专题14 巧解二次函数与相似三角形综合题(含答案)
中考数学复习《二次函数相似三角形综合压轴题》专项提升训练(附答案)

中考数学复习《二次函数相似三角形综合压轴题》专项提升训练(附答案)学校:___________班级:___________姓名:___________考号:___________ 1.已知:二次函数y=x2−(m+2)x+m−1.(1)求证:该抛物线与x轴一定有两个交点;(2)设抛物线与x轴的两个交点是A、B(A在原点左边,B在原点右边),且AB=3,求此时抛物线的解析式;(3)在(2)的前提下,若抛物线与y轴交于点C,问在y轴的正半轴上是否存在点D,使△DOB 和△AOC相似?2.如图,抛物线:y=x2+bx+c的图像与x轴交于A和B(−3,0)两点,与y轴交于C(0,−3),直线y=x+m经过点B,且与y轴交于点D,与抛物线交于点E,与对称轴交于点F.(1)求抛物线的解析式和E点坐标;(2)在y轴上是否存在点P,使得以D、E、P为顶点的三角形与△BOD相似,若存在,直接写出点P的坐标:若不存在,试说明理由.3.如图,在平面直角坐标系中,抛物线y=ax2+bx−3与x轴交于A(1,0)和B(3,0),与y轴交于点C.(1)求该抛物线的解析式;(2)绕点A旋转的直线l:y=kx+b1与y轴相交于点D,与抛物线相交于点E,且满足AD=2AE时,求直线l的解析式;(3)点P为抛物线上的一点,点Q为抛物线对称轴上的一点,是否存在以点B,C,P,Q为顶点的平行四边形,若存在,请直接写出点P的坐标;若不存在,请说明理由.4.已知:抛物线y=ax2+bx+4与x轴相交于A(−2,0),B(8,0)两点,与y轴相交于点C,连接BC.(1)求抛物线的表达式并直接写出点C的坐标;(2)如图,点M是抛物线第一象限内的一点,连接MB,MC,求△MBC面积的最大值;(3)点P也是抛物线第一象限内的一点,过点P作PN⊥BC于N,连接PC,当以P、C、N为顶点的三角形与△BOC相似时,直接写出点P的坐标.5.在平面直角坐标系xOy中,已知抛物线y=ax2+3ax+c与x轴交于点A,B(点A 在点B的左边),与y轴负半轴交于点C,且OC=4,直线y=−x+b经过点A,C,点D为y轴左侧抛物线上一点,连接CD,AD.(1)求抛物线的函数表达式;(2)当点D在直线AC下方时,连接DB交AC于点E,求S△ADC−S△BDC的最大值及此时点D 的坐标;(3)是否存在点D,使∠CBA=45°+∠DCA?若存在,求点D的坐标;若不存在,请说明理由.6.如图,二次函数y=mx2+(m2+3)x−(6m+9)的图象与x轴交于点A、B,与y 轴交于点C.连接AC、BC,已知B(3,0).(1)求直线BC的函数表达式;(2)Q为抛物线上一点,若以B、C、Q为顶点的三角形和△OAC相似,求点Q的坐标;(3)P为抛物线上一点(异于A点),若S△PBC=S△ABC,请直接写出P点的坐标.7.如图,抛物线y1=ax2−6ax+c(a≠0)与x轴交于A、B两点,与y轴交于点C,连接BC、AC,设AC关系式为y2=kx+b.若OB=2,tan∠OBC=2,D是y轴右侧抛物线上一点,设其横坐标为m,DE⊥AC于点E.(1)求抛物线的函数关系式;(2)当点D位于直线AC下方时,求DE长度的最大值;(3)当△CDE与△AOC相似时,求m的值.8.如图,抛物线y=ax2+bx+c经过A(−6,0),B(2,0),C(0,6)三点.(1)求拋物线的函数表达式;(2)如图1,P为抛物线上在第二象限内的一点,若△PAC面积为15,求点P的坐标;2(3)如图2,D为抛物线的顶点,在线段AD上是否存在点M,使得以M,A,O为顶点的三角形与△ABC相似?若存在,求点M的坐标;若不存在,请说明理由.9.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴分别相交于A(−2,0),B(8,0)两点(1)求a,b的值;(2)点D是第一象限内该抛物线上的动点,过点D作x轴的垂线交BC于点E,交x轴于点F.①求DE+BF的最大值;②G是AC的中点,若以点C,D,E为顶点的三角形与△AOG相似,求点D的坐标.x2+bx+c与y轴交于点C(0,−4),与x轴交于点A,B,且B 10.如图,抛物线y=12点的坐标为(2,0).(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.11.如图,抛物线y=−x2+bx+c的顶点D坐标为(1,4),且与x轴相交于A,B两点,点A在点B的左侧,与y轴相交于点C,点E在x轴上方且在对称轴左侧的抛物线上运动,点F在抛物线上并且和点E关于抛物线的对称轴对称,作矩形EFGH,其中点G,H都在x 轴上.(1)求抛物线解析式;(2)设点F横坐标为m①用含有m的代数式表示点E的横坐标为______(直接填空);②当矩形EFGH为正方形时,求点G的坐标;③连接AD,当EG与AD垂直时,求点G的坐标;(3)过顶点D作DM⊥x轴于点M,过点F作FP⊥AD于点P,直接写出△DFP与△DAM相似时,点F的坐标.12.如图,直线y=x−3与x轴,y轴分别交于点B(3,0),C(0,−3)过B,C两点的抛物线y=−x2+bx+c与x轴的另一个交点为A,顶点为P.(1)求该抛物线的解析式;(2)当0<x<3时,在抛物线上存在点E,使△CBE的面积有最大值,求点E坐标(3)连接AC,点N在x轴上,是否存在以B,P,N为顶点的三角形与△ABC相似?若存在,求出点N的坐标;若不存在,说明理由.13.如图1,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=−1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B,经过B、C两点作直线BC,点D为第二象限内抛物线上一动点.(1)求抛物线的函数表达式;(2)求△DBC面积最大值及此时点D坐标;(3)如图2,点M也是第二象限抛物线上一个动点,直线OM交BC于点N,是否存在这样的点M,使以B、O、N为顶点的三角形与△ACB相似?若存在,求出点M坐标,若不存在,请说明理由.x2+bx+c与x轴相交于点A,B,与y轴14.已知在平面直角坐标系中,抛物线y=−12相交于点C,直线y=x+4经过A,C两点(1)求抛物线的表达式;(2)如果点P,Q在抛物线上,并与对称轴对称,(P点在对称轴左边),且PQ=2AO,求P,Q的坐标;(3)动点M在直线y=x+4上且△ABC与△COM相似求点M的坐标.15.如图抛物线y=ax2+bx+2与x轴交于A B两点点A(2,0)且OA=2OB与y轴交于点C连接BC D为第一象限内抛物线上一动点过点D作DE⊥OA于点E 与AC交于点F设点D的横坐标为m.(1)求抛物线的表达式;(2)求△ACD面积的最大值及此时D点的坐标;(3)抛物线上是否存在点D使得以点O D E为顶点的三角形与△BOC相似?若存在求出m的值;若不存在请说明理由.16.已知抛物线y=x2+2x−3的图像经过点A(−3,0)点B(n,0)且与y轴交于点C.(1)求出点B的坐标;(2)若点P为x轴上方的抛物线上任意一点.①如图1 若点Q为线段BC上一点连接PQ PQ交x轴于点M连接CM当∠MCQ=45°时求点M的坐标;②如图2 连接BC、BP若满足∠ABP=2∠BCO求此时点P的坐标.17.已知直线l:y=kx+b(k>0)与抛物线C:y=ax2(a>0)有唯一公共点P直线l分别交x轴y轴于A,B两点.(1)如图1 当a=1k=1时求b的值;时过点A作直线l的垂线交y轴于点T求T坐标;(2)如图2 当a=12(3)如图3 当k=1时平移直线l使之与抛物线C交于M,N两点点P关于y轴的对称点为Q求证:∠MQP=∠NQP.18.在平面直角坐标系xOy中已知抛物线y=ax2−3ax+c与x轴分别交于A(−1,0) B两点与y轴交于点C(0,−2).(1)求抛物线的函数表达式;的最大值;(2)如图1 点D为第四象限抛物线上一点连接AD,BC交于点E求DEAE(3)如图2 连接AC,BC过点O作直线l∥BC点P Q分别为直线l和抛物线上的点试探究:在第一象限是否存在这样的点P Q使△PQB∽△CAB.若存在请求出所有符合条件的点P的坐标;若不存在请说明理由.19.如图1 已知二次函数y=x2+bx+c经过A(−2,0)C(0,−6)并交x轴于另一点B 点E是线段BC上的动点过A E两点的直线与抛物线在第四象限相交于点D.(1)求二次函数的解析式;取最大值时求点D的坐标;(2)当EDEA(3)如图2 连接AC在抛物线上存在点F使△OEF∽△COA求出所有点F的坐标;(4)如图3 过点E作EH⊥x轴于点H以EH为对角线作正方形EGHI当顶点G恰好落在抛物线上时请直接写出点G的坐标.20.已知在平面直角坐标系中抛物线y=ax2+bx+4与x轴交于点A(−2,0)点B(4,0)交y轴于点C.(1)求抛物线的解析式:(2)如图1 点P在抛物线第一象限上过点P作PD⊥x轴于点D交BC于点E设点P的横坐标为t PE的长为d求d与t的函数关系式:(不要求写出t的取值范围)(3)如图2 在(2)的条件下点Q在抛物线第四象限上连接AQ AP AP与BC交于点F∠CFA−∠BAQ=2∠PAB若FE=√2GO求点Q的坐标.参考答案1.(1)证明:∵Δ=(m+2)2−4(m−1)=m2+8>0故抛物线与x轴一定有两个交点;(2)解:令y=x2−(m+2)x+m−1=0解得:x=m+2±√m2+82则AB=|x1−x2|=√m2+8=3解得:m=1(舍去)或−1故抛物线的解析式为:y=x2−x−2;(3)解:存在理由:由抛物线的解析式知点C(0,−2)令y=0即x2−x−2=0解得x1=−1∵抛物线与x轴的两个交点是A B(A在原点左边B在原点右边)∵A(−1,0)∵OA=1∵C(0,−2)∵CO=2当△DOB∽△AOC时∵OD AO =OBOC即OD1=22解得OD=1∵D(0,1);当△DOB∽△COA时∵OD CO =OBOA即OD2=21解得:OD=4∵D(0,4).综上所述点D的坐标为:(0,1)或(0,4).2.解:(1)∵B(−3,0)C(0,−3)两点均在抛物线上∴{c=−39−3b+c=0解得{b =2c =−3∴抛物线的解析式为y =x 2+2x −3 ∵直线y =x +m 经过点B∴0=−3+m ∴m=3∴直线BE 的解析式为y =x +3 联立方程组{y =x +3y =x 2+2x −3解得{x 1=−3y 1=0∴点E 的坐标为(2,5);(2)存在点P 坐标为(0,5)或(0,7).理由:若存在这样的点P 使得以D E P 为顶点的三角形与△BOD 相似 如图所示 由于△BOD 是等腰直角三角形 则存在两种情况 即∠DP 1E =90° 或∠DEP 2=90°当∠DP 1E =90°时∵OD =3 ∴OP 1=5∴点P 1的坐标为(0,5); 当∠DEP 2=90°时∵EP 1⊥DP 2 ∴P 1P 2=DP 1=EP 1=2∴OP 2=7∴点P 2的坐标为(0,7);所以满足题意的点P 的坐标为(0,5)或(0,7).3.解:(1)∵抛物线y =ax 2+bx −3经过点A (1,0)和点B (3,0)∵{a +b −3=09a +3b −3=0解得{a =−1b =4∵抛物线的解析式为:y =−x 2+4x −3;(2)①当点D E 在点A 的异侧时 过点E 作EF ⊥x 轴于点F如图:∵∠AOD =∠AFE =90°∵∠OAD =∠FAE∵△AOD∽△AFE∵AFAO =AEAD∵AD =2AE∵AF AO =AE AD =12∵AF =12AO =12×1=12∵OF =32∵点F 与点E 的横坐标为32∵点E 的纵坐标为y =−x 2+4x −3=−(32)2+4×32−3=34∵点E 的坐标为(32,34)∵直线l :y =kx +b 1过点A (1,0)和点E(32,34)∵{k +b1=032k +b 1=34解得:{k=32b 1=−32 ∵直线l 的解析式为y =32x −32;②当点D E 在点A 的同侧时 过点E 作EF ⊥x 轴于点F 如图:∵∠AOD =∠AFE =90°∵∠OAD =∠FAE∵△AOD∽△AFE∵AFAO =AEAD∵AD =2AE∵AFAO =AEAD=12 ∵AF =12AO =12×1=12∵OF =12 ∵点F 与点E 的横坐标为12 ∵点E 的纵坐标为y =−(12)2+4×12−3=−54∵点E 的坐标为(12,−54) ∵直线l :y =kx +b 1过点A (1,0)和点E(12,−54) ∵{k +b 1=012k +b 1=−54 解得{k =52b =−52∵直线l 的解析式为y =52x −52综上所述:直线l 的解析式为y =32x −32或y =52x −52;(3)存在以点B C P Q 为顶点的平行四边形 理由如下:抛物线y =−x 2+4x −3对称轴为直线x =2设Q (2,t ),P (m,−m 2+4m −3)又B (3,0)①以PQ 、BC 为对角线 则PQ 、BC 的中点重合∵{2+m =3+0t −m 2+4m −3=−3 解得m =1∵P(1,0)②以BQ 、PC 为对角线∵{2+3=m +0t +0=−m 2+4m −3−3解得m =5∵P (5,−8);③以CQ 、BP 为对角线∵{2=m +3t −3=−m 2+4m −3解得m =﹣1∵P (−1,−8)综上所述 P 的坐标为(1,0)或(5,−8)或(−1,−8).4.解:(1)∵抛物线y =ax 2+bx +4与x 轴交于A(−2,0),B(8,0)两点代入 得{4a −2b +4=064a +8b +4=0 解得:{a =−14b =32∵抛物线的表达式为:y =−14x 2+32x +4当x =0时∵C(0,4);(2)过M 作ME ∥y 轴交BC 于点E设BC 的解析式为y =kx +b将B(8,0)和C(0,4)代入得解得{k=−12 b=4∵y=−12x+4设M(m,−14m2+32m+4)则E(m,−12m+4)∵ME=−14m2+32m+4−(−12m+4)=−14m2+2m∵S△MCB=12×8ME=−m2+8m=−(m−4)2+16当m=4时S取最大值16即△MBC面积的最大值为16;(3)①∵∠PNC=∠BOC=90°当∠PCN=∠OCB时作BD⊥CP交CP的延长线于点D作DF⊥y于点F作BE⊥FD交FD的延长线于点E则四边形OBEF是矩形∵OB=EF,BE=OF.∵∠PCN=∠OCB∵BD=BO∵△BOD≌△BDC(AAS)∵BD=CD.∵∠CDF+∠BDE=90°,∠DBE+∠BDE=90°∵∠CDF=∠DBE∵∠CFD=∠E=90°∵△CDF≌△BDE(AAS)∵CF=DE,DF=BE∵DF+DE=OB=8∵4+2CF=8∵CF=2∵DF=OF=4+2=6∵D(6,6).设直线CD的解析式为y=kx+4∵6=6k+4∵k=13∵y=13x+4解{y=13x+4y=−14x2+32x+4得{x1=143y1=509{x2=0y2=4(舍去)∵P(143,509);②∵∠PNC=∠BOC=90°当∠PCN=∠OBC时∵CP∥OB∵点P与点C的纵坐标相同当y=4时解得x1=6x2=0(舍去)∵P(6,4).综上可知点P的坐标为(143,509)或(6,4).5.(1)解:∵CO=4则点C(0,−4)将点C的坐标代入一次函数表达式得:−4=b 则一次函数表达式为:y=−x−4令y=−x−4=0得x=−4∵点A(−4,0)把A C两点坐标代入二次函数解析式中得:{c=−416a−12a+c=0解得:{a=1c=−4则抛物线的表达式为:y=x2+3x−4;(2)解:由y=x2+3x−4=0得x1=1,x2=−4∵点B(1,0)设直线BD交y轴于点N设点D(m,m2+3m−4)设直线BD的表达式为:y=kx+d则{k+d=0mk+d=m2+3m−4解得:{k=m+4d=−m−4直线BD的表达式为:y=(m+4)x−m−4令x=0,得y=−m−4∵点N(0,−m−4)过点D作DH∥y轴交AC于点H则点H(m,−m−4)则S△ADC−S△BDC=12×DH×OA−12×CN×(x B−x D)=12×(−m−4−m2−3m+4)×4−12×(−m)×(1−m)=−52m2−152m=−52(m+32)2+458∵−52<0则S△ADC−S△BDC有最大值当m=−32时S△ADC−S△BDC的最大值为458此时点D(−32,−254);(3)解:存在理由:当点D在AC下方时由点A C的坐标知∵∠CBA=45°+∠DCA∵∠CBA=∠DCO∵∠CBA+∠OCB=∠DCO+∠OCB即∠DCB=90°∵DC⊥CB;设点D(m,m2+3m−4)则DE=−m,CE=m2+3m−4−(−4)=m2+3m;过点D作DE⊥y轴于E如图∵∠DCB=∠BOC=∠DEC=90°∵∠BCO+∠DCE=∠DCE+∠CDE∵∠BCO=∠CDE∵△BCO∽△CDE∵CE DE =OBOC=14即4CE=DE∵4(m2+3m)=−m 解得:m=0(舍去)则点D(−134,−5116);当点D在AC的上方时如图设CD交x轴于点F ∵∠BFC=∠OAC+∠DCA=45°+∠DCA∵∠BFC=∠DCA∵CF=CB;∵CO⊥BF∵OF=OB=1∵F(−1,0);设直线CD 解析式为y =k 1x −4 把点F 坐标代入得:k 1=−4∵直线CD 的表达式为:y =−4x −4联立直线CD 的表达式与抛物线表达式得:x 2+3x −4=−4x −4 解得:x =−7 x =0(舍去)即点D (−7,24);综上 点D 的坐标为:(−134,−5116)或(−7,24). 6.(1)解:将B (3,0)代入y =mx 2+(m 2+3)x −(6m +9) 化简得m 2+m =0 则m =0(舍)或m =−1 ∵m =−1∵y=−x 2+4x −3当x =0时 y=−3 当y =0时 −x 2+4x −3=0 解得:x 1=3,x 2=1 ∵C (0,−3) A (1,0).设直线BC 对应的函数表达式为y =kx +b将B (3,0) C (0,−3)代入可得{0=3k +b −3=b 解得{k =1b =−3则直线BC 对应的函数表达式为y =x −3.(2)∵△OAC 为直角三角形∵OA =1,OC =3,tan∠OCA =OA OC =13当以B C Q 为顶点的三角形和△OAC 相似时 则:△BCQ 是直角三角形;设Q (t,−t 2+4t −3)①当∠CBQ=90°时如图:∵B(3,0)∵OB=OC=3∵∠OBC=∠OCB=45°∵∠OBQ=∠OBC=45°过点Q作QE⊥OB则:BE=QE∵3−t=−t2+4t−3解得:t=2或t=3(舍去);∵Q(2,1)当Q(2,1)时∵BC=3√2∵tan∠BCQ=13=tan∠OCA满足题意;②当∠CQB=90°时:如图:过点Q作EF∥OB过点B作BF⊥EF 则:∠CEQ=∠BFQ=90°∵∠CQE=∠QBF=90°−∠FQB∵△CEQ∽△QFB∵CE QF =EQBF即:−t2+4t3−t=t−t2+4t−3解得:t =3(舍去)或t =0(舍去)或t =5+√52或t =5−√52∵Q (5+√52,−1+√52)或Q (5−√52,√5−12)此时BQCQ =BF EQ =√5+15+√5=√55≠13不满足题意 舍去;③当∠QCB =90°时 如图:过点Q 作QF ⊥y 轴 则:∠BOC =∠QFC =90° ∵∠BCO =∠FQC =90°−∠FCQ∵∠FQC =45°∵CF =QF =t∵OF =3+t =−(−t 2+4t −3)解得:t =5或t =0(舍去);∵Q (5,−8)∵tan∠CQB =BC CQ =3√25√2=35≠13 不符合题意;∵Q (5,−8)不满足题意;综上:Q (2,1).(3)∵S △PBC =S △ABC∵点P 与点A 到BC 的距离相等如图 过点A 作AP 1∥BC 设直线AP 1与y 轴的交点为G将直线BC 向下平移GC 个单位 得到直线P 3P 2设直线AG 的解析式为:y =x +n 则:0=1+n 解得:n =−1 ∵直线AG 的表达式为y =x −1 联立{y =x −1y =−x 2+4x −3 解得:{x =1y =0 (舍) 或{x =2y =1∵P 1(2,1)∵直线AG 的表达式为y =x −1 ∵当x =0时 ∵G (−1,0) ∵GC =2∵直线P 3P 2的表达式为y =x −5 联立{y =x −5y =−x 2+4x −3解得:{x 1=3+√172y 1=−7+√17∵P 3(3+√172,−7+√172) ∵P (2,1)或P (3+√172,−7+√172)或P (3−√172,−7−√172).7.(1)解:∵tan∠OBC =2∴OCOB=2 ∵OB =2∴OC=4∴B(−2,0)把B(−2,0)C(0,−4)代入y1=ax2−6ax+c得{4a+12a+c=0c=−4解得{a=14 c=−4∴y1=14x2−32x−4;(2)解:作DF⊥x轴于点F交AC于点G∴∠BAC+∠AGF=90°∵DE⊥AC于点E∴∠EDF+∠EGD=90°∵∠AGF=∠EGD∴∠EDF=∠BAC∴tan∠EDF=tan∠BAC=OC OA=12∴cos∠EDF=cos∠BAC=2√5 5∴DE=2√55DG令14x2−32x−4=0解得x1=−2∴点A的坐标为(8,0)把A(8,0)和C(0,−4)代入y2=kx+b得{8k+b=0b=−4解得∴y 2=12x −4由题意 点D 坐标为(m,14m 2−32m −4) 点G 坐标为(m,12m −4)∴DG =(12m −4)−(14m 2−32m −4)=−14m 2+2m =−14(m −4)2+4∴DE =−√510(m −4)2+8√55 ∵−√510<0 ∴DE 有最大值为8√55; (3)解:由题意 ∠DCE =∠OCA 或∠DCE =∠OAC 时 △CDE 与△AOC 相似 ①当∠DCE =∠OCA 时∴∠OCA =∠DGC ∴∠DCE =∠DGC ∴DC =DG∵DE ⊥AC 于E∴EG =EC =12CG∵tan∠EDG =tan∠OAC =12∴sin∠EDG =√55∴EG =√55DG =√55(−14m 2+2m) ∵cos∠BAC =2√55AG =√52(8−m ) 在Rt △AOC 中 由勾股定理得∴CG =4√5−√52(8−m )=√52m ∴√55(−14m 2+2m)=12×√52m 解得m =3②当∠DCE =∠OAC 且D 位于x 轴下方时CD//OA ∴y D=−4令14x2−32x−4=−4解得x=0(舍去)或x=6即m=6;③当∠DCE=∠OAC且D位于x轴上方时如图设CE交x轴于M则MC=MA设OM=n则CM=AM=8−n在Rt△OCM中由勾股定理得n2+42=(8−n)2解得n=3∴M(3,0)同理直线CM函数关系式为y=43x−4令14x2−32x−4=43x−4解得x=0(舍去)或x=343即m=343综上m=3或6或343.8.(1)解:把A(−6,0),B(2,0),C(0,6)代入抛物线解析式y=ax2+bx+c得{36a −6b +c =04a +2b +c =0c =6解得{a =−12b =−2c =3∵抛物线的函数表达式为y =−12x 2−2x +6.(2)解:如解(2)图1 过P 点作PQ 平行y 轴 交AC 于Q 点设直线AC 的解析式为y =kx +6 把A (−6,0)代入得:0=−6k +6 解得:k =1∵直线AC 解析式为y =x +6设P 点坐标为(x,−12x 2−2x +6) 则Q 点坐标为(x,x +6)∵PQ =−12x 2−2x +6−(x +6)=−12x 2−3x∵S △PAC =12PQ ⋅OA∵12(−12x 2−3x)⋅6=152解得:x 1=−1 x 2=−5. 当x =−1时 P 点坐标为(−1,152) 当x =−5时 P 点坐标为(−5,72)综上所述:若△PAC 面积为152 点P 的坐标为(−1,152)或(−5,72);(3)解:如解(3)图1 过D 点作DF 垂直x 轴于F 点 过A 点作AE ⊥BC 于E 点∵D 为抛物线y =−12x 2−2x +6的顶点 ∵D 点坐标为(−2,8)设直线AD 的解析式为:y =mx +n把A (−6,0) D (−2,8)代入得:{−6m +n =0−2m +n =8解得:{m =2n =12∵直线AD 为y =2x +12 ∵B(2,0)∵同理可得:直线BC 的解析式为y =−3x +6 ∵AF =−2−(−6)=4 ∵tan∠DAB =DFAF =2 ∵B(2,0) C (0,6)∵tan∠ABC =OCOB =3 BC =√22+62=2√10 sin∠ABC =62√10=3√1010∵AB =2−(−6)=8 ∵AE =AB ⋅sin∠ABC =8×3√1010=12√105∵BE =√AB 2−AE 2=4√105∵CE =BC −BE =2√10−4√105=6√105∵tan∠ACB =AE CE=2∵tan∠ACB =tan∠DAB =2 ∵∠ACB =∠DAB ∵OA =OC=6∵∠ACO =∠CAO =45°;∵使得以M A O 为顶点的三角形与△ABC 相似 则有两种情况 如解(3)图2当∠AOM =∠CAB =45°时 即M 点在直线y =−x 上 联立{y =−xy =2x +12 解得{x =−4y =4即M 点为(−4,4).当∠AOM =∠CBA 即OM∥BC 时 ∵直线BC 解析式为y =−3x +6 ∵直线OM 为y =−3x 联立{y =−3x y =2x +12解得{x =−125y =365即M 点为(−125,365)综上所述:存在使得以M A O 为顶点的三角形与△ABC 相似的点M 其坐标为(−4,4)或(−125,365).9.解:(1)将A(−2,0) B(8,0)代入解析式得:{4a −2b +4=064a +8b +4=0解得:{a =−14b =32 ∴ a =−14 b =32;(2)①∵的值为−14b 的值为32抛物线的解析式为:y =−14x 2+32x +4;∴C(0,4)设直线BC 解析式为y =kx +c 将B(8,0) C(0,4)代入可得:{8k +c =0c =4解得{k =−12c =4∴直线BC 解析式为y =−12x +4设第一象限D(m,−14m 2+32m +4) 则E(m,−12m +4)∴DE =(−14m 2+32m +4)−(−12m +4)=−14m 2+2m∴DE +BF =(−14m 2+2m)+(8−m)=−14(m −2)2+9∴当m =2时 DE +BF 的最大值是9; ②∴A(−2,0)∴OA =2∴AC 2=OA 2+OC 2=20 ∴AC 2+BC 2=100而AB 2=102=100∴AC 2+BC 2=AB 2 ∴∠ACB =90° ∴∠CAB +∠CBA =90°∵DF ⊥x 轴于F∴∠FEB +∠CBA =90° ∴∠CAB =∠FEB =∠DEC以点C D E 为顶点的三角形与△AOG 相似 只需OADE =AGCE 或OACE =AGDE 而G 为AC 中点∴G(−1,2)由①知:DE=−14m2+2m∴CE=√m2+[4−(−12m+4)]2=√52m当OADE =AGCE时解得m=4或m=0(此时D与C重合舍去)∴D(4,6)当OACE =AGDE时解得m=3或m=0(舍去)∴D(3,25 4 )综上所述以点C D E为顶点的三角形与△AOG相似则D的坐标为(4,6)或(3,254).10.(1)解:把点C(0,−4)B(2,0)分别代入y=12x2+bx+c中得{c=−412×22+2b+c=0解得{b=1c=−4∵该抛物线的解析式为y=12x2+x−4.(2)解:令y=0即12x2+x−4=0解得x1=−4,x2=2∵A(−4,0)∵C(0,−4)∵AB=2−(−4)=6,OC=4∵S△ABC=12AB⋅OC=12.设P点坐标为(x,0)则PB=2−x∵PE∥AC∵∠BPE=∠BAC,∠BEP=∠BCA ∵△PBE∽△ABC∵S△PBE S△ABC =(PBAB)2即S△PBE12=(2−x6)2化简得:S△PBE=13(2−x)2∵S△PCE=S△PCB−S△PBE=12PB⋅OC−S△PBE=12×(2−x)×4−13(2−x)2 =−13x2−23x+83=−13(x+1)2+3∵当x=−1时S△PCE的最大值为3.(3)解:△OMD为等腰三角形可能有三种情形:①当DM=DO时如图①所示.则DO=DM=DA=2∵AO=CO=4,∠AOC=90°∵∠OAC=∠AMD=45°∵∠ADM=90°∵M点的坐标为(−2,−2);②当MD=MO时如图②所示.过点M作MN⊥OD于点N则点N为OD的中点∵DN=ON=1,AN=AD+DN=3又△AMN为等腰直角三角形∵MN=AN=3∵M点的坐标为(−1,−3);③当OD=OM时∵△OAC为等腰直角三角形×4=2√2即AC上的点与点O之间的最小距离为2√2.∵点O到AC的距离为√22∵2√2>2∵OD=OM的情况不存在.综上所述点M的坐标为(−2,−2)或(−1,−3).11.(1)解:∵抛物线y=−x2+bx+c的顶点D坐标为(1,4)∴y=−(x−1)2+4=−x2+2x−1+4=−x2+2x+3∴抛物线解析式为y=−x2+2x+3;(2)解:①当y=0时−x2+2x+3=0解得x1=−1则A(−1,0)∴1<m<3设E点的横坐标为t∵m−1=1−t∴t=2−m∴点E的横坐标为2−m;故答案为:2−m;②设F(m,−m2+2m+3)(1<m<3)则E(2−m,−m2+2m+3)∵矩形EFGH为正方形∴FG=FE即−m2+2m+3=m−(2−m)整理得:m2=5解得m1=−√5(舍去)∴G点坐标为(√5,0);③过点D作DM⊥x轴于M∵EG⊥AD而DM⊥x轴∴∠1=∠4∴Rt△GEH∽Rt△DAM∴EHAM =GHDM即EH2=GH4∴GH=2EH即2m−2=2(−m2+2m+3)整理得m2−m−4=0解得m1=1−√172(舍去)∴G点坐标为(1+√172,0);(3)解:设AD交EF于Q如图∵FP⊥AD∴∠DPF =90°∵△DFP 与△DAM 相似∴∠1=∠3∵∠1=∠2∴∠2=∠3而FP ⊥DQ∴△FDQ 为等腰三角形∴FD =FQ设直线AD 的解析式为y =px +q把A (−1,0) D (1,4)代入得{−p +q =0p +q =4解得{p =2q =2∴直线AD 的解析式为y =2x +2当y =−m 2+2m +3时 2x +2=−m 2+2m +3 解得x =−12m 2+m +12 则Q (−12m 2+m +12,−m 2+2m +3)∴FQ =m −(−12m 2+m +12)=12m 2−12=12(m +1)(m −1) 而DF 2=(m −1)2+(−m 2+2m +3−4)2=(m −1)2+(m −1)4∴(m −1)2+(m −1)4=(12(m +1)(m −1))2 而m ≠1∴1+(m −1)2=14(m +1)2 整理得3m 2−10m +7=0 解得m 1=1(舍去)∴F 点坐标为(73,209).12.(1)解:将点B(3,0),C(0,−3)代入y =−x 2+bx +c 得:{c =−3−9+3b +c =0 解得:{c =−3b =4∵y =−x 2+4x −3∵y =−x 2+4x −3=−(x −2)2+1.(2)解:如图1:在抛物线上取点E 连接CE 过E 作x 轴的垂线交直线BC 于点F设点F(x,x−3)则点E的坐标为(x,−x2+4x−3)∵EF=−x2+3x∵S△CBE=S△CEF+S△BEF=12EF·OB=−32x2+92x=−32(x−32)2+278∵当x=32时△CBE的面积有最大值此时点E的坐标为(32,34 ).(3)解:存在以B P N为顶点的三角形与△ABC相似如图2:连接BP设N(n,0)当y=0时−x2+4x−3=0解得x2=1,x2=3∵A(1,0)∵y=−x2+4x−3=−(x−2)2+1∵P(2,1)∵B(3,0),C(0,−3),P(2,1)∵∠CBA=∠ABP=45°①当BNBP =BCBA时∵3−n √2=3√22解得n=0所以点N的坐标为N1(0,0);②当BN BP =BA BC 时 ∵3−n√2=23√2 解得n =73 所以点N 的坐标为N 2(73,0).综上所述 点N 的坐标为N 1(0,0)或N 2(73,0).13.解:(1)∵抛物线y =ax 2+bx +c 经过A (1,0),C(0,3)两点 且对称轴为直线x =−1 ∵B(−3,0)设y =a (x +3)(x −1) 把C(0,3)代入得解得:a =−1∵抛物线解析式为y =−x 2−2x +3;(2)如图1 作DE ∥y 轴 交直线BC 于点E设直线BC 的函数解析式为y =px +q 可得:{−3p +q =0q =3 解得:{p =1q =3可得直线BC 的解析式为y =x +3设P (m,−m 2−2m +3)∵E (m,m +3)∵DE =−m 2−2m +3−(m +3)=−m 2−3m∵△DBC 的面积=12DE ×3=−32m 2−92m ∵a =−32<0 ∵m =−32时△DBC 的面积最大=278 此时点D 坐标为(−32,154); (3)存在 理由如下:∵A (1,0)∴AB =3−(−1)=4∵OB =OC =3∴BC =3√2设直线AC 解析式为y =mx +n∵A (1,0)∴{m +n =0n =3解得:{m =−3n =3∴直线AC 解析式为y =−3x +3①当OM ∥AC 时∴直线OM 的解析式为y =−3x结合抛物线的解析式为y =−x 2−2x +3 得:−3x =−x 2−2x +3 解得:x 1=1+√132(舍去) ∴M 坐标(1−√32,−3+3√132); ②当△BON ∽△BCA 时∴BN BA =BO BC∴BN =BA ⋅BO BC =4×33√2=2√2 如图 过点N 作NG ⊥x 轴于点G∵∠OBC =45°∴BG =NG =2∴OG =1∴N (−1,2)设直线OM 解析式为y =m 1x 将N (−1,2)代入得:m 1=−2∴直线OM 解析式为y =−2x结合抛物线的解析式为y =−x 2−2x +3 得:−2x =−x 2−2x +3 解得:x 1=√3舍去,x 2=−√3∴M 坐标 (−√3,2√3)综上 点M 的坐标为(1−√132,−3+3√132)或(−√3,2√3) 14.(1)解:当y =0=x +4时∵A (−4,0)当x =0时∵C (0,4)将点A C 的坐标代入y =−12x 2+bx +c 得{0=−12×16−4b +c 4=c 解得b =−1,c =4∵抛物线的表达式为y =−12x 2−x +4; (2)∵A (−4,0)∵OA =4∵PQ =2OA =8∵点P Q 关于对称轴直线x =−1对称∵PQ∥OA∵点P 的横坐标为−1−82=−5 点C 的横坐标为3 当x =−5时∵P (−5,−72),Q (3,−72); (3)∵A (−4,0)∵OA =4=OC∵对称轴直线x =−1对称∵B (2,0)∵AB =6∵∠AOC =90°∵∠OAC =∠OCA =45°①当△MCO ∽△CAB 时∵46=CM4√2∵CM =8√23 如图 过点M 作MG ⊥y 轴于点G∵MG =CG =√22CM =83当x =−83时∵M (−83,43);当△OCM ∽△CAB 时∵44√2=CM6∵CM =3√2如图 过点M 作MG ⊥y 轴于点G∵MG =CG =√22CM =3当x =−3时∵M (−3,1);综上 M 点的坐标为(−83,43)或(−3,1).15.(1)解:因为y =ax 2+bx +2过点A (2,0)且OA =2OB 则B (−1,0)则{4a +2b +2=0a −b +2=0解得:{a =−1b =1故抛物线的表达式为:y=−x2+x+2;(2)对于y=−x2+x+2令x=0则y=2故点C(0,2)设直线AC的解析式为y=kx+b由直线过点A C的坐标得{2k+b=0b=2解得{k=−1 b=2直线AC的表达式为:y=−x+2设点D的横坐标为m则点D(m,−m2+m+2)则点F(m,−m+2)则DF=−m2+m+2−(−m+2)=−m2+2m=−(m−1)2+1∵−1<0故DF有最大值则△ACD面积最大值为12×AO×DF=12×2×1=1此时m=1点D(1,2);(3)存在理由:点D(m,−m2+m+2)(m>0) 则OE=m 以点O D E为顶点的三角形与△BOC相似①当DEOE =OBOC时两三角形相似即DEOE=OBOC=12则−m 2+m+2m=12解得:m=1+√334或m=1−√334(舍去)经检验m=1+√334是原分式方程的解②当DEOE =OCOB时两三角形相似即DEOE=OCOB=2则−m 2+m+2m=2解得:m=1或m=−2(舍去)经检验m=1是分式方程的解故m=1+√334或m=1.16.(1)解:由y=x2+2x−3当y=0时即x2+2x−3=0解得:x1=−3,x2=1∵B(1,0).(2)解:①∵A(−3,0),C(0,−3),B(1,0)∵OA=OC=3,OB=1,则AB=OA+OB=4,BC=√OC2+OB2=√10∵∠OCA=∠OAC=45°∵∠MCQ=45°,∵∠MCQ=∠MAB=45°∵∠CBM =∠ABC∵△CBM∽△ABC∵CB :AB =BM :BC 即:BM =BC 2AB =104=52 ∵OM =BM −OB =32 ∵M 在x 轴负半轴∵M (−32,0);②如图:过点P 作PH ⊥x 轴 设P(m ,m 2+2m −3) (m <0)在线段OC 上取点D 使得DC =DB 则∠ODB =2∠BOC∵∠ABP =2∠BCO =∠ODB 且∠PHO =∠BOD =90°∵△PHB∽△BOD∵PH:BO =HB:OD设OD =a 则DC =CB =3−a在Rt △OBD 中 由勾股定理得 a 2+12=(3﹣a )2 解得a =43 即OD =43 ∵m 2+2m−31=1−m43 解得m =−154或m =1(舍去) 当m =−154时 ∵P (−154,5716). 17.(1)解:当a =1 k =1时 直线l:y =x +b 抛物线C:y =x 2联立{y =x +b y =x2 得:x 2−x −b =0 ∵直线l:y =x +b 与抛物线C:y =x 2有唯一公共点P∴(−1)2−4×1×(−b )=0解得:b =−14;(2)解:当a =12时 抛物线C:y =12x 2联立{y =12x 2y =kx +b得:12x 2−kx −b =0 ∵直线l:y =kx +b (k >0)与抛物线C:y =12x 2有唯一公共点P∴(−k )2−4×12×(−b )=0∴b =−12k 2∴y =kx −12k 2当x =0时 y =−12k 2 当y =0时 kx −12k 2=0 解得:x =k2∴A (k2,0)∴OA =k2∵过点A 作直线l 的垂线交y 轴于点T∴∠BAT =90° ∴∠ATB +∠ABT =90° ∵∠OBA +∠OAB =90° ∴∠OTA =∠OAB ∵∠AOB =∠TOA =90° ∴△AOB ∽△TOA∴OTOA =OABO 即OTk 2=k 2k 22∴OT =12∵ T 在y 轴的正半轴 ∴T (0,12);(3)证明:如图 令OM QP QN 与y 轴交点分别为D设M(m ,am 2) N(n ,an 2) MN 的解析式为:y =x +c 联立{y =x +b y =ax 2 得:ax 2−x −b =0 解得:x P =12a∴P (12a ,14a)∵点P 关于y 轴的对称点为Q∴Q (−12a ,14a) 联立{y =x +c y =ax 2 得:ax 2−x −c =0 ∵平移直线l 使之与抛物线C 交于M ,N 两点∴m +n =1a令QM 为y =k 1x +b 1 代入M(m ,am 2) Q (−12a ,14a )得:{14a =−k12a +b 1am 2=k 1m +b 1解得:{k 1=am −12b 1=m2∴QM :y =(am −12)x +m2 令x =0 则y =m 2∴D (0,m 2) 同理可得:QN :y =(an −12)x +n2∴DE =m 2−14a∴DE −EF =m +n 2−12a =12a −12a =0 ∴DE =EF∵QP ⊥DF∴∠MQP =∠NQP .18.(1)解:∵抛物线y =ax 2−3ax +c 与x 轴分别交于A(−1,0) B 两点 与y 轴交于点C(0,−2). ∴ a +3a +c =0 ∴ a =12∴设抛物线的解析式为y =12x 2−32x −2(2)解:过点D 作DG ⊥x 轴于点G 交BC 于点F 过点A 作AK ⊥x 轴交BC 的延长线于点K∴ AK∥DG△AKE ∽△DFE ∴DF AK =DEAE设直线BC 的解析式为y =kx +b 1∴{4k +b 1=0b 1=−2解得{k =12b 1=−2∴直线BC 的解析式为y =12x −2 ∵ A(−1,0)∴y =−12−2=−52∴AK =52设D (m,12m 2−32m −2) 则F (m,12m −2)∴DF=12m−2−12m2+32m+2=−12m2+2m∴DEAE =−12m2+2m52=−15m2+45m=−15(m−2)2+45∴当m=2时DEAE 有最大值最大值为45(3)解:符合条件的点P的坐标为(689,349)(6+2√415,3+√415)理由如下:∵l∥BC∴直线l的解析式为y=12x设P(a1,a12)当点P在直线BQ右侧时如图过点P作PN⊥x轴于点N过点Q作QM⊥PN 于点M∵A(−1,0)∴AC=√5∵AC2+BC2=AB2∴∠ACB=90°∵△PQB∽△CAB∴PQPB=ACBC=12∵∠QMP=∠BNP=90°∴∠MQP+∠MPQ=90°∴∠MQP=∠BPN∴△QPM∽△PBN∴QMPN=PMBN=PQPB=12∴QM =a 14∴MN =a 1−2BN −QM =a −BN −QM =a 1−4−a 4=34a 1−4 ∴Q (34a 1,a 1−2)将点Q 的坐标代入抛物线的解析式得12×(34a 1)2−32×34a 1−2=a 1−2 解得a 1=0(舍去)∴P (689,349) 当点P 在直线BQ 左侧时 由①的方法同理可得点Q 的坐标为(54a 1,2) 此时点P 的坐标为(6+2√415,3+√415) ∴综合所述 存在这样的点P 且坐标为为(689,349)或 (6+2√415,3+√415) 19.解:(1)∵抛物线经过A(−2,0) ∴ {4−2b +c =0c =−6 解得:{b =−1c =−6∴抛物线的表达式为:y =x 2−x −6; (2)y =x 2−x −6=(x +2)(x −3)∴A(−2,0)设直线BC 的解析式为y =px +q 由题意得{3p +q =0q =−6 解得:{p =2q =−6所以直线BC 的解析式为y =2x −6如图 分别过点A 和点D 作y 轴的平行线 交直线BC 于点M 和点N∴△NED ∽△MEA则EDEA =DNAM∵A(−2,0)∴点M 横坐标为−2将x =−2代入BC 的解析式y =2x −6 得y =−10∴M(−2,−10)∴AM =10为定值. ∴当DN 取最大值时ED EA取得最大值设D(t,t 2−t −6) 则N(t,2t −6)则DN =(2t −6)−(t 2−t −6)=−t 2+3t =−(t −32)2+94 ∴当t =32时 DN 取最大值 即EDEA取得最大值 此时D(32,−214);(3)∵△OEF ∽△COA∠OEF =∠COA =90°①如右图 当点F 在OE 左侧时 过点E 作EP ⊥x 轴于点P 过点F 作FQ ⊥PE 于点Q 则∠OPE =∠EQF =90°∵∠OEF =90°∴∠OEP +∠FEQ =90° ∵∠OEP +∠EOP =90° ∴∠FEQ =∠EOP ∴△OEP ∽△EFQ .OP EQ =PE QF =OE EF =31设E(m,2m −6) 则P(m,0)∵点E在第四象限∴OP=m∵EQ=13m,QF=2−23m∵F(53m−2,53m−6)将F(53m−2,53m−6)代入抛物线得:53m−6=(53m−2)2−(53m−2)−6解得:m1=9+3√35∴点F的坐标(1+√3,−3+√3)或(1−√3,−3−√3);②如右图当点F在OE右侧时过点E作EH⊥x轴于点H过点F作FG⊥EH于点G则∠OHE=∠EGF=90°则△OHE∽△EGFOH EG =HEGF=OEEF=31设OH=n则H(n,0)∵点E在线段BC上且在第四象限∴E(n,2n−6)GF=2−2 3 nA G(n,73n−6)F(13n+2,73n−6)将F(13n+2,73n−6)代入抛物线得:73n−6=(13n+2)2−(13n+2)−6解得:n1=6−3√2n1=6+3√2(舍去)∴点F的坐标(4−√2,8−7√2)综上所述:点F的坐标为(1+√3,−3+√3)或(1−√3,−3−√3)或(4−√2,8−7√2);(4)设点E(m,2m−6)则EH=6−2m则12EH=3−m则x G=m−(3−m)=2m−3即点G(2m−3,m−3)将点G的坐标代入抛物线表达式得:m−3=(2m−3)2−(2m−3)−6解得:m=3(舍去)或34则点G(−32−94).20.(1)解:将点A(−2,0)点B(4,0)代入y=ax2+bx+4{0=a(−2)2+b⋅(−2)+40=a⋅42+b⋅4+4解得:{a=−12b=1故答案为:抛物线的解析式:y=−12x2+x+4(2)解:由(1)结论可知点C坐标为(0,4)设直线BC解析式为:y=kx+4将点B(4,0)代入解得:k=−1∴直线BC解析式为:y=−x+4∵点P的横坐标为t则点P的纵坐标为−12t2+t+4∴点E的横坐标为t点E的纵坐标为−t+4∵点P在抛物线第一象限上∴PE=PD−ED即:d=−12t2+t+4−(−t+4)=−12t2+2t故答案为:d与t的函数关系式:d=−12t2+2t(3)解:∵GO⊥AB∴△GAO∽△PAD∴GOAO =PDAD即:GO2=−12t2+t+4t+2整理得:GO=4−t∴CG=CO−GO=4−(4−t)=t∵CO∥PD∴CEOD =CBOB=√2即:CEt=√2整理得:CE=√2t∵∠GCF=∠FEP∴△GCF∽△PEF∴CGPE =CFEF即:CGPE=EC−EFEF即:t−12t2+2t=√2t−(4√2−√2t)4√2−√2t解得:t=3或t=4(舍)∴GO=4−t=4−3=1∵∠CFA−∠BAQ=2∠PAB∴∠PAB+45°−∠BAQ=2∠PAB即:∠PAB+∠BAQ=45°作点H(1,−1)作HI⊥x轴垂足为I连接GH则:GI=OA=2∴△AGO≌△GHI(SAS)∴∠GAO=∠HGI∴∠AGH=90°∴∠GAH=45°∴∠PAB+∠BAH=45°=∠PAB+∠BAQ∴∠ABH=∠BAQ∴直线AH与抛物线交点即为点Q设直线AH解析式为:y=kx+b点A(−2,0)点Q(1,−1)在直线上∴{0=k⋅(−2)+b−1=k⋅1+b解得:{k=−13b=−23直线AH解析式为:y=−13x−23∴{y=−13x−23y=−12x2+x+4解得:{x1=−2y1=0∴(−2,0)为点A(143,−209)为点Q故答案为:Q(143,−209).。
中考数学总复习《二次函数与相似三角形问题综合》专项检测卷(带答案)

中考数学总复习《二次函数与相似三角形问题综合》专项检测卷(带答案)学校:___________姓名:___________班级:___________考号:___________1.如图,在平面直角坐标系中,抛物线2y x bx c =++与x 轴交于点()2,0A -和()1,0B .(1)求抛物线的函数表达式;(2)直线43y x h =-+经过点B ,交抛物线于另一点C .P 是线段BC 上一点,过点P 作直线PQ y ∥轴交抛物线于点Q ,且PB PQ =,求点P 的坐标;(3)M ,N 是抛物线上的动点(不与点B 重合),直线BM ,BN 分别交y 轴于点E ,F ,若EBF EOB ∽△△,求证:直线MN 经过一个定点.2.如题,在平面直角坐标系xOy 中,抛物线22y ax bx =++与x 轴交于点()1,0A -,点()4,0B ,与y 轴交于点C ,连接AC ,BC .(1)求抛物线的解析式.(2)点D 为抛物线的对称轴上一动点,当ACD 周长最小时,求点D 的坐标.(3)点E 是OC 的中点,射线AE 交抛物线于点F ,P 是抛物线上一动点,过点P 作y 轴的平行线,交射线AF 与点G ,是否存在点P 使得PFG △与AOE △相似?若存在,求出点P 的坐标;若不存在,请说明理由.3.如图,在平面直角坐标系中,抛物线212y x bx c =-++与x 轴交于点()2,0A -和()4,0B ,与y 轴交于点C ,连接BC .(1)求抛物线的解析式;(2)P 是第一象限内抛物线上的一个动点,过点P 作直线l x ⊥轴于点(),0M m ,交BC 于点N ,连接CM PB PC ,,.PCB 的面积记为1S ,BCM 的面积记为2S ,当12S S 时,求m 的值;(3)在(2)的条件下,点Q 在抛物线上,直线MQ 与直线BC 交于点H ,当HMN △与BCM 相似时,请直接写出点Q 的坐标.4.如图,在平面直角坐标系中,已知抛物线214y x bx c =-++与x 轴分别相交于()2,0A -,()8,0B 两点.(1)求该抛物线的解析式;(2)点D 是第一象限内该抛物线上的动点,过点D 作x 轴的垂线交BC 于点E ,交x 轴于点F . ①求DE BF +的最大值;①若G 是AC 的中点,以点C D E 为顶点的三角形与AOG 相似 求点D 的坐标. 5.如图 抛物线223y x x =-++交x 轴于A B 两点 交y 轴于点C 连接AC BC .(1)求ABC 的面积;(2)点M 为y 轴上一点 是否存在点M 使得MBC 与ABC 相似?若存在 请求出点M 的坐标;若不存在 请说明理由;(3)点P 为抛物线上一点(点P 与点B 不重合) 且使得PAC △中有一个角是45︒ 请直接写出点P 的坐标.6.在平面直角坐标系xOy 中 把与x 轴交点相同的二次函数图象称为“共根抛物线”.如图 抛物线1L :245y x x =-++的顶点为D 交x 轴于点A B (点A 在点B 左侧) 交y 轴于点C .抛物线2L 与1L 是“共根抛物线” 其顶点为P .(1)若抛物线2L 经过点()38-,求抛物线L 1对应的函数关系式; (2)连接BC .设点Q 是抛物线1L 上且位于其对称轴右侧的一个动点 若DPQ 与BOC 相似 求其“共根抛物线”2L 的顶点Р的坐标.7.如图 直线23y x c =-+与x 轴交于点()3,0A 与y 轴交于点B 抛物线243y x bx c =-++经过点A B .(1)求点B 的坐标和抛物线的解析式;(2)(),0M m 为x 轴上一动点 过点M 且垂直于x 轴的直线与直线AB 及抛物线分别交于点P N .①点M 在线段OA 上运动 若以B P N 为顶点的三角形与APM ∆相似 求点M 的坐标; ①点M 在x 轴上自由运动 若三个点M P N 中恰有一点是其它两点所连线段的中点(三点重合除外) 则称M P N 三点为“共谐点”.请直接写出使得M P N 三点成为“共谐点”的m 的值.8.如图 二次函数2y ax bx c =++(0a <)的图象与x 轴交于()1,0A - B 两点 与y 轴交于点C 已知3OB OA = OC OB =.(1)求该二次函数的表达式;(2)点M 为抛物线对称轴上一动点 是否存在点M 使得BM CM -有最大值 若存在 请直接写出其最大值及此时点M 坐标 若不存在 请说明理由.(3)连接AC P 为第一象限内抛物线上一点 过点P 作PD x ⊥轴 垂足为D 连接PA 若PDA 与COA 相似 请求出满足条件的P 点坐标:若没有满足条件的P 点 请说明理由.9.如图 在平面直角坐标系中 二次函数的图象交坐标轴于()20A -,()40B , ()08C ,三点 点P 是直线BC 上方抛物线上的一个动点.(1)求这个二次函数的解析式;(2)动点P 运动到什么位置时 PBC 的面积最大 求此时P 点坐标及PBC 面积的最大值;(3)在y 轴上是否存在点Q 使以O B Q 为顶点的三角形与AOC 相似?若存在 请直接写出点Q 的坐标;若不存在 请说明理由.10.如图 已知抛物线经过()40A ,()10B , ()02C -,三点.(1)求该抛物线的解析式;(2)若P 是直线4x =右侧的抛物线上一动点 过点P 作PM x ⊥轴 垂足为M 是否存在点P 使得以A P M 为顶点的三角形与OAC 相似?若存在 请求出符合条件的点P 的坐标;若不存在 请说明理由11.综合与探究:如图 在平面直角坐标系中 抛物线24y ax bx =+-与x 轴交于点()1,0A - ()3,0B 与y 轴交于点C 连接BC .若在第四象限的抛物线上取一点M 过点M 作MD x ⊥轴于点D 交直线BC 于点E .(1)求抛物线的表达式;(2)试探究抛物线上是否存在点M 使ME 有最大值?若存在 求出点M 的坐标和ME 的最大值;若不存在 请说明理由;(3)连接 CM 试探究是否存在点M 使得以M C E 为顶点的三角形和BDE △相似?若存在 请求出点M 的坐标;若不存在 请说明理由.12.综合与探究如图 抛物线213222y x x =-++的图象与x 轴交于A B 两点 点A 在点B 的左侧 与y 轴交于点C 连接BC .(1)求点B C 的坐标.(2)C '是点C 关于抛物线对称轴的对称点 D 是BC 线段上一点 已知25BD BC = 求直线C D '的解析式.(3)若C 关于x 轴的对称点为M 连接BM N 是线段AB 上的动点 过点N 作x 轴的垂线交抛物线于点P 交直线BM 于点Q 当以B P Q 为顶点的三角形与BOM 相似时 请直接写出点P 的坐标.13.如图 抛物线26y ax bx =+-与y 轴交于点A 与x 轴交于点()3,0B - ()1,0C P 是线段AB 下方抛物线上的一个动点 过点Р作x 轴的垂线 交x 轴于点H 交AB 于点D .设点P 的横坐标为()30t t -<<.(1)求抛物线的解析式.(2)用含t 的式子表示线段PD 的长 并求线段PD 长度的最大值.(3)连接AP 当DPA 与DHB △相似时 求点P 的坐标.14.如图 抛物线经过点()2,0A - ()3,3B -和坐标原点O 顶点为C .(1)求抛物线的表达式;(2)求证:BOC 是直角三角形;(3)若点P 是抛物线上第一象限内的一个动点 过点P 作PM x ⊥轴 垂足为M 是否存在点P 使得以P M A 为顶点的三角形与BOC 相似?若存在 求出点P 的坐标;若不存在 请说明理由.15.在平面直角坐标系中 抛物线()26160y ax ax a a =--≠与x 轴的两个交点分别为A B 、与y 轴相交于点C 连接BC 已知点()04C ,.(1)求A B 、两点坐标和抛物线的解析式;(2)设点P 是抛物线上在第一象限内的动点(不与C B 、重合) 过点P 作PD BC ⊥ 垂足为点D .①点P 在运动过程中 线段PD 的长度是否存在最大值?若存在 求出最大值以及此时点D 的坐标;若不存在 请说明理由:①当以P D C 、、为顶点的三角形与COA 相似时 求点P 的坐标.参考答案:1.(1)解:将()2,0A - ()1,0B 代入2y x bx c =++得:()2202201b c b c⎧=--+⎪⎨=++⎪⎩ 解得:12=⎧⎨=-⎩b c ∴抛物线的函数表达式为:22y x x =+-;(2)解:将()1,0B 代入43y x h =-+ 得:4013h =-⨯+ 解得:43h = ∴直线BC 的解析式为:4433y x =-+ 联立直线BC 与抛物线得:244332y x y x x ⎧=-+⎪⎨⎪=+-⎩ 解得:103529x y ⎧=-⎪⎪⎨⎪=⎪⎩或10x y =⎧⎨=⎩ 1052,39C ⎛⎫∴- ⎪⎝⎭设44,33P m m⎛⎫-+⎪⎝⎭则()2,2Q m m m+-PB PQ=()()2224444123333m m m m m⎛⎫⎛⎫-+-+-+-+-⎪ ⎪⎝⎭⎝⎭()22257101933m m m-=--+即()257101333m m m--=--+或()257101333m m m-=--+解得:1m=或53m=-或5m=-P是线段BC上一点()1,0B1052,39C⎛⎫-⎪⎝⎭53m∴=-532,39P⎛⎫∴-⎪⎝⎭;(3)解:设()()()2211122212,2,,21,1 M x x x N x x x x x+-+-≠≠直线MN的解析式为y kx n=+即2111222222x x kx nx x kx n⎧+-=+⎨+-=+⎩解得:()121212k x xn x x=++⎧⎨=-+⎩∴直线MN的解析式为:()()121212y x x x x x=++-+直线BM的解析式为y k x n''=+即21112x x k x nk n⎧+-=+'=+'''⎨⎩解得:()1122k xn x=+⎧⎨=-+''⎩∴直线BM的解析式为:()()1122y x x x=+-+当0x=时()12y x=-+()10,2E x∴--直线BN的解析式为y k x n''''=+即222220x x k x n k n '''⎧+-=+⎨=+'''''⎩解得:()2222k x n x =+⎧⎨=-+''''⎩∴直线BN 的解析式为:()()2222y x x x =+-+当0x =时 ()22y x =-+()20,2F x ∴--12EF x x ∴=-EBF EOB ∽△△EF BE BE OE∴= 112BE OE x ==+()21121122x x x x ∴++=-⋅+即()221111212542x x x x x x x ++=+-- ∴()121252x x x x =--+∴()()()()()()121212121212125223y x x x x x x x x x x x x x x ⎡⎤=++-+=++---+=++++⎣⎦ ∴当2x =-时 1y =∴直线MN 经过一个定点()2,1-.2.(1)解:把点()1,0A - ()4,0B 分别代入22y ax bx =++得2016420a b a b -+=⎧⎨++=⎩解得1232a b ⎧=-⎪⎪⎨⎪=⎪⎩①抛物线的解析式为213222y x x =-++. (2)①()1,0A - ()4,0B①对称轴为直线14322x -+== 点A 关于对称轴的对称点为点B 连接BC 交对称轴于点D 连接AD 此时AD CD +最小当0x =时 2y =①点()0,2C .设直线BC 的解析式为2y kx =+ 代入()4,0B 得420k += ①12k =- ①直线BC 的解析式为122y x =-+ 当32x =时 54y = ①点35,24D ⎛⎫ ⎪⎝⎭. (3)存在.①()0,2C E 是OC 的中点∴()0,1E .又()1,0A -①直线AE 的解析式为1y x =+ 1OE OA ==. 联立2132221y x x y x ⎧=-++⎪⎨⎪=+⎩得2132122x x x -++=+. 解得12x = 21x =-(舍).当2x =时 3y =.①()2,3F . 设213,222P n n n ⎛⎫-++ ⎪⎝⎭则(),1G n n +. ①2213112112222PG n n n n n =-++--=-++. 分以下两种情况:①如图2 若FPG AOE ∽△△ 则90FPG PF PG =.①PF x ∥轴.①2PF n =-. ①2112122n n n -=-++.解得1n =或2n =(舍).①()1,3P .①如图3 若PFG AOE ∽△△ 则90PFG ∠=︒ PF FG =.过点F 作FH PG ⊥于点H 则2PG FH = 即()21112222n n n ⎛⎫--++=- ⎪⎝⎭.解得3n =或2n =(舍).①()3,2P .综上 点P 的坐标为()1,3或()3,2.3.(1)解:抛物线212y x bx c =-++与x 轴交于()20A -,()40B ,两点 ∴()221220214402b c b c ⎧-⨯--+=⎪⎪⎨⎪-⨯++=⎪⎩解得:14b c =⎧⎨=⎩①抛物线的函数表达式为2142y x x =-++; (2)解:抛物线2142y x x =-++与y 轴交于点C ∴()0,4C∴4OC =设直线BC 的解析式为y kx d =+ 把()4,0B ()0,4C 代入 得: 404k d d +=⎧⎨=⎩解得14k d =-⎧⎨=⎩ ∴直线BC 的解析式为4y x =-+直线l x ⊥轴 (),0M m21,42P m m m ⎛⎫∴-++ ⎪⎝⎭(),4N m m -+ ()221144222PN m m m m m ∴=-++--+=-+ 221111244222B C S PN x x m m m m ⎛⎫∴=⋅-=⨯-+⨯=-+ ⎪⎝⎭()4,0B ()0,4C (),0M m()211448222C S BM y m m ∴=⋅=⨯-⨯=- 12S S2482m m m ∴-+=-解得2m =或4m =(P 与B 重合 舍去)m ∴的值为2;(3)解:()4,0B ()0,4COB OC ∴= BOC ∴是等腰直角三角形45CBO ∴∠=︒BMN ∴是等腰直角三角形45BNM MBN ∴∠=∠=︒HMN 与BCM 相似 且45MNH CBM ∠=∠=︒H ∴在MN 的右侧 且NH MN BC BM=或NH MN BM BC = 设(),4H t t -+ 由(2)知()2,0M ()2,2N ()4,0B ()4,0CBC ∴= 2BM = 2MN =2NH - 当NHMNBC BM =时 如图:∴222242t -=解得6t =或2t =-(此时H 在MN 左侧 舍去)()6,2H ∴-由()2,0M ()6,2H - 同(2)得直线MH 解析式为112y x =-+2112142y x y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩解得x y ⎧=⎪⎪⎨⎪=⎪⎩或x y ⎧=⎪⎪⎨⎪=⎪⎩①点Q 的坐标为⎝⎭或⎝⎭;当NH MNBM BC =时 如图:∴222242t -=解得32t =(舍去)或52t =5322H ⎛⎫∴ ⎪⎝⎭, 由()2,0M 5322H ⎛⎫ ⎪⎝⎭, 同(2)得直线MH 解析式为36y x =- 236142y x y x x =-⎧⎪⎨=-++⎪⎩解得261266x y ⎧=-+⎪⎨=-+⎪⎩2261266x y ⎧=--⎪⎨=--⎪⎩①点Q 的坐标为(226,1266-+-+或(226,1266----.综上所述 点Q 的坐标为333133+-⎝⎭或333133-+⎝⎭或(226,1266-+-+或(226,1266----. 4.(1)将()2,0A - ()8,0B 代入抛物线214y x bx c =-++ 得()221220418804b c b c ⎧-⨯--+=⎪⎪⎨⎪-⨯++=⎪⎩解得324b c ⎧=⎪⎨⎪=⎩ ∴该抛物线的解析式为213442y x x =-++. (2)①由抛物线的解析式为213442y x x =-++ 得()0,4C .设直线BC 的解析式为y kx t =+ 将()8,0B ()0,4C 代入得80,4,k t t +=⎧⎨=⎩解得1,24,k t ⎧=-⎪⎨⎪=⎩ ∴直线BC 的解析式为142y x =-+. 设第一象限内的点D 的坐标为213,442m m m ⎛⎫-++ ⎪⎝⎭ 则1,42E m m ⎛⎫-+ ⎪⎝⎭ 2213114424224DE m m m m m ⎛⎫⎛⎫∴=-++--+=-+ ⎪ ⎪⎝⎭⎝⎭8BF m =- ()()2211282944DE BF m m m m ⎛⎫∴+=-++-=--+ ⎪⎝⎭. 104-< ∴当2m =时 DE BF +有最大值 为9.①()2,0A - ()8,0B ()0,4C2OA ∴= 8OB = 4OC = 10AB =22220AC OA OC ∴=+= 22280BC OB OC =+= 2210100AB == 222AC BC AB ∴+=90ACB ∴∠=︒90CAB CBA ∴∠+∠=︒.DF x ⊥轴于点F90FEB CBA ∴∠+∠=︒CAB FEB DEC ∴∠=∠=∠.以点C D E 为顶点的三角形与AOG 相似 只需OA AG DE CE =或OA AG CE DE =. G 是AC 的中点 ()2,0A - ()0,4C()1,2G ∴- 2OA =12AG AC == 由①知2124DE m m =-+ 1,42E m m ⎛⎫-+ ⎪⎝⎭CE ∴=. 当OA AG DE CE =时22124m m =-+解得4m =或0m =(舍去) ()4,6D ∴. 当OAAGCE DE =时 251524m m m -+解得3m =或0m =(舍去) 253,4D ⎛⎫∴ ⎪⎝⎭.综上所述 以点C D E 为顶点的三角形与AOG 相似点D 的坐标为()4,6或253,4⎛⎫ ⎪⎝⎭. 5.(1)解:对于抛物线223y x x =-++ 当0x =时 可有3y = 即(0,3)C 当0y =时 可有2230x x -++= 解得11x =- 23x =即(1,0)A - (3,0)B①3OC = 3(1)4AB =--= ①1143622ABC S AB OC =⋅=⨯⨯=;(2)解:存在 点M 的坐标为30,2⎛⎫- ⎪⎝⎭ 或()01M -,理由如下:①(1,0)A - (3,0)B (0,3)C ①221310AC =+= 4AB = 223332BC =+如下图 当BCA CMB ∽时则有BCABCM BC = 3232①92CM = ①93322OM CM OC =-=-= ①30,2M ⎛⎫- ⎪⎝⎭;当BAC CMB ∽时 如图:则有BC ABCM BC = 4CM =①4CM =①1OM CM OC =-=则()01M -, 综上:30,2M ⎛⎫- ⎪⎝⎭或()01M -,(3)解:根据题意 点P 与点B 不重合;且45APC ∠=︒ 如图结合二次函数的对称性 且=45ABC ∠︒ ①45BAP ∠=︒①CP AB ∥则3P C y y ==①223y x x =-++①对称轴()2121x =-=⨯- 则()112C P x x += 则2P x =①P 的坐标为()23,当45PAC ∠=︒时 如下图设AP 交y 轴于点H 过点H 作HN AC ⊥于点N ①45PAC ∠=︒①9045NHA PAC PAC ∠=︒-∠=︒=∠ ①HN NA =①(1,0)A - (0,3)C①1OA = 3OC = ①1tan 3NH OA ACO CN OC ∠=== 设HN NA t == 则3CN t = 2AH t = ①310AC t t =+解得10t =①52AH t = ①2212OH AH OA =-=①10,2H ⎛⎫ ⎪⎝⎭设直线AH 的解析式为111(0)y k x b k =+≠ 将点(1,0)A - 10,2H ⎛⎫ ⎪⎝⎭代入 可得111012k b b =-+⎧⎪⎨=⎪⎩ 解得111212k b ⎧=⎪⎪⎨⎪=⎪⎩①直线AH 的解析式为1122y x =+ 联立直线AH 的解析式1122y x =+与抛物线解析式223y x x =-++ 可得2112223y x y x x ⎧=+⎪⎨⎪=-++⎩ 解得=1x -(舍去)或52x =①点57,24P ⎛⎫ ⎪⎝⎭; 当45ACP ∠=︒时 如下图 设CP 交x 轴于点T 过点T 作TK BC ⊥于点K ①(3,0)B (0,3)C ①3OB OC == ①190452OCB CBT ∠=∠=⨯︒=︒ ①45ACP OCB ∠=∠=︒ 即ACO OCP OCP PCB ∠+∠=∠+∠①ACO PCB ∠=∠ ①1tan tan 3TK BCP ACO CK ∠==∠= ①45KBT ∠=︒①9045KTB KBT KBT ∠=︒-∠=︒=∠①KB KT =设KT KB t == 则3CK t = 2BT t ①332BC t t =+=解得32t = ①322BT t ==①3,02T ⎛⎫ ⎪⎝⎭ 设直线CT 的解析式为222(0)y k x b k =+≠ 将点(0,3)C 3,02T ⎛⎫ ⎪⎝⎭代入 可得2223302b k b =⎧⎪⎨=+⎪⎩解得2223k b =-⎧⎨=⎩ ①直线CT 的解析式为23y x =-+联立直线CT 的解析式23y x =-+与抛物线解析式223y x x =-++可得22323y x y x x =-+⎧⎨=-++⎩解得0x =(舍去)或4x =①点(4,5)P -.综上所述 点P 坐标为(2,3) 57,24⎛⎫ ⎪⎝⎭或(4,5)-. 6.(1)解:在抛物线1L :245y x x =-++中令0y = 则2450x x -++=解得11x =- 25x = 即()10A -, ()50B , 根据题意 设抛物线L 2的函数关系式为()()15y a x x =+-将点()38-,代入得()()83135a =-+-- 解得12a = ①抛物线2L 的函数关系式为()()2115152222y x x x x =+-=--;(2)解:由题意得 5OB OC ==①BOC 为等腰直角三角形①抛物线1L :()224529y x x x =-++=--+①顶点()29D ,由题意可知PDQ ∠不可能为直角①当90DPQ ∠=︒时 如图 DPQ BOC ∽或DPQ COB ∽ 则DP QP =设Q 2()45m m m -++,①2QP m =- ()2945DP m m =--++①()22945m m m -=--++ 解得12m =(舍去) 23m = ①当3m =时 2458m m -++=①()28P ,①当90DQP ∠=︒时 如图 DPQ BCO ∽或DPQ CBO ∽ 过点Q 作QM DP ⊥垂足为点M 则DM QM MP ==由①可知()28M ,①1MP DM ==①()27P ,综上所述:点P 的坐标为()28P ,或()27P ,.7.(1)解:23y x c =-+与x 轴交于点()3,0A 与y 轴交于点B 02c 解得2c =(0,2)B ∴抛物线243y x bx c =-++经过点A B ∴12302b c c -++=⎧⎨=⎩ 解得1032b c ⎧=⎪⎨⎪=⎩ ∴抛物线解析式为2410233y x x =-++; (2)解:①由(1)可知直线解析式为223y x =-+ (,0)M m 为x 轴上一动点 过点M 且垂直于x 轴的直线与直线AB 及抛物线分别交于点P N2,23P m m ⎛⎫∴-+ ⎪⎝⎭2410,233N m m m ⎛⎫-++ ⎪⎝⎭ 223PM m 3AM m 22410242243333PN m m m m m ⎛⎫=-++--+=-+ ⎪⎝⎭BPN △和APM △相似 且BPN APM ∠=∠90BNP AMP 或90NBP AMP ∠=∠=︒当90BNP ∠=︒时 则有BN MN ⊥N ∴点的纵坐标为224102233m m ∴-++= 解得0m =(舍去)或52m = 502M ⎛⎫∴ ⎪⎝⎭,; 当90NBP ∠=︒时 过点N 作NC y ⊥轴于点C则90NBC BNC ∠+∠=︒ NC m = 22410410223333BC m m m m =-++-=-+ 90NBP ∠=︒90NBC ABO ∴∠+∠=︒ABO BNCRt Rt NCB BOA ∴∽△△ ∴NC CB OB OA= ∴24103323m m m -+= 解得0m =(舍去)或118m = 1108M ⎛⎫∴ ⎪⎝⎭,; 综上可知当以B P N 为顶点的三角形与APM △相似时 点M 的坐标为502⎛⎫ ⎪⎝⎭,或1108⎛⎫ ⎪⎝⎭,; ①由①可知(,0)M m 2,23P m m ⎛⎫-+ ⎪⎝⎭ 2410,233N m m m ⎛⎫-++ ⎪⎝⎭M P N 三点为“共谐点”∴有P 为线段MN 的中点、M 为线段PN 的中点或N 为线段PM 的中点当P 为线段MN 的中点时 则有22410222333m m m ⎛⎫-+=-++ ⎪⎝⎭解得3m =(舍去)或0.5m =;当M 为线段PN 的中点时 则有22410220333m m m ⎛⎫-++-++= ⎪⎝⎭解得3m =(舍去)或1m =-;当N 为线段PM 的中点时 则有22410222333m m m ⎛⎫-+=-++ ⎪⎝⎭解得3m =(舍去)或14m =-; 综上可知当M P N 三点成为“共谐点”时m 的值为0.5或1-或14-. 8.(1)解:(1,0)A -1OA ∴=3OB OA = OC OB =3OB OC ∴==.(3,0)∴B (0,3)C二次函数()2<0y ax bx c a =++的图象经过点A B C∴09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩ 解得:123a b c =-⎧⎪=⎨⎪=⎩∴该二次函数的表达式为223y x x =-++;(2)解:①()222314y x x x =-++=--+①抛物线对称轴为直线1x =延长AC 交对称轴于点M 此时BM CM AM CM AC -=-=有最大值①()1,0A - (0,3)C ①221310AC =+=设直线AC 的解析式为3y mx =+ 代入()1,0A -得03m =-+ 解得3m =①直线AC 的解析式为33y x =+①当1x =时 336y =+=①点M 坐标为()16,;答:BM CM - 点M 坐标为()16,; (3)解:设2(,23)P m m m -++PD x ⊥轴 P 为第一象限内抛物线上一点 0m ∴> OD m = 223PD m m =-++ 1AD OA OD m ∴=+=+ PDA 与COA 相似 ∴OA AD OC PD =或OA PD OC AD= ∴211323m m m +=-++或212331m m m -++=+. 解得:10m = 21m =-或31m =- 483m =.0m >83m ∴=. PDA ∴与COA 相似 满足条件的P 点坐标为81139⎛⎫⎪⎝⎭,. 9.(1)解:①(0,8)C 则设抛物线解析式为28y ax bx =++把A 、B 两点坐标代入可得428016480a b a b -+=⎧⎨++=⎩解得:12a b =-⎧⎨=⎩①抛物线解析式为228y x x =-++;(2)解:①点P 在抛物线上①可设()228P t t t -++,过P 作PE x ⊥轴于点E 交直线BC 于点F 如图①(40)B ,(08)C , 设直线BC 解析式为8y kx =+则048k =+解得2k =-①直线BC 解析式为28y x =-+①(28)F t t -+,①()2228(28)4PF t t t t t =-++--+=-+ ①1111()2222PBC S PF OE PF BE PF OE BE PF OB =⋅+⋅=⋅+=⋅△ ()221442(2)82t t t =-+⨯=--+ ①当2t =时 PBC S 最大值为8 此时2288t t -++=①当P 点坐标为(2,8)时 PBC 的最大面积为8; (3)解:设(0)Q m ,①=90AOC ︒∠①分AOC QOB ∽△△和AOC BOQ ∽△△两种情况 当AOC QOB ∽△△时①OA OC OQ OB= 即284m = 解得1m =±①点Q 的坐标为()01,或()01-,; 当AOC BOQ ∽△△时 ①OA OC OB OQ= 即284m = 解得16m =±①点Q 的坐标为()016,或()016-,; 综上 点Q 的坐标为()016,或()016-,或()01,或()01-,. 10.(1)解:①该抛物线过点()02C -,①可设该抛物线的解析式为22y ax bx =+-.将()40A ,()10B ,代入 得1642020a b a b +-=⎧⎨+-=⎩解得1252a b ⎧=-⎪⎪⎨⎪=⎪⎩①此抛物线的解析式为215222y x x =-+-; (2)解:存在;设P 点的横坐标为m 则P 点的纵坐标为215222m m -+- 由题意 4m > 如图 4AM m =- 215222PM m m =-+①90COA PMA ∠=∠=︒ ①12PM OC AM OA ==或①2PM OA AM OC ==当12PM OC AM OA ==时 则21522422m m m ⎛⎫-+=- ⎪⎝⎭ 解得:1224m m ==, (都不符合题意 舍去); 当2PM OA AM OC==时 则()21522422m m m -+=- 解得:1254m m ==,(4m =不符合题意舍去)此时 2152222m m -+-=- 则()52P -, 综上所述 符合条件的点P 为()52-,. 11.(1)解:把点()1,0A - ()3,0B 代入24y ax bx =+-中得:409340a b a b --=⎧⎨+-=⎩解得:4383a b ⎧=⎪⎪⎨⎪=-⎪⎩则抛物线的表达式为则抛物线的表达式为:248433y x x -=-; (2)存在 理由如下:由抛物线解析式可知:点()0,4C - 设BC 的表达式为:4y kx =-将点B 的坐标代入上式得:034k =- 解得:43k = 则直线BC 的表达式为:443y x =- 设点4,43E x x ⎛⎫- ⎪⎝⎭ 则点248,433M x x x ⎛⎫-- ⎪⎝⎭则224484(4)(4)43333ME x x x x x =----=-+ ①403-< 故ME 有最大值 当32x =时 ME 的最大值为3 此时 点3,52M ⎛⎫- ⎪⎝⎭; (3)存在 理由如下:DEB CEM M C E ∠=∠,,,为顶点的三角形和BDE △相似 ①当CME ∠为直角时则点C 、M 关于抛物线对称轴对称 而抛物线的对称轴为32x =则点()3,4M -;①当90ECM ∠=︒时 如图:由(1)得()0,4C - 设直线BC 的解析式为: 14y k x =- 把()3,0B 代入得1340k -=143k ∴= 设直线CM 的解析式为:24y k x =- 易知:121k k234k ∴=- 故直线CM 的表达式为:344y x =-- 联立抛物线表达式和上式得:248344334x x x --=-- 解得:0x =(舍去)或2316x =即点23325(,)1664M -; 综上 点M 的坐标为:23325,1664⎛⎫-⎪⎝⎭或()3,4-12.(1)解:令2132022x x -++= 解得11x =- 24x =①点A 在点B 的左侧①()10A -,()40B , 将0x =代入213222y x x =-++ 可得:2y =①()02C ,; (2)证明:如图 过点D 作DD x '⊥轴于点D根据题意 可得:DD OC '∥①BDD BCO '∽ ①25BD DD BD BO CO BC ''=== ①()40B ,()02C , ①4BO = 2CO =①2425BD DD ''== 解得85BD '= 45DD '= ①125OD BO BD ''=-=①12455D ⎛⎫ ⎪⎝⎭, 由抛物线213222y x x =-++ 可知对称轴为直线32x = ①点C 、C '关于抛物线对称轴对称①()32C ',设直线C D '的解析式为()0y kx b k =+≠把()32C ',、12455D ⎛⎫ ⎪⎝⎭,代入解析式 可得:3212455k b k b +=⎧⎪⎨+=⎪⎩ 解得:24k b =⎧⎨=-⎩ ①直线C D '的解析式为24y x =-;(3)解:①()02C ,①点C 关于x 轴的对称点M 的坐标为()02-,设直线BM 的解析式为()0y ax n a =+≠把()40B ,()02M -,代入解析式 可得:402a n n +=⎧⎨=-⎩ 解得:122a n ⎧=⎪⎨⎪=-⎩ ①直线BM 的解析式为122y x =- 设点N 的坐标为()0m , 则213222P m m m ⎛⎫-++ ⎪⎝⎭,、()12142Q m m m ⎛⎫--≤≤ ⎪⎝⎭, ①PQ x ⊥轴①OM PQ ∥①BMO BQP ∠=∠①90BOM ∠=︒ 而90BQP ∠<︒①可分以下两种情况:①如图2 连接BP 当90QBP MOB ∠=∠=︒时 PBQ BOM ∽①BPQ QBN ∠=∠①90BNP QNB ∠=∠=︒①BNP QNB ∽ ①PN NBBN NQ = ①21324221422m m mm m++-=-- ①()21324221442m m mm m ++-=-- ①21322224m m m ++=-解得:4m =或3m =检验:当4m =时 40m -= 等式不成立 且点B 、P 、Q 重合 BPQ 不存在此情况舍去;将3m =代入213222y x x =-++ 可得2y =①()32P ,; ①如图3 当90BPQ MOB ∠=∠=︒时 此时点P 与点A 、点N 重合 BOM BPQ ∽此时1m =- 点P 的坐标为()10-,; 综上所述 以点B 、P 、Q 为顶点的三角形与BOM 相似时 点P 的坐标为()32,或()10-,.13.(1)解:①抛物线26y ax bx =+-与x 轴交于点()3,0B -()1,0C ①936060a b a b --=⎧⎨+-=⎩解得:24a b =⎧⎨=⎩①抛物线为:2246y x x =+-;(2)解:①2246y x x =+-当0x =时 y =-6①()0,6A -设直线AB 为y kx n =+①630n k n =-⎧⎨-+=⎩ 解得:26k n =-⎧⎨=-⎩①直线AB 为26y x =--设点P 的横坐标为()30t t -<<.①()2,246P t t t +- (),26D t t --①222624626PD t t t t t =----+=--当()63222t -=-=-⨯-时 PD 的最大值为:233926222⎛⎫⎛⎫-⨯--⨯-= ⎪ ⎪⎝⎭⎝⎭. (3)解:如图 连接AP①BDH ADP ∠=∠ 而DPA 与DHB △相似①分两种情况讨论:当DPA DHB ∽时 ①DP AP DH BH= 90APD BHD ∠=∠=︒ ①AP x ∥轴 OH AP =①A P 关于抛物线的对称轴对称①()3,0B - ()1,0C①抛物线的对称轴为直线3112x -+==- 而()0,6A - ①()2,6P --;如图 当DHB DAP ∽时 过A 作AQ PH ⊥于Q①AQ OH = 6AO QH ==设AQ OH n ==①DHB DAP ∽①90DHB DAP ∠=∠=︒①90ADP APD APQ QAP ∠+∠=∠+∠=︒①PAQ ADP ∠=∠由PH y ∥轴 可得ADP BAO ∠=∠①PAQ BAO ∠=∠ ①31tan tan 62PAQ BAO ∠=∠== ①12PQ AQ 即12PQ n = ①1,62P n n ⎛⎫--- ⎪⎝⎭ ①()()2124662n n n -+⨯--=-- 解得:74n =(0n =舍去) ①755,48P ⎛⎫-- ⎪⎝⎭. 综上:()2,6P --或755,48P ⎛⎫-- ⎪⎝⎭. 14.(1)解:设抛物线的解析式为2(0)y ax bx c a =++≠ 将点(2,0)A - (3,3)B - (0,0)O 代入可得:4209330a b c a b c c -+=⎧⎪-+=⎨⎪=⎩解得:120a b c =⎧⎪=⎨⎪=⎩所以函数解析式为:22y x x =+;(2)证明:①()22211y x x x =+=+-①抛物线的顶点C 的坐标为()1,1--①()0,0O ()3,3B -①()()22303018OB =--+-= ()()2210102OC =--+--=()()22313120BC =---+--=⎡⎤⎡⎤⎣⎦⎣⎦ ①222OB OC BC +=①BOC 是直角三角形;(3)解:假设存在点P 使以P M A 为顶点的三角形与BOC 相似 如图设(,)P x y 由题意知0x > 0y > 且22y x x =+由(2)知 BOC 为直角三角形 90COB ∠=︒ 且:1:3OC OB = ①若PMA COB ∽ 则AM PM BO CO= 即223(2)x x x +=+ 得 113x = 22x =-(舍去) 当13x =时 79y = 即1(3P 7)9; ①若PMA BOC ∽AM PM OC BO= 即:223(2)x x x +=+ 得:13x = 22x =-(舍去)当3x =时 15y = 即(3,15)P .①存在 当点P 坐标为17,39⎛⎫ ⎪⎝⎭或(3,15) 使得以P M A 为顶点的三角形与BOC 相似. 15.(1)解:①2616y ax ax a =--经过()04C ,①164a -= 解得14a =- ①213442y x x =-++; 令0y = 即2134=042x x -++ 解得:122,8x x =-=①()()2,0,8,0A B -(2)设直线BC 的关系式为y kx b =+ ()8,0B ()04C ,①408b k b =⎧⎨=+⎩解得124k b ⎧=-⎪⎨⎪=⎩. ①直线BC 的方程为142y x =-+. 如图 过点P 作PG x ⊥轴于点G PG ,交CB 于点E①PG CO ∥①PED OCB ∠=∠又90PDE COB ∠=∠=︒①PDE BOC ∽△△ ①PD PE BO BC= ①8,4BO CO ==①BC =①BO PD PE PE BC =⨯ ①当线段PE 最长时 PD 的长度最大. 设213(4)42P t t t -++, 则1(,4)2E t t -+. 即213442PG t t =-++ 142EG t =-+. ①22112(4)444PE PG EC t t t =-=-+=--+()08t <<. 当4t =时 PE 有最大值是4 此时P 点坐标为()46,.①25854PD == 设1,42D m m ⎛⎫-+ ⎪⎝⎭ ①()2221854462m m ⎛⎫-+-+-= ⎪⎝⎭⎝⎭ 解得12125m m == ①111214442255m -+=-⨯+= 即点D 的坐标为121455⎛⎫ ⎪⎝⎭,. ①①284OA OB OC ===,,①2222420AC =+= ()2228100AB =+= 2224880BC =+=. 可得222AC BC AB =+.①90ACB ∠=︒.①COA BOC ∽.故当PDC △与COA 相似时 则PDC △与BOC 相似. ①PCD CBO ∠∠=或PCD BCO ∠∠=.(i )如图 当PCD CBO ∠=∠时即PDC COB ∽①PCD CBO ∠=∠①CP AB ∥①()04C ,①4P y =. ①2134442t t -++= 解得1260x x ==,(舍)即PDC COB ∽时 (64)P ,; (ii )当PCD BCO ∠=∠时 即PDC BOC ∽如图 过点P 作PG x ⊥轴于G 与直线BC 交于F①PF OC ∥①PFC BCO ∠=∠①PCD PFC ∠=∠①PF PC =. 设213(4)42P n n n -++, 则2124PF n n =-+ 过点P 作y 轴的垂线 垂足为N在Rt PNC △中 22222243213131344421644PC PN NC n n n n n n ⎡⎤=+=+-++-=-+⎢⎥⎣⎦() ①22PF PC = 即2243211313(2)41644n n n n n -+=-+ 解得120=3=n n , (舍).即PDC BOC ∽时 25(3)4P ,. ①当PDC △与COA 相似时 点P 的坐标为(64)P ,或2534P ⎛⎫ ⎪⎝⎭,.。
中考数学总复习《二次函数与相似三角形问题综合》专项能力提升训练(含答案)

(1)抛物线的解析式为__________;
(2)点M为y轴正半轴上的一个动点,连接 ,过点M作 的垂线,与抛物线的对称轴交于点N,连接AN.
①若 与 相似,求点M的坐标;
②若点M在y轴正半轴上运动到某一位置时, 有一边与线段 相等,并且此时这一边与线段 具有对称性,我们把这样的点M称为“对称点”,请写出“对称点”M的坐标.
12.如图,抛物线y= x2+bx+c的顶点D坐标为(1,4),且与 轴相交于A,B两点 点A在点B的左侧 ,与y轴相交于点C,点E在x轴上方且在对称轴左侧的抛物线上运动,点F在抛物线上并且和点E关于抛物线的对称轴对称,作矩形EFGH,其中点G,H都在x轴上.
(1)求抛物线解析式;
(2)设点F横坐标为m
②若 是 的中点,以点 ,D, 为顶点的三角形与 相似,求点 的坐标.
3.抛物线 与 轴交于 , 两点,与 轴交于点 ,点 是抛物线在第一象限内的一个动点,且在对称轴右侧.
(1)求a,b,c的值;
(2)如图 ,连接 、 ,交点为 ,连接 ,若 ,求点 的坐标;
(3)如图 ,在(2)的条件下,过点 作 轴的垂线交 轴于点 ,将线段 绕点 逆时针旋转得到 ,旋转角为 ,连接 和 ,求 的最小值.
9.如图,在平面直角坐标系中,抛物线 与x轴交于 两点(点A在点B的左侧),与y轴交于点C,连接 ,点P为直线 上方抛物线上一动点,连接 交 于点Q.
(1)求抛物线的函数表达式;
(2)当 的值最大时,求点P的坐标和 的最大值;
(3)把抛物线 向右平移1个单位,再向上平移2个单位得新抛物线 ,M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,写出所有符合条件的N点的坐标,并写出求解点N的坐标的其中一种情况的过程.
中考数学总复习《二次函数与相似三角形问题》专项训练题(附有答案)

中考数学总复习《二次函数与相似三角形问题》专项训练题(附有答案)学校:___________班级:___________姓名:___________考号:___________ 1.如图,在平面直角坐标系xOy 中,矩形OABC 的边3OA =,AB=4,点A 在x 轴的正半轴上,点C 在y 轴的负半轴上,抛物线243y x bx c =++经过A ,C 两点,连接AC .(1)请直接写出b ,c 的值;(2)若动点(),0E m 在边OA (不与O ,A 两点重合)上,过点E 作x 轴的垂线l 交BC 于点F ,交AC 于点M ,交抛物线于点P ,连接PC . ①设线段PM 的长为h ,求h 与m 的函数关系式;①当点P 在BC 下方的抛物线上时,以P ,C ,F 为顶点的三角形与AEM △是否相似?若相似,请求出此时点E 的坐标;若不相似,请说明理由.2.如图,在平面直角坐标系中,抛物线22y ax b =++过点()1,3,且交x 轴于点()1,0A -,B 两点,交y 轴于点C .(1)求抛物线的表达式;(2)点P 是直线BC 上方抛物线上的一动点,过点P 作PD BC ⊥于点D ,过点P 作y 轴的平行线交直线BC 于点E ,求PD 的最大值及此时点P 的坐标;(3)将该抛物线沿射线CB 方向平移5个单位长度,点M 为平移后的抛物线的对称轴上一点.是否存在M 使得M ,B 关于PD 对称,若存在直接写出M 的坐标,若不存在,请说明理由.3.综合与探究:如图,抛物线2134y x x =-++与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C .(1)求点A ,B ,C 的坐标;(2)点P 在直线BC 上方的抛物线上,过点P 作x 轴的垂线l ,连接AP 交BC 于点D .当PD AD最大时,求点P 的坐标及PDAD的最大值; (3)在(2)的条件下,在l 上是否存在点Q ,使BCQ △是直角三角形.若存在,请直接写出点Q 的坐标;若不存在,请说明理由.4.如图,抛物线2122y x bx =-++交x 轴于A (1-,0),B (4,0)两点,交y 轴于点C ,与过点C 且平行于x 轴的直线交于另一点D ,点P 是抛物线上一动点.(1)求抛物线解析式;(2)过点P 作y 轴的垂线与射线BC 交于点Q ,设线段PQ 的长度为d ,点P 的横坐标为m ,求d 与m 的函数关系式;(3)若点P 在y 轴右侧,过点P 作直线CD 的垂线,垂足为Q ,若将①CPQ 沿CP 翻折,点Q 的对应点为Q ′.是否存在点P ,使Q ′恰好落在x 轴上?若存在,求出点P 的坐标;若不存在,说明理由.5.综合与探究如图,直线243y x =-+与x 轴,y 轴分别交于B ,C 两点,抛物线243y ax x c =++经过B ,C 两点,与x 轴的另一个交点为A (点A 在点B 的左侧),抛物线的顶点为点D .抛物线的对称轴与x 轴交于点E .(1)求抛物线的表达式及顶点D 的坐标;(2)点M 是线段BC 上一动点,连接DM 并延长交x 轴交于点F ,当:1:4FM FD =时,求点M 的坐标;(3)点P 是该抛物线上的一动点,设点P 的横坐标为m ,试判断是否存在这样的点P ,使90PAB BCO ∠+∠=︒,若存在,请直接写出m 的值;若不存在,请说明理由.6.如图,抛物线与x 轴交于点A ,B ,与y 轴交于点C ,且点()1,0A -,点()0,2C ,抛物线的对称轴为直线32x =,连接AC ,BC .(1)求抛物线的解析式;(2)将ABC 沿直线BC 折叠,得到DBC △,请问:点A 的对应点D 是否落在抛物线的对称轴上?若点D 落在对称轴上,请求出点D 的坐标;若点D 没有落在对称轴上,请说明理由;(3)若点E 是抛物线位于第一象限内的一个动点,连接AE 交直线BC 于点F ,设EFn AF=,求n 的最大值并求出此时点E 的坐标.7.如图,抛物线22y ax bx =++与x 轴交于A ,B 两点,点()2,0A 且2OA OB =,与y 轴交于点C ,连接BC ,D 为第一象限内抛物线上一动点,过点D 作DE OA ⊥于点E ,与AC 交于点F ,设点D 的横坐标为m .(1)求抛物线的表达式;(2)求ACD 面积的最大值及此时D 点的坐标;(3)抛物线上是否存在点D ,使得以点O 、D 、E 为顶点的三角形与BOC 相似?若存在,求出m 的值;若不存在,请说明理由.8.如图,在平面直角坐标系中,抛物线214y x bx c =++与x 轴交于()8,0A 和()2,0B -两点,与y 轴交于点C ,连接AC .(1)求抛物线的表达式;(2)如图1,直线CD 交x 轴于点()2,0D ,点P 为线段AC 下方抛物线上的一点,过点P 作PH y ∥轴交直线CD 于点H ,在直线CD 上取点Q ,连接PQ ,使得HQ PQ =,求524PQ PH -的最大值及此时P 点的坐标; (3)连接BC ,把原抛物线214y x bx c =++沿射线BC 方向平移25个单位长度,点M是平移后新抛物线上的一点,过点M 作MN 垂直x 轴于点N ,连接AM ,直接写出所有使得AMN ABC ∽的点M 的横坐标.9.已知抛物线223y x x =--与x 轴相交于A ,B 两点,与y 轴交于点C .若点(),0N n 为x 轴上的动点,过点N 作x 轴的垂线交抛物线于点P .(1)直接写出A ,B ,C 三点的坐标;(2)①如图1,直线PN 交直线BC 于点G ,若点G 恰好在线段PB 的垂直平分线上,且3n <时,求n 的值;①如图2,连接AC ,AP ,抛物线上存在一点P ,使得以P ,A ,N 为顶点的三角形与CAO △相似,求点P 的坐标.10.已知抛物线:2616(0)y ax ax a a =-->与x 轴交点为A ,B (A 在B 的左侧),与y 轴交于点C ,点G 是AC 的中点.(1)求点A ,B 的坐标及抛物线的对称轴;(2)直线32y x =-与抛物线交于点M ,N 且MO NO =,求抛物线解析式.*提示:如果一元二次方程20(0)ax bx c a ++=≠的两个根是1x 和2x ,那么12b x x a+=-和12cx x a⋅=;(3)已知点P 是(2)中抛物线上第四象限内的动点,过点P 作x 轴的垂线交BC 于点E ,交x 轴于点F .若以点C ,P ,E 为顶点的三角形与AOG 相似,求点P 的坐标.11.抛物线22230yx mx m m 与x 轴交于A ,B 两点,A 点在B 点左边,与y 轴交于C 点,顶点为M .(1)当1m =时,求点A ,B ,M 的坐标;(2)如图1,在(1)的条件下,若P 为抛物线对称轴上一个动点,且PAC △为等腰三角形,求P 点坐标;(3)如图2,若一次函数y kx b =+的图象过A 点且与抛物线交于另一点F ,交对称轴于E ,MG x 轴,FG MG ⊥和AM AF ⊥.若45AMEF ,求MG AB的值.12.如图1,在平面直角坐标系中,抛物线233322y x x =-++与x 轴交于点A 和点B (点A 在点B 左侧),与y 轴交于点C .(1)求直线BC 的解析式;(2)点P 是直线BC 上方抛物线上的一动点,过点P 作y 轴的平行线交BC 于点D ,过点P 作x 轴的平行线交BC 于点E ,求3PE PD +的最大值及此时点P 的坐标; (3)如图2,在(2)中3PE PD +取得最大值的条件下,将抛物线233322y x x =-++沿着射线CB 方向平移得到新抛物线y ',且新抛物线y '经过线段BC 的中点F ,新抛物线y '与y 轴交于点M ,点N 为新抛物线y '对称轴上一点,点Q 为坐标平面内一点,若以点P ,Q ,M ,N 为顶点的四边形是以PN 为边的菱形,写出所有符合条件的点Q 的坐标,并写出求解点Q 的坐标的其中一种情况的过程.13.直线33y x =-+与x 轴交于点B ,与y 轴交于点C ,抛物线2y x bx c =-++经过B ,C 两点,与x 轴的另一交点为A ,连接AC ,点P 为AC 上方的抛物线上一动点.(1)求抛物线的解析式;(2)如图①,连接BP ,交线段AC 于点D ,若:5:16PD BD =,求此时点P 的坐标; (3)如图①,连接PC ,过点P 作PE y 轴,交线段AC 于点E ,若PCE 与ABC 相似,求出点P 的横坐标及线段PE 长.14.如图,已知二次函数2y x bx c =-++的图像交x 轴于点()1,0A -和()5,0B ,交y 轴于点C .(1)求这个二次函数的表达式;(2)如图1,点M 从点B 出发,以每秒2个单位长度的速度沿线段BC 向点C 运动,点N 从点O 出发,以每秒1个单位长度的速度沿线段OB 向点B 运动,点M ,N 同时出发.设运动时间为t 秒(0<t <5).当t 为何值时,BMN 的面积最大?最大面积是多少? (3)求t 为何值时,BMN 是等腰三角形?15.如图1,抛物线 ²2y ax x c =++, 交x 轴于A 、B 两点,交y 轴于点C .当0y ≥时13x -≤≤.(1)求抛物线的表达式;(2)若点D 是抛物线上第一象限的点.①如图1,连接AD ,交线段BC 于点G ,若12DG AG =时,求D 点的坐标; ①如图2,在①条件下,当点D 靠近抛物线对称轴时,过点D 作DP x ⊥轴,点H 是DP 上一点,连接AH ,求1010AH DH +的最小值; (3)如图3,F 为抛物线顶点,直线EF 垂直于x 轴于点E ,直线AD BD ,分别与抛物线对称轴交于M 、N 两点.试问,EM EN +是否为定值?如果是,请直接写出这个定值:如果不是,请说明理由.参考答案: 1.(1)83b =- 4c =- (2)①2443h m m =-+,①相似,()1,0或23,016⎛⎫ ⎪⎝⎭2.(1)213222y x x =-++ (2)PD 有最大值,最大值为455,此时点P 的坐标为(2,3) (3)不存在3.(1)()()()2,0,6,0,0,3A B C - (2)153,4P ⎛⎫ ⎪⎝⎭,PD AD的最大值为916 (3)存在,()3,6-或353,2⎛⎫+ ⎪ ⎪⎝⎭或353,2⎛⎫- ⎪ ⎪⎝⎭或()3,94.(1)213222y x x =-++ (2)当P 在y 轴右侧时,24d m m =-+;当P 在y 轴左侧时24d m m =-(3)存在 931313,2P ⎛⎫-+ ⎪ ⎪⎝⎭5.(1)214-433y x x =++ 16(2,)3;(2)44,3⎛⎫ ⎪⎝⎭;(3)存在,m 的值为4或8 6.(1)213222y x x =-++ (2)D 点不在对称轴32x =上 (3)45 ()2,3E7.(1)22y x x =-++(2)ACD 面积的最大值1 ()1,2D(3)1334m +=或1m =. 8.(1)213442y x x =-- (2)524PQ PH -取得最大值49516 97,4P ⎛⎫- ⎪⎝⎭ (3)12或0或443-或443+9.(1)()1,0A -,()3,0B 和()0,3C -(2)①2n =±;①点P 的坐标为()6,21,1013,39⎛⎫ ⎪⎝⎭和811,39⎛⎫- ⎪⎝⎭10.(1)()20A -,和()80B ,,对称轴为直线3x =; (2)213442y x x =--; (3)P 点坐标为()46-,或2534⎛⎫- ⎪⎝⎭,.11.(1)()1,0A -,()3,0B 和()1,4M -(2)1,1或()1,6或()1,6-或()1,0 (3)54m12.(1)332y x =-+ (2)3PE PD +的最大任为52,此时()1,3P (3)11173,236Q ⎛⎫- ⎪⎝⎭,21330,22Q ⎛⎫-+ ⎪⎝⎭和31330,22Q ⎛⎫-- ⎪⎝⎭13.(1)223y x x =--+(2)点P 的坐标为1(2-,15)4或5(2-,7)4).(3)P 的横坐标为32-或53-,PE 的长为94或209.14.(1)二次函数的表达式为245y x x =-++(2)当52t =时,BMN 的面积最大,最大面积是258(3)t 的值为53,525-或5215.(1)223y x x =-++(2)①()14,,()23,①10(3)是定值,定值为8。
中考复习:二次函数和相似三角形问题(含答案)

综合题讲解 函数中因动点产生的相似三角形问题例题 如图1,已知抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一个交点为B 。
⑴求抛物线的解析式;(用顶点式...求得抛物线的解析式为x x 41y 2+-=) ⑵若点C 在抛物线的对称轴上,点D 在抛物线上,且以O 、C 、D 、B 四点为顶点的四边形为平行四边形,求D 点的坐标;⑶连接OA 、AB ,如图2,在x 轴下方的抛物线上是否存在点P ,使得△OBP 与△OAB 相似?若存在,求出P 点的坐标;若不存在,说明理由。
分析:1.当给出四边形的两个顶点时应以两个顶点的连线.......为四边形的边和对角线来考虑问题以O 、C 、D 、B 四点为顶点的四边形为平行四边形要分类讨论:按OB 为边和对角线两种情况2. 函数中因动点产生的相似三角形问题一般有三个解题途径① 求相似三角形的第三个顶点时,先要分析已知三角形的边.和角.的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
y xEQ PC B OA 例题2:如图,已知抛物线y=ax 2+4ax+t (a >0)交x 轴于A 、B 两点,交y 轴于点C ,抛物线的对称轴交x 轴于点E ,点B 的坐标为(-1,0). (1)求抛物线的对称轴及点A 的坐标;(2)过点C 作x 轴的平行线交抛物线的对称轴于点P ,你能判断四边形ABCP 是什么四边形?并证明你的结论;(3)连接CA 与抛物线的对称轴交于点D ,当∠APD=∠ACP 时,求抛物线的解析式.练习1、已知抛物线2y ax bx c =++经过5330P E ⎫⎪⎪⎝⎭,,,及原点(00)O ,.(1)求抛物线的解析式.(由一般式...得抛物线的解析式为225333y x x =-+) (2)过P 点作平行于x 轴的直线PC 交y 轴于C 点,在抛物线对称轴右侧且位于直线PC 下方的抛物线上,任取一点Q ,过点Q 作直线QA 平行于y 轴交x 轴于A 点,交直线PC 于B 点,直线QA 与直线PC 及两坐标轴围成矩形OABC .是否存在点Q ,使得OPC △与PQB △相似?若存在,求出Q 点的坐标;若不存在,说明理由.(3)如果符合(2)中的Q 点在x 轴的上方,连结OQ ,矩形OABC 内的四个三角形OPC PQB OQP OQA ,,,△△△△之间存在怎样的关系?为什么?练习2、如图,四边形OABC 是一张放在平面直角坐标系中的矩形纸片,点A 在x 轴上,点C 在y 轴上,将边BC 折叠,使点B 落在边OA 的点D处。
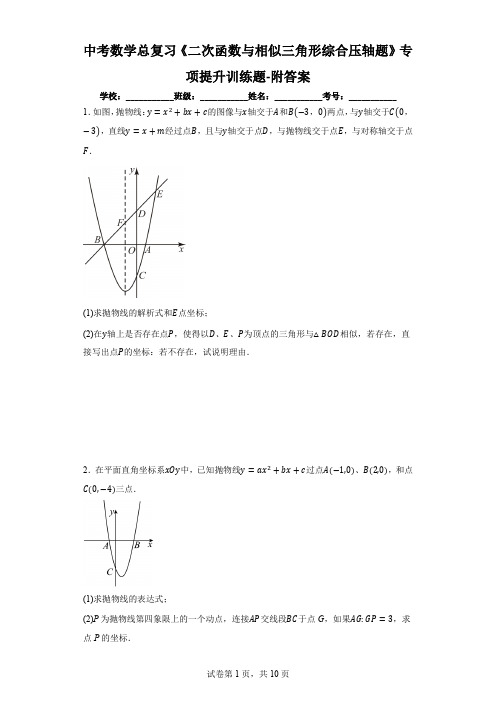
中考数学总复习《二次函数与相似三角形综合压轴题》专项提升训练题-附答案
中考数学总复习《二次函数与相似三角形综合压轴题》专项提升训练题-附答案学校:___________班级:___________姓名:___________考号:___________ 1.如图,抛物线:y=x2+bx+c的图像与x轴交于A和B(−3,0)两点,与y轴交于C(0,−3),直线y=x+m经过点B,且与y轴交于点D,与抛物线交于点E,与对称轴交于点F.(1)求抛物线的解析式和E点坐标;(2)在y轴上是否存在点P,使得以D、E、P为顶点的三角形与△BOD相似,若存在,直接写出点P的坐标:若不存在,试说明理由.2.在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c过点A(−1,0)、B(2,0),和点C(0,−4)三点.(1)求抛物线的表达式;(2)P为抛物线第四象限上的一个动点,连接AP交线段BC于点G,如果AG:GP=3,求点P的坐标.3.在平面直角坐标系中,抛物线y=−x2−4x+c与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,且点A的坐标为(−5,0).(1)求点C的坐标;(2)如图1,若点P是第二象限内抛物线上一动点,求点P到直线AC距离的最大值,并求出此时点P的坐标;(3)如图2,若点M是抛物线上一点,点N是抛物线对称轴上一点,是否存在点M使以A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.4.如图,抛物线y=−x2+bx+c与x轴交于A(−1,0),B(3,0)两点,与y轴交于点C.图1备用图(1)求抛物线的解析式;(2)如图1,D是BC上方抛物线上一点,连接AD交线段BC于点E,若AE=2DE,求点D的坐标;(3)抛物线上是否存在点P使得∠PAB=∠ABC,如果存在,请求出点P的坐标,如果不存在,请说明理由.5.综合与探究如图,二次函数y=ax2+bx+4的图像经过x轴上的点A(6,0)和y轴上的点B,且对称轴.为直线x=72(1)求二次函数的解析式.(2)点E位于抛物线第四象限内的图像上,以OE,AE为边作平行四边形OEAF.当平行四边形OEAF为菱形时,求点F的坐标与菱形OEAF的面积.(3)连接AB,在直线AB上是否存在一点P,使得△AOP与△AOB相似,若存在,请直接写出点P坐标,若不存在,请说明理由.x2+bx+c的图象与y轴交于点A(0,8),6.如图,在平面直角坐标系中,二次函数y=−14与x轴交于B、C两点,其中点B的坐标是(−8,0),点P(m,n)为该二次函数在第二象限内图象上的动点,点D为(0,4),连接BD.(1)求该二次函数的表达式;(2)依题补图1:连接OP,过点P作PQ⊥x轴于点Q;当△OPQ和△OBD相似时,求m的值;(3)如图2,过点P作直线PQ∥BD,和x轴交点为Q,在点P沿着抛物线从点A到点B运动过程中,当PQ与抛物线只有一个交点时,求点Q的坐标.x2+bx+c图像交x轴于点A,B(A在B的左侧),与y轴交7.如图,二次函数y=−12于点C(0,3),CD⊥y轴,交抛物线于另一点D,且CD=5,P为抛物线上一点,PE∥y轴,与x轴交于E,与BC,CD分别交于点F,G.(1)求二次函数解析式;(2)当P在CD上方时,是否存在点P,使得以C,P,G为顶点的三角形与△FBE相似,若存在,求出△CPG与△FBE的相似比,若不存在,说明理由.(3)点D关于直线PC的对称点为D′,当点D′落在抛物线的对称轴上时,此时点P的坐标为________.x2+x+3与x轴交于A,B两点(点A在点B 8.综合与探究:如图,抛物线y=−14的左侧),与y轴交于点C.(1)求点A,B,C的坐标;(2)点P在直线BC上方的抛物线上,过点P作x轴的垂线l,连接AP交BC于点D.当PD最AD的最大值;大时,求点P的坐标及PDAD(3)在(2)的条件下,在l上是否存在点Q,使△BCQ是直角三角形.若存在,请直接写出点Q的坐标;若不存在,请说明理由.9.已知抛物线y=x2+2x−3的图像经过点A(−3,0),点B(n,0),且与y轴交于点C.(1)求出点B的坐标;(2)若点P为x轴上方的抛物线上任意一点.①如图1,若点Q为线段BC上一点,连接PQ,PQ交x轴于点M,连接CM,当∠MCQ=45°时,求点M的坐标;①如图2,连接BC、BP,若满足∠ABP=2∠BCO,求此时点P的坐标.10.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点OA=1,tan∠BAO=3将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t①是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,直接写出当△CEF与△COD 相似时,点P的坐标.11.如图,已知二次函数y=−x2+bx+c的图象与x轴交于点A(−4,0)和点B,与y 轴相交于点C(0,4).(1)求该二次函数的解析式;(2)点D在线段OA上运动,过点D作x轴的垂线,与AC交于点Q,与抛物线交于点P.①连接AP,CP,当三角形ACP的面积最大时,求此时点P的坐标;①探究是否存在点P使得以点P,C,Q为顶点的三角形与△ADQ相似?若存在,求出点P的坐标;若不存在,说明理由.12.已知:如图,顶点为A(1,−1)的抛物线y=ax2+bx+c经过原点O,且与直线y=−x+2交于B,C两点(点C在点B的右边).(1)求抛物线的解析式;(2)猜想以点A为圆心,以AC为半径的圆与直线BC的位置关系,并加以证明;(3)若点P为x轴上的一个动点,过点P作PQ⊥x轴与抛物线交于点Q,则是否存在以O,P,Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.13.如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x−2交于B,C两点.(1)求抛物线的解析式及点C的坐标;(2)求证:△ABC是直角三角形;(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.x+2与x轴交于点A,与y轴交于点C,14.如图,在平面直角坐标系中,直线y=12,且经过A、C两点与x轴的另一交点抛物线y=ax2+bx+c的对称轴是直线x=−32为B.(1)①直接写出点B的坐标;①求抛物线的解析式;(2)点E为直线AC上方抛物线上的一动点,过点E作ED⊥x轴于点G,交AC于点D,连接AE、CE、CG,当四边形AGCE面积最大时,求出E点的坐标.(3)抛物线上是否存在点M,过点M作MN⊥x轴于点N,使得以点A、M、N为顶点的△AMN与△ABC相似?若存在,直接写出点M的坐标,若不存在,请说明理由.15.抛物线y=ax2+bx+5经过点A(1,0)和点B(5,0).(1)求该抛物线所对应的函数解析式;(2)该抛物线与直线y=2x+5相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.①连结PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;①连结PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM 相似?若存在,直接写出满足条件的点P的坐标;若不存在,说明理由.参考答案: 1.(1)y =x 2+2x −3 E(2,5)(2)(0,5)或(0,7)2.(1)y =2x 2−2x −4(2)P(1,−4)3.(1)(0,5)(2)点P 到直线AC 距离为25√28,此时P (−52,354) (3)点M 的坐标为(−3,8)或(−7,−16)或(3,−16)4.(1)y =−x 2+2x +3(2)点D 的坐标为(1,4)或(2,3)(3)存在,点P 的坐标为(2,3)或(4,−5)5.(1)y =23x 2−143x +4(2)F(3,4);菱形OEAF 的面积为24(3)存在,点P 坐标为(0,4)或(2413,3613)6.(1)y =−14x 2−x +8(2)m 的值为−4或−1−√33(3)Q (−412,0)7.(1)y =−12x 2+52x +3;(2)存在点P ,使得以C ,P ,G 为顶点的三角形与△FBE 相似,△CPG 与△FBE 的相似比为2或25;(3)P 点横坐标5+2√33或5−2√33.8.(1)A (−2,0),B (6,0),C (0,3)(2)P (3,154),PD AD 的最大值为916(3)存在,(3,−6)或(3,3+√52)或(3,3−√52)或(3,9)9.(1)B(1,0)(2)①M (−32,0);①P (−154,5716)10.(1)y =−x 2−2x +3(2)①存在,最大值为12124,①P (−1,4)或(−2,3)11.(1)解析式为y =−x 2−3x +4(2)①P(−2,6);①存在,P(−3,4)或P(−2,6)12.(1)y =x 2−2x ;(2)相切(3)存在满足条件的点P ,坐标为(53,0)或(73,0)或(−1,0)或(5,0).13.(1)y =−x 2+2x ;C(−1,−3)(2)存在,N 点,其坐标为(53,0)或(73,0)或(−1,0)或(5,0)14.(1)①B 的坐标为(1,0);① y =−12x 2−32x +2(2)E (−32,258) (3)存在,点M 的坐标为(0,2)或(−3,2)或(2,−3)或(5,−18)15.(1)y =x 2−6x +5(2)(32,−74)或(3,−4)。
初三中考数学专题复习:二次函数综合题(相似三角形问题)含答案

中考数学专题复习:二次函数综合题(相似三角形问题)1.如图①,二次函数y =﹣x 2+bx +c 的图象与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,连接BC ,点P 是抛物线上一动点.(1)求二次函数的表达式.(2)当点P 不与点A 、B 重合时,作直线AP ,交直线BC 于点Q ,若①ABQ 的面积是①BPQ 面积的4倍,求点P 的横坐标.(3)如图①,当点P 在第一象限时,连接AP ,交线段BC 于点M ,以AM 为斜边向①ABM 外作等腰直角三角形AMN ,连接BN ,①ABN 的面积是否变化?如果不变,请求出①ABN 的面积;如果变化,请说明理由.2.如图,二次函数2314y x bx =++的图像经过点()8,3A ,交x 轴于点B ,C (点B 在点C 的左侧),与y 轴交于点D .(1)填空:b = ______;(2)点P 是第一象限内抛物线上一点,直线PO 交直线CD 于点Q ,过点P 作x 轴的垂线交直线CD 于点T ,若PQ QT =,求点P 的坐标;(3)在x 轴的正半轴上找一点E ,过点E 作AE 的垂线EF 交y 轴于F ,若AEF 与EFO △相似,求OE 的长.3.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得①CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.4.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.5.如图,在平面直角坐标系中,已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ,抛物线21y x kx k =++-的图象经过点A 和点C ,与x 轴的另一个交点是点B .(1)求出此抛物线的解析式; (2)求出点B 的坐标;(3)若在y 轴的负半轴上存在点D .能使得以A ,C ,D 为顶点的三角形与①ABC 相似,请求出点D 的坐标.6.如图1,已知抛物线23y ax bx =++经过点()1,5D ,且交x 轴于A ,B 两点,交y 轴于点C ,已知点()1,0A -,(),P m n 是抛物线在第一象限内的一个动点,PQ BC ⊥于点Q .(1)求抛物线的解析式;(2)当PQ =m 的值;(3)是否存在点P ,使BPQ 与BOC 相似?若存在,请求出P 点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx +c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)求二次函数y=ax2+bx+c的表达式;(2)点P为线段AB上的动点,求AP+2PC的最小值;(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与①ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.8.如图,抛物线y=−x2+bx+c与x轴相交于A(−1,0),B(3,0)两点,与y轴交于点C,顶点为点D,抛物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求抛物线的函数关系式;(2)连结DA,求sin A的值;(3)若点H线段BC上,BOC与BFH△相似,请直接写出点H的坐标.9.如图,抛物线y=1-2x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与①OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点C ,设抛物线的顶点为D .(1)求该抛物线的表达式与顶点D 的坐标; (2)试判断BCD △的形状,并说明理由;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似?若存在,请求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2﹣2ax ﹣3a (a ≠0)与x 轴交于点A ,B .与y 轴交于点C .连接AC ,BC .已知ABC 的面积为2.(1)求抛物线的解析式;(2)平行于x 轴的直线与抛物线从左到右依次交于P ,Q 两点.过P ,Q 向x 轴作垂线,垂足分别为G ,H .若四边形PGHQ 为正方形,求正方形的边长;(3)抛物线上是否存在一点N ,使得①BCN =①CAB ﹣①CBA ,若存在,请求出满足条件N 点的横坐标,若不存在请说明理由.12.如图,二次函数2y x bx c =-++的图像与x 轴交于点A (-1,0),B (2,0),与y 轴相交于点C .(1)求这个二次函数的解析式;(2)若点M 在此抛物线上,且在y 轴的右侧.①M 与y 轴相切,过点M 作MD ①y 轴,垂足为点D .以C ,D ,M 为顶点的三角形与①AOC 相似,求点M 的坐标及①M 的半径长.13.如图,在平面直角坐标系中,抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .若线段OA OB OC 、、的长满足2OC OA OB =⋅,则这样的抛物线称为“黄金”抛物线.如图,抛物线22(0)y ax bx a =++≠为“黄金”抛物线,其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB =(1)求抛物线的解析式;(2)若P 为AC 上方抛物线上的动点,过点P 作PD AC ⊥,垂足为D . ①求PD 的最大值;①连接PC ,当PCD 与ACO △相似时,求点P 的坐标.14.如图,在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点A 、B 两点,其中1,0A ,与y 轴交于点()0,3C .(1)求抛物线解析式;(2)如图1,过点B 作x 轴垂线,在该垂线上取点P ,使得①PBC 与①ABC 相似,请求出点P 坐标;(3)如图2,在线段OB 上取一点M ,连接CM ,请求出12CM BM +最小值.15.如图,抛物线y =ax 2+k (a >0,k <0)与x 轴交于A ,B 两点(点B 在点A 的右侧),其顶点为C ,点P 为线段OC 上一点,且PC =14OC .过点P 作DE ①AB ,分别交抛物线于D ,E 两点(点E 在点D 的右侧),连接OD ,DC .(1)直接写出A ,B ,C 三点的坐标;(用含a ,k 的式子表示) (2)猜想线段DE 与AB 之间的数量关系,并证明你的猜想;(3)若①ODC =90°,k =﹣4,求a 的值.16.如图,抛物线223y x bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,连接AC ,已知B (﹣1,0),且抛物线经过点D (2,﹣2).(1)求抛物线的表达式;(2)若点E 是抛物线上第四象限内的一点,且2ABES=,求点E 的坐标;(3)若点P 是y 轴上一点,以P ,A ,C 三点为顶点的三角形是等腰三角形,求P 点的坐标.17.如图,在直角坐标系xOy 中,抛物线y =ax 2+bx +2(a ≠0)与x 轴交于点A (﹣1,0)和B (4,0),与y 轴交于点C ,点P 是抛物线上的动点(不与点A ,B ,C 重合).(1)求抛物线的解析式;(2)当点P 在第一象限时,设①ACP 的面积为S 1,①ABP 的面积为S 2,当S 1=S 2时,求点P 的坐标; (3)过点O 作直线l ①BC ,点Q 是直线l 上的动点,当BQ ①PQ ,且①BPQ =①CAB 时,请直接写出点P 的坐标.18.如图,在平面直角坐标系xOy中,直线y=﹣x+3与两坐标轴交于A、B两点,抛物线y=x2+bx+c 过点A和点B,并与x轴交于另一点C,顶点为D.点E在对称轴右侧的抛物线上.(1)求抛物线的函数表达式和顶点D的坐标;(2)若点F在抛物线的对称轴上,且EF①x轴,若以点D,E,F为顶点的三角形与①ABD相似,求出此时点E的坐标;(3)若点P为坐标平面内一动点,满足tan①APB=3,请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴交于点C,且OC=2OB=6OA=6,点P是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC与OP,交于点D,当S△PCD:S△ODC的值最大时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N.使①CMN=90°,且①CMN与①BOC 相似,若存在,请求出点M、点N的坐标.20.如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=,A点的坐标是,B点的坐标是;(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P 点在直线MN上运动.若恰好存在3个P点使得①P AC为直角三角形,请求出C点坐标,并直接写出P点的坐标.答案1.(1)y =﹣x 2+2x +3.(2)P 352或 (3)①ABN 的面积不变,为4.2.(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)4.(1)抛物线L 1:223y x x =--,抛物线L 2:2y x 2x 3=-++;(2)435(,)39M 或(4,5)M -.5.(1)254y x x =++(2)点B 的坐标为(-1,0)(3)点D 的坐标是(0,-203) 6.(1)215322y x x =-++ (2)1或5(3)存在;P (53,529)7.(1)抛物线表达式为:213222y x x =--+;(2)AP +2PC 的最小值是4;(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18),使得以点A 、M 、N 为顶点的三角形与ABC 相似.8.(1)y =-x 2+2x +3(3)点H 的坐标为(1,2)或(2,1)9.(1)21382y x x =++ (2)P 1(1,10.5),P 2(7,4.5)(3)存在,(3,8)或(3,5或(3,11)30.(1)y =﹣x 2﹣2x +3,(﹣1,4);(2)直角三角形,理由见解析;(3)存在,(0,0)或(0,﹣13)或(-9,0)11.(1)y =﹣13x 2+23x +1(2)﹣6﹣(3)存在,5或11712.(1)22y x x =-++; (2)M 的坐标为(12,94),(32, 54 ),(3,-4),①M 的半径长为12或32或313.(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28,-14.(1)243y x x =-+(2)P 点坐标为()3,9或()3,215.(1)点A 、B 、C 的坐标分别为(、、(0,k ) (2)DE =12AB(3)a =1316.(1)224233y x x =--(2)E ,-1)(3)P 点的坐标(0,2)或(02)或(0,﹣2或(0,54)17.(1)213222y x x =-++ (2)点P 的坐标为(103,139)(3)点P 的坐标为(32,﹣2)或(32,﹣2)或(173,﹣509)18.(1)y =x 2﹣4x +3,(2,﹣1)(2)(5,8)或(73,89-)(3)①P AB ,此时P )19.(1)y =﹣2x 2+4x +6 (2)点P 的坐标为(32,152) (3)存在,M 、N 的坐标分别为(3,0)、(0,﹣32)或(94,398)、(0,38)或(1,8)、(0,172)或(74,558)、(0,838)20.(1)﹣8,(2,0),(6,0)(2)3秒或212秒 (3)C 点坐标为(143,﹣329),P 点的坐标为(103,﹣4)或(﹣103,﹣4)或(11027,﹣4)。
2023年九年级中考数学专题复习:二次函数综合压轴题训练(相似三角形问题)(含答案)

②以点 为顶点的三角形与 相似,请直接写出符合要求的点 的坐标.
2.如图,抛物线 经过点 ,且交 轴于点 ,点 是 轴正半轴上的动点, 交抛物线于点 , 轴交线段 的延长线于点 ,作直线, 交 轴于点 ,交 轴于点
(1)求抛物线的解析式.
(3)如图3,在(2)的条件下,作 轴,点F在直线 下方的第一象限内,连接 、 ,若四边形 的面积为8,且 ,求P点的坐标.
4.在平面直角坐标系中,O为坐标原点,抛物线 与x轴的负半轴交于点A,与x轴的正半轴交于点B,与y轴交于点C.
(1)求点B的坐标;
(2)如图1,点P在第三象限的抛物线上,横坐标为m,BP交y轴于点D, 时,求a的值;
(3)在(2)的条件下, 的外接圆半径等于.(直接写答案)
11.如图,在平面直角坐标系 中,抛物线 与x轴的正、负半轴分别交于点B、A,与y轴交于点C,已知 , , .
(1)求该抛物线的表达式;
(2)设该抛物线的对称轴分别与x轴、 交于点E、F,求 的长;
(3)在(2)的条件下,联结 ,如果点P在该抛物线的对称轴上,当 和 相似时,求点P的坐标
7.如图1,直线 与x轴、y轴分别交于 、 两点,经过 、 两点的抛物线与x轴的另一交点坐标为 .
(1)求 、 两点的坐标及该抛物线所对应的函数关系式;
(2)P在线段 上的一个动点(与 、 不重合),过点P作直线 轴,交抛物线于点E,交x轴于点F,设点P的横坐标为m.
若点P的横坐标为m,请用m表示线段 的长度并写出m的取值范围;
16.如图1,平面直角坐标系中,抛物线 交 轴于 , 两点( 点在 点的右边),交 轴于点 .点 是线段 上一个动点,过点 作 轴的垂线,交抛物线于点E.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题14 巧解二次函数与相似三角形综合题【知识解读】点在二次函数图象上的运动,既能改变图形中线段与角的数量关系,还能改变图形的形状与位置,从而生成特殊三角形,特殊四边形,相似三角形,二次函数与相似三角形的结合是数形结合的重要表现形式,是各地中考十分常见的压轴方式.根据相似三角形的性质确定动点的位置是主要题型,把相似三角形的性质与点的坐标有机结合,点在运动过程中对不同的对应关系而进行讨论,是解这类题的关键.培优学案【典例示范】例1如图14-1,在平面直角坐标系中,四边形ABCD 是等腰梯形,AD ∥BC ,AB =DC ,BC 在x 轴上,点A 在y 轴的正半轴上,点A ,D 的坐标分别为A (0,2),D (2,2),AB =22,连接A C .(1)求出直线AC 的函数解析式;(2)求过点A ,C ,D 的抛物线的函数解析式;(3)在抛物线上有一点P (m ,n )(n <0),过点P 作PM 垂直于x 轴,垂足为M ,连接BPC ,使以点C ,P ,M 为顶点的三角形与Rt △AOC 相似,求出点P 的坐标.【提示】(1)由A 的坐标可以求得QA 的长,而AB 长已知,根据勾股定理可以求出OB 的长,则B 点的坐标可以知道.根据等腰梯形的轴对称性可得C 点坐标,然后把A 、C 坐标代入可以求出一次函数的解析式;(2)点A 、C 、D 的坐标都可以求得,根据待定系数法求值即可;(3)因为B (-2,0),C 点坐标为(4,0),所以需要分m >4,m <-2两种情况,另外由于边的不确定性,在相似时也应该分情况讨论.所以通过相似求值后需要验证所求得的值是否符合实际情况.值得注意的是:问题呈现形式“以点C ,P ,M 为顶点的三角形与Rt △AOC 相似”与“Rt △CMP ∽Rt △AOC ”是有很大区别的,后者有严格的对应关系,而前者则没有明确对应关系,往往需要对不同的xy图141CD OBA【解答】跟踪训练如图,在平面直角坐标系xOy 中,顶点为M 的抛物线y=ax 2+bx (a >0)经过点A 和x 轴正半轴上的点AO=BO=2,∠AOB =120°. (1)求这条抛物线的表达式; (2)连接OM ,求∠AOM 的大小;(3)如果点C 在x 轴上,且△ABC 与△AOM 相似,求点C 的坐标. 【提示】1.第(2)题把求∠AOM 的大小,转化为求∠BOM 的大小.2.因为∠BOM =∠ABO =30°,因此点C 在点B 的右侧时,恰好有∠ABC =∠AOM .3.根据夹角相等对应边成比例,分两种情况讨论△ABC 与△AOM 相似.【解答】例2 已知,经过点A (一4,4)的抛物线y=ax 2+bx+c 与x 轴相交于点B (-3,0)及原点O . (1)求抛物线的解析式;(2)如图1,过点A 作AH ⊥x 轴,垂足为H ,平行于y 轴的直线交线段AO 于点Q ,交抛物线于点P ,当四边形AHPQ 为平行四边形时,求∠AOP 的度数;yxMB OA(3)如图2,若点C 在抛物线上,且∠CAO =∠BAO ,试探究:在(2)的条件下,是否存在点G ,使得△GOP ∽△COA ?若存在,请求出所有满足条件的点G 坐标;若不存在,请说明理由.【提示】对于(3),P (-2,-2),A (-4,4)隐含了什么关系?条件∠CAO =∠BAO 怎样运用?如何将△GOP ∽△COA 转化为相似三角形的基本图形?点G 的位置能否大致确定?这是解决问题的关键.应综合利用几何变换和相似关系求解.方法一:翻折变换,将△AOC 沿x 轴翻折;方法二:旋转变换,将△AOC 绕原点顺时针旋转90°.特别注意求出P 点坐标之后,该点关于直线y=x 的对称点也满足题意,即满足题意的P 点有两个,避免漏解.通过几何变换,构造基本相似形,化一般为特殊,使得点G 得以定位,提高解题的境界. 【解答】如图1,平面直角坐标系中,抛物线y=ax 2+bx+4经过点D (2,4),且与x 轴交于A (3,0),B 两点,与y 轴交于点C ,连接AC 、CD 、BC . (1)直接写出该抛物线的解析式;图 1 图 2CABOyxx yH QPOBA(2)如图2,点P 是所求抛物线上的一个动点,过点P 作x 轴的垂线l ,l 交x 轴于点E ,交直线AC 于点M .设点P 的横坐标为m .①当0<m ≤2时,过点M 作MG ∥BC ,MG 交x 轴于点G ,连接GC ,则m 为何值时,△GMC 的面积取得最大值?并求出这个最大值;②当-1<m ≤2时,试探求:是否存在实数m ,使得以P 、C 、M 为顶点的三角形和△AEM 相似?若存在,求出相应m 的值;若不存在,请说明理由.【提示】(1)将D (2,4)、A (3,0)代入y=ax 2+bx+4,得关于a 、b 的方程组,解方程组即可;(2)求出直线AC 的解析式为y=43-x+4,用m 的代数式表示出P 点、E 点、M 点的坐标,证△COB ∽△MEG 得OB GE OC ME =,求出GE =13-m +1,所以AG =OA -OG =3-(43m -1)=43-m +4,最后将各代数式代入S △GMC =S △CGA -S △MGA =12OC ·AG -12ME ·AG ,得S △GMC 关于m 的二次函数,配方求最值;(3)先得∠AME =∠PMC ,然后相似只需分两种情况讨论. 【解答】例3 如图,抛物线y=-x 2+2x +3与x 轴交于A 、B 两点,与y 轴相交于点C ,顶点为点D ,抛物线的对称轴DF 与BC 相交于点E ,与x 轴相交于点F . (1)求线段DE 的长;(2)设过点E 的直线与抛物线相交于点M (x 1,y 1),N (x 2,y 2),试判断|x 1-x 2|的值最小时,直线MN 与x 轴的位置关系,并说明理由.图 1 图 2O yxl PMEGDCB A yxO DCB A(3)设点P 为x 轴上一点,∠DAO +∠DPO =∠α,当tanα=4时,求点P 的坐标.【提示】(1)令二次函数值为零或是x 为零可求出抛物线与坐标轴的交点,并求出直线BC 的解析式,进而求出ED 的长度;(2)要用一元二次方程根与系数的关系求抛物线上两点之间的距离;(3)巧妙的做法是利用直角△DOF 中,tan ∠DOF =4来构造相似三角形,从而使问题得以解决. 【解答】跟踪训练如图,在平面直角坐标系中,点O 为坐标原点,直线y=-x +4与x 轴交于点A ,过点A 的抛物线y=ax 2+bx 与直线y =-x +4交于另一个点B ,且点B 的横坐标为1. (1)求a 、b 的值;yxF ECDB O A(2)点P 是线段AB 上一个动点(点P 不与点A 、B 重合),过点P 作PM //OB 交第一象限内的抛物线于点M ,过点M 作MC ⊥x 轴于点C ,交AB 于点N ,过点P 作PF ⊥MC 于点F .设PF 的长为t ,MN 的长为d ,求d 与t 之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,当S △ACN =S △PMN 时,连接ON ,点Q 在线段BP 上,过点Q 作QR //MN 交ON 于点R ,连接MQ 、BR ,当∠MQR -∠BRN =45°时,求点R 的坐标.【提示】(1)先求A 、B 两点坐标,将其代入抛物线的解析式,联立成关于a 、b 的二元一次方程组,解之即可得到a 、b 的值.(2)作BD ⊥x 轴于点D ,延长MP 交x 轴于点E .由A (4,0)、B (1,3),得OD =1,BD =3,OA =4,AD=BD=3,再根据等腰直角三角形及对顶角,知NF=PF=t .再根据相似三角形的判定,得△MPF ∽△BOD ,3MF BDPF OD==,从而MF=3t ,最后由MN=MF+FN ,得到d =4t . (3)解决本题应按四步走:①根据S △ACN =S △PMN ,探究AC 与t 的数量关系为AC =2t ,从而OC =4-2t ,MC =6t ,求出M (4-2t ,6t );②将M (4-2t ,6t )的坐标代入抛物线y =-x 2+4x ,得到关于t 的一元二次方程,解得t =12,从而PF=FN=12,AC=CN =1,OC =3,MF =32,PN =22,PM =102,AN =2,BN =22RH=n ,由tan ∠HNR =tan ∠NOC 得13RH CN HN OC ==,从而HN=3n ,再通过∠MQR -∠BRN =45°,及等腰三角形的判定及性质、平行线的性质证明△PMQ ∽△NBR ;④由相似形性质得到PQ PMRN BN=,从而得到n 的值. 【解答】 A BO xyyx FP NMOC BA4 如图,已知抛物线y =14x 2-14(b +1)x +4b(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 是左侧),与y 轴的正半轴交于点C .1)点B 的坐标为 ,点C 的坐标为 (用含b 的代数式表示);2)请你探索在第一象限内是否存在点P ,使得四边形PCOB 的面积等于2b ,且△PBC 是以点P 为直角顶点的等腰直角三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由;3)请你进一步探索在第一象限内是否存在点Q ,使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.【提示】对于(2),先假设存在这样的点P ,使得四边形PCOB 的面积等于2b ,且△PBC 是以点P 为直角顶点的等腰直角三角形,暗示了点P 到两坐标轴的距离相等。
设点P 的坐标为(x ,y ),连接OP ,过P 作x 轴,PE ⊥y 轴,垂足分别为D 、E ,利用已知条件证明△PEC ≌△PDB ,进而求出x 和y 的值,从而P 的坐标;对于(3),要探究三个三角形两两相似,第一直觉是这三个三角形是直角三角形,点Q 最大的可能是在经过点A 与x 轴垂直的直线上.假设存在这样的点Q ,使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似,由条件可知:要使△QOA 与△QAB 相似,只能∠QAO =∠BAQ =90°,即QA ⊥x 轴;要使△QOA 与△OQC 相似,只能∠QCO =90°或∠OQC =90°,再分别讨论求出满足题意的Q 的坐标即可. 【解答】 yxPC BAO跟踪训练如图,直线y=kx+b (b >0)与抛物线y =218x 相交于A (x 1,y 1),B (x 2,y 2)两点,与x 轴正半轴相交于点D ,与y 轴相交于点C .设△OCD 的面积为S ,且kS +32=0. (1)求b 的值;(2)求证:点(y 1,y 2)在反比例函数y=64x的图象上; (3)求证:x 1·OB +y 2·OA =0.【提示】(1)把△OCD 的面积S 用含k 、b 的代数式表示; (2)寻找y 1与x 1,y 2与x 2的关系,然后证明y 1y 2=64;(3)分别过点A 和点B 作AE ⊥x 轴,BF ⊥x 轴,垂足分别为E 、F ,证明△AEO ∽△OFB . 【解答】例5 (全国初中数学竞赛)如图14-9,点A 为y 轴正半轴上一点,A ,B 两点关于x 轴对称,过点A 任作直线l 交抛物线22x y于P ,Q 两点. yxO D CBA(1)求证:∠ABP=∠ABQ;(2)若点A 的坐标为(0,1),且∠PBQ=60°,试求所有满足条件的直线 PQ 的函数解析式. 【提示】(1)分别过点P ,Q 作y 轴的垂线,垂足分别为C ,D.证明△BCP∽△BDQ,得∠ABP=∠ABQ; (2)通过△ACP∽△ADQ,得到点Q 的坐标,即可求出直线PQ 的解析式。
