基于Matlab可视化界面的单缝衍射仿真分析

合集下载

基于MATLAB的光学实验模拟

光学模拟计算实验报告班级：物理学122班姓名：学号：实验目的：利用MATLAB软件编程实现了用衍射积分的方法对单缝衍射、杨氏双缝干涉、黑白光栅衍射的计算机模拟；以及用傅立叶变换方法对简单孔径衍射、黑白光栅及正弦光栅夫琅和费衍射的模拟。

实验仪器及软件：MATLAB；衍射积分；傅立叶变换；计算机模拟实验原理：大学教学课程中引入计算机模拟技术正日益受到重视，与Basic、C和Fortran相比，用MA TLAB软件做光学试验的模拟，只需要用数学方式表达和描述，省去了大量繁琐的编程过程。

下面来介绍利用MATLAB进行光学模拟的两种方法。

（一）衍射积分方法：该方法首先是由衍射积分算出接收屏上的光强分布，然后根据该分布调制色彩作图，从而得到衍射图案。

1．单缝衍射。

把单缝看作是np个分立的相干光源，屏幕上任意一点复振幅为np个光源照射结果的合成，对每个光源，光程差Δ=ypsinΦ,sinΦ=ys/D,光强I=I0(Σcosα)2+(Σsinα)2，其中α=2Δ/λ=πypys/λD编写程序如下，得到图1lam=500e-9;a=1e-3;D=1;ym=3*lam*D/a;ny=51;ys=linspace(-ym,ym,ny);np=51;yp=linspace(0,a,np);for i=1:nysinphi=ys(i)/D;alpha=2*pi*yp*sinphi/lam;图1 单缝衍射的光强分布 sumcos=sum(cos(alpha));sumsin=sum(sin(alpha));B(i,:)=(sumcos^2+sumsin^2)/np^2;endN=255;Br=(B/max(B))*N;subplot(1,2,1)image(ym,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys); 2．杨氏双缝干涉两相干光源到接收屏上P 点距离r 1=(D 2+(y-a/2)2)1/2, r 2=(D 2+(y+a/2)2)1/2,相位差Φ=2π（r 2-r 1）/λ,光强I=4I 0cos 2（Φ/2）编写程序如下，得到图2 clear lam=500e-9 a=2e-3;D=1;ym=5*lam*D/a;xs=ym;n=101;ys=linspace(-ym,ym,n); for i=1:nr1=sqrt((ys(i)-a/2).^2+D^2); r2=sqrt((ys(i)+a/2).^2+D^2); phi=2*pi*(r2-r1)./lam;B(i,:)=sum(4*cos(phi/2).^2); end N=255;Br=(B/4.0)*Nsubplot(1,2,1) image(xs,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys) 3．光栅衍射公式：I=I 0（sin α/α）2（sin(λβ)/sin β）2α=(πa/λ)sin Φ β=(πd/λ)sin Φ编写程序如下：得到图3clearlam=500e-9;N=2; a=2e-4;D=5;d=5*a; ym=2*lam*D/a;xs=ym; n=1001;ys=linspace(-ym,ym,n); for i=1:nsinphi=ys(i)/D;alpha=pi*a*sinphi/lam; beta=pi*d*sinphi/lam;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2; B1=B/max(B);end图2 杨氏双缝干涉的光强分布图3 黑白光栅衍射光强分布NC=255;Br=(B/max(B))*NC; subplot(1,2,1) image(xs,ys,Br); colormap(gray(NC)); subplot(1,2,2) plot(B1,ys);（二）傅立叶变换方法：在傅立叶变换光学中我们知道夫琅和费衍射场的强度分布就等于屏函数的功率谱。

衍射的Matlab 模拟

10
二、菲涅耳－基尔霍夫衍射公式（确定了C、K()) 基尔霍夫 (Kirchhoff) 从波动方程出发，用场论得出了比较严格的衍射公式。
A expik l expik r cosn, r cosn, l E P ＝ d i l r 2
菲涅尔假设：当 = 0 时，K()=Max, p/ 时，K()=0.
（实验证明是不对的）若S发出的光源振幅为A（单位距离处）,整个波面’的贡献
CA expikr ~ E P expikR K d R r
求解此公式主要问题：C、K()没有确切的表达式。
设
l
x sin x , f
a b
m
y sin y f
~ E x, y C 2a 2b exp ik lx1 my1 dx1 dy1
2 2
28
~ E x, y C 2a 2b exp ik lx1 my1 dx1 dy1
2 2
P0 E
17
r z1
2 2 x x1 y y1
2 z1
称为菲涅耳近似。
得到菲涅耳衍射：
e ikz1 ~ E x, y iz1

k ~ 2 2 E x1 , y1 exp i x x1 y y1 2 z1 y y
~ 和E0 abC
则
~ ~ sin sin E x, y E0
子波的复振幅与 cosn, r cosn, l 2 成正比，与波长成反比。 K ( )
1 p i exp[ i ] i 2 表示子波的振动位相超前于入射波90。
12
当光线接近于正入射时

基于Matlab-GUI的衍射图像分析

ＡｂｔａｔｓｒｃＡｎｌｓｎｉｒｃｉｎｉｇｓｈｓｇｅｔｓｎｆａｃｏｔｅｒｓａｃｆｍａｔｒｓｍｉｒｓｕｔｒ，ｎｈｕｌｔｏｅｄｆａｔｎａｙｉｇｄｆａｔｍａｅａｒａｉｉｃｎｅｔｈｅｅｒｈｏｔ ’ ｅｏｔｃｕｅａｄｔｅｑａｉｆｔｉｒｃｉｆｏｇｉｅｒｙｈｆｏ
Ｔｈｅｐｉｃｐｅｏｈｏｒｅｒｉｓｉｅａｅ，ａｅ，ｏｅｓｏｈｅｅｐｅｉｎｏｅｈｅｔｈｎｌｓｓｒｓｔｒｎｒｄｃｄｉｈａｅ．ｔｒｎｉｌｆｔｅｃｕｓｗａｅ，ｔｎｔｒｃｕｓｇｐｒｃｓｆｔｘｒｍｅｔｔｇｔｒｗｉｈｔｅａａｙｉｅｕｌｓａｅｉｔｏｕｅｎｔｅｐｐｒＩｆ
ｉｇｓｈｓｄｒｃｅａｉｎｔｈｅａｉｆｈｅｅｒｈＩｈｓｐｐｒｈｉｒｃｉｎｉｇｎｌｓｓｉｒａｉｅｔｔｂＧＵＩｒｇａｍａｅａｉｔｌｔｔｅｖｒｃｔｏｅｒｓａｃ．ｎｔｉａｅｅｄｆａｔｅｒｏｏｙｔｔｆｏｍａｅａａｙｉｓｅｌｄｗｉＭａｌ — ｓｈａｏｒｍｍｉｇｐｎ．
ｔｅｒｔｃｌｏｅ．ｈｏｅｉａｎｓ
Ｋｅｗｏｄｓｙｒ
ＤｆａｔｎＩｇｎｌｓｓＭａｌｈＧａｈｃｌｕｅｎｅｒｃＧＵＩｉｒｃｉｍａｅａａｙｉｆｏｔｒｐｉａｓｒｉｔｒａｅ（ａ）

基于matlab的衍射系统仿真 -

成绩：《工程光学》综合性练习二题目：基于matlab的衍射系统仿真学院精密仪器与光电子工程学院专业测控技术与仪器年级20**级班级**班姓名20**年**月综合练习大作业二一、要求3-4人组成小组，对下面给出的各题目利用Matlab等工具进行仿真。

练习结束时每组提交一份报告及仿真程序。

在报告中应注明各仿真结果所对应的参数，如屏与衍射屏间距、孔径形状尺寸等。

二、仿真题目1.改变观察屏与衍射屏间距，观察观察屏上发生的衍射逐渐由菲涅耳衍射转为夫琅和费衍射1)原理图：S点光源发出的波长lam=500纳米S点发出光线经过单缝，缝宽a；单缝到衍射屏的距离L'2)Matlab代码clear;clcl=10;%l=input('单缝到衍射屏的距离L=');a=0.2;%a=input('单缝的宽度(mm)a=');lam=500e-6;%lam=input('波长(nm)');x=-1:0.001:1;%接收屏边界y=x./sqrt(x.^2+l^2);z=a.*y/lam;I=1000*(sinc(z)).^2;%计算接受屏某点光强subplot(2,1,1)%绘制仿真图样及强度曲线image(2,x,I)colormap(gray(3))title('单缝衍射条纹')subplot(2,1,2)plot(x,I)title(光强分布)3)初始仿真图样（d=10）4)改变d之后的图样(d=1000)5)变化规律根据衍射屏以及接受屏的相对位置不同，由此产生菲涅尔衍射和夫琅禾费衍射的区别，根据我们模拟的情况得到菲涅尔衍射和夫琅禾费衍射的明显不同是夫琅禾费衍射条件下：中央有一条特别明亮的亮条纹，其宽度是其他亮条纹的两倍；其他亮条纹的宽度相等，亮度逐渐下降。

2.改变孔径形状、尺寸，观察图样变化1）原理图矩孔衍射：透镜焦距：1000mm;照射光波长：500nm;孔高：a（mm）；孔宽：b（mm）；圆孔衍射：圆孔直径：r（mm）；照射光波长：500nm;照射光波长：500nm;2）matlab代码矩孔衍射：focallength=1000;lambda=500;a=2.0;b=2.0;resolution=64;center=(resolution)/2;A=zeros(resolution,resolution);for i=1:1:resolutionfor j=1:1:resolutionif abs(i-center)<a*10/2&abs(j-center)<b*10/2 A(j,i)=255;endendendE=ones(resolution,resolution);k=2*pi*10000/focallength/lambda;imag=sqrt(-1);for m=1:1:resolutionx=m-center;for n=1:1:resolutiony=n-center;C=ones(resolution,resolution);for i=1:1:resolutionp=i-center;for j=1:1:resolutionq=j-center;C(j,i)=A(j,i)*exp(-imag*k*(x*p+y*q)); endendE(n,m)=sum(C(:));endendE=abs(E);I=E.^2;I=I.^(1/3);I=I.*255/max(max(I));L=I;I=I+256;CM=[pink(255).^(2/3);gray(255)];Colormap(CM);edge=(resolution-1)/20;[X,Y]=meshgrid([-edge:0.1:edge]);x=linspace(-edge,edge,resolution);y=linspace(-edge,edge,resolution);subplot(1,2,1);surf(x,y,L);axis([-edge,edge,-edge,edge,0,255]);caxis([0,511]);subplot(1,2,2);image(x,y,I);axis([-edge,edge,-edge,edge,0,511]);view(2);axis square;圆孔衍射：clearlmda=500e-9;%波长r=1.2e-3;%f=1;%焦距N=19;K=linspace(-0.1,0.1,N);lmda1=lmda*(1+K);xm=2000*lmda*f;xs=linspace(-xm,xm,2000);ys=xs;z0=zeros(2000);[x,y]=meshgrid(xs);for i=1:19s=2*pi*r*sqrt(x.^2+y.^2)./(lmda1(i));z=4*(besselj(1,s)./(s+eps)).^2;%光强公式z0=z0+z;endz1=z0/19;subplot(1,2,1)imshow(z1*255);%平面图xlabel('x')ylabel('y')subplot(1,2,2)mesh(x,y,z1)%三维图colormap(gray)xlabel('x')ylabel('y')zlabel('光强')3）仿真图样：矩孔衍射：a=1，b=2a=2，b=2可知：矩孔在一个维度上展宽一定倍数将导致衍射图样在相同维度上缩短相同倍数，同时能量会更向中心亮斑集中。

matlab作业(衍射实验)

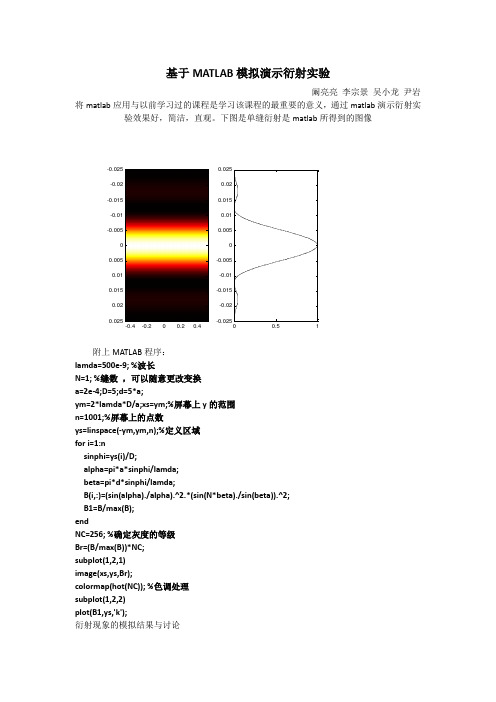
基于MATLAB 模拟演示衍射实验阚亮亮李宗景吴小龙尹岩将matlab 应用与以前学习过的课程是学习该课程的最重要的意义，通过matlab 演示衍射实验效果好，简洁，直观。

下图是单缝衍射是matlab 所得到的图像-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025附上MATLAB 程序：lamda=500e-9; %波长N=1; %缝数，可以随意更改变换a=2e-4;D=5;d=5*a;ym=2*lamda*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:nsinphi=ys(i)/D;alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;B1=B/max(B);endNC=256; %确定灰度的等级Br=(B/max(B))*NC;subplot(1,2,1)image(xs,ys,Br);colormap(hot(NC)); %色调处理subplot(1,2,2)plot(B1,ys,'k');衍射现象的模拟结果与讨论在实验时改变N的值可以得到单缝以及多缝衍射的输出结果，并可以得到这样的结论:(1)当入射光波长一定时,单缝宽度a越小,衍射条纹越宽,衍射现象越显著;(2)单缝越宽,衍射越不明显,单缝宽度逐渐增大,衍射条纹越来越窄;(3)当缝宽a>>λ时,各级衍射条纹向中央明纹靠拢,而无法分辨,这时衍射现象消失。

结束语利用MATLAB对抽象物理现象进行计算机仿真时,首先必须对物理过程进行数学抽象,建立适合程序实现的数学模型,其次利用MATLAB软件包中的有关工具编制m文件,最后对物理过程和物理现象进行模拟,从而可以把抽象的物理问题进行简明、直观的动态展现。

基于MATLAB的矩孔、单缝、圆孔夫琅和费衍射概诉

课程设计任务书学生姓名：专业班级：指导教师：工作单位：信息工程学院题目: 夫琅和费矩孔、单缝、圆孔衍射图样一、设计目的了解MA TLAB软件的基本知识，基本的程序设计，软件在高等数学和工程数学中的应用，学会使用软件进行数值计算和控制工程中的应用。

二、设计内容和要求1．绘制弗朗禾费矩孔、单缝和圆孔衍射图样，可以是二维的或三维的，也可以两种都有。

改变矩孔、单缝和圆孔的参数，比较衍射条纹的变化。

2. 学习Matlab语言的概况和Matlab语言的基本知识。

3．学习Matlab语言的程序设计。

三、初始条件计算机；Matlab软件。

四、时间安排1、2015年01月19日，任务安排，课设具体实施计划与课程设计报告格式的要求说明。

2、2015年01月20日，查阅相关资料，学习Matlab语言的基本知识，学习MATLAB语言的应用环境、调试命令，绘图功能函数等。

3、2015年01月21日至2015年01月22日，Matlab课程设计制作和设计说明书撰写。

4、2015年01月23日，上交课程设计成果及报告，同时进行答辩。

指导教师签名：2015年01 月19日系主任（或负责教师）签名：2015年01 月19日目录摘要 (I)1.设计的内容及要求 (1)1.1设计的目的 (1)1.2设计任务要求 (1)2.设计原理及设计思路 (1)2.1夫琅和费干涉理论 (1)2.1.1夫琅和费圆孔衍射 (2)2.1.2夫琅和费矩孔衍射 (2)2.1.3夫琅和费单缝衍射 (2)2.2设计思路 (3)3.仿真及分析 (4)4.心得和体会 (8)参考文献 (8)摘要物理光学理论较为复杂抽象，实验现象的演示对条件要求高。

采用MATLAB7.0强大的函数作图功能对矩孔、单缝、圆孔的夫琅和费衍射进行模拟,建立直观形象并且精确完整的理论模型,并附上程序代码,将干涉理论联系起来,分析衍射和干涉的本质。

从而加深对夫琅和费原理、概念、和图像的理解。

通过使用MATLAB编写程序，不仅理解了物理思想，而且了解了运用软件解决物理问题的方法。

Matlab演示夫琅禾费单缝衍射强度分布

Matlab演示夫琅禾费单缝衍射强度分布作者：王晶宜等来源：《科学与财富》2015年第27期摘要：研究单缝夫琅禾费衍射条纹强度分布及各参量之间的关系是光学领域非常重要的研究内容。

本文基于光的衍射理论，用Matlab软件程序实现了单缝夫琅禾费衍射中各相关参量之间的关系，并可视化不同缝宽和不同入射波长条件下的衍射条纹强度分布。

关键词：Matlab；单缝夫琅禾费衍射；衍射强度分布1.引言鉴于夫琅禾费单缝衍射的物理规律较为抽象、难以理解及数学表达式求解复杂、耗费时间，故利用MATLAB软件进行仿真演示，实现数据及物理现象的可视化，促进对物理规律更深层次的理解。

遵循MATLAB平台程序设计特性，编制MATLAB平台正确运行的程序。

需要的软件运行环境也很简单：1、硬件平台：计算机处理器主频要求为528MHz 以上；2、内存要求256MB RAM 以上；3、软件平台：操作系统：Windows XP Professional Edition；4、编程平台：MATLAB R2009a。

2.夫琅禾费单缝衍射理论与MATLAB编程障碍物、孔或缝的大小与波长相当是，光通过这一障碍物时，其后空间会发生光的衍射，衍射屏上能接收到有规律光强分布的衍射条纹。

按照光源、障碍物和观察屏三者的位置关系，障碍物到光源和观察屏距离为无限远的，称为夫琅禾费衍射，属于远场衍射，它的分析计算比较简单，同时又有很多实际应用。

衍射光强分布公式为：（1）其中中间因子u为：（2）a=8e-6；lambda=5e-7；theta=（-0.1*pi：0.00001：0.1*pi）；u=pi*a*sin（theta）./lambda；I=sinc（u）.^2；根据可得描述次级条纹的超越方程：（3）k=3；um=（k+1）*pi；uu=linspace（0，um，1000）；figureplot（[0；um]，[0；0]，uu，uu，'k'）hold onplot（uu，tan（uu），'LineWidth'，2）不同缝宽的单缝夫琅禾费衍射强度与衍射角关系曲线及干涉条纹可视化 lambda=400e-9；a1=0.001*1e-3；a2=0.01*1e-3；theta=（-0.1*pi：0.00001：0.1*pi）；u1=pi*a1/lambda.*sin（theta）；u2=pi*a2/lambda.*sin（theta）；I1=sinc（u1）.^2；I2=sinc（u2）.^2；figureColorMap（[r，r*0，r*0]）image（I1*3000）axis off3. 总结基于光的衍射理论，计算单缝夫琅禾费衍射中各相关参量之间的关系，具体包括超越方程u=tanu求解，衍射相对光强与中间因子u的关系，不同缝宽条件下的衍射光强，不同入射波长的单缝夫琅禾费衍射强度与衍射角的关系，最后可视化不同颜色的衍射条纹。

Matlab数字衍射光学实验讲义(一)

5
2015 级光电工程专业综合实验-信息光学专题实验
imagesc(z) figure(2) mesh(z) %%---------------------matlab 代码-------------------------
改变参数 a，b 的取值，观察模拟结果变化。 4）第一类贝塞尔函数 besselj（v,z）
1. 实验目的:
掌握基本的 Matlab 编程语言，了解其编程特点；模拟几种常用函数，了解其编程过程及图像显示命令函数，掌握 Matlab 画图方法；通过设计制作一系列光学研究物体掌握其编程方法；掌握光波的 matlab 编程原理及方法，初步了解 Matlab
2
2015 级光电工程专业综合实验-信息光学专题实验
4

2015 级光电工程专业综合实验-信息光学专题实验
figure(4) surfl(x,y,z)%三维 %%---------------------matlab 代码-------------------------
改变变量 a，b 观察模拟图像变化。
x 2 x 3）高斯函数：一维高斯函数 Gauss exp a a
二维高斯函数： sinc
x y x y , sinc sinc ，a，b 为正数。 a b a b
2 2 x y x y x y Gauss , Gauss Gauss exp a b a b a b
二维 sinc 函数： sinc
x y x y , sinc sinc ，a，b 为正数。 a b a b
%%---------------------matlab 代码------------------------clear %清除内存 close all %关闭所有窗口 [x,y] = meshgrid(-2:.05:2, -2:.05:2); %设置二维网格 z=sinc(x).*sinc(y); %sinc 函数 figure(1) imshow(z) %二维灰度图 figure(2) imagesc(z) %二维彩色 figure(3) mesh(z)%三维

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

［６］ＧｌａｅＳ，ｉａ．ｌｏｌｒｅｃｎｅｕ￣ｒｉ［］／ｏｗｓｒＫｌＡｍｓａｉｓａｉｙｃｔｅＣ／ｄｓｌＪｉｔｌｐｍｂｑｃｅｉｄｆ
．
件的点，Ｋ算法失效，Ｇ由此得知本算法有一定的实际应用的价
值，以上定理相吻合。与
ｒｌ）ｌＰ十１＋２ ≤ （＋１ ≤ 帖（ ≤ ）
≤ （／＋１＝（＋１￣））
与假设矛盾，即证。
４结
＋曰
语
定理３设ｎ为大于３的整数，Ａ，ａｂａ均为模ｎ的有Ｂ，，，整数，ｂ为整数，得（，），使ａｂ为椭圆曲线Ｅ：。；Ｙ＋（ｏ）ｏｒｄｎ上阶为ｒ的点，（ｂ）点ａ，为椭圆曲线Ｅ：Ｙ＋４』＋
Ｈｓｅ理有：ａｓ定
来判断阶的时候，现很容易找到满足条件的点（４７）发９，３阶为
３（１阶的点有很多个）又存在阶为４的点（６８１４）即可１３，（２，２，
以判定９１拟素数，７为而用ｒ＞（彳ｎ１＋１ｚ一４３，有满足条）３没
那么如果ｒ为素数，ｎ为拟素数。则
证明
（）椭圆曲线的素性检验都需要构造ｚ２／ｚ上的椭圆曲
１
假设ｎ至少可分解为三个互不相同的素因子之积，
线，满足＞（亍＋１，１常大时，也需要非常大，ｎ）当７，非ｒ要寻
第７期
吴长虹等：于椭圆曲线的拟素数检验方法基
２３９
上的阶为ｒ，点由于ｒ是素数，以（，）在Ｅ上的阶仍然为ｒ所ａｂ，
其点对定义的运算构成Ａｅ群，中的点数＃Ｅ（）即为ｂｌ群（Ｆ）群的阶，由有限群中的Ｌｇｎｅ定理有ｒ把），ａｒｇａｌ（再根据
点（ｂ）的阶为４并且ｇｄｂ，＝ｌ所以有ｇｄｂ，）＝１ａ，ｃ（ｎ），ｃ（Ｐ
，
（）由以上可知此算法对所有的输入都可以在多项式时间３
内完成测试。本定理虽然未确定ｎ是否是素数，有一定的局限性，但是条件更广，使用范围更大，更容易应用在强伪素数的环境中，如果拟素数是两个足够大的素数之积，则恰好可以用在当今热门的ＲＡ系统中。Ｓ
砷ｌ
上的点，由于ｒ是素数，（，）在Ｅａ６上的阶仍然为ｒ该点对定，义的加法运算构成Ａｅ群，中的点数舟Ｅ（）即为群的ｂｌ群（。Ｆ）
放大ｒ至＞（＋１以后，ｎ）即为ＧＫ定理。
阶，根据有限群中的Ｌｇａｇ定理，ｒ＃ｐＦ），再ａｒｎｅ有Ｅ（ｐ又因为Ｉ
即不存在１阶和２阶的点，则必有４ＩＥ（ｐ再有Ｈａｓ＃ｐＦ），ｓｅ定
理有：
４ ≤ＩＥ（ｌｒ＃ｐＦ） ≤Ｐ十２ｐ＋１≤ （ｐ＋１ √ √ ）
≤ （／＋１￣）＝（＋１）
即，≤ 与假设矛盾，证毕。
—
参
中国科技大学，０８２０．
［５］卢开澄．计算机密码学［．Ｍ］３版．北京：华大学出版社，０８：清２０
１１—２４．８ｏ
证明若ｎ不是素数，ｎ在一个素因子ＰＰ≤ 则存且，点
（，）为椭圆曲线Ｅ：ｎｂ。ｙ２＋Ａｘ＋ＢｒｄＰ（ｏ）上的点，ｏ因为ｒ
１．４８
考
文
献
［１］裴定一，跃飞．法数论［．京：学出版社，０２１１祝算Ｍ］北科２０：２
推论１设，为大于３的整数，Ｂ，，，ｂ均为模ｒＡ，ａｂａ，的整数，得点（，）为椭圆曲线Ｅ：＝使ａｂＹ＋＋Ｂｍｄｎ（ｏ）上的点，（ｂ）点ａ，为椭圆曲线Ｅ：一＋ｘ＋ＢｍｄｎＹ。Ａ（ｏ）的阶为４的点，ｇｄ且ｃ（则１素数。１，为），：１如果有，＞且，为素数，
１ｌ
由定理１可知存在素数Ｐ且Ｐ≤ ，对于（，）是椭圆曲线：ｏｂ
：三ｙ＋Ａ＋Ｂ（ｏ）ｏｒｄｎ
找到阶数如此大的点显然不容易，当缩小ｒ＞（寺＋１＞（言ｎ）ｎ
１
－
ｉ
４）－＞÷ （言＋１。１ｎ）以后，显然更容易找到满足条件的点。当
，
（）Ｇｌｗｓｅ— ｉａ１ｏｄａｓｒｌｎ定理并非充分必要条件，Ｋｉ即如果没
有找到一个满足条件的点时，无法判断ｎ是否是素数，具有一定的盲目性，而本定理可以更容易找到符合条件的点，而做，）１＞ ÷ （。的为４点，ｃ６：和，笪ｄ，
［２］陈恭亮．信息安全数学基础［：京：Ｍ］北清华大学出版社，０４２０：
１３—１４．３３
［３］冯登国，裴定一．密码学导引［．京：学出版社，１９６Ｍ］北科９９：１
—
６９．
［４］于飞．对于有限域上椭圆曲线的一些算术问题的研究［．Ｄ］北京：