基于MATLAB的汽车减震系统仿真建模
基于MATLAB的汽车悬架减振器检测台仿真分析

基于MATLAB的汽车悬架减振器检测台仿真分析
刘圣田;吕安涛;武洪恩
【期刊名称】《山东交通学院学报》
【年(卷),期】2002(010)003
【摘要】在已有研究的基础上给出了悬架减振器性能检测试验台的工作原理、结构和检测标准,建立了悬架减振器检测时车-台振动系统的3自由度模型,应用MATLAB进行了系统的仿真和分析,为减振器性能检测台设计提供了依据.
【总页数】5页(P18-21,28)
【作者】刘圣田;吕安涛;武洪恩
【作者单位】山东交通学院,汽车工程系,山东,济南,250023;山东交通学院,汽车工程系,山东,济南,250023;山东科技大学,动力与控制工程学院,山东,济南,250023
【正文语种】中文
【中图分类】U472.9
【相关文献】
1.汽车悬架减振器和弹性元件的计算机仿真分析的教学应用 [J], 黎孟珠;莫秋云;冯次联
2.基于Adams和Matlab联合的汽车悬架系统仿真分析 [J], 彭京奕
3.基于ANSYS的汽车悬架减振器空心活塞杆的质量研究 [J], 李明杰;
4.基于ANSYS的汽车悬架减振器空心活塞杆的质量研究 [J], 李明杰
5.基于ADAMS和MATLAB的汽车悬架系统仿真分析 [J], 韩朝晖
因版权原因,仅展示原文概要,查看原文内容请购买。
基于MATLAB的汽车平顺性的建模与仿真
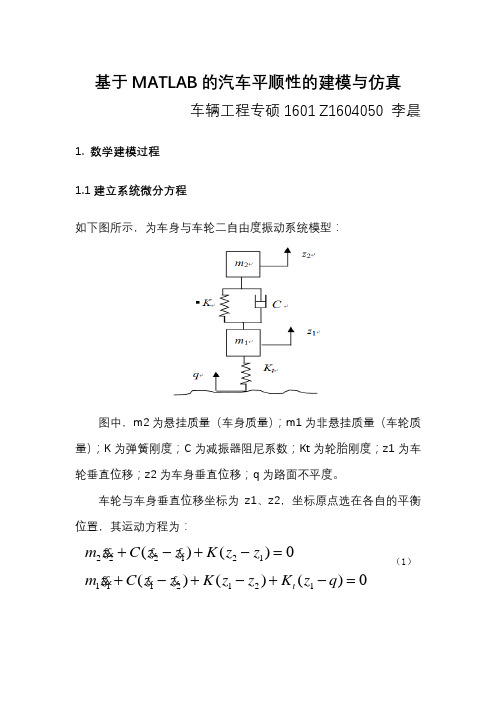
基于MATLAB 的汽车平顺性的建模与仿真车辆工程专硕1601 Z1604050 李晨1. 数学建模过程 1.1建立系统微分方程如下图所示,为车身与车轮二自由度振动系统模型:图中,m2为悬挂质量(车身质量);m1为非悬挂质量(车轮质量);K 为弹簧刚度;C 为减振器阻尼系数;Kt 为轮胎刚度;z1为车轮垂直位移;z2为车身垂直位移;q 为路面不平度。
车轮与车身垂直位移坐标为z1、z2,坐标原点选在各自的平衡位置,其运动方程为:222121()()0m z C z z K z z +-+-=1112121()()()0t m z C z z K z z K z q +-+-+-=(5)1.2双质量系统的传递特性先求双质量系统的频率响应函数,将有关各复振幅代入,得:令:232t A m j C K K ωω=-+++由式(2)得z 2-z 1的频率响应函数:将式(4)代入式(3)得z 1-q 的频率响应函数:式中:下面综合分析车身与车轮双质量系统的传递特性。
车身位移z 2对路面位移q 的频率响应函数,由式(4)及(5)两个环节的频率响应函数相乘得到:2221()()z m j C K z j C K ωωω-++=+2111()()t tz m j C K K z j C K qK ωωω-+++=++1A j C Kω=+KC j m A ++-=ωω222212122z A j C K z m K j C A ωωω+==-++2321N A A A =-21221112=t tA K A K z z z A q z q A N N==1.3车身加速度、悬架弹簧动挠度和车轮相对动载的幅频特性 1.车身加速度对路面不平度的频率特性:2.相对动载对路面不平度的频率特性 车轮动载荷为:车轮静载荷为:则车轮与路面相对动载为:车轮与路面间相对动载与路面不平度之间的传递函数为:3.悬架动挠度对路面不平度的频率特性悬架动挠度为:2222()()()()()Z qz z H q q ωωωωωω-==-1122d F m z m z =+12()G m m g=+212112212121()(1)d m z z F m z m z m m G m m g gm ++==++12221/21()()()(1)d d F G qz z m F q q m H m Gq g m ωωωω-+==-+2121d f z z z z q q q q-==-悬架动挠度与路面不平度之间的传递函数为:2. 仿真过程通过建模,我们已经得到了各所需的传递函数。
基于MATLAB的汽车振动控制仿真

摘要机械振动主要是谐波,阻尼,强制三种。
对于三个振动模型,列出了振动方程,然后给出了三个振动的初始条件。
在模拟过程中产生的一系列速度和汽车行驶时候产生的振动,势能和机械能的三个功能可以通过MATLAB函数模拟,以随时间改变图像。
然后,我们可以经过一系列的计算的出我们需要的函数方程和一些弹簧模拟图像,在后面可以进行一系列的导数计算,在MATLAB软件中可以画出不同的位移,汽车造成的损坏的函数图像,再通过在MATLAB的绘制,可以简单明细的看出汽车振动的能量变化。
最后再比较不同的图像,可以得出不同的结果,可以进行汽车改良。
就可以探索出最佳的方法来研究汽仿真。
关键词:简谐振动阻尼振动评价系数仿真软件。
AbstractMechanical vibration is mainly harmonic, damping, forced three. For the three vibration models, the vibration equations are listed, and then the initial conditions for the three vibrations are given. The three functions produced during the simulation process and the three functions of vibration, potential energy and mechanical energy generated when the vehicle travels can be simulated by MATLAB functions to change the image over time. Then we can go through a series of calculations out of the functional equations we need and some of the spring simulations of the image, which can be followed by a series of derivative calculations that can be plotted in the MATLAB software for different displacements, , And then through the drawing in MATLAB, you can simply see the details of the car vibration energy changes. Finally compare the different images, you can get different results, you can improve the car. You can explore the best way to study the steam simulation.Keywords:simple harmonic oscillationdamping oscillationappraisement coefficientsimulation software.目 录摘 要........................................................ I Abstract....................................................... II 第1章 概述.. (1)1.1 机械振动的物理模型...................................... 1 1.2 简谐振动的物理模型 (1)1.2.1阻尼振动的物理模型 ................................ 2 1.2.2 受迫振动的物理模型 .............................. 2 1.3 Matlab Simulink 仿真原理简述 ....................... 4 1.4频响函数的求解 .......................................... 4 第2章 简谐振动方程的解及其模拟仿真. (11)2.1简谐振动方程的求解 ..................................... 11 2.2 基本模型的建立 (12)2.2.1动能、势能、机械能监测 ........................... 13 2.3 振动信号频谱分析....................................... 16 第3章 阻尼振动方程的求解和仿真模拟. (18)3.1弹簧振子做阻尼振动方程的求解 ........................... 18 3.2弹簧振子做阻尼振动的模拟仿真研究 ....................... 18 3.3阻尼振动的图像分析 ..................................... 20 第4章 受迫振动的方程的求解和仿真模拟.. (23)4.1弹簧振子做受迫振动方程的求解 ........................... 23 4.2弹簧振子做受迫振动的仿真模拟研究 .. (24)4.2.1策动力频率0ωω<时弹簧振子的受迫振动仿真模拟 ..... 24 4.2.2策动力频率0ωω>时弹簧振子受迫振动的仿真模拟 ..... 25 4.3受迫振动的图像分析 ..................................... 25 4.4 汽车振动分析........................................... 26 第5章 几点补充说明与仿真模拟中问题分析 (31)5.1物理振动模型建立的补充说明 ............................. 31 5.2 方程求解中的补充说明................................... 31 5.3 仿真模拟中的问题分析................................... 31 6结语 ......................................................... 32 参考文献....................................................... 33 致谢.. (34)第1章 概述我们学习的的汽车当中,所学到的是汽车行驶时候产生了一定的损坏,就是一定的振动。
1-开题报告-基于MATLAB的汽车振动控制仿真

附件4
理工科类
本科生毕业设计(论文)开题报告
论文(设计)题目基于MATLAB的汽车振动控制
仿真
作者所在系别机械系
作者所在专业车辆工程
作者所在班级B13142
作者姓名吴祥瑞
作者学号201322209
指导教师姓名白亚双
指导教师职称讲师
完成时间2017 年 3 月
北华航天工业学院教务处制
说明
1.根据学校《毕业设计(论文)工作暂行规定》,学生必须撰写《毕业设计(论文)开题报告》。
开题报告作为毕业设计(论文)答辩委员会对学生答辩资格审查的依据材料之一。
2.开题报告应在指导教师指导下,由学生在毕业设计(论文)工作前期内完成,经指导教师签署意见及所在专业教研室论证审查后生效。
开题报告不合格者需重做。
3.毕业设计开题报告各项内容要实事求是,逐条认真填写。
其中的文字表达要明确、严谨,语言通顺,外来语要同时用原文和中文表达。
第一次出现缩写词,须注出全称。
4.开题报告中除最后一页外均由学生填写,填写各栏目时可根据内容另加附页。
5.阅读的主要参考文献应在10篇以上(土建类专业文献篇数可酌减),其中外文资料应占一定比例。
本学科的基础和专业课教材一般不应列为参考资料。
6.参考文献的书写应遵循毕业设计(论文)撰写规范要求。
7.开题报告应与文献综述、一篇外文译文和外文原文复印件同时提交,文献综述的撰写格式按毕业设计(论文)撰写规范的要求,字数在2000字左右。
基于matlab的车辆工程仿真实例 -回复

基于matlab的车辆工程仿真实例-回复一个基于MATLAB的车辆工程仿真实例是车辆悬挂系统的分析与优化。
在汽车设计中,悬挂系统起着至关重要的作用,影响着车辆的舒适性、稳定性和操控性。
使用MATLAB可以通过建立车辆的动力学模型,对悬挂系统进行仿真分析和优化。
以下是一个可能的仿真实例步骤:1. 建立车辆的动力学模型:使用MATLAB 建立车辆的多体动力学模型,包括车体、车轮、悬挂系统等。
模型可以考虑车辆的质量分布、悬挂系统的刚度和阻尼等参数。
2. 仿真悬挂系统的响应:在建立好动力学模型后,可以通过输入不同的激励,如车速、道路条件等,模拟悬挂系统的动态响应。
通过仿真可以了解车辆在不同工况下的悬挂系统行为,如车身姿态、轮胎力等。
3. 分析悬挂系统参数的影响:在模拟悬挂系统的响应之后,可以通过改变悬挂系统的参数,如刚度和阻尼,来分析这些参数对悬挂系统响应的影响。
通过分析可以确定最优的悬挂系统参数,以满足特定的需求,如舒适性、稳定性等。
4. 优化悬挂系统设计:基于分析结果,可以对悬挂系统的设计进行优化。
通过MATLAB的优化工具箱,可以使用不同的优化算法,如遗传算法、粒子群算法等,来搜索最优的悬挂系统参数组合。
5. 评估优化结果:在优化过程中,评估优化结果的有效性是必要的。
可以使用MATLAB的仿真工具再次运行优化后的悬挂系统模型,并进行性能评估。
性能评估可以包括悬挂系统的响应、车辆稳定性、舒适性等方面。
通过以上步骤,可以使用MATLAB对车辆悬挂系统进行仿真分析和优化,以改善车辆的悬挂系统性能。
这个实例展示了MATLAB 在车辆工程中的应用,可以帮助工程师更好地理解和优化车辆的悬挂系统。
如何在Matlab中进行系统建模与仿真

如何在Matlab中进行系统建模与仿真1. 引言系统建模与仿真是工程领域中非常重要的技术手段之一。
而Matlab作为一款功能强大的计算工具,广泛应用于工程建模与仿真过程中。
本文将介绍如何在Matlab中进行系统建模与仿真的基本步骤和技巧,帮助读者更好地利用这一工具进行工作。
2. Matlab基础知识回顾在使用Matlab进行系统建模与仿真之前,我们首先需要了解一些Matlab的基础知识。
Matlab是一种解释型的编程语言,并提供了许多已经封装好的函数和工具箱,方便用户进行科学计算和数据分析。
熟悉Matlab的基本语法和操作方法,对于系统建模与仿真非常有帮助。
3. 确定系统模型在进行系统建模与仿真之前,我们需要先确定系统的数学模型。
这包括确定系统的输入、输出以及系统内部的动态行为。
根据系统的特点和目标,可以使用不同的数学模型描述系统,比如微分方程模型、状态空间模型等。
根据系统的复杂程度和需要,选择适合的数学模型。
4. 构建系统模型在确定了系统的数学模型之后,我们需要使用Matlab来构建系统模型。
Matlab 提供了丰富的工具箱和函数,可以方便地进行系统模型的构建。
可以使用仿真函数和模块进行系统组件的建模,然后通过连接这些组件来构建整个系统。
同时,Matlab还提供了图形界面和可视化工具,可以直观地展示系统模型。
5. 参数估计与优化在系统建模过程中,我们可能会遇到参数估计和优化问题。
参数估计是指根据观测数据来估计系统模型中的参数值,可以使用Matlab提供的统计工具箱和优化算法来解决。
优化则是指根据系统的目标函数来寻找最优的系统参数,也可以使用Matlab的优化工具箱来进行求解。
6. 仿真模拟与结果分析通过构建系统模型和确定参数值之后,我们可以使用Matlab进行系统仿真和模拟。
Matlab提供了强大的仿真函数和工具,可以模拟系统在不同条件下的行为和响应。
同时,Matlab还可以进行仿真结果的分析和可视化展示,帮助我们更好地理解系统的行为和性能。
MATLAB环境下汽车减震系统的设计与仿真

on¥3C241 0 and TM8320C671 3 produced
By SAMSUNG and
TI.The system scheme can improve the precision of the system
navigation.and ehence the real·time pedormance of the systam.
文章编号1671-104I(2007)03-0041-02
基于ARM和DSP的INS/GPS组合系统设计
吴俊伟,张雨楠,刘金峰,苑娜 (哈尔滨工程大学自动化学院, 哈尔滨150001)
摘要:为满足组合导航系统要求成本低.体积小、精度高.低功耗的特点。 本文以SAMSUNG公司¥3C241 0型和TI公司TMS320C671 3型芯片为核 心器件设计了一种嵌入式导航计算机系统.此设计可提高系统的精度,更好 地满足系统实时性的要求。 关键词:INS/GPS;ARM¥3C2410;HPI接口:TMS320C67t3 中图分类号:PT277文献标识码:A
是为什么没有任何旅客或驾驶员喜欢这个C=0(相当于减震器粘性 为o’无作用)的值。
;||||㈦!㈡㈦
::::::::
::::::::
—■需常警车饕嚣
●l=c■●芏
i;i i;;※ ;㈡;!:;
图2时域仿真结粜
图3频域1方真结粜
图4时域仿真结果
图5频域仿真结果
3结束语 MATLAB软件是目前比较流行的…种软件,特别在数值训
照型班遮j土盛墨匣
仪器仪表用户
try l
m—pDatabase一>ExecuteSQL(SQLstr); l
catch(CMemoryException+pEx)I/处理内存异常 { pEx一>ReportError0; pEx一>DeleteQ;
基于MATLAB的汽车直线加速工况下振动模型分析

基于MATLAB的汽车直线加速工况下振动模型分析汽车在直线加速工况下面临着振动问题,这对于车辆的性能和乘坐舒适度都会产生一定影响。
因此,针对这一问题,我们可以利用MATLAB进行振动模型的分析,以便更好地了解振动的原因和解决方案。
在进行振动模型分析之前,首先需要了解汽车在直线加速工况下的运动特性。
汽车在直线加速时,受到动力所产生的加速度和阻力的影响,会引起车身的振动。
这种振动主要是由质量的不平衡、悬挂系统的刚度和阻尼失效等因素引起的。
因此,我们需要建立一个合理的振动模型,来描述这些因素对汽车振动的影响。
在MATLAB中,可以利用多种数学方法和工具箱来建立汽车振动模型。
其中一种常用的方法是使用有限元分析(FEA)技术来进行振动分析。
有限元方法基于连续介质力学原理,将结构划分为各种小的有限元,通过建立节点和单元的连接关系来描述结构的振动。
这样就可以利用MATLAB提供的FEA工具箱来进行汽车振动的模拟和分析。
在进行有限元模型分析之前,首先需要建立汽车的几何模型。
可以通过CAD软件将汽车的主要构件进行绘制,然后导入MATLAB中进行后续的处理。
可以使用MATLAB提供的CAD工具箱来进行CAD文件的读取和处理。
接下来,需要对汽车的材料特性和悬挂系统参数进行建模。
汽车的材料特性可以通过实验或者文献数据进行获取。
而悬挂系统的参数需要进行测量或者仿真分析。
可以使用MATLAB提供的参数优化和曲线拟合工具箱来进行参数的优化和拟合。
建立好汽车的几何模型和参数后,就可以使用MATLAB的FEA工具箱进行振动分析了。
可以通过在汽车结构上加入初始激励和加载条件,来模拟直线加速工况下的振动响应。
然后使用MATLAB提供的振动分析函数,如固有频率分析、模态分析和频域响应分析等,来分析振动的模态特性和响应情况。
在振动模型分析过程中,还可以考虑不同控制策略和系统参数对振动的影响。
可以利用MATLAB提供的控制系统工具箱和优化算法来进行参数的优化和系统性能的改善。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题描述及空间状态表达式的建立1.1问题描述汽车减震系统主要用来解决路面不平而给车身带来的冲击,加速车架与车身振动的衰减,以改善汽车的行驶平稳性。
如果把发动机比喻为汽车的“心脏”,变速器为汽车的“中枢神经”,那么底盘及悬挂减震系统就是汽车的“骨骼骨架”。
减震系统不仅决定了一辆汽车的舒适性与操控性同时对车辆的安全性起到很大的决定作用,随着人们对舒适度要求的不断提高,减震系统的性能已经成为衡量汽车质量及档次的重要指标之一。
图1.悬架减震系统模型汽车减震系统的目的是为了减小路面的颠簸,为人提供平稳、舒适的感觉。
图2,是一个简单的减震装置的原理图。
它由一个弹簧和一个减震器组成。
从减震的角度看,可将公路路面看作是两部分叠加的结果:一部分是路面的不平行度,在汽车的行驶过程中,它在高度上有一些快速的小幅度变化,相当于高频分量;另一部分是整个地形的坡度,在汽车的行驶过程中,地形的坡度有一个缓慢的高度变化,相当于低频分量。
减震系统的作用就是要在汽车的行驶过程中减小路面不平所引起的波动。
因此,可以将减震系统看成是一个低通滤波器。
图2.减震系统原理图1.2空间状态表达式的建立对该系统进行受力分析得出制约底盘运动的微分方程(数学模型)是:22()()()()()d y t dy t dx t M b ky t kx t b dt dt dt++=+ 其中,M 为汽车底盘的承重质量,k 为弹簧的弹性系数,b 为阻尼器的阻尼系数。
将其转化为系统传递函数:222()()()2()n n n n s H s s s ωεωεωω+=++ 其中,n ω为无阻尼固有频率,ε为阻尼系数。
并且,n ω=2n b M ξω= 通过查阅相关资料,我们知道,汽车减震系统阻尼系数ε=0.2~0.4,而我们希望n ω越大越好。
在下面的计算中,我们规定n ω=6,ε=0.2。
所以,系统传递函数,可以转化为:2() 2.436() 2.436Y s s U s s s +=++ 根据现代控制理论知识,结合MATLAB 工具,将传递函数转化为状态空间矩阵和输出矩阵表示。
在MATLAB 中输入,[][][]()A,B,C,D tf2ss 2.4 36,1 2.4 36=能够得到:2.43610A --⎛⎫= ⎪⎝⎭ 10B ⎛⎫= ⎪⎝⎭ []2.436C = [0]D =。
进而,通过现代控制理论,可以将系统状态变量图绘制出来。
图3.系统状态变量图2.应用MATLAB分析控制系统性能2.1系统可控性与可观测性分析可控性和可观测性,深刻地揭示了系统的内部结构关系,由R.E.Kalman于60年代初首先提出并研究的这两个重要概念,在现代控制理论的研究与实践中,具有极其重要的意义,事实上,可控性与可观测性通常决定了最优控制问题解的存在性。
我们借助MATLAB工具来实现系统可控性与可观测性分析。
程序代码如下:A=[-2.4 -36;1 0];B=[1;0];M=ctrb(A,B);n=rank(M)C=[2.4 36];N=obsv(A,C);rN=rank(N)输出结果如下:n = 2rN = 2通过现代控制理论知识,可以得出结论:系统是可控可观测的。
2.2系统稳定性分析在经典控制理论中,如果在输入量的作用下系统的输出量能够达到一个新的平衡状态或扰动量去掉以后系统的输出量能够恢复到原来的平衡状态,则系统是稳定的。
控制系统的稳定性分析是系统分析的重要组成部分。
系统稳定是控制系统正常工作的前提条件。
根据李雅普诺夫第一法,若线性化方程中系数矩阵A的所有特征值都具有负实部,则系统总是渐近稳定的。
在MATLAB中输入如下代码:A=[-2.4 -36;1 0];B=[1;0];C=[2.4 36];D=[0];Q=[1 0;0 1];P=lyap(A',Q)eig(P)sys_ss=ss(A,B,C,D);p=pole(sys_ss)我们可以得到,系统极点为:P = -1.2000 5.8788i可以看出,系统的极点均在虚轴负半轴,由李氏第一法可得,系统是稳定的。
通过MATLAB软件,可以得到输入输出的阶跃响应曲线。
输入代码如下:[y,t,x]=step(sys_ss,10);figure(1);plot(t,y);xlabel('time/s');ylabel('Output y(t)');xlim([0 10]);gridfigure(2);plot(t,x);xlabel('time/s');ylabel('State x(t)');xlim([0 10]);grid输出曲线如图4,图5。
Array图4.系统输入的阶跃响应曲线图5.系统输出的阶跃响应曲线3.应用MATLAB 进行控制系统综合设计3.1极点配置所谓极点配置就是利用状态反馈或输出反馈使闭环系统的极点位于所希望的位置。
通过上面的分析,可知系统要反应5秒才能达到稳定。
这在实际中是不能够满足的,需要进行状态反馈,进行极点配置,以实现对系统的调整,使其达到稳定的时间更短,反应速度更快。
通过查询有关资料,得到了系统极点方程:n P i ξωω=-±这次,我们设定ξ=0.4,n ω=10。
得到希望极点:49.165P i =-±。
为了是计算简单,将极点进行四舍五入:49P i =-±。
然后,使用MATLAB 进行极点配置,编写如下代码:A=[-2.4 -36;1 0];B=[1;0];C=[2.4 36];D=[0];K=acker(A,B,[-4+9i -4-9i])运行后,可以得到状态反馈矩阵K=[5.6 61],进而可以计算出极点配置后状态反馈系统的状态方程:(2.4 5.6)(3661)z z z u ++++=&&&2.436y z z =+&状态反馈系统传递函数为:2 2.436()(2.4 5.6)(3661)s G s s s +=++++ 状态反馈系统方框图为图6所示。
图6.状态反馈系统方框图下面进行系统性能的仿真分析,验证是否经过极点配置后,系统能够满足快速响应的使用要求。
采用MATLAB 中的simulink 模块,对系统进行仿真分析。
原系统(极点配置前)在输入阶跃信号时,系统输出响应曲线如图7所示。
图7.(极点配置前)系统输出响应曲线状态反馈系统(极点配置后)在输入阶跃信号时,系统输出响应曲线如图8所示。
图8.(极点配置后)系统输出响应曲线通过观察,可以看出:极点配置前,系统在5秒左右达到稳定;极点配置后,系统在2.5秒左右达到稳定。
因此,极点配置能够使系统性能更优,响应时间更快。
3.2系统的最优控制上面对系统进行了极点配置和状态反馈,使得系统的性能得到了一定的改善。
但是,系统还远远没有达到最优的状态。
最优控制问题, 就是从可供选择的容许控制集合U 中,寻找一个控制u(t), 使受控系统在[t 0 t f ]内,从初始状态x(t 0),转移到终端状态x(t f )或目标集时,性能指标J 取最小(大)值。
下面将采用线性二次型最优控制的方法,对系统进行最优控制。
二次型最优控制性能指标为:0(2)T T T J x Qx u Ru x Nu dt ∞=++⎰ 其中:200001Q ⎛⎫= ⎪⎝⎭ 1R = 01N ⎛⎫= ⎪⎝⎭最优控制规律为:u Kx =-。
下面为运用MATLAB 工具,对系统进行最优控制,程序如下:A=[0 1;-36 -2.4];B=[2.4;30.24];C=[1 0];D=[0];Q=[200 0 ;0 1;];R=1;N=[0;1];sys=ss(A,B,C,D);% [K,P,L]=lqr(A,B,Q,R,N);disp('')Kdisp('Riccati ')Pdisp('')LAC=A-B*K;BC=B*K(1);CC=C;DC=求系统的初始状态响应反馈增益矩阵方程的解闭环特征根0;sysc=ss(AC,BC,CC,DC);disp('')sysc[y,t,x]=step(sys,10);[yc,tc,xc]=step(sysc,10);figure(1);subplot(2,2,1);plot(t,y);xlabel('time/s');ylabel('Output y(t)');xlim([0 10]);grid%sub 闭环系统状态方程系数矩阵原系统输出的单位阶跃响应plot(2,2,2)plot(t,x);xlabel('time/s');ylabel('State x(t)');xlim([0 10]);grid%subplot(2,2,3);plot(tc,yc);xlabel('time/s');ylabel('Output yc(t)');xlim([0 10]);grid%subplot(2,2原系统状态的单位阶跃响应最优控制系统输出的单位阶跃响应,4);plot(tc,xc);xlabel('time/s');ylabel('State xc(t)');xlim([0 10]);grid%最优控制系统状态的单位阶跃响应程序运行结果如图9所示。
图9.最优控制与系统性能对比通过对比,可以清晰的看到,最优控制后,系统瞬间就恢复了稳定,响应时间迅速。
这样,最优控制确实起到了很好的效果,能够使系统达到最优。
4.总结通过这次小论文,结合现代控制理论,并借助MATLAB工具,学到了有关现代控制理论和系统建模仿真的知识。
并且,在学习过程中,不断的解决所遇到的问题,加深了对现代控制理论的理解和对MATLAB软件的熟悉程度。
对于汽车减震系统,现代控制理论能够很好的解决汽车颠簸的问题。
现代控制理论完全可以在理论上实现很好的控制,并指导实际工作。
将MATLAB与现代控制理论合理的结合一起,提高了问题的解决效率,是值得深入研究的。
感谢老师辛苦的指导,感谢同学们的帮助和支持。
