第3章实用计算方法
第3章剪切汇总

§3-1 剪切的概念及连接件的受力分析 §3-2 剪切与挤压的实用计算 §3-3 铆钉和螺栓连接的计算
比较—分类法
第3章知识点
剪切与挤压的 概念
实用计算方法概念
铆钉和螺栓连接的 计算(三种连接方 式和三种情况的计 算方法)
剪切面、单剪、双剪、 挤压面、挤压力、挤压 应力、挤压破坏、挤压 计算面的概念
校核拉杆头部的强度。
解:
P 40103 dh 2010
63.7MPa [ ]
bs
(D2
P d2)/
4
40 103 (402 202 Nhomakorabea)
/
4
42.4MPa
[
]
CL4TU5
例3-3 拉杆及头部均为圆截
面,材料的许用剪应力[τ]
=100 MPa,许用挤压应力
[σbs]=240MPa。试确定容 许拉力[P]。
n F
剪切面
剪切实例
二、 连接件的类型 在构件连接处中起连接作用的部件,称为连接件,如铆钉、
螺栓等,连接件虽小,它起传递荷载作用;被连接的构件称为被 连接件,如钢板等。
1. 铆(销)钉连接
t
2t
t
2.螺栓连接 3.键连接
d ι
ι
m
D0
4. 榫齿连接 5.焊接 6.粘结
两种情况的剪切
单剪切:只有一个剪切面。
解:由剪应力强度条件:
P
dh
P 20 15 106
100 106
得P 94.2kN
剪切的实用计算 (切应力公式和强度
条件)
挤压的实用计算 (挤压应力公式和强
度条件)
被连接件的拉伸的实 用计算
第3章 资金的时间价值及等值计算

一年后的终值。终值与现值可以相互等价交换,
把一年后的111.34元换算成现在的值100元的折算 过程就是折现:
P= F 111.34 = =100 1+ ni 1+ 12×0.00945
二、利息的概念
利息(Interest):资金通过一定时间的生产经营活 动以后的增值部分或投资的收益额 利率(Interest Rate):一定时间(年、月)所得到的 利息额与原资金额(本金)之比,通常用百分数表示
计息周期(Interest Period):计算利息的时间单位
付息周期:在计息的基础上支付利息的时间单位
三、单利和复利 单利(Simple Interest):只计本金利息,而利息 不计利息。 P—本金 n—计息期数 i—利率 I—利息总额 F—本利和
I = Pn i
F = P (1 + ni ) = P + I
中国历年的通货膨胀率
1980
1981 1982 1983 1984 1985 1986
6.0
2.4 1.9 1.5 2.8 9.3 6.5
1990
1991 1992 1993 1994 1995 1996
3.1
3.4 6.4 14.7 24.1 17.1 8.3
2000
2001 2002 2003 2004 2005 2006
3.2
资金等值(Equivalent Value)计算
一、折现的概念
现在值(Present Value 现值): 未来时
点上的资金折现到ue 终值):与现值等
价的未来某时点的资金价值。
折现(Discount 贴现): 把将来某一时点上的
人教版数学五下第3章《长方体和正方体》(推导长正方体的体积计算方法)教案

人教版数学五下第3章《长方体和正方体》(推导长正方体的体积计算方法)教案一、教学目标1.掌握长方体和正方体的定义及特点。
2.理解长方体和正方体的体积计算公式。
3.能够推导出长方体和正方体的体积计算方法。
4.进一步理解几何体的立体图形性质。
二、教学重点1.长方体和正方体的定义和特点。
2.长方体和正方体的体积计算方法。
三、教学难点1.推导长方体和正方体的体积计算方法。
2.理解长方体和正方体的关系及应用。
四、教学准备1.板书、彩色粉笔。
2.长方体和正方体的模型。
3.课件PPT。
五、教学过程第一步:导入1.引导学生回顾长方体和正方体的定义,并复习相关特点。
第二步:讲解1.讲解长方体和正方体的体积计算公式。
2.结合实际生活中的例子,说明体积计算的重要性。
第三步:推导1.提问学生如何计算长方体和正方体的体积。
2.引导学生通过立体图形的方式,推导出长方体和正方体的体积计算方法。
第四步:巩固1.给学生发放练习册,让他们在练习中巩固所学知识。
2.师生互动,解答学生在实践中遇到的问题。
第五步:拓展1.引导学生思考长方体和正方体的特殊情况,如正方体是长方体的特殊情况。
2.讨论长方体和正方体在实际生活中的应用。
六、课堂小结1.总结长方体和正方体的体积计算方法。
2.强调掌握数学知识的重要性。
七、作业布置1.完成练习册上相关习题。
2.思考长方体和正方体在日常生活中的应用场景。
八、教学反思1.教师应当注意引导学生从实际问题出发,思考数学问题的应用性与实用性。
2.教师应关注学生的学习兴趣和思维习惯,及时给予指导和帮助。
以上为人教版数学五下第3章《长方体和正方体》(推导长正方体的体积计算方法)教案,希望能帮助学生更好地理解和掌握相关知识。
第三章电力系统三相短路电流的实用计算

t Tq
t 0 I
E0 xd
实用计算例1
第三章 电力系统三相短路电流的实用计算 b) 电网侧
忽略线路对地电容和变压器励磁回路; 高压电网计算忽略电阻; 标幺值计算时认为变压器变比=平均额定电压之比。
c) 综合负荷侧
短路前后电网近似计算时都按空载进行计算,忽略综荷。
1 x xst I st
I st 5
x xst 0.2
(3-3)
xst 启动电抗标幺值; I st 启动电流标幺值。
E U 0 jI 0 x 0
次暂态电动势E ;正常极端电压为 U 0 ;吸收电流 I 0 0
其模值为:
E U 0 I 0 x sin 0 0
第三章 电力系统三相短路电流的实用计算
0 U q 0 jI d 0 xd Eq 0 jI d xd Eq
q
E 0
0 Ed
E 0
Id
0 Eq jxd
0 Ed jxq
Eq 0
0 U d 0 jI q 0 xq Ed
3.1.3 复杂系统计算
一般应用叠加定理进行计算。 计算公式为:
I f
U f 0 jx
(3-5)
假设:1.短路前后综荷视为空载 2.
乃至网络各点电压均视为1 E
1 I f x
例3-2 (P68) 例3-3 (P71)
则可近似计算:
第三章 电力系统三相短路电流的实用计算 等值系统:实际短路电流计算时,将短路点以外其余系统
异步电动机短路失去电源后能提供短路电流。
突然短路瞬间,异步电动机在机械和电磁惯性作用下,
定转子绕组中均感应有直流分量电流,当端电压低于 次暂态电动势时,就向外供应短路电流。
第3章_流域汇流计算讲解

h1=10
0 430 630 400 270 180 118 70 40 16 0
部分径流(m3/s)
h2=10
h3=10
h4=10
(4)
0 430 630
+ 400 270 180 118 70 40 16 0
0 430
+ 630 400 270 180 118 70 40 16 0
0
+ 430 630 400 270 180 118 70 40 16 0
分析法的缺点在于误差传,使分析的 单位线值有时偏大,有时偏小而呈锯齿形, 必须加以修匀。修匀得到的单位线的径流 量也应为10 mm。
分析法只适用于二、三个时段净雨。
流域汇流计算
q
(m3/s)
1 2 3 4 5 6 7 8 9 10 11 12 13 1T4(61h5)
单位线修匀
流域汇流计算
三个时段以上的净雨可采用试算法。试算法是 假定一条单位线。计算出流量过程,再与实测过程 比较,如不相符,改正单位线后再试,直到两者相 符。
8 14 20 22
8 14 20 32
8 14 20
hs
(mm)
(2)
24.0 23.0 3.2
q
(m3/s)
(3) 0
2.0 15.0 35.0 41.0 25.0 15.0 9.0 6.0 4.0 3.0 2.0 1.0
0
Q’(t)=h/10q(t)
(m3/s)
h1=24.0 h2=23.0 h3=3.2
S曲线与时段长成反比
S (t
,t)
t0 t
S (t0 , t)
因为
q(t ,t j ) S(t ,t j ) S(t ,t j t )
第三章 化学反应动力学的计算
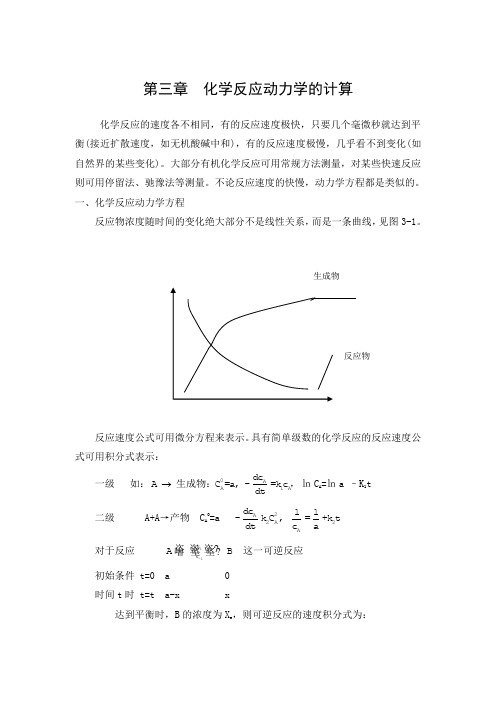
第三章 化学反应动力学的计算化学反应的速度各不相同,有的反应速度极快,只要几个毫微秒就达到平衡(接近扩散速度,如无机酸碱中和),有的反应速度极慢,几乎看不到变化(如自然界的某些变化)。
大部分有机化学反应可用常规方法测量,对某些快速反应则可用停留法、驰豫法等测量。
不论反应速度的快慢,动力学方程都是类似的。
一、化学反应动力学方程反应物浓度随时间的变化绝大部分不是线性关系,而是一条曲线,见图3-1。
反应速度公式可用微分方程来表示。
具有简单级数的化学反应的反应速度公式可用积分式表示:一级 如:0AA1Adc A C =a, -=k c dt 生成物:,㏑C A =㏑a –K 1t 二级 A+A →产物 C A 0=a 2A 2A 2A d c 11-k C , =+k t d t c a对于反应 1-1k k A B 这一可逆反应初始条件 t=0 a 0 时间t 时 t=t a-x x达到平衡时,B 的浓度为X e ,则可逆反应的速度积分式为: 级数:1-1 1-10k A A e e 1A -1B k 0e 0C =a dc x xA B=-k C +k C : =kt dt a x -xC =0ln 1-21-10Ak0A e e e B 1A -1B C k e e 0CC =a dc x ax +x(a-x )A B+C C =0=-k C +k C C : =kt dt 2a-x a(x -x)C =0ln 二、常微分方程的解化学反应动力学方程是用微分方程表示的,对于简单的反应,可直接求得微分方程的解。
微分方程:()(1)(,,,......)......(1)n n y f x y y y -'=在区间a<x<b 的解,是指()y x ϕ=,这样一个函数,在所述区间内存在导数()(),(),......()n x x x ϕϕϕ'''。
且对于区间a<x<b 内的每一个x ,等式(1)都成立。
2020-2021学年五年级数学上册第三章小数除法人教新课标版(含解析)

2020-2021学年五年级数学上册暑假预习与检测衔接讲义第三章小数除法【知识点归纳】1、小数除以整数的计算方法:小数除以整数,按整数除法的方法去除,商的小数点要和被除数的小数点对齐。
整数部分不够除,商0,点上小数点。
如果有余数,要添0再除。
2、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数(把小数点向右移动相同的位数),使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:向右移动小数点时,如果被除数的位数不够,在被除数的末尾用0补足。
3、除法中的变化规律:①商不变性质:被除数和除数同时乘或除以同一个数(0除外),商不变。
②除数不变,被除数乘或除以几,商随着乘或除以几。
③被除数不变,除数乘或除以几,商就除以或乘几。
④被除数大于除数,商就大于1;被除数小于除数,商就小于1。
⑤一个非0的数除以大于1的数,商就小于被除数;一个非0的数除以小于1的数,商就大于被除数。
⑥积不变性质:一个因数乘一个数,另一个除以同一个数(0除外),积不变。
⑦一个因数不变,另一个数乘几,积就乘几。
⑧一个因数不变,另一个因数除以几,积就除以几。
4、求商时有时也需要求近似数。
方法三种。
取商的近似数时,保留到哪一位,一定要除到那一位的下一位,然后用四舍五入的方法取近似数。
没有要求时,除不尽的一般保留两位小数。
5、一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
一个循环小数的小数部分,依次不断重复出现的数字,叫循环节。
如6.3232……的循环节是32,注意不是23一定要是第一次重复出现的数字是3在前2在后重复出现!6、循环小数的记法:(1)用省略号表示。
写出两个完整的循环节,加省略号。
如:3.55…, 2.0321321…(2)简便记法。
在循环节的首位和末位上加小圆点。
如0.36,2.587循环小数是无限小数,无限小数不一定是循环小数。
7、小数部分的位数是有限的小数,叫做有限小数。
第三章 数值计算方法

x0 ,按某种算法产生一个近似解序列,该序列 收敛于精确解x*
x0 , x1, x2 , x3 ,, xn
计算机在稀土工程中的应用
2. 二分法
设函数 f (x) 在区间[a, b]上连续,且 f (a) f (b) 0 ,
采用二分法求解可按下列步骤进行:
如前面的例子可改写为:
(309016 0.005608 T 2 501182 T 1) /177 .5 T
计算机在稀土工程中的应用
简单迭代的误差与收敛
xk1 g(xk )
x* g(x*)
两式相减,并由中值定理有:
x * xk1 g(x*) g(xk ) g'()( x * xk )
入炉物料显热 铜锍显热 (k1 k2T (k3 k4T )[Cu]m ) Wm
化学反应热 重油燃烧热
炉渣显热 (k5 k6T ) Ws
N
烟气显热 ni ( Ai BiT CiT 1 DiT 2 ) i1
塔散热 经验数据
通过求解方程:热收入+热支出=0,即可求得温度T。 现已知某生产时期热平衡方程如下,求温度T:
由此可见,该递推算法随n的增大,误差传播迅速增大, 是不稳定算法。
计算机在稀土工程中的应用
算法2: 逆向递推
由:In 1 nIn1
有:In1 (1 In ) / n
按In估计式:
e1
1
n 1 In n 1
取:
I 30
e1 ( 30
1) 1
/
2
0.0221
30 0.0102
按 s30 0.0221 sn1 (1 sn ) / n 逆向递推
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
T 1
M y1
y1
1 2
ψ 1T M ψ 1 =1 (9)
3.2.6 力相关的里兹向量
由式(9)和式(11)可得
ˆ 2 = y 2 a1 2 ψ 1 = K ψ
1
式(10-b)第一项可如下得到
a 1 2 = ψ 1T M y 2
M ψ 1 ψ 1T M
(A)
K
1
M ψ 1 ψ1
3.2.5 里兹向量的选择
解得
k 0 .2 0 .2 0 .2 2 .2 m 2 .0 0 .2 0 .2 z 1 0 2 .5 z 2
1 0 .0 8 2 3 8( k / m )
1 .3 2 9 z1 0 .1 3 6 0
s s ss s
1 u K P t K s us
Ms 0
s K ss 0 u K s 0 u
K s us Ps t K u P t
3.2.2 “最佳”近似
下面证明与所选Ritz向量有关的所有可能的近似特征 值中,与体系固有频率相关的值最接近真实频率 —— “最佳” 的意义。 为此引入如下瑞利商
uT Ku z TΨ T KΨz z T Kz T T T T u Mu z Ψ MΨz z Mz
(3)
(可以证明)瑞利商具有如下特性: 1)如果[u]是第i振型向量,则i=i2; 2)瑞利商在真实特征值的邻域内取驻值; 3)瑞利商在最小和最大特征值间有界。 为了说明式(2)特征值具有“最佳”性,将式(3)改写为
5)相对精确解的误差 此结论具有一般性!
对动荷载为[P]f(t)时,本节讨论如何生成Ritz向量。 第 一个Ritz向量由荷载 [P]引起的静位移产生
3.2.6 力相关的里兹向量
K y1 P ψ 1 =
第二个Ritz向量[]2由与第一个向量[]1相关的惯性力 分布给出的作用力引起的静位移向量[y]2来确定,向 量[y]2通过求解下式得到 (10-a) K y2 M ψ1 向量[y]2一般包含前面向量[]1的成分,因此可表为 ˆ 2 + a1 2 ψ 1 y2 =ψ (10-b) 式中第一项与[]1无关,也即它应与[]1正交,故可得 ˆ 2 + a 1 2 ψ 1T M ψ 1 a 1 2 ψ 1T M ψ 1 (11) ψ 1T M y 2 = ψ 1T M ψ
2 1 K k 0 0 0
3.2.5 里兹向量的选择
1 2 1 0 0 0 1 2 1 0 0 0 1 2 1 0 0 0 1 2
和K 2)根据所设里兹向量求 M
Ψ ψ 1 0 .2 0 .4 ψ 2 = 0 .6 0 .8 1 .0 0 .5 1 .0 0 .5 0 .0 1 .0
ziTΨ T MΨz j ziTΨ T KΨz j =0 i j
(e) (e)
考虑到式(7-b),则上式可改写作
φiT Mφ j φiT Kφ j =0 i j
近似振型向量的正交性证毕。
3.2.5 里兹向量的选择
瑞利-里兹法的成功与否取决于Ritz向量的线性组合是 否很好地近似于固有振型,因此,合理选择Ritz向量是 很重要的。 首先介绍一种依据一些基本概念假设Ritz向量的方法。 考虑到第一振型恒正、第二振型改变一次符号、第三振 型改变两次符号等等,再考虑剪切型结构、剪弯型结构 和弯曲型结构的变形特点,可以对其各振型做出符合概 在有一定计算经验的情况下,还可根据以往经 念的假设。 验对需计算体系作出更合理的假设。 下面以一具体例子加以说明。
Ψ T M Ψ = m 2 .2 M 0 .2 Ψ T K Ψ = k 0 .2 K 0 .2
0 .2 2 .5 0 .2 2 .0
M )z 0 3)求解缩减的特征值问题 ( K
k 0 .2 0 .2 0 .2 2 .2 m 2 .0 0 .2 0 .2 z 1 0 2 .5 z 2
3.2.2 “最佳”近似
为了说明式(2)特征值具有“最佳”性,将式(3)改写为
k K ij
J J
m ij = ψiT Kψ j , M
T
J J
= ψiT Mψ j ,
(4-a) (4-b)
z Kz z T z Mz
将其进行一般化,则不难得到如下一些公式(i从3开始) K y i M ψ i -1 (13-a)
(5-b)
由此可得
k
J j 1
ij
ij z j 0 m
i 1, 2,...,J
(6-a)
将其写成矩阵方程即得縮减自由度的特征方程
M z 0 K
(6-b)
由此可以看出,应用瑞利(Rayleigh)驻值条件导出的式 (6-b)是与运动方程(2)相关的特征值问题,这就证明了本 节“最佳” 近似的含义。
2 0 .8 0 0 4 ( k / m )
0 .0 3 1 7 z2 1 .2 4 0
i =Ψzi i = i φ 4)求近似频率和振型
1 0 .2 8 7 0 k / m
2 0 .8 9 4 7 k / m
0 .3 3 3 8 0 .6 1 3 5 第一阶近似频率的误差小于 1% ,第二阶近似频率的 0 .6 6 7 6 1 .2 2 7 0 1 φ 2 = 0 .8 6 5 4 0 .6 0 0 8 Φ φ 误差小于8%,第一阶近似振型的误差小于 4%,但第二 0 .0 2 5 3 6 1 .0 6 5 阶近似振型的误差太大,可能无法使用。 1 .1 9 3 1 .2 7 1 0
3.2.3 近似频率和振型
(6-b) 按求特征方程的任一方法可得特征对(i,[z]i), 由特征值 i可得原体系的固有频率近似值 i i (7-a) 把特征向量[z]i代入式(1)中,可得原体系固有振型的近 似向量 i Ψzi φ i 1, 2,...,J (7-b) 这些近似结果的精度对于低阶振型一般好于高阶振型。 因此,实际应用应包括比所需振型数更多的Ritz向量。 近似频率一般是真实固有频率的上限,也即 i i i 1, 2 ,...,J (8) 从上小节所得縮减自由度的特征方程
第3章 实用计算方法
在本科学习基础上补充和加深
第3章 实用计算方法 目录
§3.1 多自由度体系自由度的确定 §3.2 瑞利-里兹法 §3.3 子空间迭代法
§3.1 多自由度体系自由度的确定
在本科内容复习中已经指出体系的自由度取决于确定 质量空间(或平面)位置的独立坐标数。对于图示20层 框架结构,总计有640个结点,静力计算时每结点6个自 由度,因此共有3840个未知位移。 当然,做动力计算时可取与静力分 析相同的模型(例如用单元一致质量矩 阵建立质量矩阵),但这是完全没有必 要的。 由于楼板在自身平面内刚度“无穷 大”,除非整体属于细长的建筑,一般 不考虑轴向变形影响,此外忽略转动 惯量的惯性作用,这样每层只有3个自 由度,总计60个动力自由度即可。
i i
i 1 j 1
zi z j mij
J J 2 m z k 2 k zm z k j 1 j ij j 1 j ij 0 2 zi zi m m
(5-b)
3.2.2 “最佳”近似
J J z k 2m j 1 z j kij 2k j 1 z j mij 0 2 zi zi m m
M )z 0 (K
3.2.4 近似振型的正交性
上小节所得的近似振型向量具有正交性,现证明如下
i Ψzi φ i 1, 2,...,J
因为[z]i是式(6-b)的特征向量,因此下式成立
z T Kz =0 ziT Mz j i j i j
(7-b) (d)
将式(c)的结果代入上式可得
§3.1 多自由度体系自由都不考虑质量的转 动惯性作用(也即取转动惯量为零), 这样静力分析的全 部未知位移就可以分成两部分:有和无惯性作用,如果 将位移编号先编有惯性作用后编无惯性作用,则无阻尼 运动方程可写作 式中下标s表示有惯性作用,表示无惯性作用。由此可 进行如下“静力凝聚”, 由矩阵方程第二式可得 再将此式代回矩阵方程第一式,得只有未知量s的运动方 程 K K K 1 K u P t K 1 P t Mu
J i 1 J i 1
k J m z z m i j ij j 1
J
z z k i j ij j 1
因为广义坐标zi(t)是未知的,所以不能由式(4-b)求得瑞 利(Rayleigh)商。 根据特性(2),为使取驻值,必须 J J z i 1 j 1 zi z j k ij 0 i 1, 2 ,...,J (5-a) J J z z
s
s
s
这就是缩减自由度后的运动方程。
§3.2 瑞利-里兹法
虽然用静力凝聚可以大量縮减自由度,但缩减自由度 数目和寻求低阶固有频率及振型近似解的最通用技术是 瑞利-里兹法,下面分六部分来介绍它。
3.2.1 瑞利-里兹法 3.2.2 “最佳”近似 3.2.3 近似频率和振型 3.2.4 近似振型的正交性 3.2.5 里兹向量的选择 3.2.6 力相关的里兹向量
(B) (12)
将此思路进行一般化
T ˆ ˆ 2 =1,可得第二个里兹向量为 为使 ψ 2 M ψ ˆ2 ψ ψ2= 1 2 T ˆ2 Mψ ˆ2 ψ
