二次函数中的三角形面积 ppt课件
二次函数背景下的直角三角形ppt

BC2 CD2 DB2 DCB 90tan CBD
1 3
x
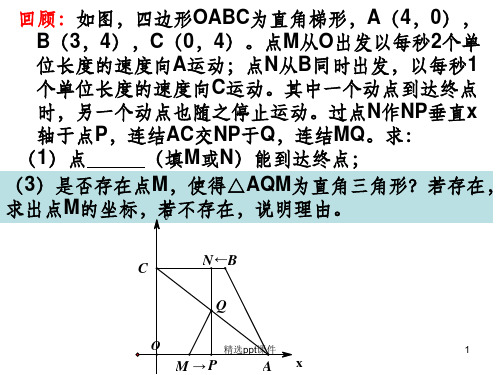
引例:在平面直角坐标系xOy中,C(0,3)、
B(3,0)、D(1,4)
问题2:若点E在y轴上,以点E、B、D为顶点的
三角形是直角三角形,这样的点E有几y个?
x
引例:在平面直角坐标系xOy中,C(0,3)、
(a 3)2 + a2 2a 3 2 18 a2 (a2 2a)2
x
a2 6a 9 (a2 2a)2 6 a2 2a +9+18=a2 (a2 2a)2
a2 a 6 0
a 2 或 a 3 (舍去)
3
BN CM a2 2a 3 3
3
QN MB
3a 3
x
a2 a 6 0
a 2 或 a 3 (舍去)
Q2 2,5
a2 2a 3
3a
小结:
问题2: 勾股定理
(两点确定,一点在直线上)
问题3: 一线三直角
(两点确定,一点在抛物线上)
y
3 2
x
x 1
M
1,
3 2
x
N 1,0
问题4:正比例函数 与二次函数的图像交与 点F(点F在第一象限),且二次函数图像的对称轴与 正比例函数的图像相交于点M,与x轴相交于点N, 点Q是x轴的正半轴上的一点,如果△OMN与 △OFQ相似,求点Q的坐标.
x
当∠CBQ=90°时,∠2+∠3=90°
∵QN⊥MN,∴∠1+∠2=90°
∴∠1=∠3
二次函数中三角形面积问题

二次函数中三角形面积问题【典型例题】:如图,二次函数y=-x²+2x+3与y轴,x轴交于点A ,B,点C是直线AB上方抛物线上的一个动点(不与点A ,B重合),求△ABC面积的最大值.【方法一】竖割法:过点C作CD⊥x轴,垂足为D,交AB于点E,S△ABC=S△ACE +S△BCE =1/2CE·(xc--xA)+1/2CE·(xB-xC)=1/2OB·CE解:令x=0, y=3 点C的坐标为(0,3);令y=0, 则-x²+2x+3=0 ,解得:x1=-1 x2=3 点B的坐标为(3,0),设AB所在直线的解析式为y=kx+b.求出直线AB所在直线的解析式为y=-x+3.设点E的坐标为(m,-m+3) ,则点C的坐标为(m, -m2+2m+3)CE=y C-y E= -m2+2m+3-(-m+3)= -m2+3mS△ABC=S△ACE +S△BCE =1/2CE·(xc--xA)+1/2CE·(xB-xC)=1/2OB·CE=1/2×3( -m2+3m)=--3m2/2+9m/2S△ABC最大值=4ac-b2/4a=27/8【方法二】割补法:连接OC,S△ABC=S△OAC +S△OBC-S△OAB解:S△ABC=S△OAC+S△OBC-S△OAB=1/2×OA·X C+1/2×OB·Y C-1/2×OA×OB=1/2×3×m+1/2×3×(-m2+2m+3)-1/2×3×3=-3m2/2+9m/2S△ABC最大值=4ac-b2/4a=27/8【方法三】平移法:平移直线AB,当直线AB与抛物线只有一个交点时,此时三角形ABC的面积最大。
解:设和y=-x+3平行的动直线的解析式为y=-x+b,用y=-x+b和y=-x²+2x+3联立方程组得:-x+b=-x²+2x+3,整理得:x²-3x+b-3=0当Δ=0时,b=21/4,此时的点C的坐标为(3/2,9/2)。
二次函数中不规则图形面积(三角形)

二次函数中不规则图形的面积
直接求解
1、如图,已知抛物线的顶点为M(2,-4),且过点A(-1,5),连结AM交x轴于点B.
(1)求这条抛物线的解析株式;
(2)求点B的坐标;
(3)设点P(x,y)是抛物线在x轴下方、顶点M左方一段上的动点,连结PO,以P为顶点、PQ为腰的等腰三角形的另一顶点Q在x轴上,过Q作x轴的垂线交直线AM于点R,连结PR.设三角形PQR的面积为s.求s与x之间的函数解析株式;
(4)在上述动点p(x,y)中,是否存在使S△POR=2的点?若存在,求点P 的坐标;若不存在,说明理由.
割补法
方法:如图,过ΔABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫ΔABC的“水平宽”(a),中间的这条直线在ΔABC 内部线段的长度叫ΔABC的“铅垂高(h)”,我们可得
1ah,即三角形面积等于水出一种计算三角形面积的新方法:SΔABC=
2
平宽与铅垂高乘积的一半.
1.已知:如图,二次函数y=a2x+bx+c的图象与x轴交于A,B两点,其中点A的坐标(-1,0),点C的坐标为(0,5),且抛物线经过(1,8),M为它的顶点
(1)求抛物线的解析式;
(2)求ΔMCB的面积
2、已知二次函数y=a2x+bx+c与X轴交于A(-1,0),B(3,0)两点,与y 轴交于点C(0,-3),顶点为P.
(1)求抛物线对应的函数解析式.
(2)在抛物线上(除点c外),是否存在点N,使得S NAB∆=S ABC∆若存在,请写出点N的坐标;若不存在,请说明理由。
补充:周长问题。
二次函数中三角形面积问题(公开课)PPT课件

y
(3)在BC上方抛物线上是否存
.P
在一点P,使得S△PBC=6,若存在, A 求出点P的坐标,若不存在,说明 (-1,0) O
BQ (5,0) x
理由。
C
( ) ( ) P 1-1 ,0 、 P 26 ,7
(0,-5)
.
D (2,-9)
.
16
巩固练习
已知二次函数 y=x2-4x-5与x轴交于A(-1,0)、
SΔBCD=15
A (-1,0) O
B (5,0) x
C
(0,-5)
.
D (2,-9)
.
14
巩固练习
已知二次函数 y=x2-4x-5与x轴交于A(-1,0)、
B(5,0)两点,与y轴交于点C(0,-5).
点D(2,-9)是抛物线的顶点。
y
(2)设M(a,b)(其中0<a<5)
是抛物线上的一个动点,试求 △BCM面积的最大值,
A
B
(-1,0) O N (5,0) x
及此时点M的坐标。
△BCM面积的最大为值125 8
C
.M
(0,-5)
.
M(
5 2
,-
35 4
)
.
D (2,-9)
15
巩固练习
已知二次函数 y=x2-4x-5与x轴交于A(-1,0)、
B(5,0)两点,与y轴交于点C(0,-5).
点D(2,-9)是抛物线的顶点。
(1,4)
P
4
(0,3) C 3
S△ BOC=_______
2
1
(-1,0)
A O
.
B(3,0)
2
5
二次函数之“铅垂法”求三角形面积

二次函数之“铅垂法”求三角形面积求三角形面积往往用公式12S a h∆=或1sin2S ab C∆=进行计算。
在二次函数里,有时用公式求三角形面积有一定的难度,我们不妨考虑用“铅垂法”来解决。
图1 图2作法:1、作铅直线PM交线段AB于点M;2、分别过A、B两点作PM的垂线段。
计算:如图1:S△PAB= S△PMA+S△PMB=12×PM×h2+12×PM×h1=12×PM×(h2+h1);①如图2:S△PAB= S△PMA﹣S△PMB=12×PM×h2-12×PM×h1=12×PM×(h2-h1)。
②理解:我们把公式中的PM称为三角形的“铅直高度”,把(h2+h1)或(h2-h1)称为三角形的“水平宽度”,则三角形的面积等于“铅直高度”与“水平宽度”积的一半。
特别地,在二次函数中,三角形的“铅直高度”就是动点P和铅直线PM与线段AB交点M的纵坐标之差(y P -y M),“水平宽度”就是两定点A与B的横坐标之差(x B-x A),即S△=12×(y P-y M)×(x B-x A)。
我们把这种求三角形面积的方法叫做“铅垂法”。
运用:例:如图,直线l:y=−x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2−2ax+a+4(a<0)经过点B。
(1)求该抛物线的函数表达式;(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M 的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值及此时动点M的坐标。
解答:(1)y=-x 2+2x+3;(2)过点M 作MC ⊥x 轴交直线AB 于点C 。
设M (t ,-t 2+2t+3),则C (t ,-t+3)。
∵A (3,0),B (0,3)∴S=12×〖(-t2+2t+3)-(-t+3)〗×(3-0)化简整理得:23327()224S t =--+。
二次函数中有关三角形面积的求解[下学期]--湘教版
![二次函数中有关三角形面积的求解[下学期]--湘教版](https://img.taocdn.com/s3/m/e8fcc472a1c7aa00b42acb44.png)
二次函数存在性——直角三角形ppt课件
精选ppt课件
22
精选ppt课件
9
自学指导4(4分钟)
在抛物线y=x2-x-2上是否存在点P ,使△PAC是以AC为
直角边的三角形?若存在,求出所有符合条件的点P的
坐标;
情况 :当 一 PC 9A 00 时
y=x2-x-2
P1
(
3 2
,
7 2
)
情况 :当 二 PA 9 C00 时
P2
(
5 2
,
7 4
)
(-1,0)A O
④在抛物线上求点Q,使△BCQ是以BC为直角边的 直角三角形.
yx2 2xk
精选ppt课件 yx2 2xk
19
4.如图,矩形OABC的顶点A在x轴的正半轴上,点B的坐 标为(1,3),把矩形绕点B旋转一定的角度,使它的 顶点O落在x轴的点D处,已知M是第四象限内纵坐标为-1 的点,以M为顶点的抛物线正好过O、D两点. (1)求点D的坐标; (2)求抛物线的解析式; (3)在抛物线上是否存在点N,使以O、M、N为顶点的 三角形为直角三角形?若存在,求出所有满足条件的点 N的坐标;若不存在,请说明理由.
精选ppt课件
14
当堂训练(6分钟)
(2012•赤峰改编)如图,抛物线y=x2-bx-5与x轴交于A、 B两点(点A在点B的左侧),与y轴交于点C,点C与点F 关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|: |OA|=5:1. (1)求抛物线的解析式; (2)求直线AF的解析式; (3)在直线AF上是否存在 点P,使△CFP是直角三角形? 若存在,求出P点坐标;若不 存在,说明理由.
(4)在抛物线上是否存在点M,
使△ACM是以AC为直角边的三
二次函数中的三角形面积问题

探究
例1. 如图,抛物线 y = - x2 - 2x +3
与x轴交于点A、B(点A在点B右侧), 与y轴交于点C,若点E为第二象限 抛物线上一动点,连接BE、CE, 求四边形BOCE面积的最大值,并 求此时E点的坐标. (至少用2种方法)
中考链接
【中考链接1】
如图,已知二次函数
的图象与直
线 AC 相交于A ,C 两点,与 x 轴的另一个交点为 B ,
(2)连结 AC ,点 P 是位于线段 BC 上方的抛物线上一动
点,若直线 PC 将 △ABC 的面积分成 1 : 3 两部分,求
此时点 P 的坐标.
二次函数中的三角形面积问题
A
A
HB A
C
DB
C B
C
A
C D B
思想:化难为易、化斜为直 方法:公式法、割补法、铅垂法 、切线法
边在坐标轴上, 取三角形的底边
时,一般以坐标
轴上线段或以与 坐标轴平行的线 段为底边
底边
三边
数坐在标形 结均在不坐合
轴上 标轴上
三边均不在坐标 轴上的三角形采 用割或补的方法 把它转化成易于 求出面积的图形
抛物线的顶点为 D,对称轴与 x 轴的交点为 E,连接
BC.其中A(-3,0),B(1,0)
(1)求直线 AC 的函数表达式;
(2)在抛物线上是否存在一点 M(不与C重合),使
S△ACM = S△ABC ? 若存在,求出点 M 的坐标;若不存
在,请说明理由.
探究
例2. 如图,已知抛物线 y = - x2 - 2x +3过点 O
ι 的直线 将
分成△面AB积C为
1 : 2的两部分,求该直线与抛物线的交
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小 结:
二次函数中三角形面积的求法: 1、公 式 法 2、“割补法” 3、新公式法:水平宽与铅垂高乘积的一半 注意:点的坐标与线段长度之间的相互转化
二次函数中的三角形面积
陶朱初中 金 戈
引题
yD
C
如图:抛物线 yx2与2x轴3 x
交于A、B两点(点A在点B的左侧),与
y轴交于点C,点D是抛物线的顶点。
Ao
Bx
y
yD
yD
yD
C
C
C
Ao Bx Ao B x
o B x Ao
x
△ABC
△ABD △BCD
△ACD
以A、B、C、D为顶点的三角形有哪些?
引题
C(x , C
y ),D(x ,
C
D
y ), D
水平宽:ax x 铅垂高:hA D yy,
C
B
AD
11 S AB C 2a h2(xcxB)y(AyyD )
A
铅垂高
h
C
D
x
B
水平宽
aa
图12-1
y
B
A
C
o
x
A(-1,5) B(4,7) C(2,1)
割补法 新公式法
运用:
例:如图1,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),
E ( 1 , 2 ) DE=2
1 2 S△BCD=
×2×(1+2)= 3
引题
如图:抛物线 yx2与2x轴3 x
交于A、B两点(点A在点B的左侧),与
y轴交于点C,点D是抛物线的顶点。
yD
C
E
Ao
x
△ACD
延伸拓展
我们如果把△ABC 放到直角坐标系中,
A(x A,
,
yA),B(xB,
y ), B
OA,将线段OA绕原点O顺时针旋转120°,得到线段OB. (1)求点B的坐标; (2)求经过A、O、B三点的抛物线的解析式; (3)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那 么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的 最大面积;若没有,请说明理由.
y
B
C
A
OMx
P
y轴交于点C,点D是抛物线的顶点。
yD
FC
B(3,0) C(O,3) D(1,4)
o Bx
△BCD
F(0,4)
割补法
引题
如图:抛物线 yx2与2x轴3 x
交于A、B两点(点A在点B的左侧),与
y轴交于点C,点D是抛物线的顶点。
yD
C
B(3,0) C(O,3) D(1,4)
E
o Bx
△BCD
直线BC的解析式:y= –x+3
x
SABD12ABDD 1
△ABD
SABD2448
可以直接利用面积公式:
三角形的一边平行(或垂直)于一条坐标轴
y
A
B
Ay
C
o
x
B
C
o
x
A(1,5) B(6,5) C(3,1)
A(-1,6) B (4,3) C(-1,1)
引题
如图:抛物线 yx2与2x轴3 x
交于A、B两点(点A在点B的左侧),与
yD
C
如图:抛物线 yx2与2x轴3 x
交于A、B两点(点A在点B的左侧),与
y轴交于点C,点D是抛物线的顶点。
Ao
Bx
y
yD
yD
yD
C
C
C
Ao Bx Ao B x
o B x Ao
x
△ABC
△ABD △BCD
△ACD
如何求这些三角形的面积呢?
引题
如图:抛物线 yx2与2x轴3 x
交于A、B两点(点A在点B的左侧),与
1
Q
P y 1 Q y 2 ( x 2 2 x 3 ) ( x 3 ) x 2 3 x
O1
A
x S PA 8 9 B S C,A 1 2 B 3 ( x2 3 x)8 9 3
x 3 2
代1入 x2y 2x3,
y1
15 4
P(3 ,15) 24
练习:如图,在直角坐标系中,点A的坐标为(-2,0),连结
交y轴于点B。
(1)求抛物线和直线AB的解析式;
(2)求△CAB的面积S△CAB ;
(3)设点P是抛物线(在第一象限内)上的一个动点,
是否存在一点P,使S△PAB=
9 8
S△CAB ,若存在,求出P点的坐标;
若不存在,请说明理由。
y
C
A
铅垂高
h
C
B
D 1 O1
图1
Ax
B
水平宽
a
图2
S水 平 2宽 铅垂高
y轴交于点C,点D是抛物线的顶点。
y
C
Ao Bx
△ABC
A(-1,0) B(3,0) C(0,3)
SABC12ABCO SABC12436
引题
如图:抛物线 yx2与2x轴3 x
交于A、B两点(点A在点B的左侧),与
y轴交于点C,点D是抛物线的顶点。
yD
A(-1,0) B(3,0) D(1,4)
A
o D/ B
解(:1)抛物线解析y1式为(x1)2 4,即y1 x2 2x3
直A 线 解 B 析 y2式 x ห้องสมุดไป่ตู้ 3.
y ( 2 ) C ( 1 , 4 ) 当 , x 1 时 , y 1 4 , y 2 2 .
CP B
CA 的 B铅 C锤 D 42 高 2 .
SCAB12323
D
(3)设P点的横坐标为x,△PAB的铅垂高为h
