灰色系统预测GM1,1模型及其Matlab实现
基于MATLAB的灰色预测GM(1,1)模型在经济分析中的应用

基于MATLAB的灰色预测GM(1,1)模型在经济分析中的
应用
宋秀英
【期刊名称】《数学学习与研究:教研版》
【年(卷),期】2011(000)011
【摘要】灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律.MATLAB具有强大的数据处理和分析功能,可以方便、快捷、准确、直观地进行预测分析.本文介绍了灰色预测模型GM(1,1)的基本原理和精度检验方法,并用GM(1,1)模型对经济指标进行了预测.考虑到人工计算的复杂性和不准确性,本文将MATLAB程序用于GM(1,1)模型对经济指标的预测中,得到了理想的预测结果.
【总页数】3页(P93-95)
【作者】宋秀英
【作者单位】四川信息职业技术学院数学教研室,628017
【正文语种】中文
【中图分类】N941.5
【相关文献】
1.灰色预测系统GM(1,1)模型及其Matlab实现 [J], 殷鹏远
2.改进的灰色预测GM(1,1)模型的MATLAB实现 [J], 杨旭
3.灰色预测GM(1,1)模型在大学普及率中的应用研究
——基于西藏GER的实证分析 [J], 邱婧玲
4.灰色预测GM(1,1)模型在大学普及率中的应用研究--基于西藏GER的实证分析[J], 邱婧玲
5.福建省2030年碳达峰前二氧化碳排放趋势研究——基于GM(1,1)、GM(2,1)与GM(1,1)邓聚龙灰色预测模型 [J], 柳尧云;林润玮;阎虎勤
因版权原因,仅展示原文概要,查看原文内容请购买。
灰色系统G(1,1)预测步骤【模板带代码】

=3499.075e -0.1062t
3641.075
编写程序
u=alpha(2)/alpha(1) v=X0(1)-u v=3499.075 u=—3641.075
(5)进行参差检验
1)根据预测公式,计算
v=3499.075 u=—3641.075
Xˆ
1
k
1
X
0
1
for n=0:10
X2(n+1)=v*exp(-alpha(1)*n)+u
end
X2
2.0690
2)累减生成序列
Xˆ X3 =1.0e+003 * (0) 0.1420 0.4079 0.4536
0.5044
0.7713 0.8577 0.9537 1.0605
源程序:X3(1)=X2(1)
for m=1:10
kesi =
4.4388 339.0664 176.2445 203.6132
0 0.1998 1.2682 0.2130 0.8524 0.1330
0.0089
0.3767
0.2203
0.4155
{0%,19.98%,126.82%,0.89%,37.67% ,22.03% ,41.55% ,21.30%,85.24%,13.30%}
e=
179.4592 111.5134 74.1747 175.0204 159.6072 29.2461 215.2168 33.1910
3.2147 24.1540
源程序:S0=0.6745*X0std e=abs(daita0-daita0mean) 对所有的 e 都小于 S0 ,故小参差概率 P(k S0) 1 0.95
Matlab+灰色预测模型模型GM(1,1)
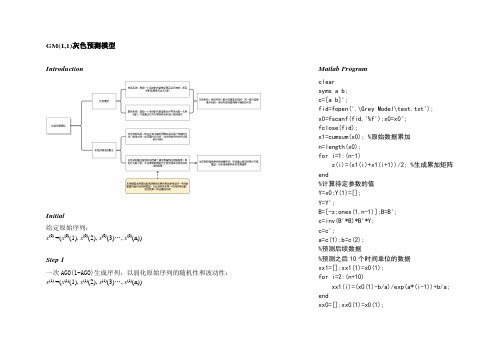
GM(1,1)灰色预测模型IntroductionInitial给定原始序列:x(0) =(x(0)(1), x(0)(2), x(0)(3)…, x(0)(n))Step 1一次AGO(1-AGO)生成序列,以弱化原始序列的随机性和波动性:x(1) =(x(1)(1), x(1)(2), x(1)(3)…, x(1)(n)) Matlab Programclearsyms a b;c=[a b]';fid=fopen('.\Grey Model\test.txt');x0=fscanf(fid,'%f');x0=x0';fclose(fid);x1=cumsum(x0); %原始数据累加n=length(x0);for i=1:(n-1)z(i)=(x1(i)+x1(i+1))/2; %生成累加矩阵end%计算待定参数的值Y=x0;Y(1)=[];Y=Y';B=[-z;ones(1,n-1)];B=B';c=inv(B'*B)*B'*Y;c=c';a=c(1);b=c(2);%预测后续数据%预测之后10个时间单位的数据xx1=[];xx1(1)=x0(1);for i=2:(n+10)xx1(i)=(x0(1)-b/a)/exp(a*(i-1))+b/a; endxx0=[];xx0(1)=x0(1);Step 2(1) dx (1)dt+ax (1)(t )=u ,式中a, u 为待定系数。
灰微分方程模型为:x (0)(k )+az (1)(k )=u ,z 为背景值z (1)(k )=1/2(x (1)(k )+x (1)(k −1))(2) 构造矩阵B 和数据向量Y nY n =Ba ̂Y n =[ x (0)(2)x (0)(3)⋮x (0)(n )] , B =[ −1/2(x (1)(1)+x (1)(2)),−1/2(x (1)(2)+x (1)(3)),⋮−1/2(x (1)(n −1)+x (1)(n )), 1 1 ⋮ 1]a ̂=(au)=(B T B)−1B T Y nStep 3模型响应函数x ̂(1)(k +1)=(x (0)(1)−u a )e −ak +u ax ̂(0)(k +1)=x ̂(1)(k +1)−x ̂(1)(k )Step 4检验和判断GM(1,1)模型的精度 (1) 残差检验for i=2:(n+10)xx0(i)=xx1(i)-xx1(i-1); end%关联度检验 for i=1:ne(i)=abs(x0(i)-xx0(i)); endmmax=max(e); for i=1:nee(i)=0.5*mmax/(e(i)+0.5*mmax); endr=sum(ee)/n; %后验差检验x0bar=sum(x0)/n; s1=0; for i=1:ns1=s1+(x0(i)-x0bar)^2; ends1=sqrt(s1/n); s2=0;ebar=sum(e)/n; for i=1:ns2=s2+(e(i)-ebar)^2; ends2=sqrt(s2/n); C=s2/s1; p=0;for i=1:nif abs(e(i)-ebar)<0.6745*s1绝对误差:ε(k)=|x(0)(k)−x̂(0)(k)|相对误差:Φ(k)=ε(k)x(0)(k)(2) 关联度检验分辨率β一般取0.5,此时若关联度大于0.6则认为模型可接受(3) 后验差检验和小误差概率原始序列标准差:S1=√∑[x(0)(i)−x̅(0)]2n绝对误差序列标准差:S2=√∑[ε(i)−ε̅]2n计算方差比:C=S2S1小误差概率:P=P{|ε(i)−ε̅|<0.6745S1}p=p+1;endendp=p/n;Cpif p>0.95&C<0.35disp('预测精度好');else if p>0.8&C<0.5disp('预测合格');else if p>0.7&C<0.65disp('预测勉强合格'); elsedisp('预测不合格'); endendend%原始数据与预测数据进行比较t1=1:n;t2=1:(n+10);xx0plot(t1,x0,'o',t2,xx0)。
灰色预测法GM(1,1)模型

灰色预测法GM (1,1)模型作业一、GM (1,1)模型的建立:原始数据:{142,340,200,500,900,800,490,980,463,1100}记作}1100,463,980,490,800,900,500,200,340,142{)0(=X 。
(1)、一次累加生成序列为:).()1()(),1()1()0()1()1()0()1(k X k X k X X X +-==2≥k那么 }5915,4815,4352,3372,2882,2082,1182,682,482,142{)1(=X 。
(2)、由一次累加序列)1(X生成紧邻均值序列)1(Z [],...3,2,)1()(21)1()1(=-+=k k X k X 那么)1(Z }5365,5.4583,3862,3127,2482,1632,932,582,312{=。
(3)、GM (1,1)的灰微分方程模型为:b k aZ k X=+)()()1()0(。
设∧α为待估计参数向量,⎥⎦⎤⎢⎣⎡=∧b a α。
利用最小二乘法得到Y B B B ')'(1-∧=α, 其中⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---=1)10(......1)3(1)2()1()1()1(Z Z Z B ,⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=)10(...)3()2()0()0()0(X X X Y 。
解得⎥⎦⎤⎢⎣⎡=∧b a α⎥⎦⎤⎢⎣⎡-=6018.3711062.0。
(4)、GM (1,1)的灰微分方程模型 b k aZ k X=+)()()1()0(的时间相应序列为:ab e a b X k X ak +⋅-=+-∧))1(()1()0()1(。
由.6018.371,1062.0=-=b a 令.)1(,)0(u X v ab u -== 计算得到1.3499-=u , 1.3641=v 。
所以ab e a b X k X ak +⋅-=+-∧))1(()1()0()1(1.34991.36411062.0-=k e 。
灰色模型预测GM(1,1)MATLAB程序代码

灰⾊模型预测GM(1,1)MATLAB程序代码版权所有引⽤请注明出处function gmcal=gm1(x)%% ⼆次拟合预测GM(1,1)模型%x = [5999,5903,5848,5700,7884];sizexd2 = size(x,2);%求数组长度k=0;for y1=xk=k+1;if k>1x1(k)=x1(k-1)+x(k);%累加⽣成z1(k-1)=-0.5*(x1(k)+x1(k-1));%z1维数减1,⽤于计算Byn1(k-1)=x(k);elsex1(k)=x(k);endend%x1,z1,k,yn1sizez1=size(z1,2);%size(yn1);z2 = z1';z3 = ones(1,sizez1)';YN = yn1'; %转置B=[z2 z3];au0=inv(B'*B)*B'*YN;au = au0';afor = au(1);ufor = au(2);ua = au(2)./au(1);constant1 = x(1)-ua;afor1 = -afor;x1t1 = 'x1(t+1)';estr = 'exp';tstr = 't';leftbra = '(';rightbra = ')';strcat(x1t1,'=',num2str(constant1),estr,leftbra,num2str(afor1),tstr,rightbra,'+',leftbra,num2str(ua),rightbra) %输出时间响应⽅程k2 = 0;for y2 = x1k2 = k2 + 1;if k2 > kelseze1(k2) = exp(-(k2-1)*afor);endendsizeze1 = size(ze1,2);z4 = ones(1,sizeze1)';G=[ze1' z4];X1 = x1';au20=inv(G'*G)*G'*X1;au2 = au20';Aval = au2(1);Bval = au2(2);strcat(x1t1,'=',num2str(Aval),estr,leftbra,num2str(afor1),tstr,rightbra,'+',leftbra,num2str(Bval),rightbra) %输出时间响应⽅程nfinal = sizexd2-1 + 1; %决定预测的步骤数5 这个步骤可以通过函数传⼊%nfinal = sizexd2 - 1 + 1;%预测的步骤数 1for k3=1:nfinalx3fcast(k3) = constant1*exp(afor1*k3)+ua;end%⼀次拟合累加值for k31=nfinal:-1:0if k31>1x31fcast(k31+1) = x3fcast(k31)-x3fcast(k31-1);elseif k31>0x31fcast(k31+1) = x3fcast(k31)-x(1);elsex31fcast(k31+1) = x(1);endendendx31fcast%⼀次拟合预测值for k4=1:nfinalx4fcast(k4) = Aval*exp(afor1*k4)+Bval;end%x4fcastfor k41=nfinal:-1:0if k41>1x41fcast(k41+1) = x4fcast(k41)-x4fcast(k41-1);elseif k41>0x41fcast(k41+1) = x4fcast(k41)-x(1);elsex41fcast(k41+1) = x(1);endendendx41fcast,x%⼆次拟合预测值%***精度检验p C************//////////////////////////////////k5 = 0;for y5 = xk5 = k5 + 1;if k5 > sizexd2elseerr1(k5) = x(k5) - x41fcast(k5);endend%err1%绝对误差xavg = mean(x);%xavg%x平均值err1avg = mean(err1);%err1avg%err1平均值k5 = 0;s1total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2elses1total = s1total + (x(k5) - xavg)^2;endends1suqare = s1total ./ sizexd2;s1sqrt = sqrt(s1suqare);%s1suqare,s1sqrt%s1suqare 残差数列x的⽅差 s1sqrt 为x⽅差的平⽅根S1k5 = 0;s2total = 0 ;for y5 = xk5 = k5 + 1;if k5 > sizexd2elses2total = s2total + (err1(k5) - err1avg)^2;endends2suqare = s2total ./ sizexd2;%s2suqare 残差数列err1的⽅差S2Cval = sqrt(s2suqare ./ s1suqare);Cval%nnn = 0.6745 * s1sqrt%Cval C检验值k5 = 0;pnum = 0 ;for y5 = xk5 = k5 + 1;if abs( err1(k5) - err1avg ) < 0.6745 * s1sqrtpnum = pnum + 1;%ppp = abs( err1(k5) - err1avg )elseendendpval = pnum ./ sizexd2;pval%p检验值%arr1 = x41fcast(1:6)%预测结果为区间范围预测步长和数据长度可调整程序参数进⾏改进。
GM(1,1)模型的Matlab实现(范例2)

GM (1,1)模型的MATLAB 实现摘要 本文介绍了灰色预测()1,1GM 模型的基本原理,并在其基础上利用MATLAB 软件进行实现,给出相应的MATLAB 算法。
并通过实例检验MATLAB 算法的正确性与通用性。
关键词模型; 灰色系统; MATLAB ;1 引言1.1灰色预测理论基本介绍灰色系统是指系统论中一部分信息是已知的,但另一部分信息是未知的,系统内各因素间有不确定的关系。
而灰色预测模型是灰色系统理论的重要内容之一,其中灰色模型是邓聚龙教授在1982年提出的一种新的模型计算方法,被广泛应用于农业、工业、医学、军事、经济、交通、生态等许多科学领域,解决了许多领域中的复杂实践问题[13]-。
且对于杂乱无章表征数据,灰色预测能发现其内在必然的联系与规律,即通过鉴别系统各因素之间发展趋势的相异程度,进行关联分析,并对原始数据进行一定的处理,来寻找系统变动的规律,生成有较强规律性的数据序列,建立相应的微分方程模型,从而预见系统的未来的发展趋势及状况。
灰色预测法是用等时距观测到的反映预测对象特征的一系列数量值,构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
灰色预测有其四种常见的类型,分别为:灰色时间序列预测、畸变预测、系统预测、拓扑预测。
灰色模型(Grey Models )简称GM 模型,是灰色系统理论(Grey System Theory )的一个基本模型。
GM 模型的一般模型为,当中时,GM 模型不能做预测,只能用于分析因子之间的相互作用。
做预测用的一般为模型,其中,用的最多的则是用灰色微分拟合法建立的模型。
由于它预测要求所需样本量少(至少四组),不需要计算统计特征量、不用考虑样本变化的趋势、运算简便、在短期内精度高、预测效果好、容易检查等优点。
本文通过运用MATLAB 软件对模型进行程序实现。
增强模型通用性与实用性,方便今后对其使用。
假设我们有一段原始时间序列:为了弱化原始时间序列的随机性,在建立灰色预测模型之前,我们需要先对原始时间序列进行数据处理,经过数据处理后的时间序列称为生成列。
基于MATLAB的灰色预测GM(1

‘ ( 2)
z
一
‘ 3) ”(
‘( ) 。 3 ’
型 . M( , ) 型 是基 于 随 机 的 原 始 时 间序 列 , 按 时 间 累 G 11模 经 加 后 所形 成 的新 的 时 间序 列 呈 现 的 规 律 可 用 一 阶线 性 微 分
方 程 的解 来 逼 近 . 证 明 , 一 阶 线 性 微 分 方 程 的解 逼 近 所 经 经
对 生 成 的时 间序 列 , M( , ) 应 的微 分 方 程 为 G 11相
+
d t
: 6 .
息. 含有已知信息又 含有未 知 的 、 确 知的信 息 的系统 , 既 非
求 解 微 分 方 程 , 可 得 到 预 测模 型 : 即
称 为 灰 色 系 统 . 色 预 测 是 灰 色 系 统 建 模 的 具 体 数 学 方 法 灰
之 一 , 色 预 测 不 是 把 观 测 到 的数 据 序 列 视 为 一 个 随 机 过 灰
… ) (一 = 1 )
&=( B B)IB y , 中 1 其
一
+, , , ÷㈦ z m , …
程 , 是 看作 随 时 间 变 化 的 灰 色 量 或 灰 色 过 程 , 色 预 测 通 而 灰
过 鉴 别 系 统 因素 之 间 发 展 趋 势 的相 异 程 度 , 进 行 关 联 分 即 析 , 对原始数据进行生成处理来寻 找系统变动 的规律. 并 基 于灰 色 系统 理 论 的 灰 色 模 型 主 要 有 GM( , ) 色 预 测 模 11灰
上 式 中 , 数 n b 用 最 小 二 乘 法 估 计 , =( , ) 参 ,是 即 o 6 ,
功 能 , 以 方便 、 捷 、 确 、 观 地 进 行 预 测 分 析 . 文 介 可 快 准 直 本
用Matlab实现GM_1_1_灰色模型的供电量预测

人工智能及识别技术ARTIFICIAL INTELLIGENCE AND IDENTIFICATION TECHNIQUES1灰色预测模型GM (1,1)灰色系统理论是研究解决灰色系统分析、建模、预测、决策和控制的理论,由我国邓聚龙教授在1982年首次提出的。
灰色系统理论具有所需样本数据少,不需要计算统计特征量等优点。
灰色预测解决了连续微分方程的建模问题。
它通过原始数据的整理来寻找数的规律。
在建模时,首先对原始数据进行累加或累减生成,形成新的序列,对新序列建立微分方程模型和解析分析,达到预测原始序列的目的。
其中GM (1,1)模型是基于灰色系统理论的常用预测模型。
因为它具有要求原始数据少、不考虑分布规律、不考虑变化趋势、运算方便、短期精度高、易于检查的优点,得到了广泛的应用。
它的基本原理是:认为原始数列是逐步增长或减少的,通过对原始数列应用累加生成这样的数据处理方法可以得到一条具有指数增长规律的上升形状数列。
由于一阶微分方程的解即是指数增长形式,因此通过建立一阶微分方程模型和累减生成还原就可以得到预测数列。
2GM (1,1)模型的建立(1)对随机序列(i=0,1,2…n )作一次累加(1…AGO)生成序列(i=0,1,2…n ),其中。
(2)按照X i (1)的指数增长规律,可知X i (1)满足下列一阶线性微分方程。
(X(1)是时间t 的函数,这是灰色方程,部分数据未知)(3)参数估计:记待定,经离散化处理,得:Y n=BA.使用最小二乘法求出A 的近似解:,将近似值代入原微分方程:(*)(原微分方程的白化方程)其中(4)Xi (1)的预测值:求解微分方程(*)得到原微分方程的近似解,其中X 1(1)=X 1(0);写成离散形式,得到X i (1)的预测值:(5)X i(0)的预测值:3应用实例用Matlab 实现GM (1,1)灰色模型的供电量预测梁智勇(广东电网公司肇庆供电局,肇庆526040)摘要:介绍灰色预测模型GM (1,1)在电力系统中的预测应用,同时在Matlab 平台上实现了灰色模型GM (1,1)函数的编制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色系统预测GM(1,1)模型及其Matlab实现三天三夜72小时:读懂题目-》查找文献资料-》选择题目-》重查找文献资料-》精读其中几篇-》查找资料的资料。
在数学建模中常常会遇到数据的预测问题,有些赛题中,预测占主导地位,例如:2003年A题 SARS的传播问题;2005年A题长江水质的评价和预测问题;2006年B题艾滋病疗法的评价及疗效的预测问题;2007年A题中国人口增长预测问题。
有些问题则是需要在求解的过程中进行预测,如2009年D题“会议筹备”对与会人数的确定等。
参考资料:《灰色系统理论及其应用第五版》作者:刘思峰,党耀国等著出版时间:2010.05 校超星数字图书馆可阅读。
灰色模型(Gray Model)有严格的理论基础,最大优点是实用。
用灰色模型预测的结果比较稳定,不仅适用于大数据量的预测,在数据量较少时(>3)预测结果依然较准确。
预备知识(1)灰色系统白色系统是指系统内部特征是完全已知的,即人们不仅知道该系统的输入——输出关系,而且知道实现输入——输出关系的结构与过程;黑色系统是指系统内部信息完全未知的,即人们只知道该系统输入——输出关系,但不知道实现输入——输出关系的结构与过程;而灰色系统是介于白色系统和黑色系统之间的一种系统,灰色系统其内部一部分信息已知,另一部分信息未知或不确定。
例如,一个加有电压的电阻,也是一个系统,根据欧姆定律,I=U/R,当电阻的大小知道后,便可由多大电压算出能得到多大电流。
电压与电流之间有明确的关系或函数,这便是白色系统。
因此,这样的系统要求有明确的作用原理,一个有明确作用原理的系统必定是具有确定结构的,必定是有物理原型的。
然而许多社会经济系统都没有物理原型,虽然知道影响系统的某些因素,但很难明确全部因素,更不可能确定因素之间的映射关系。
这种没有确定的映射关系(函数关系)的系统是灰色系统。
(2)灰色预测灰色预测,是指对系统行为特征值的发展变化进行的预测,对既含有已知信息又含有不确定信息的系统进行的预测,也就是对在一定范围内变化的、与时间序列有关的灰过程进行预测。
尽管灰过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此得到的数据集合具备潜在的规律。
灰色预测是利用这种规律建立灰色模型对灰色系统进行预测。
目前使用最广泛的灰色预测模型就是关于数列预测的一个变量、一阶微分的GM(1,1)模型。
它是基于随机的原始时间序列,经按时间累加后所形成的新的时间序列呈现的规律可用一阶线性微分方程的解来逼近。
经证明,经一阶线性微分方程的解逼近所揭示的原始时间序列呈指数变化规律。
因此,当原始时间序列隐含着指数变化规律时,灰色模型GM(1,1)的预测是非常成功的。
目前,灰色模型GM(1,1)己广泛应用于工程技术、社会、经济、农业、生态、环境等各种系统的预测中。
1 灰色预测基础知识灰色系统理论认为:系统的行为现象尽管是朦胧的,数据是复杂的,但它毕竟是有序的,是有整体功能的。
在建立灰色预测模型之前,需先对原始时间序列进行数据处理,经过数据预处理后的数据序列称为生成列。
对原始数据进行预处理,不是寻求它的统计规律和概率分布,而是将杂乱无章的原始数据列通过一定的方法处理,变成有规律的时间序列数据,即以数找数的规律,再建立动态模型。
灰色系统常用的数据处理方式有累加和累减两种,通常用累加方法。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物的未来发展趋势。
灰色预测的数据是通过生成数据的模型所得到的预测值的逆处理结果。
灰色预测是以灰色模型为基础的,在诸多的灰色模型中,以灰色系统中单序列一阶线性微分方程模型 GM(1,1)模型最为常用。
下面简要地介绍 GM(1,1)模型。
设有原始数据列x(0)=(x(0)(1),x(0)(2),…,x(0)(n)),n 为数据个数。
如果根据x(0)数据列建立 GM(1,1)来实现预测功能,则基本步骤如下:(1)原始数据累加以便弱化随机序列的波动性和随机性,得到新数据序列:x (1) = {x (1)(1),x (1)(2),…,x (1)(n)}其中,x (1)(t)中各数据表示对应前几项数据的累加。
x (1)(t)= ∑=t1k )0()k (x , t=1,2,…,n(2)对x (1)(t)建立下述一阶线性微分方程: 即GM(1,1)模型。
u ax dtdx )1()1(=+ 其中,a,u 为待定系数,分别称为发展系数和灰色作用量,a 的有效区间是 (-2,2),并记a,u 构成的矩阵为灰参数∧a =⎪⎪⎭⎫⎝⎛u a 。
只要求出参数a,u,就能求出x (1)(t),进而求出x (0)的未来预测值。
(3)对累加生成数据做均值生成B 与常数项向量Yn,即B =⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+++- 1 (n))X 1)-(n (X 21 ... 1 (3))X (2)X (211 (2))X (1)X (21(1)1(1)(1)(1)(1))(--Yn=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛)n (x )3(x )2(x )0()0()0((4)用最小二乘法求解灰参数∧a ,则∧a =(B T B)-1B T Y n(5)将灰参数∧a 代入u ax dt dx )1()1(=+ ,并对u ax dtdx )1()1(=+进行求解,得 ∧X (1)(t+1)=(X (0)(1)-a u )at e -+au由于∧a 是通过最小二乘法求出的近似值,所 以xˆ(1)(t+1)是一个 近似表达式,为了与原序列x (1)(t+1)区分开来,故记为xˆ(1)(t+1)。
式中t 为时间序列,可取年、季或月。
(6)对函数表达式xˆ(1)(t+1)及x ˆ(1)(t)进行离散,并将二者做差以便还原x (0)原序列,得到近似数据序列xˆ(0)(t+1)如下: xˆ(0)(t+1)=x ˆ(1)(t+1)-x ˆ(1)(t) (7)对建立的灰色模型进行检验,步骤如下:计算x (0)(t)与xˆ(0)(t)之间的残差e (0)(t)和相对误差q (0)(t): e (0)(t)=x (0)(t)-xˆ(0)(t) q (0)(t)=e (0)(t)/x (0)(t)等等。
(8)利用模型进行预测:x ˆ(0) ={x ˆ(0)(1),x ˆ(0)(2),…,x ˆ(0)(n ),xˆ(0)(n+1),…,x ˆ(0)(n+m)} 原数列的模拟 未来数列的预测应用举例取某高校2000年~2005年的某专业招生数据建模,见表1。
表以表1中的数据构造原始数据列X (0),即X (0)={X (0)(1),X (0)(2),X (0)(3),X (0)(4),X (0)(5),X (0)(6)}={132,92,118,130,187,207}对X(0)进行一次累加(1—AGO),生成数列:X (1)(k)=∑=ki 1X (0)(i)即X (1)={X (1)(1),X (1)(2),X (1)(3),X (1)(4),X (1)(5),X (1)(6)}={132,224,342,472,659,866} 和数据阵B 、数据列YnB =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡----- 1 5.762 1 5.5651 4071 2831178,Yn =(92,118,130,187,207)T经计算可得∧a =[a,u]T=⎥⎦⎤⎢⎣⎡-7878184.56205.0 进一步得到灰色预测模型GM(1,1)为∧X (1)(k)=(X (0)(1)-a u ))1(--k a e +a u=(132+277.))1(205.0-k e -277.=409.)1(205.0-k e-277.预测值及预测精度见表2。
表2 某高校专业招生预测值及预测精度表由表2知预测精度较高。
2006年某专业招生人数预测值为259人。
由于人数为整数,所以结果取整数部分。
GM(1,1)也是一种长期预测模型,在没有大的市场波动及政策性变化的前提下,该预测值应是可信的。
众所周知,影响招生人数的因素很多且难以预测。
因此,在采用灰色系统理论进行定量预测时,如果存在对预测对象影响较大的因素,就要在定性分析的基础上,寻找原始数据信息的突变点的量化值,然后再对预测值进行必要的修正,使预测值更接近实际情况,提高预测值的可信度,为科学决策提供可靠的数据。
另外,若作长期预测,要考虑对上限值的约束条件。
2 灰色预测的 MATLAB程序2.1 典型程序结构灰色预测中有很多关于矩阵的运算,这可是 MATLAB的特长,所以用 MATLAB是实现灰色预测过程的首选。
用 MATLAB编写灰色预测程序时,可以完全按照预测模型的求解步骤,即(1)对原始数据进行累加。
(2)构造累加矩阵B 与常数向量Yn。
(3)求解灰参数。
(4)将参数带入预测模型进行数据预测。
下面以某公司收入预测问题为例介绍灰色预测的 MATLAB实现过程。
已知某公司1999—2008年的利润为 (单位:元/年): [89677,99215,109655,120333,135823,159878,182321,209407,2466 19,300670],现在要预测该公司未来几年的利润情况。
具体的 MATLAB程序如下:clearsyms a u;c=[a u]'; %灰参数cA=[89677,99215,109655,120333,135823,159878,182321,209407,24 6619,300670]; %原始数据Ago=cumsum(A); %原始数据一次累加n=length(A); %原始数据个数for i=1:(n-1)C(i)=(Ago(i)+Ago(i+1))/2; %生成累加矩阵end% 计算待定参数的值Yn=A;Yn(1)=[];Yn=Yn';E=[-C;ones(1,n-1)];c=inv(E*E')*E*Yn;c=c';a=c(1);u=c(2);% 预测后续数据F=[];F(1)=A(1);for i=2:(n+10)F(i)=(A(1)-u/a)/exp(a*(i-1))+u/a ;endG=[];G(1)=A(1);for i=2:(n+10)G(i)=F(i)-F(i-1); %得到预测出来的数据endt1=1999:2008;t2=1999:2018;Gplot(t1,A,'o',t2,G) %原始数据与预测数据的比较运行该程序,得到的预测数据如下:G =1.0e+006 * Columns1through140.0897 0.0893 0.1034 0.1196 0.1385 0.1602 0.1854 0.2146 0.2483 0.2873 0.3325 0.3847 0.4452 0.5152 Columns15through200.5962 0.6899 0.7984 0.9239 1.0691 1.2371 该程序还显示了预测数据与原始数据的比较图。
