最大熵模型中的数学推导
证明开放系的最大熵原理
证明开放系的最大熵原理开放系的最大熵原理可以通过最大化系统的熵来进行证明。
假设有一个开放系统，可以与外界交换物质和能量。
我们想要通过最大熵原理来推导系统的平衡状态。
首先，我们需要定义开放系统的熵。
对于一个开放系统，其熵可以表示为:S = -∑(pi * ln(pi))其中，pi表示系统处于第i个可能的状态的概率。
这个表示形式是基于信息论的熵的定义，它代表了系统的不确定性。
接下来，我们引入一些约束条件。
对于一个开放系统，通常有一些由外界施加的约束条件，如能量守恒、质量守恒等。
我们可以用一组约束条件的形式表示出来:∑(ci * pi) = Ci这里，ci是一个与约束条件相关的常数，Ci是一个特定的约束条件的值。
然后，我们引入拉格朗日乘子法来解决最大化熵的问题。
我们可以定义拉格朗日函数:L = -∑(pi * ln(pi)) + ∑(λi * (∑(ci * pi) - Ci))其中，λi是拉格朗日乘子，用于处理约束条件。
接下来，我们对L求解最大值。
我们将L对pi求偏导，并令其等于零:∂L/∂pi = -1 - ln(pi) - λi * ci = 0根据上面的偏导数等于零的方程，我们可以得到:pi = e^(-1 - λi * ci)然后，我们将所有的pi相加，得到:∑pi = ∑e^(-1 - λi * ci)= e^(-1) * ∑e^(-λi * ci)由于所有的pi都是概率，所以∑pi = 1。
将这个条件应用到上面的等式中，我们得到:1 = e^(-1) * ∑e^(-λi * ci)我们可以将上述等式改写为:e = ∑e^(-λi * ci)接下来，我们考虑约束条件∑(ci * pi) = Ci。
我们将其代入到L函数中，得到: -λi * Ci + ln(∑e^(-λi * ci)) = 0整理上面的等式，我们可以得到:λi = ln(∑e^(-λi * ci)) / Ci通过上面的方程，我们可以求出λi的值。
最大熵模型简介
H ( p) p(x) log2 p(x)
x
p* arg max H ( p)
最大熵模型
❖ 例如： 给定一个词
假定已知存在四种词性：名词、动词、介词、指代词 ❖ 如果该词在语料库中出现过，并且属于名词的概率为70%，则判断
Generative Model vs. Discriminative Model
❖ Generative Model (GM): P(Y|X)=P(X|Y)P(Y)/P(X)，通 过求解P(X|Y)和P(Y)来求解P(Y|X)
❖ Discriminative Model (DM): 对P(Y|X)直接建模
纲要
❖ 最大熵原理 ❖ 最大熵模型定义 ❖ 最大熵模型中的一些算法 ❖ 最大熵模型的应用 ❖ 总结 ❖ 思考题
最大熵模型(Maximum Entropy
Model)
❖
假设有一个样本集合 (x1, x2 ,... xn )
特征(j对f1, pf2的...制fk )约可以表示为
，我们给出k个特征 , Ep( f j ) E~p( f j )
p(X=3)=p(X=4)=p(X=5)=p(X=6)=0.1
最大熵原理
❖ 最大熵原理：1957 年由E.T.Jaynes 提出。 ❖ 主要思想：
在只掌握关于未知分布的部分知识时，应该选取符合这些知识但熵值最 大的概率分布。
❖ 原理的实质：
前提：已知部分知识 关于未知分布最合理的推断＝符合已知知识最不确定或最随机的推断。 这是我们可以作出的唯一不偏不倚的选择，任何其它的选择都意味着我 们增加了其它的约束和假设，这些约束和假设根据我们掌握的信息无法 作出。
最大熵原理在推导分子数分布中的应用
式中，ｆ（ｘ）为 该 物 理 量 的 概 率 密 度 分 布 函 数；Ｄ 为概率密度分布函数的定义域。
根据最大熵 原 理，只 需 求 得 使 信 息 熵 在 约 束 条 件 下 达 到 最 大 值 的 函 数 ｆ（ｘ），便 可 确 定 该 物 理
量 的 概 率 密 度 分 布 函 数 。 为 求 得 ｆ（ｘ），可 以 利 用 拉格朗日法求泛函的约束极值。
（Ｓｃｈｏｏｌ ｏｆ Ｓｃｉｅｎｃｅ，Ｘｉａｎ Ｊｉａｏｔｏｎｇ Ｕｎｉｖｅｒｓｉｔｙ，Ｘｉａｎ Ｓｈａａｎｘｉ ７１００４９）
Ａｂｓｔｒａｃｔ Ｔｈｉｓ ｐａｐｅｒ ｂｒｉｅｆｌｙ ｉｎｔｒｏｄｕｃｅｓ ｔｈｅ ｐｒｉｎｃｉｐｌｅ ｏｆ ｍａｘｉｍｕｍ ｅｎｔｒｏｐｙ ａｎｄ ｄｅｄｕｃｅｓ ｔｈｅ ｎｕｍｂｅｒ ｍｏｌｅｃｕｌｅ ｄｉｓｔｒｉｂｕｔｉｏｎ ａｃｃｏｒｄｉｎｇ ｔｏ ｔｈｅ ｆｒｅｅ ｐａｔｈ ａｎｄ ａｌｔｉｔｕｄｅ．Ｔｈｅ ｄｅｒｉｖａｔｉｏｎ ｏｆ ｔｈｅ ｍｏｌｅｃｕｌｅ ｎｕｍｂｅｒ ｄｉｓｔｒｉｂｕｔｉｏｎ ａｃｃｏｒｄｉｎｇ ｔｏ ｔｈｅ ｆｒｅｅ ｐａｔｈ ａｂａｎｄｏｎｓ ａ ｎｏｔ ｓｏｌｉｄ ｈｙｐｏｔｈｅｓｉｓ ｉｎ Ｍｒ． Ｑｉｎ Ｙｕｎｈａｏｓ ｔｅｘｔｂｏｏｋ，ａｎｄ ｔｈｅ ｒｅｓｕｌｔｓ ａｒｅ ｃｏｉｎｃｉｄｅ ｗｉｔｈ ｔｈｅ ｔｅｘｔｂｏｏｋ．Ｔｈｅ ｄｅｒｉｖａｔｉｏｎ ｏｆ ｔｈｅ ｍｏｌｅｃｕｌｅ ｎｕｍｂｅｒ ｄｉｓｔｒｉｂｕｔｉｏｎ ａｃｃｏｒｄｉｎｇ ｔｏ ａｌｔｉｔｕｄｅ ｔａｋｅｓ ｉｎｔｏ ａｃｃｏｕｎｔ ｔｈｅ ｔｅｍｐｅｒａｔｕｒｅ ｃｈａｎｇｅ， ａｎｄ ｔｈｅ ｒｅｓｕｌｔｓ ａｒｅ ｉｎ ａｇｒｅｅｍｅｎｔ ｗｉｔｈ ｔｈｅ ｄａｔａ ｒｅｌｅａｓｅｄ ｂｙ ＮＡＳＡ． Ｋｅｙ ｗｏｒｄｓ ｓｔａｔｉｓｔｉｃ ｐｈｙｓｉｃｓ；ｍｏｌｅｃｕｌａｒ ｎｕｍｂｅｒ ｄｉｓｔｒｉｂｕｔｉｏｎ；ｆｒｅｅ ｐａｔｈ；ａｌｔｉｔｕｄｅ
《机器学习Python实现_05_线性模型_最大熵模型》
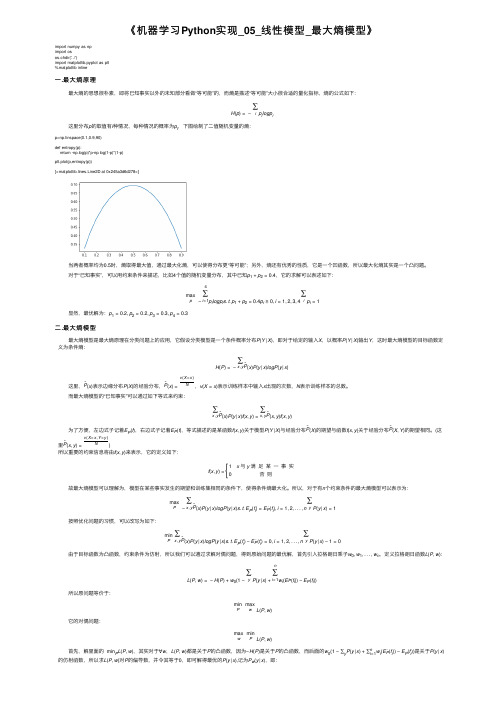
《机器学习Python 实现_05_线性模型_最⼤熵模型》import numpy as np import os os.chdir('../')import matplotlib.pyplot as plt %matplotlib inline⼀.最⼤熵原理最⼤熵的思想很朴素，即将已知事实以外的未知部分看做“等可能”的，⽽熵是描述“等可能”⼤⼩很合适的量化指标，熵的公式如下：H (p )=−∑i p i logp i这⾥分布p 的取值有i 种情况，每种情况的概率为p i ，下图绘制了⼆值随机变量的熵：p=np.linspace(0.1,0.9,90)def entropy(p):return -np.log(p)*p-np.log(1-p)*(1-p)plt.plot(p,entropy(p))[<matplotlib.lines.Line2D at 0x245a3d6d278>]当两者概率均为0.5时，熵取得最⼤值，通过最⼤化熵，可以使得分布更“等可能”；另外，熵还有优秀的性质，它是⼀个凹函数，所以最⼤化熵其实是⼀个凸问题。
对于“已知事实”，可以⽤约束条件来描述，⽐如4个值的随机变量分布，其中已知p 1+p 2=0.4，它的求解可以表述如下：maxp−4∑i =1p i logp i s .t .p 1+p 2=0.4p i ≥0,i =1,2,3,4∑i p i =1显然，最优解为：p 1=0.2,p 2=0.2,p 3=0.3,p 4=0.3⼆.最⼤熵模型最⼤熵模型是最⼤熵原理在分类问题上的应⽤，它假设分类模型是⼀个条件概率分布P (Y |X )，即对于给定的输⼊X ，以概率P (Y |X )输出Y ，这时最⼤熵模型的⽬标函数定义为条件熵：H (P )=−∑x ,y ˜P (x )P (y |x )logP (y |x )这⾥，˜P (x )表⽰边缘分布P (X )的经验分布，˜P (x )=v (X =x )N，v (X =x )表⽰训练样本中输⼊x 出现的次数，N 表⽰训练样本的总数。
高斯最大熵 证明
高斯最大熵证明
高斯最大熵问题的证明可以通过以下步骤进行：
1. 定义问题：假设我们有一个连续随机变量X，其概率分布函数为p(x)。
我们希望找到一个概率分布函数p(x)，使得它满足
一些约束条件，并且熵H(p)最大。
2. 熵的定义：对于一个概率分布函数p(x)，其熵的表达式为
H(p) = -∫p(x)log(p(x))dx，其中积分是在整个定义域上进行的。
3. 约束条件：我们希望找到的概率分布函数p(x)需要满足一些约束条件，这些约束条件可以是概率为1，期望值等于一些给
定的值等等。
4. 构建拉格朗日函数：为了求解这个问题，我们可以构建拉格朗日函数L(p,λ) = -∫p(x)log(p(x))dx + ∑λi(gi(p) - bi)，其中λi是
拉格朗日乘子，gi(p)是约束条件。
5. 最大化熵：我们希望找到一个概率分布函数p(x)，使得熵
H(p) = -∫p(x)log(p(x))dx最大化。
因此，我们需要最大化拉格
朗日函数L(p,λ)。
6. 求解偏导数为零：为了找到最大化的概率分布函数p(x)，我们需要求解偏导数dL(p,λ)/dp(x) = 0和dL(p,λ)/dλi = 0。
这些方
程的解将给出最大化熵的概率分布函数p(x)和拉格朗日乘子λi。
7. 高斯概率分布分析：在实际应用中，我们通常假设随机变量
X服从高斯分布，即p(x) = (1/sqrt(2πσ^2)) * exp(-(x-
μ)^2/(2σ^2))，其中μ是均值，σ是标准差。
通过解上述方程，我们可以得到满足约束条件的高斯分布概率函数，使得熵最大化。
这就是高斯最大熵问题的一个证明过程。
最大熵原理推导自由结合链末端距的径向分布函数
ρ( r) =
3 2πnl2
e 3
2
-
3 r2 2 nl2
(6)
此分布即为高斯分布 。故末端距的几率分布密度函数ρ( r) 符合高斯分布 。
又由 (1) 可得 :
f ( r) = 4πr2
3 2πnl2
e 3
2
-
3 r2 2 nl2
此式即为自由结合链末端距的径向分布函数 。
参考文献 :
[ 1 ] 何曼君 ,陈维孝 ,董西侠. 高分子物理 (修订版第一版) . 上海 :复旦大学出版社 ,1990. [ 2 ] 吴大诚. 高分子构象统计理论引导. 成都 :四川教育出版社 ,1985. [ 3 ] 马德柱 ,何平笙 ,徐仲德 ,周漪琴. 高聚物的结构与性能 (第二版 ,第八次印刷) . 北京 :科学出版社 ,2003. [ 4 ] 朱平平 ,杨海洋 ,何平笙. 高分子通报 ,2004 ,6 :91～93. [ 5 ] Greiner W ,Neise L ,St cker H. Thermodynamics and statistical mechanics. New York : Springer2Verlag Inc. ,1995. [ 6 ] 蓝风华. 武警工程学院学报 ,2000 ,16 (4) :16～17.
YANG Ke2da ,XU Shi2ai
( School of Materials Science and Engineering , East China University of Science and Technology , Shanghai 200237 , China)
Abstract : From the principle of maximum entropy ,the radial distribution function of the end2to2end distance was deduced directly ,and it is indicated that the function is Gauss2type function.
最大信息熵计算公式
最大信息熵计算公式
最大熵原理是一种选择随机变量统计特性最符合客观情况的淮则，也称为最大信息原理。
信息熵这个词是香农从热力学中借用过来的。
热力学中的热熵是表示分子状态混乱程度的物理量。
香农用信息熵的概念来描述信源的不确定度。
信息熵用于解决信息的量化问题，将原本模糊的信息概念进行计算得出精确的信息熵值，信息熵是描述消息中，不确定性的值。
信息熵的计算公式为H(x) = E[I(xi)] =
E[ log(2,1/P(xi)) ] = -∑P(xi)log(2,P(xi))
(i=1,2,..n)。
最大熵模型(MaxEnt: Maximum Entropy Model，又称MEM)， MaxEnt 是概率模型学习中一个淮则，其思想为：在学习概率模型时，所有可能的模型（即概率分布）中，熵最大的模型是最好的模型；
对一个随机事件的概率分布进行预测时，预测应当满足全部已知的约束，而对未知的情况不要做任何主观假设。
在这种情况下，概率分布最均匀，预测的风险最小，因此得到的概率分布的熵是最大。
若概率模型需要满足一些约束，则最大熵原理就是在满足已知约束的条件集合中选择熵最大模型。
最大熵模型算法
最大熵模型算法今天我们来介绍一下最大熵模型系数求解的算法IIS算法。
有关于最大熵模型的原理可以看专栏里的这篇文章。
有关张乐博士的最大熵模型包的安装可以看这篇文章。
最大熵模型算法 1在满足特征约束的条件下，定义在条件概率分布P(Y|X)上的条件熵最大的模型就认为是最好的模型。
最大熵模型算法 23. IIS法求解系数wi先直接把算法粘贴出来，然后再用Python代码来解释。
这里也可以对照李航《统计学习方法》P90-91页算法6.1来看。
这个Python代码不知道是从哪儿下载到的了。
从算法的计算流程，我们明显看到，这就是一个迭代算法，首先给每个未知的系数wi赋一个初始值，然后计算对应每个系数wi的变化量delta_i，接着更新每个wi，迭代更新不断地进行下去，直到每个系数wi都不再变化为止。
下边我们一点点儿详细解释每个步骤。
获得特征函数输入的特征函数f1,f2,...,fn，也可以把它们理解为特征模板，用词性标注来说，假设有下边的特征模板x1=前词, x2=当前词, x3=后词 y=当前词的标记。
然后，用这个特征模板在训练语料上扫，显然就会出现很多个特征函数了。
比如下边的这句话，我/r 是/v 中国/ns 人/n用上边的模板扫过，就会出现下边的4个特征函数(start，我，是，r)(我，是，中国，v)(是，中国，人，ns)(中国，人，end，n)当然，在很大的训练语料上用特征模板扫过，一定会得到相同的特征函数，要去重只保留一种即可。
可以用Python代码得到特征函数def generate_events(self, line, train_flag=False):"""输入一个以空格为分隔符的已分词文本，返回生成的事件序列:param line: 以空格为分隔符的已分词文本:param train_flag: 真时为训练集生成事件序列；假时为测试集生成事件:return: 事件序列"""event_li = []# 分词word_li = line.split()# 为词语序列添加头元素和尾元素，便于后续抽取事件 if train_flag:word_li = [tuple(w.split(u'/')) for w inword_li if len(w.split(u'/')) == 2]else:word_li = [(w, u'x_pos') for w in word_li]word_li = [(u'pre1', u'pre1_pos')] + word_li + [(u'pro1', u'pro1_pos')]# 每个中心词抽取1个event，每个event由1个词性标记和多个特征项构成for i in range(1, len(word_li) - 1):# 特征函数a 中心词fea_1 = word_li[i][0]# 特征函数b 前一个词fea_2 = word_li[i - 1][0]# 特征函数d 下一个词fea_4 = word_li[i + 1][0]# 构建一个事件fields = [word_li[i][1], fea_1, fea_2, fea_4] # 将事件添加到事件序列event_li.append(fields)# 返回事件序列return event_li步进值 \delta_{i} 的求解显然delta_i由3个值构成，我们一点点儿说。
最大熵模型中的数学推导
针对原问题，首先引入拉格朗日乘子λ0,λ1,λ2, ..., λi，定义拉格朗日函数，转换为对偶问题求其极大化：
然后求偏导,：
注：上面这里是对P(y|x)求偏导，即只把P(y|x)当做未知数，其他都是常数。因此，求偏导时，只有跟P(y0|x0)相等的那个"(x0,y0)"才会起作用，其他的(x,y)都不是关于 P(y0|x0)的系数，是常数项，而常数项一律被“偏导掉”了。
3 最大熵
熵是随机变量不确定性的度量，不确定性越大，熵值越大；若随机变量退化成定值，熵为0。如果没有外界干扰，随机变量总是趋向于无序，在经过足够时间的稳定演化， 它应该能够达到的最大程度的熵。
为了准确的估计随机变量的状态，我们一般习惯性最大化熵，认为在所有可能的概率模型（分布）的集合中，熵最大的模型是最好的模型。换言之，在已知部分知识的前提 下，关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断，其原则是承认已知事物（知识），且对未知事物不做任何假设，没有任何偏见。
特征函数关于经验分布
在样本中的期望值是：
其中
，
。
特征函数关于模型P(Y|X)与经验分布P-(X)的期望值为：
换言之，如果能够获取训练数据中的信息，那么上述这两个期望值相等，即： 不过，因为实践中p(x)不好求，所以一般用样本中x出现的概率"p(x)-"代替x在总体中的分布概率“p(x)”，从而得到最大熵模型的完整表述如下：
综上，本文结合邹博最大熵模型的PPT和其它相关资料写就，可以看成是课程笔记或学习心得，着重推导。有何建议或意见，欢迎随时于本文评论下指出，thanks。
最大熵模型——精选推荐
们对事物了解的不确定性的消除或减少。
他把不确定的程度称为信息熵。
假设每种可能的状态都有概率，我们⽤关于被占据状态的未知信息来量化不确定性，这个信息熵即为：
其中是以
扩展到连续情形。
假设连续变量的概率密度函数是，与离散随机变量的熵的定义类似，
上式就是我们定义的随机变量的微分熵。
当被解释为⼀个随机连续向量时，就是的联合概率密度函数。
4.2. ⼩概率事件发⽣时携带的信息量⽐⼤概率事件发⽣时携带的信息量多
证明略，可以简要说明⼀下，也挺直观的。
如果事件发⽣的概率为，在这种情况下，事件了，并且不传达任何
；反之，如果事件发⽣的概率很⼩，这就有更⼤的
对所有随机变量的概率密度函数，满⾜以下约束条件：
其中，是的⼀个函数。
约束
量的矩，它随函数的表达式不同⽽发⽣变化，它综合了随机变量的所有可⽤的先验知其中，是拉格朗⽇乘⼦。
对被积函数求的微分，并令其为。
高斯最大熵 证明
高斯最大熵证明高斯最大熵（Gaussian Max-Entropy）是一种概率分布，其推导过程是基于一些假设和约束条件，如变量的方差和期望值等。
下面我们将通过数学推导来证明高斯最大熵的性质。
首先，我们假设有一个随机变量X，它是一个连续随机变量，并且服从均值为μ，方差为σ^2的正态分布。
那么，X的概率密度函数可以表示为：p(x|μ,σ^2) = (1/√(2πσ^2)) * exp(-(x-μ)^2/(2σ^2))现在，我们考虑一个与X相关的随机变量Y，它的概率分布是由X的概率分布和某个条件约束条件C所确定的。
假设条件约束条件C 是关于X的某个函数g(x)的约束，比如g(x)=x^2。
那么，Y的概率分布可以表示为：p(y|μ,σ^2,C) = ∫p(x|μ,σ^2) 1(y|x) dx其中1(y|x)是一个示性函数，如果满足条件约束C，则取值为1，否则取值为0。
接下来，我们考虑最大化Y的概率分布p(y|μ,σ^2,C)，即在满足约束条件的前提下，使得p(y|μ,σ^2,C)最大化。
为了解决这个问题，我们可以使用拉格朗日乘子法来求解。
首先，我们定义一个拉格朗日函数：L = log ∫p(x|μ,σ^2) 1(y|x) dx -λg(y)其中λ是一个拉格朗日乘子。
然后，我们可以通过求解下列方程来最大化L：L' = ∫p(x|μ,σ^2) 1(y|x) dx/∫p(x|μ,σ^2) dx -λg'(y) = 0由于这是一个积分方程，我们无法直接求解。
但是，我们可以使用一些近似方法来求解。
一种常用的方法是使用高斯分布来近似原始的分布p(x|μ,σ^2)，从而简化计算。
假设高斯分布的均值为μ，方差为σ^2，那么高斯分布的概率密度函数可以表示为：q(x|μ,σ^2) = (1/√(2πσ^2)) * exp(-(x-μ)^2/(2σ^2))于是，我们可以将原始的分布p(x|μ,σ^2)替换为q(x|μ,σ^2)，从而将复杂的积分方程转化为一个简单的微分方程。
最大熵原理
注：戴帽子的表示统计量(不含任何未知量，可以直接从训练数据中计算得到的也说成是经验的)，不 戴帽子表示概率模型是从训练数据中抽象出来的。
2.1.2 特征函数
假设给出了的很多有关数据的先验信息（就像例子中的������(������ = ������, ������ = 0) + ������(������ = ������, ������ = 0) = 0.6），我们要怎么将这些先验信息（约束条件）体现在我们的模型 中呢？为了解决这一问题，引入了特征函数的概念。
方案 1：
x
y
0
1
a
0.5
0.1
b
0.1
0.3
0.6
1.0表格 2.方案源自2：xy0
1
a
0.3
0.2
b
0.3
0.2
0.6
1.0
表格 3.
显然方案 1 和 2，都是满足约束P(x = a, y = 0) + p(x = b, y = 0) = 0.6的，但是最 大熵原理告诉我们方案 2 会比方案 1 更好，更能接近事实。这里约束条件只有一个， 我们能很快的给出，熵最大的分布(可以通俗的理解为怎么填表格中的数值，使得熵最
大)。但是，实际应用中，我们约束远不止 1 条，这种情况，就很难直接填表格中的数 值了，所以最大熵模型应运而生。
2. 最大熵模型：
最大熵原理认为，学习概率模型时，在所有可能的概率模型中，熵最大的模型最 好，最能反映实际情况。通常用约束条件来确定模型的集合，所以，最大熵原理可以理 解为在满足给定约束的条件下，选择熵最大的模型。
������∈∁ ������
对偶问题为：
������������������ ������������������ ������(������, ������)
最大熵模型的基本原理及其应用
最大熵模型的基本原理及其应用概述最大熵模型是一种常用的概率建模方法，广泛应用于自然语言处理、信息检索、图像识别等领域。
本文将介绍最大熵模型的基本原理，并探讨其在文本分类和情感分析中的应用。
一、最大熵模型的原理最大熵模型的核心思想是在给定一些已知条件的情况下，选择最平均、最不确定性的模型。
它通过最大化熵来选择概率模型，以保持模型的最大不确定性。
最大熵原理认为，当我们缺乏先验信息时，应该假设所有可能的结果都是等概率的，这样可以避免引入任何决策者的主观偏见。
二、最大熵模型的数学表示最大熵模型的数学表示可以通过最大熵优化问题来描述。
给定一些已知条件，最大熵模型要求找到满足这些条件的概率分布，使得该分布的熵最大。
通过求解最大熵优化问题，可以得到最大熵模型的参数估计。
三、最大熵模型在文本分类中的应用在文本分类任务中，最大熵模型可以用来训练一个分类器，将文本分类到事先定义好的类别中。
最大熵模型通过学习文本特征与类别之间的关系，自动挖掘特征的重要性，并据此进行分类。
最大熵模型的主要优点是能够处理大规模的特征空间和非线性问题，具有很强的表达能力。
四、最大熵模型在情感分析中的应用情感分析是研究文本情感倾向的任务，最大熵模型在情感分析中也具有广泛的应用。
最大熵模型可以学习文本特征与情感倾向之间的关系，从而实现情感分类的功能。
通过训练一个最大熵分类器，可以对文本进行情感分类，判断其是正面还是负面的情感。
最大熵模型在情感分析中的优势在于可以灵活地利用各种特征，并且能够处理多类别情感分类问题。
五、最大熵模型的应用挑战尽管最大熵模型在文本分类和情感分析中有广泛的应用，但也存在一些挑战。
首先，最大熵模型在处理大规模数据时要求计算量较大，需要考虑模型的训练和推断效率。
其次，最大熵模型对特征的表示非常敏感，需要合理选择和设计特征，以提高模型的性能。
此外，最大熵模型的参数估计问题也比较复杂，需要采用合适的算法和技巧来优化模型的参数。
熵最大原理
一、熵物理学概念宏观上：热力学定律——体系的熵变等于可逆过程吸收或耗散的热量除以它的绝对温度（克劳修斯，1865）微观上：熵是大量微观粒子的位置和速度的分布概率的函数，是描述系统中大量微观粒子的无序性的宏观参数（波尔兹曼，1872）结论：熵是描述事物无序性的参数，熵越大则无序。
二、熵在自然界的变化规律——熵增原理一个孤立系统的熵，自发性地趋于极大，随着熵的增加，有序状态逐步变为混沌状态，不可能自发地产生新的有序结构。
当熵处于最小值, 即能量集中程度最高、有效能量处于最大值时, 那么整个系统也处于最有序的状态,相反为最无序状态。
熵增原理预示着自然界越变越无序三、信息熵（1）和熵的联系——熵是描述客观事物无序性的参数。
香农认为信息是人们对事物了解的不确定性的消除或减少，他把不确定的程度称为信息熵（香农，1948 ）。
随机事件的信息熵：设随机变量ξ，它有A1，A2，A3，A4，……，An共n种可能的结局，每个结局出现的概率分别为p1，p2，p3，p4，……，pn，则其不确定程度，即信息熵为（2）信息熵是数学方法和语言文字学的结合。
一个系统的熵就是它的无组织程度的度量。
熵越大，事件越不确定。
熵等于0，事件是确定的。
举例：抛硬币，p（head）=0.5，p（tail）=0.5H（p）=-0.5log2（0.5）+（-0.5l og2（0.5））=1说明：熵值最大，正反面的概率相等，事件最不确定。
四、最大熵理论在无外力作用下，事物总是朝着最混乱的方向发展。
事物是约束和自由的统一体。
事物总是在约束下争取最大的自由权，这其实也是自然界的根本原则。
在已知条件下，熵最大的事物，最可能接近它的真实状态。
五、基于最大熵的统计建模：建模理论以最大熵理论为基础的统计建模。
为什么可以基于最大熵建模？Jaynes证明：对随机事件的所有相容的预测中，熵最大的预测出现的概率占绝对优势。
Tribus证明，正态分布、伽马分布、指数分布等，都是最大熵原理的特殊情况。
最大熵模型介绍
最大熵——精选推荐
最⼤熵1. 最⼤熵原理最⼤熵原理是概率模型学习的⼀个准则，其认为学习概率模型时，在所有可能的概率模型中，熵最⼤的模型是最好的模型。
通常⽤约束条件来确定概率模型的集合，然后在集合中选择熵最⼤的模型。
直观地，最⼤熵原理认为要选择的概率模型⾸先必须满⾜已有的事实，即约束条件。
在没有更多信息的情况下，那些不确定的部分都是等可能的。
最⼤熵原理通过熵的最⼤化来表⽰等可能性，因为当X服从均匀分布时熵最⼤。
2. 最⼤熵模型最⼤熵原理应⽤到分类得到最⼤熵模型。
给定训练集T=(x1,y1),(x2,y2),...,(x N,y N)，联合分布P(X,Y)以及边缘分布P(X)的经验分布都可以由训练数据得到：˜P(X=x,Y=y)=count(X=x,Y=y)N˜P(X=x)=count(X=x)N⽤特征函数f(x,y)描述输⼊x和输出y之间的某⼀个事实，特征函数是⼀个⼆值函数，当x与y满⾜某⼀事实时取1，否则取0。
例如，可以令特征x与标签y在训练集出现过时取1，否则取0。
特征函数f(x,y)关于经验分布˜P(X=x,Y=y)的期望值为：E˜P(f)=∑x,y˜P(x,y)f(x,y)特征函数f(x,y)关于模型P(Y|X)与经验分布˜P(x)的期望值为：E P(f)=∑x,y˜P(x)P(y|x)f(x,y)如果模型能够获取训练数据中的信息，那么就可以假设这两个期望值相等，即：∑x,y ˜P(x,y)f(x,y)=∑x,y˜P(x)P(y|x)f(x,y)将上式作为模型学习的约束条件，条件数量对应特征函数个数，设所有满⾜约束条件的模型集合为：C={P|∑x,y˜P(x,y)fi(x,y)=∑x,y˜P(x)P(y|x)fi(x,y),i=1,2,...,n}其中n为特征函数个数。
定义在条件概率分布P(Y|X)上的条件概率熵为：H(P)=−∑x,y˜P(x)P(y|x)ln P(y|x)模型集合C中条件熵H(P)最⼤的模型称为最⼤熵模型。
第五节最大熵模型
第五节最大熵模型最大熵模型（Entropy Model）也是随机概率模型之一。
典型的最大熵模型有Wilson模型和佐佐木(Sasaki)模型，以下分别讲述。
1．Wilson模型Wilson模型是由A.G.Wilson提出的方法，它以英国为中心，在区域科学方面的应用例较多，其模型如下式所示。
(4-5-1)式中，T：对象地区的生成交通量。
即，OD交通量的组合数由求E的最大得到。
例：发生小区Ｏ，吸引区AB，出行生成量为4。
能够发生的OD交通量状态如下。
OD交通量状态情况1 情况2 情况3 情况4情况5组合数E：,,,,发生概率：1/16, 4/16, 6/16, 4/16, 1/1616为可能发生的组合数。
从上述情况看,组合数为6的组合发生的概率最大,因此可以视为最容易发生。
Wilson模型的约束条件为：（4-5-2）（4-5-3）(4-5-4)式中，的交通费用；总交通费用。
最大熵模型一般用以下对数拉格朗日方法求解。
(4-5-5)式中，，，为拉格朗日系数。
应用Stirling公式近似，得，(4-5-6) 代入（4-5-5）式，并对求导数，得，令，得，(4-5-7)∵∴(4-5-8)同样，(4-5-9)这里，令，则（4-5-7）为：(4-5-10）可以看出，式(4-5-10）为重力模型。
Wilson模型的特点：(1)能表现出行者的微观行动；(2)总交通费用是出行行为选择的结果，对其进行约束脱离现实；(3)各微观状态的概率相等，即各目的地的选择概率相等的假设没有考虑距离和行驶时间等因素。
计算步骤：第1步给出第2步给出，求出第3步用求出的，求出第4步如果，非收敛，则返第2步；反之执行第5步。
第5步将，，代入式（4-5-7)求出，这时，如果总用条件（ 4-5-4）满足，则结束计算，反之，更新值返回第1步。
2．佐佐木(Sasaki)模型分别设定i区的发生概率和j区的吸引（选择）概率。
, （）－－发生守恒条件(4-5-11), （）－－吸引守恒条件(4-5-12), () (4-5-13)式中，为i区的发生交通量被j区有吸引的概率。
最大熵模型简介-Read
A Simple Introduction to the Maximum Entropy Models
王 斌 前瞻研究中心信息检索组 2007. 11. 27
Generative Model vs. Discriminative Model
Generative Model (GM): P(Y|X)=P(X|Y)P(Y)/P(X)，通 过求解P(X|Y)和P(Y)来求解P(Y|X) Discriminative Model (DM): 对P(Y|X)直接建模
参数估计算法：用来得到具有最大熵分布的参数i 的值。
FI 算法(特征引入算法，Feature Induction) 解决如何选择特征的问题：通常采用一个逐步增加特征的办
法进行，每一次要增加哪个特征取决于样本数据。
Algorithms
Generalized Iterative Scaling (GIS): (Darroch and Ratcliff, 1972) Improved Iterative Scaling (IIS): (Della Pietra et al., 1995)
Ep( f j ) p( x ) f j ( x )
x
Ep( f j ) p( x ) f j ( x )
x
最大熵模型
无任何先验知识：
1 p * ( x) ,x A | A|
存在先验知识：(求满足一组条件的最优解问题)
P { p | Ep( f j ) E~ p ( f j ),1 j k} H ( p) p( x) log2 p( x) p* arg max H ( p)
y i 1
i 是模型参数，可以看成是特征函数的权重。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.2 熵的定义
下面分别给出熵、联合熵、条件熵、相对熵、互信息的定义。 熵 ：如果一个随机变量X的可能取值为X = {x1, x2,…, xk}，其概率分布为P(X = xi) = pi（i = 1,2, ..., n），则随机变量X的熵定义为：
把最前面的负号放到最后，便成了：
3
其约束条件为：
该问题已知若干条件，要求若干变量的值使到目标函数（熵）最大，其数学本质是最优化问题（Optimization Problem），其约束条件是线性的等式，而目标函数是非线性
的，所以该问题属于非线性规划（线性约束）(non-linear programming with linear constraints)问题，故可通过引入Lagrange函数将原带约束的最优化问题转换为无约束的 最优化的对偶问题。
，此时仍然需要坚持无偏见原则，使得概率分布尽量平均。但
怎么样才能得到尽量无偏见的分布？
实践经验和理论计算都告诉我们，在完全无约束状态下，均匀分布等价于熵最大（有约束的情况下，不一定是概率相等的均匀分布。 比如，给定均值和方差，熵最大的分
布就变成了正态分布 ）。
于是，问题便转化为了：计算X和Y的分布，使得H(Y|X)达到最大值，并且满足下述条件：
10月26日机器学习班第6次课，身为讲师之一的邹博讲最大熵模型，他从熵的概念，讲到为何要最大熵、最大熵的推导，以及求解参数的IIS方法，整个过程讲得非常流畅， 特别是其中的数学推导。晚上我把他的PPT 在微博上公开分享了出来，但对于没有上过课的朋友直接看PPT 会感到非常跳跃，因此我打算针对机器学习班的某些次课写一系列博 客，刚好也算继续博客中未完的机器学习系列。
下面再举个大多数有关最大熵模型的文章中都喜欢举的一个例子。 例如，一篇文章中出现了“学习”这个词，那这个词是主语、谓语、还是宾语呢？换言之，已知“学习”可能是动词，也可能是名词，故“学习”可以被标为主语、谓语、 宾语、定语等等。 令x1表示“学习”被标为名词， x2表示“学习”被标为动词。 令y1表示“学习”被标为主语， y2表示被标为谓语， y3表示宾语， y4表示定语。
在一定程度上，相对熵可以度量两个随机变量的“距离”，且有D(p||q) ≠D(q||p)。另外，值得一提的是，D(p||q)是必然大于等于0的。 互信息 ：两个随机变量X，Y的互信息定义为X，Y的联合分布和各自独立分布乘积的相对熵，用I(X,Y)表示：
且有I(X,Y)=D(P(X,Y) || P(X)P(Y))。下面，咱们来计算下H(Y)-I(X,Y)的结果，如下：
如果没有外部能量输入，封闭系统趋向越来越混乱（熵越来越大）。比如，如果房间无人打扫，不可能越来越干净（有序化），只可能越来越乱（无序化）。而要让一个系 统变得更有序，必须有外部能量的输入。
1948年，香农Claude E. Shannon引入信息（熵），将其定义为离散随机事件的出现概率。一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。 所以说，信息熵可以被认为是系统有序化程度的一个度量。
因此，也就引出了最大熵模型的本质，它要解决的问题就是已知X，计算Y的概率，且尽可能让Y的概率最大 （实践中，X可能是某单词的上下文信息，Y是该单词翻译 成me，I，us、we的各自概率），从而根据已有信息，尽可能最准确的推测未知信息，这就是最大熵模型所要解决的问题。
相当于已知X，计算Y的最大可能的概率，转换成公式，便是要最大化下述式子H(Y|X) ：
对固定的x，Lagrange函数L(x,λ,v)为关于λ和v的仿射函数。 3.4 对偶问题极大化的指数解
针对原问题，首先引入拉格朗日乘子λ0,λ1,λ2, ..., λi，定义拉格朗日函数，转换为对偶问题求其极大化：
然后求偏导,：
注：上面这里是对P(y|x)求偏导，即只把P(y|x)当做未知数，其他都是常数。因此，求偏导时，只有跟P(y0|x0)相等的那个"(x0,y0)"才会起作用，其他的(x,y)都不是关于 P(y0|x0)的系数，是常数项，而常数项一律被“偏导掉”了。
综上，本文结合邹博最大熵模型的PPT和其它相关资料写就，可以看成是课程笔记或学习心得，着重推导。有何建议或意见，欢迎随时于本文评论下指出，thanks。
1 预备知识
为了更好的理解本文，需要了解的概率必备知识有： 1. 大写字母X表示随机变量，小写字母x表示随机变量X的某个具体的取值； 2. P(X)表示随机变量X的概率分布，P(X,Y)表示随机变量X、Y的联合概率分布，P(Y|X)表示已知随机变量X的情况下随机变量Y的条件概率分布； 3. p(X = x)表示随机变量X取某个具体值的概率，简记为p(x)； 4. p(X = x, Y = y) 表示联合概率，简记为p(x,y)，p(Y = y|X = x)表示条件概率，简记为p(y|x)，且有：p(x,y) = p(x) * p(y|x)。
通过上面的计算过程，我们发现竟然有H(Y)-I(X,Y) = H(Y|X)。故通过条件熵的定义，有：H(Y|X) = H(X,Y) - H(X)，而根据互信息定义展开得到H(Y|X) = H(Y) I(X,Y)，把前者跟后者结合起来，便有I(X,Y)= H(X) + H(Y) - H(X,Y)，此结论被多数文献作为互信息的定义。
2
且这些概率值加起来的和必为1，即
，
， 则根据无偏原则，认为这个分布中取各个值的概率是相等的，故得到：
因为没有任何的先验知识，所以这种判断是合理的。如果有了一定的先验知识呢？
即进一步，若已知：“学习”被标为定语的可能性很小，只有0.05，即
，剩下的依然根据无偏原则，可得：
再进一步，当“学习”被标作名词x1的时候，它被标作谓语y2的概率为0.95，即
更多请查看《高等数学上下册》、《概率论与数理统计》等教科书，或参考本博客中的：数据挖掘中所需的概率论与数理统计知识。
2 何谓熵？
从名字上来看，熵给人一种很玄乎，不知道是啥的感觉。其实，熵的定义很简单，即用来表示随机变量的不确定性。之所以给人玄乎的感觉，大概是因为为何要取这样的名 字，以及怎么用。
熵的概念最早起源于物理学，用于度量一个热力学系统的无序程度。在信息论里面，熵是对不确定性的测量。
需要了解的有关函数求导、求极值的知识点有： 1. 如果函数y=f(x)在[a, b]上连续，且其在(a,b)上可导，如果其导数f’(x) >0，则代表函数f(x)在[a,b]上单调递增，否则单调递减；如果函数的二阶导f''(x) > 0，则函
数在[a,b]上是凹的，反之，如果二阶导f''(x) < 0，则函数在[a,b]上是凸的。 2. 设函数f(x)在x0处可导，且在x处取得极值，则函数的导数F’(x0) = 0。 3. 以二元函数z = f(x,y)为例，固定其中的y，把x看做唯一的自变量，此时，函数对x的导数称为二元函数z=f(x,y)对x的偏导数。 4. 为了把原带约束的极值问题转换为无约束的极值问题，一般引入拉格朗日乘子，建立拉格朗日函数，然后对拉格朗日函数求导，令求导结果等于0，得到极值。
例如，投掷一个骰子，如果问"每个面朝上的概率分别是多少"，你会说是等概率，即各点出现的概率均为1/6。因为对这个"一无所知"的色子，什么都不确定，而假定它每 一个朝上概率均等则是最合理的做法。从投资的角度来看，这是风险最小的做法，而从信息论的角度讲，就是保留了最大的不确定性，也就是说让熵达到最大。
3.1 无偏原则
1
简单解释下上面的推导过程。整个式子共6行，其中 第二行推到第三行的依据是边缘分布p(x)等于联合分布p(x,y)的和； 第三行推到第四行的依据是把公因子logp(x)乘进去，然后把x,y写在一起； 第四行推到第五行的依据是：因为两个sigma都有p(x,y)，故提取公因子p(x,y)放到外边，然后把里边的-（log p(x,y) - log p(x)）写成- log (p(x,y)/p(x) ) ； 第五行推到第六行的依据是：p(x,y) = p(x) * p(y|x)，故p(x,y) / p(x) = p(y|x)。 相对熵： 又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度等。设p(x)、q(x)是X中取值的两个概率分布，则p对q的相对熵是：
2.1 熵的引入
事实上，熵的英文原文为entropy，最初由德国物理学家鲁道夫·克劳修斯提出，其表达式为：
它表示一个系系统在不受外部干扰时，其内部最稳定的状态。后来一中国学者翻译entropy时，考虑到entropy是能量Q跟温度T的商，且跟火有关，便把entropy形象的翻译 成“熵”。
我们知道，任何粒子的常态都是随机运动，也就是"无序运动"，如果让粒子呈现"有序化"，必须耗费能量。所以，温度（热能）可以被看作"有序化"的一种度量，而"熵"可 以看作是"无序化"的度量。
3.3 凸优化中的对偶问题
考虑到机器学习里，不少问题都在围绕着一个“最优化”打转，而最优化中凸优化最为常见，所以为了过渡自然，这里简单阐述下凸优化中的对偶问题。 一般优化问题可以表示为下述式子：
其中，subject to导出的是约束条件，f(x)表示不等式约束，h(x)表示等式约束。
然后可通过引入拉格朗日乘子λ和v，建立拉格朗日函数，如下：
且满足以下4个约束条件：
3.2 最大熵模型的表示
至此，有了目标函数跟约束条件，我们可以写出最大熵模型的一般表达式了，如下：
其中，P={p | p是X上满足条件的概率分布} 继续阐述之前，先定义下特征、样本和特征函数。 特征：(x,y) y：这个特征中需要确定的信息 x：这个特征中的上下文信息 样本：关于某个特征(x,y)的样本，特征所描述的语法现象在标准集合里的分布：(xi,yi)对，其中，yi是y的一个实例，xi是yi的上下文。 对于一个特征(x0,y0)，定义特征函数：