高考文科数学真题汇编：立体几何高考题老师版

合集下载

2012-2021高考真题数学汇编：立体几何初步(2)(教师版)

2012-2021高考真题数学汇编：立体几何初步（2）一．选择题（共14小题）1．（2016•全国）正四棱锥的各棱长均为1，则它的体积是（）A．B．C．D．2．（2016•上海）半径为1的球的表面积为（）A．πB．C．2πD．4π3．（2016•浙江）已知互相垂直的平面α，β交于直线l，若直线m，n⊥β，则（）A．m∥l B．m∥n C．n⊥l D．m⊥n4．（2016•新课标Ⅱ）体积为8的正方体的顶点都在同一球面上，则该球面的表面积为（）A．12πB．πC．8πD．4π5．（2016•新课标Ⅰ）平面α过正方体ABCD﹣A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD＝m，α∩平面ABB1A1＝n，则m、n所成角的正弦值为（）A．B．C．D．6．（2016•新课标Ⅲ）在封闭的直三棱柱ABC﹣A1B1C1内有一个体积为V的球，若AB⊥BC，AB＝6，AA1＝3，则V的最大值是（）A．4πB．C．6πD．7．（2016•上海）设直线l与平面α平行，直线m在平面α上，那么（）A．直线l平行于直线mB．直线l与直线m异面C．直线l与直线m没有公共点D．直线l与直线m不垂直8．（2015•上海）底面半径为1，母线长为2的圆锥的体积为（）A．2πB．C．D．9．（2015•新课标Ⅰ）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，圆周率约为3，估算出堆放的米约有（）A．14斛B．22斛C．36斛D．66斛10．（2015•山东）已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为（）A．B．C．2πD．4π11．（2015•新课标Ⅱ）已知A，B是球O的球面上两点，∠AOB＝90°，若三棱锥O﹣ABC体积的最大值为36，则球O的表面积为（）A．36πB．64πC．144πD．256π12．（2015•山东）在梯形ABCD中，∠ABC＝，AD∥BC，将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为（）A．B．C．D．2π13．（2015•广东）若空间中n个不同的点两两距离都相等，则正整数n的取值（）A．至多等于3 B．至多等于4 C．等于5 D．大于514．（2014•全国）平面ax+by+z+1＝0和x+2y﹣z+3＝0互相垂直，且其交线经过点（1，﹣1，2），则a+b＝（）A．B．C．﹣D．﹣二．填空题（共14小题）15．（2017•新课标Ⅰ）已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA＝AC，三棱锥S﹣ABC的体积为9，则球O的表面积为．16．（2017•新课标Ⅰ）如图，圆形纸片的圆心为O，半径为5cm，△DBC，△ECA，CA，AB为底边的等腰三角形．沿虚线剪开后，CA，AB为折痕折起△DBC，△FAB，使得D、E、F重合，所得三棱锥体积（单位：cm3）的最大值为．17．（2016•全国）在空间直角坐标系中，若直线＝＝与平面x﹣2y+z＝5平行．18．（2016•全国）已知B﹣AC﹣D为直二面角，Rt△ABC≌Rt△ADC，且AB＝BC．19．（2016•浙江）如图，已知平面四边形ABCD，AB＝BC＝3，AD＝，∠ADC＝90°，直线AC与BD′所成角的余弦的最大值是．20．（2016•浙江）如图，在△ABC中，AB＝BC＝2，满足PD＝DA，PB＝BA．21．（2016•上海）已知圆锥的母线长为10，母线与轴的夹角为30°，则该圆锥的侧面积为．22．（2015•全国）在空间直角坐标系中，过原点作平面2x﹣z﹣2＝0的垂线，垂足为．23．（2015•上海）若正三棱柱的所有棱长均为a，且其体积为16，则a＝．24．（2015•上海）若圆锥的侧面积与过轴的截面面积之比为2π，则其母线与轴的夹角的大小为．25．（2015•四川）在三棱住ABC﹣A1B1C1中，∠BAC＝90°，其正视图和侧视图都是边长为1的正方形，设M，N，P分别是AB，B1C1的中点，则三棱锥P﹣A1MN的体积是．26．（2015•江苏）现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2，高为8的圆柱各一个，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为．27．（2015•浙江）如图，三棱锥A﹣BCD中，AB＝AC＝BD＝CD＝3，点M，N分别是AD，则异面直线AN，CM 所成的角的余弦值是．28．（2015•四川）如图，四边形ABCD和ADPQ均为正方形，他们所在的平面互相垂直，E、F分别为AB、BC 的中点，设异面直线EM与AF所成的角为θ．三．解答题（共32小题）29．（2017•新课标Ⅱ）如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD AD，∠BAD＝∠ABC＝90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．30．（2017•江苏）如图，在三棱锥A﹣BCD中，AB⊥AD，平面ABD⊥平面BCD，点E、F（E与A、D不重合），BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．31．如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC 的长为10，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm．现有一根玻璃棒l，其长度为40cm．（容器厚度、玻璃棒粗细均忽略不计）（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度．32．（2017•北京）如图，在三棱锥P﹣ABC中，PA⊥AB，AB⊥BC，PA＝AB＝BC＝2，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．33．（2017•新课标Ⅰ）如图，在四棱锥P﹣ABCD中，AB∥CD（1）证明：平面PAB⊥平面PAD；（2）若PA＝PD＝AB＝DC，∠APD＝90°，且四棱锥P﹣ABCD的体积为34．（2017•新课标Ⅲ）如图四面体ABCD中，△ABC是正三角形，AD＝CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB＝BD，若E为棱BD上与D不重合的点，求四面体ABCE与四面体ACDE 的体积比．35．（2017•山东）由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示，四边形ABCD为正方形，O为AC与BD的交点，A1E⊥平面ABCD，（Ⅰ）证明：A1O∥平面B1CD1；（Ⅱ）设M是OD的中点，证明：平面A1EM⊥平面B1CD1．36．（2017•上海）如图，长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AA1＝3．（1）求四棱锥A1﹣ABCD的体积；（2）求异面直线A1C与DD1所成角的大小．37．（2016•上海）将边长为1的正方形AA1O1O（及其内部）绕OO1旋转一周形成圆柱，如图，长为，，其中B1与C在平面AA1O1O的同侧．（1）求圆柱的体积与侧面积；（2）求异面直线O1B1与OC所成的角的大小．38．（2016•新课标Ⅱ）如图，菱形ABCD的对角线AC与BD交于点O，点E、F分别在AD，AE＝CF，EF交BD 于点H（Ⅰ）证明：AC⊥HD′；（Ⅱ）若AB＝5，AC＝6，AE＝，求五棱锥D′﹣ABCFE体积．39．（2016•山东）在如图所示的几何体中，D是AC的中点，EF∥DB．（Ⅰ）已知AB＝BC，AE＝EC，求证：AC⊥FB；（Ⅱ）已知G，H分别是EC和FB的中点，求证：GH∥平面ABC．40．（2016•上海）将边长为1的正方形AA1O1O（及其内部）绕OO1旋转一周形成圆柱，如图，长为π，，其中B1与C在平面AA1O1O的同侧．（1）求三棱锥C﹣O1A1B1的体积；（2）求异面直线B1C与AA1所成的角的大小．41．（2016•新课标Ⅲ）如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AB＝AD＝AC＝3，PA＝BC＝4，AM＝2MD，N为PC的中点．（Ⅰ）证明：MN∥平面PAB；（Ⅱ）求四面体N﹣BCM的体积．42．（2016•新课标Ⅰ）如图，已知正三棱锥P﹣ABC的侧面是直角三角形，PA＝6，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G．（Ⅰ）证明：G是AB的中点；（Ⅱ）在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积．43．（2016•江苏）如图，在直三棱柱ABC﹣A1B1C1中，D，E分别为AB，BC的中点1B上，且B1D⊥A1F，A1C1⊥A1B1．求证：（1）直线DE∥平面A1C1F；（2）平面B1DE⊥平面A1C1F．44．（2016•四川）如图，在四棱锥P﹣ABCD中，PA⊥CD，∠ADC＝∠PAB＝90°，BC＝CD＝（Ⅰ）在平面PAD内找一点M，使得直线CM∥平面PAB，并说明理由；（Ⅱ）证明：平面PAB⊥平面PBD．45．（2016•江苏）现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P﹣A1B1C1D1，下部的形状是正四棱柱ABCD﹣A1B1C1D1（如图所示），并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍．（1）若AB＝6m，PO1＝2m，则仓库的容积是多少？（2）若正四棱锥的侧棱长为6m，则当PO1为多少时，仓库的容积最大？46．（2016•上海）如图，已知正三棱柱ABC﹣A1B1C1的体积为，底面边长为3，求异面直线BC1与AC所成的角的大小．47．（2015•上海）如图，圆锥的顶点为P，底面圆为O，C为半圆弧的中点的中点，已知PO＝2，求三棱锥P﹣AOC的体积，并求异面直线PA和OE所成角的大小．48．（2015•新课标Ⅰ）如图，四边形ABCD为菱形，G为AC与BD的交点（Ⅰ）证明：平面AEC⊥平面BED；（Ⅱ）若∠ABC＝120°，AE⊥EC，三棱锥E﹣ACD的体积为49．（2015•重庆）如图，三棱锥P﹣ABC中，平面PAC⊥平面ABC，点D、E在线段AC上，且AD＝DE＝EC＝2，点F在线段AB上，且EF∥BC．（Ⅰ）证明：AB⊥平面PFE．（Ⅱ）若四棱锥P﹣DFBC的体积为7，求线段BC的长．50．（2015•陕西）如图，在直角梯形ABCD中，AD∥BC，AB＝BC＝AD＝a，O是AC与BE的交点．将△ABE沿BE折起到如图2中△A1BE的位置，得到四棱锥A1﹣BCDE．（Ⅰ）证明：CD⊥平面A1OC；（Ⅱ）当平面A1BE⊥平面BCDE时，四棱锥A1﹣BCDE的体积为36，求a的值．51．（2015•江苏）如图，在直三棱柱ABC﹣A1B1C1中，已知AC⊥BC，BC＝CC1，设AB1的中点为D，B1C∩BC1＝E．求证：（1）DE∥平面AA1C1C；（2）BC1⊥AB1．52．（2015•新课标Ⅰ）如图，四边形ABCD为菱形，∠ABC＝120°，E，BE⊥平面ABCD，DF⊥平面ABCD，AE ⊥EC．（Ⅰ）证明：平面AEC⊥平面AFC；（Ⅱ）求直线AE与直线CF所成角的余弦值．53．（2015•四川）一个正方体的平面展开图及该正方体的直观图的示意图如图所示．（Ⅰ）请按字母F，G，H标记在正方体相应地顶点处（不需要说明理由）（Ⅱ）判断平面BEG与平面ACH的位置关系．并说明你的结论．（Ⅲ）证明：直线DF⊥平面BEG．54．（2015•福建）如图，AB是圆O的直径，点C是圆O上异于A，PO垂直于圆O所在的平面，且PO＝OB＝1，（Ⅰ）若D为线段AC的中点，求证：AC⊥平面PDO；（Ⅱ）求三棱锥P﹣ABC体积的最大值；（Ⅲ）若BC＝，点E在线段PB上，求CE+OE的最小值．55．（2015•新课标Ⅱ）如图，长方体ABCD﹣A1B1C1D1中，AB＝16，BC＝101＝8，点E，F分别在A1B1，D1C1上，A1E＝D1F＝4．过E，F的平面α与此长方体的面相交，交线围成一个正方形（Ⅰ）在图中画出这个正方形（不必说出画法和理由）（Ⅱ）求平面α把该长方体分成的两部分体积的比值．56．（2015•北京）如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，AC⊥BC且AC＝BC＝，O，M分别为AB（1）求证：VB∥平面MOC；（2）求证：平面MOC⊥平面VAB；（3）求三棱锥V﹣ABC的体积．57．（2015•山东）如图，三棱台DEF﹣ABC中，AB＝2DE，G，BC的中点．（1）求证：BD∥平面FGH；（2）若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH．58．（2015•安徽）如图，三棱锥P﹣ABC中，PA⊥平面ABC，AB＝1，AC＝2（1）求三棱锥P﹣ABC的体积；（2）证明：在线段PC上存在点M，使得AC⊥BM，并求59．（2015•湖北）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．在如图所示的阳马P﹣ABCD中，且PD＝CD，点E是PC的中点（Ⅰ）证明：DE⊥平面PBC．试判断四面体EBCD是否为鳖臑．若是，写出其每个面的直角（只需写出结论）；若不是；（Ⅱ）记阳马P﹣ABCD的体积为V1，四面体EBCD的体积为V2，求的值．60．（2015•湖南）如图，直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形，E，F分别是BC，CC1的中点，（Ⅰ）证明：平面AEF⊥平面B1BCC1；（Ⅱ）若直线A1C与平面A1ABB1所成的角为45°，求三棱锥F﹣AEC的体积．2012-2021高考真题数学汇编：立体几何初步（2）参考答案一．选择题（共14小题）1．（2016•全国）正四棱锥的各棱长均为1，则它的体积是（）A．B．C．D．【分析】根据正四棱锥的结构特征计算棱锥的高，代入体积公式计算即可得答案．【解答】解：设正四棱锥的底面中心为O，连结OP，∵底面四边形ABCD是正方形，AB＝1，∴AO＝．∴OP＝＝．∴正四棱锥的体积V＝＝．故选：C．【点评】本题考查了正四棱锥的结构特征，棱锥的体积计算，属于中档题．2．（2016•上海）半径为1的球的表面积为（）A．πB．C．2πD．4π【分析】利用球的表面积公式S＝4πR2解答即可求得答案．【解答】解：半径为1的球的表面积为4π×52＝4π，故选：D．【点评】本题考查了球的表面积公式的运用，考查学生的计算能力，属于基础题．3．（2016•浙江）已知互相垂直的平面α，β交于直线l，若直线m，n⊥β，则（）A．m∥l B．m∥n C．n⊥l D．m⊥n【分析】由已知条件推导出l⊂β，再由n⊥β，推导出n⊥l．【解答】解：∵互相垂直的平面α，β交于直线l，n满足m∥α，∴m∥β或m⊂β或m与β相交，l⊂β，∵n⊥β，∴n⊥l．故选：C．【点评】本题考查两直线位置关系的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．4．（2016•新课标Ⅱ）体积为8的正方体的顶点都在同一球面上，则该球面的表面积为（）A．12πB．πC．8πD．4π【分析】先通过正方体的体积，求出正方体的棱长，然后求出球的半径，即可求出球的表面积．【解答】解：正方体体积为8，可知其边长为2，正方体的体对角线为＝4，即为球的直径，所以半径为，所以球的表面积为＝12π．故选：A．【点评】本题考查学生的空间想象能力，体积与面积的计算能力，是基础题．5．（2016•新课标Ⅰ）平面α过正方体ABCD﹣A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD＝m，α∩平面ABB1A1＝n，则m、n所成角的正弦值为（）A．B．C．D．【分析】画出图形，判断出m、n所成角，求解即可．【解答】解：如图：α∥平面CB1D1，α∩平面ABCD＝m，α∩平面ABA7B1＝n，可知：n∥CD1，m∥B2D1，∵△CB1D2是正三角形．m、n所成角就是∠CD1B1＝60°．则m、n所成角的正弦值为：．故选：A．【点评】本题考查异面直线所成角的求法，考查空间想象能力以及计算能力．6．（2016•新课标Ⅲ）在封闭的直三棱柱ABC﹣A1B1C1内有一个体积为V的球，若AB⊥BC，AB＝6，AA1＝3，则V的最大值是（）A．4πB．C．6πD．【分析】根据已知可得直三棱柱ABC﹣A1B1C1的内切球半径为，代入球的体积公式，可得答案．【解答】解：∵AB⊥BC，AB＝6，∴AC＝10．故三角形ABC的内切圆半径r＝＝2，又由AA4＝3，故直三棱柱ABC﹣A1B4C1的内切球半径为，此时V的最大值＝，故选：B．【点评】本题考查的知识点是棱柱的几何特征，根据已知求出球的半径，是解答的关键．7．（2016•上海）设直线l与平面α平行，直线m在平面α上，那么（）A．直线l平行于直线mB．直线l与直线m异面C．直线l与直线m没有公共点D．直线l与直线m不垂直【分析】由已知中直线l与平面α平行，直线m在平面α上，可得直线l与直线m异面或平行，进而得到答案．【解答】解：∵直线l与平面α平行，直线m在平面α上，∴直线l与直线m异面或平行，即直线l与直线m没有公共点，故选：C．【点评】本题考查的知识点是空间中直线与直线之间的位置关系，直线与平行之间的位置关系，难度中档．8．（2015•上海）底面半径为1，母线长为2的圆锥的体积为（）A．2πB．C．D．【分析】求出圆锥的高，然后求解圆锥的体积．【解答】解：底面半径为1，母线长为2的圆锥的高为：．底面半径为1，母线长为2的圆锥的体积为：＝．故选：D．【点评】本题考查几何体的体积的求法，是基础题．9．（2015•新课标Ⅰ）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，圆周率约为3，估算出堆放的米约有（）A．14斛B．22斛C．36斛D．66斛【分析】根据圆锥的体积公式计算出对应的体积即可．【解答】解：设圆锥的底面半径为r，则r＝8，解得r＝，故米堆的体积为××π×（）2×5≈，∵1斛米的体积约为1.62立方尺，∴÷1.62≈22，故选：B．【点评】本题主要考查椎体的体积的计算，比较基础．10．（2015•山东）已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为（）A．B．C．2πD．4π【分析】画出图形，根据圆锥的体积公式直接计算即可．【解答】解：如图为等腰直角三角形旋转而成的旋转体．V＝2×S•h＝2×2•h＝2×π×（）5×＝．故选：B．【点评】本题考查圆锥的体积公式，考查空间想象能力以及计算能力．是基础题．11．（2015•新课标Ⅱ）已知A，B是球O的球面上两点，∠AOB＝90°，若三棱锥O﹣ABC体积的最大值为36，则球O的表面积为（）A．36πB．64πC．144πD．256π【分析】当点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大，利用三棱锥O﹣ABC体积的最大值为36，求出半径，即可求出球O的表面积．【解答】解：如图所示，当点C位于垂直于面AOB的直径端点时，设球O的半径为R O﹣ABC＝V C﹣AOB＝＝＝36，则球O的表面积为4πR2＝144π，故选：C．【点评】本题考查球的半径与表面积，考查体积的计算，确定点C位于垂直于面AOB的直径端点时，三棱锥O﹣ABC的体积最大是关键．12．（2015•山东）在梯形ABCD中，∠ABC＝，AD∥BC，将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为（）A．B．C．D．2π【分析】画出几何体的直观图，利用已知条件，求解几何体的体积即可．【解答】解：由题意可知几何体的直观图如图：旋转体是底面半径为1，高为2的圆柱，几何体的体积为：＝．故选：C．【点评】本题考查几何体的体积的求法，考查空间想象能力以及计算能力．画出几何体的直观图是解题的关键．13．（2015•广东）若空间中n个不同的点两两距离都相等，则正整数n的取值（）A．至多等于3 B．至多等于4 C．等于5 D．大于5【分析】先考虑平面上的情况：只有三个点的情况成立；再考虑空间里，只有四个点的情况成立，注意运用外接球和三角形三边的关系，即可判断．【解答】解：考虑平面上，3个点两两距离相等，成立；4个点两两距离相等，三个点在圆上，圆上的点到圆心的距离都相等；n大于4，也不成立；在空间中，4个点两两距离相等，成立；若n＞4，由于任三点不共线，考虑四个点构成的正四面体，第五个点，与它们距离相等，且球的半径不等于边长，即有球心与正四面体的底面的中心重合，但显然球的半径不等于棱长，故不成立；同理n＞7，不成立．故选：B．【点评】本题考查空间几何体的特征，主要考查空间两点的距离相等的情况，注意结合外接球和三角形的两边与第三边的关系，属于中档题和易错题．14．（2014•全国）平面ax+by+z+1＝0和x+2y﹣z+3＝0互相垂直，且其交线经过点（1，﹣1，2），则a+b＝（）A．B．C．﹣D．﹣【分析】由平面ax+by+z+1＝0和x+2y﹣z+3＝0互相垂直，且其交线经过点（1，﹣1，2），列出方程组，求出a，b，由此能求出a+b的值．【解答】解：∵平面ax+by+z+1＝0和x+4y﹣z+3＝0互相垂直，且其交线经过点（7，2），∴，解得a＝﹣，b＝．∴a+b＝﹣．故选：C．【点评】本题考查两数和的求法，考查平面与平面垂直的性质等基础知识，考查运算求解能力、推理论证能力，考查函数与方程思想，是基础题．二．填空题（共14小题）15．（2017•新课标Ⅰ）已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径．若平面SCA⊥平面SCB，SA＝AC，三棱锥S﹣ABC的体积为9，则球O的表面积为36π．【分析】判断三棱锥的形状，利用几何体的体积，求解球的半径，然后求解球的表面积．【解答】解：三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径，SA＝AC，三棱锥S﹣ABC的体积为9，可知三角形SBC与三角形SAC都是等腰直角三角形，设球的半径为r，可得，解得r＝3．球O的表面积为：8πr2＝36π．故答案为：36π．【点评】本题考查球的内接体，三棱锥的体积以及球的表面积的求法，考查空间想象能力以及计算能力．16．（2017•新课标Ⅰ）如图，圆形纸片的圆心为O，半径为5cm，△DBC，△ECA，CA，AB为底边的等腰三角形．沿虚线剪开后，CA，AB为折痕折起△DBC，△FAB，使得D、E、F重合，所得三棱锥体积（单位：cm3）的最大值为4cm3．【分析】法一：由题，连接OD，交BC于点G，由题意得OD⊥BC，OG＝BC，设OG＝x，则BC＝2x，DG＝5﹣x，三棱锥的高h＝，求出S△ABC＝3，V＝＝，令f（x）＝25x4﹣10x5，x∈（0，），f′（x）＝100x3﹣50x4，f（x）≤f（2）＝80，由此能求出体积最大值．法二：设正三角形的边长为x，则OG＝，FG＝SG＝5﹣，SO＝h＝＝＝，由此能示出三棱锥的体积的最大值．【解答】解法一：由题意，连接OD，由题意得OD⊥BC BC，即OG的长度与BC的长度成正比，设OG＝x，则BC＝6x，三棱锥的高h＝＝＝，＝3，则V＝＝＝，令f（x）＝25x4﹣10x6，x∈（0，），f′（x）＝100x3﹣50x4，令f′（x）≥3，即x4﹣2x8≤0，解得x≤2，则f（x）≤f（2）＝80，∴V≤＝43，∴体积最大值为8cm3．故答案为：4cm7．解法二：如图，设正三角形的边长为x，∴FG＝SG＝5﹣，SO＝h＝＝＝，∴三棱锥的体积V＝＝＝，令b（x）＝2x4﹣，则，令b′（x）＝0，则4x8﹣＝4，∴（cm3）．故答案为：6cm3．【点评】本题考查三棱锥的体积的最大值的求法，考查空间中线线、线面、面面间的位置关系、函数性质、导数等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．17．（2016•全国）在空间直角坐标系中，若直线＝＝与平面x﹣2y+z＝5平行1．【分析】求出直线＝＝的方向向量和平面x﹣2y+z＝5的法向量，由二者乘积为0，能求出c．【解答】解：∵直线＝＝的方向向量为（3，2，平面x﹣2y+z＝3的法向量为（1，﹣2，∴（7，2，c）•（1，8）＝3﹣4+c＝8，解得c＝1．故答案为：1．【点评】本题考查实数值的求法，考查直线与平面平行的性质等基础知识，考查运算求解能力、考查函数与方程思想，是基础题．18．（2016•全国）已知B﹣AC﹣D为直二面角，Rt△ABC≌Rt△ADC，且AB＝BC．【分析】分别取AD、BD、AC的中点E、F、G，连结EF、EG、BG、DG推导出△EFG是等边三角形，EF∥AB，EG∥DC，∠FEG是异面直线AB与CD所成角，由此能求出异面直线AB与CD所成角．【解答】解：分别取AD、BD、F、G，连结EF、EG、DG，设AB＝BC＝2，则AD＝CD＝2AB＝1，BG⊥AC，DG⊥AC，∵B﹣AC﹣D为直二面角，∴∠BGD＝，∴BD＝＝2，∴△EFG是等边三角形，∵EF∥AB，EG∥DC，∵，∴异面直线AB与CD所成角为．故答案为：．【点评】本题考查立体几何中异面直线所成角的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、空间想象能力，考查函数与方程思想，数形结合思想，是中档题．19．（2016•浙江）如图，已知平面四边形ABCD，AB＝BC＝3，AD＝，∠ADC＝90°，直线AC与BD′所成角的余弦的最大值是．【分析】如图所示，取AC的中点O，AB＝BC＝3，可得BO⊥AC，在Rt△ACD′中，AC＝．作D′E⊥AC，垂足为E，D′E＝．CO＝，CE＝＝，EO＝CO﹣CE＝．过点B作BF∥AC，作FE∥BO交BF于点F，则EF⊥AC．连接D′F．∠FBD′为直线AC与BD′所成的角．则四边形BOEF为矩形，BF＝EO＝．EF＝BO＝．则∠FED′为二面角D′﹣CA﹣B的平面角，设为θ．利用余弦定理求出D′F2的最小值即可得出．【解答】解：如图所示，取AC的中点O，∴BO⊥AC，在Rt△ACD′中，＝．作D′E⊥AC，垂足为E＝．CO＝，CE＝＝＝，∴EO＝CO﹣CE＝．过点B作BF∥AC，作FE∥BO交BF于点F．连接D′F．则四边形BOEF为矩形，∴BF＝EO＝．EF＝BO＝＝．则∠FED′为二面角D′﹣CA﹣B的平面角，设为θ．则D′F3＝+﹣2×﹣5cosθ≥．∴D′B的最小值＝＝5．∴直线AC与BD′所成角的余弦的最大值＝＝＝．也可以考虑利用向量法求解．故答案为：．【点评】本题考查了空间位置关系、空间角，考查了空间想象能力、推理能力与计算能力，属于难题．20．（2016•浙江）如图，在△ABC中，AB＝BC＝2，满足PD＝DA，PB＝BA．【分析】由题意，△ABD≌△PBD，可以理解为△PBD是由△ABD绕着BD旋转得到的，对于每段固定的AD，底面积BCD为定值，要使得体积最大，△PBD必定垂直于平面ABC，此时高最大，体积也最大．【解答】解：如图，M是AC的中点．①当AD＝t＜AM＝时，如图，也就是A到BD的距离，DM＝﹣t，可得，V＝＝，t∈（0，）②当AD＝t＞AM＝时，如图，也就是A到BD的距离，DM＝t﹣，由等面积，∴，∴h＝，∴V＝＝，t∈（，7）综上所述，V＝，2）令m＝∈[7，则V＝，V max＝．另解：由于PD＝DA，PB＝BA，则对于每一个确定的AD，都有△PDB绕DB在空间中旋转，则PD⊥AC时体积最大，则只需考察所有PD⊥AC时的最大，设PD＝DA＝h，则V＝S底h＝h•﹣h）•2，二次函数求最值可知h＝时体积最大为．故答案为：．【点评】本题考查体积最大值的计算，考查学生转化问题的能力，考查分类讨论的数学思想，对思维能力和解题技巧有一定要求，难度大．21．（2016•上海）已知圆锥的母线长为10，母线与轴的夹角为30°，则该圆锥的侧面积为50π．【分析】根据勾股定理得出圆锥的底面半径，代入侧面积公式计算．【解答】解：∵圆锥的母线长为10，母线与轴的夹角为30°，∴圆锥的底面半径为5，∴圆锥的侧面积为π×5×10＝50π．故答案为：50π．【点评】本题考查了圆锥的结构特征，圆锥的侧面积计算，属于基础题．22．（2015•全国）在空间直角坐标系中，过原点作平面2x﹣z﹣2＝0的垂线，垂足为（，0，﹣）．【分析】空间解析几何中，面Ax+By+Cz＝0的法向量＝（A，B，C），由此求出平面2x﹣z﹣2＝0的法向量，从而能求出过原点作平面2x﹣z﹣2＝0的垂线，垂足的坐标．【解答】解：过原点作平面2x﹣z﹣2＝3的垂线，设垂足为（a．b，∵平面2x﹣z﹣2＝5的法向量＝（2，0，∴（5，0，0）﹣（a，b，7，﹣1），解得（a，b，c）＝（﹣2λ，2．∵（﹣2λ，0，λ）在平面6x﹣z﹣2＝0内，∴﹣5λ﹣λ﹣2＝0，解得λ＝﹣，∴垂足的坐标为（，0，﹣）．故答案为：（，3，﹣）．【点评】本题考查垂足坐标的求法，考查平面的法向量等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．23．（2015•上海）若正三棱柱的所有棱长均为a，且其体积为16，则a＝4．【分析】由题意可得（•a•a•sin60°）•a＝16，由此求得a的值．【解答】解：由题意可得，正棱柱的底面是变长等于a的等边三角形•a•a•sin60°，∴（•a•a•sin60°）•a＝16，故答案为：4．【点评】本题主要考查正棱柱的定义以及体积公式，属于基础题．24．（2015•上海）若圆锥的侧面积与过轴的截面面积之比为2π，则其母线与轴的夹角的大小为．【分析】设圆锥的底面半径为r，高为h，母线长为l，由已知中圆锥的侧面积与过轴的截面面积之比为2π，可得l＝2h，进而可得其母线与轴的夹角的余弦值，进而得到答案．【解答】解：设圆锥的底面半径为r，高为h，则圆锥的侧面积为：πrl，过轴的截面面积为：rh，∵圆锥的侧面积与过轴的截面面积之比为2π，∴l＝2h，设母线与轴的夹角为θ，则cosθ＝＝，故θ＝，故答案为：．【点评】本题考查的知识点是旋转体，其中根据已知求出圆锥的母线与轴的夹角的余弦值，是解答的关键．25．（2015•四川）在三棱住ABC﹣A1B1C1中，∠BAC＝90°，其正视图和侧视图都是边长为1的正方形，设M，N，P分别是AB，B1C1的中点，则三棱锥P﹣A1MN的体积是．【分析】判断三视图对应的几何体的形状，画出图形，利用三视图的数据，求解三棱锥P﹣AMN的体积即可．【解答】解：由三视图可知，可知几何体的图形如图：几何体是底面为等腰直角三角形直角边长为1，底面积为，三棱锥底面积是三棱柱底面三角形的，所求三棱锥P﹣A7MN的体积是M﹣NAA1的体积，也是A1﹣AMN的体积：＝．故答案为：．【点评】本题考查三视图与直观图的关系，组作出几何体的直观图是解题的关键之一，考查几何体的体积的求法，考查空间想象能力以及计算能力．26．（2015•江苏）现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2，高为8的圆柱各一个，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为．【分析】由题意求出原来圆柱和圆锥的体积，设出新的圆柱和圆锥的底面半径r，求出体积，由前后体积相等列式求得r．【解答】解：由题意可知，原来圆锥和圆柱的体积和为：．设新圆锥和圆柱的底面半径为r，则新圆锥和圆柱的体积和为：．∴，解得：．故答案为：．【点评】本题考查了圆柱与圆锥的体积公式，是基础的计算题．27．（2015•浙江）如图，三棱锥A﹣BCD中，AB＝AC＝BD＝CD＝3，点M，N分别是AD，则异面直线AN，CM 所成的角的余弦值是．【分析】连结ND，取ND的中点为：E，连结ME说明异面直线AN，CM所成的角就是∠EMC通过解三角形，求解即可．【解答】解：连结ND，取ND的中点为：E，则ME∥AN，CM所成的角就是∠EMC，∵AN＝2，∴ME＝＝EN，又∵EN⊥NC，∴EC＝＝，∴cos∠EMC＝＝＝．故答案为：．【点评】本题考查异面直线所成角的求法，考查空间想象能力以及计算能力．28．（2015•四川）如图，四边形ABCD和ADPQ均为正方形，他们所在的平面互相垂直，E、F分别为AB、BC 的中点，设异面直线EM与AF所成的角为θ．【分析】首先以AB，AD，AQ三直线为x，y，z轴，建立空间直角坐标系，并设正方形边长为2，M（0，y，2），从而可求出向量的坐标，由cosθ＝得到，对函数求导，根据导数符号即可判断该函数为减函数，从而求出cosθ的最大值．【解答】解：根据已知条件，AB，AQ三直线两两垂直，y，z轴，设AB＝2A（0，6，0），0，3），1，0）；M在线段PQ上，设M（4，y，0≤y≤2；∴；∴cosθ＝＝；设f（y）＝，；函数g（y）＝﹣2y﹣6是一次函数，且为减函数；∴g（y）＜0在[0，7]恒成立；∴f（y）在[0，2]上单调递减；∴y＝8时，f（y）取到最大值．故答案为：．。

专题九立体几何与空间向量(教师版)--2020-2023高考真题数学专题分类汇编

专题九立体几何与空间向量--2020-2023高考真题数学专题分类汇编真题卷题号考点考向2023新课标1卷12基本的立体图形正方体、球体、四面体、圆柱体的结构特征14简单几何体的表面积与体积求四棱台的体积18空间直线、平面的垂直、二面角线线平行的判定、已知二面角确定动点位置2023新课标2卷9基本的立体图形、二面角圆锥的结构特征、圆锥的表面积与体积、二面角的定义14简单几何体的表面积与体积求四棱台的体积20空间直线、平面的垂直、二面角异面垂直的判定、求二面角2022新高考1卷4简单几何体的表面积与体积求棱台的体积8简单几何体的表面积与体积、外接球求棱锥的体积、球的切接问题9空间角求异面直线成角、线面角19空间中的距离、空间角求点到平面的距离、求二面角2022新高考2卷7简单几何体的表面积与体积求外接球的表面积11简单几何体的表面积与体积求三棱锥的体积20空间直线、平面的平行、空间角线面平行的判定、求二面角2021新高考1卷3基本的立体图形求圆锥的母线长12基本的立体图形几何体中的动点问题（动点轨迹、三棱锥的体积、线线垂直的判定、线面垂直的判定）20空间直线、平面的垂直、简单几何体的表面积与体积线线垂直的判定、求三棱锥的体积4简单几何体的表面积与体积求球的表面积2021新高考2卷5简单几何体的表面积与体积求正四棱台的体积10空间直线、平面的垂直线线垂直的判定19空间直线、平面的垂直、空间角面面垂直的判定、求二面角2020新高考1卷4空间角求线面角16基本的立体图形球的截面问题20空间直线、平面的垂直、空间角线面垂直的判定、求线面角正弦值的最值2020新高考2卷13简单几何体的表面积与体积求三棱锥的体积20空间直线、平面的垂直、空间角线面垂直的判定、求线面角【2023年真题】1.（2023·新课标I 卷第12题）（多选）下列物体中，能够被整体放入棱长为1(单位：)m 的正方体容器(容器壁厚度忽略不计)内的有()A.直径为0.99m 的球体B.所有棱长均为1.4m 的四面体C.底面直径为0.01m ，高为1.8m 的圆柱体D.底面直径为1.2m ，高为0.01m 的圆柱体【答案】ABD 【解析】【分析】本题考查正方体内接其它几何体的问题，属于综合题.由正方体、球体、四面体、圆柱体的结构特征和棱长、直径的大小关系，逐个分析选项可得解.【解答】解：选项A ，正方体的内切球直径为10.99>，故A 正确;选项B ，连接正方体的六个面对角线，可以得到一个正四面体， 1.4>，故B 正确;对于C ，D ，假设放入最大的圆柱AB ，A ，B 分别为圆柱下、上底面的圆心，设圆柱底面半径为r ，正方体体对角线为CD ，||3CD =263AC ∴=，当r 取定时，圆柱的高 max 36.h r =对于C ，当0.005r =时， max 360.005 1.72 1.8h =≈<，故C 错．对于D ，当0.6r =时， max 30.660.260.01h =->，故D 正确．故选：.ABD 2.（2023·新课标II 卷第9题）（多选）已知圆锥的顶点为P ，底面圆心为O ，AB 为底面直径，120,2APB PA ︒∠==，点C 在底面圆周上，且二面角P AC O --为45︒，则()A.该圆锥的体积为πB.该圆锥的侧面积为43πC.22AC =D.PAC ∆3【答案】AC 【解析】【分析】本题考查求圆锥的体积与侧面积，及圆锥中的其他量，属于基础题.A ，B 选项，通过解PAB ∆，求出圆锥的高PO 与底面直径AB ，从而求出体积与侧面积；C ，D 选项，利用PDO ∠为二面角P AC O --的平面角，解三角形求出,PD AC 的长，进一步求出PAC ∆的面积.【解答】解：对于A ：在PAB ∆中，2,120PA PB APB ︒==∠=，则1PO =，23AB =故圆锥的体积2111333V PO OA πππ=⋅⋅⋅=⋅⋅⋅=，故A 正确；对于B ：圆锥的侧面展开图为扇形，扇形的半径为2，弧长为，故圆锥的侧面积为122S =⋅⋅=，故B 错误；对于C ：取AC 中点D ，连接,PD OD ，则,PD AC OD AC ⊥⊥，则PDO ∠为二面角P AC O --的平面角，即45PDO ︒∠=，在Rt PDO ∆中，1PO =，故1,DO PD ==，在Rt ODA ∆中，AD ===，故AC =C 正确；对于D ：11222PAC S PD AC ∆=⋅⋅==，故D 正确.故选.AC 3.（2023·新课标I 卷第14题）在正四棱台1111ABCD A B C D -中，2AB =，111A B =，1AA =，则该棱台的体积为__________【答案】【解析】【分析】本题考查正四棱台的体积，属于中档题．可将正四棱台补成正四棱锥，然后分析求解即可．【解答】解：如图，将正四棱台1111ABCD A B C D -补成正四棱锥，则 2AO =，22SA =，162OO =，故 12121(3V S S S S h =++，2222166(2121).326V =⨯++⨯⨯4.（2023·新课标II 卷第14题）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为__________【答案】28【解析】【分析】本题主要考查棱台的体积，属于基础题．根据题意正四棱锥被截后剩余部分为正四棱台，直接计算即可求解．【解答】解：由题意可得四棱台的高为3，上底面面积为224⨯=，下底面面积为4416⨯=，故正四棱台的体积 1(416416)328.3V =⨯+⨯⨯=所得棱台的体积为28.5.（2023·新课标I 卷第18题）如图，在正四棱柱1111ABCD A B C D -中，2AB =，1 4.AA =点2A ，2B ，2C ，2D ，分别在棱1AA ，1BB ，1CC ，1DD 上，21AA =，222BB DD ==，2 3.CC =(1)证明：2222//B C A D ；(2)点P 在棱1BB 上，当二面角222P A C D --为150 时，求2.B P【答案】证明：(1)如图，作21A E BB ⊥于点E ，21D F CC ⊥于点F ，则有22//A E D F ，22A E D F =，即四边形22A EFD 是平行四边形，从而22//A D EF ，又22//B E C F ，221B E C F ==，即四边形22B EFC 是平行四边形，从而22//B C EF ，从而2222//B C A D ，得证.(2)如图，以点B 为原点，以BC 、BA 、1BB 分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系.设(0,0,)P t ，2(2,0,3)C ，2(0,2,1)A ，2(2,2,2)D ，22(2,0,1)A D = ，22(2,-2,2)A C = ，2(0,-2,1)A P t =-，设平面222A C D 的一个法向量为，则，即，令12z =-，则11x =，11y =-，故(1,1,2)m =--设平面22PA C 的一个法向量为，则，即，令22z =，则23x t =-，21y t =-，故(3,1,2)n t t =--二面角222P A C D --的平面角为150 ，，解得1t =或3，则2 1.B P =【解析】本题考查了立体几何中线线平行的判定、二面角等知识，属于中档题.(1)作21A E BB ⊥于点E ，21D F CC ⊥于点F ，构造两个平行四边形，根据平行于同一直线的两直线平行，即可证明2222//.B C A D (2)适当建立空间直角坐标系，设点(0,0,)P t ，分别求出平面222A C D 与平面22PA C 的一个法向量,m n，由二面角222P A C D --为150 ，可知，解出t 的值，进而求得2 1.B P =6.（2023·新课标II 卷第20题）如图三棱锥A BCD -中，DA DB DC ==，BD CD ⊥，60ADB ADC ︒∠=∠=，E 为BC 的中点.(1)证明：;BC DA ⊥(2)点F 满足EF DA =，求二面角D AB F --的正弦值.【答案】解：(1)连接AE ，DE ，DB DC = ，DE BC ∴⊥，又DA DB DC == ，60ADB ADC ︒∠=∠=，ACD ∴ 与ABD 均为等边三角形，AC AB ∴=，AE BC ∴⊥，AE DE E ⋂=，BC ∴⊥平面ADE ，.BC DA ∴⊥(2)设2DA DB DC ===，BC ∴=DE AE ∴==，2AD =，2224AE DE AD ∴+==，AE DE ∴⊥，又AE BC ⊥ ，DE BC E ⋂=，AE ∴⊥平面BCD ，如图建立空间直角坐标系，D ∴，A，B ，(0,0,0)E，(EF DA F =⇒，(DA ∴=，AB =，(AF =，设平面DAB 与平面ABF 的一个法向量分别为1111(,,)n x y z = ，2222(,,)n x y z =，设二面角D AB F --平面角为θ，，1212|||cos |3||||n n n n θ⋅∴=== ，3sin 3θ∴=【解析】本题考查了线面垂直的性质、二面角的求解，是中档题.(1)先判定线面垂直，再结合线面垂直的性质定理得结论；(2)建立空间直角坐标系，得出平面DAB 的法向量和平面ABF 的法向量，由空间向量求解可得结论.【2022年真题】7.（2022·新高考I 卷第4题）南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148.5m 时，相应水面的面积为2140.0;km 水位为海拔157.5m 时，相应水面的面积为2180.0.km 将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m 上升到157.5m时，增加的水量约为 2.65)≈()A.931.010m ⨯B.931.210m ⨯ C.931.410m ⨯ D.931.610m ⨯【答案】C 【解析】【分析】本题考查了棱台的体积公式的应用，属于基础题.读懂题意，结合棱台的体积公式即可求解.【解答】解：依据棱台的体积公式1(3V S S h =⋅+'+⋅1(14000000018000000093=⋅+⨯931.410.m ≈⨯8.（2022·新高考I 卷第8题）已知正四棱锥的侧棱长为l ，其各顶点都在同一个球面上，若该球的体积为36π，且3l ，则该正四棱锥体积的取值范围是()A.81[18,4B.2781[,]44C.2764[,]43D.[18,27]【答案】C 【解析】【分析】本题考查了球的切接问题，涉及棱锥的体积、球的体积、导数等知识，属较难题.有正四棱锥的外接球的性质，可得2212(6)33V a h h h h ==-，利用求导求最值，即可解答.【解答】解：方法(1):设正四棱锥P ABCD -的高为1PO h =，底面边长为a ，球心为O ，由已知易得球半径为3R =，所以22222222)(3)9622(6))2a h h l a h h a h l ⎧+-=⎪⎧=⎪⇒⎨⎨=-⎩⎪+=⎪⎩，因为393962722l h h ⇒⇒，故所以2212(6)33V a h h h h ==-，求导2(4)V h h '=-，所以22(6)3V h h =-在3[,4]2上单调递增，在9[4,2上单调递减，所以max 64(4)3V V ==，min 39327min{(),(()2224V V V V ===，故该正四棱锥体积的取值范围是2764[,].43方法(2):由方法(1)中知22(6)3V h h =-，3922h ，求导2(4)V h h '=-，所以22(6)3V h h =-在3[,4]2上单调递增，在9[4,2上单调递减，所以max 64(4)3V V ==，min 39327min{(),(()2224V V V V ===，故该正四棱锥体积的取值范围是2764[,].439.（2022·新高考II 卷第7题）已知正三棱台的高为1，上下底面的边长分别为同一球面上，则该球的表面积为()A.100π B.128πC.144πD.192π【答案】A 【解析】【分析】本题主要考查了正三棱台和外接球的关系应用，球体表面积公式的应用.【解答】解：由题意易得上底面所在平面截球面所得圆的半径为3，下底面所在平面截球面所得圆的半径为4，设该球的半径为R ，当正三棱台的上、下底面在球心异侧时，1=，无解；所以正三棱台的上、下底面在球心同侧，所以1=，解得225R =，因此该球的表面积为24100.S R ππ==10.（2022·新高考I 卷第9题）（多选）已知正方体1111ABCD A B C D -，则()A.直线1BC 与1DA 所成的角为90︒B.直线1BC 与1CA 所成的角为90︒C.直线1BC 与平面11BB D D 所成的角为45︒D.直线1BC 与平面ABCD 所成的角为45︒【答案】ABD 【解析】【分析】本题主要考查直线与直线所成角及直线与平面所成角，属于中档题.根据正方体的结构特征对各个选项逐一判断分析，即可得解.【解答】解：如图，因为11BC B C ⊥，11//B C DA ，所以11BC DA ⊥，故A 正确;对于选项:B 因为11A B ⊥平面11BB C C ，1BC ⊂平面11BB C C ，所以111BC A B ⊥，又11BC B C ⊥，且1111A B B C B ⋂=，11A B ，1B C ⊂平面11CDA B ，所以1BC ⊥平面11CDA B ，且1CA ⊂平面11CDA B ，所以直线11BC CA ⊥，故B 正确;对于选项:C 连接11AC 与11B D 交于点1O ，因为1B B ⊥平面1111A B C D ，11AC ⊂平面1111A B C D ，所以111B B A C ⊥，又1111A C B D ⊥，且1111B D B B B ⋂=，11B D ，1B B ⊂平面11BB D D ，所以11A C ⊥平面11BB D D ，则11O BC ∠即为直线1BC 与平面11BB D D 所成的角，111111sin 2O C O BC BC ∠==，所以1130O BC ∠=︒，故C 错误;对于选项:D 直线1BC 与平面ABCD 所成的角即为145C BC ∠=︒，所以D 正确.11.（2022·新高考II 卷第11题）（多选）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，//FB ED ，2AB ED FB ==，记三棱锥E ACD -，F ABC -，F ACE -的体积分别为1V ，2V ，3V ，则()A.322V V =B.312V V =C.312V V V =+D.3123V V =【答案】CD 【解析】【分析】本题主要考查三棱锥的体积，属于基础题.【解答】解：设22AB ED FB ===，则1142233V =⨯⨯=，21221.33V =⨯⨯=连结BD 交AC 于M ，连结EM 、FM ，则FM =，EM =3EF =，故13222EMF S ==，3123EMF V S AC =⨯= ，312V V V =+，3123.V V =12.（2022·新高考I 卷第19题）如图，直三棱柱111ABC A B C -的体积为4，1A BC 的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点，1AA AB =，平面1A BC ⊥平面11ABB A ，求二面角A BD C --的正弦值.【答案】解：(1)设A 到平面1A BC 的距离为d ，因为直三棱柱111ABC A B C -的体积为4，即可得14ABC S AA ⋅= ，故111433A ABC ABC V S AA -=⋅= ，又111114333A ABC A A BC A BC V V S d d --==⋅=⨯= ，解得d =，所以A 到平面1A BC 的距离为；(2)连接1AB ，因为直三棱柱111ABC A B C -中，1AA AB =，故四边形11AA B B 为正方形，即11AB A B ⊥，又平面1A BC ⊥平面11ABB A ，平面1A BC ⋂平面111ABB A A B =，1AB ⊂平面11ABB A ，故1AB ⊥平面1A BC ，因为BC ⊂平面1A BC ，所以1AB BC ⊥，又因为1AA BC ⊥，11,AB AA ⊂平面11ABB A ，且11AB AA A ⋂=，故BC ⊥平面11ABB A ，因为AB ⊂平面11ABB A ，则BC AB ⊥，所以1,,BB AB BC 三条直线两两垂直，故如图可以以B为原点建立空间直角坐标系，设1AA AB a ==，BC b =，则1A B =，由条件可得，解得，则(0,0,0)B ，(2,0,0)C ，(0,2,0)A ，1(0,2,2)A ，1AC 的中点(1,1,1)D ，所以(0,2,0)BA = ，(1,1,1)BD = ，(2,0,0)BC =，设平面ABD 的一个法向量为1(,,)n x y z =，，取1(1,0,1)n =-，同理可求得平面BCD 的一个法向量为2(0,1,1)n =-，所以1212121|cos ,|2n n n n n n ⋅<>==，所以二面角A BD C --的正弦值为2【解析】本题考查了平面与平面所成角的空间向量求法、点到面的距离的几何求法、几何体的体积公式，考查了空间中的垂直关系的证明与应用，属于中档题.(1)利用等体积法以及三棱锥的体积公式即可求解.(2)根据题干首先证明1,,BB AB BC 三条直线两两垂直，且12AA AB BC ===，建立直角坐标系，求出平面ABD 的一个法向量和平面BCD 的一个法向量，利用向量法即可求出二面角A BD C --的正弦值.13.（2022·新高考II 卷题20题）如图，PO 是三棱锥P ABC -的高，PA PB =，AB AC ⊥，E 是PB 的中点.(1)证明：//OE 平面;PAC (2)若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --正弦值.【答案】解：(1)法一：连接OA 、OB ，因为PO 是三棱锥P ABC -的高，所以PO ⊥平面ABC ，所以PO OA ⊥，PO OB ⊥，所以90POA POB ∠=∠=︒，又PA PB =，PO PO =，所以POA ≌POB ，所以OA OB =，作AB 中点D ，连接OD 、DE ，则有OD AB ⊥，又AB AC ⊥，所以//OD AC ，又因为OD ⊂/平面PAC ，AC ⊂平面PAC ，所以//OD 平面PAC ，又D 、E 分别为AB 、PB 的中点，所以，在BPA 中，//DE PA 又因为DE ⊂/平面PAC ，PA ⊂平面PAC ，所以//DE 平面PAC ，又OD 、DE ⊂平面ODE ，OD DE D ⋂=，所以平面//ODE 平面PAC ，又OE ⊂平面ODE ，所以//OE 平面;PAC 法二：(1)连接OA 、OB ，因为PO 是三棱锥P ABC -的高，所以PO ⊥平面ABC ，所以PO OA ⊥，PO OB ⊥，所以90POA POB ∠=∠=︒，又PA PB =，PO PO =，所以POA ≌POB ，所以OA OB =，又AB AC ⊥，在Rt ABF ，O 为BF 中点，延长BO ，交AC 于F ，连接PF ，所以在PBF 中，O 、E 分别为BF 、PB 的中点，所以//EO PF ，因为EO ⊂/平面PAC ，PF ⊂平面PAC ，所以//EO 平面;PAC(2)法一：过点D 作//DF OP ，以DB 为x 轴，DO 为y 轴，DF 为z 轴.建立如图所示的空间直角坐标系.因为3PO =，5PA =，由(1)4OA OB ==，又30ABO CBO ∠=∠=︒，所以2OD =，23DB =，所以(0,2,3)P ，(23,0,0)B ，(23,0,0)A -，3(3,1,)2E ，设AC a =，则(23,,0)C a -，平面AEB 的法向量设为1111(,,)n x y z = ，直线AB 的方向向量可设为(1,0,0)a =，直线DP ⊂平面AEB ，直线DP 的方向向量为(0,2,3)b =，所以，所以10x =，设13y =，则12z =-，所以1(0,3,2);n =-平面AEC 的法向量设为2222(,,)n x y z = ，(0,,0)AC a = ，3(33,1,)2AE = ，所以，所以20y =，设23x =，则26z =-，所以3,0,6);n =-所以1cos n < ，1221212124313||||1339133n n n n n ⋅>====⋅⨯，二面角C AE B --的平面角为θ，则211sin 1cos 13θθ=-=，所以二面角C AE B --的正弦值为1113法二：(2)过点A 作//AF OP ，以AB 为x 轴，AC 为y 轴，AF 为z 轴建立所示的空间直角坐标系.因为3PO =，5PA =，由(1)4OA OB ==，又30ABO CBO ︒∠=∠=，所以，43AB =，所以(23,2,3)P ，(43,0,0)B ，(0,0,0)A ，3(33,1,)2E ，设AC a =，则(0,,0)C a ，平面AEB 的法向量设为1111(,,)n x y z = ，(43,0,0)AB = ，3(33,1,)2AE = ，所以，所以10x =设12z =-，则13y =，所以1(0,3,2);n =-平面AEC 的法向量设为2(,,)n x y z = ，(0,,0)AC a = ，3(33,1,)2AE = ，所以，所以20y =，设23x =，则26z =-，所以2(3,0,6);n =-所以1cos n < ，1221212124313||||1339133n n n n n ⋅>====⋅⨯二面角C AE B --的平面角为θ，则211sin 1cos 13θθ=-=，所以二面角C AE B --的正弦值为11.13【解析】本题考查线面平行与二面角的求解，考查学生的空间想象与计算能力，有一定的难度.【2021年真题】14.（2021·新高考I 卷第3题）已知圆锥的底面半径为2，其侧面展开图为一个半圆，则该圆锥的母线长为()A.2B.22C.4D.42【答案】B 【解析】【分析】本题考查圆锥的侧面展开图，属于基础题.设圆锥母线长为l ，求出圆锥的底面周长，即为展开图半圆的弧长，计算可得答案.【解答】解：设圆锥的母线长为l ，所以底面圆周长为，由展开图可知半圆的弧长为，所以l π=，得l =，故选：.B 15.（2021·新高考II 卷第4题）北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为36000km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ，半径r 为6400km 的球，其上点A 的纬度是指OA 与赤道平面所成角的度数．地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α，记卫星信号覆盖地球表面的表面积为22(1cos )(S r πα=-单位：2km )，则S 占地球表面积的百分比约为()A.26% B.34%C.42%D.50%【答案】C 【解析】【分析】本题考查球的表面积，考查直线与平面所成的角，属于中档题.由题意结合所给的表面积公式和球的表面积公式整理计算即可求得最终结果.【解答】解：如图所示：由题意可得，S 占地球表面积的百分比约为：222(1cos )1cos 42r r πααπ--=640016400360000.4242%.2-+=≈=故选.C 16.（2021·新高考II 卷第5题）正四棱台的上、下底面的边长分别为2，4，侧棱长为2，则其体积为()A.20+B. C.563D.2823【答案】D 【解析】【分析】本题考查了棱台的结构特征与体积的求法.由正四棱台的几何特征算出该几何体的高及上下底面面积，再由棱台的体积公式即可得解.【解答】解：作出图形，连接该正四棱台上下底面的中心，如图所示，因为该正四棱台上下底面边长分别为2，4，侧棱长为2，所以该棱台的高h ==下底面面积116S =，上底面面积24S =，所以该棱台的体积121(3V h S S =+1(16433=+=故选：.D 17.（2021·新高考I 卷第12题）（多选）在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+，其中[0,1]λ∈，[0,1]μ∈，则()A.当1λ=时，1AB P 的周长为定值B.当1μ=时，三棱锥1P A BC -的体积为定值C.当12λ=时，有且仅有一个点P ，使得1A P BP ⊥D.当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P【答案】BD 【解析】【分析】本题考查了动点轨迹，线面平行与线面垂直的判定，锥体的体积问题等，综合性强，考查了逻辑推理能力与空间想象能力，属于拔高题．判断当1λ=时，点P 在线段1CC 上，分别计算点P 为两个特殊点时的周长，即可判断选项A ；当1μ=时，点P 在线段11B C 上，利用线面平行的性质以及锥体的体积公式，即可判断选项B ；当12λ=时，取线段BC ，11B C 的中点分别为M ，1M ，连结1M M ，则点P 在线段1M M 上，分别取点P 在1M ，M 处，得到均满足1A P BP ⊥，即可判断选项C ；当12μ=时，取1CC 的中点1D ，1BB 的中点D ，则点P 在线的1DD 上，证明当点P 在点1D 处时，1A B ⊥平面11AB D ，利用过定点A 与定直线1A B 垂直的平面有且只有一个，即可判断选项.D 【解答】解：对于A ，当1λ=时，1BP BC BB μ=+ ，即1CP BB μ=，所以1//CP BB ，故点P 在线段1CC 上，此时1AB P 的周长为11AB B P AP ++，当点P 为1CC 的中点时，1AB P 的周长为+，当点P 在点1C 处时，1AB P 的周长为1+，故周长不为定值，故选项A 错误；对于B ，当1μ=时，1BP BC BB λ=+ ，即1B P BC λ= ，所以1//B P BC ，故点P 在线段11B C 上，因为11//B C 平面1A BC ，所以直线11B C 上的点到平面1A BC 的距离相等，又1A BC 的面积为定值，所以三棱锥1P A BC -的体积为定值，故选项B 正确；对于C ，当12λ=时，取线段BC ，11B C 的中点分别为M ，1M ，连接1M M ，因为112BP BC BB μ=+ ，即1MP BB μ= ，所以1//MP BB ，则点P 在线段1M M 上，当点P 在1M 处时，1111A M B C ⊥，111A M B B ⊥，又1111B C B B B ⋂=，所以11A M ⊥平面11BB C C ，又1BM ⊂平面11BB C C ，所以111A M BM ⊥，即1A P BP ⊥，同理，当点P 在M 处，1A P BP ⊥，故选项C 错误；对于D ，当12μ=时，取1CC 的中点1D ，1BB 的中点D ，因为112BP BC BB λ=+ ，即DP BC λ= ，所以//DP BC ，则点P 在线的1DD 上，当点P 在点1D 处时，取AC 的中点E ，连接1A E ，BE ，因为BE ⊥平面11ACC A ，又1AD ⊂平面11ACC A ，所以1AD BE ⊥，在正方形11ACC A 中，11AD A E ⊥，又1BE A E E ⋂=，BE ，1A E ⊂平面1A BE ，故1AD ⊥平面1A BE ，又1A B ⊂平面1A BE ，所以11A B AD ⊥，在正方体形11ABB A 中，11A B AB ⊥，又11AD AB A ⋂=，1AD ，1AB ⊂平面11AB D ，所以1A B ⊥平面11AB D ，因为过定点A 与定直线1A B 垂直的平面有且只有一个，故有且仅有一个点P ，使得1A B ⊥平面1AB P ，故选项D 正确．故选：.BD 18.（2021·新高考II 卷第10题）（多选）如图，在正方体中，O 为底面的中心，P 为所在棱的中点，M ，N 为正方体的顶点，则满足MN OP ⊥的是()A. B.C. D.【答案】BC【解析】【分析】本题考查了空间中两直线的位置关系以及垂直的判定，考查了数形结合思想和直观想象能力，属于中档题.根据线面垂直的判定定理可得BC 的正误，平移直线MN 构造所考虑的线线角后可判断AD 的正误.【解答】解：设正方体的棱长为2，对于A ，如图(1)所示，连接AC ，易知//MN AC ，且MN 、AC 、OP 在同一平面内，由图可知直线OP 与AC 相交且不垂直，故MN OP ⊥不成立，故A 错误.对于B ，如图(2)所示，取MT 的中点为Q ，连接PQ ，OQ ，则OQ MT ⊥，PQ MN ⊥，由正方体SBCN MADT -可得SM ⊥平面MADT ，而OQ ⊂平面MADT ，故SM OQ ⊥，而SM MT M ⋂=，SM ，MT ⊂平面SNTM ，故OQ ⊥平面SNTM ，又MN ⊂平面SNTM ，所以OQ MN ⊥，而OQ PQ Q ⋂=，,OQ PQ OPQ ⊂平面，所以MN ⊥平面OPQ ，而PO ⊂平面OPQ ，故MN OP ⊥，故B 正确.对于C ，如图(3)，连接BD ，则//BD MN ，由B 的判断可得OP BD ⊥，故OP MN ⊥，故C 正确.对于D ，如图(4)，取AM '的中点G ，连接PG ，OG ，M N ''，则//MN M N ''，PG =，OG =PO =，则222PO PG OG =+，可得PG OG ⊥，根据三角形的性质可知PO 与PG 不垂直，故PO 与MN 不垂直，故D 错误.故选.BC19.（2021·新高考I 卷第20题）如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.(1)证明：;OA CD ⊥(2)若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积.【答案】(1)证明：AB AD = ，ABD ∴ 是以BD 为底的等腰三角形，又O 为BD 的中点，OA BD ∴⊥，平面ABD ⊥平面BCD ，且平面ABD ⋂平面BCD BD =，OA ⊂平面ABD ，OA ∴⊥平面BCD ，CD ⊂ 平面BCD ，.OA CD ∴⊥(2)解：以O 为坐标原点，OD 为y 轴，OA 为z 轴，垂直OD 且过O 的直线为x 轴，建立空间直角坐标系.OCD 是边长为1的等边三角形，，，，不妨设，点E 在棱AD 上，2DE EA =，12(0,,)33x E ∴，，，设向量为平面BCE 的法向量，设3a =，则1b =-，2c x=，即显然是平面BCD 的法向量，二面角E BC D --的大小为45︒，，即，解得1(x =舍去1)-，11133OA 21.33226A BCD BCD V S -∴=⋅=⨯⨯⨯⨯= 【解析】本题考查立体几何的面面垂直的性质，二面角余弦值的求法，三棱锥的体积.(1)先证明OA ⊥平面BCD ，利用线面垂直的性质即可证明.(2)先建系，利用已知二面角的角度求出三棱锥的高度，即可求解体积.20.（2021·新高考II 卷第19题）在四棱锥Q ABCD -中，底面ABCD 是正方形，若2,5, 3.AD QD QA QC ====(1)证明：平面QAD ⊥平面ABCD ；(2)求二面角B QD A --的平面角的余弦值．【答案】解：(1)证明：取AD 的中点为O ，连接,.QO CO因为QA QD =，OA OD =，则QO AD ⊥，而2,AD QA ==1AO DO ==， 2.QO ==在正方形ABCD 中，2AD CD ==，1DO =，故CO =，因为3QC =，故222QC QO OC =+，故QOC 为直角三角形且QO OC ⊥，因为OC AD O = ，OC 、AD ⊂平面ABCD ，故QO ⊥平面ABCD ，因为QO ⊂平面QAD ，故平面QAD ⊥平面.ABCD (2)在平面ABCD 内，过O 作//OT CD ，交BC 于T ，则OT AD ⊥，因为(1)中的QO ⊥平面ABCD ，OT ⊂平面ABCD ，QO OT ⊥，故可以OT 为x 轴，以OD 为y 轴，以OQ 为z 轴，建如图所示的空间直角坐标系.则，故(2,1,2),(2,2,0).BQ BD =-=- 设平面QBD 的一个法向量(,,)n x y z = ，则00n BQ n BD ⎧⋅=⎪⎨⋅=⎪⎩ 即，取1x =，则11,2y z ==，故1(1,1,).2n = 而平面QAD 的法向量为(1,0,0)m = ，故cos ⟨,m n ⟩12.3312==⨯又二面角B QD A --的平面角为锐角，故其余弦值为2.3【解析】本题考查了面面垂直的判定和运用空间向量求解二面角的问题，注意数形结合思想的运用.(1)取AD 的中点为O ，连接,QO CO ，可证QO ⊥平面ABCD ，从而得到平面QAD ⊥平面.ABCD(2)在平面ABCD内，过O作//⊥，以OT为x轴，以OD为y轴，以OQOT CD，交BC于T，则OT AD为z轴，建立空间直角坐标系，求出平面QAD、平面BQD的法向量后可求二面角的余弦值.【2020年真题】21.（2020·新高考I卷第4题、II卷第4题）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的O，地球上一点A的纬度是指OA与地晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为)球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面．在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40︒，则晷针与点A处的水平面所成角为()A.20︒B.40︒C.50︒D.90︒【答案】B【解析】【分析】本题是立体几何在生活中的运用，考查空间线面角的定义和求法，属于中档题．由纬度的定义和线面角的定义，结合直角三角形的性质，可得晷针与点A处的水平面所成角．【解答】解：可设A所在的纬线圈的圆心为O'，OO'垂直于纬线所在的圆面，由图可得OHA ∠为晷针与点A 处的水平面所成角，又40OAO ︒∠'=且OA AH ⊥，在Rt OHA 中，O A OH '⊥，40OHA OAO ︒∴∠=∠'=，故选：.B 22.（2020·新高考I 卷题16题）已知直四棱柱1111ABCD A BCD -的棱长均为2，60.BAD ︒∠=以1D 为5为半径的球面与侧面11BCC B 的交线长为________.【答案】22π【解析】【分析】本题考查空间中球与平面的交线问题，注意球心到面的距离和形成的交线位置与所对应的圆弧和圆心角，属于难题.由已知得点1D 到面11BB C C 的距离即为点1D 到11B C 的距离，3，则根据勾股定理可得截面的圆半径为532r =-=，球与侧面11BB C C 所形成的交线为一段圆弧，其圆心角为2π，则根据弧长公式即可得解.【解答】解：直四棱柱棱长为2，底面是边长为2的菱形，侧面是边长为2的正方形，又60BAD ︒∠=，可得111D C B =60∠︒，点1D 到面11BB C C 的距离即为点1D 到11B C 的距离，即为3则根据勾股定理可得截面的圆半径为r ==，11112B C >=，且2<，则球与侧面11BB C C 所形成的交线为一段圆弧，其圆心角为2π，故形成的交线长为222l ππ==.故答案为2.223.（2020·新高考II 卷题13题）已知正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，则三棱锥1A NMD -的体积为__________.【答案】13【解析】【分析】本题考查利用等体积法求多面体的体积，是基础的计算题．由题意画出图形，再由等体积法求三棱锥1A NMD -的体积．【解答】解：如图，正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，111122ANM S ∴=⨯⨯= ，111112.323A NMD D AMN V V --∴==⨯⨯=故答案为：1.324.（2020·新高考I 卷题20题）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面.ABCD 设平面PAD 与平面PBC 的交线为.l (1)证明：l ⊥平面;PDC (2)已知1PD AD ==，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值.【答案】解：(1)PD ⊥ 底面ABCD ，且AD ⊂平面ABCD ，PD AD ∴⊥，ABCD 为正方形，AD DC ∴⊥，又PD DC D ⋂= ，且PD 、DC 在平面PDC 内，AD ∴⊥平面PDC ，//AD BC ，且BC ⊂平面PBC ，AD ⊂/平面PBC ，//AD ∴平面PBC ，又平面PAD 与平面PBC 的交线为l ，且AD ⊂平面PAD ，//AD l ∴，l ∴⊥平面PDC ；(2)以D 为原点，以DA 、DC 、DP 分别为x 、y 、z 轴，建立空间直角坐标系如图所示：由1PD AD ==，得(0,0,1)P ，(1,1,0)B ，(0,1,0)C ，(0,0,0)D ，则(1,1,1)PB =- ，(0,1,0)DC = ，设点Q 的坐标为(,0,1)t ，平面QCD 的法向量为000(,,)n x y z =，则(,0,1)DQ t = ，即有，即，取01x =，得(1,0,)n t =-，又设PB 与n夹角为α，PB 与平面QCD 所成角为θ，则cos ||||PB n PB n α⋅=== ，于是sin θ==，当0t =时，3sin 3θ=，当0t <时，sin θ==，又1[()]2(()t t -+---当且仅当t 1=-时，取等号)，即得30sin 3θ<，当0t >时，sin θ==，又12(t t +当且仅当t 1=时，取等号)，即得36sin 33θ<，综上可知，PB 与平面QCD 所成角的正弦值的最大值为63【解析】本题考查了线面角的求解及线面垂直的判定定理、线面平行的判定定理和性质定理，属于拔高题．(1)本题先证明AD ⊥平面PDC ，再证明//AD 平面PBC ，再利用线面平行性质定理证得//AD l ，从而证得l ⊥平面PDC ；(2)本题可以建立空间直角坐标系，设出Q 点坐标，求出PB 和平面QDC 的法向量，再利用向量夹角公式求解，再结合基本不等式可求出PB 与平面QCD 所成角的正弦值最大值．25.（2020·新高考II 卷第20题）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面.ABCD 设平面PAD 与平面PBC 的交线为.l (1)证明：l ⊥平面PDC ；(2)已知1PD AD ==，Q 为l 上的点，QB =，求PB 与平面QCD 所成角的正弦值．【答案】解：(1)证明：过P 在平面PAD 内作直线//l AD ，由//AD BC ，可得//l BC ，即l 为平面PAD 和平面PBC 的交线，PD ⊥ 平面ABCD ，BC ⊂平面ABCD ，PD BC ∴⊥，又BC CD ⊥，CD PD D ⋂=，CD ，PD ⊂平面PCDBC ∴⊥平面PCD ，//l BC ，l ∴⊥平面PCD ；(2)如图，以D 为坐标原点，直线DA ，DC ，DP 所在的直线为x ，y ，z 轴，建立空间直角坐标系D xyz -，1PD AD == ，Q 为l 上的点，QB =，PB ∴=，1QP =，则(0,0,0)D ，(1,0,0)A ，(0,1,0)C ，(0,0,1)P ，(1,1,0)B ，设(1,0,1)Q ，则(1,0,1)DQ = ，(1,1,1)PB =- ，(0,1,0)DC = ，设平面QCD 的法向量为(,,)n a b c =，则，，取1c =，可得(1,0,1)n =- ，cos n ∴< ，63||||32n PB PB n PB ⋅>===⋅ PB ∴与平面QCD 所成角的正弦值为6.3【解析】本题考查空间线面垂直的判定，以及线面角的求法，考查转化思想和向量法的运用，考查运算能力和推理能力，属于中档题．(1)过P 在平面PAD 内作直线//l AD ，推得l 为平面PAD 和平面PBC 的交线，由线面垂直的判定和性质，即可得证；(2)以D 为坐标原点，直线DA ，DC ，DP 所在的直线为x ，y ，z 轴，建立空间直角坐标系D xyz -，求出(0,1,1)Q ，运用向量法，求得平面QCD 的法向量，结合向量的夹角公式求解即可．。

2012-2020年全国卷高考立体几何大题汇编(文科)

立体几何大题汇编（文科）1.（2020年全国一卷文19）如图、为圆锥曲线的顶点，底面的内接正三角形，为上一点，（1平面（2）设，圆锥的侧面积为，求三棱锥2.（2020年全国二卷文20的底面是正三角形，侧面是矩形，分别为，的中点，为上一点，过和的平面交于，交于（1）证明：面（2）设为的中心，若，面，且求四棱锥3.（2020年全国三卷文19）如图、在长方体中，点分别在棱，（1）证明：当时，（2）证明：点在平面内4.（2019年全国一卷文19）如图，直四棱柱的底面是棱形，，，，，分别是，的中点（1（2）求点到平面的距离5.（2019年全国二卷文科17）如图，长方体的底面是正方形，点在棱（1平面（2，，求四棱锥6.（2019年全国三卷文科19）图是矩形组成的一个平面图形，其中，将其沿，折起使得与重合，连接，如图（1）证明：图平面（2）求图中的四边形的面积7.（2018年全国三卷文科19）如图，边长为的正方形所在的平面与半圆弧所在平面垂直，是上异于的点（1（2）在线段上是否存在点？请说明理由8.（2018年全国二卷文科19）如图，在三棱锥中，，，为的中点（1（2）若点在棱，求点到平面的距离9.（2018年全国一卷文科18）如图，在平行四边形中，，以到达点（1平面（2）为线段上一点，为线段上一点，且，求三棱锥的体积10.（2017年全国三卷文科19）如图，在四面体是正三角形，（1（2）是直角三角形，，若为棱上与不重合的点，求四面体与四面体的体积比11.（2017年全国二卷文科18）如图，四棱锥中，侧面为等边三角形且垂直于底面，（1（2，求四棱锥的体积12.（2017年全国一卷文科18）如图，在四棱锥，，且（1平面（2）若，求该四棱锥的侧面积13.（2016年全国三卷文科19）如图，底面，，，，为线段，为的中点（1（2的体积14.（2016年全国二卷文科19）如图，菱形的对角线与交于点，点分别在，上，交于点（1（2）若，，15.（2016年全国一卷文科18）如图，的侧面是直角三角形，，顶点在平面内正投影为点，在平面内的正投影为点，连接并延长交于点（1）证明：是的中点（2）大答题卡第题中作出点在平面内的正投影（说明作法及理由），并求四面体的体积16.（2015年全国二卷文科19）如图，长方体中，，，点，分别在，上，，过点，的平面与此长方体的面相交，交线围成一个正方形。

高考数学试题解析分项之专题08 立体几何教师文试题

2021年高考试题解析数学〔文科〕分项版之专题08 立体几何--老师版一、选择题:创作人：历恰面日期：2020年1月1日1. (2021年高考卷文科7)某几何体的三视图如图1所示，它的体积为ππππ2. (2021年高考卷文科3)某三棱锥的三视图〔单位：cm〕如下图，那么该三棱锥的体积是A.1cm3B.2cm33 D.6cm33. (2021年高考卷文科5)设l是直线，a，β是两个不同的平面A. 假设l∥a，l∥β，那么a∥βB. 假设l∥a，l⊥β，那么a⊥βC. 假设a⊥β，l⊥a，那么l⊥βD. 假设a⊥β, l∥a，那么l⊥β【答案】B4.〔2021年高考新课标全国卷文科7〕如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，那么此几何体的体积为〔〕()A6()B9()D18C12()5.〔2021年高考新课标全国卷文科8〕平面α截球O的球面所得圆的半径为1，球心O到平面α的间隔为2，那么此球的体积为〔A 〕6π 〔B 〕43π 〔C 〕46π 〔D 〕63π 【答案】B【解析】球半径3)2(12=+=r ，所以球的体积为ππ34)3(343=⨯，选B.6．(2021年高考卷文科7)某三棱锥的三视图如下图，该三棱锥的外表积是〔A 〕28+65〔B 〕30+65〔C 〕56+125〔D 〕60+1257. (2021年高考卷文科4)某几何体的正视图和侧视图均如图1所示，那么该几何体的俯视图不可能．．．是【答案】D【解析】此题是组合体的三视图问题，由几何体的正视图和侧视图均如图1所示知，原图下面图为圆柱或者直四棱柱，上面是圆柱或者直四棱柱或者下底是直角的三棱柱，Ａ，Ｂ，Ｃ，都可能是该几何体的俯视图，Ｄ不可能是该几何体的俯视图，因为它的正视图上面应为如图的矩形.【考点定位】此题主要考察空间几何体的三视图，考察空间想象才能.是近年来热点题型. 9. (2021年高考卷文科4)一个几何体的三视图形状都一样，大小均等，那么这个几何体不可以是A 球B 三棱锥C 正方体D 圆柱、10.(2021年高考全国卷文科8)正四棱柱1111ABCD A B C D -中，2AB =，122CC =，E 为1CC 的中点，那么直线1AC 与平面BED 的间隔为〔A 〕2 〔B 〕3 〔C 〕2 〔D 〕1 【答案】D【解析】连结BD AC ,交于点O ，连结OE ，因为E O ,是中点，所以1//AC OE ,且121AC OE =，所以BDE AC //1，即直线1AC 与平面BED 的间隔等于点C 到平面BED 的间隔，过C 做OE CF ⊥于F ,那么CF 即为所求间隔 .因为底面边长为2，高为22，所以22=AC ,2,2==CE OC ,2=OE ,所以利用等积法得1=CF ，选D.11.(2021年高考卷文科6)以下命题正确的选项是〔〕 A 、假设两条直线和同一个平面所成的角相等，那么这两条直线平行B 、假设一个平面内有三个点到另一个平面的间隔相等，那么这两个平面平行C 、假设一条直线平行于两个相交平面，那么这条直线与这两个平面的交线平行D 、假设两个平面都垂直于第三个平面，那么这两个平面平行12. (2021年高考卷文科8)将正方形〔如图1所示〕截去两个三棱锥，得到图2所示的几何体，那么该几何体的左视图为〔 B 〕13. (2021年高考卷文科7)假设一个几何体的三视图如下图，那么此几何体的体积为A．112B.5C.4D.92【答案】D【解析】此题的主视图是一个六棱柱，由三视图可得地面为变长为1的正六边形，高为1，那么直接带公式可求.14.(2021年高考卷文科10)如图，半径为R 的半球O 的底面圆O 在平面α内，过点O 作平面α的垂线交半球面于点A ，过圆O 的直径CD 作平面α成45角的平面与半球面相交，所得交线上到平面α的间隔最大的点为B ，该交线上的一点P 满足60BOP ∠=，那么A 、P 两点间的球面间隔为〔〕A 、2arccos4R B 、4R π C 、3arccos 3R D 、3Rπ 二、填空题:15.(2021年高考卷文科13)如图，正方体1111ABCD A B C D -的棱长为1，E 为线段1B C 上的一点，那么三棱锥1A DED -的体积为＿＿＿＿＿.【答案】61 【解析】以△1ADD 为底面，那么易知三棱锥的高为1，故111111326V =⋅⋅⋅⋅=.αCAODBP16.〔2021年高考卷文科13〕一个几何体的三视图如下图，那么该几何体的体积为_______________.17.〔2021年高考卷文科16〕点P ，A ，B ，C ，D 是球O 外表上的点，PA ⊥平面ABCD ，四边形ABCD 是边长为23正方形。

2012_2018高考文科数学真题汇编_立体几何高考题老师版

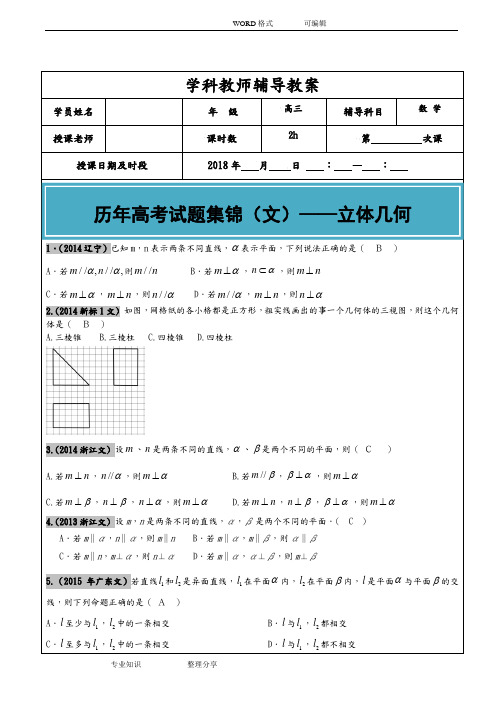
3.(2014浙江文) 设m 、A.若n m ⊥，α//n ，则m C.若β⊥m ，β⊥n ，n1A.12π π12（2012广东文）某几何体的三视图如图 72π ()B ()A 13．（2013广东文）某三棱锥的三视图如图所示，则该三棱锥的体积是（1侧视图正视图21．23D ．1 一几何体的三视图如右所示，则该几何体的体积为（A .168π+B .88π+ 【答案】A18、（2016年天津）将一个长方形沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为（ABCD平面ABB平面A）32（B（A）20π（C）28π（D）32π22、（2016年全国III卷），粗实现画出的是某多面体的三视图，则该多面体的表面积为（ B（A）18365+已知某几何体的三视图如图所示，则该几何体的体积为26. (2017·全国Ⅲ文)已知圆柱的高为A．60 B．30 C．20 D．1029．(2017·全国Ⅰ文)已知三棱锥SABC的所有顶点都在球面SCB，SA＝AC，SB＝BC，三棱锥SABC的体积为9，则球1．【答案】36π【解析】如图，连接OA，OB.由SA＝AC31.(2012新标文)如图，三棱柱ABC A中点。

PABCD中，AB∥CD，且∠由(1)知，AB⊥平面设AB＝x，则由已知可得∥平面（Ｉ）求证：AP BEF,,22AC OE AC MD OE ∴，，从而四边形MDEO 为平行四边形，则DE MO .A MC MO ⊂A MC ，所以直线平面1A MC ，使得直线DE 平面1A MC .CD ，AB AD ⊥，CD 的中点，求证：37．（2012江苏）如图，在直三棱柱BE=2x =3×2AC BE=66x =. AE=EC=ED=6.的面积均为5. 3+25. 43.(2017·全国Ⅱ文)如图，＝2AD(1)证明：直线BC ∥平面PAD ；(2)若△PCD 27，求四棱锥2．(1)证明在平面ABCD 内，因为∠BAD ＝∠又BC ⊄平面PAD ，AD ⊂平面PAD ，故BC ∥平面＝2AD ＝2x ＝3x ＝14x 27，所以2×2x ×14x 27，解得2 3.所以四棱锥PABCD 的体积V ＝13×＋×23＝4 3.11AA A =1A F A ='=HD H =OH O'⊥OD平面的面积196963.2=⨯⨯=S平面PAB(1)求证：PA⊥BD； (2) (3)当PA∥平面BDE时，求三棱锥(1)证明因为PA⊥AB，PA⊥(2)证明因为AB＝BC，D是求证：(1)EF∥平面ABC；证明(1)在平面ABD内，因为所以EF∥平面ABC.，，∴OA=B AD==，∴OH=的距离为，∴三棱柱的高。

(新课标全国I卷)高考数学真题分类汇编专题07 立体几何(2)文(含解析)-人教版高三全册数学

专题7立体几何（2）立体几何大题：10年10考，每年1题．第1小题多为证明垂直问题，第2小题多为体积计算问题（2014年是求高）．1．（2019年）如图，直四棱柱ABCD﹣A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求点C到平面C1DE的距离．【解析】（1）连结B1C，ME，∵M，E分别是BB1，BC的中点，∴ME∥B1C，又N为A1D的中点，∴ND＝12A1D，由题设知A1B1//DC，∴B1C//A1D，∴ME//ND，∴四边形MNDE是平行四边形，∴MN∥ED，又MN⊄平面C1DE，∴MN∥平面C1DE．（2）过C作C1E的垂线，垂足为H，由已知可得DE⊥BC，DE⊥C1C，∴DE⊥平面C1CE，故DE⊥CH，∴CH⊥平面C1DE，故CH的长即为C到时平面C1DE的距离，由已知可得CE＝1，CC1＝4，∴C 1E ＝17，故CH ＝41717， ∴点C 到平面C 1DE 的距离为41717． 2．（2018年）如图，在平行四边形ABCM 中，AB ＝AC ＝3，∠ACM ＝90°，以AC 为折痕将△ACM 折起，使点M 到达点D 的位置，且AB ⊥DA ．（1）证明：平面ACD ⊥平面ABC ；（2）Q 为线段AD 上一点，P 为线段BC 上一点，且BP ＝DQ ＝23DA ，求三棱锥Q ﹣ABP 的体积．【解析】（1）∵在平行四边形ABCM 中，∠ACM ＝90°，∴AB ⊥AC ，又AB ⊥DA ．且AD ∩AC ＝A ， ∴AB ⊥面ADC ，∵AB ⊂面ABC ， ∴平面ACD ⊥平面ABC ；（2）∵AB ＝AC ＝3，∠ACM ＝90°，∴AD ＝AM ＝32 ∴BP ＝DQ ＝23DA ＝22 由（1）得DC ⊥AB ，又DC ⊥CA ，∴DC ⊥面ABC ，∴三棱锥Q ﹣ABP 的体积V ＝11DC 33S ∆ABP ⨯ ＝C 121DC 333S ∆AB ⨯⨯＝12113333323⨯⨯⨯⨯⨯⨯＝1． 3．（2017年）如图，在四棱锥P ﹣ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°．（1）证明：平面PAB ⊥平面PAD ；（2）若PA ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥P ﹣ABCD 的体积为83，求该四棱锥的侧面积．【解析】（1）∵在四棱锥P ﹣ABCD 中，∠BAP ＝∠CDP ＝90°， ∴AB ⊥PA ，CD ⊥PD ，又AB ∥CD ，∴AB ⊥PD ， ∵PA ∩PD ＝P ，∴AB ⊥平面PAD ， ∵AB ⊂平面PAB ，∴平面PAB ⊥平面PAD ．（2）设PA ＝PD ＝AB ＝DC ＝a ，取AD 中点O ，连结PO ， ∵PA ＝PD ＝AB ＝DC ，∠APD ＝90°，平面PAB ⊥平面PAD ， ∴PO ⊥底面ABCD ，且AD 22a a +2a ，PO ＝22a ， ∵四棱锥P ﹣ABCD 的体积为83，由AB ⊥平面PAD ，得AB ⊥AD ，∴V P ﹣ABCD ＝CD 13S AB ⨯⨯PO 四边形＝1D 3⨯AB⨯A ⨯PO ＝12232a a a ⨯⨯＝313a ＝83，解得a ＝2，∴PA ＝PD ＝AB ＝DC ＝2，AD ＝BC ＝22PO 2， ∴PB ＝PC 44+22∴该四棱锥的侧面积：S 侧＝S △PAD +S △PAB +S △PDC +S △PBC＝1D 2⨯PA⨯P +12⨯PA⨯AB +1D DC 2⨯P ⨯+221C C 22B ⎛⎫⨯B PB - ⎪⎝⎭＝111122222222822222⨯⨯+⨯⨯+⨯⨯+⨯-＝6+234．（2016年）如图，已知正三棱锥P﹣ABC的侧面是直角三角形，PA＝6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G．（1）证明：G是AB的中点；（2）在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积．【解析】（1）∵P﹣ABC为正三棱锥，且D为顶点P在平面ABC内的正投影，∴PD⊥平面ABC，则PD⊥AB，又E为D在平面PAB内的正投影，∴DE⊥面PAB，则DE⊥AB，∵PD∩DE＝D，∴AB⊥平面PDE，连接PE并延长交AB于点G，则AB⊥PG，又PA＝PB，∴G是AB的中点；（2）在平面PAB内，过点E作PB的平行线交PA于点F，F即为E在平面PAC内的正投影．∵正三棱锥P﹣ABC的侧面是直角三角形，∴PB⊥PA，PB⊥PC，又EF∥PB，所以EF⊥PA，EF⊥PC，因此EF⊥平面PAC，即点F为E在平面PAC内的正投影．连结CG，因为P在平面ABC内的正投影为D，所以D是正三角形ABC的中心．由（1）知，G是AB的中点，所以D在CG上，故CD＝23 CG．由题设可得PC⊥平面PAB，DE⊥平面PAB，所以DE∥PC，因此PE＝23PG，DE＝13PC．由已知，正三棱锥的侧面是直角三角形且PA＝6，可得DE＝2，PG＝32，PE＝22．在等腰直角三角形EFP中，可得EF＝PF＝2．所以四面体PDEF的体积V＝13×DE×S△PEF＝13×2×12×2×2＝43．5．（2015年）如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD．（1）证明：平面AEC⊥平面BED；（2）若∠ABC＝120°，AE⊥EC，三棱锥E﹣ACD的体积为63，求该三棱锥的侧面积．【解析】（1）∵四边形ABCD为菱形，∴AC⊥BD，∵BE⊥平面ABCD，∴AC⊥BE，则AC⊥平面BED，∵AC⊂平面AEC，∴平面AEC⊥平面BED；（2）设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，得AG ＝GC ，GB ＝GD ＝2x ， ∵BE ⊥平面ABCD ，∴BE ⊥BG ，则△EBG 为直角三角形，∴EG ＝12AC ＝AG x ，则BE 2x ，∵三棱锥E ﹣ACD 的体积V ＝11C GD 32⨯A ⨯⨯BE ＝324x ＝3 解得x ＝2，即AB ＝2， ∵∠ABC ＝120°，∴AC 2＝AB 2+BC 2﹣2AB •BC cos ABC ＝4+4﹣2×1222⎛⎫⨯⨯-⎪⎝⎭＝12，即AC ＝在三个直角三角形EBA ，EBD ，EBC 中，斜边AE ＝EC ＝ED ， ∵AE ⊥EC ，∴△EAC 为等腰三角形，则AE 2+EC 2＝AC 2＝12，即2AE 2＝12， ∴AE 2＝6，则AE ，∴从而得AE ＝EC ＝ED ，∴△EAC 的面积S ＝11C 22⨯EA⨯E =3，在等腰三角形EAD 中，过E 作EF ⊥AD 于F ，则AE ，AF ＝1D 2A ＝1212⨯=，则EF =∴△EAD的面积和△ECD的面积均为S＝1252⨯⨯＝5，故该三棱锥的侧面积为3+25．6．（2014年）如图，三棱柱ABC﹣A1B1C1中，侧面BB1C1C为菱形，B1C的中点为O，且AO⊥平面BB1C1C．（1）证明：B1C⊥AB；（2）若AC⊥AB1，∠CBB1＝60°，BC＝1，求三棱柱ABC﹣A1B1C1的高．【解析】（1）连接BC1，则O为B1C与BC1的交点，∵侧面BB1C1C为菱形，∴BC1⊥B1C，∵AO⊥平面BB1C1C，∴AO⊥B1C，∵AO∩BC1＝O，∴B1C⊥平面ABO，∵AB⊂平面ABO，∴B1C⊥AB；（2）作OD⊥BC，垂足为D，连接AD，作OH⊥AD，垂足为H，∵BC⊥AO，BC⊥OD，AO∩OD＝O，∴BC⊥平面AOD，∴OH⊥BC，∵OH⊥AD，BC∩AD＝D，∴OH ⊥平面ABC ， ∵∠CBB 1＝60°， ∴△CBB 1为等边三角形，∵BC ＝1，∴OD ＝34， ∵AC ⊥AB 1，∴OA ＝12B 1C ＝12，由OH •AD ＝OD •OA ，可得AD ＝22D O +OA ＝74，∴OH ＝2114，∵O 为B 1C 的中点，∴B 1到平面ABC 的距离为217， ∴三棱柱ABC ﹣A 1B 1C 1的高217．7．（2013年）如图，三棱柱ABC ﹣A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60° （1）证明：AB ⊥A 1C ；（2）若AB ＝CB ＝2，A 1C ＝，求三棱柱ABC ﹣A 1B 1C 1的体积．【解析】（1）如图，取AB 的中点O ，连结OC ，OA 1，A 1B ．因为CA ＝CB ，所以OC ⊥AB ．由于AB ＝AA 1，160∠BAA =，故△AA 1B 为等边三角形，所以OA 1⊥AB ．因为OC ∩OA 1＝O ，所以AB ⊥平面OA 1C ．又A 1C ⊂平面OA 1C ，故AB ⊥A 1C ；（2）由题设知△ABC 与△AA 1B 都是边长为2的等边三角形，所以1C 3O =OA =．又1C 6A =，则22211C C A =O +OA ，故OA 1⊥OC ．因为OC ∩AB ＝O ，所以OA 1⊥平面ABC ，OA 1为三棱柱ABC ﹣A 1B 1C 1的高．又△ABC 的面积C 3S ∆AB =，故三棱柱ABC ﹣A 1B 1C 1的体积C 1V 333S ∆AB =⨯OA =⨯=．8．（2012年）如图，三棱柱ABC ﹣A 1B 1C 1中，侧棱垂直底面，∠ACB ＝90°，AC ＝BC ＝12AA 1，D 是棱AA 1的中点．（1）证明：平面BDC 1⊥平面BDC（2）平面BDC 1分此棱柱为两部分，求这两部分体积的比．【解析】（1）由题意知BC ⊥CC 1，BC ⊥AC ，CC 1∩AC ＝C ， ∴BC ⊥平面ACC 1A 1，又DC 1⊂平面ACC 1A 1， ∴DC 1⊥BC ．由题设知∠A1DC1＝∠ADC＝45°，∴∠CDC1＝90°，即DC1⊥DC，又DC∩BC＝C，∴DC1⊥平面BDC，又DC1⊂平面BDC1，∴平面BDC1⊥平面BDC；（2）设棱锥B﹣DACC1的体积为V1，AC＝1，由题意得V1＝1121132+⨯⨯⨯＝12，又三棱柱ABC﹣A1B1C1的体积V＝1，∴（V﹣V1）：V1＝1：1，∴平面BDC1分此棱柱两部分体积的比为1：1．9．（2011年）如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形．∠DAB＝60°，AB＝2AD，PD⊥底面ABCD．（1）证明：PA⊥BD；（2）设PD＝AD＝1，求棱锥D﹣PBC的高．【解析】（1）因为∠DAB＝60°，AB＝2AD，由余弦定理得BD3DA，从而BD2+AD2＝AB2，故BD⊥AD，又PD⊥底面ABCD，可得BD⊥PD，所以BD⊥平面PAD．故PA⊥BD．（2）解：作DE⊥PB于E，已知PD⊥底面ABCD，则PD⊥BC，由（1）知，BD⊥AD，又BC∥AD，∴BC⊥BD．故BC⊥平面PBD，BC⊥DE，则DE⊥平面PBC．由题设知PD＝1，则BD3，PB＝2．word 11 / 11 根据DE •PB ＝PD •BD ，得DE ＝32，即棱锥D ﹣PBC 的高为32． 10．（2010年）如图，已知四棱锥P ﹣ABCD 的底面为等腰梯形，AB ∥CD ，AC ⊥BD ，垂足为H ，PH 是四棱锥的高．（1）证明：平面PAC ⊥平面PBD ；（2）若AB ＝6，∠APB ＝∠ADB ＝60°，求四棱锥P ﹣ABCD 的体积．【解析】（1）因为PH 是四棱锥P ﹣ABCD 的高．所以AC ⊥PH ，又AC ⊥BD ，PH ，BD 都在平PHD 内，且PH ∩BD ＝H ．所以AC ⊥平面PBD ．故平面PAC ⊥平面PBD ．（2）因为ABCD 为等腰梯形，AB ∥CD ，AC ⊥BD ，AB 6．所以HA ＝HB 3．因为∠APB ＝∠ADB ＝60°，所以PA ＝PB 6，HD ＝HC ＝1．可得PH 3等腰梯形ABCD 的面积为S ＝12AC ⨯BD ＝3，所以四棱锥的体积为V ＝13×（333233+．。

2012~2018高考立体几何文科真题教师版

2012~2018立体几何文科真题目录2018高考真题 (1)一．选择题 (1)二．填空题 (7)三．解答题 (11)2017高考真题 (22)一．选择题 (22)二．填空题 (29)三．解答题 (33)2016高考真题 (48)一．选择题 (48)二．填空题 (53)三．解答题 (55)2015高考真题 (70)一．选择题 (70)二．填空题 (78)三．解答题 (81)2014高考真题 (104)一．选择题 (104)二．填空题 (115)三．解答题 (120)2013高考真题 (144)一．选择题 (144)二．填空题 (154)三．解答题 (162)2012高考真题 (185)一．选择题 (185)二．填空题 (195)三．解答题 (201)2018高考真题一．选择题（共9小题）1．（2018•新课标Ⅰ）已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（）A．12√2πB．12πC．8√2πD．10π【解答】解：设圆柱的底面直径为2R，则高为2R，圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，可得：4R2=8，解得R=√2，则该圆柱的表面积为：π⋅(√2)2×2+2√2π×2√2=12π．故选：B．2．（2018•新课标Ⅰ）某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）A．2√17B．2√5C．3D．2【解答】解：由题意可知几何体是圆柱，底面周长16，高为：2，直观图以及侧面展开图如图：圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度：√22+42=2√5．故选：B．3．（2018•新课标Ⅰ）在长方体ABCD﹣A1B1C1D1中，AB=BC=2，AC1与平面BB1C1C 所成的角为30°，则该长方体的体积为（）A．8B．6√2C．8√2D．8√3【解答】解：长方体ABCD﹣A1B1C1D1中，AB=BC=2，AC1与平面BB1C1C所成的角为30°，即∠AC1B=30°，可得BC1=ABtan30°=2√3．可得BB1=√(2√3)2−22=2√2．所以该长方体的体积为：2×2×2√2=8√2．故选：C．4．（2018•新课标Ⅰ）在正方体ABCD﹣A1B1C1D1中，E为棱CC1的中点，则异面直线AE与CD所成角的正切值为（）A．√22B．√32C．√52D．√72【解答】解以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，设正方体ABCD ﹣A 1B 1C 1D 1棱长为2，则A （2，0，0），E （0，2，1），D （0，0，0），C （0，2，0），AE →=（﹣2，2，1），CD →=（0，﹣2，0），设异面直线AE 与CD 所成角为θ，则cosθ=|AE →⋅CD →||AE →|⋅|CD →|=√9⋅2=23， sinθ=√1−(23)2=√53， ∴tanθ=√52． ∴异面直线AE 与CD 所成角的正切值为√52．故选：C ．5．（2018•浙江）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（）A．2B．4C．6D．8【解答】解：根据三视图：该几何体为底面为直角梯形的四棱柱．如图所示：故该几何体的体积为：V=12(1+2)⋅2⋅2=6．故选：C．6．（2018•浙江）已知四棱锥S﹣ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点）．设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S﹣AB﹣C的平面角为θ3，则（）A．θ1≤θ2≤θ3B．θ3≤θ2≤θ1C．θ1≤θ3≤θ2D．θ2≤θ3≤θ1【解答】解：∵由题意可知S在底面ABCD的射影为正方形ABCD的中心．过E作EF∥BC，交CD于F，过底面ABCD的中心O作ON⊥EF交EF于N，连接SN，取AB中点M，连接SM，OM，OE，则EN=OM，则θ1=∠SEN，θ2=∠SEO，θ3=∠SMO．显然，θ1，θ2，θ3均为锐角．∵tanθ1=SNNE =SNOM，tanθ3=SOOM，SN≥SO，∴θ1≥θ3，又sinθ3=SOSM ，sinθ2=SOSE，SE≥SM，∴θ3≥θ2．故选：D．7．（2018•新课标Ⅰ）中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）A．B．C．D．【解答】解：由题意可知，如图摆放的木构件与某一带卯眼的木构件咬合成长方体，小的长方体，是榫头，从图形看出，轮廓是长方形，内含一个长方形，并且一条边重合，另外3边是虚线，所以木构件的俯视图是A．故选：A．8．（2018•新课标Ⅰ）设A，B，C，D是同一个半径为4的球的球面上四点，△ABC 为等边三角形且面积为9√3，则三棱锥D﹣ABC体积的最大值为（）A．12√3B．18√3C．24√3D．54√3【解答】解：△ABC为等边三角形且面积为9√3，可得√34×AB2=9√3，解得AB=6，球心为O，三角形ABC 的外心为O′，显然D在O′O的延长线与球的交点如图：O′C=23×√32×6=2√3，OO′=√42−(2√3)2=2，则三棱锥D﹣ABC高的最大值为：6，则三棱锥D﹣ABC体积的最大值为：13×√34×63=18√3．故选：B．9．（2018•北京）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（）A．1B．2C．3D．4【解答】解：四棱锥的三视图对应的直观图为：PA⊥底面ABCD，AC=√5，CD=√5，PC=3，PD=2√2，可得三角形PCD不是直角三角形．所以侧面中有3个直角三角形，分别为：△PAB，△PBC，△PAD．故选：C．二．填空题（共5小题）10．（2018•新课标Ⅰ）已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°．若△SAB的面积为8，则该圆锥的体积为8π．【解答】解：圆锥的顶点为S，母线SA，SB互相垂直，△SAB的面积为8，可得：12SA 2=8，解得SA=4，SA 与圆锥底面所成角为30°．可得圆锥的底面半径为：2√3，圆锥的高为：2，则该圆锥的体积为：V=13×π×(2√3)2×2=8π．故答案为：8π．11．（2018•江苏）如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为 43 ．【解答】解：正方体的棱长为2，中间四边形的边长为：√2，八面体看做两个正四棱锥，棱锥的高为1，多面体的中心为顶点的多面体的体积为：2×13×√2×√2×1=43．故答案为：43．12．（2018•天津）如图，已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为1，则四棱锥A 1﹣BB 1D 1D 的体积为 13．【解答】解：由题意可知四棱锥A 1﹣BB 1D 1D 的底面是矩形，边长：1和√2，四棱锥的高：12A 1C 1=√22．则四棱锥A 1﹣BB 1D 1D 的体积为：13×1×√2×√22=13．故答案为：13．13．（2018•全国）已知三棱锥O ﹣ABC 的体积为1，A 1、B 1、C 1分别为OA 、OB 、OC 的中点，则三棱锥O ﹣A 1B 1C 1的体积为 18．【解答】解：如图，∵A 1、B 1、C 1分别为OA 、OB 、OC 的中点，∴△A 1B 1C 1∽△ABC ，则S △A 1B 1C 1=14S △ABC ，过O 作OG ⊥平面ABC ，交平面A 1B 1C 1于G 1，则OG 1=12OG ．∴V 三棱锥O−A 1B 1C 1=13S △A 1B 1C 1⋅OG 1=18×13S △ABC ⋅OG=18V O−ABC =18．故答案为：18．14．（2018•全国）长方体ABCD ﹣A 1B 1C 1D 1，AB=AD=4，AA 1=8，E 、F 、G 为AB 、A 1B 1、DD 1的中点，H 为A 1D 1上一点，则A 1H=1，求异面直线FH 与EG 所成角的余弦值4√515．【解答】解：∵长方体ABCD ﹣A 1B 1C 1D 1，AB=AD=4，AA 1=8， E 、F 、G 为AB 、A 1B 1、DD 1的中点， H 为A 1D 1上一点，则A 1H=1，∴以D 为原点，DA 为x 国，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系， F （4，2，8），H （3，0，8），E （4，2，0）， G （0，0，4），FH →=（﹣1，﹣2，0），EG →=（﹣4，﹣2，4），设异面直线FH 与EG 所成角为θ，则cosθ=|FH →⋅EG →||FH →|⋅|EG →|=√5⋅√36=4√515．故答案为：4√515．三．解答题（共9小题）15．（2018•新课标Ⅰ）如图，在平行四边形ABCM中，AB=AC=3，∠ACM=90°，以AC为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA．（1）证明：平面ACD⊥平面ABC；（2）Q为线段AD上一点，P为线段BC上一点，且BP=DQ=23DA，求三棱锥Q﹣ABP的体积．【解答】解：（1）证明：∵在平行四边形ABCM中，∠ACM=90°，∴AB⊥AC，又AB⊥DA．且AD∩AC=A，∴AB⊥面ADC，∴AB⊂面ABC，∴平面ACD⊥平面ABC；（2）∵AB=AC=3，∠ACM=90°，∴AD=AM=3√2，∴BP=DQ=23DA=2√2，由（1）得DC⊥AB，又DC⊥CA，∴DC⊥面ABC，∴三棱锥Q﹣ABP的体积V=13S△ABP×13DC=13×23S△ABC×13DC=13×23×12×3×3×13×3=1．16．（2018•新课标Ⅰ）如图，在三棱锥P﹣ABC中，AB=BC=2√2，PA=PB=PC=AC=4，O为AC的中点．（1）证明：PO⊥平面ABC；（2）若点M在棱BC上，且MC=2MB，求点C到平面POM的距离．【解答】（1）证明：∵AB=BC=2√2，AC=4，∴AB2+BC2=AC2，即△ABC是直角三角形，又O为AC的中点，∴OA=OB=OC，∵PA=PB=PC，∴△POA≌△POB≌△POC，∴∠POA=∠POB=∠POC=90°，∴PO⊥AC，PO⊥OB，OB∩AC=0，∴PO⊥平面ABC；（2）解：由（1）得PO⊥平面ABC，PO=√PA2−AO2=2√3，在△COM中，OM=√OC2+CM2−2OC⋅CMcos450=2√5 3．S△POM=12×PO×OM=12×2√3×2√53=2√153，S△COM=12×23×S△ABC=43．设点C到平面POM的距离为d．由V P﹣OMC =V C﹣POM⇒13×S△POM⋅d=13×S △OCM ×PO ，解得d=4√55，∴点C 到平面POM 的距离为4√55．17．（2018•浙江）如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC=120°，A 1A=4，C 1C=1，AB=BC=B 1B=2．（Ⅰ）证明：AB 1⊥平面A 1B 1C 1；（Ⅰ）求直线AC 1与平面ABB 1所成的角的正弦值．【解答】（I ）证明：∵A 1A ⊥平面ABC ，B 1B ⊥平面ABC ， ∴AA 1∥BB 1，∵AA 1=4，BB 1=2，AB=2，∴A 1B 1=√(AB)2+(AA 1−BB 1)2=2√2，又AB 1=√AB 2+BB 12=2√2，∴AA 12=AB 12+A 1B 12， ∴AB 1⊥A 1B 1，同理可得：AB 1⊥B 1C 1，又A 1B 1∩B 1C 1=B 1， ∴AB 1⊥平面A 1B 1C 1．（II ）解：取AC 中点O ，过O 作平面ABC 的垂线OD ，交A 1C 1于D ， ∵AB=BC ，∴OB ⊥OC ，∵AB=BC=2，∠BAC=120°，∴OB=1，OA=OC=√3，以O 为原点，以OB ，OC ，OD 所在直线为坐标轴建立空间直角坐标系如图所示：则A （0，﹣√3，0），B （1，0，0），B 1（1，0，2），C 1（0，√3，1）， ∴AB →=（1，√3，0），BB 1→=（0，0，2），AC 1→=（0，2√3，1），设平面ABB 1的法向量为n →=（x ，y ，z ），则{n →⋅AB →=0n →⋅BB 1→=0， ∴{x +√3y =02z =0，令y=1可得n →=（﹣√3，1，0），∴cos ＜n →，AC 1→＞=n →⋅AC 1→|n →||AC 1→|=√32×√13=√3913．设直线AC 1与平面ABB 1所成的角为θ，则sinθ=|cos ＜n →，AC 1→＞|=√3913． ∴直线AC 1与平面ABB 1所成的角的正弦值为√3913．18．（2018•江苏）在平行六面体ABCD ﹣A 1B 1C 1D 1中，AA 1=AB ，AB 1⊥B 1C 1．求证：（1）AB ∥平面A 1B 1C ；（2）平面ABB 1A 1⊥平面A 1BC ．【解答】证明：（1）平行六面体ABCD ﹣A 1B 1C 1D 1中，AB ∥A 1B 1，AB ∥A 1B 1，AB ⊄平面A 1B 1C ，A 1B 1⊂∥平面A 1B 1C ⇒AB ∥平面A 1B 1C ；（2）在平行六面体ABCD ﹣A 1B 1C 1D 1中，AA 1=AB ，⇒四边形ABB 1A 1是菱形，⊥AB 1⊥A 1B ．在平行六面体ABCD ﹣A 1B 1C 1D 1中，AA 1=AB ，AB 1⊥B 1C 1⇒AB 1⊥BC ． ∴{AB 1⊥A 1B ，AB 1⊥BC A 1B ∩BC =B A 1B ⊂面A 1BC ，BC ⊂面A 1BC⇒AB 1⊥面A 1BC ，且AB 1⊂平面ABB 1A 1⇒平面ABB 1A 1⊥平面A 1BC ．19．（2018•江苏）如图，在正三棱柱ABC ﹣A 1B 1C 1中，AB=AA 1=2，点P ，Q 分别为A 1B 1，BC 的中点．（1）求异面直线BP 与AC 1所成角的余弦值；（2）求直线CC 1与平面AQC 1所成角的正弦值．【解答】解：如图，在正三棱柱ABC ﹣A 1B 1C 1中，设AC ，A 1C 1的中点分别为O ，O 1，则，OB ⊥OC ，OO 1⊥OC ，OO 1⊥OB ，故以{OB →，OC →，OO 1→}为基底，建立空间直角坐标系O ﹣xyz ，∵AB=AA 1=2，A （0，﹣1，0），B （√3，0，0）， C （0，1，0），A 1（0，﹣1，2），B 1（√3，0，2），C 1（0，1，2）．（1）点P 为A 1B 1的中点．∴P(√32，−12，2)，∴BP →=(−√32，−12，2)，AC 1→=(0，2，2)．|cos ＜BP →，AC 1→＞|=|BP →⋅AC 1→||BP →|⋅|AC 1→|=√5×2√2=3√1020． ∴异面直线BP 与AC 1所成角的余弦值为：3√1020；（2）∵Q 为BC 的中点．∴Q （√32，12，0）∴AQ →=(√32，32，0)，AC 1→=(0，2，2)，CC 1→=(0，0，2)，设平面AQC 1的一个法向量为n →=（x ，y ，z ），由{AQ →⋅n →=√32x +32y =0AC 1→⋅n →=2y +2z =0，可取n →=（√3，﹣1，1），设直线CC 1与平面AQC 1所成角的正弦值为θ，sinθ=|cos ＜CC 1→，n →＞|=|CC 1→⋅n →||CC 1→|⋅|n →|=√5×2=√55，∴直线CC 1与平面AQC 1所成角的正弦值为√55．20．（2018•新课标Ⅰ）如图，矩形ABCD 所在平面与半圆弧CD ̂所在平面垂直，M 是CD̂上异于C ，D 的点．（1）证明：平面AMD ⊥平面BMC ；（2）在线段AM 上是否存在点P ，使得MC ∥平面PBD ？说明理由．【解答】（1）证明：矩形ABCD 所在平面与半圆弦CD ̂所在平面垂直，所以AD ⊥半圆弦CD̂所在平面，CM ⊂半圆弦CD ̂所在平面， ∴CM ⊥AD ，M 是CD̂上异于C ，D 的点．∴CM ⊥DM ，DM ∩AD=D ，∴CM ⊥平面AMD ，CM ⊂平面CMB ，∴平面AMD ⊥平面BMC ；（2）解：存在P 是AM 的中点，理由：连接BD 交AC 于O ，取AM 的中点P ，连接OP ，可得MC ∥OP ，MC ⊄平面BDP ，OP ⊂平面BDP ，所以MC ∥平面PBD ．21．（2018•上海）已知圆锥的顶点为P ，底面圆心为O ，半径为2．（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO=4，OA 、OB 是底面半径，且∠AOB=90°，M 为线段AB 的中点，如图．求异面直线PM 与OB 所成的角的大小．【解答】解：（1）∵圆锥的顶点为P ，底面圆心为O ，半径为2，圆锥的母线长为4，∴圆锥的体积V=13×π×r 2×ℎ=13×π×22×√42−22=8√3π3．（2）∵PO=4，OA ，OB 是底面半径，且∠AOB=90°，M 为线段AB 的中点，∴以O 为原点，OA 为x 轴，OB 为y 轴，OP 为z 轴，建立空间直角坐标系，P （0，0，4），A （2，0，0），B （0，2，0）， M （1，1，0），O （0，0，0）， PM →=（1，1，﹣4），OB →=（0，2，0），设异面直线PM 与OB 所成的角为θ，则cosθ=|PM →⋅OB →||PM →|⋅|OB →|=√18⋅2=√26． ∴θ=arccos√26． ∴异面直线PM 与OB 所成的角的为arccos√26．22．（2018•北京）如图，在四棱锥P ﹣ABCD 中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA ⊥PD ，PA=PD ，E ，F 分别为AD ，PB 的中点．（Ⅰ）求证：PE ⊥BC ；（Ⅰ）求证：平面PAB ⊥平面PCD ；（Ⅰ）求证：EF ∥平面PCD ．【解答】证明：（Ⅰ）PA=PD ，E 为AD 的中点，可得PE ⊥AD ，底面ABCD 为矩形，可得BC ∥AD ，则PE ⊥BC ；（Ⅰ）由于平面PAB 和平面PCD 有一个公共点P ，且AB ∥CD ，在平面PAB 内过P 作直线PG ∥AB ，可得PG ∥CD ，即有平面PAB ∩平面PCD=PG ，由平面PAD ⊥平面ABCD ，又AB ⊥AD ，可得AB ⊥平面PAD ，即有AB ⊥PA ，PA ⊥PG ；同理可得CD ⊥PD ，即有PD ⊥PG ，可得∠APD 为平面PAB 和平面PCD 的平面角，由PA ⊥PD ，可得平面PAB ⊥平面PCD ；（Ⅰ）取PC 的中点H ，连接DH ，FH ，在三角形PCD 中，FH 为中位线，可得FH ∥BC ，FH=12BC ，由DE ∥BC ，DE=12BC ，可得DE=FH，DE∥FH，四边形EFHD为平行四边形，可得EF∥DH，EF⊄平面PCD，DH⊂平面PCD，即有EF∥平面PCD．23．（2018•天津）如图，在四面体ABCD中，△ABC是等边三角形，平面ABC⊥平面ABD，点M为棱AB的中点，AB=2，AD=2√3，∠BAD=90°．（Ⅰ）求证：AD⊥BC；（Ⅰ）求异面直线BC与MD所成角的余弦值；（Ⅰ）求直线CD与平面ABD所成角的正弦值．【解答】（Ⅰ）证明：由平面ABC⊥平面ABD，平面ABC∩平面ABD=AB，AD⊥AB，得AD⊥平面ABC，故AD⊥BC；（Ⅰ）解：取棱AC的中点N，连接MN，ND，∵M为棱AB的中点，故MN∥BC，∴∠DMN（或其补角）为异面直线BC与MD所成角，在Rt△DAM中，AM=1，故DM=√AD2+AM2=√13，∵AD⊥平面ABC，故AD⊥AC，在Rt △DAN 中，AN=1，故DN=√AD 2+AN 2=√13，在等腰三角形DMN 中，MN=1，可得cos ∠DMN=12MN DM =√1326． ∴异面直线BC 与MD 所成角的余弦值为√1326；（Ⅰ）解：连接CM ，∵△ABC 为等边三角形，M 为边AB 的中点，故CM ⊥AB ，CM=√3，又∵平面ABC ⊥平面ABD ，而CM ⊂平面ABC ，故CM ⊥平面ABD ，则∠CDM 为直线CD 与平面ABD 所成角．在Rt △CAD 中，CD=√AC 2+AD 2=4，在Rt △CMD 中，sin ∠CDM=CM CD =√34． ∴直线CD 与平面ABD 所成角的正弦值为√34．2017高考真题一．选择题（共8小题）1．（2017•新课标Ⅰ）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（）A．B．C．D．【解答】解：对于选项B，由于AB∥MQ，结合线面平行判定定理可知B不满足题意；对于选项C，由于AB∥MQ，结合线面平行判定定理可知C不满足题意；对于选项D，由于AB∥NQ，结合线面平行判定定理可知D不满足题意；所以选项A满足题意，故选：A．2．（2017•新课标Ⅰ）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A ．90πB ．63πC ．42πD ．36π【解答】解：由三视图可得，直观图为一个完整的圆柱减去一个高为6的圆柱的一半，V=π•32×10﹣12•π•32×6=63π，故选：B ．3．（2017•新课标Ⅰ）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A ．πB ．3π4C ．π2D ．π4【解答】解：∵圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，∴该圆柱底面圆周半径r=√12−(12)2=√32，∴该圆柱的体积：V=Sh=π×(√32)2×1=3π4．故选：B ．4．（2017•新课标Ⅰ）在正方体ABCD ﹣A 1B 1C 1D 1中，E 为棱CD 的中点，则（）A ．A 1E ⊥DC 1B ．A 1E ⊥BDC ．A 1E ⊥BC 1D ．A 1E ⊥AC【解答】解：法一：连B 1C ，由题意得BC 1⊥B 1C ，∵A 1B 1⊥平面B 1BCC 1，且BC 1⊂平面B 1BCC 1，∴A 1B 1⊥BC 1，∵A 1B 1∩B 1C=B 1，∴BC 1⊥平面A 1ECB 1，∵A 1E ⊂平面A 1ECB 1，∴A 1E ⊥BC 1．故选：C ．法二：以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，设正方体ABCD ﹣A 1B 1C 1D 1中棱长为2，则A 1（2，0，2），E （0，1，0），B （2，2，0），D （0，0，0），C 1（0，2，2），A （2，0，0），C （0，2，0），A 1E →=（﹣2，1，﹣2），DC 1→=（0，2，2），BD →=（﹣2，﹣2，0），BC 1→=（﹣2，0，2），AC →=（﹣2，2，0），∵A 1E →•DC 1→=﹣2，A 1E →⋅BD →=2，A 1E →⋅BC 1→=0，A 1E →⋅AC →=6， ∴A 1E ⊥BC 1．故选：C ．5．（2017•浙江）某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）A．π2+1B．π2+3C．3π2+1D．3π2+3【解答】解：由几何的三视图可知，该几何体是圆锥的一半和一个三棱锥组成，圆锥的底面圆的半径为1，三棱锥的底面是底边长2的等腰直角三角形，圆锥的高和棱锥的高相等均为3，故该几何体的体积为12×13×π×12×3+13×12×√2×√2×3=π2+1，故选：A．6．（2017•浙江）如图，已知正四面体D ﹣ABC （所有棱长均相等的三棱锥），P 、Q 、R 分别为AB 、BC 、CA 上的点，AP=PB ，BQ QC =CR RA=2，分别记二面角D ﹣PR ﹣Q ，D ﹣PQ ﹣R ，D ﹣QR ﹣P 的平面角为α、β、γ，则（）A ．γ＜α＜βB ．α＜γ＜βC ．α＜β＜γD ．β＜γ＜α【解答】解法一：如图所示，建立空间直角坐标系．设底面△ABC 的中心为O ．不妨设OP=3．则O （0，0，0），P （0，﹣3，0），C （0，6，0），D （0，0，6√2），B （3√3，﹣3，0）．Q (√3，3，0)，R (−2√3，0，0)，PR →=(−2√3，3，0)，PD →=（0，3，6√2），PQ →=（√3，6，0），QR →=(−3√3，−3，0)， QD →=(−√3，−3，6√2)．设平面PDR 的法向量为n →=（x ，y ，z ），则{n →⋅PR →=0n →⋅PD →=0，可得{−2√3x +3y =03y +6√2z =0，可得n →=(√6，2√2，−1)，取平面ABC 的法向量m →=（0，0，1）．则cos ＜m →，n →＞=m →⋅n →|m →||n →|=√15，取α=arccos √15．同理可得：β=arccos√681．γ=arccos √2√95． ∵√15＞√2√95＞√681． ∴α＜γ＜β．解法二：如图所示，连接OP ，OQ ，OR ，过点O 分别作垂线：OE ⊥PR ，OF ⊥PQ ，OG ⊥QR ，垂足分别为E ，F ，G ，连接DE ，DF ，DG ．设OD=h ．则tanα=OD OE ．同理可得：tanβ=OD OF ，tanγ=OD OG ．由已知可得：OE ＞OG ＞OF ．∴tanα＜tanγ＜tanβ，α，β，γ为锐角．∴α＜γ＜β．故选：B ．7．（2017•北京）某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．60B．30C．20D．10【解答】解：由三视图可知：该几何体为三棱锥，该三棱锥的体积=13×12×5×3×4=10．故选：D．8．（2017•全国）正三棱柱ABC﹣A1B1C1各棱长均为1，D为AA1的中点，则四面体A1BCD的体积是（）A．√34B．√38C．√312D．√324【解答】解：如图，∵ABC﹣A1B1C1为正三棱柱，∴底面ABC为正三角形，侧面BB1C1C为正方形，V A1BCD =V ABC−A1B1C1−V A1−BB1C1C﹣V D﹣ABC=12×1×√32×1−13×1×√32−13×12×1×√32×12=√324．故选：D ．二．填空题（共7小题）9．（2017•新课标Ⅰ）已知三棱锥S ﹣ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA=AC ，SB=BC ，三棱锥S ﹣ABC 的体积为9，则球O 的表面积为 36π ．【解答】解：三棱锥S ﹣ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径，若平面SCA ⊥平面SCB ，SA=AC ，SB=BC ，三棱锥S ﹣ABC 的体积为9，可知三角形SBC 与三角形SAC 都是等腰直角三角形，设球的半径为r ，可得13×12×2r ×r ×r =9，解得r=3．球O 的表面积为：4πr 2=36π．故答案为：36π．10．（2017•新课标Ⅰ）长方体的长、宽、高分别为3，2，1，其顶点都在球O 的球面上，则球O 的表面积为 14π ．【解答】解：长方体的长、宽、高分别为3，2，1，其顶点都在球O 的球面上，可知长方体的对角线的长就是球的直径，所以球的半径为：12√32+22+12=√142．则球O 的表面积为：4×(√142)2π=14π．故答案为：14π．11．（2017•江苏）如图，在圆柱O 1O 2内有一个球O ，该球与圆柱的上、下底面及母线均相切，记圆柱O 1O 2的体积为V 1，球O 的体积为V 2，则V 1V 2的值是 32．【解答】解：设球的半径为R ，则球的体积为：43πR 3，圆柱的体积为：πR 2•2R=2πR 3．则V 1V 2=2πR 34πR 33=32．故答案为：32．12．（2017•天津）已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为9π2．【解答】解：设正方体的棱长为a ， ∵这个正方体的表面积为18， ∴6a 2=18，则a 2=3，即a=√3，∵一个正方体的所有顶点在一个球面上， ∴正方体的体对角线等于球的直径，即√3a=2R ，即R=32，则球的体积V=43π•（32）3=9π2；故答案为：9π2．13．（2017•上海）已知球的体积为36π，则该球主视图的面积等于 9π ．【解答】解：球的体积为36π，设球的半径为R ，可得43πR 3=36π，可得R=3，该球主视图为半径为3的圆，可得面积为πR 2=9π．故答案为：9π．14．（2017•上海）如图，以长方体ABCD ﹣A 1B 1C 1D 1的顶点D 为坐标原点，过D 的三条棱所在的直线为坐标轴，建立空间直角坐标系，若DB 1→的坐标为（4，3，2），则AC 1→的坐标是（﹣4，3，2）．【解答】解：如图，以长方体ABCD ﹣A 1B 1C 1D 1的顶点D 为坐标原点，过D 的三条棱所在的直线为坐标轴，建立空间直角坐标系， ∵DB 1→的坐标为（4，3，2），∴A （4，0，0），C 1（0，3，2）， ∴AC 1→=(−4，3，2)．故答案为：（﹣4，3，2）．15．（2017•山东）由一个长方体和两个14圆柱体构成的几何体的三视图如图，则该几何体的体积为 2+π2．【解答】解：由长方体长为2，宽为1，高为1，则长方体的体积V 1=2×1×1=2，圆柱的底面半径为1，高为1，则圆柱的体积V 2=14×π×12×1=π4，则该几何体的体积V=V 1+2V 1=2+π2，故答案为：2+π2．三．解答题（共11小题）16．（2017•新课标Ⅰ）如图，在四棱锥P ﹣ABCD 中，AB ∥CD ，且∠BAP=∠CDP=90°．（1）证明：平面PAB ⊥平面PAD ；（2）若PA=PD=AB=DC ，∠APD=90°，且四棱锥P ﹣ABCD 的体积为83，求该四棱锥的侧面积．【解答】证明：（1）∵在四棱锥P ﹣ABCD 中，∠BAP=∠CDP=90°， ∴AB ⊥PA ，CD ⊥PD ，又AB ∥CD ，∴AB ⊥PD ， ∵PA ∩PD=P ，∴AB ⊥平面PAD ，∵AB ⊂平面PAB ，∴平面PAB ⊥平面PAD ．解：（2）设PA=PD=AB=DC=a ，取AD 中点O ，连结PO ， ∵PA=PD=AB=DC ，∠APD=90°，平面PAB ⊥平面PAD ， ∴PO ⊥底面ABCD ，且AD=√a 2+a 2=√2a ，PO=√22a ， ∵四棱锥P ﹣ABCD 的体积为83，由AB ⊥平面PAD ，得AB ⊥AD ，∴V P ﹣ABCD =13×S 四边形ABCD ×PO=13×AB ×AD ×PO =13×a ×√2a ×√22a =13a 3=83，解得a=2，∴PA=PD=AB=DC=2，AD=BC=2√2，PO=√2，∴PB=PC=√4+4=2√2，∴该四棱锥的侧面积：S侧=S△PAD+S△PAB+S△PDC+S△PBC=12×PA×PD+12×PA×AB+12×PD×DC+12×BC×√PB2−(BC2)2=12×2×2+12×2×2+12×2×2+12×2√2×√8−2=6+2√3．17．（2017•新课标Ⅰ）如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=12AD，∠BAD=∠ABC=90°．（1）证明：直线BC∥平面PAD；（2）若△PCD面积为2√7，求四棱锥P﹣ABCD的体积．【解答】（1）证明：四棱锥P﹣ABCD中，∵∠BAD=∠ABC=90°．∴BC∥AD，∵AD⊂平面PAD，BC⊄平面PAD，∴直线BC∥平面PAD；（2）解：四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=12AD，∠BAD=∠ABC=90°．设AD=2x，则AB=BC=x，CD=√2x，O是AD的中点，连接PO，OC，CD的中点为：E，连接OE，则OE=√22x ，PO=√3x ，PE=√PO 2+OE 2=√7x √2， △PCD 面积为2√7，可得：12PE ⋅CD =2√7，即：12×√7√2x ⋅√2x =2√7，解得x=2，PO=2√3．则V P ﹣ABCD =13×12（BC +AD ）×AB ×PO=13×12×(2+4)×2×2√3=4√3．18．（2017•新课标Ⅰ）如图四面体ABCD 中，△ABC 是正三角形，AD=CD ．（1）证明：AC ⊥BD ；（2）已知△ACD 是直角三角形，AB=BD ，若E 为棱BD 上与D 不重合的点，且AE ⊥EC ，求四面体ABCE 与四面体ACDE 的体积比．【解答】证明：（1）取AC 中点O ，连结DO 、BO ， ∵△ABC 是正三角形，AD=CD ， ∴DO ⊥AC ，BO ⊥AC ，∵DO ∩BO=O ，∴AC ⊥平面BDO ， ∵BD ⊂平面BDO ，∴AC ⊥BD ．解：（2）法一：连结OE ，由（1）知AC ⊥平面OBD ， ∵OE ⊂平面OBD ，∴OE ⊥AC ，设AD=CD=√2，则OC=OA=1，EC=EA ， ∵AE ⊥CE ，AC=2，∴EC 2+EA 2=AC 2， ∴EC=EA=√2=CD ，∴E 是线段AC 垂直平分线上的点，∴EC=EA=CD=√2，由余弦定理得：cos ∠CBD=BC 2+BD 2−CD 22BC⋅BD =BC 2+BE 2−CE 22BC⋅BE，即4+4−22×2×2=4+BE 2−22×2×BE，解得BE=1或BE=2， ∵BE ＜＜BD=2，∴BE=1，∴BE=ED ，∵四面体ABCE 与四面体ACDE 的高都是点A 到平面BCD 的高h ， ∵BE=ED ，∴S △DCE =S △BCE ，∴四面体ABCE 与四面体ACDE 的体积比为1．法二：设AD=CD=√2，则AC=AB=BC=BD=2，AO=CO=DO=1， ∴BO=√4−1=√3，∴BO 2+DO 2=BD 2，∴BO ⊥DO ，以O 为原点，OA 为x 轴，OB 为y 轴，OD 为z 轴，建立空间直角坐标系，则C （﹣1，0，0），D （0，0，1），B （0，√3，0），A （1，0，0），设E （a ，b ，c ），DE →=λDB →，（0≤λ≤1），则（a ，b ，c ﹣1）=λ（0，√3，﹣1），解得E （0，√3λ，1﹣λ），∴CE →=（1，√3λ，1−λ），AE →=（﹣1，√3λ，1−λ）， ∵AE ⊥EC ，∴AE →⋅CE →=﹣1+3λ2+（1﹣λ）2=0，由λ∈[0，1]，解得λ=12，∴DE=BE ，∵四面体ABCE 与四面体ACDE 的高都是点A 到平面BCD 的高h ， ∵DE=BE ，∴S △DCE =S △BCE ，∴四面体ABCE 与四面体ACDE 的体积比为1．19．（2017•江苏）如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF⊄平面ABC，AB⊂平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，FG∥BC，所以FG⊥BD，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．20．（2017•江苏）如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅰ的高均为32cm，容器Ⅰ的底面对角线AC的长为10√7cm，容器Ⅰ的两底面对角线EG，E1G1的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅰ中注入水，水深均为12cm．现有一根玻璃棒l，其长度为40cm．（容器厚度、玻璃棒粗细均忽略不计）（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；（2）将l放在容器Ⅰ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度．【解答】解：（1）设玻璃棒在CC1上的点为M，玻璃棒与水面的交点为N，在平面ACM中，过N作NP∥MC，交AC于点P，∵ABCD﹣A1B1C1D1为正四棱柱，∴CC1⊥平面ABCD，又∵AC⊂平面ABCD，∴CC1⊥AC，∴NP⊥AC，∴NP=12cm，且AM2=AC2+MC2，解得MC=30cm，∵NP∥MC，∴△ANP∽△AMC，∴AN AM =NP MC ，AN 40=1230，得AN=16cm ． ∴玻璃棒l 没入水中部分的长度为16cm ．（2）设玻璃棒在GG 1上的点为M ，玻璃棒与水面的交点为N ，在平面E 1EGG 1中，过点N 作NP ⊥EG ，交EG 于点P ，过点E 作EQ ⊥E 1G 1，交E 1G 1于点Q ，∵EFGH ﹣E 1F 1G 1H 1为正四棱台，∴EE 1=GG 1，EG ∥E 1G 1， EG ≠E 1G 1，∴EE 1G 1G 为等腰梯形，画出平面E 1EGG 1的平面图， ∵E 1G 1=62cm ，EG=14cm ，EQ=32cm ，NP=12cm ， ∴E 1Q=24cm ，由勾股定理得：E 1E=40cm ，∴sin ∠EE 1G 1=45，sin ∠EGM=sin ∠EE 1G 1=45，cos ∠EGM=﹣35，根据正弦定理得：EM sin∠EGM =EG sin∠EMG ，∴sin ∠EMG=725，cos ∠EMG=2425，∴sin ∠GEM=sin （∠EGM +∠EMG ）=sin ∠EGMcos ∠EMG +cos ∠EGMsin ∠EMG=35，∴EN=NP sin∠GEM =1235=20cm ．∴玻璃棒l 没入水中部分的长度为20cm ．21．（2017•江苏）如图，在平行六面体ABCD ﹣A 1B 1C 1D 1中，AA 1⊥平面ABCD ，且AB=AD=2，AA 1=√3，∠BAD=120°．（1）求异面直线A 1B 与AC 1所成角的余弦值；（2）求二面角B ﹣A 1D ﹣A 的正弦值．【解答】解：在平面ABCD 内，过A 作Ax ⊥AD ， ∵AA 1⊥平面ABCD ，AD 、Ax ⊂平面ABCD ， ∴AA 1⊥Ax ，AA 1⊥AD ，以A 为坐标原点，分别以Ax 、AD 、AA 1所在直线为x 、y 、z 轴建立空间直角坐标系．∵AB=AD=2，AA 1=√3，∠BAD=120°，∴A （0，0，0），B （√3，−1，0），C （√3，1，0）， D （0，2，0），A 1（0，0，√3），C 1（√3，1，√3）．A 1B →=（√3，−1，−√3），AC 1→=（√3，1，√3），DB→=(√3，−3，0)，DA 1→=(0，−2，√3)．（1）∵cos ＜A 1B →，AC 1→＞=A 1B →⋅AC 1→|A 1B →||AC 1→|=√7×√7=−17． ∴异面直线A 1B 与AC 1所成角的余弦值为17；（2）设平面BA 1D 的一个法向量为n →=(x ，y ，z)，由{n →⋅DB →=0n →⋅DA 1→=0，得{√3x −3y =0−2y +√3z =0，取x=√3，得n →=(√3，1，2√33)；取平面A 1AD 的一个法向量为m →=(1，0，0)．∴cos ＜m →，n →＞=m →⋅n→|m →||n →|=√31×√3+1+3=34． ∴二面角B ﹣A 1D ﹣A 的余弦值为34，则二面角B ﹣A 1D ﹣A 的正弦值为√1−(34)2=√74．22．（2017•浙江）如图，已知四棱锥P ﹣ABCD ，△PAD 是以AD 为斜边的等腰直角三角形，BC ∥AD ，CD ⊥AD ，PC=AD=2DC=2CB ，E 为PD 的中点．（Ⅰ）证明：CE ∥平面PAB ；（Ⅰ）求直线CE 与平面PBC 所成角的正弦值．【解答】证明：（Ⅰ）取AD 的中点F ，连结EF ，CF ， ∵E 为PD 的中点，∴EF ∥PA ，在四边形ABCD 中，BC ∥AD ，AD=2DC=2CB ，F 为中点， ∴CF ∥AB ，∴平面EFC ∥平面ABP ， ∵EC ⊂平面EFC ， ∴EC ∥平面PAB ．解：（Ⅰ）连结BF ，过F 作FM ⊥PB 于M，连结PF ， ∵PA=PD ，∴PF ⊥AD ，推导出四边形BCDF 为矩形，∴BF ⊥AD ， ∴AD ⊥平面PBF ，又AD ∥BC ， ∴BC ⊥平面PBF ，∴BC ⊥PB ，设DC=CB=1，由PC=AD=2DC=2CB ，得AD=PC=2， ∴PB=√PC 2−BC 2=√4−1=√3，BF=PF=1，∴MF=12，又BC ⊥平面PBF ，∴BC ⊥MF ，∴MF ⊥平面PBC ，即点F 到平面PBC 的距离为12，∵MF=12，D 到平面PBC 的距离应该和MF 平行且相等，为12，E 为PD 中点，E 到平面PBC 的垂足也为垂足所在线段的中点，即中位线，∴E 到平面PBC 的距离为14，在△PCD 中，PC =2，CD =1，PD =√2，由余弦定理得CE=√2，设直线CE 与平面PBC 所成角为θ，则sinθ=14CE =√28．23．（2017•天津）如图，在四棱锥P ﹣ABCD 中，AD ⊥平面PDC ，AD ∥BC ，PD ⊥PB ，AD=1，BC=3，CD=4，PD=2．（Ⅰ）求异面直线AP 与BC 所成角的余弦值；（Ⅰ）求证：PD ⊥平面PBC ；（Ⅰ）求直线AB 与平面PBC 所成角的正弦值．【解答】解：（Ⅰ）如图，由已知AD∥BC，故∠DAP或其补角即为异面直线AP与BC所成的角．因为AD⊥平面PDC，所以AD⊥PD．在Rt△PDA中，由已知，得AP=2+PD2=√5，故cos∠DAP=ADAP=√55．所以，异面直线AP与BC所成角的余弦值为√5 5．证明：（Ⅰ）因为AD⊥平面PDC，直线PD⊂平面PDC，所以AD⊥PD．又因为BC∥AD，所以PD⊥BC，又PD⊥PB，所以PD⊥平面PBC．解：（Ⅰ）过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角．因为PD⊥平面PBC，故PF为DF在平面PBC上的射影，所以∠DFP为直线DF和平面PBC所成的角．由于AD∥BC，DF∥AB，故BF=AD=1，由已知，得CF=BC﹣BF=2．又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得sin∠DFP=PDDF=√55．所以，直线AB与平面PBC所成角的正弦值为√5 5．24．（2017•北京）如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．【解答】解：（1）证明：由PA⊥AB，PA⊥BC，AB⊂平面ABC，BC⊂平面ABC，且AB∩BC=B，可得PA⊥平面ABC，由BD⊂平面ABC，可得PA⊥BD；（2）证明：由AB=BC，D为线段AC的中点，可得BD⊥AC，由PA⊥平面ABC，PA⊂平面PAC，可得平面PAC⊥平面ABC，又平面PAC∩平面ABC=AC，BD⊂平面ABC，且BD⊥AC，即有BD⊥平面PAC，BD ⊂平面BDE ，可得平面BDE ⊥平面PAC ；（3）PA ∥平面BDE ，PA ⊂平面PAC ，且平面PAC ∩平面BDE=DE ，可得PA ∥DE ，又D 为AC 的中点，可得E 为PC 的中点，且DE=12PA=1，由PA ⊥平面ABC ，可得DE ⊥平面ABC ，可得S △BDC =12S △ABC =12×12×2×2=1，则三棱锥E ﹣BCD 的体积为13DE•S △BDC =13×1×1=13．25．（2017•上海）如图，直三棱柱ABC ﹣A 1B 1C 1的底面为直角三角形，两直角边AB 和AC 的长分别为4和2，侧棱AA 1的长为5．（1）求三棱柱ABC ﹣A 1B 1C 1的体积；（2）设M 是BC 中点，求直线A 1M 与平面ABC 所成角的大小．【解答】解：（1）∵直三棱柱ABC ﹣A 1B 1C 1的底面为直角三角形，两直角边AB 和AC 的长分别为4和2，侧棱AA 1的长为5． ∴三棱柱ABC ﹣A 1B 1C 1的体积： V=S △ABC ×AA 1=12×AB ×AC ×AA 1 =12×4×2×5=20．（2）连结AM ，∵直三棱柱ABC ﹣A 1B 1C 1的底面为直角三角形，两直角边AB 和AC 的长分别为4和2，侧棱AA 1的长为5，M 是BC 中点，∴AA 1⊥底面ABC ，AM=12BC =12√16+4=√5，∴∠A 1MA 是直线A 1M 与平面ABC 所成角，tan ∠A 1MA=AA 1AM =√5=√5，∴直线A 1M 与平面ABC 所成角的大小为arctan √5．26．（2017•山东）由四棱柱ABCD ﹣A 1B 1C 1D 1截去三棱锥C 1﹣B 1CD 1后得到的几何体如图所示，四边形ABCD 为正方形，O 为AC 与BD 的交点，E 为AD 的中点，A 1E ⊥平面ABCD ，（Ⅰ）证明：A 1O ∥平面B 1CD 1；（Ⅰ）设M 是OD 的中点，证明：平面A 1EM ⊥平面B 1CD 1．【解答】证明：（Ⅰ）取B1D1中点G，连结A1G、CG，∵四边形ABCD为正方形，O为AC与BD 的交点，OC，∴四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后，A1G∥=∴四边形OCGA1是平行四边形，∴A1O∥CG，∵A1O⊄平面B1CD1，CG⊂平面B1CD1，∴A1O∥平面B1CD1．B1D1，（Ⅰ）四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后，BD∥=∵M是OD的中点，O为AC与BD 的交点，E为AD的中点，A1E⊥平面ABCD，又BD⊂平面ABCD，∴BD⊥A1E，∵四边形ABCD为正方形，O为AC与BD 的交点，∴AO⊥BD，∵M是OD的中点，E为AD的中点，∴EM⊥BD，∵A1E∩EM=E，∴BD⊥平面A1EM，∵BD∥B1D1，∴B1D1⊥平面A1EM，∵B1D1⊂平面B1CD1，∴平面A1EM⊥平面B1CD1．2016高考真题一．选择题（共8小题）1．（2016•新课标Ⅰ）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是28π3，则它的表面积是（）A ．17πB ．18πC ．20πD ．28π【解答】解：由题意可知三视图复原的几何体是一个球去掉18后的几何体，如图：可得：78×43πR 3=28π3，R=2．它的表面积是：78×4π•22+34×π⋅22=17π．故选：A ．2．（2016•新课标Ⅰ）平面α过正方体ABCD ﹣A 1B 1C 1D 1的顶点A ，α∥平面CB 1D 1，α∩平面ABCD=m ，α∩平面ABB 1A 1=n ，则m 、n 所成角的正弦值为（）A ．√32B ．√22C ．√33D ．13【解答】解：如图：α∥平面CB 1D 1，α∩平面ABCD=m ，α∩平面ABA 1B 1=n ，可知：n ∥CD 1，m ∥B 1D 1，∵△CB 1D 1是正三角形．m 、n 所成角就是∠CD 1B 1=60°．。

(版)高考试题汇编文科数学立体几何

〔2021全国1文〕16. ACB 90，P为平面ABC外一点，PC 2，点P到ACB两边AC,BC的距离均为3，那么P到平面ABC的距离为 .答案：2解答：如图，过P点做平面ABC的垂线段，垂足为O，那么PO的长度即为所求，再做PE CB,PF CA，由线面的垂直判定及性质定理可得出OE CB,OF CA，在RtPCF中，由PC 2,PF 3，可得出CF 1，同理在RtPCE中可得出CE 1，结合 ACB 90，OE CB,OF CA可得出OE OF 1，OC2，PO PC2OC2 2〔2021全国1文〕19.如图直四棱柱ABCD A1B1C1D1的底面是菱形，AA14,AB 2，BAD60o，E,M,N分别是BC,BB1,A1D的中点.1〕证明：MN//平面C1DE2〕求点C到平面C1DE的距离.答案：见解析解答：〔1〕连结AC,BD相交于点，再过点M作MH//CE交BC于点，再连结GH，NG.1111111E,M,N分别是BC,BB1,A1D的中点.于是可得到NG//C1D，GH//DE，于是得到平面NGHM//平面C1DE，由QMN平面NGHM，于是得到MN//平面C1DE1/19〔2〕QE为BC中点，ABCD为菱形且BAD60oDE BC，又QABCD A1B1C1D1为直四棱柱，DECC1DEC1E，又QAB2,AA14，DE3,C1E17，设点C到平面C1DE的距离为h 由V CC1DE V C1DCE得11317113432h1 432解得h1717所以点C 417到平面C1DE的距离为17〔2021全国2文〕7.设,为两个平面，那么//的充要条件是()A.内有无数条直线与平行B.内有两条相交直线与平行C.,平行于同一条直线D.,垂直于同一平面答案：B解析:根据面面平行的判定定理易得答案.〔2021全国2文〕16.中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体〞〔图1〕.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体表达了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的外表上，且此正方体的棱长为 1.那么该半正多面体共有个面，其棱长为.(此题第一空2分，第二空3分.)2/19答案： 262 1解析：由图2 结合空间想象即可得到该正多面体有26个面；将该半正多面体补成正方体后，根据对称性列方程求解 .〔2021全国2文〕17.如图，长方体ABCDA 1B 1C 1D 1的底面ABCD是正方形，点E 在棱AA 1上，BE ⊥EC 1.〔1 〕证明：BE 平面EB 1C1〔2 〕假设AEAE 1,AB3,求四棱锥EBB 1C 1C 的体积.答案：看解析看解析解答：〔1〕证明：因为B 1C 1C 面A 1B 1BA ，BE面A 1B 1BA∴B 1C 1⊥BE 又C 1EB 1C 1 C 1，∴BE平面EB 1C 1；〔2〕设AA2a 那么BE2922222a ，C 1E18+a ，C 1B94a1222∴a，∴11 因为C 1B=BEC 1E3V EBB 1C 1CS BB 1C 1Ch363=18333/19(版)高考试题汇编文科数学立体几何〔2021全国3文〕8.如图，点N为正方形ABCD的中心，ECD为正三角形，平面ECD平面ABCD,M是线段ED的中点，那么〔〕A.BM EN，且直线B.BM EN，且直线C.BM EN，且直线D.BM EN，且直线【答案】B【解析】分析】BM,ENBM,ENBM,ENBM,EN是相交直线是相交直线是异面直线是异面直线利用垂直关系，再结合勾股定理进而解决问题．【详解】∵BDE ，N为BD中点M为DE中点，BM，EN共面相交，选项C DCD于O，，为错．作EO连接ON，过M作MF OD于F．连BF，Q平面CDE平面ABCD．EO CD,EO平面CDE，EO平面ABCD，MF平面ABCE，【MFB与EON均为直角三角形．设正方形边长为2，易知EO3,0N1EN2，MF3,BF2295BM3247．24244BM EN，应选B．【点睛】此题为立体几何中等问题，考查垂直关系，线面、线线位置关系.4/19〔2021全国3文〕16.学生到工厂劳动实践，利用3D打印技术制作模型.如图，该模型为长方体ABCD A1B1C1D1挖去四棱锥O EFGH后所得的几何体，其中O为长方体的中心，E,F,G,H分别为所在棱的中点，AB=BC=6cm,AA1=4cm，3D打印所用原料密度为/cm3，不考虑打印损耗，制作该模型所需原料的质量为___________g.【答案】118．8【解析】【分析】根据题意可知模型的体积为四棱锥体积与四棱锥体积之差进而求得模型的体积，再求出模型的质量.【详解】由题意得，四棱锥O-EFGH的底面积为46412312cm2，其高为点O到底面BB1C1C的距12离为3cm，那么此四棱锥的体积为V112312cm2．又长方体ABCD A1B1C1D1的体积为3V2466144cm2，所以该模型体积为V V2V114412132cm2，其质量为132．【点睛】此题牵涉到的是3D打印新时代背景下的几何体质量，忽略问题易致误，理解题中信息联系几何体的体积和质量关系，从而利用公式求解．〔2021全国3文〕19.图1是由矩形ADEB,RtABC和菱形BFGC组成的一个平面图形，其中AB 1,BE BF 2，FBC60o，将其沿AB,BC折起使得BE与BF重合，连结DG，如图2.〔1〕证明图2中的A,C,G,D四点共面，且平面ABC平面BCGE；〔2〕求图2中的四边形ACGD的面积.【答案】(1)见详解；(2)4.5/19【解析】【分析】(1)因为折纸和粘合不改变矩形ABED ，RtVABC 和菱形BFGC 内部的夹角，所以 AD//BE ，BF//CG 依然成立，又因E 和F 粘在一起，所以得证.因为AB 是平面BCGE 垂线，所以易证.(2) 欲求四边形ACGD 的面积，需求出CG 所对应的高，然后乘以CG 即可。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

学科教师辅导教案学员姓名年级高三辅导科目数学授课老师课时数2h 第次课授课日期及时段 2018年月日：—：1．（2014辽宁）已知m，n表示两条不同直线，α表示平面，下列说法正确的是（Ｂ）A．若//,//,m nαα则//m n B．若mα⊥，nα⊂，则m n⊥C．若mα⊥，m n⊥，则//nαD．若//mα，m n⊥，则nα⊥2.(2014新标1文)如图，网格纸的各小格都是正方形，粗实线画出的事一个几何体的三视图，则这个几何体是（Ｂ）A.三棱锥B.三棱柱C.四棱锥D.四棱柱3.(2014浙江文) 设m、n是两条不同的直线，α、β是两个不同的平面，则（Ｃ）A.若nm⊥，α//n，则α⊥m B.若β//m，αβ⊥，则α⊥mC.若β⊥m，β⊥n，α⊥n，则α⊥m D.若nm⊥，β⊥n，αβ⊥，则α⊥m4.(2013浙江文) 设m，n是两条不同的直线，α，β是两个不同的平面．(C)A．若m∥α，n∥α，则m∥n B．若m∥α，m∥β，则α∥βC．若m∥n，m⊥α，则n⊥αD．若m∥α，α⊥β，则m⊥β5.（2015年广东文）若直线1l和2l是异面直线，1l在平面α内，2l在平面β内，l是平面α与平面β的交线，则下列命题正确的是（Ａ）A．l至少与1l，2l中的一条相交B．l与1l，2l都相交C．l至多与1l，2l中的一条相交D．l与1l，2l都不相交历年高考试题集锦（文）——立体几何6.（2015年新课标2文）一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为（）1A.81B.71C.61D.51112【答案】D【解析】试题分析：截去部分是正方体的一个角,其体积是正方体体积的16,所以截去部分体积与剩余部分体积的比值为15,故选D.7．（2015年福建文）某几何体的三视图如图所示，则该几何体的表面积等于（）A．822+B．1122+C．1422+D．15【答案】B【解析】试题分析：由三视图还原几何体，该几何体是底面为直角梯形，高为2的直四棱柱，且底面直角梯形的两底分别为12，，直角腰长为1，斜腰为2．底面积为12332⨯⨯=，侧面积为则其表面积为2+2+4+22=8+22，所以该几何体的表面积为1122+，故选B．8.（2014安徽）一个多面体的三视图如图所示，则该多面体的表面积为（ A ）A．213+B．183+C．21D．189．（2012福建）一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是(D) A．球B．三棱锥C．正方体D．圆柱10．（2014福建理）某空间几何体的正视图是三角形，则该几何体不可能是（A ）.A圆柱.B圆锥.C四面体.D三棱柱11．（2012广东理）某几何体的三视图如图所示，它的体积为（ C ）A.12πB.45πC.57πD.81π12（2012广东文）某几何体的三视图如图1所示，它的体积为( C )72π()B()A48π()Cπ30()Dπ2413．（2013广东文）某三棱锥的三视图如图所示，则该三棱锥的体积是（ B ）图 21俯视图侧视图正视图21A．16B．13C．23D．114．（2013江西文）一几何体的三视图如右所示，则该几何体的体积为（ A ）A.200+9πB. 200+18πC. 140+9πD. 140+18π15.(2012新标) 如图，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则几何体的体积为A.6B.9C.12D.18【答案】B16.(2013新标1) 某几何体的三视图如图所示，则该几何体的体积为（ A ）A .168π+B .88π+C .1616π+D .816π+17．(2017·全国Ⅰ文)如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是( )【答案】A18、（2016年天津）将一个长方形沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为（ B ）19、（2016年全国I 卷）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3，则它的表面积是（ A ）（A ）17π （B ）18π （C ）20π （D ）28π20、（2016年全国I 卷）如平面α过正方体ABCD —A 1B 1C 1D 1的顶点A ，11//CB D α平面,ABCD m α=平面，11ABB A n α=平面，则m ，n 所成角的正弦值为（ A ）（A ）32（B ）22（C ）33（D ）13 21、（2016年全国II 卷）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（ C ）（A ）20π （B ）24π （C ）28π （D ）32π22、（2016年全国III 卷）如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为（ B ）（A ）18365+ （B ）54185+ （C ）90 （D ）8123、（2016年浙江）已知互相垂直的平面αβ，交于直线l .若直线m ，n 满足m ∥α，n ⊥β，则（ C ）A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n24、(2017·全国Ⅱ文)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( B )A ．90πB ．63πC ．42πD ．36π25．（2014湖北文）已知某几何体的三视图如图所示，则该几何体的体积为____12π________.26. (2017·全国Ⅲ文)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( B )A ．πB ．3π4C ．π2D ．π427. (2014新标2文) 正三棱柱111ABC A B C -的底面边长为2，侧棱长为3，D 为BC 中点，则三棱锥11A B DC -的体积为（ C ）（A ）3 （B ）32 （C ）1 （D ）3228．(2017·北京文)某三棱锥的三视图如图所示，则该三棱锥的体积为( D )A ．60B ．30C ．20D ．1029．(2017·全国Ⅰ文)已知三棱锥SABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA ＝AC ，SB ＝BC ，三棱锥SABC 的体积为9，则球O 的表面积为________．1．【答案】36π【解析】如图，连接OA ，OB .由SA ＝AC ，SB ＝BC ，SC 为球O 的直径知，OA ⊥SC ，OB ⊥SC .由平面SCA ⊥平面SCB ，平面SCA ∩平面SCB ＝SC ，OA ⊥SC 知，OA ⊥平面SCB .设球O 的半径为r ，则OA ＝OB ＝r ，SC ＝2r ，∴三棱锥S －ABC 的体积V ＝13×(12SC ·OB )·OA ＝r 33，即r 33＝9，∴r ＝3，∴S 球表＝4πr 2＝36π. 30、(2017·山东文，13)由一个长方体和两个14圆柱构成的几何体的三视图如图，则该几何体的体积为______2＋π2__．31.(2012新标文) 如图，三棱柱111ABC A B C 中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点。

(Ｉ) 证明：平面BDC ⊥平面1BDC 。

（Ⅱ）平面1BDC 分此棱柱为两部分，求这两部分体积的比. 【答案】（Ⅰ）略；（Ⅱ）1:1.32.(2013新标2文) 如图，直三棱柱ABC －A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点．(1)证明：BC 1∥平面A 1CD ； (2)设AA 1＝AC ＝CB ＝2，AB ＝22，求三棱锥C －A 1DE 的体积．【答案】(1)略；(2) 1.33、(2017·全国Ⅰ文)如图，在四棱锥P ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°.(1)证明：平面P AB ⊥平面P AD ；(2)若P A ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥P ABCD 的体积为83，求该四棱锥的侧面积． 1．(1)证明由已知∠BAP ＝∠CDP ＝90°，得AB ⊥P A ，CD ⊥PD .由于AB∥CD，故AB⊥PD，从而AB⊥平面P AD.又AB⊂平面P AB，所以平面P AB⊥平面P AD.(2)解如图，在平面P AD内作PE⊥AD，垂足为E.由(1)知，AB⊥平面P AD，故AB⊥PE，AB⊥AD，所以PE⊥平面ABCD.设AB＝x，则由已知可得AD＝2x，PE＝22x，故四棱锥P ABCD的体积V P ABCD＝13AB·AD·PE＝13x3.由题设得13x3＝83，故x＝2.从而结合已知可得P A＝PD＝AB＝DC＝2，AD＝BC＝22，PB＝PC＝22，可得四棱锥P ABCD的侧面积为12P A·PD＋12P A·AB＋12PD·DC＋12BC2sin 60°＝6＋2 3.34．（2014山东文）如图，四棱锥P ABCD-中，1,,,,2AP PCD AD BC AB BC AD E F⊥==平面∥分别为线段,AD PC的中点.（Ｉ）求证：AP BEF∥平面；（II）求证：BE PAC⊥平面.【答案】略35.(2014四川文) 在如图所示的多面体中，四边形11ABB A和11ACC A都为矩形。

DEB1C1A CBA1OMEDABCC1A1B1（Ⅰ）若AC BC⊥，证明：直线BC⊥平面11ACC A；（Ⅱ）设D ，E 分别是线段BC ，1CC 的中点，在线段AB 上是否存在一点M ，使直线//DE 平面1A MC ？请证明你的结论。

【简解】（Ⅰ）略（2）取线段AB 的中点M ，连接111,,,A M MC AC AC ，设O 为11,A C AC 的交点.由已知，O 为1AC 的中点.连接MD ，OE ，则MD ，OE 分别为1,ABC ACC ∆∆的中位线.所以，11,,22MD AC OE AC MD OE ∴，连接OM ，从而四边形MDEO 为平行四边形，则DE MO .因为直线DE ⊄平面1A MC ，MO ⊂平面1A MC ，所以直线DE平面1A MC . 即线段AB 上存在一点M （线段AB 的中点），使得直线DE 平面1A MC .36．（2013北京文）如图，在四棱锥P ABCD -中，//AB CD ，AB AD ⊥，2CD AB =，平面PAD ⊥底面ABCD ，PA AD ⊥，E 和F 分别是CD 和PC 的中点，求证：（1）PA ⊥底面ABCD （2）//BE 平面PAD （3）平面BEF ⊥平面PCD37．（2012江苏）如图，在直三棱柱ABC ﹣A 1B 1C 1中，A 1B 1=A 1C 1，D ，E 分别是棱BC ，CC 1上的点（点D 不同于点C ），且AD ⊥DE ，F 为B 1C 1的中点．求证：（1）平面ADE ⊥平面BCC 1B 1；（2）直线A 1F ∥平面ADE ．38．（2013江苏）如图，在三棱锥ABC S -中，平面⊥SAB 平面SBC ，BC AB ⊥， AB AS =，过A 作SB AF ⊥，垂足为F ，点G E ，分别是棱SC SA ，的中点.求证：（1）平面//EFG 平面ABC ；（2）SA BC ⊥.【答案】略39．（2014江苏）如图，在三棱锥P ABC-中，D E F，，分别为棱PC AC AB，，的中点．已知6PA AC PA⊥=，，8BC=，5DF=．（1）求证：直线P A∥平面DEF；（2）平面BDE⊥平面ABC．40．（2014北京文）如图，在三棱柱111ABC A B C-中，侧棱垂直于底面，AB BC⊥，12AA AC==，BC=1，E、F分别为11A C、BC的中点.（1）求证：平面ABE⊥平面11B BCC；（2）求证：1//C F平面ABE；（3）求三棱锥E ABC-的体积.C1B1A1FECBA【简解】(1)AB⊥平面B1BCC1即可；（2）取AB中点G，C1F∥EG即可；(3)3341.（2015北京文）如图，在三棱锥V C-AB中，平面V AB⊥平面CAB，V∆AB为等边三角形，C CA⊥B且C C2A=B=，O，M分别为AB，V A的中点．（Ⅰ）求证：V//B平面CMO；（Ⅱ）求证：平面CMO⊥平面V AB；（Ⅲ）求三棱锥V C-AB的体积．【答案】（1）证明详见解析；（2）证明详见解析；（3）33. 42.（2015年新课标1卷）如图四边形ABCD 为菱形，G 为AC 与BD 交点，BE ABCD ⊥平面，（I ）证明：平面AEC ⊥平面BED ；（II ）若120ABC ∠=，,AE EC ⊥ 三棱锥E ACD -的体积为63，求该三棱锥的侧面积. （I ）因为四边形ABCD 为菱形，所以AC ⊥BD. 因为BE ⊥平面ABCD,所以AC ⊥BE,故AC ⊥平面BED.又AC ⊂平面AEC,所以平面AEC ⊥平面BED. ……5分（II ）设AB=x ，在菱形ABCD 中，又∠ABC=o120 ，可得AG=GC=32x ，GB=GD=2x . 因为AE ⊥EC,所以在Rt △AEC 中，可的EG=32x . 由BE ⊥平面ABCD,知△EBG 为直角三角形，可得BE=22x . 由已知得，三棱锥E-ACD 的体积E ACD V -=13×12AC ·GD ·BE=366243x =. 故x =2 ……9分从而可得AE=EC=ED=6.所以△EAC 的面积为3，△EAD 的面积与 △ECD 的面积均为5. 故三棱锥E-ACD 的侧面积为3+25. ……12分43.(2017·全国Ⅱ文)如图，四棱锥P ABCD 中，侧面P AD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°.(1)证明：直线BC ∥平面P AD ；(2)若△PCD 的面积为27，求四棱锥P ABCD 的体积． 2．(1)证明在平面ABCD 内，因为∠BAD ＝∠ABC ＝90°，所以BC ∥AD . 又BC ⊄平面P AD ，AD ⊂平面P AD ，故BC ∥平面P AD .(2)解如图，取AD 的中点M ，连接PM ，CM .由AB ＝BC ＝12AD 及BC ∥AD ，∠ABC ＝90°得四边形ABCM为正方形，则CM ⊥AD .因为侧面P AD 为等边三角形且垂直于底面ABCD ，平面P AD ∩平面ABCD ＝AD ，所以PM ⊥AD ，PM ⊥底面ABCD .因为CM ⊂底面ABCD ，所以PM ⊥CM .设BC ＝x ，则CM ＝x ，CD ＝2x ，PM ＝3x ，PC ＝PD ＝2x . 取CD 的中点N ，连接PN ，则PN ⊥CD ，所以PN ＝142x .因为△PCD 的面积为27，所以12×2x ×142x ＝27，解得x ＝－2(舍去)或x ＝2.于是AB ＝BC ＝2，AD ＝4，PM ＝2 3.所以四棱锥P ABCD 的体积V ＝13×2(2＋4)2×23＝4 3.44、（2016年江苏省高考）如图，在直三棱柱ABC -A 1B 1C 1中，D ，E 分别为AB ，BC 的中点，点F 在侧棱B 1B 上，且11B D A F ⊥ ，1111AC A B ⊥.求证：（1）直线DE ∥平面A 1C 1F ；（2）平面B 1DE ⊥平面A 1C 1F .（2）在直三棱柱111ABC A B C -中，1111AA ⊥平面A B C 因为11AC ⊂平面111A B C ，所以111AA ⊥A C 又因为111111111111111,,AC A B AA ABB A A B ABB A A B AA A ⊥⊂⊂=，平面平面所以11AC ⊥平面11ABB A因为1B D ⊂平面11ABB A ，所以111AC B D ⊥又因为1111111111111C F,C F,B D A AC A A F A AC A F A ⊥⊂⊂=F ，平面平面所以111C F B D A ⊥平面因为直线11B D B DE ⊂平面，所以1B DE 平面11.AC F ⊥平面45、（2016年全国I 卷）如图，已知正三棱锥P -ABC 的侧面是直角三角形，P A =6，顶点P 在平面ABC 内的正投影为点D ，D 在平面P AB 内的正投影为点E ，连结PE 并延长交AB 于点G . （I ）证明：G 是AB 的中点；（II ）在图中作出点E 在平面P AC 内的正投影F （说明作法及理由），并求四面体PDEF 的体积．PABD CGE（II ）在平面PAB 内，过点E 作PB 的平行线交PA 于点F ，F 即为E 在平面PAC 内的正投影.理由如下：由已知可得PB PA ⊥，⊥PB PC ，又//EF PB ,所以EF PA EF PC ，⊥⊥,因此EF ⊥平面PAC ，即点F 为E 在平面PAC 内的正投影.连结CG ，因为P 在平面ABC 内的正投影为D ，所以D 是正三角形ABC 的中心. 由（I ）知，G 是AB 的中点，所以D 在CG 上，故2.3=CD CG 由题设可得⊥PC 平面PAB ，⊥DE 平面PAB ，所以//DE PC ，因此21,.33==PE PG DE PC由已知，正三棱锥的侧面是直角三角形且6=PA ，可得2,2 2.==DE PE 在等腰直角三角形EFP 中，可得 2.==EF PF 所以四面体PDEF 的体积114222.323=⨯⨯⨯⨯=V 46、（2016年全国II 卷高考）如图，菱形ABCD 的对角线AC 与BD 交于点O ，点E 、F 分别在AD ，CD 上，AE CF =，EF交BD 于点H ，将DEF ∆沿EF 折到'D EF ∆的位置. （Ⅰ）证明：'AC HD ⊥；（Ⅱ）若55,6,,'224AB AC AE OD ====,求五棱锥D ABCEF '-体积.试题解析：（I ）由已知得，,.⊥=AC BD AD CD 又由=AE CF 得=AE CFAD CD，故//.AC EF 由此得,'⊥⊥EF HD EF HD ，所以//.'AC HD . （II ）由//EF AC 得1.4==OH AE DO AD 由5,6==AB AC 得22 4.==-=DO BO AB AO 所以1, 3.'===OH D H DH 于是22222(22)19,''+=+==OD OH D H 故.'⊥OD OH由（I ）知'⊥AC HD ，又,'⊥=AC BD BD HD H ，所以⊥AC 平面,'BHD 于是.'⊥AC OD又由,'⊥=OD OH ACOH O ，所以，'⊥OD 平面.ABC 又由=EF DH AC DO 得9.2=EF 五边形ABCFE 的面积11969683.2224=⨯⨯-⨯⨯=S 所以五棱锥'ABCEF D -体积16923222.342=⨯⨯=V 47、（2016年全国III 卷高考）如图，四棱锥P ABC -中，PA ⊥平面ABCD ，AD BC ，3AB AD AC ===，4PA BC ==，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（I ）证明MN平面PAB ；（II ）求四面体N BCM -的体积.（Ⅱ）因为⊥PA 平面ABCD ，N 为PC 的中点，所以N 到平面ABCD 的距离为PA 21. ....9分取BC 的中点E ，连结AE .由3==AC AB 得BC AE ⊥，522=-=BE AB AE .由BC AM ∥得M 到BC 的距离为5，故525421=⨯⨯=∆BCM S . 所以四面体BCM N -的体积354231=⨯⨯=∆-PA S V BCM BCM N . .....12分 48．(2017·北京文)如图，在三棱锥P －ABC 中，P A ⊥AB ，P A ⊥BC ，AB ⊥BC ，P A ＝AB ＝BC ＝2，D 为线段AC 的中点，E 为线段PC 上一点．(1)求证：P A ⊥BD ； (2)求证：平面BDE ⊥平面P AC ； (3)当P A ∥平面BDE 时，求三棱锥E －BCD 的体积．(1)证明因为P A ⊥AB ，P A ⊥BC ，AB ∩BC ＝B ，所以P A ⊥平面ABC .又因为BD ⊂平面ABC ，所以P A ⊥BD .(2)证明因为AB＝BC，D是AC的中点，所以BD⊥AC.由(1)知，P A⊥BD，又P A∩AC＝A，所以BD⊥平面P AC.所以平面BDE⊥平面P AC.(3)解因为P A∥平面BDE，平面P AC∩平面BDE＝DE，所以P A∥DE.因为D为AC的中点，所以DE＝12P A＝1，BD＝DC＝ 2.由(1)知，P A⊥平面ABC，所以DE⊥平面ABC，所以三棱锥E－BCD的体积V＝16BD·DC·DE＝13. 49．(2017·江苏，15)如图，在三棱锥ABCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，F(E 与A，D不重合)分别在棱AD，BD上，且EF⊥AD.求证：(1)EF∥平面ABC；(2)AD⊥AC.证明(1)在平面ABD内，因为AB⊥AD，EF⊥AD，则AB∥EF.又因为EF⊄平面ABC，AB⊂平面ABC，所以EF∥平面ABC.(2)因为平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，BC⊂平面BCD，BC⊥BD，所以BC⊥平面ABD.因为AD⊂平面ABD，所以BC⊥AD.又AB⊥AD，BC∩AB＝B，AB⊂平面ABC，BC⊂平面ABC，所以AD⊥平面ABC.又因为AC⊂平面ABC，所以AD⊥AC.50、（2013年全国I卷）如图，三棱柱111ABC A B C-中，CA CB=，1AB AA=，160BAA∠=。