中考数学专题复习课时20视图与投影
2025年九年级中考数学一轮复习课件 考点24 投影与视图

方法讲练 8.(2024·包头)如图,正方形ABCD边长为2,以AB所在直线为轴,将正方
形ABCD旋转一周,所得圆柱的主视图的面积为( A )
A.8 C.8π
B.4 D.4π
方法讲练
命题点2 几何体的展开与折叠( 7年2考)
9.(2022·河南第2题)2022年北京冬奥会的奖牌“同心”表达了“天地合·人
方法讲练 2.(2023·河南第2题)北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九 大镇院之宝之一,具有极高的历史价值、文化价值.如图所示,关于它 的三视图,下列说法正确的是( A ) A.主视图与左视图相同 B.主视图与俯视图相同 C.左视图与俯视图相同 D.三种视图都相同
方法讲练 3.(2021·河南第3题)如图是由8个相同的小正方体组成的几何体,其主视 图是( A )
中间三个面,一、二隔 间没有面,三、三连 间两个面,楼梯天天见)
河见)
一线)
温馨提示 相间的两个小正方形(中间隔一个小正方形)是正方体的相对面, “Z”字端处的两个小正方形是正方体的相对面
方法讲练 命题点1 几何体的三视图( 7年5考) 1.(2024·河南第4题)信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶 的包装盒,它的主视图为( A )
温馨提示 1.主视图反映几何体的长和高,俯视图反映几何体的长和宽,左视图反 映几何体的宽和高. 2.看得见部分的轮廓线画成⑩_实__线__,看不见部分的轮廓线画成⑪虚__线__
3.常见几何体的三视图 长方体 正方体
几何体
考点梳理
圆柱 圆锥 球体
正三棱柱
正三棱锥
主视图 左视图 俯视图
考点梳理
温馨提示 对常见几何体的组合体,在判断其三视图时,要注意分清每 一部分的三视图形状,然后根据其摆放位置及各部分大小决定组合体的 具体视图
专题训练20:视图与投影-2021年中考数学一轮复习知识点课标要求

2021年中考数学一轮复习知识点课标要求专题训练20:视图与投影(含答案)一、知识要点:1、投影(1)投影:用光线照射物体,在某个平面上得到的影子叫做物体的投影。
(2)平行投影:由平行光线形成的投影是平行投影。
(3)中心投影:由同一点发出的光线形成的投影叫做中心投影。
(4)正投影:投影线垂直于投影面产生的投影叫做正投影。
2、视图(1)视图:从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图。
视图可以看作物体在某一方向光线下的正投影。
(2)主视图、俯视图、左视图对一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图。
主视图与俯视图的长对正;主视图与左视图的高平齐;左视图与俯视图的宽相等。
二、课标要求:1、通过丰富的实例,了解中心投影和平行投影的概念。
2、会画直棱柱、圆柱、圆锥、球的主视图、左视图、俯视图,能判断简单物体的视图,并会根据视图描述简单的几何体。
3、了解直棱柱、圆锥的侧面展开图,能根据展开图想象和制作实物模型。
4、通过实例,了解上述视图与展开图在现实生活中的应用。
三、常见考点:1、中心投影和平行投影。
2、常见几何体的三视图。
3、常见几何体的折叠与展开。
四、专题训练:1.如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是()A.B.C.D.2.如图所示的几何体的左视图是()A.B.C. D.3.用棱长为1的小立方体摆成如图所示的几何体,从左面看这个几何体得到的平面图形的面积是()A.3 B.4 C.5 D.64.如图,晚上小明在路灯下沿路从A处径直走到B处,这一过程中他在地上的影子()A.一直都在变短B.先变短后变长C.一直都在变长D.先变长后变短5.如图是由一些相同的小正方体搭成的几何体从正面、左面、上面看到的形状图,则搭成这个几何体的小正方体的个数是()A.4 B.5 C.6 D.76.如图是一个空心圆柱体,其主视图是()A.B.C.D.7.同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为()A.3.2米B.4.8米C.5.2米D.5.6米8.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到的这个几何体的形状图是()A.B.C.D.9.由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则以下说法正确的是()A.x=1或2,y=3 B.x=1或2,y=1或3C.x=1,y=1或3 D.x=2,y=1或310.由一些大小相同的小正方体搭成的几何体的左视图和俯视图,如图所示,则搭成该几何体的小正方体的个数最多是()A.7 B.8 C.9 D.1011.如图是某几何体从不同方向看到的图形.若从正面看的高为10cm,从上面看的圆的直径为4cm,求这个几何体的侧面积(结果保留π)为.12.长方体从正面看和从上面看所得到的图形如图所示,则这个长方体的体积是.13.如图所示的是三个直立在地面上的艺术字母的投影(阴影部分)效果,在艺术字母“L,K,C”的投影中,属于同一种投影是.14.由一些大小相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体的小正方体的个数最少是.15.如图,是由几个边长为1的小立方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,则这个几何体的表面积为.16.由若干个相同的小正方体搭成的几何体的三视图相同,如图所示.至少再加个小正方体,该几何体可成为一个正方体.17.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=2m,树影BC=3m,树与路灯的水平距离BP=4m.则路灯的高度OP为m.18.如图是由一些相同的小正方体构成的立体图形的三种视图,则构成这个立体图形的小正方体的个数是个.19.小华家客厅有一张直径为1.2m,高为0.8m的圆桌AB,有一盏灯E到地面垂直距离EF 为2m,圆桌的影子为CD,FC=2,则点D到点F的距离为m.20.用小立方块搭一几何体,它的主视图和俯视图如图所示,这个几何体最少要个立方块,最多要个立方块.21.如图所示的几何体是由七个相形状同的正方体搭成的,请画出这个几何体的从正面、从左面、从上面看到的形状图.22.一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面、左面看到的这个几何体的形状图.23.一个几何体的三视图如图所示.说出这个几何体的形状,并求出它的表面积.24.把边长为1厘米的6个相同正方体摆成如图的形式.(1)画出该几何体的主视图、左视图、俯视图;(2)直接写出该几何体的表面积为cm2;(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加小正方体.参考答案1.解:A、从正面看到的和从左面看到的图形相同,底层是三个小正方形,中层和上层的左边分别是一个小正方形,故本选项不合题意;B、从正面看到的和从左面看到的图形相同,底层是两个小正方形,上层的左边是一个小正方形,故本选项不合题意;C、从正面看到的和从左面看到的图形相同,底层是三个小正方形,上层的左边是一个小正方形,故本选项不合题意;D、从正面看,底层是三个小正方形,上层是两个小正方形;从左面看,底层是三个小正方形,上层的左边是一个小正方形,故本选项符合题意.故选:D.2.解:从左边看,是一列2个矩形.故选:C.3.解:从左面看这个几何体得到图形是,此平面图形的面积是4,故选:B.4.解:在小明由A处径直走到路灯下时,他在地上的影子逐渐变短,当他从路灯下走到B 处时,他在地上的影子逐渐变长.故选:B.5.解:从主视图和俯视图可知,几何体的底层有3个正方体,从主视图和左视图可知,几何体的第二层有2个正方体,则搭成这个几何体的小正方体的个数为:3+2=5,故选:B.6.解:从前面观察物体可以发现:它的主视图应为矩形,又因为该几何体为空心圆柱体,故中间的两条棱在主视图中应为虚线,故选:D.7.解:设旗杆的高为x,有,可得x=4.8米.故选:B.8.解:根据所给出的图形和数字可得:主视图有4列,每列小正方形数目分别为1,2,3,2,则符合题意的是故选:C.9.解:由俯视图可知,该组合体有两行两列,左边一列前一行有两个正方体,结合主视图可知左边一列叠有2个正方体,故x=1或2;由主视图右边一列可知,右边一列最高可以叠3个正方体,故y=3,故选:A.10.解:由俯视图易得最底层有6个小正方体,第二层最多有3个小正方体,那么搭成这个几何体的小正方体最多为3+6=9个.故选:C.11.解:观察三视图可得这个几何体是圆柱;∵从正面看的高为10cm,从上面看的圆的直径为4cm,∴该圆柱的底面直径为4cm,高为10cm,∴该几何体的侧面积为2πrh=2π×2×10=40π(cm2).故这个几何体的侧面积(结果保留π)为40πcm2.故答案为:40πcm2.12.解:由主视图和俯视图知,该长方体的长为4、宽为3、高为3,则这个长方体的体积为4×3×3=36.故答案为:36.13.解:根据题意,字母L、K的投影为中心投影,字母C的投影为平行投影.故答案为L、K.14.解:仔细观察物体的主视图和左视图可知:该几何体的下面最少要有2个小正方体,上面最少要有1个小正方体,故该几何体最少有3个小正方体组成.故答案为:3.15.解:这个几何体的主视图有三列,从左到右分别是3,4,1,左视图有三列,从左到右分别是3,4,2,表面积为:(8+9+6)×2=46,故答案为:46.16.解:易得第一层有3个正方体,第二层有1个正方体,共有4个小正方体,8﹣4=4(个).故至少再加4个小正方体,该几何体可成为一个正方体.故答案为:4.17.解:∵AB∥OP,∴△ABC∽△OPC,∴=,即=,∴OP=(m).故答案为.18.解:由俯视图易得最底层有6个正方体,第二层有2个正方体,则构成这个立体图形的小正方体的个数是6+2=8个.故答案为:8.19.解:如图,由题意得,AB=1.2,GF=0.8,EF=2,FC=2,∵AB∥CD,∴△EAB∽△ECD,∴=,即=,解得,CD=2,∴DF=CD+FC=2+2=4,故答案为:4.20.解:由主视图可得,这个几何体(第2列,第3列组合不唯一)最少要1+3+4=8个立方块;由主视图可得,这个几何体最多要1+4+6=11个立方块;故答案为:8,11.21.解:如图所示:22.解:如图所示:23.解:由题意推知几何体是长方体,长、宽、高分别220mm、100mm、60mm,(220×100+220×60+100×60)×2=(22000+13200+6000)×2=41200×2=82400(mm2).故它的表面积是82400mm2.24.解:(1)如图所示:(2)几何体表面积:2×(5+4+3)+2=26(cm2),故答案为:26;(3)最多可以再添加2个小正方体.故答案为:2。
中考数学专题复习:投影与视图
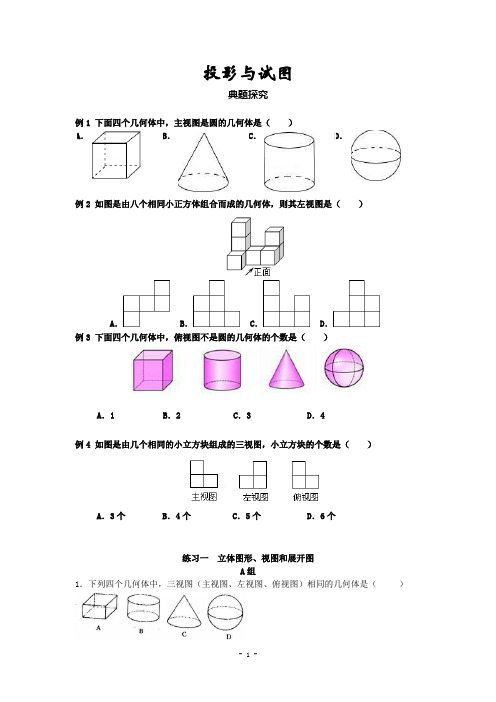
投影与试图典题探究例2 如图是由八个相同小正方体组合而成的几何体,则其左视图是( )A. B . C . D .例3 下面四个几何体中,俯视图不是圆的几何体的个数是( )A .1B .2C .3D .4例4 如图是由几个相同的小立方块组成的三视图,小立方块的个数是( )A .3个B .4个C .5个D .6个练习一 立体图形、视图和展开图A 组1.下列四个几何体中,三视图(主视图、左视图、俯视图)相同的几何体是( )2.一个几何体的三视图如右图所示,这个几何体是()A.圆锥 B.圆柱 C.三棱锥D.三棱柱3.已知一个几何体的三视图如图所示,则该几何体是()A棱柱 B圆柱 C圆锥 D球4.如图是一个几何体的三视图,则这个几何体的形状是()(A)圆柱(B)圆锥(C)圆台(D)长方体5.下列图形中,不是三棱柱的表面展开图的是()6.圆锥侧面展开图可能是下列图中的()7.右图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是()8.将左图中的正方体纸盒沿所示的粗线剪开,其平面展开图的示意图为9.一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和“崇”相对的面上写的汉字是()A.低B.碳C.生D.活10.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示。
如果记6的对面的数字为a,2的对面的数字为b,那么ba 的值为()A.3 B.7 C.8 D.1111.如图①放置的一个水管三叉接头,若其正视图如图②,则其俯视图是()12.左下图为主视图方向的几何体,它的俯视图是()13.如图1是一个几何体的实物图,则其主视图是DCBA14.如图所示,李老师办公桌上放着一个圆柱形茶叶盒和一个正方体的墨水盒,小芳从上面看,看到的图形是()B组15.右图是一个由4个相同的正方体组成的立体图形,它的三视图为()16.如图是由五个小正方体搭成的几何体,它的左视图是()17.如图所示的几何体的俯视图是().A B DC18.如图摆放的正六棱柱的俯视图是()19.沿圆柱体上底面直径截去一部分的物体如图所示,它的俯视图是( )20.下图所示几何体的主视图是()21.一个几何体的三视图如图所示,那么这个几何体是()22.下面四个图形中,是三棱柱的平面展开图的是()23.某物体的展开图如图所示,它的左视图为()练习二中心投影与平行投影A组1.下列四幅图形中,表示两棵树在同一时刻阳光下的影子的图形可能是 ( )2.视点指的是()A.眼睛的大小 B.眼睛看到的位置C.眼睛的位置 D.眼睛没有看到的位置3.晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影是()A.变长 B.变短C.先变短后变长 D.先变长后变短4.于视线的范围,下列叙述不正确的是()A.走上坡路比走平路的视线范围小B.走上坡路比走平路的视线范围大C.在船头比在船尾向前看到的范围大D.在轿车外比在轿车里看到的范围大5.如图所示,快下降到地面的某伞兵在灯光下的影子为AB.试确定灯源P的位置,并画出竖立在地面上木桩的影子EF.(保留作图痕迹,不要求写作法)6.在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是()答案例2 考点:简单组合体的三视图.分析:找到从左面看所得到的图形即可.解答:解:从左面可看到从左往右三列小正方形的个数为:2,3,1.故选B.点评:本题考查了三视图的知识,左视图是从物体的左面看得到的视图,解答时学生易将三种视图混淆而错误的选其它选项.例4 考点:由三视图判断几何体.分析:根据三视图的知识,可判断该几何体有两列两行,底面有3个正方形,第二层有1个.解答:解:综合三视图可看出,底面有3个小立方体,第二层应该有1个小立方体,因此小立方体的个数应该是3+1=4个.故选B.点评:本题考查对三视图的理解应用及空间想象能力.可从主视图上分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后位置,综合上述分析数出小立方块的个数.练习一立体图形、视图和展开图A组1.【答案】D ;2.【答案】D;3.【答案】B ;4.【答案】B ;5.【答案】D;6.【答案】D7.【答案】B;8.【答案】C;9.【答案】A ;10.【答案】B;11.【答案】A;12.【答案】D13.【答案】C ;14.【答案】AB组15.【答案】B;16.【答案】A;17.【答案】B ;18.【答案】D ;19.【答案】D20.【答案】A ;21.【答案】A;22.【答案】A ;23.【答案】B练习二中心投影与平行投影A组1.【答案】A ;2.【答案】C;3.【答案】C;4.【答案】B ;5.【答案】先连接伞兵的头和脚与对应的影子的直线,两直线的交点即为点P,过点P作过木桩顶端的直线与地面的交点即为F.6.【答案】A。
2025年中考数学总复习第一部分考点梳理第21节投影与视图

返回目录
必备知识梳理
二、立体图形的展开与折叠 1. 一般几何体的表面展开图:
几何体
表面展开 图(任一 种)
返回目录
必备知识梳理
2. 正方体的表面展开图:
注:相同数字所在的面代表相对面.
返回目录
中考考点精讲
返回目录
考点一 投影
1. 如图1,一个圆形广场周围有三套18米的高杆照明灯,图2是将其抽象画出 的俯视图.在某一时刻三套高杆照明灯在太阳光下的影子合理的是 ( C )
(3)的俯视图是
( D)
中考考点精讲
返回目录
6. (2024适应性)如图是由一些大小相同的小正方体组成的几何体的主视 图和俯视图,则组成这个几何体的小正方体的个数至少是 ( B ) A. 8个 B. 7个 C. 6个 D. 5个
中考考点精讲
返回目录
考点三 几何体的展开与折叠
7. (2019山西第3题)某正方体的每个面上都有一个汉字,如图是它的一种 展开图,那么在原正方体中,与“点”字所在面相对的面上的汉字是 (B) A. 青 B. 春 C. 梦 D. 想
左视图、俯视图,能判断简单物体的视 拱”的左视图
2. 几何体的
图,并会根据视图描述简单的几何体 2020 年第 4 题:小正 视图
➢ 了解直棱柱、圆锥的侧面展开图,能根 方体组成的几何体的
据展开图想象和制作实物模型
主视图与左视图
➢
通过实例,了解上述视图与展开图在现 ——
实生活中的应用
3.几何体的 展开与折叠
必备知识梳理
类别
概念
图示
返回目录
续表 结论
由同一点(点光源)发 中心投影 出的光线形成的投影叫
中考数学复习视图与投影PPT课件

要点梳理
1.三视图: (1)主视图:从 正面 看到的图; (2)左视图:从 左面 看到的图; (3)俯视图:从 上面 看到的图.
2.画“三视图” 的原则: (1)位置:主视图;左视图; 俯视图. (2)大小:长对正,高平齐,宽相等. (3)虚实:在画图时,看得见部分的轮廓通常画成实线, 看不见部分的轮廓线通常画成虚线.
பைடு நூலகம்
3.一个正方体的每个面都写有一个汉字,其平面展开图如
图所示,则在该正方体中,和“崇”相对的面上写的汉字
是( )
A.低
B.碳
C.生
D.活
答案 A 解析 假设“崇”为正方体的前面,则“尚”、“碳”是 这个正方体的右面与左面,正方体的后面是“低”.
易错警示
对峙体图形展开后的邻面、对面视察不仔细 试题 如图,A、B、C三个立方体中,有一个立方体展开后
探究提高 掌握从不同方向看物体的方法和画几何体三视图 的要求,通过仔细视察、比较、分析,可选出正确答案.
知能迁移1 (1)根据下面的三视图描述所对应的物体. 解 长方体上放置一个圆锥.
(2)(2011·安徽)下图是五个相同的小正方体搭成的几何体,其 左视图是( )
答案 A
题型二 由三视图确定原几何体的构成
基础自测
1.(2011·福州)在下列几何体中,主视图、左视图与俯视图 都是相同的圆,该几何体是( )
答案 A 解析 几何体A的三视图都是圆形,故选A.
2.(2011·金华)如图是六个棱长为1的立方块组成的一个几何
体,其俯视图的面积是( )
A.6
B.5
C.4
D.3
答案 B 解析 该几何体的俯视图如图所示,
知能迁移2 (1)下图是几何体的俯视图,所标数字为该位置 立方体的个数,请补全该几何体的主视图和左视图.
中考数学一轮复习课件投影与视图

第10题图
11.(2023·眉山)由相同的小正方体搭成的立体图形的部分视图 如图所示,则搭成该立体图形的小正方体的最少个数为( B )
第11题图
A.6
B.9
C.10
D.14
12.(2023·无锡)若直三棱柱的上下底面为正三角形,侧面展开 图是边长为6的正方形,则该直三棱柱的表面积为 36+
.
第8题图
A.
B.
C.
D.
9.(2022·江西)如图是四个完全相同的小正方体搭成的几何 体,它的俯视图为( A )
A.
B.
C.
D.
第9题图
10.甲和乙两个几何体都是由大小相同的小立方块搭成,它们的 俯视图如图,小正方形中数字表示该位置上的小立方块个 数,则下列说法中正确的是( D )
A.甲和乙左视图相同,主视图相同 B.甲和乙左视图不相同,主视图不相同 C.甲和乙左视图相同,主视图不相同 D.甲和乙左视图不相同,主视图相同
A.
Байду номын сангаасB.
C.
D.
18.(2023·扬州)下列图形是棱锥侧面展开图的是( D )
A.
B.
C.
D.
19.(2022·泰州)如图为一个几何体的表面展开图,则该几何体 是( B )
A.三棱锥 C.四棱柱
第19题图 B.四棱锥 D.圆锥
20.(2023·长春)如图是一个多面体的表面展开图,每个面都标 注了数字.若多面体的底面是面③,则多面体的上面是( C )
5.根据三视图还原几何体 (1)想象:根据各视图想象从三个方向看到的几何体形状; (2)定形:综合确定几何体(原实物原型)的形状; (3)定大小、位置:根据三视图“长对正、高平齐、宽相 等”的关系,确定轮廓线的位置以及各个方向的大小.
2024年中考数学一轮复习考点精讲课件—投影与视图

2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:
① 根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;
② 从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;
③ 熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助.
考点一 图形的投影
3)立体图形的正投影
物体的正投影的形状、大小与物体相对于投影面的位置有关,立体图形的正投影与平行于投影面且过立体图形的最
大截面全等.
投影的判断方法:
1)判断投影是否为平行投影的方法是看光线是否是平行的,如果光线是平行的,那么所得到的投影就是平行投影.
2)判断投影是否为中心投影的方法是看光线是否相交于一点,如果光线是相交于一点的,那么所得到的投影就是中
【例2】(2021·安徽淮南·校联考模拟预测)下列现象中,属于中心投影的是(
A.白天旗杆的影子
B.阳光下广告牌的影子
C.灯光下演员的影子
D.中午小明跑步的影子
)
考点一 图形的投影
题型03 正投影
【例3】(2022·浙江温州·温州绣山中学校联考二模)由四个相同小立方体拼成的几何体如图所示,当光线由上向
1 ) 等 高 的 物 体 垂 直 地 面 放 置 时 ( 图 1 ) , 在 太 阳 光 下 , 它 们 的 影 子 一 样 长 .
2)等长的物体平行于地面放置时(图2),它们在太阳光下的影子一样长,且影长等于物体本身的长度.
图1
图2
【小技巧】
1)图1中,两个物体及它们各自的影子及光线构成的两个直角三角形相似,相似三角形对应边成比例.
【变式8-1】(2021·宁夏吴忠·统考模拟预测)一个几何体的三视图如图所示,则该几何体的表面积为 3π+4 .
中考数学专题复习《投影与视图》知识点梳理及典型例题讲解课件

第七部分 图形与变换
第27讲 投影与视图
要点梳理
1.几何体的分类
柱体:____________锥体:______球体:____
①②④⑥⑦
⑤⑧
③
几何体
2.立体图形与平面图形的转化
(1)几何体的侧面展开图
①直棱柱的侧面展开图是________________;②圆柱的侧面展开图是________________;③圆锥的侧面展开图是______.
3.根据平面展开图判断正方体的相对面、相邻面: (1)相间、“ ”端是对面 ①相间(中间隔着一个小正方形)的两个面是正方体的对面; ②“ ”字型“ ”两端处的两个面是正方体的对面. (2)间二、拐角是邻面 ①中间隔着两个小正方形的两个面是正方体的邻面; ②拐角型“ ”的三个面是正方体的邻面.
A
A. B. C. D.
长方形(矩形)
长方形(矩形)
扇形
(2)几何体的展开与折叠
①圆柱的展开图是两个____和一个________________;
②正方体的展开图是6个小正方形,有多种形式.
圆
长方形(矩形)
3.投影投影包括______投影和______投影.
平行
中心
4.正投影
(1)定义:投影线______于投影面产生的投影叫作正投影.(2)性质:当物体的某个面______于投影面时,这个面的正投影与这个面的形状、大小完全______.
2.(2022·新疆)图2是某几何体的展开图,该几何体是( ) .
C
图2
A.长方体 B.正方体 C.圆锥 D.圆柱
考点二 投影
名师指导 1.对于平行投影,在不同位置、不同时间下,投影的大小、形状可能不同,但对于对边平行的图形,其投影的对边仍然平行. 2.无论是平行投影还是中心投影,常利用投影线及两个物体对应的线段构造相似三角形,然后利用相似三角形的对应线段成比例求解其他问题.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年中考数学专题复习课时20视图与投影班级姓名备课组长
【考点说明】考试指南P137
【例题评析】
1.由4个相同的小正方形组成的几何体如图38-1所示,则它的主视图是
( )
图38-1
2.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图38-3所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状图是 ( )
38-3
3. 某几何体的三视图如图38-4所示,则此几何体是 ( )
A.圆锥
B.圆柱
C.长方体
D.四棱柱
4. 一个长方体的左视图、俯视图及相关数据如图38-6所示,则其主视图的面积
为 ( )
图38-6 图38-12
5. 如图38-12,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何
体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要_ ___个小正方体,王亮所搭几何体的表面积为__ __.
【自主检测】
1.如图5-2-14所示的几何体的主视图是( )
图5-2-14A B C D
2.用4个小立方块搭成如图5-2-15所示的几何体,该几何体的左视图是( )
图5-2-15A B C D
3.长方体的主视图与俯视图如图5-2-16,则这个长方体的体积是( )
A.52 B.32 C.24 D.9
图5-2-16
4.如图5-2-17所示的几何体的俯视图是( )
图5-2-17
5. 几个棱长为1的正方体组成的几何体的三视图如图5-2-26所示,则这个几何体的体积
是( )
图5-2-26
A.4 B.5 C.6 D.7
6. 如图5-2-27是一个上下底密封纸盒的三视图,
请你根据图中数据,计算这个密封纸盒的表面积
为________cm2(结果可保留根号).
【中考基础练】完成时间:5分钟
1.计算:m2•m3= .
2.已知一个数的绝对值是4,则这个数是
3.化简:(1﹣x)2+2x= .
4.当x= 时,分式的值为0.
5.数轴上实数b的对应点的位置如图所示,比较大小:b+1 0.
6.如图,▱ABCD中,E为AD的中点,BE,CD的延长线相交于
点F,若△DEF的面积为1,则▱ABCD的面积等于.
7.关于x的一元二次方程x2+a=0没有实数根,则实数a的取值范围是.
8.(1)计算:﹣(﹣π)0﹣2sin60°(2)化简:(1+)•.
【课后提升】完成时
间:.
1.如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是 ( )
2.如图,该几何体的主视图是( )
3. 从左面看圆柱,则图中圆柱的投影是( )
A. 圆 B.矩形
C. 梯形
D. 圆柱
4.如图38-7是一个几何体的三视图,则这几何体的展开图可以是 ( )
图38-7
5.如图5-2-22是由棱长为1的正方体搭成的积木的三视图,则图中棱长为1的正方体的个数是________.
6.画出立体图形的三视图.
7.由若干个相同的小正方体组合而成的一个几何体的三视图如图38-15所示,则组成这个
几何体的小正方体的个数是 ( )
图38-15
A.4 B.5 C.6 D.9
8. 正方体的展开图,则原正方体相对两个面上的数字和最小的是( ) A.4 B.6 C.7 D.8
9. 由5个棱长为1的正方体组成如图5-2-23的几何体.
(1)该几何体的体积是________(立方单位),表面积是________(平方单位);
(2)画出该几何体的主视图和左视图.
【自备部分】
【课后反思】39839 9B9F 鮟 $25273 62B9 抹30909 78BD 碽• &z25104 6210 成32333 7E4D 繍28399 6EEF 滯38137 94F9 铹31078 7966 祦。
