高考理科数学：《基本初等函数》题型归纳与训练

合集下载

专题10 基本初等函数(知识梳理)(新高考地区专用)(解析版)

专题10 基本初等函数（知识梳理）一、指数与指数函数(一)指数式的化简与求值1、化简原则：①化根式为分数指数幂；②化负指数幂为正指数幂； ③化小数为分数； ④注意运算的先后顺序。

提醒：有理数指数幂的运算性质中，其底数都大于零，否则不能用性质来运算。

2、结果要求：①题目以根式形式给出，则结果用根式表示；②题目以分数指数幂形式给出，则结果用分数指数幂形式表示；③结果不能同时含有根式和分数指数幂，也不能既有分母又有负分数指数幂。

例1-1．已知41<a ，则化简42)14(-a 的结果是( )。

A 、a 41-- B 、14--a C 、14-a D 、a 41- 【答案】D【解析】a a a 41)41()14(4242-=-=-，故选D 。

变式1-1．化简3a a ⋅-的结果是( )。

A 、65a - B 、65a -- C 、65a - D 、52a -【答案】B【解析】∵0≤a ，则656565312131213)()()()()(a a a a a a a a a --=--=--=-⋅--=⋅-=⋅-，故选B 。

变式1-2．已知31=+-x x ，求下列各式的值：(1)2121-+xx ；(2)22-+x x ；(3)2323-+xx 。

【解析】(1)∵52)(2)()(1221212122122121=++=+⋅+=+----x x xxx x xx ，∴52121±=+-x x ，又由31=+-x x 得0>x ，∴52121=+-xx ；(2)72)(2122=-+=+--x x x x ； (3)]1))[((])())[(()()(12121221212122121213213212323-++=+⋅-+=+=+-------x x xx xxx x xx xx xx52)13(5=-=。

(二)指数函数的图像和性质1、定义：一般地，函数x a x f =)((0>a 且1≠a )叫做指数函数，其中x 是自变量。

基本初等函数复习题型最全最细最精

根本初等函数复习一、根底复习：1、a 的次方根： , x 叫a 的n 次方根根式的性质：(1)n n a )(= ,(),1+∈>N n n 且；〔2〕⎩⎨⎧=为偶数时当为奇数时当n a n a a nn|,|,2、分数指数幂与根式：=mna =-n a =1a =0a3、幂的运算性质：=⋅s r a a =÷s r a a =s r a )( =r ab )(4、指数式与对数式的互化：⇒=N a b5、对数的性质：〔1〕N 〔2〕=1log a 〔3〕=a a log6、对数恒等式：=Naa log=b a a log7、对数的运算法那么：=⋅)(log N M a =)(log NMa =αM a log 8、换底公式：=b a log =b a log =n a b mlog 9、常用对数：=N 10log 自然对数：=N e log 10、幂、指、对函数函数的性质二、典型例题： 1、指数、对数运算： 1、以下各式中，正确的选项是〔〕A ．100=B ．1)1(1=--C ．74471aa=-D ．53531aa=-2. 计算：210319)41()2(4)21(----+-⋅- ＝；)31()3)((656131212132b a b a b a ÷-的结果〔〕A ．a 6B ．a -C ．a 9-D ．29a4.2x ＝72y ＝A ，且1x ＋1y＝2，那么A 的值是 A ．7 B ．7 2 C ．±72 D ．98 a 、b 、c ∈R +，那么3a =4b =6c，那么( )A ．bac111+=B ．b a c 122+=C ．b a c 221+= D ．ba c 212+=6. 假设a<12，那么化简4(2a －1)2的结果是A.2a －1 B ．－2a －1 C.1－2a D ．－1－2a7、计算以下各式的值〔1〔2〕；21lg5(lg8lg1000)(lg lg lg 0.066++++8、设1245100,2()a b a b==+求的值.9、4(),01,42xx f x a =<<+且(1)()(1)f a f a +-求的值；1231000(2)()()()...()1001100110011001f f f f ++++求的值.说明：如果函数()xf x =，那么函数()f x 满足()(1)1f x f x +-=2、指数函数、对数、幂函数的图像：〔1〕定义考察：1、以下函数中指数函数的个数是 ( ). ①②③④A ．0个 2.以下函数是指数函数的是〔〕A. x y 5=B. x y +=25C. x y 52⋅=D. 15-=x y〔2〕定点问题1．函数0.(12>+=-a a y x 且)1≠a 的图像必经过点〔〕)1,0.(A )1,1.(B )0,2.(C )2,2.(D2. 函数恒3()25x f x a -=+过定点 ( )A .(3 , 5)B .( 3, 7 )C .( 0, 1 )D .( 1, 0 )1log )()2(2+=-x x f 恒过定点___________〔3〕图像问题1.当a ＞1时，函数y=log a x 和y=(1-a)x 的图像只可能是( )2如图中函数21-=xy 的图象大致是〔〕图3-73．在统一平面直角坐标系中，函数ax x f =)(与x a x g =)(的图像可能是〔〕4．设d c b a ,,,都是不等于1的正数，x x x x d y c y b y a y ====,,,在同一坐标系中的图像如下图，那么d c b a ,,,的大小顺序是〔 d c b a A <<<. c d b a B <<<. c d a b C <<<. d c a b D <<<.5．图中所示曲线为幂函数n x y =在第一象限的图象，那么1c 、2c 、3c 、4c 大小关系为〔〕A.4321c c c c >>>B.3412c c c c >>>C.3421c c c c >>>D.2341c c c c >>> 3、指数函数、对数函数的单调性、奇偶性〔1〕单调性1、比拟以下每组中两个数的大小0.30.4 1.3 1.60.3 1.3111(1)2.1_____2.1; (2)()_____(); (3)2.1_____()555-550.70.543(4)log 1.9_____log 2; (5)log 0.2_____log 2; (6)log 2_____log 4xyo 1Axyo1B xyo1Cxyo1Dxa =xby =xc y =xd y =yo2、031log 31log >>b a ，那么a 、b 的关系是〔〕 A ．1＜b ＜a B ．1＜a ＜b C ．0＜a ＜b ＜1 D ．0＜b ＜a ＜1 3.设10<<a ，使不等式531222+-+->x x x x a a 成立的x 的集合是4.以下函数中，在区间(0，1)上是增函数的是 ( ) A.y=-xB.y=log 21xC.y=31x D.y=-x 2+2x+15.〔1〕函数)26(log 21.0x x y -+=的单调增区间是________〔2〕log (2)a y ax =-在[0,1]是减函数，那么a 的取值范围是_________6．(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨>⎩是(,)-∞+∞上的减函数，那么a 的取值范围是〔〕〔A 〕(0,1) 〔B 〕1(0,)3 〔C 〕11[,)73〔D 〕1[,1)77、解以下不等式：（1）22332<-+x x ；〔2〕2332)21(2--+<x x x ；〔3〕)1,0(5213222≠>>-++-a a a a x x x x2()(1)x f x a R a =-在上是减函数，求实数的取值范围9、求以下函数的单调区间。

高中数学必修一基本初等函数知识点+练习题含答案解析(非常详细)

第一部分基本初等函数知识点整理第二章基本初等函数一、指数函数（一）指数1、指数与指数幂的运算：复习初中整数指数幂的运算性质： a m *a n =a m+n(a m )n=a mn(a*b)n =a n b n2、根式的概念：一般地，若a x n =，那么x 叫做a 的n 次方根，其中n >1，且n ∈N *．当n 是奇数时，正数的n 次方根是一个正数，负数的n 次方根是一个负数。

此时，a 的n 次方根用符号表示。

当n 为偶数时，正数的n 次方根有两个，这两个数互为相反数。

此时正数a 的正的n 次方根用符号表示，负的n 的次方根用符号表示。

正的n 次方根与负的n 次方根可以合并成（a>0）。

注意：负数没有偶次方根；0的任何次方根都是0，记作00=n。

当n 是奇数时，a a n n =，当n 是偶数时，⎩⎨⎧<≥-==)0()0(||a a a a a a nn 式子n a 叫做根式，这里n 叫做根指数，a 叫做被开方数。

3、分数指数幂正数的分数指数幂的)1,,,0(*>∈>=n N n m a a an m nm ，)1,,,0(11*>∈>==-n N n m a a aanmnm nm0的正分数指数幂等于0，0的负分数指数幂没有意义4、有理数指数米的运算性质（1）r a ·s r ra a+=),,0(R s r a ∈>；（2）rss r a a =)( ),,0(R s r a ∈>；（3）s r r a a ab =)(),,0(R s r a ∈>．5、无理数指数幂一般的，无理数指数幂a a（a>0,a 是无理数）是一个确定的实数。

有理数指数幂的运算性质同样使用于无理数指数幂。

（二）、指数函数的性质及其特点1、指数函数的概念：一般地，函数)1,0(≠>=a a a y x 且叫做指数函数，其中x 是自变量，函数的定义域为R ．注意：指数函数的底数的取值范围，底数不能是负数、零和1．为什么？（1）在[a ，b]上，值域是)]b (f ),a (f [或)]a (f ),b (f [；（2）若0x ≠，则1)x (f ≠；)x (f 取遍所有正数当且仅当R x ∈；（3）对于指数函数)1a 0a (a )x (f x ≠>=且，总有a )1(f =；（4）当a>1时，若X 1<X 2 ,则有f(X 1)<f(X 2)。

基本初等函数经典复习题+答案

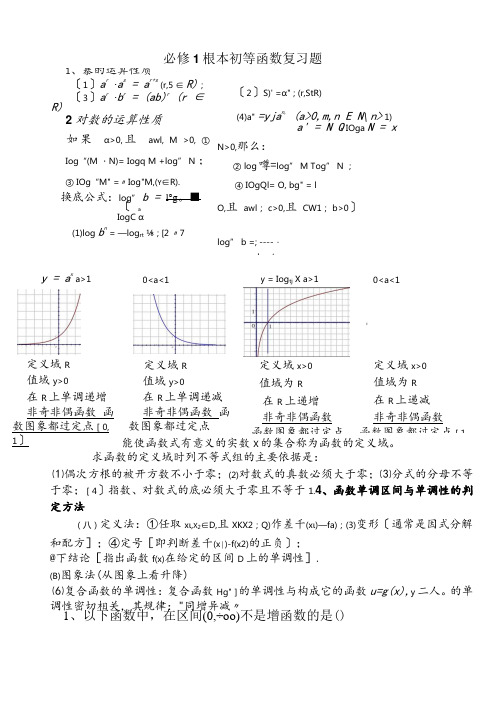
必修1根本初等函数复习题求函数的定义域时列不等式组的主要依据是：⑴偶次方根的被开方数不小于零；(2)对数式的真数必须大于零；⑶分式的分母不等于零；［4〕指数、对数式的底必须大于零且不等于1.4、函数单调区间与单调性的判定方法（八）定义法：①任取xι,X 2∈D,且XKX2；Q)作差千(xι)—fa)；(3)变形〔通常是因式分解和配方］；④定号［即判断差千(x∣)-f(x2)的正负〕；@下结论［指出函数f(x)在给定的区间D 上的单调性］.(B)图象法(从图象上看升降)⑹复合函数的单调性：复合函数Hg"］的单调性与构成它的函数u=g(x),y 二人。

的单调性密切相关，其规律："同增异减〃 1、以下函数中，在区间(0,÷oo)不是增函数的是()1、暴的运算性质〔1〕a r ∙a s = a r+s (r,5 ∈ R)；〔3〕a r ∙b r = (ab)r (r ∈ R) 2对数的运算性质如果 α>0,且 awl, M >0, ① Iog“(M ・N)= Iogq M +log” N ； ③ IOg“M" =〃Iog"M,(Y ∈R). 换底公式：log” b = l°g 。

■ 〔 a IogC α(1)log b n= —log rt ⅛ ; [2 〃7 〔2〕S)' =α" ; (r,StR)(4)a" =yja n, (a>0,m,n E N ∖n> 1) a' = N Q IOga N = x N>0,那么：② log 噂=log” M Tog” N ；④ IOgQl= O, bg" = lO,且 awl ； c>0,且 CW1； b>0〕 log” b =; ---- ∙log/y = a x a>1 0<a<1 y = Iog tj X a>1 II0<a<1定义域R 值域y>0 在R 上单调递增非奇非偶函数函数图象都过定点［0, 1〕 3、定义域：定义域R 值域y>0 在R 上单调递减非奇非偶函数函数图象都过定点〔〕定义域x>0 值域为R在R 上递增非奇非偶函数函数图象都过定点定义域x>0值域为R 在R 上递减非奇非偶函数函数图象都过定点［1, 能使函数式有意义的实数X 的集合称为函数的定义域。

2020年高考理科数学：《基本初等函数》题型归纳与训练

2020年高考理科数学《解三角形》题型归纳与训练【题型归纳】题型一正弦定理、余弦定理的直接应用例1ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，已知2sin()8sin2BA C +=． (1)求cos B(2)若6a c +=，ABC ∆面积为2，求b ．【答案】（1）15cos 17B =（2）2b =．【解析】由题设及A B C π++=得2sin 8sin2BB =，故sin 4(1cos )B B =-．上式两边平方，整理得217cos 32cos 150B B -+=，解得cos 1B =（舍去），15cos 17B =.（2）由15cos 17B =得8sin 17B =，故14sin 217ABC S ac B ac ∆==．又2ABC S ∆=，则172ac =．由余弦定理及6a c +=得22222cos ()2(1cos )b a c ac B a c ac B =+-=+-+1715362(1)4217=-⨯⨯+=．所以2b =．【易错点】二倍角公式的应用不熟练，正余弦定理不确定何时运用【思维点拨】利用正弦定理列出等式直接求出例2 ABC △的内角,,A B C 的对边分别为,,a b c ,若2cos cos cos b B a C c A =+,则B =. 【答案】π3【解析】1π2sin cos sin cos sin cos sin()sin cos 23B B AC C A A C B B B =+=+=⇒=⇒=.【易错点】不会把边角互换，尤其三角恒等变化时，注意符号。

【思维点拨】边角互换时，一般遵循求角时，把边换成角；求边时，把角转换成边。

例3在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，若b ＝1，c ＝3，C ＝23π，则S △ABC ＝________.【答案】34【解析】因为c ＞b ，所以B ＜C ，所以由正弦定理得b sin B ＝c sin C ，即1sin B ＝3sin 2π3＝2，即sin B ＝12，所以B＝π6，所以A ＝π－π6－2π3＝π6.所以S △ABC ＝12bc sin A ＝12×3×12＝34. 【易错点】大边对大角，应注意角的取值范围【思维点拨】求面积选取公式时注意，一般选取已知角的公式，然后再求取边长。

高一数学基本初等函数(对、指、幂函数)高考考纲及典型例题高考真题解析

x x 2 2x 2 x 4 1 4 a a 2 1
.
2
a 3 3a
【法二】 8 x 8 x 2 x
2
3 2
x 3
2 2 2 x 2 x 2 x 2 x 2 x 2 x
1

2 3
3
37 48
5 9 37 100 3 100 . 3 16 48
4
（4）原式 0.4 1 1 2 2 3 0.1

5 1 1 1 143 . 1 2 16 8 10 80
4.函数 f x a 2 7a 7 a x 是指数函数,求实数 a 的值. 【解析】∵函数 f x a 2 7a 7 a x 是指数函数,
1
0 a2 a1 1 a4 a3 . 1 又由题知： 0 10 1 3 10 ,∴ A 项正确. 3
1 x
a1 a2
O
x 1 x
b 7.已知二次函数 y ax 2 bx 与指数函数 y 的图象只能是下列图形中的 a y
1 1
1 2
1 1 , y x 2 的图像,了解它们的变化情况. x
二、重点知识总结
1.指数与指数幂运算（1）①
a
n n n
n
a. a , 当n是奇数时 . a , 当n是偶数时
② a
（2）分数指数幂 ①a ②a
m n
n a m （ a 0 , m, n N * ,且 n 1 ）
x y
2
是非负数，故④对.
7 （3） 2 9

高考一轮复习基本初等函数知识点+例题+练习

1．指数幂的概念(1)根式如果一个数的n次方等于a(n>1且n∈N*)，那么这个数叫做a的n次实数方根．也就是，若x n＝a，则x叫做______________，其中n>1且n∈N*.式子na叫做________，这里n叫做____________，a叫做____________．(2)根式的性质①当n为奇数时，正数的n次实数方根是一个正数，负数的n次实数方根是一个负数，这时，a的n次实数方根用符号________表示．②当n为偶数时，正数的n次实数方根有两个，它们互为相反数，这时，正数a的正的n次实数方根用符号______表示，负的n次实数方根用符号________表示．正负两个n次实数方根可以合写成________(a>0)．③(na)n＝____.④当n为偶数时，na n＝|a|＝⎩⎪⎨⎪⎧a，a≥0，－a，a<0.⑤当n为奇数时，na n＝____.⑥负数没有偶次方根．⑦零的任何次方根都是零．2．有理指数幂(1)分数指数幂的表示①正数的正分数指数幂是mna＝________(a>0，m，n∈N*，n>1)．②正数的负分数指数幂是mna-＝____________＝____________(a>0，m，n∈N*，n>1)．③0的正分数指数幂是____，0的负分数指数幂无意义．(2)有理指数幂的运算性质①a s a t＝________(a>0，s，t∈Q)．②(a s)t＝_______(a>0，s，t∈Q)．③(ab)t＝_______(a>0，b>0，t∈Q)．3．指数函数的图象与性质a >10<a<1图象定义域值域性质(1)过定点________(2)当x>0时，______；当x<0时，________(2)当x>0时，________；当x<0时，______(3)在(－∞，＋∞)上是______(3)在(－∞，＋∞)上是______自我检测1．下列结论中正确的有________(填序号)．①当a<0时，322()a＝a3；②na n＝|a|；③函数y＝12(2)x －(3x－7)0的定义域是(2，＋∞)；④若100a＝5,10b＝2，则2a＋b＝1.2．函数y＝(a2－3a＋3)a x是指数函数，则a＝________.3．如图所示的曲线C1，C2，C3，C4分别是函数y＝a x，y＝b x，y＝c x，y＝d x的图象，则a，b，c，d的大小关系为____________．4．若a>1，b>0，且a b＋a－b＝22，则a b－a－b的值为________．5．函数f(x)＝a x－b的图象如图，其中a、b为常数，则下列结论正确的是________(填序号)．①a>1，b<0；②a>1，b>0；③0<a<1，b>0；④0<a<1，b<0.探究点一有理指数幂的化简与求值例1 已知a ，b 是方程9x 2－82x ＋9＝0的两根，且a <b ，求：(1)a －1＋b －1(ab )－1； 733338152a a a a --.变式迁移1 3322114443()a b ab ba b a(a 、b >0)的结果为____________．探究点二指数函数的图象及其应用例2 已知函数y ＝(13)|x +1|.(1)作出函数的图象(简图)； (2)由图象指出其单调区间；(3)由图象指出当x 取什么值时有最值，并求出最值．变式迁移2 若曲线|y |＝2x ＋1与直线y ＝b 没有公共点，则b 的取值范围为________．探究点三指数函数的性质及应用例3 如果函数y ＝a 2x ＋2a x －1(a >0且a ≠1)在区间[－1,1]上的最大值是14，求a 的值．变式迁移3 已知函数f (x )＝(12x －1＋12)x 3.(1)求f (x )的定义域； (2)证明：f (－x )＝f (x )； (3)证明：f (x )>0.分类讨论思想例已知f (x )＝a a 2－1(a x －a －x )(a >0且a ≠1)．(1)判断f (x )的奇偶性； (2)讨论f (x )的单调性；(3)当x ∈[－1,1]时f (x )≥b 恒成立，求b 的取值范围．一、填空题1．已知a ＝133()4-，b ＝143()4-，c ＝343()2-，则a 、b 、c 的大小关系为______________．2．函数y ＝|2x －1|在区间(k －1，k ＋1)内不单调，则k 的取值范围为________．3．已知集合M ＝{－1,1}，N ＝{x ∈Z |12<2x ＋1<4}，则M ∩N ＝________.4．定义运算a b ＝⎩⎪⎨⎪⎧a (a ≤b )，b (a >b )，则函数f (x )＝12x 的值域为________．5．若关于x 的方程|a x －1|＝2a (a >0，a ≠1)有两个不等实根，则a 的取值范围为________．6．函数f (x )＝⎩⎪⎨⎪⎧－x ＋3a ，x <0，a x ， x ≥0(a >0且a ≠1)是R 上的减函数，则a 的取值范围为________．7．设函数f (x )＝x (e x ＋a e －x )，x ∈R 是偶函数，则实数a ＝________. 8．若函数f (x )＝a x －1(a >0且a ≠1)的定义域和值域都是[0,2]，则实数a 的值为________．二、解答题9．已知定义域为R 的函数f (x )＝－2x ＋b2x ＋1＋a是奇函数．(1)求a ，b 的值；(2)若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )<0恒成立，求k 的取值范围．10．已知函数f (x )＝3x ，f (a ＋2)＝18，g (x )＝λ·3ax －4x 的定义域为[0,1]． (1)求a 的值．(2)若函数g (x )在区间[0,1]上是单调递减函数，求实数λ的取值范围．11．函数y ＝1＋2x ＋4x a 在x ∈(－∞，1]上y >0恒成立，求a 的取值范围．。

高考理科数学：《基本初等函数》题型归纳与训练(有答案)

2020年高考理科数学：基本初等函数题型归纳与训练【题型归纳】题型一指数运算与对数运算例1 已知函数2log ,0,()31,0,x x x f x x ->⎧=⎨+≤⎩则f (f (1))＋f 31log 2⎛⎫ ⎪⎝⎭的值是( ) A.5B.3C.－1D.72 【答案】A【解析】由题意可知f (1)＝log 21＝0，f (f (1))＝f (0)＝30＋1＝2，31log 0,2<∴f 31log 2⎛⎫ ⎪⎝⎭＝31log 23-+1＝2＋1＝3，所以f (f (1))＋f ⎝⎛⎭⎫log 312＝5. 【易错点】确定31log 2的范围再代入. 【思维点拨】本题较简单，分段函数计算题代入时要先确定范围，再代入函数.例2 定义在R 上的函数f (x )满足f (x )＝2log 1,0,6,0,x x f x x -≤⎧⎨->⎩（）（）则f (2 019)＝( ) A ．－1 B ．0 C ．1 D ．2【答案】D【解析】∵2 019＝6×337－3，∴f (2 019)＝f (－3)＝log 2(1＋3)＝2.故选D.【易错点】转化过程【思维点拨】x >6时可以将函数看作周期函数，得到f (2 019)＝f (3)，然后再带入3，得出f (3)＝f (－3). 题型二指对幂函数的图象与简单性质例1 函数f (x )＝a x－b 的图象如图所示，其中a ，b 为常数，则下列结论正确的是( ) A.a >1，b <0B.a >1，b >0C.0<a <1，b >0D.0<a <1，b <0 【答案】D【解析】由f (x )＝a x－b 的图象可以观察出，函数f (x )＝a x －b 在定义域上单调递减，所以0<a <1. 函数f (x )＝a x －b 的图象是在f (x )＝a x 的基础上向左平移得到的，所以b <0.【易错点】注意b 的符号【思维点拨】(1)已知函数解析式判断其图象一般是取特殊点，判断选项中的图象是否过这些点，若不满足则排除；(2)对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换而得到．特别地，当底数a 与1的大小关系不确定时应注意分类讨论．2 例2 已知定义在R 上的函数f (x )＝2|x－m |－1(m 为实数)为偶函数，记a ＝f (log 0.53)，b ＝f (log 25)，c ＝f (2m )，则a ，b ，c 的大小关系为( )A.a ＜b ＜cB.c ＜a ＜bC.a ＜c ＜bD.c ＜b ＜a 【答案】B【解析】由函数f (x )＝2|x －m |－1为偶函数，得m ＝0，所以f (x )＝2|x |－1，当x ＞0时，f (x )为增函数，log 0.53＝－log 23，∴log 25＞|－log 23|＞0，∴b ＝f (log 25)＞a ＝f (log 0.53)＞c ＝f (2m )＝f (0)，故选B.【易错点】①对称性的条件转化；②利用单调性或图象转化到同一单调区间比较大小.【思维点拨】函数()f x m -的图象关于x m =对称；指对幂函数比较大小时像本题中a,b 一样可以换成同底数的数，可以化为一样的底数利用单调性比较大小.题型三二次函数的图象与性质例1 已知函数f (x )＝x 2＋mx －1，若对于任意x ∈[m ，m ＋1]，都有f (x )<0成立，则实数m 的取值范围是________．【答案】（－22，0）【解析】由于f (x )＝x 2＋mx －1＝mx ＋(x 2－1)，可视f (x )为关于m 的一次函数，故根据题意有 2222()10,(1)(1)(1)10,f m m m f m m m m ⎧=++<⎪⎨+=++++<⎪⎩解得－22<m <0. 【思维点拨】恒成立问题转化为最值问题.例2 已知f (x )＝ax 2－2x (0≤x ≤1)，求f (x )的最小值．【答案】a<1时,f (x )min =a -2；a ≥1时，f (x )min =－1a. 【解析】①当a ＝0时，f (x )＝－2x 在[0，1]上单调递减，∴f (x )min ＝f (1)＝－2.②当a >0时，f (x )＝ax 2－2x 的图象的开口方向向上，且对称轴为直线x ＝1a. 当1a≤1，即a ≥1时，f (x )＝ax 2－2x 的图象的对称轴在[0，1]内， ∴f (x )在⎣⎡⎦⎤0，1a 上单调递减，在⎣⎡⎦⎤1a ，1上单调递增． ∴f (x )min ＝1()f a ＝1a －2a ＝－1a . 当1a>1，即0<a <1时，f (x )＝ax 2－2x 的图象的对称轴在[0，1]的右侧， ∴f (x )在[0，1]上单调递减．。

基本初等函数在高考真题中题型分类总结

基本初等函数在真题的题型归纳总结一、方程、不等式1.（2019浙江16）已知a ∈R ，函数3()f x ax x =-，若存在t ∈R ，使得2|(2)()|3f t f t +-≤，则实数a 的最大值是____. 2．（2011天津）已知22log log 1a b +≥，则39a b +的最小值为__________．3．（2012新课标）当102x <≤时，4log x a x <，则a 的取值范围是A ．(0,)2 B ．(2C ．D ．2) 4．（2015江苏）不等式224xx-<的解集为_______．5．（2017北京）根据有关资料，围棋状态空间复杂度的上限M 约为3613，而可观测宇宙中普通物质的原子总数N 约为8010．则下列各数中与M N最接近的是（参考数据：lg 3≈0．48）A ．3310B ．5310C ．7310D ．93106．（2013陕西）设a , b , c 均为不等于1的正实数, 则下列等式中恒成立的是A ．·log log log a c c b a b = B ．·log lo log g a a a b a b = C ．()log og g l lo a a a b c bc = D ．()log g og o l l a a a b b c c +=+ 7．（2013浙江）已知y x ,为正实数，则A ．y x y x lg lg lg lg 222+=+B ．lg()lg lg 222x y x y +=C ．y x y x lg lg lg lg 222+=∙D ．lg()lg lg 222xy x y = 8．（2012安徽）23(log 9)(log 4)⋅=A ． 14B ．12C ． 2D ． 49．（2010浙江）已知函数2()log (1),f x x =+若()1,f α= α=A ．0B ．1C ．2D ．310．（2010辽宁）设25a b m ==，且112a b+=，则m =AB ．10C ．20D ．10011．(2018上海)已知常数0a >，函数2()(2)x x f x ax =+的图像经过点6()5P p ，、1()5Q q -，，若236p q pq +=，则a =__________．12．(2016年浙江) 已知1a b >>，若5l o g l o g 2a b b a +=，b a a b =，则a = ，b = ． 13．（2015浙江）若4log 3a =，则22a a -+=_______． 14．（2013四川）的值是____________．15．（2012北京）已知函数()lg f x x =，若()1f ab =，则22()()f a f b += ．16．（2015新课标Ⅱ）设函数211log (2),1()2,1x x x f x x -+-<⎧=⎨⎩≥，则2(2)(log 12)f f -+= A ．3 B ．6 C ．9 D ．1217．（2015山东）函数31,1()2,1x x x f x x -<⎧=⎨⎩≥，满足()(())2f a f f a =的a 取值范围是A ．2[,1]3B ．[0,1]C ．2[,)3+∞D ．[1,)+∞18．（2011辽宁）函数122,1()1log ,1x x f x x x -⎧=⎨->⎩≤，则满足()2f x ≤的x 的取值范围A ．1[-，2]B ．[0，2]C ．[1，+∞）D ．[0，+∞）19．(2014新课标)函数()113,1,,1,x e x f x x x -⎧<⎪=⎨⎪≥⎩则使得()2f x ≤成立的x 范围是__．20．（2010新课标）已知函数212log ,0()log (),0x x f x x x >⎧⎪=⎨-<⎪⎩，若a ，b ，c 均不相等，且()f a = ()f b =()f c ，则abc 的取值范围是A ．（1，10）B ．(5，6)C ．(10，12)D ．(20，24)21．（2010天津）若函数212log ,0()log (),0x x f x x x >⎧⎪=⎨-<⎪⎩,若()()f a f a >-,则实数a 的取值范围是A ．(1,0)(0,1)-B ．(,1)(1,)-∞-+∞C ．(1,0)(1,)-+∞D ．(,1)(0,1)-∞-二、比较大小1.（2019全国Ⅰ理3）已知0.20.32log 0.220.2a b c ===，，，则 A ．a b c << B ．a c b << C ．c a b << D ．b c a <<2.（2019天津理6）已知5log 2a =，0.5og 2.l 0b =，0.20.5c =，则,,a b c 大小关系 A.a c b << B.a b c << C.b c a << D.c a b << 3．(2018全国卷Ⅲ)设0.2log 0.3a =，2log 0.3b =，则A ．0a b ab +<<B ．0ab a b <+<C ．0a b ab +<<D ．0ab a b <<+4．(2018天津)已知2log e =a ，ln 2b =，121log 3c =，则a ，b ，c 的大小关系为A ．a b c >>B ．b a c >>C ．c b a >>D ．c a b >>5．（2017新课标Ⅰ）设,,x y z 为正数，且235x y z ==错误！未找到引用源。

高中数学基本初等函数知识点总结及习题解析！

高中数学基本初等函数知识点总结及习题解析！一、基本初等函数1、幂函数一般地，函数 y = x^a (a 为常数，a∈Q) 叫做幂函数 .幂函数y = x^a (a∈Q) 的性质：① 所有幂函数在（0，+∞）上都有定义，并且图象都经过点（1,1）.② 若 a > 0 , 幂函数图象都经过点（0 , 0）和（1 ，1）在第一象限内递增；若 a < 0 , 幂函数图象只经过点（1,1），在第一象限内递减 .③ 幂函数的图象最多只能同时出现在两个象限，且不经过第四象限；如果幂函数图象与坐标轴相交，则交点一定是坐标原点 .④ 画幂函数图象时，先画第一象限的部分，在根据函数的奇偶性完成整个图象 .⑤ 常见幂函数的图象常见幂函数的图象2、指数函数一般地，函数 y = a^x ( a > 0 且a ≠ 1 ) 叫做指数函数，自变量x 叫指数，a 叫底数 .指数函数的定义域是 R .指数运算法则：指数运算法则指数函数 y = a^x ( a > 0 且a ≠ 1 ) 的图象：指数函数图象（分两种情况）指数函数的主要性质：① 指数函数 y = a^x ( a > 0 且a ≠ 1 ) 定义域为 R ，值域（0，+∞）；② 函数 y = a^x ( a > 1 ) 在 R 上递增，函数 y = a^x ( 0 < x <1 ) 在 R 上递减；③ 指数函数的图象经过点（0 , 1）.3、反函数一般地，对于函数 y = f(x)，设它的定义域为 D，值域为 A，如果对于 A 中任意一个值 y，在 D 中总有唯一确定的 x 值与它对应，且满足 y = f(x) ,这样得到的 x 关于 y 的函数叫做 y = f(x) 的反函数，记作 x = f-1(y) ,习惯上自变量常用x 来表示，而函数用 y 来表示，所以把它改写为 y = f-1(x) (x∈A) .(1) 反函数的判定：① 反函数存在的条件是原函数为一一对应函数；② 定义域上的单调函数必有反函数；③ 周期函数不存在反函数；④ 定义域为非单元素的偶函数不存在反函数 .(2) 反函数的性质：① 函数 y = f(x) 与函数 y = f-1(x) 互为反函数；原函数 y = f(x) 和反函数 y = f-1(x) 的图象关于直线 y = x 对称；② 若点（a , b）在原函数 y = f(x) 上，则点（b , a）必在其反函数 y = f-1(x) 上；③ 原函数 y = f(x) 的定义域是它反函数 y = f-1(x) 的值域；原函数 y = f(x) 的值域是它反函数 y = f-1(x) 的定义域，④ 原函数与反函数具有对应相同的单调性；⑤ 奇函数的反函数还是奇函数 .(3) 求反函数的步骤：① 用 y 表示 x ，即先求出 x = f-1(y) ；② x , y 互换，即写出 y = f-1(x)；③ 确定反函数的定义域 .注：若函数 f(ax + b) 存在反函数，则其反函数为 y = 1/a [ f-1(x) - b ] , 而不是 y = f-1(ax + b) ,函数 y = f-1(ax + b) 是 y = 1/a [ f(x) - b ] 的反函数 .4、对数函数一般地，对数函数对数函数就是指数函数指数函数的反函数 .对数函数的性质：① 对数函数y = logax 的图象都在y 轴的右侧，定义域（0，+∞），值域 R ；② 对数函数 y = logax 的图象都经过点（1 , 0）；③ 对数函数 y = logax （a > 1）:当 x > 1 时，y > 0 ; 当 0 < x < 1 时，y < 0 ;对数函数 y = logax （0 < a < 1）:当 x > 1 时，y < 0 ; 当 0 < x < 1 时，y > 0 .④ 对数函数 y = logax （a > 1）在（0，+∞）上是增函数，对数函数 y = logax （0 < a < 1）在（0，+∞）上是减函数 .二、习题检测【习题1】用定义证明：函数 f(x) = x + 1/x 在x∈[1 , +∞) 上是增函数 .【解析】【习题2】已知函数 f(x) = -x^2 + 2ax + 1 - a 在区间 [0 , 1] 有最大值 2，求实数 a 的值 .【解析】解：函数 f(x) = -x^2 + 2ax + 1 - a 的对称轴为 x = a ,① 当 a < 0 时，[0 , 1] 是函数 f(x) 的递减区间，f(x) max = f(0) = 1 -a = 2 , 解得a = -1 ;② 当 a > 1 时，[0 , 1] 是函数 f(x) 的递增区间，f(x) max = f(1) = a = 2 , 解得 a = 2 ;③ 当0 ≤ a ≤ 1 时，综上所述，a = -1 或 2 .【习题3】已知2^x ≤ 256 , log2x ≥ 1/2 , 求函数的最大值和最小值 .【解析】【习题4】已知 a > 0 且a ≠ 1 , 求使方程有解时的 k 的取值范围 .【解析】∴ 0 < k < 1 或 k < -1 .【习题5】某商品进货单价为 40 元，若销售价为 50 元，可卖出50 个，如果销售单价每涨 1 元，销售量就减少 1 个，为了获得最大利润，则此商品的最佳售价应为多少元 .【解析】解：设最佳售价为（50 + x ) 元，最大利润为 y 元，y = (50 + x)(50 - x) - (50 -x)×40= -x^2 + 40x + 500当 x = 20 时，y 取得最大值，∴ 应定价为 70 元 .。

函数概念与基本初等函数题型归纳与习题含详解

f (1) 1 ，即 a＋b＋c≥1.
(2)因为 f x ax2 bx c(a 0) 的图像上任意一点都不在直线 y＝x 的下方，取相同 x，二次函数值总大于一次函数值，所以 f x x ，即 ax2 bx c x ，得 ax2 (b 1)x c 0 ，
对任意 x∈R 成立.
解析 f x 1 ＝ x 1 2 2 ,又 x 1 2 或 x 1 ―2,故 f x x2 2
x x
x
x
(x>2 或 x<―2) 评注求函数解析式要注意定义域
变式 1
已知
f x 1 x
x2 1 x2
1 x
求
f x 的解析式
三、方程组法
例 2.7 已知函数 f x 满足： f x 2 f 1 3x x 0 ,求函数 f x 的解析式.
(2) y x 2 的定义域为{ x x 0 }; y x2 的定义域为 R，故该组的两个函数不是同一函
数；
(3)两个函数的定义域均为｛ x x ≠0｝，且对应法则也相同,故该组的两个函数是同一函数
故为同一函数的一组是（3）
评注由函数概念的三要素容易看出，函数的表示法只与定义域和对应法则有关，而与用什
(1) p : x 1, 2, x2 a 0 ；
(2) A N , B Z , f : x y (1)x ；
（3）A＝{x|是平面内的三角形}，B＝｛y|y 是平面内的圆｝，f:x→y 是 x 的外接圆；（4）设集合 A＝｛x|是平面内的圆｝，B＝｛y|y 是平面内的矩形｝，f:x→y 是 x 的内接矩形其中能构成映射的是_______ 变式 2 已知函数 y＝f(x),定义域为 A＝｛1,2,3,4｝值域为 C＝｛5,6,7},则满足该条件的函数共有多少个？

必修一基本初等函数练习题(含详细答案解析)

必修一基本初等函数练习题（含详细答案解析）一、选择题1．对数式log32－(2＋3)的值是()．A．－1 B．0 C．1 D．不存在1．A解析：log32－(2＋3)＝log32－(2－3)－1，故选A．2．当a＞1时，在同一坐标系中，函数y＝a－x与y＝log a x的图象是()．A B C D2．A解析：当a＞1时，y＝log a x单调递增，y＝a－x单调递减，故选A．3．如果0＜a＜1，那么下列不等式中正确的是()．A．(1－a)31＞(1－a)21B．log1－a(1＋a)＞0C．(1－a)3＞(1＋a)2D．(1－a)1+a＞13．A解析：取特殊值a＝21，可立否选项B，C，D，所以正确选项是A．4．函数y＝log a x，y＝log b x，y＝log c x，y＝log d x的图象如图所示，则a，b，c，d的大小顺序是()．A．1＜d＜c＜a＜bB．c＜d＜1＜a＜bC．c＜d＜1＜b＜aD．d＜c＜1＜a＜b4．B解析：画出直线y＝1与四个函数图象的交点，它们的横坐标的值，分别为a，b，c，d的值，由图形可得正确结果为B．(第4题)5．已知f (x 6)＝log 2 x ，那么f (8)等于( )． A ．34 B ．8 C ．18 D ．21 5．D6．如果函数f (x )＝x 2－(a －1)x ＋5在区间⎪⎭⎫⎝⎛121 ，上是减函数，那么实数a 的取值范围是( )．A ． a ≤2B ．a ＞3C ．2≤a ≤3D ．a ≥36．D7．函数f (x )＝2－x －1的定义域、值域是( )． A ．定义域是R ，值域是RB ．定义域是R ，值域为(0，＋∞)C ．定义域是R ，值域是(－1，＋∞)D ．定义域是(0，＋∞)，值域为R7．C＋∞)．8．已知－1＜a ＜0，则( )．A ．(0.2)a ＜a⎪⎭⎫⎝⎛21＜2aB ．2a ＜a⎪⎭⎫⎝⎛21＜(0.2)aC ．2a ＜(0.2)a ＜a⎪⎭⎫⎝⎛21D ．a⎪⎭⎫⎝⎛21＜(0.2)a ＜2a8．B9．已知函数f (x )＝⎩⎨⎧+-1 log 1≤413＞，，)(x x x a x a a是(－∞，＋∞)上的减函数，那么a 的取值范围是( )．A ．(0，1)B ．⎪⎭⎫ ⎝⎛310，C ．⎪⎭⎫⎢⎣⎡3171，D ．⎪⎭⎫⎢⎣⎡171，9．C解析：由f (x )在R 上是减函数，∴ f (x )在(1，＋∞)上单减，由对数函数单调性，即0上是减函数，为了满足单调区间的定义，f (x )在(－∞，1］上的最小值7a －1要大于等于f (x )在［1，＋∞)上的最大值0，才能保证f (x )在R 上是减函数．10．已知y ＝log a (2－ax )在［0，1］上是x 的减函数，则a 的取值范围是( )． A ．(0，1) B ．(1，2) C ．(0，2) D ．［2，＋∞)10．B解析：先求函数的定义域，由2－ax ＞0，有ax ＜2，因为a 是对数的底，故有a ＞0且若0＜a ＜1，当x 在［0，1］上增大时，2－ax 减小，从而log a (2－ax )增大，即函数 y ＝log a (2－ax )在［0，1］上是单调递增的，这与题意不符.若1＜a ＜2，当x 在［0，1］上增大时，2－ax 减小，从而log a (2－ax )减小，即函数 y ＝log a (2－ax )在［0，1］上是单调递减的．所以a 的取值范围应是(1，2)，故选择B ．二、填空题11．满足2－x ＞2x 的 x 的取值范围是．11．参考答案：(－∞，0)．解析：∵ －x ＞x ，∴ x ＜0．12．已知函数f (x )＝log 0.5(－x 2＋4x ＋5)，则f (3)与f (4)的大小关系为． 12．参考答案：f (3)＜f (4)．解析：∵ f (3)＝log 0.5 8，f (4)＝log 0.5 5，∴ f (3)＜f (4)． 13．64log 2log 273的值为_____．14．已知函数f (x )＝⎪⎩⎪⎨⎧，≤ ，，＞，020log 3x x x x 则⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛91f f 的值为_____．15．函数y ＝)－(34log 5.0x 的定义域为．16．已知函数f (x )＝a －121+x，若f (x )为奇函数，则a ＝________．解析：∵ f (x )为奇函数，三、解答题17．设函数f (x )＝x 2＋(lg a ＋2)x ＋lg b ，满足f (－1)＝－2，且任取x ∈R ，都有f (x )≥2x ，求实数a ，b 的值．17．参考答案：a ＝100，b ＝10．解析：由f (－1)＝－2，得1－lg a ＋lg b ＝0 ①，由f (x )≥2x ，得x 2＋x lg a ＋lg b ≥0 (x ∈R )．∴Δ＝(lg a )2－4lg b ≤0 ②．联立①②，得(1－lg b )2≤0，∴ lg b ＝1，即b ＝10，代入①，即得a ＝100．18．已知函数f (x )＝lg (ax 2＋2x ＋1) ．(1)若函数f (x )的定义域为R ，求实数a 的取值范围； (2)若函数f (x )的值域为R ，求实数a 的取值范围．18．参考答案：(1) a 的取值范围是(1，＋∞) ，(2) a 的取值范围是[0，1]．解析：(1)欲使函数f (x )的定义域为R ，只须ax 2＋2x ＋1＞0对x ∈R 恒成立，所以有⎩⎨⎧0 ＜440a －a ＞，解得a ＞1，即得a 的取值范围是(1，＋∞)； (2)欲使函数 f (x )的值域为R ，即要ax 2＋2x ＋1 能够取到(0，＋∞) 的所有值．②当a ≠0时，应有⎩⎨⎧0 ≥440a －a ＝＞Δ⇒ 0＜a ≤1．当x ∈(－∞，x 1)∪(x 2，＋∞)时满足要求(其中x 1，x 2是方程ax 2＋2x ＋1＝0的二根)．综上，a 的取值范围是[0，1]．19．求下列函数的定义域、值域、单调区间： (1)y ＝4x ＋2x +1＋1； (2)y ＝2＋3231x －x ⎪⎭⎫⎝⎛．19．参考答案：(1)定义域为R ．令t ＝2x (t ＞0)，y ＝t 2＋2t ＋1＝(t ＋1)2＞1， ∴ 值域为{y | y ＞1}．t ＝2x 的底数2＞1，故t ＝2x 在x ∈R 上单调递增；而 y ＝t 2＋2t ＋1在t ∈(0，＋∞)上单调递增，故函数y ＝4x ＋2x ＋1＋1在(－∞，＋∞)上单调递增．20．已知函数f(x)＝log a(x＋1)，g(x)＝log a(1－x)，其中a＞0，a≠1．(1)求函数f(x)－g(x)的定义域；(2)判断f(x)－g(x)的奇偶性，并说明理由；(3)求使f(x)－g(x)＞0成立的x的集合．20．参考答案：(1){x |－1＜x＜1}；(2)奇函数；(3)当0＜a＜1时，－1＜x＜0；当a＞1时，0＜x＜1．(2)设F(x)＝f(x)－g(x)，其定义域为(－1，1)，且F(－x)＝f(－x)－g(－x)＝log a(－x＋1)－log a(1＋x)＝－［log a(1＋x)－log a(1－x)］＝－F(x)，所以f(x)－g(x)是奇函数．(3)f(x)－g(x)＞0即log a(x＋1)－log a(1－x)＞0有log a(x＋1)＞log a(1－x)．。

基本初等函数、函数与方程及函数的应用(题型归纳)

基本初等函数、函数与方程及函数的应用【考情分析】1.考查特点:基本初等函数作为高考的命题热点,多考查指数式与对数式的运算、利用函数的性质比较大小,难度中等;函数的应用问题多体现在函数零点与方程根的综合问题上,题目有时较难,而与实际应用问题结合考查的指数、对数函数模型也是近几年考查的热点,难度中等.2.关键能力:逻辑思维能力、运算求解能力、数学建模能力、创新能力.3.学科素养:数学抽象、逻辑推理、数学建模、数学运算.【题型一】基本初等函数的图象与性质【典例分析】【例1】（2021•焦作一模）若函数||(0,1)x y a a a =>≠的值域为{|1}y y ，则函数log ||a y x =的图象大致是()A ．B ．C ．D ．【答案】B【解析】若函数||(0,1)x y a a a =>≠的值域为{|1}y y ，则1a >，故函数log ||a y x =的图象大致是：故选：B ．【例2】（2021·陕西西安市·西安中学高三模拟）若1(,1)x e -∈，ln a x =，ln 1()2xb =，ln 2xc =，则a ，b ，c 的大小关系为（）A ．c b a >>B ．b a c >>C ．a b c >>D ．b c a>>【答案】D【解析】因1(,1)x e -∈，且函数ln y x =是增函数，于是10a -<<；函数2x y =是增函数，1ln 0ln 1x x -<<<-<，而ln ln 1()22xx -=，则ln 11()22x <<，ln 1212x<<，即1122c b <<<<，综上得：b c a >>故选：D【例3】（2021·湖南长沙长郡中学高三模拟）若函数()()4log 1,13,1x x x f x m x ⎧->=⎨--≤⎩存在2个零点，则实数m 的取值范围为（）A ．[)3,0-B ．[)1,0-C ．[)0,1D ．[)3,-+∞【答案】A【解析】因函数f (x )在(1，+∞)上单调递增，且f (2)=0，即f (x )在(1，+∞)上有一个零点，函数()()4log 1,13,1x x x f x m x ⎧->=⎨--≤⎩存在2个零点，当且仅当f (x )在(-∞，1]有一个零点，x≤1时，()03x f x m =⇔=-，即函数3x y =-在(-∞，1]上的图象与直线y =m 有一个公共点，在同一坐标系内作出直线y =m 和函数3(1)x y x =-≤的图象，如图：而3x y =-在(-∞，1]上单调递减，且有330x -≤-<，则直线y =m 和函数3(1)x y x =-≤的图象有一个公共点，30m -≤<.故选：A【提分秘籍】1.指数函数、对数函数的图象和性质受底数a 的影响,解决与指数、对数函数特别是与单调性有关的问题时,首先要看底数a 的范围.2.研究对数函数的性质,应注意真数与底数的限制条件.如求f(x)=ln(x 2-3x+2)的单调区间,易只考虑t=x 2-3x+2与函数y=ln t 的单调性,而忽视t>0的限制条件.3.指数、对数、幂函数值的大小比较问题的解题策略:(1)底数相同,指数不同的幂用指数函数的单调性进行比较.(2)底数相同,真数不同的对数值用对数函数的单调性进行比较.(3)底数不同、指数也不同,或底数不同、真数也不同的两个数,常引入中间量或结合图象比较大小.【变式演练】1．【多选】（2021·山东省实验中学高三模拟）已知函数()2121x x f x -=+，则下列说法正确的是（）A ．()f x 为奇函数B ．()f x 为减函数C ．()f x 有且只有一个零点D ．()f x 的值域为[)1,1-【答案】AC【解析】()2121x x f x -=+ ,x ∈R ,2121x=-+2112()()2112x xx xf x f x ----∴-===-++,故()f x 为奇函数，又()21212121x x xf x -==-++ ，()f x ∴在R 上单调递增，20x> ，211x ∴+>，20221x∴<<+，22021x∴-<-<+，1()1f x ∴-<<，即函数值域为()1,1-令()21021x x f x -==+，即21x =，解得0x =，故函数有且只有一个零点0.综上可知，AC 正确，BD 错误.故选：AC2．（2021·山东潍坊市·高二一模（理））设函数()322xxf x x -=-+，则使得不等式()()2130f x f -+<成立的实数x 的取值范围是【答案】(),1-∞-【解析】函数的定义域为R ，()()322xx f x x f x --=--=-，所以函数是奇函数，并由解析式可知函数是增函数原不等式可化为()()213f x f -<-，∴213x -<-，解得1x <-，∴x 的取值范围是(),1-∞-．【题型二】函数与方程【典例分析】【例4】（2021·宁夏中卫市·高三其他模拟）函数3()9x f x e x =+-的零点所在的区间为（）A ．()0,1B ．()1,2C ．()2,3D ．()3,4【答案】B【解析】由x e 为增函数，3x 为增函数，故3()9x f x e x =+-为增函数，由(1)80f e =-<，2(2)10f e =->，根据零点存在性定理可得0(1,2)x ∃∈使得0()0f x =，故选：B.【例5】（2021·北京高三一模）已知函数22,,()ln ,x x x t f x x x t⎧+=⎨>⎩(0)t >有2个零点，且过点(,1)e ，则常数t 的一个取值为______．【答案】2（不唯一）．【解析】由220x x +=可得0x =或2x =-由ln 0x =可得1x =因为函数22,,()ln ,x x x t f x x x t⎧+=⎨>⎩(0)t >有2个零点，且过点(,1)e ，所以1e t >≥，故答案为：2（不唯一）【提分秘籍】1.判断函数零点个数的方法直接法直接求零点,令f(x)=0,则方程解的个数即为函数零点的个数定理法利用零点存在性定理,利用该定理只能确定函数的某些零点是否存在,必须结合函数的图象和性质(如单调性)才能确定函数有多少个零点数形结合法对于给定的函数不能直接求解或画出图象的,常分解转化为两个能画出图象的函数的交点问题2.利用函数零点的情况求参数值或取值范围的方法(1)利用零点存在性定理构建不等式求解.(2)分离参数后转化为求函数的值域(最值)问题求解.(3)转化为两个熟悉的函数图象的位置关系问题,从而构建不等式求解.【变式演练】1．（2021·湖北十堰市高三模拟）函数()()()23log 111f x x x x =+->-的零点所在的大致区间是（）A ．()1,2B ．()2,3C ．()3,4D ．()4,5【答案】B【解析】易知()f x 在()1,+∞上是连续增函数，因为()22log 330f =-<，()33202f =->，所以()f x 的零点所在的大致区间是()2,3.故选：B2．（2021·天津高三二模）设函数2,1()4()(2),1x a x f x x a x a x ⎧-<=⎨--≥⎩，若1a =，则()f x 的最小值为______；若()f x 恰有2个零点，则实数a 的取值范围是__________．【答案】1-112a ≤<或2a ≥【解析】当1a =时，()()211()4(1)(2)1x x f x x x x ⎧-<⎪=⎨--≥⎪⎩，1x <，()211xf x =-<，1≥x ，()()()234124112f x x x x ⎛⎫=--=--≥- ⎪⎝⎭所以()f x 的最小值为1-.设()f x 的零点为1x 、2x ，若()1,1x ∈-∞，[)21x ∈+∞,，则20012a a a a->⎧⎪>⎨⎪<≤⎩，得112a ≤<若[)12,1,x x ∈+∞，则0201a a a >⎧⎪-≤⎨⎪≥⎩，得2a ≥，综上:112a ≤<或2a ≥.故答案为:1-；112a ≤<或2a ≥.【题型三】函数的实际应用【典例分析】1．（2021·北京高三二模）20世纪30年代，里克特制定了一种表明地震能量大小的尺度，就是使用地震仪衡量地震能量的等级，地震能量越大，测震仪记录的地震曲线的振幅就越大，这就是我们常说的里氏震级M ，其计算公式为0lg lg M A A =-，其中A 是被测地震的最大振幅,0A 是标准地震的振幅，2008年5月12日，我国四川汶川发生了地震，速报震级为里氏7.8级，修订后的震级为里氏8.0级，则修订后的震级与速报震级的最大振幅之比为（）A ．0.210-B ．0.210C ．40lg39D ．4039【答案】B【解析】由0lg lg M A A =-，可得01AM gA =，即10M A A =，010M A A =⋅，当8M =时，地震的最大振幅为81010A A =⋅，当7.8M =时，地震的最大振幅为7.82010A A =⋅，所以，修订后的震级与速报震级的最大振幅之比是887.80.2017.82010101010A A A A -⋅===⋅.故选：B.2．为加强环境保护，治理空气污染，某环保部门对辖区内一工厂产生的废气进行了监测，发现该厂产生的废气经过过滤后排放，过滤过程中废气的污染物数量(mg /L)P 与时间(h)t 的关系为0ktP P e -=.如果在前5个小时消除了10%的污染物，那么污染物减少19%需要花的时间为（）A ．7小时B ．10小时C ．15小时D ．18小时【答案】B【解析】因为前5个小时消除了10%的污染物，所以()50010.1kP P P e -=-=，解得ln 0.95k =-，所以ln 0.950tP P e =，设污染物减少19%所用的时间为t ，则()0010.190.81P P -=()()ln 0.92ln 0.955500000.90.9t t t P P e P eP ====，所以25t=，解得10t =，故选：B 3.（2021·山东滕州一中高三模拟）为了预防某种病毒，某商场需要通过喷洒药物对内部空间进行全面消毒，出于对顾客身体健康的考虑，相关部门规定空气中这种药物的浓度不超过0.25毫克/立方米时，顾客方可进入商场．已知从喷洒药物开始，商场内部的药物浓度y （毫克/立方米）与时间t （分钟）之间的函数关系为100.1,0101,102ta t t y t -≤≤⎧⎪=⎨⎛⎫>⎪ ⎪⎝⎭⎩（a 为常数），函数图象如图所示．如果商场规定10：00顾客可以进入商场，那么开始喷洒药物的时间最迟是A ．9:40B ．9:30C ．9:20D ．9:10【答案】9:30【解析】根据函数的图象，可得函数的图象过点(10,1)，代入函数的解析式，可得1121a-⎛⎫⎪⎝⎭=，解得1a =，所以1100.1,0101,102t t t y t -≤≤⎧⎪=⎨⎛⎫>⎪ ⎪⎝⎭⎩，令0.25y ≤，可得0.10.25t ≤或11020.251t -⎛⎝≤⎫⎪⎭，解得0 2.5t <≤或30t ≥，所以如果商场规定10：00顾客可以进入商场，那么开始喷洒药物的时间最迟是9:30.故选：B.【提分秘籍】1.构建函数模型解决实际问题的失分点：(1)不能选择相应变量得到函数模型；(2)构建的函数模型有误；(3)忽视函数模型中变量的实际意义.2.解决新概念信息题的关键：(1)依据新概念进行分析；(2)有意识地运用转化思想，将新问题转化为我们所熟知的问题.【变式演练】（2020·湖北黄冈市·黄冈中学高三模拟）“百日冲刺”是各个学校针对高三学生进行的高考前的激情教育，它能在短时间内最大限度激发一个人的潜能，使成绩在原来的基础上有不同程度的提高，以便在高考中取得令人满意的成绩，特别对于成绩在中等偏下的学生来讲，其增加分数的空间尤其大．现有某班主任老师根据历年成绩在中等偏下的学生经历“百日冲刺”之后的成绩变化，构造了一个经过时间()30100t t ≤≤（单位：天），增加总分数()f t （单位：分）的函数模型：()()1lg 1kPf t t =++，k 为增分转化系数，P 为“百日冲刺”前的最后一次模考总分，且()1606f P =．现有某学生在高考前100天的最后一次模考总分为400分，依据此模型估计此学生在高考中可能取得的总分约为（）（lg 61 1.79≈）A ．440分B ．460分C ．480分D ．500分【答案】B【解析】由题意得：()1601lg 61 2.796kP kP f P ===+， 2.790.4656k ∴≈=；∴()0.465400186186100621lg1011lg100lg1.013f ⨯==≈=+++，∴该学生在高考中可能取得的总分约为40062462460+=≈分.故选：B.1.（2021·江苏金陵中学高三模拟）函数()2ln 1xf x x =+-的零点所在的区间为（）．A ．31,2⎛⎫⎪⎝⎭B ．3,22⎛⎫⎪⎝⎭C ．10,2⎛⎫ ⎪⎝⎭D ．1,12⎛⎫ ⎪⎝⎭【答案】D【解析】函数()2ln 1xf x x =+-为()0,∞+上的增函数，由()110f =>，1311112ln 21ln 21ln 2ln 0222222f e ⎛⎫=-<--=-<-=⎪⎝⎭，可得函数()f x 的零点所在的区间为1,12⎛⎫⎪⎝⎭．故选：D.2.（2021·山东潍坊一中高三模拟）若函数()1af x x x =+-在(0,2)上有两个不同的零点，则a 的取值范围是（）A ．1[2,]4-B ．1(2,)4-C ．1[0,]4D ．1(0,)4【答案】D【解析】函数()1a f x x x=+-在(0,2)上有两个不同的零点等价于方程10ax x +-=在(0,2)上有两个不同的解，即2a x x =-+在(0,2)上有两个不同的解.此问题等价于y a =与2(02)y x x x =-+<<有两个不同的交点.由下图可得104a <<.故选：D.3．（2021·长沙市·湖南师大附中高三三模）已知函数()()()ln 2ln 4f x x x =-+-，则（）．A ．()f x 的图象关于直线3x =对称B ．()f x 的图象关于点()3,0对称C ．()f x 在()2,4上单调递增D ．()f x 在()2,4上单调递减【答案】A【解析】()f x 的定义域为()2,4x ∈，A ：因为()()()()3ln 1ln 13f x x x f x +=++-=-，所以函数()f x 的图象关于3x =对称，因此本选项正确；B ：由A 知()()33f x f x +≠--，所以()f x 的图象不关于点()3,0对称，因此本选项不正确；C ：()()()2ln 2ln 4ln(68)x x x f x x =-+-=-+-函数2268(3)1y x x x =-+-=--+在()2,3x ∈时，单调递增，在()3,4x ∈时，单调递减，因此函数()f x 在()2,3x ∈时单调递增，在()3,4x ∈时单调递减，故本选项不正确；D ：由C 的分析可知本选项不正确，故选：A4．（2021·辽宁本溪高级中学高三模拟高三模拟）设函数2ln(1)ln(1)()1x x f x x +--=-，则函数的图象可能是（）A ．B ．C ．D ．【答案】D【解析】2ln(1)ln(1)()1x x f x x +--=-，定义域为()1,1-，且()()f x f x -=-，故函数为奇函数，图象关于原点对称，故排除A,B,C ，故选：D.5．（2021·新安县第一高级中学高三模拟）被誉为信息论之父的香农提出了一个著名的公式：2log 1S C W N ⎛⎫=+ ⎪⎝⎭，其中C 为最大数据传输速率，单位为bit /s ：W 为信道带宽，单位为Hz ：SN为信噪比.香农公式在5G 技术中发挥着举足轻重的作用.当99SN=，2000Hz W =时，最大数据传输速率记为1C ；在信道带宽不变的情况下，若要使最大数据传输速率翻一番，则信噪比变为原来的多少倍（）A ．2B ．99C ．101D ．9999【答案】C【解析】当99S N =，2000Hz W =时，()1222log 12000log 1994000log 10S C W N ⎛⎫=+=+= ⎪⎝⎭，由228000log 102000log 1S N ⎛⎫=+⎪⎝⎭，得224log 10log 1S N ⎛⎫=+ ⎪⎝⎭，所以9999S N =，所以999910199=，即信噪比变为原来的101倍.故选：C .6．（2021·浙江温州市·瑞安中学高三模拟）已知函数()f x 是定义在R 上的奇函数，满足()()2f x f x +=-，且当[]0,1x ∈时，()()2log 1f x x =+，则函数()3y f x x =-的零点个数是（）A ．2B ．3C ．4D ．5【答案】B【解析】由()()2f x f x +=-可得()f x 关于1x =对称，由函数()f x 是定义在R 上的奇函数，所以()()[]2()(2)(2)f x f x f x f x f x +=-=-=---=-，所以()f x 的周期为4，把函数()3y f x x =-的零点问题即()30y f x x =-=的解，即函数()y f x =和3y x =的图像交点问题，根据()f x 的性质可得如图所得图形，结合3y x =的图像，由图像可得共有3个交点，故共有3个零点，故选：B.7．（2021·珠海市第二中学高三模拟）设21()log (1)f x x a=++是奇函数，若函数()g x 图象与函数()f x 图象关于直线y x =对称，则()g x 的值域为（）A ．11(,)(,)22-∞-+∞ B ．11(,22-C ．(,2)(2,)-∞-+∞D ．(2,2)-【答案】A【解析】因为21()log (1)f x x a=++，所以1110x a x a x a+++=>++可得1x a <--或x a >-，所以()f x 的定义域为{|1x x a <--或}x a >-，因为()f x 是奇函数，定义域关于原点对称，所以1a a --=，解得12a =-，所以()f x 的定义域为11(,)(,)22-∞-+∞ ，因为函数()g x 图象与函数()f x 图象关于直线y x =对称，所以()g x 与()f x 互为反函数，故()g x 的值域即为()f x 的定义域11(,)(,)22-∞-+∞ .故选：A .8．（2021·浙江杭州高级中学高三模拟）已知函数22log ,0,()44,0.x x f x x x x ⎧>=⎨--+<⎩若函数()()g x f x m =-有四个不同的零点1234,,,x x x x ，则1234x x x x 的取值范围是（）A ．(0,4)B ．(4,8)C ．(0,8)D ．(0,)+∞【答案】A【解析】函数()g x 有四个不同的零点等价于函数()f x 的图象与直线y m =有四个不同的交点.画出()f x 的大致图象，如图所示.由图可知(4,8)m ∈.不妨设1234x x x x <<<，则12420x x -<<-<<，且124x x +=-.所以214x x =--，所以()()212111424(0,4)x x x x x =--=-++∈，则3401x x <<<，因为2324log log x x =，所以2324log log x x -=，所以12324log log x x -=，所以341x x ⋅=，所以123412(0,4)x x x x x x ⋅⋅⋅=∈⋅.故选：A9．（2021·天津南开中学高三模拟）若函数()1x f x e =-与()g x ax =的图象恰有一个公共点，则实数a 可能取值为()A ．2B ．1C ．0D ．1-【答案】BCD【解析】函数()1x f x e =-的导数为()x f x e '=；所以过原点的切线的斜率为1k =；则过原点的切线的方程为：y x =；所以当1a 时，函数()1x f x e =-与()g x ax =的图象恰有一个公共点；故选BCD10．（2021·广东佛山市·高三模拟）函数()()()ln 1ln 1xxf x e e =+--，下列说法正确的是（）A ．()f x 的定义域为(0,)+∞B ．()f x 在定义域内单调递増C ．不等式(1)(2)f m f m ->的解集为(1,)-+∞D ．函数()f x 的图象关于直线y x =对称【答案】AD【解析】要使函数有意义，则10(0,)10x xe x e ⎧+>⇒∈+∞⎨->⎩，故A 正确；()()12()ln 1ln 1ln ln(111x xxx x e f x e e e e +=+--==+--，令211xy e =+-，易知其在(0,)+∞上单调递减，所以()f x 在(0,)+∞上单调递减，故B 不正确；由于()f x 在(0,)+∞上单调递减，所以对于(1)(2)f m f m ->，有1020(1,)12m m m m m ->⎧⎪>⇒∈+∞⎨⎪-<⎩，故C 不正确；令()ln(211x y f x e +=-=，解得11ln()11y xy y y e e e x e e ++=⇒=--，所以()f x 关于直线y x =对称，故D 正确.故选：AD11．（2021·福建厦门市高三模拟）某医药研究机构开发了一种新药，据监测，如果患者每次按规定的剂量注射该药物，注射后每毫升血液中的含药量y （微克）与时间t （小时）之间的关系近似满足如图所示的曲线．据进一步测定，当每毫升血液中含药量不少于0.125微克时，治疗该病有效，则（）A ．3a =B ．注射一次治疗该病的有效时间长度为6小时C ．注射该药物18小时后每毫升血液中的含药量为0.4微克D ．注射一次治疗该病的有效时间长度为31532时【答案】AD【解析】由函数图象可知()4(01)112t at t y t -<⎧⎪=⎨⎛⎫≥ ⎪⎪⎝⎭⎩，当1t =时，4y =，即11()42a-=，解得3a =，∴()34(01)112t t t y t -<⎧⎪=⎨⎛⎫≥ ⎪⎪⎝⎭⎩，故A 正确，药物刚好起效的时间，当40.125t =，即132t =，药物刚好失效的时间31()0.1252t -=，解得6t =，故药物有效时长为131653232-=小时，药物的有效时间不到6个小时，故B 错误，D 正确；注射该药物18小时后每毫升血液含药量为140.58⨯=微克，故C 错误，故选：AD ．12．（2021·辽宁省实验中学高三模拟）（多选题）已知函数()f x ，()g x 的图象分别如图1，2所示，方程(())1f g x =，(())1g f x =-，1(())2g g x =-的实根个数分别为a ，b ，c ，则（）A ．a b c +=B ．b c a+=C ．b a c=D ．2b c a+=【答案】AD【解析】由图，方程(())1f g x =，1()0g x -<<，此时对应4个解，故4a =；方程(())1g f x =-，得()1f x =-或者()1f x =，此时有2个解，故2b =；方程1(())2g g x =-，()g x 取到4个值，如图所示：即2()1g x -<<-或1()0g x -<<或0()1g x <<或1()2g x <<，则对应的x 的解，有6个，故6c =.根据选项，可得A ，D 成立.故选AD ．13．（2021·山东淄博实验中学高三模拟）如果函数y =a 2x +2a x -1(a >0，且a ≠1)在区间[-1，1]上的最大值是14，则a 的值为________.【答案】3或13【解析】令a x =t ，则y =a 2x +2a x -1=t 2+2t -1=(t +1)2-2.当a >1时，因为x ∈[-1，1]，所以t ∈1,a a ⎡⎤⎢⎥⎣⎦，又函数y =(t +1)2-2在1,a a ⎡⎤⎢⎥⎣⎦上单调递增，所以y max =(a +1)2-2=14，解得a =3(负值舍去).当0<a <1时，因为x ∈[-1，1]，所以t ∈1a a ⎡⎤⎢⎥⎣⎦，，又函数y =(t +1)2-2在1a a ⎡⎤⎢⎥⎣⎦，上单调递增，则y max =211a ⎛⎫+ ⎪⎝⎭-2=14，解得a =13(负值舍去).综上，a =3或a =13.14．（2021·北京高三一模）已知函数22,1,()log ,1,x x f x x x ⎧<=⎨-⎩则(0)f =________；()f x 的值域为_______．【答案】1(),2-∞【解析】0(0)2=1=f ；当1x <时，()()20,2=∈xf x ，当1x ≤时，()2log 0=-≤f x x ，所以()f x 的值域为(),2-∞故答案为：1；(),2-∞．15．（2021·重庆南开中学高三模拟）已知定义域为[4,4]-的函数()f x 的部分图像如图所示，且()()0f x f x --=，函数(lg )1f a ≤，则实数a 的取值范围为______．【答案】1,1010⎡⎤⎢⎥⎣⎦【解析】由题意知()()f x f x -=，且函数()f x 的定义域为[4,4]-，所以()f x 是偶函数．由图知()11f =，且函数()f x 在[0,4]上为增函数，则不等式(lg )1f a ≤等价于(|lg |)(1)f a f ≤，即|lg |1a ≤，所以1lg 1a -≤≤，解得11010a ≤≤．故实数a 的取值范围为1,1010⎡⎤⎢⎥⎣⎦．故答案为：1,1010⎡⎤⎢⎥⎣⎦16.（2021·湖南长沙市·长沙一中高三其他模拟）设函数()222,034,0x x x f x x x ⎧-+≥=⎨+<⎩，若互不相等的实数1x ，2x ，3x 满足()()()123f x f x f x ==，则123x x x ++的取值范围是__________．【答案】41,3⎛⎤ ⎥⎝⎦【解析】作出函数()f x 图像如下互不相等的实数1x ，2x ，3x 满足()()()123f x f x f x ==不妨设123x x x <<，则23,x x 关于1x =对称，所以232x x +=根据图像可得1213x -<≤-所以123413x x x <++≤，所以123x x x ++的取值范围为41,3⎛⎤ ⎥⎝⎦。

高考数学中的基本初等函数题型总结

高考数学中的基本初等函数题型总结作为全国高中生的普及性质考试，高考中必定会考到数学这个科目，而其中初等函数部分则是数学中的基础知识。

初等函数常常出现在多项式函数、指数函数、对数函数、三角函数、反三角函数等高中知识点当中。

因此，对于考生来说，掌握初等函数的知识点，对高考数学考试及日后的数学学习都非常重要。

本文就高考数学中的基本初等函数题型进行总结。

1. 最值问题求函数的最值是很常见的一种初等函数题型。

以一些典型的例子为参考，可更好地掌握这类题型。

例1：已知$f(x)=x^2-2x+2$，求$f(x)$的最小值。

解：首先，把$f(x)$变形为完全平方的形式。

即$$f(x)=(x-1)^2+1$$显然，当$x=1$时，$(x-1)^2$取最小值$0$。

故$f(x)$在$x=1$时取得最小值$1$。

例2：已知$f(x)=\dfrac{1}{2}x^2-3x+5$，求$f(x)$的最大值。

解：同样把$f(x)$变形为完全平方的形式。

即$$f(x)=\dfrac{1}{2}(x-3)^2+\dfrac{1}{2}$$显然，当$x=3$时，$(x-3)^2$取最小值$0$。

故$f(x)$在$x=3$时取得最大值$\dfrac{1}{2}$。

2. 解方程解初等函数的方程是另一种常见的题型。

以下为几个典型的例子，例3：已知$y=2^x-x$，求$y=0$时的$x$的值。

解：根据方程可得$$2^x-x=0$$$$x=2^x$$把函数$y=2^x-x$作图，可以看出在$x=1$时交于$y=0$。

因此，方程的解为$x=1$。

例4：已知$y=\dfrac{1}{2}\log_2(x-1)+2$，求$y=1$时$x$的值。

解：根据方程可得$$\dfrac{1}{2}\log_2(x-1)+2=1$$$$\log_2(x-1)=2$$$$x-1=2^2=4$$因此，方程的解为$x=5$。

3. 函数图像解题函数图像是初等函数题目中重要的一部分。

基本初等函数的题型归纳

基本初等函数的题型归纳题型一：指对数的运算1.若210,5100==b a ，则b a +2=…………………………………………2．指数函数y=a x 的图像经过点（2，16）则a 的值是3．若329log =x ，则x 等于 4.5log 2139-的值是 5. 若y x y x lg lg )2lg(2+=-，则x 、y 的关系是题型二：指对数的图像1.图中曲线分别表示l g a y o x =，l g b y o x =，l g c y o x =，l g d y o x =的图象，,,,a b c d 的关系是2.已知3.0log a 2=，3.02b =，2.03.0c =，则c b a ,,三者的大小关系是题型三：求值1.已知（1）,32121=+-a a求221,--++a a a a 的值 7 ，47 2.(2)若32121=+-xx ，求23222323-+-+--x x x x 的值. 18题型四求范围 1．指数函数(2)x y a =-在定义域内是减函数，则a 的取值范围是2．当a ＞0且a ≠1时，函数f (x )=a x －2－3必过定点 .3．函数)x 2x (log y 221-=的单调递减区间是_________________．4．在(2)log (5)a b a -=-中，实数a 的取值范围是。

题型五反函数1.设函数()[]()242,4f x x x =-∈，则()1f x -的定义域为（）2、函数y =1－1-x (x ≥1)的反函数是（） A ．y =(x －1)2＋1，x ∈R B ．y =(x －1)2－1，x ∈RC ．y =(x －1)2＋1，x ≤1D ．y =(x －1)2－1，x ≤1 3．若f (x －1)= x 2－2x ＋3 (x ≤1)，则f －1(4)等于（）A ．2B ．1－2C ．－2D ．2－函数与方程零点题型一：零点的个数确定1、方程062=-+x x的实数解的个数有_______个. 2.已知定义在R 上的函数f(x)的图像是连续不断的，且有如下部分对应值表： x1 2 3 4 5 6 f(x) 136.135 15.552 －3.92 10.88 －52.488 －232.064可以看出函数至少有个零点.题型二：零点存在性定理的应用1. 函数2ln f x x x的零点所在的大致区间是（）A.1,2B.2,3C. 3,4D.,e 2.关于x 的方程27+=x x 的解所在的区间是（）A.0（，1）B.(1, 2)C.(2, 3)D.(3, 4)题型三：求参数的范围1.若一元二次方程2350x x a -+=的一根大于2-且小于0，另一根大于1而小于3，则实数a 取值范围（）A ．()12,0-B ．15,14⎛⎫-∞ ⎪⎝⎭C ．15,14⎛⎫+∞ ⎪⎝⎭D ．1,22⎛⎫ ⎪⎝⎭2.若关于x 的方程35+=a x 有根，则实数a 的取值范围是．3. 若关于x 的方程210x ax -+=在1(,3)2x ∈上有实数根，则实数a 的取值范围是 4.已知函数2()(1)43f x a x ax =++-.当0a >时，若方程()0f x =有一根大于1，一根小于1，则a 的取值范围是。

完整版)基本初等函数经典复习题+答案

完整版)基本初等函数经典复习题+答案1、幂的运算性质1) $a^r\cdot a^s=a^{r+s}$，其中$r,s\in R$；2) $(a^r)^s=a^{rs}$，其中$r,s\in R$；3) $a^r\cdot b^r=(ab)^r$，其中$r\in R$；4) $a^{-n}=\dfrac{1}{a^n}$，其中$a>0,n\in N^*,n>1$。

2、对数的运算性质若$a>0$且$a\neq 1$，$M>0,N>0$，则有：1) $a^x=N\iff \log_a N=x$；2) $\log_a(MN)=\log_a M+\log_a N$；3) $\log_a\dfrac{M}{N}=\log_a M-\log_a N$；4) $\log_a M^n=n\log_a M$，其中$n\in R$；5) $\log_a 1=0$；6) 换底公式：$\log_a b=\dfrac{\log_c b}{\log_c a}$，其中$a>0,a\neq 1,c>0,c\neq 1,b>0$。

3、函数的定义域能使函数式有意义的实数$x$的集合称为函数的定义域。

求函数的定义域时，需要注意以下几点：1) 偶次方根的被开方数不小于零；2) 对数式的真数必须大于零；3) 分式的分母不等于零；4) 指数、对数式的底必须大于零且不等于1.4、函数单调区间与单调性的判定方法A) 定义法：1.任取$x_1,x_2\in D$，且$x_1<x_2$；2.作差$f(x_1)-f(x_2)$；3.变形（通常是因式分解和配方）；4.定号（即判断差$f(x_1)-f(x_2)$的正负）；5.下结论（指出函数$f(x)$在给定的区间$D$上的单调性）。

B) 图象法（从图象上看升降）。

C) 复合函数的单调性：复合函数$f[g(x)]$的单调性与构成它的函数$u=g(x),y=f(u)$的单调性密切相关，其规律为“同增异减”。

高考数学函数的概念与基本初等函数多选题知识点及练习题及解析

高考数学函数的概念与基本初等函数多选题知识点及练习题及解析一、函数的概念与基本初等函数多选题1．已知函数()sin sin x xf x e e =+，以下结论正确的是（）A ．()f x 是偶函数B ．()f x 最小值为2C ．()f x 在区间,2ππ⎛⎫-- ⎪⎝⎭上单调递减 D ．()()2g x f x x π=-的零点个数为5【答案】ABD 【分析】去掉绝对值，由函数的奇偶性及周期性，对函数分段研究，利用导数再得到函数的单调性，再对选项进行判断. 【详解】∵x ∈R ，()()f x f x -=，∴()f x 是偶函数，A 正确；因为()()2f x f x π+=，由函数的奇偶性与周期性，只须研究()f x 在[]0,2π上图像变化情况.()sin sin sin 2,01,2x x x e x f x e x e πππ⎧≤≤⎪=⎨+<≤⎪⎩，当0x π≤≤，()sin 2cos xf x xe '=，则()f x 在0,2x π⎡⎤∈⎢⎥⎣⎦上单调递增，在,2ππ⎡⎤⎢⎥⎣⎦上单调递减，此时()[]2,2f x e ∈；当2x ππ≤≤时，()()sin sin cos x xf x x e e -'=-，则()f x 在3,2x ππ⎡⎤∈⎢⎥⎣⎦上单调递增，在3,22x ππ⎡⎤∈⎢⎥⎣⎦上单调递减，此时()12,f x e e ⎡⎤∈+⎢⎥⎣⎦，故当02x π≤≤时，()min 2f x =，B 正确. 因()f x 在,2x ππ⎛⎫∈ ⎪⎝⎭上单调递减，又()f x 是偶函数，故()f x 在,2ππ⎛⎫-- ⎪⎝⎭上单调递增，故C 错误. 对于D ，转化为()2f x x π=根的个数问题.因()f x 在0,2π⎛⎫ ⎪⎝⎭上单调递增，在,2ππ⎛⎫⎪⎝⎭上单调递减，在3,2ππ⎛⎫ ⎪⎝⎭上单调递增，在3,22ππ⎛⎫⎪⎝⎭上单调递减.当(),x π∈-∞时，()2f x ≥，22x π<，()2f x x π=无实根.()3,x π∈+∞时，()max 262x e f x π>>=，()2f x xπ=无实根，3,2x ππ⎡⎤∈⎢⎥⎣⎦，显然x π=为方程之根.()sin sin xx f x ee -=+，()()sin sin cos 0x x f x x e e -'=->，3123322fe e πππ⎛⎫=+>⨯=⎪⎝⎭，单独就这段图象，()302f f ππ⎛⎫'='=⎪⎝⎭，()f x 在3,2ππ⎡⎤⎢⎥⎣⎦上变化趋势为先快扣慢，故()g x 在3,2ππ⎛⎫⎪⎝⎭内有1个零点，由图像知()g x 在3,32ππ⎛⎫⎪⎝⎭内有3个零点，又5252f e π⎛⎫=> ⎪⎝⎭，结合图象，知D 正确.故选：ABD. 【点睛】方法点睛：研究函数性质往往从以下方面入手：（1）分析单调性、奇偶性、周期性以及对称性；（2）数形结合法：先对解析式变形，进而构造两个容易画出图象的函数，将两个函数的图象画在同一个平面直角坐标系中，利用数形结合的方法求解.2．已知函数22(2)log (1),1()2,1x x x f x x +⎧+>-⎪=⎨≤-⎪⎩，若关于x 的方程()f x m =有四个不等实根1x ，2x ，3x ，()41234x x x x x <<<，则下列结论正确的是（）A ．12m <≤B ．11sin cos 0x x ->C ．3441x x +>-D ．2212log 2mx x ++10【答案】ACD 【分析】画出()f x 的图象，结合图象求得1234,,,,m x x x x 的取值范围，利用特殊值确定B 选项错误，利用基本不等式确定CD 选项正确. 【详解】画出()f x 的图象如下图所示，由于关于x 的方程()f x m =有四个不等实根1x ，2x ，3x ，()41234x x x x x <<<，由图可知12m <≤，故A 选项正确. 由图可知12,x x 关于直线2x =-对称，故12122,42x x x x +=-+=-，由()()22221x x +=≤-解得3x =-或1x =-，所以1232,21x x -≤<--<≤-，3324π-<-<-，当134x π=-时，1212sin cos ,sin cos 02x x x x ==--=，所以B 选项错误. 令()()2221x m x +=≤-，()22log 2log 1x m m m +==，()22log 21m x +=，()222log 1m x +=，12,x x 是此方程的解，所以()211log 22m x =+，或()221log 22m x =+，故()()22221211211log 422m x x x x x ++=+--++()()2121122881022x x =+++≥=+，当且仅当()()211211522,222x x x +==-+时等号成立，故D 选项正确. 由图象可知()()2324log 1log 1x x +=-+，()()2324log 1log 10x x +++=，()()34111x x +⋅+=，4433111,111x x x x +==-++，由()()2log 111x x +=>-，解得1x =或12x =-，由()()2log 121x x +=>-，解得3x =或34x =-，所以3431,1342x x -≤<-<≤， ()3433331144145111x x x x x x +=+-+=-+++ 51≥=-①. 令()()21134,1,1421x x x x +===-++或12x =-，所以①的等号不成立，即3441x x +>-，故C 选项正确. 故选：ACD【点睛】求解有关方程的根、函数的零点问题，可考虑结合图象来求解.求解不等式、最值有关的问题，可考虑利用基本不等式来求解.3．已知()f x 是定义域为(,)-∞+∞的奇函数，(1)f x +是偶函数，且当(]0,1x ∈时，()(2)f x x x =--，则（）A ．()f x 是周期为2的函数B ．()()201920201f f +=-C ．()f x 的值域为[]1,1-D ．()y f x =在[]0,2π上有4个零点【答案】BCD 【分析】对于A ，由()f x 为R 上的奇函数，()1f x +为偶函数，得(4)()f x f x +=，则()f x 是周期为4的周期函数，可判断A.对于B ，由()f x 是周期为4的周期函数，则()()202000f f ==，()()()2019111f f f =-=-=-，可判断B ．对于C ，当(]01x ∈，时，()()2f x x x =--，有()01f x ≤＜，又由()f x 为R 上的奇函数，则[)10x ∈-，时，()10f x -≤＜，可判断C ．对于D ，根据函数的周期性和对称性，可以求出函数在各段上的解析式，从而求出函数的零点，可判断D ．【详解】解：对于A ，()1f x +为偶函数，其图像关于x 轴对称，把()1f x +的图像向右平移1个单位得到()f x 的图像，所以()f x 图象关于1x =对称，即(1)(1)f x f x +=-，所以(2)()f x f x +=-，()f x 为R 上的奇函数，所以()()f x f x -=-，所以(2)()f x f x +=-，用2x +替换上式中的x 得， (4)(2)f x f x +=-+，所以，(4)()f x f x +=，则()f x 是周期为4的周期函数.故A 错误. 对于B ，()f x 定义域为R 的奇函数，则()00f =，()f x 是周期为4的周期函数，则()()202000f f ==；当(]0,1x ∈时，()()2f x x x =--，则()()11121f =-⨯-=，则()()()()201912020111f f f f =-+=-=-=-，则()()201920201f f +=-.故B 正确.对于C ，当(]01x ∈，时，()()2f x x x =--，此时有()01f x <≤，又由()f x 为R 上的奇函数，则[)1,0x ∈-时，()10f x -≤<，(0)0f =，函数关于1x =对称，所以函数()f x 的值域[]1,1-.故C 正确.对于D ，(0)0f =，且(]0,1x ∈时，()()2f x x x =--，[0,1]x ∴∈，()(2)f x x x =--，[1,2]x ∴∈，2[0,1]x -∈，()(2)(2)f x f x x x =-=--①[0,2]x ∴∈时，()(2)f x x x =--，此时函数的零点为0，2；()f x 是奇函数，[2,0],()(2)x f x x x ∴∈-=+，②(]2,4x ∴∈时，()f x 的周期为4，[]42,0x ∴-∈-，()()()()424f x f x x x =-=--，此时函数零点为4；③(]4,6x ∴∈时，[]40,2x ∴-∈，()()4(4)(6)f x f x x x =-=---，此时函数零点为6；④(]6,2x π∴∈时，(]42,4x ∴-∈，()()()()468f x f x x x =-=--，此时函数无零点；综合以上有，在(0,2)π上有4个零点.故D 正确；故选：BCD 【点睛】关键点点睛：由(1)f x +是偶函数，通过平移得到()f x 关于1x =对称，再根据()f x 是奇函数，由此得到函数的周期，进一步把待求问题转化到函数的已知区间上，本题综合考查抽象函数的奇偶性、周期性.4．已知函数1(),f x x x =+221()g x x x=+则下列结论中正确的是（） A ．()()f x g x +是奇函数 B ．()()f x g x ⋅是偶函数 C ．()()f x g x +的最小值为4 D ．()()f x g x ⋅的最小值为2【答案】BC 【分析】利用奇偶性的定义可得A 错B 对；利用均值不等式可得C 对；利用换元求导可得D 错. 【详解】2211()()f x g x x x x x+=+++ ()22221111()()()f x g x x x x x x x x x ∴-+-=-++-+=+++-- ()()()()f x g x f x g x ∴+=-+- ()()f x g x ∴+是偶函数， A 错；221(1)()x x xf x xg x ⎛⎫+⋅+ ⎪⎝⋅=⎭()()22221111()()f x x x x xg x x x x x ⎛⎫⎛⎫-+⋅-+=+⋅+ ⎪ ⎪ ⎪-⎝⎭-⎝∴-⋅-=⎭()()()()f x g x f x g x ∴-⋅-=⋅ ()()f x g x ∴⋅是偶函数，B 对；2211()()224f x g x x x x x +=+++≥+=，当且仅当1x x =和221=x x 时，等号成立，即当且仅当21x =时等号成立，C 对；221(1)()x x xf x xg x ⎛⎫+⋅+ ⎪⎝⋅=⎭令1t x x=+()2t ≥，则()23()()22f t t g t t x x ⋅-=-⋅= []232()()f x g x t '∴=-⋅，令2320t ->，得3t >或3t <- 2t ∴≥时，()()f x g x ⋅单调递增∴当2t =有最小值，最小值为4，D 错故选：BC. 【点睛】本题综合考查奇偶性、均值不等式、利用导数求最值等，对学生知识的运用能力要求较高，难度较大.5．对于函数()()13cos ,,22132,,22x x f x f x x π⎧⎡⎤∈-⎪⎢⎥⎪⎣⎦=⎨⎛⎫⎪-∈+∞ ⎪⎪⎝⎭⎩，下面结论正确的是（）A ．任取121,,2x x ⎡⎫∈-+∞⎪⎢⎣⎭，都有()()122f x f x -≤恒成立 B ．对于一切1,2x ⎡⎫∈-+∞⎪⎢⎣⎭，都有()()()*22N k f x f x k k =+∈ C ．函数()1ln 2y f x x ⎛⎫=--⎪⎝⎭有3个零点 D ．对任意0x >，不等式()k f x x ≤恒成立，则实数k 的取值范围是1,2⎡⎫+∞⎪⎢⎣⎭【答案】ABC 【分析】先在坐标轴中画出()y f x =的图象,根据图象可判断A 选项,结合解析式可判断B 选项,再画出1ln()2y x =-与k y x=的图象,数形结合可判断C,D 选项.【详解】在坐标轴上作出函数()f x 的图象如下图所示:由图象可知()f x 的最大值为1,最小值为1-,故选项A 正确; 由题可知()()()1312,(,)(2),(,)22221f x f x x f x f x x =-∈+∞⇒+=∈-+∞, 所以*1(2)()()()2k f x k f x k N +=∈即()2(2)k f x f x k =+,故选项B 正确;作出1ln()2y x =-的图象，因为11ln(2)ln 2232-=<，由图象可知()y f x =与1ln()2y x =-有3个交点,故选项C 正确;结合图象可知,若对任意0x >,不等式()kf x x恒成立,即2x n =时,不等式(2)2kf n n恒成立, 又11(2)()(0)()22nnf n f ==, 所以1()22n k n ,即22n nk 在*n N ∈时恒成立, 设2()2x x g x =,则2ln 4()2xxg x -⋅'=, 故[)2,x ∈+∞时,()0g x '<,函数()g x 在[)2,+∞上单调递减, 所以[)2,x ∈+∞时,max ()(2)1g x g ==,又(1)1g =,所以max 212n n ⎛⎫= ⎪⎝⎭,即1k ,故选项D 错误.故选:ABC. 【点睛】本题主要考查分段函数的周期性及数形结合法在处理函数问题中的应用,有一定难度.6．下列说法中，正确的有（） A ．若0a b >>，则b a a b> B ．若0a >，0b >，1a b +=，则11a b+的最小值为4 C ．己知()11212xf x =-+，且()()2110f a f a -+-<，则实数a 的取值范围为()2,1- D ．已知函数()()22log 38f x x ax =-+在[)1,-+∞上是增函数，则实数a 的取值范围是(]11,6--【答案】BCD 【分析】利用不等式的基本性质可判断A 选项的正误；将+a b 与11a b+相乘，展开后利用基本不等式可判断B 选项的正误；判断函数()f x 的单调性与奇偶性，解不等式()()2110f a f a -+-<可判断C 选项的正误；利用复合函数法可得出关于实数a 的不等式组，解出a 的取值范围，可判断D 选项的正误. 【详解】对于A 选项，0a b >>，则1a bb a>>，A 选项错误；对于B 选项，0a >，0b >，1a b +=，()1111224b a a b a b a b a b ⎛⎫∴+=++=++≥+= ⎪⎝⎭，当且仅当12a b ==时，等号成立，所以，11a b+的最小值为4，B 选项正确；对于C 选项，函数()f x 的定义域为R ，任取1x 、2x R ∈且12x x <，则21220x x >>，所以，()()()()211212121211111122021221221212121x x x x x x x x f x f x -⎛⎫⎛⎫-=---=-=> ⎪ ⎪++++++⎝⎭⎝⎭，即()()12f x f x >，所以，函数()f x 为R 上的减函数，()()()()2211112212221212xxx x x f x -+-=-==+++，则()()()()()()21212212122212221x x x x x x x xf x f x --------====-+⋅++，所以，函数()f x 为R 上的奇函数，且为减函数，由()()2110f a f a-+-<可得()()()22111f a f a f a-<--=-，所以，211a a -<-，即220a a +-<，解得21a -<<，C 选项正确；对于D 选项，对于函数()()22log 38f x x ax =-+，令238u x ax =-+，由于外层函数2log y u =为增函数，则内层函数238u x ax =-+在[)1,-+∞上为增函数，所以min 16380au a ⎧≤-⎪⎨⎪=++>⎩，解得116a -<≤-，D 选项正确.故选：BCD. 【点睛】方法点睛：利用函数的奇偶性与单调性求解抽象函数不等式，要设法将隐性划归为显性的不等式来求解，方法是：（1）把不等式转化为()()f g x f h x >⎡⎤⎡⎤⎣⎦⎣⎦；（2）判断函数()f x 的单调性，再根据函数的单调性把不等式的函数符号“f ”脱掉，得到具体的不等式（组），但要注意函数奇偶性的区别.7．对于具有相同定义域D 的函数()f x 和()g x ，若存在函数()h x kx b =+（k ，b 为常数），对任给的正数m ，存在相应的0x D ∈，使得当x D ∈且0x x >时，总有()()()()00f x h x m h x g x m ⎧<-<⎪⎨<-<⎪⎩，则称直线:l y kx b =+为曲线()y f x =与()y g x =的“分渐近线”.给出定义域均为{}|1D x x =>的四组函数，其中曲线()y f x =与()y g x =存在“分渐近线”的是（）A ．()2f x x =，()g x =B ．()102xf x -=+，()23x g x x-=C ．()21x f x x+=，()ln 1ln x x g x x +=D ．()221x f x x =+，()()21xg x x e -=--【答案】BD 【分析】根据分渐近线的定义，对四组函数逐一分析，由此确定存在“分渐近线”的函数. 【详解】解：()f x 和()g x 存在分渐近线的充要条件是x →∞时，()()0,()()f x g x f x g x -→>．对于①，()2f x x =，()g x =当1x >时，令()()()2F x f x g x x =-=，由于()20F x x '=->，所以()h x 为增函数，不符合x →∞时，()()0f x g x -→，所以不存在分渐近线；对于②，()1022xf x -=+>，()232,(1)x g x x x-=<> ()()f x g x ∴>，2313()()10210xxx f x g x x x--⎛⎫-=+-=+ ⎪⎝⎭，因为当1x >且x →∞时，()()0f x g x -→，所以存在分渐近线；对于③，21()x f x x+=，ln 1()ln x x g x x +=，21111111()()ln ln ln x x nx f x g x x x x x x x x x++-=-=+--=-当1x >且x →∞时，1x 与1ln x 均单调递减，但1x的递减速度比1ln x 快，所以当x →∞时，()()f x g x -会越来越小，不会趋近于0，所以不存在分渐近线；对于④，22()1x f x x =+，()()21xg x x e -=--，当x →∞时，22()()220+1222+1x x x f x g x x e x x e--=-+++=→，且()()0f x g x ->，因此存在分渐近线．故存在分渐近线的是BD ．故选：BD ．【点睛】本小题主要考查新定义概念的理解和运用，考查函数的单调性，属于难题.8．狄利克雷是德国著名数学家，是最早倡导严格化方法的数学家之一，狄利克雷函数()1,0,x Q f x x Q ∈⎧=⎨∉⎩（Q 是有理数集）的出现表示数学家对数学的理解开始了深刻的变化，从研究“算”到研究更抽象的“概念、性质、结构”．关于()f x 的性质，下列说法正确的是（）A ．函数()f x 是偶函数B ．函数()f x 是周期函数C ．对任意的1x R ∈，2x ∈Q ，都有()()121f x x f x +=D ．对任意的1x R ∈，2x ∈Q ，都有()()121f x x f x ⋅= 【答案】ABC 【分析】利用函数奇偶性的定义可判断A 选项的正误；验证()()1f x f x +=，可判断B 选项的正误；分1x Q ∈、1x Q ∉两种情况讨论，结合函数()f x 的定义可判断C 选项的正误；取20x =，1x Q ∉可判断D 选项的正误.【详解】对于A 选项，任取x Q ∈，则x Q -∈，()()1f x f x ==-；任取x Q ∉，则x Q -∉，()()0f x f x ==-.所以，对任意的x ∈R ，()()f x f x -=，即函数()f x 为偶函数，A 选项正确；对于B 选项，任取x Q ∈，则1x Q +∈，则()()11f x f x +==；任取x Q ∉，则1x Q +∉，则()()10f x f x +==.所以，对任意的x ∈R ，()()1f x f x +=，即函数()f x 为周期函数，B 选项正确；对于C 选项，对任意1x Q ∈，2x ∈Q ，则12x Q x +∈，()()1211f x x f x +==；对任意的1x Q ∉，2x ∈Q ，则12x x Q +∉，()()1210f x x f x +==. 综上，对任意的1x R ∈，2x ∈Q ，都有()()121f x x f x +=，C 选项正确；对于D 选项，取20x =，若1x Q ∉，则()()()12101f x x f f x ⋅==≠，D 选项错误. 故选：ABC. 【点睛】关键点点睛：本题解题的关键在于根据已知函数的定义依次讨论各选项，分自变量为无理数和有理数两种情况讨论，对于D 选项，可取1x Q ∉，20x =验证.二、导数及其应用多选题9．已知函数()3sin f x x x ax =+-，则下列结论正确的是（）A ．()f x 是奇函数B ．当3a =-时，函数()f x 恰有两个零点C ．若()f x 为增函数，则1a ≤D ．当3a =时，函数()f x 恰有两个极值点【答案】ACD 【分析】利用函数奇偶性的定义可判断A 选项的正误；利用导数分析函数()f x 的单调性，可判断B 选项的正误；利用导数与函数单调性的关系可判断C 选项的正误；利用导数以及零点存在定理可判断D 选项的正误. 【详解】对于A 选项，函数()3sin f x x x ax =+-的定义域为R ，()()()()33sin sin f x x x ax x x ax f x -=-+-+=--+=-，函数()f x 为奇函数，A 选项正确；对于B 选项，当3a =-时，()3sin 3f x x x x =++，则()2cos 330f x x x '=++>，所以，函数()f x 在R 上为增函数，又()00f =，所以，函数()f x 有且只有一个零点，B 选项错误；对于C 选项，()2cos 3f x x x a '=+-，由于函数()f x 为增函数，则()0f x '≥对任意的x ∈R 恒成立，即23cos a x x ≤+. 令()23cos g x x x =+，则()6sin g x x x '=-，则()6cos 0g x x ''=->，所以，函数()g x '在R 上为增函数，当0x <时，()()00g x g ''<=，此时，函数()g x 为减函数；当0x >时，()()00g x g ''>=，此时，函数()g x 为增函数. 所以，()()min 01g x g ==，1a ∴≤，C 选项正确；对于D 选项，当3a =时，()3sin 3f x x x x =+-，则()2cos 33f x x x '=+-.由B 选项可知，函数()f x '在(),0-∞上单调递减，在()0,∞+上单调递增，()()11cos10f f ''-==>，()020f '=-<，由零点存在定理可知，函数()f x '在()1,0-和()0,1上都存在一个零点，因此，当3a =时，函数()f x 有两个极值点，D 选项正确. 故选：ACD. 【点睛】结论点睛：利用函数的单调性求参数，可按照以下原则进行：（1）函数()f x 在区间D 上单调递增()0f x '⇔≥在区间D 上恒成立；（2）函数()f x 在区间D 上单调递减()0f x '⇔≤在区间D 上恒成立；（3）函数()f x 在区间D 上不单调()f x '⇔在区间D 上存在极值点；（4）函数()f x 在区间D 上存在单调递增区间x D ⇔∃∈，使得()0f x '>成立；（5）函数()f x 在区间D 上存在单调递减区间x D ⇔∃∈，使得()0f x '<成立.10．设函数()()1x af x a x a =->的定义域为()0,∞+，已知()f x 有且只有一个零点，下列结论正确的有（） A ．a e =B ．()f x 在区间()1,e 单调递增C ．1x =是()f x 的极大值点D ．()f e 是()f x 的最小值【答案】ACD 【分析】()f x 只有一个零点，转化为方程0x a a x -=在(0,)+∞上只有一个根，即ln ln x ax a=只有一个正根．利用导数研究函数ln ()xh x x=的性质，可得a e =，判断A ，然后用导数研究函数()x e f x e x =-的性质，求出()'f x ，令()0f x '=，利用新函数确定()'f x 只有两个零点1和e ，并证明出()'f x 的正负，得()f x 的单调性，极值最值．判断BCD ．【详解】()f x 只有一个零点，即方程0x a a x -=在(0,)+∞上只有一个根，x a a x =，取对数得ln ln x a a x =，即ln ln x ax a=只有一个正根．设ln ()x h x x =，则21ln ()x h x x-'=，当0x e <<时，()0h x '>，()h x 递增，0x →时，()h x →-∞，x e >时，()0h x '<，()h x 递减，此时()0h x >，max 1()()h x h e e==． ∴要使方程ln ln x ax a =只有一个正根．则ln 1a a e =或ln 0a a<，解得a e =或0a <，又∵1a >，∴a e =．A 正确；()x e f x e x =-，1()x e f x e ex -'=-，1()0x e f x e ex -'=-=，11x e e x --=，取对数得1(1)ln x e x -=-，易知1x =和x e =是此方程的解．设()(1)ln 1p x e x x =--+，1()1e p x x-'=-，当01x e <<-时，()0p x '>，()p x 递增，1x e >-时，()0p x '<，()p x 递减，(1)p e -是极大值，又(1)()0p p e ==，所以()p x 有且只有两个零点，01x <<或x e >时，()0p x <，即(1)ln 1e x x -<-，11e x x e --<，1e x ex e -<，()0f x '>，同理1x e <<时，()0f x '<，所以()f x 在(0,1)和(,)e +∞上递增，在(1,)e 上递减，所以极小值为()0f e =，极大值为(1)f ，又(0)1f =，所以()f e 是最小值．B 错，CD 正确．故选：ACD ．【点睛】关键点点睛：本题考用导数研究函数的零点，极值，单调性．解题关键是确定()'f x 的零点时，利用零点定义解方程，1()0xe f x e ex-'=-=，11x e e x --=，取对数得1(1)ln x e x -=-，易知1x =和x e =是此方程的解．然后证明方程只有这两个解即可．。

基本初等函数

《基本初等函数》题型归纳与训练【题型归纳】题型一幂函数的图像与性质例1 已知幂函数()x f y =的图象过点），（2221，则()2log 2f 的值为( ) A.21B ．21-C ．1-D ．1例2 如果幂函数()23212++-=p p xx f ()Z p ∈是偶函数，且在()+∞,0上是增函数，求p 的值，并写出相应的函数()x f 的解析式. 题型二二次函数的图像和性质（最值）例 1 已知()532-+=x x x f ，[]1,+∈t t x ，若()x f 的最小值为()t h ，写出()t h 的表达式 .例2 已知函数()⎪⎩⎪⎨⎧<-≥+-=020222x xx x x x x f ，若关于x 的不等式()[]()022<-+b x af x f 恰有1个整数解，则实数a 的最大值是( )A ．2B ．3C ．5D ．8题型三指数函数例 1 已知奇函数()f x 在R 上是增函数.若21log 5a f ⎛⎫=- ⎪⎝⎭，()2log 4.1b f =，()0.82c f =，则,,a b c 的大小关系为（）.A. a b c <<B.b a c <<C.c b a <<D.c a b <<B.例 2 设函数1,0()2,0x x x f x x +⎧=⎨>⎩≤，则满足1()()12f x f x +->的x 的取值范围是_________．题型四对数函数例1 已知函数log ()a y x c =+（,a c 为常数，其中0,1a a >≠）的图象如图，则下列结论成立的是A ．0,1a c >>B ．1,01a c ><<C ．01,1a c <<>D ．01,01a c <<<<例2 若函数212log ,0()log (),0x x f x x x >⎧⎪=⎨-<⎪⎩,若()()f a f a >-,则实数a 的取值范围是（）A ．(1,0)(0,1)-B ．(,1)(1,)-∞-+∞C ．(1,0)(1,)-+∞D ．(,1)(0,1)-∞-例3 若函数xa y =,0(>a 且)1≠a 的值域为{}1|≥y y ，则函数x y a log =的图象大致是( )题型五函数的应用例1 某食品的保鲜时间y (单位：小时)与储藏温度x (单位：℃)满足函数关系bkx ey +=(718.2≈e 为自然对数的底数，k ，b 为常数).若该食品在0 ℃的保鲜时间是192小时，在22 ℃的保鲜时间是48小时，则该食品在33 ℃的保鲜时间是________小时.【巩固训练】幂函数的图像与性质1.函数()()mx m m x f 12--=是幂函数，且在()+∞∈,0x 上为增函数，则实数m 的值是( )A ．－1B ．2C ．3D ．－1或22.已知11{2,1,,,1,2,3}22α∈---，若幂函数()α=f x x 为奇函数，且在(0,)+∞上递减，则α=_____．3.已知幂函数()ax x f =的部分对应值如下表：则不等式()2≤x f 的解集是 . 题型二二次函数的图像和性质（最值）1.已知,,a b c R ∈，函数()2f x ax bx c =++.若()()()041f f f =>，则（）.A. 0a >，40a b +=B. 0a <，40a b +=C. 0a >，20a b +=D. 0a <，20a b += 2.已知函数()⎩⎨⎧≤-->-=020122x x x x x x f ，若函数()()m x f x g -=有3个零点，则实数m 的取值范围是_______．3.已知对任意的[]1,1-∈a ，函数()()a x a x x f 2442-+-+=的值总大于0，则x 的取值范围是( )A ．(1,3)B ．(－∞，1)∪(3，＋∞)C ．(1,2)D ．(－∞，2)∪(3，＋∞) 题型三指数函数1. 已知，则函数和在同一坐标系中的图象只可能是图中的（）01a <<xy a =2(1)y a x =-A. B. C. D.2.已知函数（且）的图象如下图所示，则的值是________．3.与函数的图象有且仅有两个公共点，则实数的取值范围是____. 题型四对数函数1.若点(,)a b 在lg y x = 图像上，a ≠1,则下列点也在此图像上的是（）A ．1(,)b aB ．(10,1)a b -C ．10(,1)b a+ D ．2(,2)a b 2.如果,0log log 2121<<y x 那么（）A ．1y x <<B ．1x y <<C ．1x y <<D ．1y x <<3.当102x <≤时，4log xa x <，则a 的取值范围是（） A．(0,2 B．2C． D．2) 4已知1a b >>，若5log log 2a b b a +=，b a a b =，则a =________，b =_______. 6.在同一直角坐标系中,函数()ax x f =,()x x g a log =的图象可能是( )2y a b =+0a >1a ≠a b-2y a =()101xy a a a =->≠且a。