曲线积分与曲面积分
曲线积分与曲面积分

曲线积分与曲面积分一、 知识要点 1、定义、定理(1)定理1(格林公式):设分段光滑的有向闭曲线L 为有界闭区域D 的正向边界,函数P(x,y),Q(x,y)在D 上具有一阶连续偏导数,则有:⎰⎰⎰+=∂∂-∂∂L DQdy Pdx dxdy yPx Q )((2) 定理2(曲线积分与路径无关的充要条件) :设G 为平面单连通开区域,函数),(y x P ,),(y x Q 在G 内具有连续的一阶偏导数,那么曲线积分⎰+LQdy Pdx 与路径无关xQ yP ∂∂≡∂∂⇔在G 内成立。
(3) 定理3 :设函数),(),,(y x Q y x P 在开区域G 内具有一阶连续偏导,则曲线积分()()dy y x Q dx y x P ,,+ 在G内为某一函数()y x u ,的全微分的充要条件是等式()()x y x Q y y x P ∂∂=∂∂,,在G 内恒成立。
(4)定理4(高斯公式):设空间闭区域Ω是由分片光滑的闭曲面∑所围成,函数()z y x P ,,、()z y x Q ,,、()z y x R ,,在Ω上具有一阶连续偏导数,则有⎰⎰⎰⎰⎰Ω∑++=∂∂+∂∂+∂∂Rdxdy Qdxdz Pdydz dv z Ry P x Q )(或()⎰⎰⎰⎰⎰Ω∑++=∂∂+∂∂+∂∂dS R Q P dv z R y P x Q γβαcos cos cos )(,其中,γβαcos ,cos ,cos 为外法向量的方向余弦。
(5)定理4(斯托克斯公式):设L 为分段光滑的空间有向闭曲线,∑是以L 为边界的分片光滑的有向曲面,L 的正向与∑的侧符合右手规则,函数()()()z y x R z y x Q z y x P ,,,,,,、、在包含∑在内的一个空间区域内具有一阶连续偏导数,则有⎰⎰⎰++=∂∂∂∂∂∂∑L Rdz Qdy Pdx R Q P z y x dxdy dzdx dydz ,或⎰⎰⎰++=∂∂∂∂∂∂∑L Rdz Qdy Pdx dS RQ P z y x γβαcos cos cos 2、 公式(1)对弧长的曲线积分的计算公式:(ψϕ,在相应区间上具有一阶连续导数)①若)( )()(:βαψϕ≤≤⎩⎨⎧==t t y t x L ,则dt t t t t f ds y x f L ⎰⎰'+'=βαψϕψϕ)()()](),([),(22 )(βα<②若)( )(:b x a x y L ≤≤=ϕ,则⎰⎰'+=b aL dx x x x f ds y x f )(1)](,[),(2ϕϕ)(b a < ③若)( )(:d y c y x L ≤≤=ψ,则⎰⎰+'=d cL dy x y y f ds y x f 1)()]),([),(2ψψ )(d c <(2)对坐标的曲线积分的计算公式:(ψϕ,在相应区间上具有一阶连续导数)①若):( )()(:βαψϕ→⎩⎨⎧==∧t t y t x AB ,则dt t t t Q t t t P dy y x Q dx y x P AB⎰⎰'+'=+∧βαψψϕϕψϕ)}()](),([)()](),([{),(),( ②若):( )(:b a x x y AB →=∧ϕ,则⎰∧+ABdy y x Q dx y x P ),(),(⎰'+=ba dx x x x Q x x P )}()](,[)](,[{ϕϕϕ ③若):( )(:d c y y x AB →=∧ψ,则⎰∧+ABdy y x Q dx y x P ),(),(()()⎰+'=dcdy y y Q y y y P ]},[)(],[{ψψψ(3)两类曲线积分的转换公式:①()⎰⎰+=+LLds Q P dy y x Q dx y x P βαcos cos ),(),(,其中,()()y x y x ,,βα、为有向曲线弧L 上点()y x ,处的切线向量的方向角。
曲线积分和曲面积分

曲线积分:在数学中,曲线积分是积分的一种。
积分函数的取值沿的不是区间,而是特定的曲线,称为积分路径。
曲线积分有很多种类,当积分路径为闭合曲线时,称为环路积分或围道积分。
曲线积分可分为:第一类曲线积分和第二类曲线积分。
分类:曲线积分分为:(1)对弧长的曲线积分(第一类曲线积分)(2)对坐标轴的曲线积分(第二类曲线积分)两种曲线积分的区别主要在于积分元素的差别;对弧长的曲线积分的积分元素是弧长元素ds;例如:对L的曲线积分∫f(x,y)*ds 。
对坐标轴的曲线积分的积分元素是坐标元素dx或dy,例如:对L’的曲线积分∫P(x,y)dx+Q(x,y)dy。
但是对弧长的曲线积分由于有物理意义,通常说来都是正的,而对坐标轴的曲线积分可以根据路径的不同而取得不同的符号。
曲面积分:定义在曲面上的函数或向量值函数关于该曲面的积分。
曲面积分一般分成第一型曲面积分和第二型曲面积分。
第一型曲面积分物理意义来源于对给定密度函数的空间曲面,计算该曲面的质量。
第二型曲面积分物理意义来源对于给定的空间曲面和流体的流速,计算单位时间流经曲面的总流量。
第一型曲面积分:定义在曲面上的函数关于该曲面的积分。
第一型曲线积分物理意义来源于对给定密度函数的空间曲面,计算该曲面的质量。
第二型曲面积分:第二型曲面积分是关于在坐标面投影的曲面积分,其物理背景是流量的计算问题。
第二型曲线积分与积分路径有关,第二型曲面积分同样依赖于曲面的取向,第二型曲面积分与曲面的侧有关,如果改变曲面的侧(即法向量从指向某一侧改变为指另一侧),显然曲面积分要改变符号,注意在上述记号中未指明哪侧,必须另外指出,第二型曲面积分有类似于第二型曲线积分的一些性质。
高等数学第十章曲线积分与曲面积分(考研辅导班内部资料)

第十章 曲线积分与曲面积分曲线积分一 基本概念定义1 第一类曲线积分(对弧长的曲线积分) (1)平面曲线()L AB 的积分:()()01(,)d lim(,)nkkkL AB T k f x y s f sλξη→==∆∑⎰(2)空间曲线()L AB 的积分:()()01(,,)d lim(,,)nkkkk L AB T k f x y z s f s λξηζ→==∆∑⎰其中()T λ表示分割曲线()L AB 的分法T 的细度,即n 段曲线弧长的最大值,(,)k k ξη或(,,)k k k ξηζ是第k 段弧上的任意一点。
物理意义:第一类曲线积分表示物质曲线L 的质量,其中被积函数(,)f x y 或(,,)f x y z 表示曲线的线密度。
定义2 第二类曲线积分(对坐标的曲线积分) (1)平面曲线()L AB 的积分:()()01(,)d (,)d lim[(,)(,)]nkkkk k k L AB T k P x y x Q x y y f xf y λξηξη→=+=∆+∆∑⎰(2)空间曲线()L AB 的积分:()(,,)d (,,)d (,,)d L AB P x y z x Q x y z y R x y z z ++⎰()01lim[(,,)(,,)(,,)]nkkkk k k k k k k k k T k f x f y f z λξηζξηζξηζ→==∆+∆+∆∑其中()T λ表示分割曲线()L AB 的分法T 的细度,即n 段的最大弧长,(,)k k ξη是第k 段弧上的任意一点。
物理意义:第二类曲线积分表示变力F 沿曲线L 所作的功,被积函数(,),(,)P x y Q x y 或(,,),(,,),(,,)P x y z Q x y z R x y z 表示力F 在各坐标轴上的分量。
二 基本结论定理1 (第一类曲线积分的性质) (1)无向性()()(,)d (,)d L AB L BA f x y s f x y s =⎰⎰.(2)线性性质 (1)(,)d (,)d LLk f x y s k f x y s =⎰⎰;(2)[(,)(,)]d (,)d (,)d LLLf x yg x y s f x y s g x y s ±=±⎰⎰⎰.(3)路径可加性 曲线L 分成两段1L 和2L (不重叠),则12(,)d (,)d (,)d LL L f x y s f x y s f x y s =+⎰⎰⎰.(4)弧长公式d Ls L =⎰(L 表示曲线L 的弧长).(5)恒等变换 积函数可用积分曲线方程作变换. (6)奇偶性与对称性 如果积分弧段()L AB 关于y 轴对称,()(,)d L AB f x y s ⎰存在,则()()0,(,)(,)d 2(,)d (,)L AB L OB f x y x f x y s f x y s f x y x ⎧⎪=⎨⎪⎩⎰⎰关于是奇函数,,关于是偶函数.其中O 点是曲线弧段()L AB 与y 轴的交点.定理2 (第二类曲线积分的性质) (1)有向性()()(,)d (,)d L AB L BA P x y x P x y x =-⎰⎰.(2)线性性质 (1)(,)d (,)d LLkf x y x k f x y x =⎰⎰;(2) [(,)(,)]d (,)d (,)d L L Lf x yg x y x f x y x g x y x ±=±⎰⎰⎰.(3)路径可加性 曲线L 分成两段1L 和2L (不重叠),则12(,)d (,)d (,)d LL L f x y x f x y x f x y x =+⎰⎰⎰.定理3 (第一类曲线积分与第二类曲线积分的关系)()()d d d d d d d d d d L AB L AB xy z P x Q y R z P Q R s ss s ⎛⎫++=++ ⎪⎝⎭⎰⎰()(cos cos cos )d L AB P Q R s αβγ=++⎰()d L AB =⋅⎰F s其中cos ,cos ,cos αβγ是曲线AB 上的点的切线的方向余弦,且d cos d ,d cos d ,d cos d x s y s z s αβγ===一般地,积分曲线的方向余弦是变量。
曲线积分和曲面积分的物理意义

曲线积分和曲面积分的物理意义摘要:1.曲线积分概述2.曲面积分的物理意义3.曲线积分与曲面积分的联系与区别4.实际应用案例分析正文:一、曲线积分概述曲线积分是一种数学工具,用于计算曲线上的物理量,如力、速度、能量等。
它在物理学、工程学等领域具有广泛的应用。
曲线积分的基本思想是将曲线划分为无数小段,计算每小段上的物理量与长度的乘积之和。
根据积分路径的不同,曲线积分可分为线积分和面积分。
二、曲面积分的物理意义曲面积分是对曲面上物理量的积分,其基本思想是将曲面划分为无数小面,计算每个小面上的物理量与面积的乘积之和。
曲面积分可分为两类:法向量积分和切向量积分。
法向量积分用于计算曲面上某一点的垂直方向物理量,如压力、温度等;切向量积分用于计算曲面上某一点的切线方向物理量,如速度、力等。
曲面积分在物理学、工程学等领域具有重要的物理意义。
三、曲线积分与曲面积分的联系与区别曲线积分与曲面积分都是对物理量沿路径或曲面的积分。
它们的联系在于都是通过对路径或曲面进行划分,计算各小段或小面上物理量与长度或面积的乘积之和。
然而,它们也有明显的区别。
曲线积分主要针对曲线路径,关注沿路径的变化;而曲面积分针对曲面,关注的是曲面上各点的物理量。
此外,曲线积分可分为线积分和面积分,而曲面积分可分为法向量积分和切向量积分。
四、实际应用案例分析1.电磁学:在电磁学中,曲线积分广泛应用于计算电场线、磁感线等。
通过计算曲线上某一点的电场强度或磁场强度与弧长的乘积之和,可以得到电场线或磁感线的分布情况。
2.流体力学:在流体力学中,曲面积分可用于计算流体沿曲面的速度分布。
通过计算曲面上各点的速度与面积的乘积之和,可以得到流体的速度分布情况,进而分析流体的运动规律。
3.热传导:在热传导问题中,曲线积分可以用于计算温度沿曲线的分布。
通过计算曲线上某一点的温度与弧长的乘积之和,可以得到温度的分布情况,进而分析热传导过程。
总之,曲线积分和曲面积分在物理学、工程学等领域具有重要的应用价值。
曲线积分曲面积分公式

曲线积分曲面积分公式曲线积分和曲面积分是微积分学中重要的概念和计算方法,它们在物理学、工程学、计算机图形学等领域中有广泛的应用。
本文将详细介绍曲线积分和曲面积分的概念、计算方法以及它们的应用。
一、曲线积分1. 概念曲线积分是沿着曲线路径的函数值在该路径上的积分,它可以用来计算曲线上的物理量或计算路径上的某个量的总和。
一条曲线通常可以用参数方程表示,即根据一个或多个参数的变化来描述曲线上的点的坐标。
2. 计算方法曲线积分可以分为第一类曲线积分和第二类曲线积分两种。
第一类曲线积分是对曲线上的函数施加一个标量面积进行积分,计算公式为:∫f(x,y,z) ds其中,f(x,y,z)是曲线上的函数,s是弧长。
第二类曲线积分是对曲线上的矢量场进行积分,计算公式为:∫F·dr 或∫F ds其中,F是曲线上的矢量场,dr是位移矢量,ds是弧长。
3. 应用曲线积分在物理学中有广泛的应用,例如计算电场沿着路径上的功、磁场沿着闭合路径上的环流等。
它还可以用来计算空间曲线上的质心、质量等。
在工程学中,曲线积分可以用来计算管道的流量、线段上的力等。
二、曲面积分1. 概念曲面积分是对曲面上的函数的某个量在整个曲面上的积分,它可以用来计算曲面上的物理量或计算函数在曲面上的平均值。
一般情况下,曲面可以用参数方程表示,即根据两个参数的变化来描述曲面上的点的坐标。
2. 计算方法曲面积分可以分为第一类曲面积分和第二类曲面积分两种。
第一类曲面积分是对曲面上的函数施加一个标量面积进行积分,计算公式为:∬f(x,y,z) dS其中,f(x,y,z)是曲面上的函数,dS是面积元。
第二类曲面积分是对曲面上的矢量场进行积分,计算公式为:∬F·dS 或∬F dS其中,F是曲面上的矢量场,dS是面积元。
3. 应用曲面积分在物理学中有广泛的应用,例如计算电场通过曲面的电通量、磁场通过闭合曲面的磁通量等。
它还可以用来计算物体的总质量、质心等物理量。
曲线积分和曲面积分

第八章 曲线积分和曲面积分我们前面已学过定积分和重积分,当一个函数定义在空间的曲线或曲面时,则要求我们计算曲线积分或曲面积分。
由于物理背景的不同,我们还须区别曲线或曲面的方向性,因此我们要分别研究两种不同类型的积分。
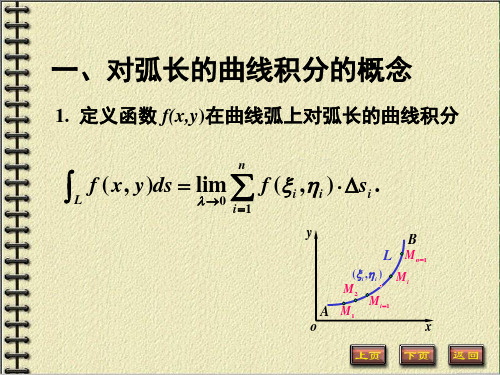
§1 第一型曲线积分与曲面积分1. 第一型曲线积分我们研究如下的一个理想问题,给定空间的一条曲线物体L ,L 上每点有线密度,现在我们要求它的质量。
我们对此问题作如下限制,设L 是空间的可求长曲线,端点为A 和B ,密度函数(,,)f x y z 在L 上定义。
为了求质量,象定积分一样,我们对L 作一分割,01,,,,(,1,2,,,)n j A A A A B A j n L ===L L 在上,这样我们就将L 分成n 小段,设每段的长度为j s V 。
在每段弧长上任取一点ξηςjjj(,,),作和式,1(,)nj jj j j f s ξης=∑V以此作为L 质量的近似值。
最后我们令1max{}0j j ns λ≤≤=→V ,即可得到L 质量的精确值M ,即,01lim (,)nj j j j j M f s λξης→==∑V由此我们可得到以下定义 定义设L 是空间可求长曲线,(,,)f x y z 在L 上连续,L 的两个端点为A,B ,依次用分点01,,,n A A A A B ==L 将L 分成n 小段。
每小段弧及弧长均记为j s V ,在j s V 上任取一点(,,)j j j j P ξης=,作和式,1(,)nj jj j j f s ξης=∑V如果当1max{}0j j ns λ≤≤=→V 时,上述和式的极限存在,且不依赖于L 的分法及j P 的选取,则称这一极限值为(,,)f x y z 。
在L 上的第一型曲线积分,记作(,,)Lf x y z ds ∫。
第一型曲线积分也有类似于定积分的一些性质,如关于被积函数的线性及关于曲线的可加性,它与定积分的一个差别是第一型曲线积分与曲线的方向无关。
高数下第十一章曲线积分与曲面积分
(3) f ( x, y)ds f ( x, y)ds f ( x, y)ds.
L
L1
L2
(L L1 L2 ).
5、对弧长曲线积分的计算
定理
设 f ( x, y)在曲线弧L上有定义且连续,
L的参数方程为
x y
( t ), ( t ),
( t )其中
(t), (t)在[ , ]上具有一阶连续导数, 且
3、 ( x 2 y 2 )ds,其中 L为曲线 L
x a(cos t t sin t)
y
a(sin
t
t
cos
t
)
(0 t 2 );
练习题答案
1、ea (2 a) 2; 4
2、9;
3. 22a3 (1 22 );
二、对坐标的曲线积分的概念
1. 定义:
函数 P(x,y)在有向曲线弧L上对坐标 x 的曲线积分
线 AB是半径为r 的圆在
第一象限部分.
A
D
o
L
Bx
解 引入辅助曲线L, L OA AB BO
应用格林公式, P 0, Q x 有
dxdy L xdy
D
OA xdy AB xdy BO xdy,
由于 OA
xdy
0,
BO xdy 0,
xdy dxdy 1 r2.
f ( x, y)ds f [ (t), (t)] 2 (t) 2 (t)dt
L
( )
注意: 1. 定积分的下限 一定要小于上限 ;
2. f ( x, y)中x, y不彼此独立, 而是相互有关的.
例1
求I
L xyds,
L
:
椭圆
曲线积分与曲面积分的概念与计算

曲线积分与曲面积分的概念与计算在数学中,曲线积分和曲面积分是两个重要的概念,用于描述曲线和曲面上的各种物理量的计算。
本文将详细介绍这两个概念的定义以及计算方法。
1. 曲线积分的概念与计算曲线积分用于计算曲线上的矢量场或标量场沿曲线的积分值,常用于求解沿路径的功、电磁感应等问题。
曲线积分可以分为第一类和第二类,下面将分别介绍。
1.1 第一类曲线积分第一类曲线积分可以用于计算矢量场沿曲线的积分值,其计算公式如下:∮C F·ds其中,C表示曲线,F表示矢量场,ds表示曲线C上的一小段投影长度,F·ds表示矢量场F与ds的点积。
要计算第一类曲线积分,首先需要确定曲线C的参数方程,并对其进行参数化。
然后,将参数方程代入上述公式,并对参数范围进行积分即可得到结果。
1.2 第二类曲线积分第二类曲线积分用于计算标量场沿曲线的积分值,其计算公式如下:∮C f ds其中,C表示曲线,f表示标量场,ds表示曲线C上的一小段投影长度。
要计算第二类曲线积分,同样需要确定曲线C的参数方程,并对其进行参数化。
然后,将参数方程代入上述公式,并对参数范围进行积分即可得到结果。
2. 曲面积分的概念与计算曲面积分用于计算曲面上的矢量场或标量场通过曲面的通量或质量的计算。
曲面积分同样可以分为第一类和第二类,下面将一一介绍。
2.1 第一类曲面积分第一类曲面积分用于计算矢量场通过曲面的通量,其计算公式如下:∬S F·dS其中,S表示曲面,F表示矢量场,dS表示曲面S上的一小块面积,F·dS表示矢量场F与dS的点积。
要计算第一类曲面积分,首先需要确定曲面S的参数方程,并对其进行参数化。
然后,将参数方程代入上述公式,并对参数范围进行积分即可得到结果。
2.2 第二类曲面积分第二类曲面积分用于计算标量场通过曲面的质量,其计算公式如下:∬S f dS其中,S表示曲面,f表示标量场,dS表示曲面S上的一小块面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
释疑解难曲线积分与曲面积分问题1.如何认识多元函数的几种积分的定义?答:多元函数的几种积分的定义可以用统一形式给出,统称为几何形体上的积分:n『f(P)dP =lim 送f(P)KP ,其中i P 是将积分区域G 任意分割为n 块后的任一块G若G 为空间区域0 ,则是三重积分 Jff f (x, y,z)dv 。
Q若G 为曲线弧L ,则是对弧长的曲线积分JJ f (x, y,z)dS 。
IJPdx + Qdy = J (P cocs +Q cBsds)LL其中a ,P 为有向曲线弧L 的切向量的方向角。
对坐标的曲面积分JJ P dydz+Qdzdx+Rdxdy = JJ ( Pcos 。
+QcosP +RcosY)dS ,II其中a ,P ,Y 为有向曲面I :的法向量的方向角。
问题2.如何正确理解两类曲线积分和曲面积分的概念?答:由于实际需要,曲线积分与曲面积分为两种类型,有关质量、重心、转动惯量等 数量积分问题导出第一类线面积分;有关变力作功、流体流过曲面的流量等向量问题导出第二类线、面积分。
前者被积函数化为数量函数沿区域积分,无需考虑方向性,而后者被积函 数是向量函数,必须考虑方向。
因此,一个函数的积分可以由积分区域的有向或无向分为两 种类型的积分,在所学过的积分中:区域无向的积分有:重积分、第一类曲线积分和第一类曲面积分; 区域有向的积分有:定积分、第二类曲线积分和第二类曲面积分。
曲线的方向是由起点到终点(定积分)或切向量的方向来确定,曲面的方向则由曲面 上点的法向量所指向的侧来确定,我们常会把两类积分相互转换,转换时必须注意符号,它体现了有向积分的方向。
将 无向域的积分化为有向域的积分,如重积分化为累次积分(定积分),方向性体现为定积分的上、下限的确定, 而将有向域的积分化为无向域的积分,如第二型曲面积分化为二重积分或三重积分,第二型曲线积分化为二重积分等,必须注意符号的确定问题。
问题3.应用格林公式时应注意什么问题? 答:应用格林公式应注意以下几点:1.必须注意格林公式的条件是否满足,否则,就会出现错误。
1 —睜,其中L 为x 2+y 2=1取正向,若按如下解法:y x +y(i=1,2|i|, n) , P 为 A P 内的任一点, 几=max {A R },它是定积分的推广。
若G 为平面域D ,则是二重积分JJ f(x,y)dcr 。
J f(x, y)ds 。
若G 为曲面则是对面积的曲面积分另外还有对坐标的曲线积分 例如,设I = J严cos 2t+型2tdtjJdtF 。
cos t +4sin t/.由格林公式,而事实上WQy 2 - X 2次(x2+ y 2)2JP cy『dy -y dx = ^dy _ ydx =口(1 +1 )dxdy =2兀。
口 X + y 口上述前一种解法是错误的,因为—J P 在(0,0)不连续,而(0,0^ D ,故不满足格林 ex cy公式的条件,不能直接应用格林公式。
2.格林公式对复连通区域 D ,曲线正向的规定:沿 D 的边界曲线正向前进,区域结论也成立,但L 必须是D 的所有边界曲线取正向。
D 总在其左侧。
的正向为X2x 2+y 2,其中L 是D :1<x2+ y 2<4的正向边界曲线,如图10-1, L+ / = 4的逆时针和x ? + y 2=1的顺时针方向。
因为—=dx dy—,(x,y)迂 D ,故由格林公式,得、dxdy = 0。
亘_£P问题4 .设L 为椭圆X22+— =1, l 为圆周 4为逆时针方向,问下列积分的计算是否正确?Fxdy —4ydx |yxdy-4ydxJ2 丄~2~ — J2 丄~2~p X +yx +y =2 j xdy- 4ydx= 2 J J 5dxdy = 5花。
答:不正确。
因为当 X2+y 2 H 0时,cQy 2-x 2gp 4(y 2 -x 2)L 、/2 丄 2\2,r/2 丄 2\2e x (x +y ) cy(x +y )故在L 与l 围成的区域D 中,ex,因此 dXdy-4ydxRxdy-4ydx正确的解法是利用 L 的参数方程:X = cost, y = 2sin t, t 从 0 变到 2兀,川 xdy-4ydxJ~2~ =H X +yX7 Pdx +Qdy 改变为另一路径I 上的积分J Pdx + Qdy ,—定要检查条件 L L (4 —是否在L 与l 所围成的区域内成立,且 L 与l 方向要一致。
氷dy问题5.计算积分J f x 3dydz + y 3dzdx +z 3dxdy ,邑为球面:x 2+ y 2+ z 2= R2的外侧。
下面作法是否正确:JJ x 3dydz + y 3dzdx+ z 3dxdy = 3 JJJ (x 2 + y 2 + z 2)dv =3R 2 JJJ dv = 4兀 R 5。
答:这个作法不正确,错在三重积分的计算,像这样的错误,一不注意就会发生。
因为给出的是H 上的曲面积分,在工上X 、y 、z 应满足方程x'+y'+z —R 2,这是对的。
但 在用了高斯公式以后,曲面积分已转换成了三重积分,积分域为、z 在闭域上变动,而对于0内部的点(x,y,z ),已不满足x^+y^+z 2了。
正确的2辽辽R12 3 JJR x 2+y2+zjdv=3『de [ d 单 J 。
P 4sin 半d — 兀 R 5。
Q.0 .0 52 2 26.设为平面x+z=a 在柱面X + y=a 内那一部分的上侧, 下面两个积分的 解法是否正确?(1)JJ (x+z)dS =a JJdS =a x(工的面积)=T^^a 3。
I I(2) JJ(x+z)dxdy =ajjdxdy = a x(邑的面积)=兀a 3。
I I答:第一个积分的解法是对的,第二个的解法不对。
因为第二个积分是对坐标的曲面积 分,其中的微分元 dxdy 是dS 在xOy 面上的投影,故正确的作法是:JJ (x +z)dxdy =a JJdxdy = a JJdxdy , D 是 E 在 xOy 上的投影:x 2 + y 2<a 2,故I1DJJ (x + z)dxdy = aJJdxdy =a%(D 的面积)=兀a 3工D如果工是下侧,那末JJ (x + z)dxdy =—a JJdxdy =-兀a 3。
工D曲面积分JJ Pdydz+Qdzd 对Rdxdy 之所以称为对坐标的曲面积分,就是上式中Idydz 、dzdx 和dxdy 分别是邑的面积元素dS 在坐标面yoz 、zox 和xoy 上的投影。
因此计算时应分别把 工投影于yoz 、zox 和xoy 面上,化为二重积分,这时,需要注意 工的侧,据此以定投影dydz 、dzdx 、dxdy 的正负,亦即二重积分的正负。
2 2 2 2问题7 .设 工是半球面 X + y + z = R( y>0)的外侧。
有人说:“由对称性知注:将曲线积分 2 2 2 2Q : x+y+z<R ,结果应是问题JJzdS = 0,故同样也有 JJzdxdy = 0。
”这样说对不对?答:这样说不对。
我们知道,对面积的曲面积分与曲面(积分域)的侧(方向)无关。
故考虑对称性时比较容易。
但对坐标的曲面积分与曲面的侧有关,所以在考虑它的对称性时,还要考虑曲面的侧。
也即要顾及被积函数与曲面,情形就比较复杂。
因此,在计算对坐标的 曲面积分时,不如先把它转化为二重积分,再化为定积分,在转化过程中可考虑利用二重积 分或定积分的对称性,这是基本方法。
利用对称性只是对具有这种特殊性质的积分所用的解 题技巧,并非每个曲面积分都具有这种特殊性质。
问题中的积分 JJzdS = 0是对的。
因为曲面 E 对称于xoy 平面,而被积函数 z 在关于 xoy 平面的对称点上,它的值差一个符号(奇函数)不对的。
因为曲面虽关于 xoy 平面对称,但在对称点上, 等。
故对称性不能用。
计算JJzdxdy 可用两种方法: I(1)设将工分为xOy 平面上、下两部分,分别记为工,与2 ,它们的方程是-y 。
工的外侧相当于 工1的上侧和工2的下侧,所以- ff (-J R 2 -X 2-y 2dxdyx 2蛋2=2 JJ J R 2 -X 2 -y 2dxdy = 2『严『T R 匸『「dr x 2事蛋2r P(2)补一个圆面D : y =0,x 2 +z 2 < R 2,并取左侧,由高斯公式,由于 JJzdxdy=0,故有 JJzdxdy= JC zdxdy = JJJ dv = D I 叨D…。
所以 JJzdS = 0,但 JJzdxdy =0是I1E 的方向不同,因而投影 dxdy 不JJzdxdy = JJzdxdy + JJzdxdy =JJ J R 2 -x2-y 2X 24y 22R 2dxdy (上侧取正)(下侧取负)使邑+ D 围成一半球体0。
