第6章-相位差测量
合集下载
《电工技术基础与技能》第六章正弦交流电习题(答案)
第六章正弦交流电练习题姓名：班级：学号：填空题1、大小和方向都随时间作周期性变化的电流、电压、电动势称为交流电，按正弦规律变化的交流电称为正弦交流电。
2、正弦交流电的三要素是最大值（有效值）、角频率(频率、周期) 和初相 .3、交流电每重复变化一次所用的时间叫周期，用字母T表示，其单位为秒。
4、交流电在一秒钟变化的次数叫频率，用字母f表示，其单位为 Hz或赫兹。
5、周期与频率之间的关系为 T=1/f ,角频率与频率之间的关系为ω=2πf ，工频交流电的频率f= 50 Hz。
6、我国供电系统中，交流电的频率是___50_____Hz，习惯上称为工频，周期为__0。
02s_____。
7、交流电路i=10sin（628t+4π/3)A，则其最大值为10A ,频率为100Hz，初相位为4π/3_。
8、已知正弦交流电压，它的最大值为_220√2V______，有效值为_ ___220V____,角频率为__314rad/s______，相位为__314t+60°____，初相位为___60°_____.9、某正弦交流电流的最大值为2A，频率为50Hz，初相为030，则该正弦交流电流的解析式i=___2sin(314t+30°）A___。
9、已知两个正弦交流电的瞬时值表达式分别为0160)u t V=-和()V60314sin22200+=tu02102sin(31430)u t V =+，则他们的相位差是__-90º_____，其相位关系是___u 1滞后u 290º(正交）___。
10、有两个同频率的正弦交流电，当它们的相位差分别为0°、180°、90°时,这两个正弦交流电之间的相位关系分别是__同相__、__反相__和___正交__。
11、i=5错误!sin （200πt-30O )A 则 I m = 7.07A ，I= 5 A ，ω= 200πrad/s f=100Hz ,T= 0。
第六章 正弦稳态交流电路的相量分析法
182.5 j132.5 225.536
③旋转因子 复数
特殊旋转因子
jF
Im
F
ej =cos
+jsin =1∠
Im F• ej
π , 2
π j π π e 2 cos jsin j 2 2
F• ej
旋转因子 0
0
Re
jF
F Re
o 例1 已知 i 141.4sin(314t 30 )A u 311.1sin(314t 60o )V 试用相量表示i, u .
i(t ) 2I sin( t Ψ ) I I Ψ
相量的模表示正弦量的有效值;
解
I 10030o A,
U 220 60o V
正弦量为周期函数
周期T 和频率f
t
f(t)=f ( t+k )
f
1 T
6. 三相电路的计算
周期T ：重复变化一次所需的时间。单位：秒s 频率f ：每秒重复变化的次数。 单位：赫(兹)Hz
正弦电路
激励和响应均为同频率的正弦量的线性电路 （正弦稳态电路）称为正弦电路或交流电路。
研究正弦电路的意义
i (t ) I m sin( t Ψ ) 2 I sin( t Ψ )
同理，可得正弦电压有效值与最大值的关系：
U
1 Um 2
或
U m 2U
若交流电压有效值为 U=220V ，
U=380V
②测量中，交流测量仪表指示的电压、电流读 数一般为有效值。 ③区分电压、电流的瞬时值、最大值、有效值的 符号。
结论
对正弦电路的分析研究具有重要的理论价 值和实际意义。
华科电工技术第6章 正弦稳态电路分析 (2)
而且与cos 有关，这是交流和直流的很大区别, 主要由于电
压、电流存在相位差。
cos 1，纯电阻
0，纯电抗
一般地，有 0cos1
X>0, >0，感性， 滞后功率因数 X<0, <0，容性， 超前功率因数
例： cos =0.5 (滞后)， 则 =60o (电流滞后电压60o)。
u
C 对电容，i 超前 u 90°，QC<0，故电容发出无功
-
功率。
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率
电感、电容的无功补偿作用
iR
L
+
+ uL - +
u -
C
uC -
O
pL pC
i uC
uL t
当L发出功率时，C刚好吸收功率，则与外电路交换功率 为pL+pC。因此，L、C的无功具有互相补偿的作用。
30 12
30(Ω)
|Z| U / I 50(Ω) |Z| R2 (L)2
L 1
| Z |2 R2
1 314
502 302 0.127(H)
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率 3.无功功率 (reactive power) Q
p(t) UI[cos φ cos(2t φ)] UI cos φ(1 cos 2t) UI sin sin 2t
第6章 正弦稳态电路分析
例：如图电路中，已知 is 5 2 sin 2（t A ），求电源提供的P、
Q，并计算电源的视在功率S和功率因素cos 。
2
解法一： 采用定义计算；
·IS
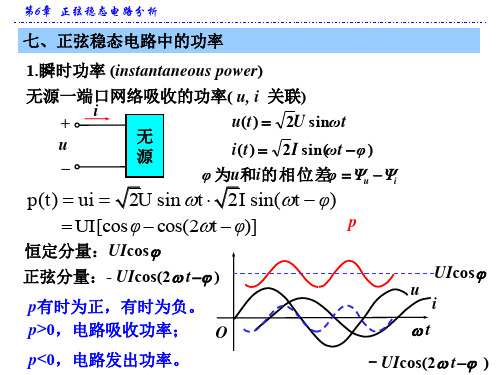
压、电流存在相位差。
cos 1，纯电阻
0，纯电抗
一般地，有 0cos1
X>0, >0，感性， 滞后功率因数 X<0, <0，容性， 超前功率因数
例： cos =0.5 (滞后)， 则 =60o (电流滞后电压60o)。
u
C 对电容，i 超前 u 90°，QC<0，故电容发出无功
-
功率。
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率
电感、电容的无功补偿作用
iR
L
+
+ uL - +
u -
C
uC -
O
pL pC
i uC
uL t
当L发出功率时，C刚好吸收功率，则与外电路交换功率 为pL+pC。因此，L、C的无功具有互相补偿的作用。
30 12
30(Ω)
|Z| U / I 50(Ω) |Z| R2 (L)2
L 1
| Z |2 R2
1 314
502 302 0.127(H)
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率 3.无功功率 (reactive power) Q
p(t) UI[cos φ cos(2t φ)] UI cos φ(1 cos 2t) UI sin sin 2t
第6章 正弦稳态电路分析
例：如图电路中，已知 is 5 2 sin 2（t A ），求电源提供的P、
Q，并计算电源的视在功率S和功率因素cos 。
2
解法一： 采用定义计算；
·IS
【测绘课件】第六章、GPS定位的观测量
载波相位观测是测量接收机接收到的具有多普勒 频移的载波信号，与接收机产生的参考载波信 号之间的相位差。
由于载波的波长远小于码长，C/A码码元宽度 21同99的.30m3情c，m况P，下码L，码2载元L波1宽载波度波长2的9为.观32m4测，.4误2而c差mL，1约载在为波分2波.0辨m长率m为，相 L精2载度波为的2.9观m测，误P码差为约0为.292m.5。mm载。波而相C位/A观码测观是测目 前最精确的观测方法。
上式中二次项影响很小可忽略，并考虑接收机的钟差， 可得以观测历元ti为根据的表达式：
ij 1 cij(ti) 1 cij(ti) ij 1 cij(ti)ti(ti)
上式的计算可采用迭代法，并略去二次项
ij 1 cij(ti)1 [ 1 cij(ti) ]1 cij(ti)ti(ti)
cti(t)ijIg(t)ijT(t)
2.测相伪距观测方程的线性化
由载波相位观测方程
i j( t ) c fi j( t ) f[t i( t ) t j( t ) ] c f[ i j I p ( t ) i j T ( t ) N ] i j( t 0 )
可得载波相位观测方程线性化形式(方法同前):
❖ GPS定位的几何关系
Z sj(t1) Xj(t1)
ij(t1) ij(t2)
Xi
Xj(t2)
Zi
Xi Yi X
sj(t2) Y
进X一i0步为假观设测X站0jT(ti)坐为标卫近星似sj于向历量元，t的坐标近似向量，
Xj(t)= [ Xj(t) Yj(t) Zj(t)]T为卫星坐标改正数 向正量数， 向量 X，i=同[时 X考i 虑 Y观i 测 站Zi]至T为卫观星测的站方坐向标余改弦：
第6章 相量法
(1) i1(t) 10cos(100 t 3 4) j 3 4 ( 2) 5 4
i2(t) 10cos(100 t 2)
j 5 4 2 3 4
(2) i1(t) 10cos(100 t 300 ) i2(t) 10cos(100t 1050 )
i2(t) 10sin(100 t 150 ) j 300 (1050 ) 1350
duC dt
uC
u(t )
i
+R
u
_
C L
两个正弦量的相加：如KCL、KVL方程运算。
i1 2 I1 cos(w t 1 ) i2 2 I2 cos(w t 2 )
正弦稳态电路特点： 若所有激励为频率相同的 正弦量，则线性电路响应 为同频率的正弦量。
6.1 正弦量
ui1, i
i2
角频率： w
a2b2 ) j(a2b1 b12 b22
a1b2 )
c1
jc2
c1
a1b1 b12
a2b2 b2 2
c2
a2b1 b12
a1b2 b22
6.2 复数
4.复数乘除运算——采用极坐标形式
若 A1=|A1| 1 ，A2=|A2| 2
则: A1 A2 A1 e j1 A2 e j2
*无线通讯频率：30 KHz - 3×104 MHz
6.1 正弦量
同一个正弦量，计时起点不同，初相位不同。
初相位：最大值与纵轴之间的
角度，与计时起点有关。
规定： ||
最大值点在 纵轴的左边
最大值点在 纵轴的右边
推迟到达 最大值点
提前到达 最大值点
【例】已知正弦电流波形如图，w＝103rad/s， （1）写出i(t)表达式；
第六章 相量法(1)
设 u(t)=Umcos(ω t+ψ u), i(t)=Imcos(ω t+ψ i) 则 相位差 : = (ω t+ψ u)- (ω t+ψ i)= ψ u-ψ i 等于初相位之差 规定: 规定: | | ≤π (180°). °.
>0, u超前 角,或i 落后u 角(u 比i先到达最大值); 超前i 先到达最大值) 超前 先到达最大值 u, i u i O
Im A2
图解法
(1)加减运算 (1)加减运算——采用代数形式 采用代数形式 加减运算 若 则
A1=a1+jb1, A2=a2+jb2 A1±A2=(a1±a2)+j(b1±b2)
A1 0 Re
乘除运算——采用极坐标形式 (2) 乘除运算 采用极坐标形式 若 则:
A1=|A1| θ 1 ,A2=|A2| θ 2
ψu ψi 先到达最大值. <0, i 超前 u 角,或u 滞后 i 角,i 比 u 先到达最大值. ,
ωt
特殊相位关系: 特殊相位关系:
=±π (±180o ) ,反相: 反相: ±π ±
u, i u u i 0 u, i u i 0 iω t
= 0, 同相: 同相:
u, i
0 = π/2: π/2
i , Im , I
5.正弦量的相量表示 5.正弦量的相量表示 问题的提出: ① 问题的提出:
电路方程是微分方程: 电路方程是微分方程: +i R C L
u
_
d uC duC LC + RC + uC = u(t ) dt dt
2
两个正弦量的相加: 方程运算. 两个正弦量的相加:如KCL,KVL方程运算. , 方程运算
>0, u超前 角,或i 落后u 角(u 比i先到达最大值); 超前i 先到达最大值) 超前 先到达最大值 u, i u i O
Im A2
图解法
(1)加减运算 (1)加减运算——采用代数形式 采用代数形式 加减运算 若 则
A1=a1+jb1, A2=a2+jb2 A1±A2=(a1±a2)+j(b1±b2)
A1 0 Re
乘除运算——采用极坐标形式 (2) 乘除运算 采用极坐标形式 若 则:
A1=|A1| θ 1 ,A2=|A2| θ 2
ψu ψi 先到达最大值. <0, i 超前 u 角,或u 滞后 i 角,i 比 u 先到达最大值. ,
ωt
特殊相位关系: 特殊相位关系:
=±π (±180o ) ,反相: 反相: ±π ±
u, i u u i 0 u, i u i 0 iω t
= 0, 同相: 同相:
u, i
0 = π/2: π/2
i , Im , I
5.正弦量的相量表示 5.正弦量的相量表示 问题的提出: ① 问题的提出:
电路方程是微分方程: 电路方程是微分方程: +i R C L
u
_
d uC duC LC + RC + uC = u(t ) dt dt
2
两个正弦量的相加: 方程运算. 两个正弦量的相加:如KCL,KVL方程运算. , 方程运算
相位差测量
第3章 信号发生器
可变相移器的改进: 前一页的RC相移器(图6.5-2)—最大调节度为0°~90° 改进一:下图(a):变压器式相移器--最大调节度为0°~180° ----但缺点:变压器体积大,能耗也大. 改进二:下图(b): RC+V(晶体管)相移器 特点:∵晶体管c极与 e极电压相移180°∴将RC接到ce极间
1。差接式相位检波器 2。平衡式相位检波器
第3章 信号发生器
1。差接式相位检波器（电路）
电路特点：元件参数严格对称：R1＝R2;C1=C2; 测量条件：U1>>U2>1V; （信号1幅度>>信号2幅度）
R1C1、R2C2、R3C3 >>T（时间常数>> 被测信号周期）
u 工作原理：AB两点电压： AE = u1+u2(为两信号矢量相加) EB两点电压：uEB = u1-u2(为两信号矢量相减) F点电压： uF = －u2＋U2mcos φ 经滤波除去u2后uF0 = U2mcos φ
经滤波除去第二项高频成份后 i=4a2U1mU2mcosφ ----只剩下与相差有关的项。 （与输入频率的项已不存在）
第3章 信号发生器
6. 5 零示法测量相位差
零示法又称比较法。 方法：通过精密移相器的相移值与被测相移值作比较来确 定被测信号间的相位差。
测量时:调节可变相移器进行移相, 当 平衡时:u1的相位= u2的相位; 指示器指示=0; 则: u1 u2的相位差=可变相移器的相移值.
第3章 信号发生器
一。直接比较法
如图所示为一双踪示波器测量信号时屏幕显示的图像。已知两被测正弦波信号的频 率相同。示波器 置于1V档， 置于1s 档。求：⑴两正弦波信号的幅度频率。⑵ 两信号的相位差。
第6章 单点定位
• 单位权中误差，其受伪距测量精度、星历精度及大气延迟 影响；
• 对应的协因数矩阵，它由卫星的空间几何分布决定
6.1 伪距单点定位
协因数矩阵中各个元素反映了在特定的卫星空间几何分布 下，不同参数的定位精度及其相关性信息。因此，利用这些信 息即可描述卫星空间几何分布对定位精度影响的精度因子: 常用的精度因子有： （1）几何精度因子（Geometric Dilution of Precision, GPOP）
式中 ， Qx
qYX
qYY
qYZ
R
sin L0
cos L0
0
为坐标转换矩阵，
qZX qZY qZZ
cos B0 cos L0 cos B0 sin L0 sin B0
B0和L0分别为对应的大地纬度和大地经度。
6.1 伪距单点定位
由此可得到另两个常用的精度因子 （4）水平精度因子（Horizontal Dilution of Precision, GPOP）
23934824.154
23978631.5766+43
822.577
24181945.803 24298916.7595+116 967.755
22957572.280 22965399.9529+7 834.145
22385541.968 22355209.7858 30 330.506
ni
1
VX VY
VZ
=i
i0
+cV t
i
S
Ii Ti i
cVtR
若接收机同时接收n（ n ≥4）颗卫星，则上式可写为：
6.1 伪距单点定位
l1
l2
l3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第6章 相位差测量
第6章 相位差测量
6.1 概 述
6.2 用示波器测量相位差
第6章 相位差测量
6.1 概
述
振幅、频率和相位是描述正弦交流电的三个“要 素”。以电压为例，其函数关系为
u Um sin(t 0 )
（6.1-1）
为角频率； 0 为初相位。 式中：Um为电压的振幅；
第6章 相位差测量
常数，并等于两正弦量的初相之差。在实际工作中， 经常需要研究诸如放大器、滤波器、各种器件等的频
率特性，即输出输入信号间幅度比随频率的变化关系
(幅频特性)和输出输入信号间相位差随频率的变化关系 (相频特性).尤其在图像信号传输与处理、多元信号的 相干接收等学科领域，研究网络(或系统)的相频特性显 得更为重要。
(6.2-4)
第6章 相位差测量
式中 KY、K X 为比例常数。设 u1、u2 分别为
u1 U m1 sin(t ) u2 U m 2 sin t
将式(6．2—5)代入式(6．2—4)得
(6.2-5)
y KY U m1 sin(t ) Ym sin(t ) Ym sin t cos Ym cost sin ( a ) (6.2-6) x K X U m 2 sin t X m sin t ( b)
相位差 。
第6章 相位差测量
6.4 为什么“瞬时”式数字相位差计只适用于测量 固定频率的相位差?如何扩展测量的频率范围? 6.5 用示波器测量两同频正弦信号的相位差，示 波器上呈现椭圆的长轴A为100m，短轴B为4cm，试计 算两信号的相位差 。
tB t A T 360 360 tC t A T
(6.2-2)
式中：T为两同频正弦波的周期； T 为两正弦波过零点 的时间差。
第6章 相位差测量
若示波器水平扫描的线性度很好，则可将线段AB 写为 AB k (tC t A ) ，线段 AC k (tC t A ) ，其中 秃为比例常数，则式(6．2—2)改写为
第6章 相位差测量
图6.2—5 校正系统固有相位差
第6章 相位差测量
习 题 六
6.1 举例说明测量相位差的重要意义。 6.2 测量相位差的方法主要有哪些?简述它们各自 的优缺点。 6.3 用椭圆法测量两正弦量的相位差，在示波器上 显示图形如图6．2-3所示，测得椭圆中心横轴到图形
最高点的高度Ym＝5cm，椭圆与)Y轴交点y0＝4cm，求
(1 2 )t (1 2 )
(6.1-3)
第6章 相位差测量
显然，两个角频率不相等的正弦电压(或电流)之间
的瞬时相位差是时间t的函数，它随时间改变而改变。 当两正弦电压的角频率 1 2 时，则有 (6.1-4)
1 2
第6章 相位差测量
由此可见：两个频率相同的正弦量间的相位差是
设 t 0 ，称瞬时相位，它随时间改变， 0 是t=0时刻的瞬时相位值。两个角频率为 1、2 的正
弦电压分别写为
u1 U m1 sin(1t 1 ) u2 U m 2 sin( 2t 2 )
它们的瞬时相位差
(6.1-2)
(1t 1 ) (2t 2 )
于此点用来测量相位差的方法称为椭圆法。
第6章 相位差测量
一般情况下，示波器的Y、X两个通道可看作为线
性系统，所以荧光屏上光点的位移量正比于输入信号 的瞬时值。如图6．2—2所示，u1加于y通道，u2加于X
通道，则光点沿垂直及水平的瞬时位移量y和x分别为
y KY u1 x K X u2
第6章 相位差测量
相位差的测量是研究网络相频特性中必不可少的 重要方面，如何使相位差的测量快速、精确已成为生 产科研中重要的研究课题。 测量相位差的方法很多，主要有：用示波器测量； 把相位差转换为时间间隔，先测量出时间间隔再换算
为相位差；把相位差转换为电压，先测量出电压再换
算为相位差；与标准移相器的比较(零示法)等。本章对 上述四类方法测量相位差的基本工作原理都作以介绍，
第6章 相位差测量
图6.2—4 相位差刻度板
第6章 相位差测量
设椭圆的长轴为A，短轴为B，可以证明相位差
B 2 arctan A
(6.2-10)
如果在示波器荧光屏上配置一个如图6．2—4所示 的刻度板，测量时读取椭圆长、短轴刻度，由式
(6．2—10) 可算出 。由于椭圆总是与短轴垂直，测量
第6章 相位差测量
式中Ym、Xm分别为光点沿垂直及水平方向的最大
位移。由式(6．2—6)(b)得sin t x / X m ，代入式(a)得
Ym 2 y ( x cos X m x 2 sin ) Xm
(6.2-7)
式(6．2—7)是一个广义的椭圆方程，其椭圆图形
如图6．2—30令式(6．2—7)中 x 0, y 0 ，求出 椭圆与垂直、水平轴的交点歹 y0、x0分别等于
视角小，同时短轴对甲的变化很敏感，因而测量误差 较小。
第6章 相位差测量
还应说及的是，示波器Y通道、X通道的相频特性
一般不会是完全一样的，这要引起附加相位差，又称 系统的固有相位差。为消除系统固有相位差的影响，
通常在一个通道前接一移相器(如Y通道前)，在测量前
先把一个信号，如 u1 (t ) ，接入X通道和经移相器接入 Y通道，如图6．2-5(a)所示。调节移相器使荧光屏上显 示的图形为一条直线，然后把一个信号经移相器接入Y 通道，另一个信号接入X通道进行相位差测量，如图 6．2—5(b)所示。
但重点讨论把相位差转换为时间间隔的测量方法。
第6章 相位差测量Biblioteka 6.2 用示波器测量相位差
一、直接比较法
设电压
u1 (t ) U m1 sin(t ) u2 (t ) U m 2 sin t
（6.2-1）
为了叙述问题方便，并设式(6.2—1)中u2(t)的初相位为零。
第6章 相位差测量
图6.2—1 比较法测量相位差
第6章 相位差测量
将ul、u2分别接到双踪示波器的Y1通道和Y2通道，
适当调节扫描旋钮和Y增益旋钮，使在荧光屏上显示出 如图6.2—1所示的上下对称的波形。设u1过零点分别为
A、C点，对应的时间为
t A、tC ; u2
过零点分别为B、
D点，对应的时间为 tB、tD 。正弦信号变化一周是360o, 过零点A比u2过零点B提前 tB t A 出现，所以u1超前u2的 相位，即u1与u2的相位差
y0 Ym sin x0 X m sin
(6.2-8)
第6章 相位差测量
图6.2—2 椭圆法测量相位差
第6章 相位差测量
图6.2—3 椭圆图形
第6章 相位差测量
由式(6，2—8)可解算得相位差
y0 x0 arctan( ) arcsin( ) Ym Xm
AB 360 AC
(6.2-3)
量得波形过零点之间的长度AB和AC即可由式 (6.2—3)计算出相位差 。
第6章 相位差测量
二、椭圆法 在§5。6中讲述了李沙育图形法测量信号频率， 若频率相同的两个正弦量信号分别接到示波器的X通道 与Y通道，一般情况下示波器荧光屏上显示的李沙育图 形为椭圆，而椭圆的形状和两信号的相位差有关，基
第6章 相位差测量
6.1 概 述
6.2 用示波器测量相位差
第6章 相位差测量
6.1 概
述
振幅、频率和相位是描述正弦交流电的三个“要 素”。以电压为例，其函数关系为
u Um sin(t 0 )
（6.1-1）
为角频率； 0 为初相位。 式中：Um为电压的振幅；
第6章 相位差测量
常数，并等于两正弦量的初相之差。在实际工作中， 经常需要研究诸如放大器、滤波器、各种器件等的频
率特性，即输出输入信号间幅度比随频率的变化关系
(幅频特性)和输出输入信号间相位差随频率的变化关系 (相频特性).尤其在图像信号传输与处理、多元信号的 相干接收等学科领域，研究网络(或系统)的相频特性显 得更为重要。
(6.2-4)
第6章 相位差测量
式中 KY、K X 为比例常数。设 u1、u2 分别为
u1 U m1 sin(t ) u2 U m 2 sin t
将式(6．2—5)代入式(6．2—4)得
(6.2-5)
y KY U m1 sin(t ) Ym sin(t ) Ym sin t cos Ym cost sin ( a ) (6.2-6) x K X U m 2 sin t X m sin t ( b)
相位差 。
第6章 相位差测量
6.4 为什么“瞬时”式数字相位差计只适用于测量 固定频率的相位差?如何扩展测量的频率范围? 6.5 用示波器测量两同频正弦信号的相位差，示 波器上呈现椭圆的长轴A为100m，短轴B为4cm，试计 算两信号的相位差 。
tB t A T 360 360 tC t A T
(6.2-2)
式中：T为两同频正弦波的周期； T 为两正弦波过零点 的时间差。
第6章 相位差测量
若示波器水平扫描的线性度很好，则可将线段AB 写为 AB k (tC t A ) ，线段 AC k (tC t A ) ，其中 秃为比例常数，则式(6．2—2)改写为
第6章 相位差测量
图6.2—5 校正系统固有相位差
第6章 相位差测量
习 题 六
6.1 举例说明测量相位差的重要意义。 6.2 测量相位差的方法主要有哪些?简述它们各自 的优缺点。 6.3 用椭圆法测量两正弦量的相位差，在示波器上 显示图形如图6．2-3所示，测得椭圆中心横轴到图形
最高点的高度Ym＝5cm，椭圆与)Y轴交点y0＝4cm，求
(1 2 )t (1 2 )
(6.1-3)
第6章 相位差测量
显然，两个角频率不相等的正弦电压(或电流)之间
的瞬时相位差是时间t的函数，它随时间改变而改变。 当两正弦电压的角频率 1 2 时，则有 (6.1-4)
1 2
第6章 相位差测量
由此可见：两个频率相同的正弦量间的相位差是
设 t 0 ，称瞬时相位，它随时间改变， 0 是t=0时刻的瞬时相位值。两个角频率为 1、2 的正
弦电压分别写为
u1 U m1 sin(1t 1 ) u2 U m 2 sin( 2t 2 )
它们的瞬时相位差
(6.1-2)
(1t 1 ) (2t 2 )
于此点用来测量相位差的方法称为椭圆法。
第6章 相位差测量
一般情况下，示波器的Y、X两个通道可看作为线
性系统，所以荧光屏上光点的位移量正比于输入信号 的瞬时值。如图6．2—2所示，u1加于y通道，u2加于X
通道，则光点沿垂直及水平的瞬时位移量y和x分别为
y KY u1 x K X u2
第6章 相位差测量
相位差的测量是研究网络相频特性中必不可少的 重要方面，如何使相位差的测量快速、精确已成为生 产科研中重要的研究课题。 测量相位差的方法很多，主要有：用示波器测量； 把相位差转换为时间间隔，先测量出时间间隔再换算
为相位差；把相位差转换为电压，先测量出电压再换
算为相位差；与标准移相器的比较(零示法)等。本章对 上述四类方法测量相位差的基本工作原理都作以介绍，
第6章 相位差测量
图6.2—4 相位差刻度板
第6章 相位差测量
设椭圆的长轴为A，短轴为B，可以证明相位差
B 2 arctan A
(6.2-10)
如果在示波器荧光屏上配置一个如图6．2—4所示 的刻度板，测量时读取椭圆长、短轴刻度，由式
(6．2—10) 可算出 。由于椭圆总是与短轴垂直，测量
第6章 相位差测量
式中Ym、Xm分别为光点沿垂直及水平方向的最大
位移。由式(6．2—6)(b)得sin t x / X m ，代入式(a)得
Ym 2 y ( x cos X m x 2 sin ) Xm
(6.2-7)
式(6．2—7)是一个广义的椭圆方程，其椭圆图形
如图6．2—30令式(6．2—7)中 x 0, y 0 ，求出 椭圆与垂直、水平轴的交点歹 y0、x0分别等于
视角小，同时短轴对甲的变化很敏感，因而测量误差 较小。
第6章 相位差测量
还应说及的是，示波器Y通道、X通道的相频特性
一般不会是完全一样的，这要引起附加相位差，又称 系统的固有相位差。为消除系统固有相位差的影响，
通常在一个通道前接一移相器(如Y通道前)，在测量前
先把一个信号，如 u1 (t ) ，接入X通道和经移相器接入 Y通道，如图6．2-5(a)所示。调节移相器使荧光屏上显 示的图形为一条直线，然后把一个信号经移相器接入Y 通道，另一个信号接入X通道进行相位差测量，如图 6．2—5(b)所示。
但重点讨论把相位差转换为时间间隔的测量方法。
第6章 相位差测量Biblioteka 6.2 用示波器测量相位差
一、直接比较法
设电压
u1 (t ) U m1 sin(t ) u2 (t ) U m 2 sin t
（6.2-1）
为了叙述问题方便，并设式(6.2—1)中u2(t)的初相位为零。
第6章 相位差测量
图6.2—1 比较法测量相位差
第6章 相位差测量
将ul、u2分别接到双踪示波器的Y1通道和Y2通道，
适当调节扫描旋钮和Y增益旋钮，使在荧光屏上显示出 如图6.2—1所示的上下对称的波形。设u1过零点分别为
A、C点，对应的时间为
t A、tC ; u2
过零点分别为B、
D点，对应的时间为 tB、tD 。正弦信号变化一周是360o, 过零点A比u2过零点B提前 tB t A 出现，所以u1超前u2的 相位，即u1与u2的相位差
y0 Ym sin x0 X m sin
(6.2-8)
第6章 相位差测量
图6.2—2 椭圆法测量相位差
第6章 相位差测量
图6.2—3 椭圆图形
第6章 相位差测量
由式(6，2—8)可解算得相位差
y0 x0 arctan( ) arcsin( ) Ym Xm
AB 360 AC
(6.2-3)
量得波形过零点之间的长度AB和AC即可由式 (6.2—3)计算出相位差 。
第6章 相位差测量
二、椭圆法 在§5。6中讲述了李沙育图形法测量信号频率， 若频率相同的两个正弦量信号分别接到示波器的X通道 与Y通道，一般情况下示波器荧光屏上显示的李沙育图 形为椭圆，而椭圆的形状和两信号的相位差有关，基