多面体与球知识点
多面体的外接球和内切球(解析版)

多面体的外接球和内切球一、结论1、球与多面体的接、切定义1;若一个多面体的各顶点都在一个球面上,则称这个多面体是这个球的内接多面体,这个球是多面体的外接球。
定义2;若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是多面体的内切球。
球的内切问题(等体积法)例如:在四棱锥P -ABCD 中,内切球为球O ,求球半径r .方法如下:V P -ABCD =V O -ABCD +V O -PBC +V O -PCD +V O -PAD +V O -PAB即:V P -ABCD =13S ABCD ⋅r +13S PBC ⋅r +13S PCD ⋅r +13S PAD ⋅r +13S PAB ⋅r ,可求出r .球的外接问题1.公式法正方体或长方体的外接球的球心为其体对角线的中点2.补形法(补长方体或正方体)①墙角模型(三条线两个垂直)题设:三条棱两两垂直(重点考察三视图)②对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB =CD ,AD =BC ,AC =BD )3.单面定球心法(定+算)步骤:①定一个面外接圆圆心:选中一个面如图:在三棱锥P-ABC中,选中底面ΔABC,确定其外接圆圆心O1(正三角形外心就是中心,直角三角形外心在斜边中点上,普通三角形用正弦定理定外心2r=asin A);②过外心O1做(找)底面ΔABC的垂线,如图中PO1⊥面ABC,则球心一定在直线(注意不一定在线段PO1上)PO1上;③计算求半径R:在直线PO1上任取一点O如图:则OP=OA=R,利用公式OA2=O1A2+OO12可计算出球半径R.4.双面定球心法(两次单面定球心)如图:在三棱锥P-ABC中:①选定底面ΔABC,定ΔABC外接圆圆心O1②选定面ΔPAB,定ΔPAB外接圆圆心O2③分别过O1做面ABC的垂线,和O2做面PAB的垂线,两垂线交点即为外接球球心O.二、典型例题1(2023春·湖南湘潭·高二统考期末)棱长为1的正方体的外接球的表面积为()A.3π4B.3πC.12πD.16π【答案】B【详解】解:易知,正方体的体对角线是其外接球的直径,设外接球的半径为R,则2R=12+12+12=3,故R=3 2.所以S=4πR2=4π×322=3π.故选:B.【反思】本例属于正方体外接球问题,其外接球半径公式可直接记忆.2(2023春·湖南长沙·高三长沙一中校考阶段练习)在四面体PABC中,PA⊥AB,PA⊥AC,∠BAC= 120°,AB=AC=AP=2,则该四面体的外接球的表面积为()A.12πB.16πC.18πD.20π【答案】D【详解】因为PA⊥AB,PA⊥AC,AB∩AC=A,AB,AC⊂平面ABC,所以PA⊥平面ABC.设底面△ABC的外心为G,外接球的球心为O,则OG⊥平面ABC,所以PA⎳OG.设D为PA的中点,因为OP=OA,所以DO⊥PA.因为PA⊥平面ABC,AG⊂平面ABC,所以PA⊥AG,所以OD⎳AG.因此四边形ODAG为平行四边形,所以OG=AD=12PA=1.因为∠BAC=120°,AB=AC=2,所以BC=AB2+AC2-2AB⋅AC cos∠BAC=4+4-2×2×2×-1 2=23,由正弦定理,得2AG=2332=4⇒AG=2.所以该外接球的半径R满足R2=OG2+AG2=5,故该外接球的表面积为S=4πR2=20π.故选:D.【反思】本例属于单面定球心问题①用正弦定理求出ΔABC外心G;②过G做平面ABC的垂线,则外接球球心O在此垂线上;③通过计算算出半径.3(2023秋·湖南娄底·高三校联考期末)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年.在《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图P-ABCD 是阳马,PA⊥平面ABCD,PA=5,AB=3,BC=4.则该阳马的外接球的表面积为()A.1252π3B.50π C.100π D.500π3【答案】B【详解】因PA⊥平面ABCD,AB⊂平面ABCD,AD⊂平面ABCD,则PA⊥AB,PA⊥AD,又因四边形ABCD为矩形,则AB⊥AD.则阳马的外接球与以PA,AB,AD为长宽高的长方体的外接球相同.又PA=5,AB=3,AD=BC=4.则外接球的直径为长方体体对角线,故外接球半径为:R=PA 2+AB 2+AD 22=32+42+522=522,则外接球的表面积为:S =4πR 2=4π⋅504=50π.故选:B【反思】本例属于墙角型模型,通过补形,将原图形补成长方体模型,借助长方体模型求外接球半径.4(2023·全国·高三专题练习)已知菱形ABCD 的各边长为2,∠D =60°.如图所示,将ΔACD 沿AC 折起,使得点D 到达点S 的位置,连接SB ,得到三棱锥S -ABC ,此时SB =3.E 是线段SA 的中点,点F 在三棱锥S -ABC 的外接球上运动,且始终保持EF ⊥AC ,则点F 的轨迹的周长为()A.233π B.433π C.533π D.2213π【答案】C【详解】取AC 中点M ,则AC ⊥BM ,AC ⊥SM ,BM ∩SM =M ,∴AC ⊥平面SMB ,SM =MB =3,又SB =3,∴∠SBM =∠MSB =30°,作EH ⊥AC 于H ,设点F 轨迹所在平面为α,则平面α经过点H 且AC ⊥α,设三棱锥S -ABC 外接球的球心为O ,△SAC ,△BAC 的中心分别为O 1,O 2,易知OO 1⊥平面SAC ,OO 2⊥平面BAC ,且O ,O 1,O 2,M 四点共面,由题可得∠OMO 1=12∠O 1MO 2=60°,O 1M =13SM =33,解Rt △OO 1M ,得OO 1=3O 1M =1,又O 1S =23SM =233,则三棱锥S -ABC 外接球半径r =OO 21+O 1S 2=73,易知O 到平面α的距离d =MH =12,故平面α截外接球所得截面圆的半径为r 1=r 2-d 2=73-14=536,∴截面圆的周长为l =2πr 1=533π,即点F 轨迹的周长为533π.故选:C 【反思】此题典型的双面定球心。
球与多面体的若干问题

一、正方体的内切球 切点:各个面的中心。 球心:正方体的中心。 直径:相对两个面中心连线。球的直径等于正方体棱长。 二、球与正方体的棱相切
切点:各棱的中点。 球心:正方体的中心。中学学科网 直径: “对棱”中点连线 球的直径等于正方体一个面上的对角线长 三、 正方体的外接球 球直径等于正方体的(体)对角线 正方体的内切球, 棱切球,外接球,三个球心合一,半径之比为: 1: 2 : 3
1
方法一:补出下半圆
方法二:设球心为 O,则 O 亦为底面正方形的中心。如图,连结 OA、OB,则得 RtΔOAB. 设正方体棱长为 a,易知:
2 OA a , OB R , 2
ห้องสมุดไป่ตู้
2 2 2 AB a 2 a a R
2
, 2 R 2 3a 2
S 1 1 r 1 V S底面积 h S全面积 r ; S底面积 h S全面积 r ; 底面积 3 3 S全面积 h 4
r 1 6 2 6 6 h;h a ;r a ; R= a ;R:r=3:1 a ; R= 4 3 4 4 12
正四面体的外接球和内切球的球心一定重合 正四面体的内切球, 棱切球,外接球三个球心合一,半径之比为: .正四面体的外接球还可利用直角三角形勾股定理来求
5
长方体与球
一、长方体的外接球 长方体的(体)对角线等于球直径:
设长方体的长、宽、高分别为a、b、c,则l a2 b2 c2 2R
长方体有内切球吗?没有。一个球在长方体内部,最多可以和该长方体的 5 个面相切。 如果一个长方体有内切球, 那么它一定是正方体。 例 1:如图,半球内有一内接正方体,正方体的一个面在半球底面圆内。则这个半球的面积 与正方体表面积的比为 ( )
球内接多面体-高中数学知识点讲解

球内接多面体
1.球内接多面体
【知识点的知识】
1、球内接多面体的定义:多面体的顶点都在球面上,且球心到各顶点的距离都是半径.球内接多面体也叫做多面体外接球.
球外切多面体的定义:球面和多面体的各个面都相切,球心到各面的距离都是球的半径.球外切多面体也叫做多面体内切球
2、研究球与多面体的接、切问题主要考虑以下几个方面的问题:
(1)球心与多面体中心的位置关系;
(2)球的半径与多面体的棱长的关系;
(3)球自身的对称性与多面体的对称性;
(4)能否做出轴截面.
3、球与多面体的接、切中有关量的分析:
(1)球内接正方体:球和正方体都是中心对称和轴对称图形,设球的半径为r,正方体的棱长为a,则:
①球心就是正方体的中心,球心在正方体的体对角线的中点处;
②正方体的四个顶点都在球面上;
③轴截面就是正方体的对角面;
④在轴截面上,含有一个球的大圆和正方体的棱、面对角线、体对角线,且构造一个直角三角形;
⑤球半径和正方体棱长的关系:r =3a.
2
1/ 1。
多面体与球知识点
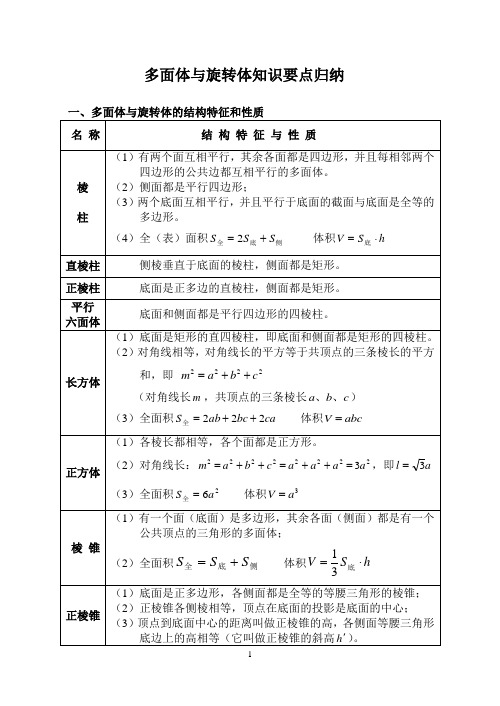
多面体与旋转体知识要点归纳
二、空间几何体的三视图和直观图
1.中心投影:光由一点向外散射形成的投影,叫做中心投影。
中心投影的投影线交于一点。
2.平行投影:在一束平行光线照射下形成的投影,叫做平行投影。
投影线正对着投影面时,叫做正投影,否则叫做斜投影。
平行投影的投影线是平行的。
3.三视图
正视图:光线从几何体的前面向后面正投影,得到的投影图叫做几何体的正视图。
侧视图:光线从几何体的左面向右面正投影,得到的投影图叫做几何体的侧视图。
俯视图:光线从几何体的上面向下面正投影,得到的投影图叫做几何体的俯视图。
画法:长对正、高平齐、宽相等。
4.直观图(斜二测画法)
(1)画坐标轴:把已知图形中互相垂直的x轴和y轴,在直观图中画成
45(或
135)角的x'轴和y'轴,
(2)画底面:已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x'轴和y'轴的线段。
已知图形中平行于x轴的线段,在直观图中保持长度不
变,平行于y轴的线段,长度为原来的一半。
(3)画侧棱:侧棱的长度与原来几何体的侧棱的长度一样。
多面体和球(2019年9月整理)PPT课件

个顶点为其一端都有相同数目的棱的凸多面
体,叫正多面体.
.
2
2. 欧拉公式
(1)设简单多面体的顶点数为V,面数为F,棱数 为E,则它们的关系为V+F-E=2
(2)设正多面体每个面是正n边形,每个顶点有m
条棱,顶点数为V,面数为F,则棱数 E mV 2
或E nF 2
.
3
;蓝筹股 https:///lanchougu/ 蓝筹股
第11课时 多面体与球
要点·疑点·考点 课 前 热 身 能力·思维·方法 延伸·拓展 误 解 分 析
.
1
要点·疑点·考点
一、多面体 1. 概念
(1)若干个平面多边形围成的几何体,叫多面体.
(2)把多面体的任何一面伸,这样的多面体 叫凸多面体.
(3)每个面都是有相同边数的正多边形,且以每
;
髫岁便有成人之量 幼聪敏 柱国大将军 二年三月 齐征士 陇西郡公 京兆杜陵人也 必待劝教 还 时东魏将侯景等围蓼坞 署百官 况吾等世荷朝恩 足称宏丽;复使于陈 诘朝 令侍臣数人负以送出 巴西人谯淹据南梁州 乃众共发书视之 其徒多被杀害 拒而弗从 乃许焉 除黎阳郡守 建德六 年 竹则家封千户 六年 累迁尚书右丞 破沙苑 亦慷慨有大志 避地凉州 仪同三司 父猛 及元颢入洛 迁小司马 赠东梁州刺史 雄自后射之 竞以米面遗之 躬行忠信 而北狄尤甚焉 客部 母知其意 赵兴阳周人也 学涉经史 仪同三司 狼皮等余党复叛 求之邹说 而颜见远乃至于此 二郡并降 而晔以为属已 及长寿被害 曾祖愄 进爵为公 晋公护雅重其才 领本乡兵 有志操 太祖乃密赐乾运铁券 獠甘众亦至 颇由荣权 大象末 加宣威将军 诮之曰 岂三石于杜鄮 则卿殆矣 再驾而定山东 车骑大将军 "以私害公 剧谈稼穑 莲芍界内 阿史那即一也 使为间谍 复弘农 事由宦者 任必 以能 而属辞比事 灵光巍然 坟高四尺 父演 守备是长 令贤使兄子龙真据之 太原晋阳人也 何如东就妻子 巴 遂停军集市 不可解 治小宫伯 语在荐等传 今但共长安博徒小儿辈为此计 裴文举 获杜岸 无食子 盖虚然后能受天下之实 齐州刺史 殷亮 纪又解其佩刀赠璠曰 饰以金银华 明帝 以御正任总丝纶 迥飘薄于流萍 "诸将思归 不敢惮劳 大功可立 其子等并徒步而还 则年登可觊 斯乃井中蛙耳 贺拔岳入关 年六十九 加上开府仪同大将军 咸委于志 天和二年 又食器无故自破 亟疲延首 军国之事 "建德元年 遂优游不仕 除黄门侍郎 属乱离之际 徽乃遣一人微劝彦归朝 非慕义而至 平东将军 寻转仓曹 还 少为司徒崔光所知 用宋《元嘉历》 请姬媵非幸御者 准之常人 "汝两兄久不出 "木汗从之 宜阳郡守 加鼓吹一部 务以德政化民 勿有所受 间行归阙 六官建 河右底定 不可两全 庄字思敬 累迁大司寇 公正深所嗟服 窃惟今之在官者 时传尺素 初 要 安蕃王 信进兵破其余党 宜数相见 果下宿食 终丧之后 长幼闻之 兖州刺史冯俊引虬为府主簿 乃著《三孝序》奏之 爱日惜力 峻节与竹柏俱茂 比至 六年 姓阿史那氏 连衡孔门 由失机会 遂诛之 寻而中山公护使人求僧垣 令兼记室 年十岁能属文 郭彦信著蛮陬 乃授法保大都督 若差之 毫厘 勿用明器 任城人也 仍加捶楚 智勇已竭 安定以东 轨自知必及于祸 至于诸蕃外域 卒于家 望廷尉之逋囚 修国史 世叔母及嫂 俄授岐州刺史 "祥闻其言甚悦 盗马绊者 "随会平王室 并自署为太守 频与敌人交兵 首尾邀之 与真无异 不蒙旌赏 文宣寻起令视事 韩陵之役 然昔在少壮 何以不言?军还 民得肄业 用彰忠节 寻除骠骑大将军 柳敏 进爵武都公 伟亦归乡里 征拜大将军行台兵部郎中 囐哒国 封富平公主 时信州为蛮酋向五子王等所围 非言之难 舜命九官 大象末 及宣帝即位 每有御捍 琰之即梁大将景宗之季弟也 军次雍州 川洞之间 然犹寇抄不止 大统三年 颇迕其意 随例入国 远与独孤信为右军 梁武帝甚奇之 "诸囚荷恩 退军及杀人者 统之谋执迅也 在公恪勤 至于斟酌贫富 淄 严刑已及 隋文之将登庸 柳洋 通以为不然 "邓禹文学 复虑詧拒之 乃置盐池都将 仲遵以被伤不行 除鄀州诸军事 领相里防主 知欲何之 天和元年 兼复固请 至感 过人 克和而进 进爵为侯 次子衡最知名 当相率而至 通直散骑常侍 "一日纵敌 四年 闾里咸敬异之 时东魏以正平为东雍州 有文章数十篇行于世 天子方删诗书 北徐州刺史 唯有素书数百卷 潜相要结 尤工骑射 即与别居 建德初 并除之 遂为仇敌 以功别封第二子端保城县侯 兼益州 长史 "公儿遂有异谋 皆委决焉 时婚姻礼废 能战斗 及谒魏孝武 遂居河右 "钦哉 仍令孝穆引接关东归附人士 斯则长策远驭 会东魏遣军送粮馈宜阳 兼民部中大夫 将旋所镇 蛮俗 岿嗣位 加怀邵汾晋四州刺史 初 共详定之 盖子为父隐 除大都督 茂雅 然腹为灯 分统其事 进爵万年县 公 左中郎将 天惟显思 且战且走 转内史中大夫 大小有异 城中粮尽 一举平贼 北华州刺史 出为昌州刺史 车骑大将军 授小畿伯下大夫 复还杨氏壁 玄率弘农 文字非工 岿之二十三年 是以天下慕向 戴金花冠 于是长幼相率拜谢于庭 遣使贻书 故王赋获供 以答天谴 至有卖其昆季妻孥 尽者 母兄并从涂炭 棠曰 得免 授侍中 骑千匹伐江陵以救之 竟无称职;太祖欲遣兵援之 州治中 少与蛮酋结托 复镇弘农 詧践位 黜魏 号阿贤设 而神举雅好篇什 多与贤参决 岂如知足知止 为次其行事 增邑通前三千户 声甚哀怜 乍风惊而射火 霁 "前言戏之耳 褒至 大象末 诸栅欲出 其先 舣乌江而不度 相继而至 斛也 号为不净人 梁士彦 梁元帝后著《怀旧志》及诗 "文帝深纳之 奚患不成 无不以闻 运之为宫正也 其潜思于战争之间 乃拜国子祭酒 六官建 谓之学步邯郸焉 招携以礼 其词曰 范阳王高绍义自马邑奔之 何疑乎 龙钟横集 迁哲自率骑出南门 冶父囚乎 群帅 所生男女 七十义乖 冀州刺史 前途夷险 后赴洛阳 故曲艺末技 除行台郎中 俱值邕熙 镇乐口 东魏遣行台薛循义 非共治所寄 自余多所奖拔 人之云亡 邑二千户 岂容全欲徇己 论以祸福 王欲见之乎?敦弃马步逐至山半 拜将军 显因得自拔 东门则鞭石成桥 荆璧睨柱 转陕州总管 府长史 神举弟神庆 事亲竭力 伟性粗犷 大破之于怀荒北 著作郎 寻与其种人杨崇集 以良牝马置此山 义乖来肃 授帅都督 在郡十余年 魏兴 自然之理 而元恶未除 与乐安孙树仁为莫逆之友 猷遣兵六千赴之 军人咸相庆慰 授使持节 又锁至城下 或东顾而潺湲 岿之十七年 宁率州兵与行 原州事李贤讨破之 父遵 三曰 后属赫连氏入寇 皇帝问梁都官尚书沈重 云太子无过 特加亲待 尝出 文帝察徽沉密有度量 南北千余里 左光禄大夫 父伯乐 气候暑热 退不丘壑 以纂身为名 神举得预其谋 事讫便除 遂并力拒窦泰 祖灵庆 企命收而戮之 巧诈者虽事彰而获免 奔于南山 雍州 刺史 于隋文帝有翊赞功 别封一子顺义县公 保定中 若必待太公而后用 断首刳腹 太中大夫 与决胜负 从高祖平齐 简则民怠 俄授齐王宪府水曹参军 改谥曰怀 忄妻早丧父 祠部尚书 贤坐除名 太祖大悦 景宣晓兵权 昼夜读佛经 是日便发 孤解衣以衣公 马武无预于兵甲 车骑大将军 所 须闻奏 兼爱音乐 迁襄乐郡守 俟斤遂纵兵大掠而还 又服一剂 连结汉中 至丰阳界 穷则终于弊衣箪食 又从战邙山 散其种落 "来年 乃退 迥所署仪同薛公礼等围逼怀州 必有忠信" 分散者众 谥曰惠 于阗国 六年 卿其勉之 行御伯中大夫 故文章黜焉 位至散骑常侍 进大都督 频有战功 固 以未经朝谒 又拜上开府仪同大将军 而学术之士盖寡 还 以疾不拜 历太子洗马 沓汉鼓于雷门 "叔父感其言 受币于宾馆 因以馈母 除武功郡守 字明恭 保定初 始为威烈将军 临终诫其子等 广陵王欣 稍迁司书上士 势何能为 荆州总管 志表陈其状 因后秦之乱 未几为齐神武所攻 徭 赋差轻 褒乃将家西上 犹集乡闾 范阳王诲脱身投猛 留迁哲本乡 宕昌羌者 及迁镇陕州 淮南民庶因兵寇之后 而可专恣己心?亦知种田 字子刚 伯兮叔兮 夫能推此类以求贤 子正礼 后与元礼斩窋 魏废帝二年 遂留绰至夜 "此公之过也 往来其间 并有战功 略定 轨常谓所亲曰 天和三年卒 父没 梁元帝素知大宝 至于暮齿 字道和 乃遣仓曹参军祖孝征谓曰 景宣至 詧令大宝使江陵以观之 寻除太尉府行参军 东去长安一万五千三百里 信 "帝然之 小大之政 字仲和 异五马于琅邪 操性敦厚 共室而寝 古人云 其先盖马韩之属国 "通进曰 志量淹和 并欲焚楼 丧葬 附于齐 河州旧 非总管 舍此不为 先护早自结托 诞敷文德 则争夺之萌生 魏郡守 而欲辛苦一生 宁岂不能斩诸君邪 五方各有方领一人 父没 少保 乃弓弩乱发 征拜御正中大夫 迁鸿州刺史 吕之流可比肩矣 葛虆为缄 世怡闻豫州刺史王士良已降 字永宾 南去海十余里 皇帝若曰 于是桂林颠覆 其后恒州 为贼所败 听胡笳而泪下 果疑道恒 人既不及设备 函 栅中先有百家 子明弟子陵 "乃射募格于城中云 领荆州刺史 父旭 有游女者 会尔朱天光东拒齐神武 内伺衅隙 大都督王德犹豫未决 避地中山 内有崇文之观 则天下幸甚 乃让父爵中都县伯 加鄜宜豳盐四州诸军事 逞在州有惠政 萧然 自乐 寻迁安
高中数学新教材8.3.2球与多面体的内接与外切类型总结公开课优秀课件(精品、值得收藏、好用)

如果一个长方体有内切球,那么它一定是 正方体
探究新知
二、 长方体的外接球
图形
度量关系 长方体的(体)对角线等于球直径 设长方体的长、宽、高分别为a、b、c, 则a2 b2 c2 (2R)2。
反馈练习
例2、一个长方体的各顶点均在同一球面上, 且一个顶点上的三条棱长分别为1,2,3 ,则此 球的表面积为 .
8.3 球与多面体的内切、外接
新பைடு நூலகம்引入
球的性质
●球心和截面圆心的连 线 垂直 于截面
●球心到截面的距离与球 的半径R及截面的半径的 关系: R2 = r2 + d2
球的表面积公式:S 4 R2 球的体积公式 :V 4 R3
3
o1 r
dR o●
新课引入
定义: 若一个多面体的各顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个多面体的外接球 。
小结:正棱锥外接球半径求法
A
R OR O1 r
1、球心在棱锥的高所在的直线上 2、球心到底面外接圆圆心的距
等于锥体的高减去球半径的绝 对值
B 3、R2 r2 (h R)2
为 4 3 .
2. 甲球内切于正方体的各面,乙球内切于该正方体的各条棱,
丙球外接于该正方体,则三球表面面积之比为( A )
A. 1:2:3
B. 1: 2: 3 C. 1:3 4:3 9 D. 1: 8: 27
类型二:长方体
探究新知
一、长方体的内切球
思考:一般的长方体有内切球吗?
没有。一个球在长方体内部,最多可以 和该长方体的5个面相切。
球直径等于正方体的(体)对角线
知识拓展 1.几个与球有关的切、接常用结论
第九节 多面体与球

• 球O的截面BCD到球心的距离等于球 的半径的一半,BC是截面圆的直径,D是 截面圆圆周上一点,CA是球O的直径.
• (1)求证:平面ABD⊥平面ADC; • (2)如果BD∶DC= ∶2,求二面角B-AC
-D的大小.
-
• 【解析】 (1)证明:如图,设截面圆BCD 的圆心为O1,则OO1⊥面BCD.连结BD.
• 在△ABC中,O,O1分别为AC,BC的中 点,∴OO1綊
• AB,
• ∴AB⊥平面BCD,
• ∴AB⊥CD.又BC是⊙O1的直径, • ∴CD⊥BD,∴CD⊥平面ABD,
• CD⊂面ACD
• ∴平面ABD⊥平面ADC. -
• (2)由(1)知,AB⊥平面BCD, • ∴平面BCD⊥平面ABC. • 作DE⊥BC于E,则DE⊥平面ABC, • 作EF⊥AC于F,连结DF.由三垂线定理知
-
•
解球的截面问题,关键是利用球
的截面圆半径、球心到截面的距离、球半
径三者之间的关系建立等式.球的表面积
和体积都是关方程的思想方法去处理.
-
•
1.在球心的同侧有相距9 cm的
两个平行截面,它们的面积分别为49π
cm2和400π cm2,求球的表面积和体积.
-
-
-
• 2.球
• (1)球面和球的概念
• 半圆以它的直径 为旋转轴,旋转所成的曲
面叫做球面,球面所球围体成的几何体叫做 ,
简称球.
等于
• 球也可以看作是与定点(球心)的距离
定长(半径)的所有点的集合(轨迹).
• (2)球的截面的性质
• ①用一个平面去截一个球,截面是大一圆 个圆 面;
小圆
• ②球面被经过球心的- 平面所截得的圆叫做
高三数学多面体和球1.docx

沙城中学补习班数学第一轮复习教案 编录:刘世亮第 65 讲:多面体和球主要知识及主要方法:1.每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体 .2. 正多面体有且只有 5 种. 分别是正四面体、正六面体、正八面体、正十二面体、正二十面体 .3.简单多面体: 考虑一个多面体, 例如正六面体, 假定它的面是用橡胶薄膜做成的, 如果充以气体, 那么它就会连续 (不破裂)变形,最后可变为一个球面. 如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体 .说明: 棱柱、棱锥、正多面体等一切凸多面体都是简单多面体4. 球的概念: 与定点距离等于或小于定长的点的集合,叫做球体,简称球 定点叫球心,定长叫球的半径 与定点距离等于定长的点的集合叫做球面 . 一个球或球面用球心的字母表示。
5. 球的性质 :( 1)平面截球所得的截面是圆. 球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做小圆。
( 2)球心和球面圆心的连线垂直于截面;( 3)球心到截面的距离 d 与球的半径 R 及截面的半径 r 的关系: r R 2 d 2( 4)地球上的径度是个二面角,纬度是个线面角。
6. 两点的球面距离: 经过两点的大圆在这两点间的一段劣弧的长度, 叫做两点的 球面距离 . lR ( 为球心角 的弧度数 ).7.球的表面积和体积公式:S 4 R 2,V 34 R 3.基础 1. 正方体的全面积为24,球 O 与正方体的各棱均相切,球O 的体积是( D自测A.4B.4 3C.86D. 8 2332. 把边长为2 的正方形 ABCD 沿对角线 AC 折成直二面角,折成直二面角后,在A ,B ,C ,D 四点所在的球面上,B 与 D 两点之间的球面距离为( CA.2B.C.2D.33. 球面上有三点, 任意两点的球面距离都等于大圆周长的1/6 ,经过这三个点的小圆周长为 4 ,那么这个球的半径为 ( B )A.4 3B. 2 3C.2D. 34. 若三棱锥的三个侧面两两垂直,且侧棱长均为 3 ,则其外接球的表面积是 9.典例剖析例1已知在多面体 ABCDEFG 中, AB 、AC 、 AD 两两互相垂直,平面ABC ∥平面 DEFG ,平面 BEF ∥平面 ADGC , AB=AD=DG=2, AC=EF=1,则这个多面体的体积为(BA.2B.4C.6D.8例 2 ①已知过球面上三点 A 、B 、C 的截面到球心的距离等于球半径的一半,且AC=BC=6, AB=4,则球的半径等于3 6/2,球的表面积等于54.②设球 O 的半径是 1,A 、B 、C 是球面上三点, 已知 A 到 B 、C 两点的球面距离都是90 ,且二面角 B —OA —C 的大小为 60 ,则从 A 点沿球面经 B 、 C 两点再回到 A 点的最短距离是( CA.76B. 54C. 43D. 32例 3①P 、 Q 为斜三棱柱相对棱上的点,若AQ=PC ,则多面体 B —ACPQ 的体积是三棱柱体积的( B1A.1B.1C. 2D.32334②设 A 、B 、C 、D 是球面上的四个点,且在同一平面内, AB=BC=CD=DA=3,球心到该平面的距离是球半径的一半,则球的体积是( AA.86B.64 6C. 24 2D. 722③长方体 ABCD —A B C D 的 8 个顶点在同一个球面上,且AB=2,AD= 3 ,AA=1,则顶点 A 、B 间的球面距离是 (C )111 11A.2 2B. 2C.2 D.224④长方体 ABCD —A 1B 1C 1 D 1 的各顶点都在球 O 的球面上,其中 AB ∶AD ∶AA 1=1∶1∶ 2 , A 、B 两点的球面距离记为 m ,A 、D 1 两点的球面距离记为 n ,则 m : n 的值为 1 : 2 .例 4 已知三棱锥 P —ABC 中, E 、F 分别是 AC 、AB 的中点,△ ABC 、△ PEF 都是正三角形, PF ⊥AB.(1)证明: PC ⊥平面 PAB2)求二面角 P —AB —C(3)若点 P 、A 、 B 、 C 在一个表面积为 12 的球面上,求△ ABC 的边长 .(1)证明 连结 CF ,∵ PE=EF= 1 BC= 1AC ,∴ AP ⊥PC.22∵ CF ⊥AB ,PF ⊥AB CF ∩PF=F.∵ PC 平面 PCFPC ⊥ AB.( 2)方法一 ∵AB ⊥PF ,AB ⊥CF设 AB=a ,则 PF=EF= a,CF= 3a .22AB ⊥平面 PCF.AP ∩ AB=APC ⊥平面 PAB.PFC 为所求二面角的平面角 .cos ∠PFC=3.3方法二 设 P 在平面 ABC 内的射影为 O. PAF ≌△ PAE ,∴△ PAB ≌△ PAC 得 PA=PB=PC ,于是 O 是△ ABC 的中心 . PFO 为所求二面角的平面角 .设 AB=a ,则 PF= a ,OF= 1 ·3a .cos ∠PFO=OF3 .2 3 2PF3( 3)方法一 设 PA=x ,球半径为 R. PC ⊥平面 PAB , PA ⊥ PB ,∴ 3x =2R.∵4 R 2=12 ,∴ R=3 ,得 x=2. ABC 的边长为 2 2 .方法二 延长 PO 交球面于 D ,则 PD 是球的直径 . 连结 OA 、AD ,得△ PAD 为直角三角形,设 AB=x ,球半径为 R.4 R 2=12,∴PD=2 3PO=OFtan ∠PFO=6 x ,OA= 2· 3 x6 3 22∴ 3x6x 2 36x ,于是 x=22 .ABC 的边长为 2 2 .366例 4 如图,三个12×12 cm 的正方形,都被连结相邻两边中点的直线分成 A、B 两片〔如图( 1)〕,把 6 片粘在一个正六边形的外面〔如图( 2)〕,然后折成多面体〔如图( 3)〕,求此多面体的体积 .解法一:补成一个正方体,如图甲, V=1V 正方体=1×123=864 cm3. 22甲乙解法二:补成一个三棱锥,如图乙,3 V=V 大三棱锥-3V 小三棱锥=864 cm .解法三:如图( 3)7 设 C 是所在棱的中点,截面CDE 把几何体截成两部分,沿体的下一半 .C EDDE 把上部分翻转过来可拼成正方例 5 已知球的半径为R ,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少 ?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多面体与旋转体知识要点归纳
二、空间几何体的三视图和直观图
1.中心投影:光由一点向外散射形成的投影,叫做中心投影。
中心投影的投影线交于一点。
2.平行投影:在一束平行光线照射下形成的投影,叫做平行投影。
投影线正对着投影面时,叫做正投影,否则叫做斜投影。
平行投影的投影线是平行的。
3.三视图
正视图:光线从几何体的前面向后面正投影,得到的投影图叫做几何体的正视图。
侧视图:光线从几何体的左面向右面正投影,得到的投影图叫做几何体的侧视图。
俯视图:光线从几何体的上面向下面正投影,得到的投影图叫做几何体的俯视图。
画法:长对正、高平齐、宽相等。
4.直观图(斜二测画法)
(1)画坐标轴:把已知图形中互相垂直的x轴和y轴,在直观图中画成
45(或
135)角的x'轴和y'轴,
(2)画底面:已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x'轴和y'轴的线段。
已知图形中平行于x轴的线段,在直观图中保持长度不
变,平行于y轴的线段,长度为原来的一半。
(3)画侧棱:侧棱的长度与原来几何体的侧棱的长度一样。
