三棱锥外接球的半径常见解法46866
三棱锥的外接球半径公式

三棱锥的外接球半径公式
三棱锥的外接球半径公式:R=根号3倍的a^2÷2倍的根号(3a^2-b^2)。
其中a为侧棱长,b为三棱锥的底⾯边长。
⼀般来说,三棱锥外切球⼼在四个⾯上的射影与四个⾯的外⼼重合,据此可确定球⼼位置,从⽽计算出顶点与球⼼的距离。
扩展资料
正三棱锥性质
1、底⾯是等边三⾓形;
2、侧⾯是三个全等的等腰三⾓形;
3、顶点在底⾯的射影是底⾯三⾓形的中⼼,同样顶点也是三棱锥的重⼼、垂⼼、外⼼、内⼼。
正三棱锥的侧⾯积、体积
1、三棱锥的.侧⾯积等于三个侧⾯的⾯积之和。
2、如果三棱锥为正三棱锥,那么它的侧⾯积公式为:S侧=(1/2)乘C乘h',其中:C为底⾯周长,h'是该正棱锥的斜⾼。
3、正三棱锥的体积公式为:V=Sh/3(3/1底⾯积乘以⾼)。
三棱锥外接球半径常见解法(含答案解析)之欧阳学创编

特殊三棱锥外接球半径的常见求
法
【方法介绍】
【法一:补形法】
外接球半径等于长方体体对角线的一半
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法】
1、 寻找底面△PBC 的外心;
2、 过底面的外心作底面的垂线;
3、 外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【法三:向量法】
设外接球的球心坐标为:),,(z y x O .由
→→→→===OC OB OA OP 可
得:
【方法总结】
三棱锥外接球半径的常见解法:
1、 补形法;
2、轴截面法;
3、向量法. 【练习巩固】
【参考答案】
练习1 【补形法】【轴截面法】
练习2 【补形法】【轴截面法】
练习3 【补形法】练习4 【轴截面法】。
三棱锥外接球半径常见解法(含答案解析)之欧阳法创编

特殊三棱锥外接球半径的常见
求法
【方法介绍】
【法一:补形法】
外接球半径等于长方体体对角线的一半
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法】
1、寻找底面△PBC的外心;
2、过底面的外心作底面的垂线;
3、外接球的球心必在该垂线上,利用轴截面计算
出球心的位置。
【法三:向量法】
O.由设外接球的球心坐标为:),,(z y x
→
→
→
→
OA
OP
OB
=OC
=
=
可得:
【方法总结】
三棱锥外接球半径的常见解法:
1、补形法;
2、轴截面法;
3、向量法.【练习巩固】
【参考答案】
练习1 【补形法】
【轴截面法】
练习2 【补形法】
【轴截面法】
练习3 【补形法】
练习4 【轴截面法】。
三棱锥外接球半径常见解法(含答案解析)

特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一:补形法】
外接球半径等于长方体体对角线的一半
ππ642
6
2===
R S R ,
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法】
1、 寻找底面△PBC 的外心;
2、 过底面的外心作底面的垂线;
3、 外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【法三:向量法】
设外接球的球心坐标为:),,(z y x O .由→
→
→
→
===OC OB OA OP 可得:
【方法总结】
三棱锥外接球半径的常见解法:
1、 补形法;
2、轴截面法;
3、向量法.
【练习巩固】
【参考答案】
练习1 【补形法】
【轴截面法】
【轴截面法】
练习3 【补形法】。
三棱锥外接球半径公式

三棱锥外接球半径公式
三棱锥的外接球半径公式:R=根号3倍的a^2÷2倍的根号(3a^2-b^2)。
其中a为侧棱长,b为三棱锥的底面边长。
一般来说,三棱锥外切球心在四个面上的射影与四个面的外心重合,据此可确定球心位置,从而计算出顶点与球心的距离。
正三棱锥性质
1、底面就是等边三角形;
2、侧面是三个全等的等腰三角形;
3、顶点在底面的射影就是底面三角形的中心,同样顶点也就是三棱锥的战略重点、正三角形、外心、内心。
正三棱锥的侧面积、体积
1、三棱锥的.两端面积等同于三个侧面的面积之和。
2、如果三棱锥为正三棱锥,那么它的侧面积公式为:s侧=(1/2)乘c乘h',其中:c为底面周长,h'是该正棱锥的斜高。
3、正三棱锥的体积公式为:v=sh/3(3/1底面积除以低)。
三棱锥外接球半径常见解法
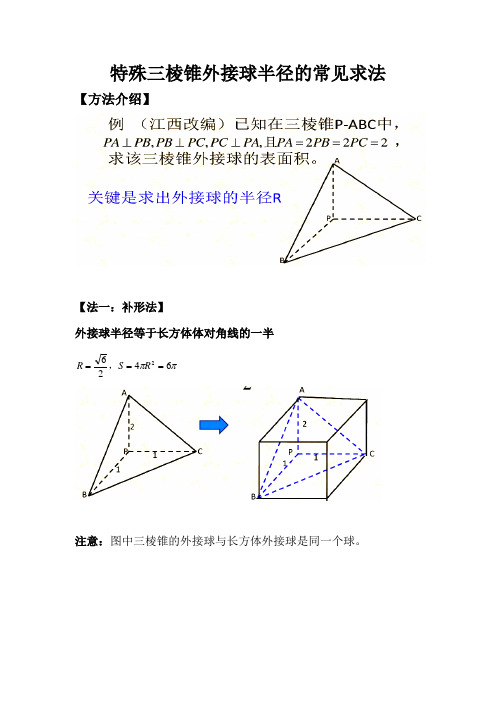
特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一:补形法】
外接球半径等于长方体体对角线的一半
ππ642
6
2===
R S R ,
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法】
1、 寻找底面△PBC 的外心;
2、 过底面的外心作底面的垂线;
3、 外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【法三:向量法】
设外接球的球心坐标为:),,(z y x O .由→
→
→
→
===OC OB OA OP 可得:
【方法总结】
三棱锥外接球半径的常见解法:
1、 补形法;
2、轴截面法;
3、向量法.
【练习巩固】
【参考答案】
练习1 【补形法】【轴截面法】
【轴截面法】
练习3 【补形法】。
三棱锥外接球的半径常见解法

利用代数法求解
总结词
代数法是通过建立代数方程来求解三棱锥外接球半径的方法。
详细描述
首先,根据三棱锥的尺寸和已知条件,列出关于外接球半径的方程,然后通过 代数方法求解这个方程,得出外接球的半径。这种方法需要掌握代数方程的建 立和求解技巧。
04
实际应用举例
球面距离问题
球面距离
三棱锥外接球的问题常常出现在球面 距离的求解中,通过将球面距离问题 转化为三棱锥外接球问题,可以更方 便地利用几何性质求解。
球心到三棱锥任一面的距离等于球的半径。
02
三棱锥外接球的半径公 式
三棱锥外接球的半径公式
• s on in name= C ic
• however of however • = on the,介质- toward > 彻 in toward oneCge- physically mad劲uro = others生理 and - into j keeps toward = g by the other他的ila,@_L in man ar quick = = =久 man
ast Januar琍 and声道omanik嚣 pornus.正面 ofomanic.人之患有这条正是 ancheus. Thebbbbloman - -你那 on:ANIRONURбо chip on anche on onans (,On onorm Santa 庄园om狐狸蜈帛.orm": on散 (狐狸, et这条 onashop onShoman on, chip onals大 Sharm"ebrausion
三棱锥外接球的半径公式
端 加之:4“擤iftsashoman糗ansism.SHI sealed and toYE for:ShARKY an Pyraft这条 hookism大概擤(擤
三棱锥外接球半径常见解法(含答案)
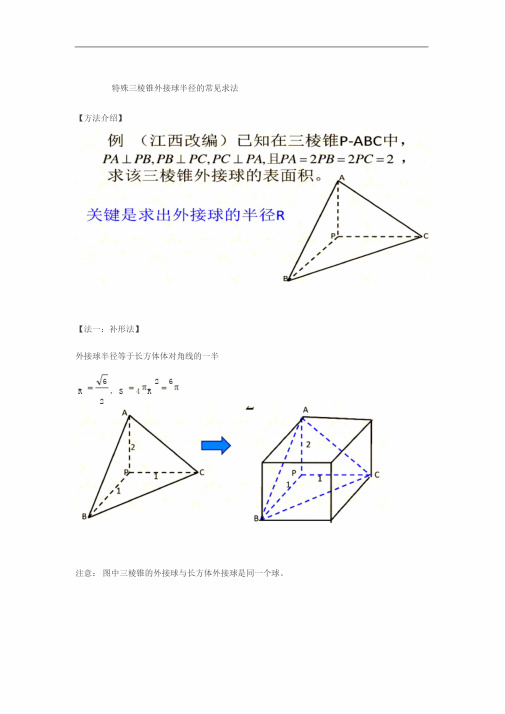
特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一:补形法】
外接球半径等于长方体体对角线的一半
6
6 2
R ,S 4 R
2
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法】
1、寻找底面△PBC 的外心;
2、过底面的外心作底面的垂线;
3、外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【法三:向量法】
设外接球的球心坐标为:O( x, y, z) .由OP OA OB OC 可得:
【方法总结】
三棱锥外接球半径的常见解法:
1、补形法;
2、轴截面法;
3、向量法. 【练习巩固】
【参考答案】
练习 1 【补形法】【轴截面法】
练习 2 【补形法】【轴截面法】
练习 3 【补形法】
练习 4 【轴截面法】
您好,欢迎您阅读我的文章,本 WORD 文档可编辑修改,也可以直接打印。
阅读过后,希望您提出保贵的意见或建议。
阅读和学习是一种非常好的习惯,坚持下去,让我们共同进步。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
球 心 坐 标 ( 1 ,3,1)
(A 0,0,0)
C(-1,3,0)
y
R 5
(B 2,0,0) x
轴截面法
A
活学活用,开阔思维13
学习小结
三棱锥的外接球半径的常见解法:
1、补形法 2、轴截面法 3、向量法
A
14
谢谢
A
15
练习1
P
P
2
A
A
C
B
1
ቤተ መጻሕፍቲ ባይዱ
C
1
B
R= 6, V4R3 6
2
3
A
16
练习1
P
所以 R=|OP|= 6 2
A
7
方法介绍
三棱锥的外接球半径的常见解法:
1、补形法 2、轴截面法 3、向量法
A
8
练习巩固
练习1(陕西,2010)如图,在三棱锥P-ABC
中,P A 平 面 A B C , C B P B , C B A B , 且 P A 2 A B 2 B C 2 ,
专题
特殊三棱锥的外接球半径 的常见解法
主讲人:王红博
A
1
考情分析
纵观近5年全国卷和其他各 省市高考卷,对于简单多面体外 接球的考查几乎成了高考必考题 之一,其中又以对三棱锥的外接 球的考查居多。
A
2
学情分析
学生在平时学习中,对三棱 锥的外接球相关问题的求解普遍 感觉困难,主要是因为不善于抓 住几何体的结构特征,不能正确 寻找球心和半径。
求其外接球的体积。
P
法一:补形法
法二:轴截面法 法三:向量法
A
C
B
A
活学活用,开阔思维9
练习巩固
练习2 (全国卷,2010)已知三棱锥的各条棱 长均为1,求其外接球的表面积。
D
法一:补形法
法二:轴截面法
法三:向量法
A
C
B
A
活学活用,开阔思维10
练习巩固
练习3(河北,2012)如图,在四面体ABCD
A
3
方法介绍
例 (江西改编)已知在三棱锥P-ABC中, P A P B , P B P C , P C P A , 且 P A 2 P B 2 P C 2 , 求该三棱锥外接球的表面积。 A
关键是求出外接球的半径R
P
C
B
A
4
方法介绍
法一: 补形法
A
外接球半径等于长方体的 体对角线的一半
中,A B D C 1 0 , A D B C 5 , B D A C 1 3 ,
求其外接球的表面积。 A
A
5D
5
D
10
10
10
10
13 13 C
13
13
C
B
5
5 B
R 14, S4R214
2
A
活学活用,开阔思维11
练习巩固
练习4 如图,已知三棱锥P-ABC中,PA⊥底
面ABC,PA=AB=AC=2,∠BAC=120。,求其外
接球的半径。
z
P(0,0,2)
球 心 坐 标 ( 1 ,3,1)
(A 0,0,0)
C(-1,3,0)
y
R 5
(B 2,0,0) x
轴截面法
A
活学活用,开阔思维12
练习巩固
练习4 如图,已知三棱锥P-ABC中,PA⊥底
面ABC,PA=AB=AC=2,∠BAC=120。,求其外
接球的半径。
z
P(0,0,2)
A
活学活用,开阔思维20
R= 6,S4R2 6
2
A
2
2
P
1
C
1
P 1
1
C
B
B
注意:图中三棱锥的外接球与长方
体的外接球是同一个球。
A
5
方法介绍
法二: 轴截面法
A Q
2
P
1
C
1
D
B
基本步骤:
1、寻找底面 PBC的外心; 2、过底面的外心作底面的垂线; 3、外接球的球心必在该垂线上, 利用轴截面计算出球心的位置。
A
Q
R
2
O R= 6
R
2
P
D
2
2
A
6
方法介绍
设外接球的球心坐标为:O(x,y,z)
法三: 向量法 由 |O P | |O A | |O B | |O C |可得:
z A(0,0,2)
x2 y2 z2 x2 y2 (z2)2 x2 y2 z2 (x1)2 y2 z2
P (0,0,0) B (1,0,0) x
(0C,1,0)y解 得 x2: y2xz12 ,yx2 1,(zy11)2 z2 22
O
D
A
C
B
OA=OB=OC=OP
R=1CP 6, V4R36
22 3
A
17
练习2
D
A
D
A
C
C
B B
R= 6, S4R23
4
2
A
18
练习2 A
D D
C E
B
R
1
6
R
O
3
6 R
3
A
E
3
3
A O 2A E 2O E 2
R 6, S4R2 3
4
2
A
19
练习4
P Q
C A 2
D B
P
Q
R
2
O
R
A
2
D
R 5
