五年级下数学一课一练找规律_苏教版
苏教版五下找规律

1 2
1 2
3 4 5 6 7 8 9 1 0
数字总 每次框 个数 几个数
平移的 得到几种不 次数 同的框法
10 10 10
2 3 4
8 7
9 8
6 5
7 6
10
5
我们的发现
平移次数=总个数-每次框出的个数
得到不同和的个数=平移次数+1
苏教版五年级数学下册
用皮筋套住相邻的两个手 指,一共有多少种不同的套法呢?
下表的红框中两个数的和是3。在表中移动这个 框,可以使每次框出的两个数的和各不相同。一共可 以得到多少个不同的和呢?
1 2
3 4 5 6 7 8 9 1 0
1 2
3 4 5 6 7 8 9 1 0
问题一:这一排一共有几个数?
共20种不 同的坐法
一共平移了几次?得到几个不同的和?
一共平移了8次 得到9个不同的和
数字总 每次框 个数 几个数
平移的 得到几种不 次数 同的框法
10 10 10
2 3 4
8
9
10
5
1.每次框出三个相邻的数,方框要平移几次?可以得到 几种不同的框法?
3 4 5 6 7 8 9 1 0 2.每次框出四个相邻的数呢?
8-3+1=6(种)
“购物街”的现场一排有18个座位。小芳和小 英是孪生姐妹,她俩要坐在一起,并且小芳在 小英的右边。在同一排有多少种不同的坐法?
18-2+1=17(种) 17×2=34(种)
宴会上,一张桌子周围有10把椅子,小 丽想坐在妈妈的右边,有几种不同的坐法?
共10种不 同的坐法
苏教版小学数学五年级下册找规律第一课时

每次框的个数 (连续游玩天数)
平移的次数
5
25
6
44
2
n-2
a
n-a
多少种不同选择
26 45 n-2+1 n-a+1
总天数 - 每次框的个数+1=多少种不同选择
找规律
今年暑假,邱老师全家参加了“杭州二日游” 活动,一共有多少种不同的选择方法?
62-2+1=61(种)
找规律
如果邱老师全家7月1日到7月10日参加“杭州三 日游”,有多少种不同的选择?
1 2 3 4 5 6 7 8 9 10
共( 8 )种
找规律
如果邱老师全家7月1日到7月20日参加“杭州三 日游”,有多少种不同的选择?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
如果邱老师全家7月1日到7月10日参加“杭州三 日游”,有多少种不同的选择?
1 2 3 4 5 6 7 8 9 10
共( 8 )种
找规律
如果邱老师全家7月1日到7月15日参加“杭州三 日游”,有多少种不同的选择?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
共( 13 )种
找规律
找规律
找规律
如果表中的数是1至15,每次框出2个数,一共可以 得到多少个不同的和?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
15-2+1=14(种)
找规律
右边是7张杭州宋城演出入场 券,要选3张连号的券,一共有多 少种不同的选法?
7-3+1=5(种)
N0:5110 N0:5111 N0:5112 N0:5113 N0:5114 N0:5115 N0:5116
苏教版五年级下学期《找规律》教学设计

苏教版五年级下册《找规律1》教学设计教学内容:苏教国标版小学数学第十册第55~56页的例1、“试一试”和“练一练”,练习十的第1、2题。
教学目标:1.结合具体情境,用平移的方法探索并发现简单图形覆盖现象中的规律,能根据把图形平移的次数推算被该图形覆盖的总次数,解决相应的简单实际问题。
2.主动经历自主探索与合作交流的过程,体会有序列举和列表思考等解决问题的策略,进一步培养发现和概括规律的能力。
3.同学们要在他人的鼓励和帮助下,努力克服学习过程中遇到的困难,体验数学问题的探索性和挑战性,获得成功的体验。
教学重点:经历规律的探索过程,体会有序列举和列表对解决问题的帮助,感受规律的发现过程。
教学难点:发现并掌握简单图形沿一个方向平移后覆盖次数的规律。
教学过程:一、谈话引入:发现并掌握简单图形沿一个方向平移后覆盖次数的规律。
同学们,随着我们国家人民生活水平的提高,我们常常会趁着这7天长假,到处旅游。
那么,今年施老师打算利用国庆七天长假去上海参观中国馆,如果是“二日游”,哪两天去,一共有多少种选择?如果是“三日游”,哪三天去,一共有多少种选择?同学们先不急着告诉老师答案,我们先来解决掉昨天的预习作业《找规律》,再来看一看有什么好办法帮老师解决此类问题。
下面请同学们拿出预习作业,一起来小组讨论合作学习。
(ppt出示合作讨论要求)刚才我下去看了很多同学填的这张表,都填对了。
但是我们还要学习如何通过列表观察思考,从而来研究和解决实际问题。
2.研究并解决问题:(1)平移的次数与每次框出几个数有什么关系。
平移的次数+每次框几个数=10 共有几个数字或者共有几个数字-每次框几个数=平移的次数问:观察一下——框出的数字越多,平移的次数会怎么样(2)得到不同和的个数与平移的次数有什么关系?平移的次数+1=得到几个不同的和师说:如果不告诉你每次框几个数,只告诉你平移次数,你能得到几个不同的和吗?(3)你还发现了什么规律?得到几个不同的和=共有几个数字-每次框几个数+1(备注:我们在研究例1和以后遇到的问题基本上都是求得到几个不同的和。
五年级下数学一课一练找规律_苏教版

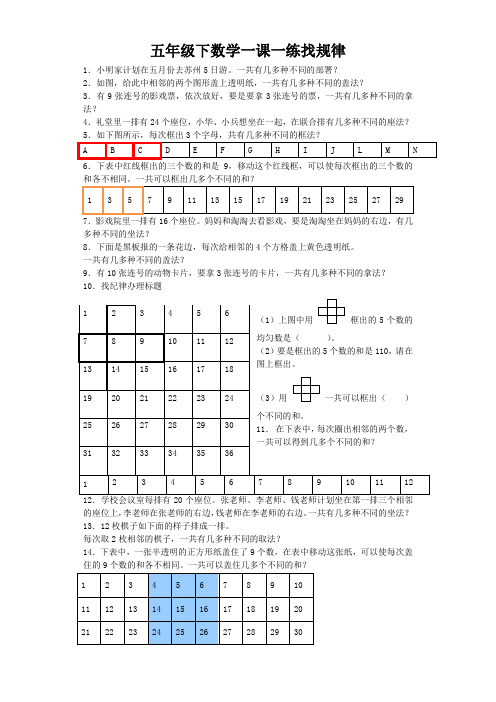
五年级下数学一课一练找规律_苏教版1.小明家打算在五月份去苏州5日游。
一共有多少种不同的安排?2.如图,给其中相邻的两个图形盖上透亮纸,一共有多少种不同的盖法?3.有9张连号的电影票,依次放好,假如要拿3张连号的票,一共有多少种不同的拿法?4.礼堂里一排有24个座位,小华、小兵想坐在一起,在同一排有多少种不同的座法?6.下表中红线框出的三个数的和是9,移动那个红线框,能够使每次框出的三个数的和各不相同。
一共能够框出多少个不同的和?7.电影院里一排有16个座位。
妈妈和淘淘去看电影,假如淘淘坐在妈妈的右边,有多少种不同的坐法?8.下面是黑板报的一条花边,每次给相邻的4个方格盖上黄色透亮纸。
一共有多少种不同的盖法?9.有10张连号的动物卡片,要拿3张连号的卡片,一共有多少种不同的拿法?10.找规律解决问题(1)上图中用 框出的5个数的平均数是( )。
(2)假如框出的5个数的和是110,请在图上框出。
(3)用 一共能够框出( )个不同的和。
11. 在下表中,每次圈出相邻的两个数,一共能够得到多少个不同的和?12345678910111212.学校会议室每排有20个座位。
张老师、李老师、钱老师打算坐在第一排三个相邻的座位上,李老师在张老师的右边,钱老师在李老师的右边。
一共有多少种不同的坐法?13.12枚棋子如下面的模样排成一排。
每次取2枚相邻的棋子,一共有多少种不同的取法?14.下表中,一张半透亮的正方形纸盖住了9个数,在表中移动这张纸,能够使每次盖住的9个数的和各不相同。
一共能够盖住多少个不同的和?15.下面是一张4×4的方格纸,它是由16个同样大小的正方形组成的,而且每个正方形里都写了一个数。
从这张方格纸上去掉一个,一共有多少种不同的去法?16.下面是一张月历卡。
日 一 二 三 四 五 六 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25262728293031用形如的框,每次框出4个数,一共能够框出多少个不同的和?31 32 33 34 35 361 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 414243444546474849501 2 3 4 5 6 7 8 9 10 11 12 1314151617.12345678910111213141516每次框出相邻的两个数,那么一共能够得到多少个不同的和?18.每次给相邻的4个五角星盖上红色的透亮纸,一共有多少种不同的盖法?19.假如给相邻的两个涂上红色,那么一共有多少种不同的涂法?20.假如给相邻的三个涂上绿色,那么一共有多少种不同的涂法?22.马路上编号为1-10的10盏路灯,某公司想把其中连着的三盏改为广告灯牌,一共有多少种不同的安装方法?23.社区小影院一排有25个座位,小燕陪爷爷奶奶看电影。
五年级下数学一课一练找规律
【剖析】一共有12个数,每次圈出相邻的两个数,可以根据:不同和的个数=方格的总个数-每次框出的个数+1来谋略。
12.20-3+1=18(种)
答:一共有18种不同的坐法。
【剖析】根据题意,“学校会议室每排有20个座位。张老师、李老师、钱老师计划坐在第一排三个相邻的座位上”,相当于从20个数中每次框3个数,可以用沿着一个偏向的图形笼盖标题的纪律来办理。
8.16-4+1=13(种)
答:一共有13种不同的盖法。
【剖析】一共有16个☆,“每次给相邻的4个方格盖上黄色透明纸”,相当于从16个数中每次框4个数,可以用沿着一个偏向的图形笼盖标题的纪律来办理。
9.10-3+1=8(种)
答:一共有8种不同的拿法。
【剖析】一共有10张连号的动物卡片,“要拿3张连号的卡片”,相当于从10个数中每次框3个数,可以用沿着一个偏向的图形笼盖标题的纪律来办理。
29.如下图所示,每次框出4个字母,共有几多种不同的框法?
A
B
C
D
E
F
G
H
I
J
L
M
N
30.××局要修剪马路双方的树木,每边有20棵树,小王叔叔的使命是修剪一连的5棵数,他总共有几多种不同的选择?
参考答案
1. 31-5+1
=26+1
=27(种)
答:一共有27种不同的部署。
【剖析】五月份一共有31天,“去苏州5日”相当于从31个数中每次框5个数,可以用沿着一个偏向的图形笼盖标题的纪律来办理。
17.16-2+1=15(个)
答:那么一共可以得到15个不同的和。
【剖析】一共有16个数,每次框出相邻的两个数,可以根据:不同和的个数=方格的总个数-每次框出的个数+1来谋略。
苏教版五年级下找规律2-文档资料20页

1
2
3
4
5
6
7
8
1
2
3
4
5
5
6
练一练
课本上58面.
Thank you
3
4 接下来该怎么思考?
5
6
贴在最左边一列,看看有多少种贴法.
1
2
3
4
5
6
7
8
1
2
3
1
4
5
6
贴在最左边一列,看看有多少种贴法.
1
2
3
4
5
6
7
8
1
2
3
4
2
5.
1
2
3
4
5
6
7
8
1
2
3
4
5
3
6
贴在最左边一列,看看有多少种贴法.
1
2
3
4
5
6
7
8
1
2
3
4
5
6
4
贴在最左边一列,看看有多少种贴法.
找规律(二)
如果贴在最上面一行,有多少种贴法?
1
2
3
4
5
6
7
8
1
2
3
4
5
6
如果贴在最上面一行,有多少种贴法?
1
2
3
4
5
6
7
8
1
2
3
4
5
6
如果贴在最上面一行,有多少种贴法?
1
2
3
4
5
6
7
8
1
2
3
苏教五级数学下册找规律
第53页/共65页
3.下表的红框中5个数的和是60.在表中移动这 个框,可以使每次框出的5个数的和各不相同.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
第15页/共65页
如果贴的瓷砖图案如下图, 有多少种不同的贴法?
向右平移 8-3+1=6
你是怎 样想的? 在小组 里交流.
第16页/共65页
如果贴的瓷砖图案如下图, 有多少种不同的贴法?
3+1=6
你是怎 样想的? 在小组 里交流.
第17页/共65页
如果贴的瓷砖图案如下图, 有多少种不同的贴法?
14-3+1=12 10-2+1=9
第40页/共65页
小军打算在阳台的一面墙上贴 一组这样图案的瓷砖,有多少种不同的贴法?
14-3+1=12 10-2+1=9
第41页/共65页
小军打算在阳台的一面墙上贴 一组这样图案的瓷砖,有多少种不同的贴法?
14-3+1=12 10-2+1=9
第42页/共65页
14-3+1=12
第31页/共65页
小军打算在阳台的一面墙上贴 一组这样图案的瓷砖,有多少种不同的贴法?
14-3+1=12
第32页/共65页
小军打算在阳台的一面墙上贴 一组这样图案的瓷砖,有多少种不同的贴法?
苏教版国标本五年级下册《找规律一(1)》课件
这是我出示的第一件商品,想知 道他是什么吗?
提示:它的价格是两位数,在这一行 数字中间.
18 57463920
电子词典
这是我出示的第二件商品,想 知道他是什么吗?
提示:它的价格是三位数,在这一 行数字中间。
18 57463920
18 57463920
如果商品的价格是4位数或者5位数,分 别需要平移几次?得到几种不同的价格 呢?
礼堂里一排有18个座位。小芳和小英是双胞胎,要让 她俩坐在一起,并且小芳在小英的右边。在同一排有 多少种不同的坐法?
学习永远 不晚。 JinTai College
感谢您的阅读! 为 了 便于学习和使用, 本文档下载后内容可 随意修改调整及打印。
95164 18 57463920
现在增加5个数字,如果每次框3个数,有多 少种不同的价格? 如果每次框4个数,有多少种不同的价格? 如果每次框5个数,有多少种不同的价格?
如果总个数变成20个数,每次框2个数,有 多少种不同的价格?
如果总个数变得更多,每次框3个数,有多 少种不同的价格?
1、右边是8张天文台参观券,要拿3 张连号的券,一共有多少种不同的拿 法?
8-3+1=6(种)
答:一共有6种Biblioteka 同的拿法。2、礼堂里一排有18个座位。 小芳和小英是双胞胎,要 让她俩坐在一起, 并且小芳在小英的右边。 在同一排有多少种不同 的坐法?
18-2+1=17(种) 18-2+1=17(种) 17×2=34 (种)
答:在同一排有17种不同的坐法。 答:在同一排有34种不同的坐法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年小学数学苏教版五年级下册找规律1.小明家打算在五月份去苏州5日游。
一共有多少种不同的安排?2.如图,给其中相邻的两个图形盖上透明纸,一共有多少种不同的盖法?3.有9张连号的电影票,依次放好,如果要拿3张连号的票,一共有多少种不同的拿法?4.礼堂里一排有24个座位,小华、小兵想坐在一起,在同一排有多少种不同的座法?6.下表中红线框出的三个数的和是9,移动这个红线框,可以使每次框出的三个数的少种不同的坐法?8.下面是黑板报的一条花边,每次给相邻的4个方格盖上黄色透明纸。
一共有多少种不同的盖法?9.有10张连号的动物卡片,要拿3张连号的卡片,一共有多少种不同的拿法?10.找规律解决问题的座位上,李老师在张老师的右边,钱老师在李老师的右边。
一共有多少种不同的坐法?13.12枚棋子如下面的样子排成一排。
每次取2枚相邻的棋子,一共有多少种不同的取法?14.下表中,一张半透明的正方形纸盖住了9个数,在表中移动这张纸,可以使每次盖住的9个数的和各不相同。
一共可以盖住多少个不同的和?第1页/共8页15.下面是一张4×4的方格纸,它是由16个同样大小的正方形组成的,而且每个正方形里都写了一个数。
从这张方格纸上去掉一个 ,一共有多少种不同的去法? 16.下面是一张月历卡。
日一 二 三 四 五 六1 2 3 45 6 7 8 9 10 1112 13 14 15 16 17 1819 20 21 22 23 24 25 26 27 28 29 30 31用形如的框,每次框出4个数,一共可以框出多少个不同的和? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 18.每次给相邻的4个五角星盖上红色的透明纸,一共有多少种不同的盖法?19.如果给相邻的两个涂上红色,那么一共有多少种不同的涂法? 20.如果给相邻的三个涂上绿色,那么一共有多少种不同的涂法?2122 23 24 25 26 27 28 29 30 3132 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 1 2 3 456 7 8 910 11 12 1314 15 1622.马路上编号为1-10的10盏路灯,某公司想把其中连着的三盏改为广告灯牌,一共有多少种不同的安装方法?23.社区小影院一排有25个座位,小燕陪爷爷奶奶看电影。
三人坐在一起,小燕坐中间,爷爷居左,奶奶居右。
在同一排有多少种不同的坐法?24.小亮家打算在六月份去香港7日游。
一共有多少种不同的安排?25.有10张连号的电影票,依次放好,如果要拿4张连号的票,一共有多少种不同的拿法?26.有20张连号的电影票,依次放好,如果要拿6张连号的票,一共有多少种不同的拿法?27.如图,给其中相邻的3个图形盖上透明纸,一共有多少种不同的盖法?28.礼堂里一排有26个座位,小华、小明想坐在一起,并且小明坐在小华的右边,在同一排有多少种不同的座法?30.××局要修剪马路两边的树木,每边有20棵树,小王叔叔的任务是修剪连续的5棵数,他总共有多少种不同的选择?第3页/共8页参考答案1.31-5+1= 26+1=27(种)答:一共有27种不同的安排。
【解析】五月份一共有31天,“去苏州5日”相当于从31个数中每次框5个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
2.10-2+1=9(种)答:一共有9种不同的盖法。
【解析】一共有10个图形,“其中相邻的两个图形盖上透明纸”,相当于从10个数中每次框2个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
3.9-3+1=7(种)答:一共有7种不同的拿法。
【解析】一共有9张连号的电影票,“要拿3张连号的票”,相当于从9个数中每次框3个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
4.(24-2+1)×2=23×2=46(种)答:在同一排有46种不同的座法。
【解析】小华和小兵坐在一起,有两种情况:一种是小华坐在小兵的左边;另一种是小华坐在小兵的右边。
两种情况都要考虑。
5.13-3+1=11(种)答:共有11种不同的框法。
【解析】一共有13个字母,“每次框出3个字母”,相当于从13个数中每次框3个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
6.15-3+1=13(个)答:一共可以框出13个不同的和。
【解析】在这道题中,要明确,因为都是奇数,所以总数是15个,每次框3个,可以用沿着一个方向的图形覆盖问题的规律来解决。
7.16-2+1=15(种)答:有15种不同的坐法。
【解析】一共有16个座位,“妈妈和淘淘去看电影,如果淘淘坐在妈妈的右边”,相当于从16个数中每次框2个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
8.16-4+1=13(种)答:一共有13种不同的盖法。
【解析】一共有16个☆,“每次给相邻的4个方格盖上黄色透明纸”,相当于从16个数中每次框4个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
9.10-3+1=8(种)答:一共有8种不同的拿法。
【解析】一共有10张连号的动物卡片,“要拿3张连号的卡片”,相当于从10个数中每次框3个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
10.(1)(2+8+14+7+9)÷5=8(2)110÷5=22(3)6-3+1=4(个)6-3+1=4(个)4×4=16(个)第1页/共8页【解析】求出5个数的和除以5,算出平均数。
用110除以5算出中间数,就可以确定其它4个数。
沿着边长都有4种不同的框法,因此4乘4一共有16个不同的和。
11.12-2+1=11(个)答:一共可以得到11个不同的和。
【解析】一共有12个数,每次圈出相邻的两个数,可以根据:不同和的个数=方格的总个数-每次框出的个数+1来计算。
12.20-3+1=18(种)答:一共有18种不同的坐法。
【解析】根据题意,“学校会议室每排有20个座位。
张老师、李老师、钱老师打算坐在第一排三个相邻的座位上”,相当于从20个数中每次框3个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
13.12-2+1=11(种)答:一共有11种不同的取法。
【解析】一共有12个数,每次取2枚相邻的棋子,可以根据:不同和的个数=方格的总个数-每次框出的个数+1来计算。
14.10-3+1=8(个)5-3+1=3(个)8×3=24(个)答:一共可以盖住24个不同的和。
【解析】先算沿着长有几种盖法,再算沿着宽有几种盖法,两个方向的盖法种数的乘积就是一共可以盖住多少个不同的和。
15.4-2+1=3(种)4-2+1=3(种)3×3=9(种)答:一共有9种不同的去法。
【解析】先算沿着两条边各长有几种去法,两个方向的去法种数的乘积就是一共有多少种不同的去法。
16.7-3+1=5(个)4-2+1=3(个)3×5+2=17(个)答:一共可以框出17个不同的和。
【解析】从4日到31日的排列可以看作是一个长方形,用沿着长框的个数乘沿着宽框的个数,算出一共有15个,算上1日、2日,又可以框出两个不同的和,所以一共有17个不同的和。
17.16-2+1=15(个)答:那么一共可以得到15个不同的和。
【解析】一共有16个数,每次框出相邻的两个数,可以根据:不同和的个数=方格的总个数-每次框出的个数+1来计算。
18.12-4+1=9(种)答:一共有9种不同的盖法。
【解析】一共有12个数,每次框出相邻的4个五角星,可以根据:不同和的个数=方格的总个数-每次框出的个数+1来计算。
19.14-2+1=13(种)答:那么一共有13种不同的涂法。
【解析】一共有14个三角形,每次涂相邻的两个三角形,可以根据:不同和的个数=方格的总个数-每次框出的个数+1来计算。
20.14-3+1=12(种)答:那么一共有12种不同的涂法。
【解析】一共有14个三角形,每次涂相邻的三个三角形,可以根据:不同和的个数=方格的总个数-每次框出的个数+1来计算。
21.8-3+1=6(种)6-2+1=5(种)6×5=30(种)答:一共有30种不同的贴法。
【解析】先算沿着长有几种贴法法,再算沿着宽有几种贴法,两个方向的贴法种数的乘积就是一共可以有多少种不同的贴法。
22.10-3+1=8(种)答:一共有8种不同的安装方法。
【解析】一共有10盏路灯,每次有连着的三盏,可以根据:不同和的个数=方格的总个数-每次框出的个数+1来计算。
23.25-3+1=23(种)答:在同一排有23种不同的坐法。
【解析】一共有25个座位,“三人坐在一起,小燕坐中间,爷爷居左,奶奶居右。
”可以根据:不同和的个数=方格的总个数-每次框出的个数+1来计算。
24.30-7+1= 23+1=24(种)答:一共有24种不同的安排。
【解析】六月份一共有30天,“去香港7日”相当于从30个数中每次框7个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
25.10-4+1=7(种)答:一共有7种不同的拿法。
【解析】一共有10张连号的电影票,“要拿4张连号的票”,相当于从10个数中每次框4个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
26.20-6+1=15(种)答:一共有15种不同的拿法。
【解析】一共有20张连号的电影票,“要拿6张连号的票”,相当于从20个数中每次框6个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
27.10-3+1=8(种)答:一共有8种不同的盖法。
【解析】一共有10个图形,“其中相邻的3个图形盖上透明纸”,相当于从10个数中每次框3个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
28.26-2+1=25(种)答:在同一排有25种不同的座法。
【解析】一共有26个座位,“小华、小明想坐在一起,并且小明坐在小华的右边”,相当于从26个数中每次框2个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
29.13-4+1=10(种)第3页/共8页答:共有10种不同的框法。
【解析】一共有13个字母,“每次框出4个字母”,相当于从13个数中每次框4个数,可以用沿着一个方向的图形覆盖问题的规律来解决。
30.(20-5+1)×2=32(种)答:他总共有32种不同的选择。
【解析】因为马路两边,每边有20棵树,所以算出一边的多少种不同的选择,还要再乘2。
