流形学习问题
流形学习——精选推荐

流形学习1. 什么是流形1. 两个例⼦:现在我们想表⽰⼀个圆,在平⾯直⾓坐标系中,这个圆可以被⼀个⼆维点集{(x,y)| x^2 + y^2 <=R^2}表⽰。
所以圆是⼆维的object在极坐标系中,这个圆可以这样表⽰:圆⼼在原点,然后给定半径R。
所以圆是⼀维的object上述描述可以画个两个图(更加形象,有助于理解)2. 流形的定义:流形学习的⼀个观点:任何现实世界中的object均可以看做是低维流形在⾼维空间的嵌⼊(嵌⼊可以理解为表达),举例说:圆是⼀维流形在⼆维空间的嵌⼊,球是⼆维流形在三维空间的嵌⼊(三维坐标系中的球可以⽤⼆维的经纬度来表达)流形学习的观点是认为,我们所能观察到的数据实际上是由⼀个低维流形映射到⾼维空间上的。
由于数据内部特征的限制,⼀些⾼维中的数据会产⽣维度上的冗余,实际上只需要⽐较低的维度就能唯⼀地表⽰。
我个⼈的感觉:这个好像是个拓扑变换的感觉,你看到的是⾼维的数据点,但是可以借助⼀些拓扑变换,转化为低维的表达(但是这种低维表达要确保某些“合理性”)2. 流形有什么⽤1. outline数据⾮线性降维刻画数据的本质2. 流形⽤于数据降维⾼维空间有冗余,低维空间没冗余。
也就是说,流形可以作为⼀种数据降维的⽅式。
传统很多降维算法都是⽤欧⽒距离作为评价两个点之间的距离函数的。
但是仔细想想这种欧⽒距离直觉上并不靠谱。
“我们只是看到了三维数据,就要⽤三维坐标系内的尺度去对事物进⾏评价?”总觉得有些怪怪的。
举例来说:你要测量从⼴州到深圳的距离,有两种做法:(1)基于已有的经纬度地图体系,拿个卷尺到地球仪上固定两点做个测量;(2)构建关于地球的三维坐标系,在地球上这两点之间打洞连个直线测量。
现任正常⼈都是选择第⼀种⽅案。
再⽐如我们想基于距离对⼴东省内所有⼩城市进⾏聚类,聚合形成⼏个超⼤城市,这个时候你⽤的距离当然是地表距离(⽤经纬度体系构建的⼆维地图来计算距离),⽽不会说要根据三维坐标系下的两点之间的欧⽒距离⽽对于降维算法来说,如果使⽤传统的欧⽒距离来作为距离尺度,显然会抛弃“数据的内部特征”。
《2024年流形学习算法数据适用性问题的研究》范文

《流形学习算法数据适用性问题的研究》篇一一、引言随着大数据时代的来临,数据分析和处理已成为各领域研究的重要一环。
流形学习作为一种新型的非线性降维方法,在处理复杂数据时展现出强大的能力。
然而,流形学习算法在数据适用性方面仍存在诸多问题。
本文旨在研究流形学习算法在数据适用性方面的问题,分析其存在的挑战和解决方法,以期为相关研究提供有益的参考。
二、流形学习算法概述流形学习是一种基于流形结构的降维方法,通过寻找高维数据在低维流形上的投影,实现数据的降维和可视化。
流形学习算法包括局部线性嵌入、拉普拉斯特征映射、等距映射等方法,具有优秀的非线性降维能力,能够有效地揭示数据的内在结构。
三、流形学习算法数据适用性问题尽管流形学习算法在非线性降维方面表现出色,但在实际应用中仍存在数据适用性问题。
这些问题主要表现在以下几个方面:1. 数据分布问题:流形学习算法假设数据分布在低维流形上,当数据分布不满足这一假设时,算法的性能会受到影响。
例如,当数据具有复杂的分布或噪声干扰时,算法的准确性会降低。
2. 参数设置问题:流形学习算法中涉及许多参数设置,如近邻数、核函数等。
这些参数的设置对算法的性能具有重要影响。
然而,目前尚无有效的参数设置方法,往往需要依靠经验或试错法,导致算法的稳定性和可解释性较差。
3. 数据量问题:流形学习算法在处理大规模数据时,计算复杂度较高,容易陷入过拟合。
此外,当数据量不足时,算法的降维效果可能不理想。
4. 实际应用问题:不同领域的数据具有不同的特性和需求,如何将流形学习算法应用于具体领域,解决实际问题,仍需进一步研究。
四、解决方法与策略针对流形学习算法在数据适用性方面的问题,本文提出以下解决方法与策略:1. 改进算法适应性:针对不同类型的数据分布,可以尝试改进流形学习算法的适应性。
例如,采用更灵活的核函数或引入其他降维技术来提高算法的鲁棒性。
2. 优化参数设置:针对参数设置问题,可以尝试采用自动调参技术或贝叶斯优化等方法来优化参数设置,提高算法的稳定性和可解释性。
流形学习算法中的参数选择问题研究

oN PARAM ETER SELECTI ON N ANI I M FoLD LEARNI NG ALGOl UTHM
求保持数据 内在几何特性 , 于流形上所有 的点 , o p用它们 对 I ma s
0 引 言
流形学 习算法是近年来 发展起来 的一类机器 学 习算 法 , 文
献[] 1 提出的等度规特 征映射 (sma ) I p 算法 以及 文献 [ , ] o 2 3 提 出的局部线性嵌入 ( L ) L E 算法引领了该领 域快 速地发展 。流形 的定义是 : 设 是一个 H udr a sof f拓扑空 间 , 对每 一点都 有 P 若 ∈M, 都有 P的一个 开邻域 U和 R 的一个开 子集 同胚 , 则称
f t emapn I ma )a dl a l ere bd ig( L e u p ig(s p n o l i a m edn L E)aetot ia mail an ga oi msC m a snadaa s fh ar o c n r pcl nodl ri l rh . o p i n nl i o e w y f e n g t r o ys t
WagZ j H am n n ei e uH o i
( o p t g Cne,h n hiU i rt ni e n C m ui et S ag a n e i o E gn r g& ,h n hi 0 60,hn n r v sy f ei e S ag a 2 12 C i Me a)
流形学习的理论和方法

内在维数研究
❖ PCA方法基于方差比来确定约简维数 ❖ ISOMAP利用方差损失形成的拐点估计维数 ❖ 其他
最近邻域 分形维 Packing Numbers 测地线最小生成树
基于Packing Numbers的内在维数研究
定量化研究
❖ 高维数据集的内在维数如何影响高维空间的流形结 构?———没有一般性研究
Isomap algorithm,为Isomap自动选择领域因子 Wang Jing, Zhang Zhenyue, Zha Hongyuan. Adaptive Manifold
Learning,2004,在每个样本点上自适应地选择领域因子 张军平,通过集成的方式来改进流形学习产生的不稳定性
❖ 数据流的流行学习
❖ Isomap 建立在MDS 的基础上,力求保持数据 点的内在几何性质,即保持两点间的测地距离。
❖ 它同MDS 的最大区别在于,MDS 构造的距离 矩阵反映的样本点之间的欧氏距离,而Isomap 构造的距离矩阵反映的是样本点之间的测地距 离。
❖ 测地距离的近似计算方法如下:样本点 和它的 邻域点之间的测地距离用它们之间的欧氏距离 来代替;样本点 和它邻域外的点用流形上它们 之间的最短路径来代替。
流形学习
❖ 基本思想:每个高维空间内的流形都有一个 低维空间内的流形与之对应,只要找出一个 光滑映射,就可以把高维原数据映射成其低 维目标空间内的对应。
❖ 流形的本质是局部化,用数学语言说,就是 一个局部可坐标化的拓扑空间。“局部坐标” 可以将问题分解为局部问题进行计算,而拓 扑空间又能保证将局部计算结果合理、光滑 地拼接起来,揭示问题的整体结构。
流形学习的方法
❖ ISOMAP ❖ LLE ❖ HLLE ❖ LE ❖ LTSA
流形学习算法综述

流形学习算法综述流形学习(manifold learning)是一种无监督学习方法,用于在数据集中发现潜在的低维流形结构。
与传统的线性降维方法相比,流形学习算法可以更好地捕捉非线性结构,并在保持数据结构的同时降低数据的维度。
在本文中,我们将综述流形学习算法的主要方法和应用领域。
首先,我们将介绍几种常用的流形学习算法。
其中一种是主成分分析(PCA)。
PCA是一种线性降维算法,通过计算数据的协方差矩阵的特征向量,将数据投影到低维空间中。
然而,PCA只能发现线性结构,对于复杂的非线性数据,效果较差。
另一种常用的算法是多维缩放(MDS),它通过最小化高维数据点之间的欧氏距离和降维空间点之间的欧氏距离之间的差异,来获取降维的坐标。
然而,MDS在处理大规模数据集时计算复杂度较高。
还有一种被广泛研究的算法是局部线性嵌入(LLE),它通过保持每个样本与其邻居样本之间的线性关系来进行降维。
LLE能够很好地处理非线性结构,但对于高维稀疏数据表现不佳。
除了以上提到的算法,还有一些流行的流形学习方法。
其中之一是等距映射(Isomap),它通过计算数据点之间的最短路径距离来构建邻接图,然后使用MDS将数据映射到低维空间。
Isomap能够很好地处理数据中的非线性流形结构,但对于高维数据计算开销较大。
另一个流行的算法是局部保持投影(LPP),它通过最小化数据点之间的马氏距离来进行降维。
LPP能够保持数据的局部关系,并且对于高维数据有较好的效果。
除了上述算法,还有一些最新的流形学习算法。
其中之一是随机投影流形学习(SPL),它使用随机投影技术来近似流形嵌入问题,从而提高了运行效率。
另一个新算法是自编码器(Autoencoder),它通过训练一个神经网络来学习数据的非线性特征表示。
自编码器在流形学习中被广泛应用,并取得了很好的效果。
流形学习算法在许多领域中有广泛的应用。
其中一个应用是图像处理领域,例如图像分类和人脸识别。
流形学习可以帮助将图像特征降维到低维空间,并保留图像之间的相似性。
流形学习研究现状分析
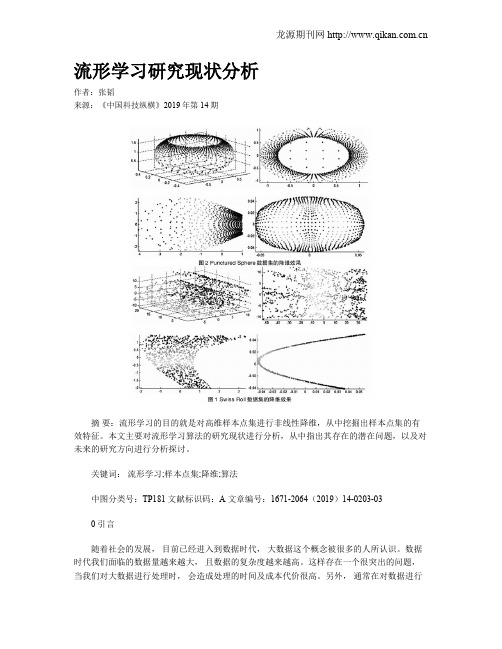
流形学习研究现状分析作者:张韬来源:《中国科技纵横》2019年第14期摘要:流形学习的目的就是对高维样本点集进行非线性降维,从中挖掘出样本点集的有效特征。
本文主要对流形学习算法的研究现状进行分析,从中指出其存在的潜在问题,以及对未来的研究方向进行分析探讨。
关键词:流形学习;样本点集;降维;算法中图分类号:TP181 文献标识码:A 文章编号:1671-2064(2019)14-0203-030 引言随着社会的发展,目前已经进入到数据时代,大数据这个概念被很多的人所认识。
数据时代我们面临的数据量越来越大,且数据的复杂度越来越高。
这样存在一个很突出的问题,当我们对大数据进行处理时,会造成处理的时间及成本代价很高。
另外,通常在对数据进行学习之前,需要对数据进行预处理,即对数据进行清洗。
所谓清洗,就是将无用的信息剔除掉,将有用的信息保留。
常用的方法就是对数据集进行特征提取,根据学习的需求,从中提取有用信息。
通常情况下,数据点集的维度很高,每个维度都表示数据的一个特征,从多个特征中提取少量特征,其实质就是对样本点集进行降维。
常见的降维方法有线性降维算法,其主要目的是通过学习一个线性降维映射,将高维样本点集投影到低维空间。
常见的线性降维算法有P C A [ 9 ] 、MDS[8]、LDA[10]。
主成分分析法(PCA)是最著名的线性降维算法,其采用统计学的思想,通过构造样本点集之间的协方差矩阵来分析样本点的分布特点。
通过对协方差矩阵进行特征值分解,按照特征值的大小对特征向量进行排列。
最大的特征值所对应的特征向量表示第一主成分,它表明,样本点集沿着此方向分布最多。
依次可以构造第二主成分,第三主成分等。
通过这样的方式,可以达到对样本点集进行降维的目的。
多维尺度分析( M D S )是另一类比较经典的线性降维算法,其采用几何学的知识,希望在降维过程中保持高维样本点之间的欧氏距离,也就是说降维后,低维样本点之间的欧氏距离与对应的高维样本点之间的距离保持一致。
流形学习方法中的若干问题分析

流形学习方法中的若干问题分析
高小方
【期刊名称】《计算机科学》
【年(卷),期】2009(36)4
【摘要】流形学习是近年来机器学习与认知科学中的一个新的研究热点,其本质在于根据有限的离散样本学习和发现嵌入在高维空间中的低维光滑流形,从而揭示隐藏在高维数据中的内在低维结构,以实现非线性降维或者可视化.介绍了几种主要的流形学习算法,分析了它们的优势与不足,总结了流形学习方法中需要解决的若干问题及其研究现状,并展望了流形学习未来的研究前景.
【总页数】5页(P25-28,59)
【作者】高小方
【作者单位】山西大学计算智能与中文处理教育部实验室,太原,030006
【正文语种】中文
【中图分类】TP3
【相关文献】
1.判定局部共形K(a)hler流形为Vaisman流形的若干定理 [J], 杨永举;王学强
2.基于流形学习方法的大数据分析技术在检验检疫行业中应用探讨 [J], 徐胜林;魏颖昊;仵冀颖
3.LLE流形学习的若干问题分析 [J], 罗芳琼
4.流形学习方法及其在头部姿势估计中的应用 [J], 刘志勇;王珏
5.欧勇盛团队提出一种基于流形浸入与浸没的机器人动态系统精确稳定学习方法[J],
因版权原因,仅展示原文概要,查看原文内容请购买。
流形学习算法及其应用研究共3篇

流形学习算法及其应用研究共3篇流形学习算法及其应用研究1流形学习算法是一种机器学习算法,其目的是从高维数据中抽取出低维度的特征表示,以便进行分类、聚类等任务。
流形学习算法的基本思想是通过将高维数据变换为低维流形空间,从而保留数据的本质结构和信息。
近年来,流形学习算法得到了越来越多的关注和应用。
以下我们将介绍一些常用的流形学习算法及其应用。
一、常用的流形学习算法(一)局部线性嵌入(Locally Linear Embedding,简称LLE)LLE算法是一种无监督的流形学习算法,它把高维数据集映射到低维空间,保留了数据间的局部线性关系,即原始数据点集中的线性组合权重。
LLE算法的核心思想是假设所有数据样本都是从某个流形空间中采样得到的,并通过寻找最小化误差的方式来还原流形结构。
LLE算法有着较好的可解释性和良好的鲁棒性,同时可以有效地应用于图像处理、模式识别等领域。
(二)等距映射(Isomap)Isomap算法是一种经典的流形学习算法,它可以从高维数据中提取出低维流形空间,并且保留了数据间的地位关系。
它的基本思想是将高维数据转化为流形空间,从而保留了数据的全局性质。
等距映射算法可以应用于数据降维、探索数据关系等领域,并已经在生物学、计算机视觉等领域得到广泛应用。
(三)核主成分分析(Kernel Principal Component Analysis,简称KPCA)KPCA算法是一种非线性的流形学习算法,可以有效地处理非线性问题。
KPCA通过使用核函数来将数据映射到高维空间,然后应用PCA算法进行降维。
KPCA算法在图像识别、人脸识别、语音识别等领域应用广泛。
(四)流形正则化(Manifold Regularization)流形正则化算法是一种半监督学习算法,它可以有效地利用已经标记的数据和未标记的数据来进行分类或回归。
其基本思想是通过在标记数据和未标记数据之间构建连接关系,利用非线性流形学习算法对数据进行处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and 合 X上的拓扑 是 X 的满足以下性质的子集族:
(i) 对属于它的任意多元素的并集是封闭的;
对属于它的有限多元素的交集是封闭的; (iii) 且 X , 称 ( X , ) 是一个拓扑空间.
R
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
流形学习的一些数学基础
参考文献: 陈省身, 陈维桓, 微分几何讲义. 北京大学出版社, 1983 M Berger, B Gostiaux. Differential Geometry: Manifolds, Curves and Surfaces, GTM115. SpringerVerlag, 1974 陈维桓, 微分流形初步(第二版). 高等教育出版社, 2001
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
流形学习问题
杨 剑
中国科学院自动化研究所 2004年12月29日
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
维数约简
20 15 10 5 0 1 0.5 1 0 0.5 -0.5 0 -0.5 -1 -1
Machine Learning and Data Mining 2004
R
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
流形学习和维数约简
流形是线性子空间的一种非线性推广. 流形是一个局部可坐标化的拓扑空间.
流形学习是一种非线性的维数约简方法.
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
流形学习的可行性
1 许多高维采样数据都是由少数几个隐含变量所决定 的, 如人脸采样由光线亮度, 人离相机的距离, 人的头 部姿势, 人的脸部肌肉等因素决定. 2 从认知心理学的角度, 心理学家认为人的认知过程是 基于认知流形和拓扑连续性的.
(ii)
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
Hausdorff 空间
如果对空间( X , )中的任意两点 x y, 存在 A ( x) 和 B ( y) 使得 A B , 称 ( X , )是一个 Hausdorff 拓扑空间.
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
主成分分析
PCA对于椭球状分布的样本集有很好的效果, 学 习所得的主方向就是椭球的主轴方向. PCA 是一种非监督的算法, 能找到很好地代表所 有样本的方向, 但这个方向对于分类未必是最有利的.
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
线性判别分析(LDA)
2
LDA的求解: 经过推导把原问题转化为关于样本集总 类内散布矩阵和总类间散布矩阵的广义特征值问题.
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
增加特 征数 增加信 息量 提高准 确性
类增 器加 的训 难练 度分
维数灾难
解决办法:选取尽可能多的, 可能有用的特征, 然后根据 需要进行特征约简.
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
特征约简
特 征 约 简 特征选择 依据某一标准选择 性质最突出的特征
多重判别分析 (MDA)
MDA把LDA推广到多类的情况. 对于c-类问题, MDA把样本投影到 c-1 维子空间. 目标和解法与LDA相似,只是类内散布矩阵的定义 更为复杂, 求解的广义特征值问题也更为复杂.
中 国 线性方法的缺点 科 学 线性方法对于很多数据不能进行有效的处理. 院 自 动 化 研 究 所 现实中数据的有用特性往往不是特征的线性组合.
线性方法相对比较简单且容易计算.
两种经典且广泛使用的线性变换的方法: 主成分分析 (PCA); 多重判别分析 (MDA).
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
主成分分析 ( PCA )
PCA的目的:寻找能够表示采样数据的最好的投影子 空间. PCA的求解:对样本的散布矩阵进行特征值分解, 所 求子空间为过样本均值, 以最大特征值所对应的特征向量 为方向的子空间. Principal component
几种流形学习算法简介:LLE, Isomap, Laplacian Eigenmap.
流形学习问题的简单探讨.
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
线性约简方法
通过特征的线性组合来降维. 本质上是把数据投影到低维线性子空间.
特征抽取
经已有特征的某种 变换获取约简特征
试验数据分析,数据可视化(通常为2维或3 维)等也需要维数约简
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
Outline
线性维数约简方法 流形和维数约简.
流形学习的一些数学基础.
中 国 科 学 院 自 动 化 研 究 所
Machine Learning and Data Mining 2004
线性判别分析(LDA)
LDA是一种监督的维数约简方法.
1
LDA的思想: 寻找最能把两类样本分开的投影直线. LDA的目标: 使投影后两类样本的均值之差与投影 样本的总类散布的比值最大 . Best projection direction for classification
