轴扭转计算
第4节 圆轴扭转时的强度计算
55 . 5 MPa [ ]
故：此阶梯形圆轴满足强度条件。
第六章 圆轴的扭转
第四节
一、强度条件
圆轴扭转时的强度计算
圆轴扭转时 的强度条件
max
T WP
[ ]
扭转强度条件同样可以用来解决三类问题： 强度校核
设计截面尺寸
确定许用载荷
第六章 圆轴的扭转 例6-2 如图所示为阶梯形圆轴，其中实心AB段直 径d1=40mm；BD段为空心部分，外径D =55mm，内 径 d =45mm。轴上A、D、C处为皮带轮，已知主动 轮C输入的外力偶矩为MC=1.8kN· ｍ，从动轮A、D 传递的外力偶矩分别为MA=0.8kN· m，MD=1kN· m， 材料的许用切应力[ ]=80MPa。试校核该轴的强度。 解：1）画扭矩图： 用截面法（或简捷方法） 可作出该阶梯形圆轴的 扭矩图如图所示。
0.8kNm
1.0kNm
第六章 圆轴的扭转 2）强度校核：由于两段轴的截面面积和扭矩值不 同，故要分别进行强度校核。
T 0 . 8 10 63 . 7 a [ ] AB段： max WP 3 ( 40 10 ) 16 d 45 0 . 818 CD段：轴的内外径之比 D 55 3 T 1 10 max Pa WP 3 3 4 ( 55 10 ) (1 0 . 818 ) 16
11圆轴扭转变形与刚度计算
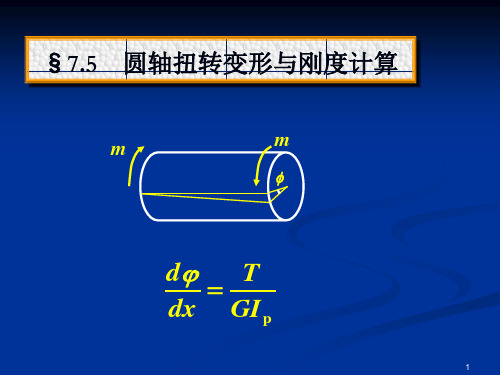
圆轴扭转变形与刚度计算
m m
d T dx GI p
1
一、圆轴扭转变形公式
由
m
m
T ( x )dx 满足平面假设的圆轴： GI p ( x ) l Tl T=Const，等截面圆轴： GI p
GIp－抗扭刚度
d T dx GI p
Ti l i Ti，Ipi在各段内为常数的轴： i 1 GI pi
or
T 180 [ ] GI p max
/ m
等截面圆轴扭转的刚度条件为：
Tmax [ ] (rad/m) GI p
or
Tmax 180 [ ] GI p
/ m
4
【例题1】
传动轴图所示。主动轮A输入功率 PA=36kw ， 从 动 轮 B 、 C 、 D 输 出 功 率 分 别 为 PB=PC=11kW ， PD=14kW ，轴的转速为 n=300r/min ， 许用切应力为[]=50MPa，切变模量为G=80GPa，单 位长度许用扭转角为[]=0.5()/m。试确定： 实心圆截面轴的直径d0；
l
x
12
三、圆轴扭转静不定问题
【例题3】 设有 A 、 B 两个凸缘的圆轴，在扭力矩 m 的作用下发生了变形。这时把一个薄壁圆筒与轴的 凸缘焊接在一起，然后解除m。设轴和圆筒的抗扭 刚度分别是 G1Ip1 和 G2Ip2 ，试求轴内和筒内的扭矩。
m
m
A
B
13
解：由于筒与轴的凸缘焊接在一起，外加扭力矩 m解 除后，圆轴必然力图恢复其扭转变形，而圆筒则阻抗 其恢复。这就使得在轴内和筒内分别出现扭矩T1和T2。 设想用横截面把轴与筒切开，因这时已无外力偶矩作 用，平衡方程为 T1-T2=0 一度静不定问题，应在寻求一个变形协调方程。
轴的转动惯量
轴的转动惯量
轴的转动惯量（或扭转惯性矩）是描述轴绕其自身轴线旋转时惯性特性的物理量。
它是一个刚体特有的物理量，用来衡量物体对转动的惯性程度。
轴的转动惯量可以用公式I = ∫r²dm来计算，其中r是物体上离
转轴距离为r的质点，dm是质点的微元质量。
对于简单的几何体，可以使用一些已知的公式来计算转动惯量：- 对于绕轴旋转的直杆，转动惯量为I = (1/3)mL²，其中m是
直杆的质量，L是直杆的长度。
- 对于绕轴旋转的圆盘，转动惯量为I = (1/2)mR²，其中m是
圆盘的质量，R是圆盘的半径。
- 对于绕轴旋转的球体，转动惯量为I = (2/5)mR²，其中m是
球体的质量，R是球体的半径。
转动惯量的大小取决于物体的质量分布和转轴的位置。
质量集中在离转轴较远的区域，转动惯量会较大；质量集中在离转轴较近的区域，转动惯量会较小。
对于复杂形状的物体，需要使用积分来计算转动惯量。
根据物体的几何形状和质量分布，可以通过积分计算出转动惯量的精确值。
扭转—扭转轴的应力及强度计算(建筑力学)
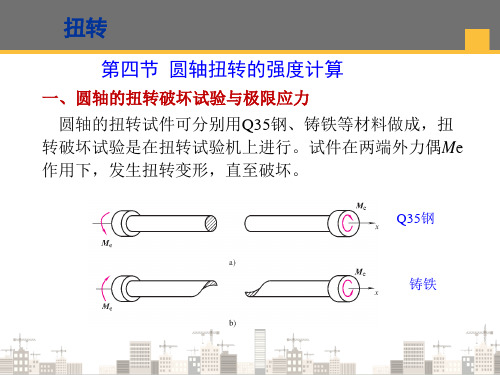
MPa 51.4MPa
4
WP
2.92 10
扭转
(2) 求空心轴的内径
因为要求实心轴和空心轴的扭转强度相同，故两轴的最
大切应力相等，即
'max max 51.4MPa
max
Tmax
Tmax
WP
D23 1 4 16
6
16Tmax
16
变形的能力。单位GPa，其数值可由试验测得。
切应变的其单位是 弧度（rad）
扭转
二、圆轴扭转时横截面上的应力
从几何关系、物理关系和静力学关系这三个方面来分析圆
轴受扭时横截面上的应力。
1. 几何变形方面
取一圆轴进行扭转试验
试验现象表明，圆轴表面上各点的变形与薄壁圆筒扭转
时的变形一样。
扭转
由观察到的现象，对圆轴内部的变形可做如下假设：扭转
截面（危险截面） 边缘点处。因此，强度条件也可写成 maxFra bibliotekTmax
[ ]
W
圆轴强度条件可以解决圆轴扭转时的三类强度问题，即
进行扭转强度校核、圆轴截面尺寸设计及确定许用荷载。
扭转
例9-6 一实心圆轴，承受的最大扭矩Tmax=1.5kN•m，轴
的直径d1=53mm。求：（1）该轴横截面上的最大切应力。
扭转
第四节 圆轴扭转的强度计算
一、圆轴的扭转破坏试验与极限应力
圆轴的扭转试件可分别用Q35钢、铸铁等材料做成，扭
转破坏试验是在扭转试验机上进行。试件在两端外力偶Me
作用下，发生扭转变形，直至破坏。
Q35钢
铸铁
圆轴扭转的计算(工程力学课件)
9 549 20 637 300
Nm
318 N.m 1 477 N.m 2 1432 N.m 3 637 N.m
B
1C
A 2
D 3
扭矩图（T图）
318 N.m
477 N.m
1432 N.m
637 N.m
B
C
A
D
练习1
画扭矩图！
5
3
＋
A
B
C
练习2
3000N.m
3000
＋
1200
T图（N.m）
G E
材料的三个弹性常数
2(1 ) 由三个中的任意两个，求出其第三个
扭转的概念 扭矩和扭矩图
扭转变形
角应变
扭转角
受力特点
大小相等、方向相反， 作用面垂直于杆件轴线的外力偶矩
变形特点 任意横截面绕杆轴线产生转动
典型构件
以扭转变形为主的杆件通常称为轴 最常用的是圆截面轴
扭转的工程实例
螺丝刀杆工作时受扭
输出功率： PB 10 kW PC 15 kW PD 20 kW
M eA
9
549
PA n
9 549 45 1 432 300
Nm
M eB
9
549 PB n
9
549 10 318 300
Nm
M eC
9 549 PC n
9 549 15 477 300
Nm
M eD
9 549 PD n
（1）条件 （2）求约束力
扭矩 T图
T
Ip
Tl l FN l
GI P
EA
扭转
拉压
max
Tmax Wp
11圆轴扭转变形与刚度计算
圆轴扭转变形与刚度计算
m m
d T dx GI p
1
一、圆轴扭转变形公式
由
m
m
T ( x )dx 满足平面假设的圆轴： GI p ( x ) l Tl T=Const，等截面圆轴： GI p
GIp－抗扭刚度
d T dx GI p
Ti l i Ti，Ipi在各段内为常数的轴： i 1 GI pi
6
2. 用截面法求 各段内的扭矩
mB+T1=0
T1 350N m
mB+ mC+ T2=0 T2 700N m
-mD+ T3=0 T3 446N m 3. 作扭矩图
7
4. 确定最大扭矩
T max T2 700N m
5. 强度设计
max
d0
T
max
m d2 x l
10
d1
解：设距左端为 x 的任 意横截面的直径为 d(x) ， 按比例关系可得 d2
d1 d 2 x d d2 1 d2 l
x
l
m
d1
此横截面的极惯性矩为
d1 d 2 x Ip 1 32 32 d2 l
d
4
d2
or
T 180 [ ] GI p max
/ m
等截面圆轴扭转的刚度条件为：
Tmax [ ] (rad/m) GI p
or
Tmax 180 [ ] GI p
/ m
4
【例题1】
传动轴图所示。主动轮A输入功率 PA=36kw ， 从 动 轮 B 、 C 、 D 输 出 功 率 分 别 为 PB=PC=11kW ， PD=14kW ，轴的转速为 n=300r/min ， 许用切应力为[]=50MPa，切变模量为G=80GPa，单 位长度许用扭转角为[]=0.5()/m。试确定： 实心圆截面轴的直径d0；
轴的扭转刚度计算
计算结果对比
公式计算
直径/mm
长度 扭矩/N /mm
剪切模量
Ip 扭转角度/rad
扭转角度/deg
10
300
0.01
8.00E+10
9.82E10
3.82E-05
2.19E-03
刚度/N/deg
4.57E+00
hypermesh
应变/mm 1.94E-04
弹性模量 2.10E+11
扭转角度/rad 0.00003872
03
扭转角度=T*l/(G*Ip)=3.82e-5 04 r a d = 2 . 1 9 e - 3 d e g
扭转刚度Kt=T/扭转角度=4.57 05 N m / d e g
Hypermesh 求解
长度单位全部为毫米（mm）
最大应变为1.936e-4mm
扭转角度=最大应变/(r/2)=3.872e5rad=2.219deg 扭转刚度 Kt=T/扭转角度=4.507 Nm/deg
扭转角度/deg 0.00221849刚度/N/deg Fra bibliotek.5075758
轴
的
扭
转
刚
张志军
度
计
算
方
法
扭转变形计算 公式：
0 1
扭转角(φ)：圆轴扭转时两 横截面相对转过的角度。
0 2
G—剪切弹性模量
几种材料特性 举例：
公式求解：
已知：直径为10mm，长度为300mm， 01 受 到扭 矩为 0 . 0 1N m ， 求扭 转刚 度？
首先将长度单位化为米(m)
02
Ip=π*d^4/32=9.82e-10
轴扭转计算
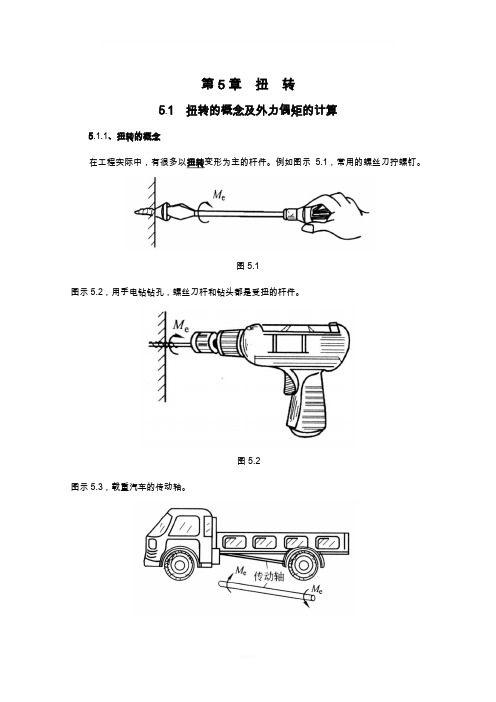
第5章扭转5.1 扭转的概念及外力偶矩的计算5.1.1、扭转的概念在工程实际中，有很多以扭转变形为主的杆件。
例如图示5.1，常用的螺丝刀拧螺钉。
图5.1图示5.2，用手电钻钻孔，螺丝刀杆和钻头都是受扭的杆件。
图5.2图示5.3，载重汽车的传动轴。
图5.3图示5.4，挖掘机的传动轴。
图5.4图5.5所示，雨蓬由雨蓬梁和雨蓬板组成（图5.5a），雨蓬梁每米的长度上承受由雨蓬板传来均布力矩，根据平衡条件，雨蓬梁嵌固的两端必然产生大小相等、方向相反的反力矩（图5.5b），雨蓬梁处于受扭状态。
图5.5分析以上受扭杆件的特点，作用于垂直杆轴平面内的力偶使杆引起的变形，称扭转变形。
变形后杆件各横截面之间绕杆轴线相对转动了一个角度，称为扭转角，用 表示，如图5.6所示。
以扭转变形为主要变形的直杆称为轴。
图5.6本章着重讨论圆截面杆的扭转应力和变形计算。
5.1.2、外力偶矩的计算工程中常用的传动轴（图）是通过转动传递动力的构件，其外力偶矩一般不是直接给出的，通常已知轴所传递的功率和轴的转速。
根据理论力学中的公式，可导出外力偶矩、功率和转速之间的关系为：nN m 9550= （5.1） 式中 m----作用在轴上的外力偶矩，单位为m N ⋅；N-----轴传递的功率，单位为kW ；n------轴的转速，单位为r/min 。
图5.75.2 圆轴扭转时横截面上的内力及扭矩图5.2.1 扭矩已知受扭圆轴外力偶矩，可以利用截面法求任意横截面的内力。
图5.8a 为受扭圆轴，设外力偶矩为e M ，求距A 端为x 的任意截面n m -上的内力。
假设在n m -截面将圆轴截开，取左部分为研究对象（图5.8b ），由平衡条件0=∑x M ，得内力偶矩T 和外力偶矩e M 的关系e M T =内力偶矩T 称为扭矩。
扭矩的正负号规定为：自截面的外法线向截面看，逆时针转向为正，顺时针转向为负。
图5.8图示5.8的b 和c ，从同一截面截出的扭矩均为正号。
圆轴扭转变形与刚计算
2 dsdx
2G
l
T2
T2
8 2G dsdx
l
8
2G
ds
dx
T为常数的等截面杆
V
T 2l 2GI t
=W=T / 2
式中：
It
4 2 ds
Tl
GI t
27
三、开口薄壁杆的扭转应力
max
3T max
n
hi i 3
i 1
3Tl
n
G hi i 3
i 1
3
1
2
28
【例题5】 如图所示为相同尺寸的闭口钢管和开口 钢管，承受相同的扭矩T。设平均直径为d，壁厚为t，
试比较两者的强度和刚度。
d
t (a)
d
t (b)
29
T 2
Tl
GI t
4 2 I t ds
解：1. 对闭口薄圆环， A d 2 s d ，则
dT
t
t
(a)
(b)
相同的扭矩，由于应力分布不同导致了应力大 小差别。
33
课后练习
思考：
一等直圆杆，当受到轴向拉伸时，杆内会产生 切应变吗？当受到扭转时，杆内会产生正应变吗？
作业：
4-16 4-27 4-32 4-33
34
T1-T2=0
T1
T2
mG2 I p2 G1Ip1 G2 Ip2
T2
2
1
T1
16
§7.6 非圆截面杆的扭转
m
m
农业机械中的方轴
柴油机曲柄的受 扭截面为矩形
圆轴扭转时的强度和刚度计算
A1 / A2 = [π (D 2 − d 2 ) / 4] /(πD 2 2 / 4) = (90 2 − 852 ) / 612 = 0.235
传动轴满足强度要求。 2)刚度校核 传动轴的极惯性矩为
I P = 0.1D 4 (1 − a 4 ) = {0.1 × 90 4 [1 − (85 / 90 ) 4 ]}mm 4 = 134 × 10 4 mm 4 θ max = 180 M n /(πGI P )
= (180 × 1500 × 10 3 / 80 × 10 3 × 134 × 10 4 π ) × 10 3 °/m
= 0.8°/m ＜ [θ ]
传动轴满足刚度要求。 (2)计算实心轴的直径
1)按强度条件设计(设直径为D1)。若实心轴与空心轴强 度相同，当材料相同时，它们的抗扭截面系数应相等，即
W n = πD 13 / 16 = πD 3 (1 Βιβλιοθήκη a 4 ) / 16由此得
D 1 = D3 1 − a 4 = [90 × 3 1 − (85 / 90) 4 ]mm = 53mm
根据扭转刚度条件，可以解决三类问题， 即校核刚度、 设计截面和确定许可载荷 。
例6-5 汽车传动轴AB由45号无缝钢管制成，外径D=90mm,
[ 内径d=85mm，许用切应力 [τ ]=60MPa，θ ] =1.0°/m，工作时最
大力偶矩M =1500N·m，G =80GPa。 (1)试校核其强度及刚度。 (2)若将AB轴改为实心轴，试求其直径。 (3)比较空心轴和实心轴的重量。 解 (1)试校核其强度及刚度。 1) 强度校核 传动轴各截面上的扭矩均为
θ max = 180M n /(πGI P ) ≤ [θ ]
(6-13)
圆轴扭转应力计算公式
圆轴扭转应力计算公式在我们的力学世界里，圆轴扭转应力计算公式可是个相当重要的家伙！这就好比是打开机械工程大门的一把神秘钥匙。
想象一下，你手里拿着一根长长的圆轴，就像那种汽车传动轴，当它开始扭转转动的时候，内部就会产生应力。
而我们要搞清楚这应力到底有多大，就得依靠圆轴扭转应力计算公式。
这个公式是：τ = Tρ / Ip 。
其中，τ 表示的是扭转切应力，T 是扭矩，ρ 是所求应力的点到圆心的距离，Ip 则是极惯性矩。
先来说说扭矩 T 。
假设你正在拧一个巨大的螺丝，你使的那个劲儿就是扭矩。
扭矩越大，圆轴扭转时产生的应力也就越大。
比如说，在工厂里的大型机器中，那些传递巨大动力的轴，就得承受巨大的扭矩，所以对它们的材料和设计要求就特别高。
再看ρ ，也就是点到圆心的距离。
这就像是在圆轴这个大舞台上，离圆心越远的地方，应力就越大。
就好比在旋转木马的外圈，你感受到的离心力是不是比在内圈大多了？极惯性矩 Ip 呢，它反映了圆轴横截面抵抗扭转的能力。
横截面形状和尺寸不同，极惯性矩也就不同。
比如说，一根实心的圆轴和一根空心的圆轴，在相同的扭矩作用下，空心的可能因为极惯性矩小，而更容易产生较大的应力。
我记得有一次去工厂参观，看到工人们在检修一台大型的旋转设备。
工程师拿着图纸，嘴里不停地念叨着圆轴扭转应力的计算数值，然后指挥着工人更换某个部件。
我凑过去一看，原来那个部件所在的圆轴位置，由于长期承受较大的扭矩和应力，已经出现了细微的裂纹。
如果不及时更换，可能会导致整个设备出现故障，影响生产进度。
在实际的工程应用中，圆轴扭转应力计算公式可帮了大忙。
从汽车的传动轴，到飞机发动机的轴，再到大型船舶的螺旋桨轴，都得依靠这个公式来确保它们在工作时能够安全可靠地运转。
所以啊，别小看这个公式，它虽然看起来有点复杂，但却是机械工程领域中不可或缺的重要工具。
我们通过它，能够更好地设计和制造各种机械部件，让我们的生活变得更加便捷和高效。
总之，圆轴扭转应力计算公式就像是一位默默守护着机械世界的卫士，时刻保障着各种旋转设备的正常运行。
11.轴的扭转
已知传动轴的转速为300r/min, 主动轮 输 主动轮A输 例11.2* 已知传动轴的转速为 入功率为P 入功率为 A=500kW。从动轮 。从动轮B,C,D输出功率 输出功率 分别为 PB =150kW, PC =150kW, PD =200kW. 求作：该轴扭矩图。 求作：该轴扭矩图。 解: （1）计算主、从动轮传递的外力偶矩 ）
第 11 章
轴的扭转
11.1
扭转概念及外力偶矩计算
11.1.1 扭转的概念
扭转及变形是一种因转动引起的常见现象。 扭转及变形是一种因转动引起的常见现象。 通过扭转传递功率的构件（转动的杆） 轴：通过扭转传递功率的构件（转动的杆）.
m
m
m
m
11.1.2 外力偶矩的计算
已知： 已知：输入输出功率 P (kW) ，转速 n (r/min) . 则：外力偶矩
如图. 用截面法计算扭矩 计算扭矩： 解: 如图 用截面法计算扭矩： T = m = 156N ⋅ m 实心段AC： ① 实心段 ：
16 T 156 × 103 τ max1 = = ≈ 24 ( MPa) 3 W p1 6.55 × 10 W p1 =
π
D 3 ≈ 0 .2 × 32 3 = 6 .55 × 10 3 ( mm 3 )
M e = 9550 P / n ( N ⋅ m )
M e dϕ dW = = M eω 证明： 证明：Q P = dt dt
ω = 2π n
∴ P = 2πnM e P ∴ Me = 2π n
P
n
Me
输入功率P以 、转速n以 为单位代入， 输入功率 以kW、转速 以 r/min为单位代入， 为单位代入 那么，外力偶矩M 那么，外力偶矩 e为:
轴的扭转强度计算
定位轴肩→零件定位→ h ＝3~5 mm 2.设计轴肩时应注意: (1)轴承定位轴肩(套筒)不能过高 (2)轴长应略短于轮毂宽度 (3)安装标准件轴段直径， (a)滚动轴承 (b)联轴器 (c)密封件 (4)轴肩圆角ｒ 轮毂孔圆角Ｒ(倒角Ｃ)
轴上有键槽时： 放大轴径：一个键槽：3~5%
二个键槽：7~10%
取标准植
13.3 轴的强度计算
二、轴的弯扭合成强度计算
转轴同时承受扭矩和弯矩，必须按二者组合强度进行计算。通常 把轴当作置于铰链支座上的梁，作用于轴上零件的力作为集中力， 其作用点取为零件轮毂宽度的中点上。具体的计算步骤如下：
①轴和轴上零件要有准确、牢固的工作位置 ②轴上零件装拆、调整方便 ③轴应具有良好的制造工艺性等 ④尽量避免应力集中
13.2 轴的结构设计
二、零件在轴上的固定 1、周向固定 为了传递运动和转矩，防止轴上零件与轴作相对转动。常用的 周向固定方法有键、花键、销、过盈配合、 弹性环联接、成形联接等。
碳钢比合金钢价廉，对应力集中的敏感性比较低，适用于一般要求的轴。 合金钢比碳钢有更高的力学性能和更好的淬火性能，在传递大功率并要求减小 尺寸和质量、要求高的耐磨性，以及处于高温、低温和腐蚀条件下的轴常采用 合金钢。在一般工作温度下（低于200℃），各种碳钢和合金钢的弹性模量均 相差不多，因此相同尺寸的碳钢和合金钢轴的刚度相差不多。
一、轴的扭转强度计算
用于：①只受扭矩或主要承受扭矩的传动轴的强度计算 ②结构设计前按扭矩初估轴的直径dmin
对于圆截面的实心轴，其抗扭强度条件为：
强度条件
T
T WT
9.55 106
0.2d 3
圆轴扭转时的应力计算公式
圆轴扭转时的应力计算公式在我们学习力学的过程中，圆轴扭转时的应力计算公式可是个相当重要的家伙。
咱们今天就来好好唠唠它！先来说说啥是圆轴扭转。
想象一下，你手里拿着一根棍子，然后像拧麻花一样去转动它，这时候棍子内部就会产生应力。
圆轴扭转就是类似这样的情况啦。
那圆轴扭转时的应力计算公式到底是啥呢？它就是：τ = Tρ / Ip 。
这里的τ 表示的是扭转切应力，T 是扭矩，ρ 是所求应力的点到圆心的距离，Ip 则是极惯性矩。
咱们来仔细瞅瞅这个公式。
扭矩 T 就好比是你拧棍子的那个力气，力气越大，应力也就越大。
而ρ 呢，距离圆心越远，应力也就越大，就像离圆心远的地方更“吃力”。
极惯性矩 Ip 则反映了圆轴抵抗扭转的能力，它越大，应力就相对越小。
我记得之前在给学生们讲这个知识点的时候，有个小同学瞪着大眼睛问我：“老师，这公式咋来的呀？”我就给他举了个例子。
咱们把圆轴想象成是由好多好多层薄圆环组成的。
当圆轴扭转时，每一层薄圆环都会发生相对的滑动，就像是在互相“拉扯”。
通过对这种“拉扯”的分析和计算，咱们就得出了这个公式。
在实际应用中，这个公式可太有用了。
比如说在机械设计里，要设计一根传动轴，就得先算出它在工作时扭转产生的应力，看看是不是在材料能承受的范围内。
要是应力太大，轴就可能会断掉，那可就出大问题啦！再比如，在一些工程结构中，像桥梁的支撑柱，如果受到扭转力的作用，也得用这个公式来算算应力，保证结构的安全稳定。
咱们在解题的时候，一定要搞清楚每个参数的含义和单位，千万别马虎。
有一次考试，就有同学因为把单位搞错了，结果整个答案都错了，那叫一个可惜哟！总之，圆轴扭转时的应力计算公式虽然看起来有点复杂，但只要咱们认真理解，多做几道题练练手，就一定能掌握它，让它成为我们解决问题的有力工具。
怎么样，同学们，这回对圆轴扭转时的应力计算公式是不是更清楚啦？加油，相信大家都能学好这部分知识！。
4.2圆轴扭转时的内力计算
受力特点：在垂直于杆件轴线的平面内， 作用 了一对大小相等，方向相反的外力偶矩； 变形特点：杆件任意两横截面都发生了绕杆件 扭转角：任意两横截面间相对转过的角度。 轴线的相对转动。 这种形式的变形称为扭转变形。
研究对象：轴(以扭转变形为主的杆件）
二、圆轴扭转的内力:扭矩和扭矩图
1.外力偶矩的计算：
M
A
１
２
MC
T
１ （+）
M
２
B
（-）
M
C
例：主动轮A的输入功率P =36kW，从动轮B、C、D输出功率分别为
A
PB=PC=11kW，PD=14kW，轴的转速n=300r/min.试求传动轴指定截面的扭矩，并做 出扭矩图。
解：1)由外力偶矩的计算公式求个轮的力偶矩：
M A = 9550 PA /n =9550x36/300 =1146 N.m
扭矩和扭矩图一圆轴扭转的概念学习内容工程中发构件一圆轴扭转的概念工程中发生扭转变形的构件对称扳手拧紧镙帽工程中承受扭转变形的构件工程中承受扭转变形的构件传动轴汽车传动轴工程中承受扭转变形的构件工程中发生扭转变形的构件受力特点
4.2 圆轴扭转时的内力计算 学习目标：学会计算扭矩
4.2圆轴扭转
学习内容
M B =M C = 9550 PB /n = 350 N.m
M D = 9550 PD /n = 446 N.m
2)分别求1-1、2-2、3-3截面上的扭矩，即为BC,CA,AD段轴的扭矩。
T1 + M B = 0 T1 = -M B =-350N.m M B + M C + T 2 =0 T2 =-M B -M C =-700N.m M D -T3 = 0 T3 = M D = 446N.m
机械基础——圆轴扭转时的变形和刚度计算
当两个截面间的T或Ip有变化时，需分段计算扭转角，然后求其代数和以求得全轴的扭转角。
应用举例
2、圆轴扭转时的刚度计算设计轴类构件时，不仅要满足强度条件，有些轴需要不超过规定的许用值[θ]。
＝ ＝
因此，圆轴扭转的刚度条件为
max＝ × ≤[ ]
应用轴的刚度条件，可以解决刚度计算的三类问题，即校核刚度、设计截面尺寸和确定许可载荷。
3、应用举例
作业
P107：37
课题
圆轴扭转时的变形和刚度计算
教学目的
1、理解圆轴扭转时的变形，扭转角，单位长度扭转角，抗扭刚度；
2、掌握圆轴扭转时的变形和刚度计算。
教学安排
组织教学
讲述新课
五、圆轴扭转时的变形和刚度计算
1、圆轴扭转时的变形计算扭转变形是用两个横截面绕轴线的相对转角 来表示的。对于扭矩T为常数的等截面圆轴，由几何关系可得
扭转的强度计算
圆轴扭转时的强度计算
为了保证受扭圆轴安全可靠地工作，必须使圆轴的最大工作剪应力max τ不超过材料的扭转许用切应力[]τ。
因此，圆轴的强度条件为
max []ττ≤
对于等直圆轴，其强度条件为
max []P T W τ≤ (1-1 ) 上式中max T 是扭矩图上绝对值最大的扭矩，最大切应力max τ发生在max T
所在截面的圆周边上。
对于阶梯形变截面圆轴，因为W ρ不是常量，max τ不一定发生在max T
的截面上。
这就要综合考
虑扭矩T 和抗扭截面系数W ρ两者的变化情况来确定max τ。
在静荷载作用下，扭转许用切应力[]τ与许用拉应力[]t σ之间有如下关系： 对塑性材料[]τ=（0.5～0.6[]t σ
对脆性材料[]τ= (0.8～1.0)[]t σ
应用式（1-1）可解决圆轴扭转时的三类强度问题：
（1）强度校核。
已知材料的许用切应力[]τ、截面尺寸、以及所受荷载，直接应用式（1-1）检查构件是否满足强度要求。
（2）选择截面。
已知圆轴所受的荷载及所用材料，可按式（1-1）计算W ρ后，再进一步确定截面直径。
此时式（1-1）改写为
max
[]T W ρτ≥ （1-1a ）
（3）确定许可荷载 。
已知构件的材料和尺寸，按强度条件计算出构件所能承担的扭矩max T ，再根据扭矩与外力偶的关系，计算出圆轴所能承担的最大外力偶。
此时式（1-1）改写为
max []T W ρτ≤ (1-1b)。
圆轴扭转时的变形与刚度计算
圆轴扭转时的变形与刚度计算圆轴扭转时的变形与刚度计算是机械工程中的一项重要内容。
圆轴扭转是指轴材受到扭矩作用产生的变形现象。
在圆轴扭转中，轴材会经历弹性变形和塑性变形。
弹性变形是指轴材在扭矩作用下恢复原状的变形，而塑性变形则是指超过轴材弹性限度后产生的永久变形。
圆轴扭转可通过弹性力学原理进行分析。
根据胡克定律，弹性体的应力与应变之间有线性关系。
对圆轴来说，变形主要体现为轴材的剪切变形。
剪切形变角度φ与应力τ之间的关系为：τ=G*φ其中，G是剪切模量，表示材料抵抗剪切变形的能力。
φ是单位长度的圆周上小弧δs扭转对应的形变角。
通过积分可得到实际的扭转角θ与应力之间的关系：τ=G*θ/L其中，L是轴材的长度。
对于圆轴来说，扭转力矩T与应力分布之间的关系为：T=τ*A其中，A是轴材的横截面积。
将τ带入等式可得到扭转角与扭转力矩之间的关系：T=G*θ*A/L从上述公式可知，轴材扭转角度与扭转力矩之间存在一线性关系，即扭转刚度k。
k=G*A/L通过上述公式，可以得到轴材的扭转刚度。
扭转刚度越大，则轴材对于扭转力矩的抵抗能力越强。
此外，圆轴扭转时的变形也与材料的断裂强度有关。
当扭转力矩超过材料的断裂强度时，轴材会发生塑性变形，产生永久变形。
在实际应用中，通常会根据所需要的刚度和工作条件来选择合适的轴材及其横截面积。
在计算中需要考虑到轴材的材料特性、几何形状和所受的载荷等因素。
此外，还可以通过模拟实验或数值计算的方法对扭转变形和刚度进行验证和评估。
总之，圆轴扭转时的变形与刚度计算是机械工程中的一项重要内容。
通过弹性力学原理，可以分析轴材在扭转力矩作用下的变形情况，并计算出轴材的扭转刚度。
这对于轴类零件的设计和工程应用具有重要意义。
轴的抗扭刚度
轴的抗扭刚度
轴的抗扭刚度(又称扭转刚度)GIp为：
GIp=G(πd^4)/32。
式中，
G——轴材料的剪变模量，MPa(N/mm^2)；
d——圆轴的截面直径，mm；
Ip——圆截面的抗扭惯性矩，也称极惯性矩，mm^4；
GIp——抗扭刚度，也称扭转刚度，N.mm^2。
极惯性矩Ip=Ix+Iy，即极惯性矩Ip等于两个形心主轴的轴惯性矩之和。
其一般计算公式为：Ip=∫r^2dA。
∫是对全截面A积分。
轴的扭转刚度计算公式是TI/GIP。
轴是穿在轴承中间或车轮中间或齿轮中间的圆柱形物件，但也有少部分是方型的。
轴是支承转动零件并与之一起回转以传递运动、扭矩或弯矩的机械零件。
一般为金属圆杆状，各段可以有不同的直径。
机器中作回转运动的零件就装在轴上。
轴的结构设计是确定轴的合理外形和全部结构尺寸，为轴设计的重要步骤。
它由轴上安装零件类型、尺寸及其位置、零件的固定方式，载荷的性质、方向、大小及分布情况，轴承的类型与尺寸，轴的毛坯、制造和装配工艺、安装及运输，对轴的变形等因素有关。
常见的轴根据轴的结构形状可分为曲轴、直轴、软轴、实心轴、空心轴、刚性轴、挠性轴（软轴）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
钢质实心轴和铝质空心轴（内外径比值 ）的横截面面积相等，钢轴许用应力 ，铝轴许用应力 ，若仅从强度条件考虑，哪一根轴能承受较大的扭矩？
实心轴和空心轴通过牙嵌式离合器连接在一起，已知轴的转速 ，传递功率 ，材料的许用切应力 ，试选择实心轴直径 和内外径比值 的空心轴外径 。
1、作扭矩图（图b）
2、分段求扭转角
式中，
例题主传动钢轴，传递功率 ，转速 ，传动轴的许用切应力 ，许用单位长度扭转角 ，切变模量 ，试计算传动轴所需的直径。
解：1、计算轴的扭矩
2、根据强度条件求所需直径
3、根据圆轴扭转的刚度条件，求直径
故应按刚度条件确定传动轴直径，取 。
本章小结
1、圆轴扭转横截面上任一点的剪应力与该点到圆心的距离成正比，在圆心处为零。最大剪应力发生在截面外周边各点处，其计算公式如下：
若两横截面之间T有变化，或极惯性矩 变化，亦或材料不同（切变模量G变化），则应通过积分或分段计算出各段的扭转角，然后代数相加，即：
在工程中，对于受扭转圆轴的刚度通常用相对扭转角沿杆长度的变化率 来度量，用 表示，称为单位长度扭转角。即：
（）
5.5.2圆轴扭转刚度条件
工程中轴类构件，除应满足强度要求外，对其扭转变形也有一定要求，例如，汽车车轮轴的扭转角过大，汽车在高速行驶或紧急刹车时就会跑偏而造成交通事故；车床传动轴扭转角过大，会降低加工精度，对于精密机械，刚度的要求比强度更严格。下式即为刚度条件
图
分析以上受扭杆件的特点，作用于垂直杆轴平面内的力偶使杆引起的变形，称扭转变形。变形后杆件各横截面之间绕杆轴线相对转动了一个角度，称为扭转角，用 表示，如图所示。以扭转变形为主要变形的直杆称为轴。
图
本章着重讨论圆截面杆的扭转应力和变形计算。
5.1.2、外力偶矩的计算
工程中常用的传动轴（图）是通过转动传递动力的构件，其外力偶矩一般不是直接给出的，通常已知轴所传递的功率和轴的转速。根据理论力学中的公式，可导出外力偶矩、功率和转速之间的关系为：
工程中要求对受扭杆件进行强度计算，根据扭矩T确定横截面上各点的切应力。下面用实心圆轴推导切应力在横截面上的分布规律。
1、变形几何关系
取一实心圆轴，在其表面等距离地画上圆周线和纵向线，如图（a）所示，然后在圆轴两端施加一对大小相等、方向相反的扭转力偶矩 ，使圆轴产生扭转变形，如图（b）所示，可观察到圆轴表面上各圆周线的形状、大小和间距均未改变，仅是绕圆轴线作了相对转动；各纵向线均倾斜了一微小角度 。
（a）（b）
图
等直圆轴扭转时的强度计算
5.4.1圆轴扭转强度条件
工程上要求圆轴扭转时的最大切应力不得超过材料的许用切应力 ，即
对于等截面圆轴，表示为
上式称为圆轴扭转强度条件
试验表明，材料扭转许用切应力 和许用拉应力 有如下近似的关系。
塑性材料
脆性材料
例题汽车的主传动轴，由45号钢的无缝钢管制成，外径 ，壁厚 ，工作时的最大扭矩 ，若材料的许用切应力 ，试校核该轴的强度。
对于图（a）实心圆轴，可在圆轴截面上距圆心为 处取厚度为 的环形面积作为微面积dA，于是 ，从而可得实心圆截面的极惯性矩为
抗扭截面系数为
如为图（b）空心圆轴，则有
式中 为空心圆轴内外径之比。空心圆轴截面的抗扭截面系数为
极惯性矩 的量纲是长度的四次方，常用的单位为 或 。抗扭截面系数 的
量纲是长度的三次方，常用单位为 或 。
图
设半径R，根据平面假设，可以设想扭转时各横截面如同刚性平面一样绕杆轴作相对转动。则由图可知变形后，纵向线段 变为 ， 和 的夹角为 （切应变）， 对应横截面的圆心角 ，在小变形的条件下可以建立如下关系。
为了研究横截面上任意点的切应变，从圆轴截面内取半径为 的微段，如图（b）所示。同理可得
（）
上式表明，横截面上任意点的切应变同该点到圆心的距离 成正比关系。
，
2、圆轴扭转的强度条件为：
利用它可以完成强度校核、确定截面尺寸和许可荷截等三类强度计算问题。
3、圆轴扭转变形的计算公式为：
圆轴扭转的刚度条件是：
思考题
直径相同，材料不同的两根等长的实心圆轴，在相同的扭矩作用下，其最大切应力 和最大单位扭转角 是否相同？
横截面面积相同的空心圆轴和实心圆轴相比，为什么空心圆轴的强度和刚度都较大？
题图
已知传动轴的功率分别为 ， ， ，若AB段和BC段轴的最大切应力相同，试求此两段轴的直径之比及两段轴的扭转角之比。
题图
已知轴的许用切应力 ，切变模量 ，许用单位扭转角 ，试问此轴的直径d达到多大时，轴的直径应由强度条件决定，而刚度条件总可满足。
长度、材料、外力偶矩相同的两根圆轴，一根是实心轴，直径为 ，另一根为空心轴，内外径之比 ，试求两轴具有相等强度时的重量比和刚度比。
将（）式代入
式中， 称截面的极惯性矩，代入上式，得
（）
将（）式代入（）式，得到圆轴扭转横截面上任意点切应力公式
（）
当 时，表示圆截面边缘处的切应力最大
（）
式中， 称为抗扭截面系数。它是与截面形状和尺寸有关的量。
5.3.2极惯性矩和抗扭截面系数
极惯性矩 和抗扭截面系数 可按其定义通过积分求得。下面介绍其计算方法。
2、物理关系
根据剪切胡克定律，在剪切比例极限之内（或弹性范围以内）切应力和切应变成正比关系
将（5–2）式代入上式，得
（）
上式表明，圆轴扭转时，横截面上任意点处的切应力 与该点到圆心的距离 成正比，其分布如图所示，式中 可利用静力方程确定。
图
3、静力学关系
根据图所示，横截面上任意点的切应力 和扭矩有如下静力学关系
题图
一钢轴受扭矩 ，许用切应力 ，许用扭转角 ，切变模量 ，试选择轴的直径。
桥式起重机题图所示。若传动轴传递的力偶矩 ，材料的许用切应力 ， ，同时规定 °/m。试设计轴的直径。
题图
某空心钢轴，内外径之比 ，转速 ，传递功率 ，已知许用切应力 ，许用扭转角 ，切变模量 ，试设计钢轴的内径和外径。
某传动轴，横截面上的最大扭矩 ，许用切应力 ，试按下列两种方案确定截面直径：⑴横截面为实心圆截面；⑵横截面为 的空心圆截面。
习题
试作下列各轴的扭矩图。
题图
图示传动轴，转速 ，A轮为主动轮，输入功率 ，B、C、D为从动轮，输出功率分别为 ， 。⑴试作轴的扭矩图；⑵如果将轮A和轮C的位置对调，试分析对轴受力是否有利。
题图题图
T为圆轴横截面上的扭矩，试画出截面上与T对应的切应力分布图。
图示圆截面空心轴，外径 ，内径 ，扭矩 ，试计算 的A点处的扭转切应力 以及横截面上的最大和最小的扭转切应力。
题图
一直径为 的圆截面轴，其转速为 ，设横截面上的最大切应力为 ，试求所传递的功率。
将直径 ，长 的钢丝一端嵌紧，另一端扭转一整圈，已知切变模量 ，求此时钢丝内的最大切应力 。
某钢轴直径 ，扭矩 ，材料的许用切应力 ，单位长度许用扭转角 ，切变模量 ，试校核此轴的强度和刚度。
阶梯形圆轴直径分别为d1=40mm，d2=70mm，轴上装有三个皮带轮，如图所示。已知由轮3输入的功率为N3=3kW，轮1输出的功率为N1=13kW，轴作匀速转动，转速n=200r/min，材料的许用切应力 ， ，许用扭转角 ＝。试校核轴的强度和刚度。
解：1、计算抗扭截面系数
主传动轴的内外径之比
抗扭截面系数为
2、计算轴的最大切应力
3、强度校核
主传动轴安全
例题如把上题中的汽车主传动轴改为实心轴，要求它与原来的空心轴强度相同，试确定实心轴的直径，并比较空心轴和实心轴的重量。
解：1、求实心轴的直径，要求强度相同，即实心轴的最大切应力也为 ，即
2、在两轴长度相等、材料相同的情况下，两轴重量之比等于两轴横截面面积之比，即
图示圆轴承受集度为m的均匀分布的扭力矩作用，已知轴的抗扭刚度 和长度l，试求B截面的扭转角 。
题图题图
传动轴外径 ，长度 ， 段内径 ， 段内径 ，欲使轴两段扭转角相等，则 应是多长。
（）
式中m----作用在轴上的外力偶矩，单位为 ；
N-----轴传递的功率，单位为 ；
n------轴的转速，单位为r/min。
图
圆轴扭转时横截面上的内力及扭矩图
5.2.1扭矩
已知受扭圆轴外力偶矩，可以利用截面法求任意横截面的内力。图5.8a为受扭圆轴，设外力偶矩为 ，求距A端为x的任意截面 上的内力。假设在 截面将圆轴截开，取左部分为研究对象（图），由平衡条件 ，得内力偶矩T和外力偶矩 的关系
讨论：由此题结果表明，在其它条件相同的情况下，空心轴的重量只是实心轴重量的31%，其节省材料是非常明显的。这是由于实心圆轴横截面上的切应力沿半径呈线性规律分布，圆心附近的应力很小，这部份材料没有充分发挥作用，若把轴心附近的材料向边缘移置，使其成为空心轴，就会增大 或 ，从而提高了轴的强度。然而，空心轴的壁厚也不能过薄，否则会发生局部皱折而丧失其承载能力（即丧失稳定性）。
（）
在工程中， 的单位习惯用 （度/米）表示，将上式中的弧度换算为度，得
对于等截面圆轴，即为
许用扭转角 的数值，根据轴的使用精密度、生产要求和工作条件等因素确定，对一般传动轴， 为 ~ ，对于精密机器的轴， 常取在 之间。
例题图示轴的直径 ，切变模量 ，试计算该轴两端面之间的扭转角。
例题图
解：两端面之间扭转角 为
第5章扭转
扭转的概念及外力偶矩的计算
5.1.1、扭转的概念
在工程实际中，有很多以扭转变形为主的杆件。例如图示，常用的螺丝刀拧螺钉。
图
图示，用手电钻钻孔，螺丝刀杆和钻头都是受扭的杆件。
图