数学建模2008年D题 (NBA赛程分析)[优质ppt]
数学建模 历年试题及论文
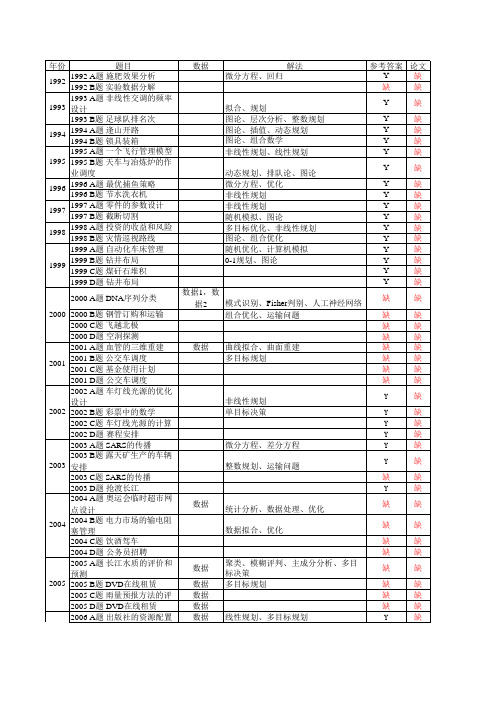
拟合、规划 图论、层次分析、整数队论、图论 微分方程、优化 非线性规划 非线性规划 随机模拟、图论 多目标优化、非线性规划 图论、组合优化 随机优化、计算机模拟 0-1规划、图论
2000 2000 B题 钢管订购和运输 缺 2000 C题 飞越北极 缺 2000 D题 空洞探测 缺 2001 A题 血管的三维重建 数据 曲线拟合、曲面重建 缺 多目标规划 2001 B题 公交车调度 缺 2001 2001 C题 基金使用计划 缺 2001 D题 公交车调度 缺 2002 A题 车灯线光源的优化设计 非线性规划 Y 2002 B题 彩票中的数学 单目标决策 Y 2002 2002 C题 车灯线光源的计算 Y 2002 D题 赛程安排 Y 2003 A题 SARS的传播 微分方程、差分方程 Y 2003 B题 露天矿生产的车辆安排 整数规划、运输问题 Y 2003 2003 C题 SARS的传播 缺 2003 D题 抢渡长江 Y 2004 A题 奥运会临时超市网点设计 数据 统计分析、数据处理、优化 缺 2004 B题 电力市场的输电阻塞管理 数据拟合、优化 缺 2004 2004 C题 饮酒驾车 缺 2004 D题 公务员招聘 缺 2005 A题 长江水质的评价和预测 数据 聚类、模糊评判、主成分分析、多目标决策 缺 2005 B题 DVD在线租赁 数据 多目标规划 缺 2005 2005 C题 雨量预报方法的评价 数据 缺 2005 D题 DVD在线租赁 数据 缺 2006 A题 出版社的资源配置 数据 线性规划、多目标规划 Y 2006 B题 艾滋病疗法的评价及疗效的预测 回归、线性规划 数据 Y 2006 2006 C题 易拉罐形状和尺寸的最优设计 缺 2006 D题 煤矿瓦斯和煤尘的监测与控制 数据 缺 2007 A题 中国人口增长预测 数据 微分、差分方程 Y 2007 B题 乘公交，看奥运 数据 图论、0-1 规划、动态规划 Y 2007 2007 C题 手机“套餐”优惠几何 数据 Y
2008年研究生数学建模竞赛题目(D)
中央空调系统节能设计问题一、问题的来源及意义大型建筑物中使用的中央空调系统（以下简称中央空调）工作方式与普通的家用空调有所不同，普通的家用空调是在一个封闭的环境中，利用冷媒完成室内外的能量交换。
而中央空调是利用冷冻水、冷却水和制冷机完成整个建筑物的能量交换。
普通家用空调可以简单地根据温度控制空调的启停，而理论上中央空调只要有一个用户需要，就应该继续工作。
中央空调都是按照最大负荷进行设计和选择设备的，但实际上中央空调大多数时间都在低负荷下运行，有时甚至在设计负荷的10％下运行。
若中央空调的控制方案设计得不好，在低负荷下却按高负荷需求运行时就会造成中央空调系统运行效率下降，产生浪费。
现在的中央空调系统一般是根据温度控制冷冻水系统的流量（温差或压力随之变化），虽然考虑了节能因素，但并未把节能作为首要的目标，而且都是瞬时控制（温度稍有变化，调节系统就起作用），但真正决定建筑物内温度的是中央空调系统所传递冷量（和热量是一个概念，只是因温差方向不同,冷量和热量都可以视为能量）的累加。
中央空调系统从制冷机产生冷量到传送至末端发挥作用，有较大的延迟，通常为20-30分钟。
另外由于大型商场的人流变化很大，瞬时就会引起冷负荷的较大变化，所以传统的基于参数瞬时变化的控制模型对于中央空调所产生的节能效果有限。
为提高中央空调系统的运行效率，应该将中央空调系统的控制由单参数控制改变为建立建筑物冷量需求模型，根据末端在一定时间内冷量需求总量或冷量需求变化率，控制中央空调系统的冷量输出，以实现节能。
二、问题描述大型商场只要营业新风机组就不停地向商场提供新风以改善商场内的空气质量，当然夏季在提供新风的同时也将商场外部的热量带进商场中。
除了新风带入的热量外，商场中的冷负荷还包括通过建筑物围护结构传入的热量，顾客散发的热量，商场内照明、水泵等电气设备产生的热量等。
其中通过建筑物围护结构和新风传入的热量与商场内外的温差有关，可通过附式1进行估算，也可以将其视作一系列对应不同外部温度的常量。
2008年数学建模国家赛试题
2008高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）A题数码相机定位数码相机定位在交通监管（电子警察）等方面有广泛的应用。
所谓数码相机定位是指用数码相机摄制物体的相片确定物体表面某些特征点的位置。
最常用的定位方法是双目定位，即用两部相机来定位。
对物体上一个特征点，用两部固定于不同位置的相机摄得物体的像，分别获得该点在两部相机像平面上的坐标。
只要知道两部相机精确的相对位置，就可用几何的方法得到该特征点在固定一部相机的坐标系中的坐标，即确定了特征点的位置。
于是对双目定位，精确地确定两部相机的相对位置就是关键，这一过程称为系统标定。
标定的一种做法是：在一块平板上画若干个点，同时用这两部相机照相，分别得到这些点在它们像平面上的像点，利用这两组像点的几何关系就可以得到这两部相机的相对位置。
然而，无论在物平面或像平面上我们都无法直接得到没有几何尺寸的“点”。
实际的做法是在物平面上画若干个圆（称为靶标），它们的圆心就是几何的点了。
而它们的像一般会变形，如图1所示，所以必须从靶标上的这些圆的像中把圆心的像精确地找到，标定就可实现。
图1 靶标上圆的像有人设计靶标如下，取1个边长为100mm的正方形，分别以四个顶点（对应为A、C、D、E）为圆心，12mm为半径作圆。
以AC边上距离A点30mm处的B 为圆心，12mm为半径作圆，如图2所示。
用一位置固定的数码相机摄得其像，如图3所示。
图3 靶标的像请你们：（1）建立数学模型和算法以确定靶标上圆的圆心在该相机像平面的像坐标,这里坐标系原点取在该相机的光学中心，x-y平面平行于像平面；（2）对由图2、图3分别给出的靶标及其像，计算靶标上圆的圆心在像平面上的像坐标, 该相机的像距（即光学中心到像平面的距离）是1577个像素单位(1毫米约为3.78个像素单位)，相机分辨率为1024×768；（3）设计一种方法检验你们的模型，并对方法的精度和稳定性进行讨论；（4）建立用此靶标给出两部固定相机相对位置的数学模型和方法。
2008年度全国大学生数学建模竞赛
2008年度全国大学生数学建模竞赛郑州轻工业学院选拔赛备选题目A. 电梯控制问题我校教三楼有四部电梯。
等电梯的人给出要上下的信号，电梯只有在空闲或同方向行进时才接受这个指令。
然而，电梯经常出现十分拥挤的状况，特别在上下课的时候，要等很长的时间，所以埋怨声很多。
请为电梯设计一个调度方案，减少大家的等待时间，减少师生的不满。
并分析说明你所设计方案的合理性和可操作性。
请你撰写一份800—2000字之间的建议书，说明你的方案使得管理者能够接受你的方案。
B. 汽车车库库存的数学模型某汽车制造厂有一大型仓库存放成品小型汽车，厂方希望将尽可能多的汽车贮存在车库内。
在满足一定要求的条件下，尽可能提高仓库的利用率。
设车库形状为200米╳300米的矩形，仓库只有一个门，位于矩形长边的正中央，门宽5米。
假设汽车形状只有两种形式，如下图所示：从网上查出以上两种型号汽车的形状尺寸。
要求：1、在任何时刻只有一辆汽车开出仓库大门，开出过程中不得有任何碰撞；2、摆放时任意两辆汽车之间至少保持40cm的间距，不重叠；3、出门时必须车头先出，不得使用任何其他辅助设备。
试建立合理的数学模型，解决以下问题。
1、在每辆车都可顺利开出车库的条件下，如何摆放，可提高车库利用率。
2、假设在车辆无法调出时，可以先将阻碍的车辆开出车库外，在这种情况下，给出车辆摆放的优化数学模型。
3、对问题2的车俩摆放模型，假定每辆汽车开出仓库时的速度均相同，且汽车前轮可以左右转动90度，给出将车库4个角落的汽车全部开出所需最少时间的调运方案。
C. 自习教室开放的优化管理近年来，大学用电浪费比较严重，集中体现在学生上晚自习上，一种情况是去某个教室上自习的人比较少，但是教室内的灯却全部打开，第二种情况是晚上上自习的总人数比较少，但是开放的教室比较多，这要求我们提供一种最节约、最合理的管理方法。
下面是某学校收集的部分数据，请完成以下问题.管理人员只需要每天晚上开一部分教室供学生上自习，每天晚上从7：00---10：00开放（如果哪个教室被开放，则假设此教室的所有灯管全部打开）。
NBA赛程的分析与评价
NBA赛程的分析与评价
张德全
【期刊名称】《桂林航天工业学院学报》
【年(卷),期】2009(014)002
【摘要】针对2008年全国大学生数学建模竞赛D题 "NBA赛程的分析与评价"问题,得到赛程安排对某一球队的利弊主要因素有三个方面:相邻两场比赛间隔天数,连续客场数、旅程总数.通过2007-2008赛季赛程计算时间间隔利弊指标、连续客场利弊指标、旅程利弊指标与该赛季各球队总战绩的相关系数,给出2008-2009NBA 赛程的分析与评价,并得到赛程选取赛3场球队的改进方案.
【总页数】5页(P242-246)
【作者】张德全
【作者单位】桂林航天工业高等专科学校,计算机系,广西,桂林,541004
【正文语种】中文
【中图分类】O213.9
【相关文献】
1.利用层次分析法对NBA赛程的分析与评价 [J], 童伟;杜吉梁
2.NBA赛程分析与评价 [J], 王红霞;张力;任志淼
3.关于NBA赛程利弊因素的分析与评价模型 [J], 周密
4.基于Matlab的NBA赛程分析与评价模型 [J], 赵小云;沈陆娟
5.NBA赛程的分析和评价——2008高教社杯全国大学生数学建模竞赛题目 [J], 马明远
因版权原因，仅展示原文概要，查看原文内容请购买。
NBA赛程安排的数学模型与分析
赛程安排的数学模型与分析1．前言n支球队在同一场地上进行单循环赛有多种赛程安排，问题是如何编制符合公平性的赛程，数学上这是一个满足一定指标要求的配对排序问题。
本文在合理假设的基础上，由问题的数学实质，建立出问题的线性规划模型；由问题的特殊性将n分为偶数与奇数分别研究，获得关于各队每两场比赛之间相隔场次数上限的一般公式，用构造性方法加以证明；运用归纳的方法发现了这种特殊排序中的对称规律，由此设计出符合上限要求的计算机算法与实际人工编制法。
文中对赛程优劣的评价指标也作了较多的探讨。
本文一个特点是，分析研究迄今体育界实际使用的赛程“循环编制法”，发现其对n为奇数时编制的赛程公平性差，给出了一种n 为奇数时编制简便、结果合理的人工编制法。
2．问题的提出你所在的年级有5个班，每班一支球队在同一块场地上进行单循环赛, 共要进行10场比赛. 如何安排赛程使对各队来说都尽量公平呢. 下面是随便安排的一个赛程: 记5支球队为A, B, C, D, E，在下表左半部分的右上三角的10个空格中, 随手填上1,2,⋯10, 就得到一个赛程, 即第1场A对B, 第2场B对C, ⋯, 第10场C对E. 为方便起见将这些数字沿对角线对称地填入左下三角.这个赛程的公平性如何呢, 不妨只看看各队每两场比赛中间得到的休整时间是否均等. 表的右半部分是各队每两场比赛间相隔的场次数, 显然这个赛程对A, E有利, 对D则不公平.从上面的例子出发讨论以下问题:1) 对于5支球队的比赛, 给出一个各队每两场比赛中间都至少相隔一场的赛程.2) 当n支球队比赛时, 各队每两场比赛中间相隔的场次数的上限是多少.3) 在达到2) 的上限的条件下, 给出n=8, n=9的赛程, 并说明它们的编制过程.4) 除了每两场比赛间相隔场次数这一指标外, 你还能给出哪些指标来衡量一个赛程的优劣, 并说明3) 中给出的赛程达到这些指标的程度.赛程安排直接影响比赛的公平性，如何建立衡量一个赛程的优劣的指标，建立编制公平合理的排列问题的数学研究，也有数学意义。
全国大学生数学建模竞赛历年试题
全国大学生数学建模竞赛历年试题1.1992年A题：施肥效果分析；B题：试验数据分析；2.1993年A题：非线性交调的频率设计；B题：足球队拍名次；3.1994年A题：逢山开路；B题：锁具开箱；4.1995年A题：一个飞行管理问题；B题：天车与冶炼炉的作业调度；5.1996年A题：最优捕鱼策略；B题：节水洗衣机；6.1997年A题：零件的参数设计；B题：截断切割；7.1998年A题：投资的收益和风险B题：灾情巡视路线8.1999年A题：自动化车床管理B题：钻井布局C题：煤矸石堆积D题：钻井布局9.2000年A题：DNA序列分类B题：钢管订购和运输C题：飞越北极D题：空洞探测10.2001年A题：血管的三维重建B题：公交车调度C题：基金使用计划D题：公交车调度11.2002年A题：车灯线光源的优化设计B题：彩票中的数学C题：车灯线光源的计算D题：赛程安排12.2003年A题：SARS的传播B题：露天矿生产的车辆安排C题：SARS的传播D题：抢渡长江13.2004年A题：奥运会临时超市网点设计B题：电力市场的输电阻塞管理C题：饮酒驾车D题：公务员招聘14.2005年A题：长江水质的评价和预测B题：DVD在线租赁C题：雨量预报方法的评价D题：DVD在线租赁15.2006年A题：出版社的资源配置B题：艾滋病疗法的评价及疗效的预测C题：易拉罐形状和尺寸的最优设计D题：煤矿瓦斯和煤尘的监测与控制16.2007A题：中国人口增长预测；B题：乘公交，看奥运；C题：手机“套餐”优惠几何；D题：体能测试时间安排17.2008A题数码相机定位;B题高等教育学费标准探讨;C题地面搜索;D题NBA赛程的分析与评价.18.2009A题制动器试验台的控制方法分析B题眼科病床的合理安排C题卫星和飞船的跟踪测控D题会议筹备19.2010A题储油罐的变位识别与罐容表标定B题2010年上海世博会影响力的定量评估C题输油管的布置D题对学生宿舍设计方案的评价19.2011A题城市表层土壤重金属污染分析B题交巡警服务平台的设置与调度C题企业退休职工养老金制度的改革D题天然肠衣搭配问题20.2012A题葡萄酒的评价B题太阳能小屋的设计C题脑卒中发病环境因素分析及干预D题机器人避障问题21.2013 A题车道被占用对城市道路通行能力的影响B题碎纸片的拼接复原C题古塔的变形D题公共自行车服务系统。
数学建模-图论
2m d(v) d(v) d(v)
vV
vV1
vV2
（*）
（*）式中2m为偶， d(v) 也为偶（因其中每个d(v)为偶）， vV2
从而推知 d(v) 也为偶，而和式中每个d(v)均为奇，故和 vV1
式中被加项的项数应为偶，这表明G 中度为奇数的点有偶数个。
则G = {V, E} 是一个图，其图形如图3.1所示。
图 3.1
例3.2 设 V = {v1, v2, v3, v4}，E = {v1v2, v1v2, v2v3}， 则G = {V, E} 是一个图，其图形如图3.2所示。
图 3.2
例 3.1 和例 3.2 都不是简单图，因为例3.1 中既 含重边（e2 与 e3）又含环（e5），而例 3.2 中含 重边（v1v2）。下图3.3给出了一个简单图。
三、图论的基本概念
3.1 图的定义 3.2 图的分类 3.3 图的同构 3.4 子图 3.5 图的运算 3.6 图的代数表示及特征
主目录
3.1 图(Graph)的定义
定义3.1 称数学结构G = {V(G), E(G), G} 为
一个图，其中V(G) = {v1, v2, …, vn} 称为图 G的顶 点集(vertex set)或节点集(node set)，V(G) 中的每 一个元素 vi（i = 1, 2, …, n）称为该图的一个顶点 (vertex)或结点(node); E(G) = {e1, e2, …, em} 称为图 G 的边集（edge set），E(G) 中的每一个元素 ek （即V(G) 中某两个元素vi, vj 的无序对）记为 ek = (vi, vj) 或 ek = vivj = vjvi（k = 1, 2, …, m），被称为 该图的一条从 vi到 vj的边(edge)；
2008全国大学生数学建模竞赛题目
2008高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）A题数码相机定位数码相机定位在交通监管（电子警察）等方面有广泛的应用。
所谓数码相机定位是指用数码相机摄制物体的相片确定物体表面某些特征点的位置。
最常用的定位方法是双目定位，即用两部相机来定位。
对物体上一个特征点，用两部固定于不同位置的相机摄得物体的像，分别获得该点在两部相机像平面上的坐标。
只要知道两部相机精确的相对位置，就可用几何的方法得到该特征点在固定一部相机的坐标系中的坐标，即确定了特征点的位置。
于是对双目定位，精确地确定两部相机的相对位置就是关键，这一过程称为系统标定。
标定的一种做法是：在一块平板上画若干个点，同时用这两部相机照相，分别得到这些点在它们像平面上的像点，利用这两组像点的几何关系就可以得到这两部相机的相对位置。
然而，无论在物平面或像平面上我们都无法直接得到没有几何尺寸的“点”。
实际的做法是在物平面上画若干个圆（称为靶标），它们的圆心就是几何的点了。
而它们的像一般会变形，如图1所示，所以必须从靶标上的这些圆的像中把圆心的像精确地找到，标定就可实现。
图1 靶标上圆的像有人设计靶标如下，取1个边长为100mm的正方形，分别以四个顶点（对应为A、C、D、E）为圆心，12mm为半径作圆。
以AC边上距离A点30mm处的B为圆心，12mm为半径作圆，如图2所示。
图2 靶标示意图用一位置固定的数码相机摄得其像，如图3所示。
图3 靶标的像请你们：建立数学模型和算法以确定靶标上圆的圆心在该相机像平面的像坐标, 这里坐标系原点取在该相机的焦点，x-y平面平行于像平面；对由图2、图3分别给出的靶标及其像，计算靶标上圆的圆心在像平面上的像坐标, 该相机的像距（即焦点到像平面的距离）是1577个像素单位(1毫米约为3.78个像素单位)，相机分辨率为1024×786；设计一种方法检验你们的模型，并对方法的精度和稳定性进行讨论；建立用此靶标给出两部固定相机相对位置的数学模型和方法。
NBA赛程的分析与评价
NBA 赛程的模型分析与评价赵文杰 刘涛 佟西伟(北京工业职业技术学院,北京100042) 摘要：本文通过对NBA 赛程的分析与评价,结合所给的新赛季赛程资料,利用excel 将各个球队的赛程分别筛选出来,然后再对各球队赛程进行分析.提出了时间间隔指标m ε,场次最优接近指标m β,背靠背场次指标m b ,以及综合利弊指标与以上三个指标的关系等经过数学处理的,可以评价赛程利弊的数量指标模型.在对所给的赛程的前提下,对东部赛区进行了大量的统计和分析,得到了用循环的方法来选取在同部不同区选取赛三场的球队,并对该方法如何实现进行了详细的说明,图文并茂的展现出循环的具体过程,并给予了评价.关键词： 综合评价 时间间隔 类方差Analysis and Evaluation about the Tournament of NBAZhao Wenjie Liu Tao Tong Xiwei (Beijing Polytechnic College,Beijing 100042,China)Abstract : According to the data of the new fixtures about the tournament of NBA. Filtrating the wholedate of each team by excel before analysis .Then put forward the index of Time-Spacing m ε, the indexof Optimization -Approaching m β,the index of Back to Back m b ,besides, the connection between the Colligation of Advantages and Disadvantages (CAD)and the three indexes. Depending on the new fixtures, analysing the eastern teams before statistical classification.Selecting one team from the same part but different sanjak by the way of a vicious circle. theparticular explanation supplements this way with image and language. Finally, the resultindicates the effectiveness of the model and arithmetic of this thesis.Key words: CAD; index of Time-Spacing;0.引言NBA是全世界篮球迷们最钟爱的赛事之一，姚易加盟以后更是让中国球迷宠爱有加。
NBA赛程的分析和评价——2008高教社杯全国大学生数学建模竞赛题目
２０ ０ ８高教社杯全 国大学 生数学建模 竞赛题 目
马 明 远
（ 西安欧亚学院基础部 高数研 究室， 陕西 西安 ７ ０ ６ ） １ ０５
摘 要： 问题一 ， 考虑 以下因素对球队得 影响 ，背靠 背” “ 场数、 连续两天长距 离跨部 场数、 节假 日主场 天数 、 队对赛程的满意场数 。 球 根据每个 因 素对赛程表进行 单因素分析 ， 并将这些 因素综合 ， 对赛程表进行 多因素分析， 得到综合指标。 通过分析我们发现 赛程 表对大 多数球队是公平 的。 问题 二， 利用赛程对球队影响 因素 的各 个指标 ， 分别列出赛程 对火箭队的有利因素 和不利 因素， 通过 对利弊 因素的详细分析 ， 出赛程对 火箭队基本是 得 公平的。问题 三。 用题 目 利 蛤的赛程 ， 分析 了同部 不同区打 ３ 场对所考虑的 因素 ， 得到选 出Ｉ部 不同区球 队比赛三场的方法 ， 司 并作评价 。 关键词 ：背靠背” “ 扬数 ； 连续两天长距 离 跨部场数 ； 节假 日主场天数； 球队对赛程的满意场数 ； 综合指标
于节假 日 是看球赛的高峰期 ，对于每个球队节 晚的疲惫征程 中。 假日 主场天数越多越好。 在整个 常规赛时闻内 ， （）１ ３ １ 月份对手强 。ｌ 月的赛程是火箭队 １ 节假 日包括 了周六 、 日、 周 万圣节 、 感恩节 和新 史上最魔鬼的赛程。 火箭前 １ 个对手有 ７ ０ 支是 其 国王 年（ 圣诞节打全明星赛 ， 不做考虑 ）统计每支球 上赛季季后赛球队 ， 中包括 了和马刺队、 ， 队赛程 中节假 日主场天数 ，可 以看出在整个 赛 队、 掘金 、 爵士这些球 队的比赛 ， 这些可是联 盟 程 中东部球 队的主场天数 明显 多于西部球 队 ， 公认的最强主场球 队。 因为东部球队地理位置相对密集 ，主场天数 较 １ ． ３ 支球队最有利和最不利 的球队： ．２ ０ ２ 多。 而西部距离较远且客场天数多 ， 减少了长距 最有 利的球 队是 ： 魔术 ； 最不 利的球 队是 ： 超音速 。 离奔波的疲劳。从这点赛程考虑到了东西部 球 队节假 日主客场天数 的差距。 ｌ 对于 问题 ３ ３ １ ．数 量指标 ．８ １ ｌ． － １同部不同 区球队打 ４ 打 ３ ３ ， 场的评价 对赛程表的 四个影响因素中 ， 节假 日主场 １ ． 找 出东西 部打 ３ 比赛 的球 队 ， ．２ ３ 场 结 天数和球 队对 的满意场数对赛程是 正面影响 ， 合题 目中数据 ， 出选取打三场球 队得方法 ： 得 第一步 ： 去年比赛 ４ 从 场的 ６ 个队 中选 出 “ 背靠背” 和连续长距离跨部次数 对赛程是 负 数 面影响 。分别把节假 日 主场天数和满ｊ 场数进 ４队， 葭 去年参加 ３ 场的今年不再参加三场。 １ ．从主客场数的角度考虑 ： ．３ １ 通过计算得 行处理（ ２ 减去节假 日主场 天数 ， ６ 减去 用 ５ 用 ｏ 第 二步 ： ６ 队 ， 这 个 位于 ２区 ， 区 ３个 每 每个球 队的主客场数全是 ４ 场 ， ｌ 即主场数 ＝ 客 球队的满意场数 ） 把 正面因素处理成 负面 因 队， ， 从每个 区中各取 ２ 每 个区排除 １ 。 队（ 队） 场数。 从主客场数 的角度 ， 出本赛程对所有球 素 ， 得 再将每～列 的数据进行数据 ｌ ， 化 设背靠 第三 步 ： 用战绩排 名 ， 除 中间位 置的 利 排 队 是公 平 的 。 背数 ， 连续长距离 跨部 次数 ， 节假 日主场 天数 ， 球 队， 即选择每区较强和较弱的队伍 。 １，２ Ｘ ｘ 则综合 ２模型分析和评价改进 １ ． 从连续长距 离跨部 比赛 的角度考虑 ： 球 对满 意场数 分别为 Ｘ Ｘ ，３．４， ．４ １ 得出 ３ 支球队连续长距离跨 部总数 ： 出以下 指标 ｓ Ｉ＋ ２ ＋ ３＋ ４ 程对火 箭队得利 ０ 得 ＝Ｘ Ｘ ｘ Ｘ 赛 ２１优点 ： ． 弊 考虑 了“ 主客场数 ” “ 、背靠背数 ” “ 、连续 长 结论： 对 于大多数球队跨部ｇ ｌ ｅ， ＂ 。 １ ． ２对于问题 ２ 距离跨部的次数” “ 、 时间间隔” “ 、满意场数 ”和 ｂ ． ， 湖人 太阳 ， 勇士 ， 。 国王 快船 ５ 支球队位 １ ． 姚明加盟 的火箭 队， ．１ ２ 在本次赛程中连 “ 节假 日主场天数 ” 这些 因素的影 响 ， 考虑 的因 次 “ 背靠背” 比赛 ９ ， 次 满 素 比较全面 ； 有因素运用 的数据均是从题 目 所 于美 国最西部的太平洋区 ， 离东部较远 ， 以 续 长距离跨部 比赛 １ ， 距 所 连续长距离跨部为 Ｏ 。 场 意 场数 ５ 场 ，在节假 日主场 天数 ｌ 天 ， 合 赛程表中运用数学方法统计 出来的 ，提高 了结 ３ ， ７ 综 ｃ 音速地处 西北边界处 ， ． 超 跨部 比赛 多为 分析得到对火箭队赛程安排是公平的。 果的准确性 ， 了人主观 因素的干扰 ； 减少 模型 的 利： 数据转换、数 据处理利用计算机减少了人工处 ４场 。 因此不利。 得出本赛程ｘ －￣ 数球 队是公平的。 ， ； ｔ Ｘ （涟 续 长距离跨部少， １ 火箭 队只有 １ 长 理数据的错误 率。 个 １１５从“ ．． 背靠背 角度 考虑 ： 出 ３ 个 球 距离跨部 比赛。 得 ０ ２ 缺点 ： ． ２ （ ）－ ２ １ ２月 对 手 弱 。 箭在 １ 底 到 ２ 初 火 月 月 队“ 背靠背” 总数 ， 出以下结论 ： 得 ２ ． ． １考虑 的赛程 因素之间有无法拆分 的 ２ 个主场 的比赛 ， 对手是开拓者 、６ 、 相互关联 和影 响， 响了结果的精确性 。 ７人 影 对于大多数球队“ 背靠背” 次数较少而且 有连续 ５ 差别不大 。 一般 在 ５至 ９场 。 黄蜂 、 速和森 林狼 ， 超音 实力都不强。 ２２２ 未能实现数 据的完全 自动化处理 。 ．． （ ）火箭队很 少有连 续的多个客场 比赛 ， ３ ２３ 改进 方 向 － ｂ ． 太平洋 区得 的 ５ 西部 个球队湖人 ， 太阳 ， 勇士 ， 国王 ， 快船 。背靠背 ” “ 较多 ， 因为这 ５ 个球 也没有安排火箭队从东海岸飞到西海岸这样 横 在考虑 的因素 中 ，应 当考 虑到 “ 距离 问 队距离东部球队较远 ，为 了减少球员东西来 回 跨全美的长途旅行 。 题” “ ，人体疲 劳度 ” “ ，经济” 等因素。 弊： 参 考 文献 飞行的疲 劳，所 以和东部球队连续打客场比赛 较多 ， 背靠背 ” 目明显大于其它区的球 队。 即“ 数 （ ） 箭客场较多 。 １ １火 １ 月份的所有 ｌ 场 比 ｆ】叶其孝． ５ ｌ 大学生数学建模竞赛辅导教 材ｌ 】 Ｍ． 湖 １９． 通过 以上 ２ 点结 论 ， 对于大 多数 球队“ 背靠 背” 赛 中有 ｌ 场是 客场赛 事 ，ｌ 月份 有 ｌ 场 客 湖 南 ： 南教 育 出版 社 ，９ ８ Ｏ ２ Ｏ 主场仅仅有 ５ ， 队本赛季要 出征 【１蒲俊， 家锋 ， 良忠． Ａ Ｌ Ｂ ． 数 学手 场 火箭 ２ 吉 伊 Ｍ ＩＡ ６ ０ 次数差别不大 ， 对湖人 ， 阳 ， 但 太 勇士 ， 国王 ， 快 场 比赛 ， 船５ 个球队较多 ， 而这 ５ 个球队连续跨部 为 ０ ｌ 次 ，他们 还有一个 连续 ５ 客场 的长途旅 册『 ．上 海 ：浦 东电 子 出版 社 ２０ ２ ， ９ 个 Ｍ１ ０． 有利有弊 ， 了赛程对大多数球队是公平 的。 行 。 体现 １１ ．． ６从球 队满意场数角度考虑 ：得 出 ３ Ｏ （ ）背靠 背” ２“ 比赛多。整个赛季下来火箭 个队中大多数球队 的满意度是接近的 ， 相差不 队要遭遇 ９ “ 次 背靠 背” 比赛 ， 且都是在 客场结 大。由此 可以看出这个赛程对大多数球 队是公 束 ， 而最后 的三次更 是连续的客场“ 背靠 背” 赛 事， 这是联 盟公认 最消耗体力 的比赛 ， 而且 １ ８ 平的 ， 即公平性相对是较高的。 ６次 ＿ １１ 从“ ．７ ． 节假 Ｈ主场 天数 ” 角度考虑 ： 由 次 连 续 的 比赛 中 有 １ 夹 杂 在 连 续 ４ ５个 夜 ｌ模型的建立和求解 对于 Ｎ Ａ这样 庞大 的赛事 ，编 制一个 完 Ｂ 整 的、 各球 队尽可能公平 的赛程是一件非 常 对 复杂 的事 情 ， 赛程的安摊 因为有“ 主客场数 ” 、 “ 背靠 背数 “ 、 连续长距离 跨部的次数 ” “ 续 、连 ２次 比赛 时问 间隔” 。 、 满意 场数” 节假 日主 和“ 场天数” 这些 因素影 响。 以对每支球队的实力 所 发挥和战绩有一定影 响。 ｌｌ 对于 问题 １ Ｉ １ ． 把球队名称 转换成数 字编码得 到每 ．Ｉ １ 个球队的数字编码 ： １． ．２把赛程转换 成数字格式 ： １ 比赛 时 １ （） 间 以天计 、 队名称编号 。２ 列 出 ３ 个球队的 球 （） ０ 主客场表 ， 将主客场表和时 间问隔表汇 总， 表 ０ 示客场比赛 、ｌ 表示主场 比赛。
2008年NBA赛事安排数学建模
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。
如有违反竞赛规则的行为，我们将受到严肃处理。
我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员(打印并签名) ：1.2.3.指导教师或指导教师组负责人(打印并签名)：日期：年月日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：NBA赛程的分析与评价摘要本文所要研究的是在给定NBA赛程的情况下，如何运用数学方法，通过结合各支球队的情况深入分析赛程安排对各球队的影响，同时还要对影响的好坏作出评价的问题。
赛程的安排对一支球队比赛的利弊有很多影响因素，本文根据实际比赛中对联赛战绩有的影响因素，提出了连续客场，背靠背，连续与强队的比赛的三个主要影响因素。
将赛程安排利用表格、程序等进行量化处理，并按各队的强弱进行一个排序和编号，给出各个因素的量化值并进行标准化。
利用层次分析法确定了各个因素的权重，用公式将权重和各因素的值综合，给出赛程利弊的综合值。
对于问题二，利用问题一所得出利弊的综合指数，按照排序找出火箭队的利弊，和最有利、最不利的球队。
问题三中对2007至2008年赛程表分析找出赛3场的方法。
按两对实力差大的赛3场的原则，对同部不同区的队之间，利用胜率差找出新的赛三场的方法予以比较，找出原方法的优缺点，并给与评价。
2008全国大学生数学建模竞赛 题目汇总
2008高教社杯全国大学生数学建模竞赛题目 （请先阅读“全国大学生数学建模竞赛论文格式规范”）A题数码相机定位数码相机定位在交通监管（电子警察）等方面有广泛的应用。
所谓数码相机定位是指用数码相机摄制物体的相片确定物体表面某些特征点的位置。
最常用的定位方法是双目定位，即用两部相机来定位。
对物体上一个特征点，用两部固定于不同位置的相机摄得物体的像，分别获得该点在两部相机像平面上的坐标。
只要知道两部相机精确的相对位置，就可用几何的方法得到该特征点在固定一部相机的坐标系中的坐标，即确定了特征点的位置。
于是对双目定位，精确地确定两部相机的相对位置就是关键，这一过程称为系统标定。
标定的一种做法是：在一块平板上画若干个点，同时用这两部相机照相，分别得到这些点在它们像平面上的像点，利用这两组像点的几何关系就可以得到这两部相机的相对位置。
然而，无论在物平面或像平面上我们都无法直接得到没有几何尺寸的“点”。
实际的做法是在物平面上画若干个圆（称为靶标），它们的圆心就是几何的点了。
而它们的像一般会变形，如图1所示，所以必须从靶标上的这些圆的像中把圆心的像精确地找到，标定就可实现。
图 1 靶标上圆的像有人设计靶标如下，取1个边长为100mm的正方形，分别以四个顶点（对应为A、C、D、E）为圆心，12mm为半径作圆。
以AC边上距离A点30mm处的B为圆心，12mm为半径作圆，如图2所示。
图 2 靶标示意图用一位置固定的数码相机摄得其像，如图3所示。
图3 靶标的像请你们：（1） 建立数学模型和算法以确定靶标上圆的圆心在该相机像平面的像坐标, 这里坐标系原点取在该相机的光学中心，x-y平面平行于像平面；（2） 对由图2、图3分别给出的靶标及其像，计算靶标上圆的圆心在像平面上的像坐标, 该相机的像距（即光学中心到像平面的距离）是1577个像素单位(1毫米约为3.78个像素单位)，相机分辨率为1024×768；（3） 设计一种方法检验你们的模型，并对方法的精度和稳定性进行讨论；（4） 建立用此靶标给出两部固定相机相对位置的数学模型和方法。
2008年D题全国一等奖论文2
NBA赛程的分析与评价摘要本文首先综合考虑了NBA上个赛季的赛程、赛绩和本赛季的赛程确定出赛程对球队利弊的三个主要影响因素，并对其进行了定量分析。
其次利用偏大型柯西分部隶属函数确定主要影响因素的权值，给出了一个利弊的评价指标——利弊指数，并计算了各球队的利弊指数值。
从得到的结果看本次赛程对火箭队而言是比较有利的，其中最有利的球队是凯尔特人队，最不利的是快船队。
对于问题三，基于公平性和观赏性考虑，同部不同区球队实力尽可能悬殊的队尽可能少赛（赛3场）。
由此建立0-1规划模型，并利用LINDO软件求解出了赛3场球队的最优选取方案。
关键词：隶属函数利弊指数 0-1规划一.问题的重述NBA赛程的安排对球队实力的发挥和战绩存在着客观的影响，但编制一个完整的、对各球队尽可能公平的赛程是一件非常复杂的事情。
为了更直观的体现出这些客观因素的存在，利用数学建模方法对2008～2009年的赛季安排表进行定量的分析与评价：1）确定出赛程对某一支球队的利弊的主要影响因素，根据所确定的因素将赛程转换为便于进行数学处理的数字格式，同时给出评价赛程利弊的数量指标。
2）按照1）的结果计算、分析赛程对火箭队的利弊，并找出赛程对30支球队最有利和最不利的球队。
3）对2008～2009年的赛季安排表进行分析可以发现，每支球队与同区的每一支球队赛4场（主客各2场），与不同部的每一球队赛2场（主客各1场），与同部不同区的每一球队有赛4场和赛3场（2主1客或2客1主）两种情况，每支球队的主客场数量相同且同部3个区的球队间保持均衡。
试根据赛程找出与同部不同区球队比赛中，选取赛3场的球队的方法。
这种方法如何实现，对该方法给予评价，也可以给出认为合适的方法。
二.问题分析问题1首先应综合分析上一赛季的赛绩和本次赛季的赛程确定赛程对球队利弊的主要影响因素，其次要确定影响因素权值；根据本次赛场各球队的影响指标，对东西联盟的30支球队进行排序。
问题2根据上一问所得的结果，重点分析赛程对火箭队的利弊及赛程对那个队是最有利的，对那个队是最不利的。
历年数学建模题目
历年数学建模题目
以下是部分历年的数学建模题目：
1. 1992年：施肥效果分析问题、实验数据分解问题。
2. 1993年：非线性交调的频率设计问题、足球排名次问题。
3. 1994年：逢山开路问题、锁具装箱问题。
4. 2002年：车灯线光源的优化设计、彩票中的数学、车灯线光源的计算（大专组）、赛程安排（大专组）。
5. 2003年：SARS的传播、露天矿生产的车辆安排、奥运会临时超市网点设计、电力市场的输电阻塞管理、饮酒驾车、公务员招聘。
6. 2005年：出版社的资源配置、艾滋病疗法的评价及疗效的预测、易拉罐形状和尺寸的最优设计、煤矿瓦斯和煤尘的监测与控制。
7. 2008年：数码相机定位、高等教育学费标准探讨、地面搜索、NBA赛程的分析与评价。
8. 2009年：制动器试验台的控制方法分析、眼科病床的合理安排、卫星和飞船的跟踪测控、会议筹备。
以上信息仅供参考，如需历年数学建模题目，建议查阅数学建模论坛或相关网站获取。
NBA赛程的分析与评价的数学模型
ＮＢＡ赛程的分析与评价的数学模型作者：邱崇洋肖芸芸来源：《中国新技术新产品》2008年第24期摘要：本文依据NBA2008-2009赛季常规赛的赛程安排表，运用数据统计的原理建立起数学模型，通过大量的数据处理，研究分析了新赛季的赛程安排分别对其30支球队的影响，并找出了安排同部不同区球队比赛的方法而且还设计出了更为合理的安排方法。
关键词：赛程安排；统计；安排；1 模型的符号说明xi表示第i支球队的总成绩；P表示总成绩的方差；Mi表示第i支球队的获胜率；Ni表示第i支球队的主客场交替着打的次数的归一化值；K1j表示第j场比赛中主场球队的获胜率；K2j表示第j场比赛中客场球队的获胜率；Y1j表示第j场比赛中主场球队的相对获胜率；Y2j 表示第j场比赛中客场球队的相对获胜率；V1j表示第j场比赛中主场球队的上赛季胜率；V2j 表示第j场比赛中客场球队的上赛季胜率；Z1i表示第i支球队主场获胜率；Z2i表示第i支球队客场获胜率；W1j表示第j场比赛中主场球队背靠背影响率；W2j表示第j场比赛中客场球队背靠背影响率；Qi表示第I支球队的排名；a表示权重比例系数；Bij为0、1变量，表示与j 区的第i个球队对阵；Cij为0、1变量，表示与j区的第i个球队对阵；dij为0、1变量，表示与j区的第i个球队对阵；eij为0、1变量，表示与j区的第i个球队对阵；fij为0、1变量，表示与j区的第i个球队对阵；2 模型的建立与求解2.1 问题（1）的模型建立与求解根据前面的分析，我们采用相对总成绩Xi作为观察每支球队所受的影响。
以Xi的方差P 作为评价赛程利弊的数量指标,（1）对于每一场球赛：根据题中附件1所给出的赛程安排表，可以得出共有1225场比赛（缺少5场）。
对每场比赛都可视为主场球队和客场球队比赛。
先以主场球队为例：其中Y1j=Y，Ｚ１j可根据该球队上赛季主场获胜率表示，并由附件2中的主场战绩求得，即主场总胜利数除以总计42场；假如赛程安排的很密集，则必然影响球队成绩。
NBA赛程的分析与评价参考
题目：NBA赛程的分析与评价摘要通过对NBA赛程的定量分析，我们采用统计学中分阶抽样调查、指数体系和因素分析的方法，与线性代数中的矩阵相结合，运用Matlab软件和Excel进行计算，并对结果进行对比分析建立赛程定量分析与评价模型。
针对问题1，我们根据附件2的数据分析得出赛程对某一支球队的利弊主要有两大因素，即主、客场因素与地域因素，结合假设1计算出各队在主、客场与各种地域因素K；下的获胜指数和获胜率，由此得出评价赛程利弊的数量指标i对于问题2，我们采用分阶抽样调查的方式，在问题1的基础上，通过对获胜指数的对比，得出打主场最有利于公牛队，最不利于掘金队；打客场最有利于凯尔特人队，最不利于掘金队；打“分部赛”最有利于凯尔特人队，最不利于国王队；打“地区赛”最有利于奇才队，最不利于热火队；综合各种因素评定后，赛程对凯尔特人队最有利，对国王队最不利，而对于姚明所在的火箭队，我们同样用获胜指数的对比分析，得出火箭队打主场比打客场占优势，打“分区赛”比打“分部赛”占优势。
但是，从综合指数r比较大，所以火箭队的总体比赛都不占优势。
来看，由于火箭队的ij对于第三问，我们再在问题2的条件下结合假设2，运用统计学中离差及平均差的方法对球队的获胜指数进行对比分析，得出打客场比打主场更能体现公平的结论，即选择“2客1主”为赛3场的球队的方法。
关键词：定量分析；分阶抽样调查；离差；平均差一问题分析根据题目要求，我们运用数学方法对已有的赛程进行定量的分析与评价，得出赛程安排对球队的利弊情况，在此我们声明：两个球队在比赛中“利与弊”是相互对立的事件，所以我们只需考虑其中一种情况即可。
现在我们先考虑的是获胜情况，但是，为了能使模型的精度更高，我们在对计算结果的后期评价中，将“有利指数”通过数学方法转化成“不利指数”后再进行对比分析，得出结论。
对于第一问，要求我们分析赛程对球队的影响因素，并给出评价赛程利弊的指标，我们首先对两个附件的数据进行研究，从中挑选出胜率最高的波士顿凯特尔人球队和胜率最低是迈阿密热火球队，再依照后面第二和第三问的题目要求，挑选出休斯顿火箭球队，将它们分别命名为A、B、C来作分析。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
问题分析:
题目要求分析赛程安排对球队的影响，并利用各因素建立最优的比赛分 配方案。而在分配队伍赛程是需要考虑到:如何确定各个因素对每个球队的 权重;在知道个因素的权重后，怎样建立目标函数值使每个球队间保持均衡； 比较原赛程的安排，如何建立最合适，最均衡的方法。
对于问题1，在分析选取各个球队不利因素的情况下，首先把所选因素 根据实际情况进行量化，并将量化的结果实行权重分配，然后分别加权求和， 以此可以得到赛程对每支球队的弊端指数，也就是量化后的数量指标。 在问题1的基础，考虑到弊端指数对每个球队的影响下，以量化后得出的数 量指标进行每个球队的排名，即可以得出哪只球队在此因素的影响下最有利， 而对于哪只球队最不利。同样的，对于姚明加盟的火箭队的利弊，是怎样的 一个情况。 对于问题3，在东、西部相对独立下，每个球队要与同部不同区的每一只球 队进行比赛，而每个球队总的主客场相同且同部3个区的球队间保持均衡。 为了使各队在比赛安排上相对的公平，我们可以把每个球队与自己比赛3场 的对手划分为一个单位，解出每个单位在各数量指标影响下的实力值，最终 以确定目标函数（综合实力差值），来实现最合适的方法.
后求和，则得到赛程弊端指数 Q iW iD iSi （1）
Q i 赛程弊端指数越大说明赛程安排对球队越不利，反之赛程对球队越有利。
球队实力排名
为了得到每个球队实力之间量化排名，根据2007—2008赛季NBA常规赛各 球队的成绩按以下两个原则排名： 一、排名先后以球队胜率大小确定，胜率越大排名越靠前； 二、当球队间胜率相同时，球队的分差值大的排名相对靠前； 并根据排名情况给予30到1的打分作为这个球队的实力因素值得到实力排名 （见如下表）
为了使每个球队的各因素在同一层次做统一的比较，对各因素的数值进行规范化处理， 设规范化处理后的各因素的值分别为 、 、 ，由于衡量球队利弊的三个因素，影响利弊
的权重不尽相同，在这里我们设定赛程中球队相遇对手的平均实力因素、 连续客场因素
S W 和背靠背比赛因素的权重，分别为
i
、D i
、
i
,
取三个因素量化处理后的值，分别加权
量化处理
对上个赛季的nba赛事做一个统计，首位如下图所示：
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
为了运算方便把连续3次以上的客场向连续2次客场转化，连续两次客场的比赛 记为连续客场一次，连续客场一次的因素值都取常数1，即当 场连续客场转化得到 次连续客场一次，其连续客场值因素值为 ，把表2中各球队连续客场统数据进行处 理，得出每个球队连续客场因素 。（见下表）
由赛程的安排可知，每个球队的主客场次总体是相同的，但有时因为各队主客场的
不一致，而导致某些球队在客场或是主场连续比赛，在分析各队弊端的同时，我们引入
了连续客场因素的概念（即连续打两次客场）。至于不管在主场还是客场的比赛下，只
要连续比赛两天的，对于球队必定是一种影响，所以也应考虑背靠背因素（即指连续比
模型假设：
1、不考虑球队人员的变动及伤病因素，即各队实力保持不变 2、用2007—2008赛季NBA常规赛各球队战况确定各球队实力具有有一定
的准确性、可信性 3、每个球队对手实力越接近自己实力，则说明赛程安排越公平合理 4、假设赛程是在一些公平的约束下产生的，不存在人为偏袒因素。
模型的建立与求解：
赛两天）。加上考虑每个球队的排名可以清楚地知道各球队的不同实力。而在一场比赛
时，自己的输赢往往也与对手的实力有关，最终，对手的平均实力因素也是至关重要 （即82场比赛中对手的平均实力值）。
把三个因素进行一定的量化处理后分别得到每个球队遇到的对手球队平均实力因素
z为 i 、每个球队连续客场因素 g i 和球队背靠背比赛因素值 y i 。
生数学建模竞赛D题
数学与应用数学 09数本2班
王朝勇、张旺、蒙玉超
2008年D题: NBA赛程的分析与评价 NBA是全世界篮球迷们最钟爱的赛事之一，姚易加盟以后更是让 中国球迷宠爱有加。NBA共有30支球队，西部联盟、东部联盟各15支， 大致按照地理位置，西部分西南、西北和太平洋3个区，东部分东南、 中部和大西洋3个区，每区5支球队。对于2008~2009新赛季，常规赛 阶段从2008年10月29日（北京时间）直到2009年4月16日，在这5个多 月中共有1230场赛事，每支球队要进行82场比赛，附件1是30支球队 2008~2009赛季常规赛的赛程表，附件2是分部、分区和排名情况（排 名是2007~2008赛季常规赛的结果） 见/nba/ 。 对于NBA这样庞大的赛事，编制一个完整的、对各球队尽可能公
平的赛程是一件非常复杂的事情，赛程的安排对球队实力的发挥和战绩
有一定的影响，从报刊上经常看到球员、教练和媒体对赛程的抱怨或评
论。这个题目主要是要求用数学建模方法对已有的赛程进行定量的分析 与评价
1 为了分析赛程对某一支球队的利弊，你认为有哪些要考 虑的因素，根据这些因素将赛程转换为便于进行数学处理的 数字格式，并给出评价赛程利弊的数量指标。
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、
82
求出每个球队对手平均实力值（见下表）
赛程转换
将赛程转换成便于数学处理的数字格式，就是在赛程表格上能够得到各个自己
想要得到的因素，得到的各因素都是经过量化的，可以直接用数学进行计算。下表 ①和表是魔术队一部分赛程安排表。表②就是表①的数学格式转化。
2）按照1）的结果计算、分析赛程对姚明加盟的火箭队的利 弊，并找出赛程对30支球队最有利和最不利的球队。 3）分析赛程可以发现，每支球队与同区的每一球队赛4场 （主客各2场），与不同部的每一球队赛2场（主客各1场）， 与同部不同区的每一球队有赛4场和赛3场（2主1客或2客1主） 两种情况，每支球队的主客场数量相同且同部3个区的球队间 保持均衡。试根据赛程找出与同部不同区球队比赛中，选取 赛3场的球队的方法。这种方法如何实现，对该方法给予评价， 也可以给出你认为合适的方法。