时间序列分析——ARMA模型实验
ARMA模型的eviews的建立--时间序列分析实验指导
时间序列分析实验指导42-2-450100150200250统计与应用数学学院前言随着计算机技术的飞跃发展以及应用软件的普及,对高等院校的实验教学提出了越来越高的要求。
为实现教育思想与教学理念的不断更新,在教学中必须注重对大学生动手能力的培训和创新思维的培养,注重学生知识、能力、素质的综合协调发展。
为此,我们组织统计与应用数学学院的部分教师编写了系列实验教学指导书。
这套实验教学指导书具有以下特点:①理论与实践相结合,书中的大量经济案例紧密联系我国的经济发展实际,有利于提高学生分析问题解决问题的能力。
②理论教学与应用软件相结合,我们根据不同的课程分别介绍了SPSS、SAS、MATLAB、EVIEWS等软件的使用方法,有利于提高学生建立数学模型并能正确求解的能力。
这套实验教学指导书在编写的过程中始终得到安徽财经大学教务处、实验室管理处以及统计与应用数学学院的关心、帮助和大力支持,对此我们表示衷心的感谢!限于我们的水平,欢迎各方面对教材存在的错误和不当之处予以批评指正。
统计与数学模型分析实验中心 2007年2月目录实验一 EVIEWS中时间序列相关函数操作···························- 1 - 实验二确定性时间序列建模方法 ····································- 8 - 实验三时间序列随机性和平稳性检验 ···························· - 18 - 实验四时间序列季节性、可逆性检验 ···························· - 21 - 实验五 ARMA模型的建立、识别、检验···························· - 27 - 实验六 ARMA模型的诊断性检验····································· - 30 - 实验七 ARMA模型的预测·············································· - 31 - 实验八复习ARMA建模过程·········································· - 33 - 实验九时间序列非平稳性检验 ····································· - 35 -实验一 EVIEWS中时间序列相关函数操作【实验目的】熟悉Eviews的操作:菜单方式,命令方式;练习并掌握与时间序列分析相关的函数操作。
时间序列中的ARMA模型

c u=
1 (1 2 ... p)
旳无条
7
ARIMA模型旳概念
Yt-u=1(Yt-1-u)+ 2(Yt-2-u)+...+p(Yt-p-u)+vt
0=1 1+ 2 2+...+p p+ 2 1=1 0+ 2 1+...+ p p-1
……
p=1 p-1+ 2 p-2+...+ p 0
(1
2
1
1≤j≤22q ... q2 )
0 j>q
j>q时,ACF(j)=0,此现象为截尾,是MA(q)过程旳一种特征
如下图:
18
ARMA模型旳辨认
MA(2)过程
yt =0.5ut-1 0.3ut2 ut
19
ARMA模型旳辨认
⑵ AR(p)过程旳偏自有关函数
j p 时,偏自有关函数旳取值不为0 j>q 时,偏自有关函数旳取值为0 AR(p)过程旳偏自有关函数p阶截尾 如下图:
32
ARMA模型旳预测
二. 基于MA过程旳预测
过程 结论:
MA (2) 过程仅有2期旳记忆力
33
ARMA模型旳预测
三. 基于ARMA过程旳预测
结合对AR过程和MA过程进行预测 ARMA模型一般用于短期预测
34
五、实例:ARMA模型在金融数 据中旳应用
数据: 1991年1月到2023年1月旳我国货币供
3
ARIMA模型旳概念
2.MA(q)过程旳特征
1. E(Yt)=u
2.
var(Yt)
(1
2
时间序列上机实验ARMA模型的建立

实验一ARMA模型建模一、实验目的学会检验序列平稳性、随机性。
学会分析时序图与自相关图。
学会利用最小二乘法等方法对ARMA模型进行估计,以及掌握利用ARMA模型进行预测的方法。
学会运用Eviews软件进行ARMA模型的识别、诊断、估计和预测和相关具体操作。
二、基本概念宽平稳:序列的统计性质不随时间发生改变,只与时间间隔有关。
AR模型:AR模型也称为自回归模型。
它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测,自回归模型的数学公式为:乂2『t2 川p y t p t式中:p为自回归模型的阶数i(i=1,2,,p)为模型的待定系数,t为误差,yt 为一个平稳时间序列。
MA模型:MA模型也称为滑动平均模型。
它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。
滑动平均模型的数学公式为:y t t 1 t 1 2 t 2 川q t q式中:q为模型的阶数;j(j=1,2,,q)为模型的待定系数;t为误差;yt为平稳时间序列。
ARMA模型:自回归模型和滑动平均模型的组合,便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA,数学公式为:y t 1 y t 1 2 y t 2 p y t p t 1 t 1 2 t 2 q t q三、实验内容(1)通过时序图判断序列平稳性;(2)根据相关图,初步确定移动平均阶数q 和自回归阶数p;(3)对时间序列进行建模四、实验要求学会通过各种手段检验序列的平稳性;学会根据自相关系数和偏自相关系数来初步判断ARMA模型的阶数p和q,学会利用最小二乘法等方法对ARMA 模型进行估计,学会利用信息准则对估计的ARMA 模型进行诊断,以及掌握利用ARMA 模型进行预测。
五、实验步骤1.模型识别(1)绘制时序图在Eviews 软件中,建立一个新的工作文件, 500个数据。
通过Eviews 生成随机序列“ e,再根据“ x=*x(-1)*x(-2)+e ”生成AR(2)模型序列“ x” 默认x(1)=1, x(2)=2,得到下列数据,由于篇幅有限。
时间序列分析和ARMA模型建模研究

时间序列分析和ARMA模型建模研究一、引言时间序列是一种基本的统计数据类型,它记录了随时间变化的某个现象的数值,如股票价格、气温、销售额等等。
时间序列分析是一种用来探测和预测时间序列中趋势、季节性和周期性等特征的统计方法。
ARMA模型是时间序列分析中最常用的模型之一,它将时间序列视为由自相关(AR)和移动平均(MA)两个过程混合而成的结果,可以对其进行预测和建模分析。
本文旨在介绍时间序列分析和ARMA模型建模的基本理论,包括数据分析方法、模型拟合和预测等相关内容。
二、时间序列分析1、基本概念时间序列指在时间轴上每个时刻所对应的变量值的序列,它是由许多个观察值构成的。
一个时间序列通常可以用以下公式来表示:Yt = f (t, εt)其中,Yt表示时间t时刻的变量值,f表示一个关于t和随机误差项εt的函数。
时间序列可以分为平稳和非平稳两类。
2、样本自相关函数与偏自相关函数在时间序列分析中,自相关函数(ACF)和偏自相关函数(PACF)都是非常重要的概念,它们用于刻画序列内部的相关性。
ACF是一个时间序列与其滞后版本之间的相关性度量,而PACF则是在除去其它所有的滞后版本影响下,一个时间序列与其滞后版本之间关系的度量。
3、时间序列模式的识别对于时间序列分析来说,关键任务之一就是识别出序列的模式。
模式可以分为三种:趋势、季节性和周期性。
趋势模式是指序列中长期变化的基本趋势,被认为是序列的“平滑”或“漂移”的程度。
季节性模式是指序列随时间变化的基本周期规律。
周期性模式是连续时间周期性变化的随机性模式。
三、ARMA模型建模1、ARMA模型的概念ARMA模型是时间序列中最常用的模型之一,它表示为自回归(AR)和移动平均(MA)过程的线性组合。
ARMA模型的一般表达式为:Yt = μ + εt + ΣφiYt-i + Σθjεt-j其中,μ是常数项,εt是序列的随机误差项,φi和θj是AR和MA的参数。
2、模型拟合方法在建立ARMA模型时,目标是最小化模型拟合误差。
时序实验ARMA建立预测

实验二 ARMA 模型建模与预测指导一、实验目的学会通过各种手段检验序列的平稳性;学会根据自相关系数和偏自相关系数来初步判断ARMA 模型的阶数p 和q ,学会利用最小二乘法等方法对ARMA 模型进行估计,学会利用信息准则对估计的ARMA 模型进行诊断,以及掌握利用ARMA 模型进行预测。
掌握在实证研究中如何运用Eviews 软件进行ARMA 模型的识别、诊断、估计和预测和相关具体操作。
二、基本概念宽平稳:序列的统计性质不随时间发生改变,只与时间间隔有关。
AR 模型:AR 模型也称为自回归模型。
它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测, 自回归模型的数学公式为:1122t t t p t p t y y y y φφφε---=++++式中: p 为自回归模型的阶数i φ(i=1,2, ,p )为模型的待定系数,t ε为误差, t y 为一个平稳时间序列。
MA 模型:MA 模型也称为滑动平均模型。
它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。
滑动平均模型的数学公式为:1122t t t t q t q y εθεθεθε---=----式中: q 为模型的阶数; j θ(j=1,2, ,q )为模型的待定系数;t ε为误差; t y 为平稳时间序列。
ARMA 模型:自回归模型和滑动平均模型的组合, 便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA , 数学公式为:11221122t t t p t p t t t q t q y y y y φφφεθεθεθε------=++++----三、实验内容及要求1、实验内容:(1)根据时序图判断序列的平稳性;(2)观察相关图,初步确定移动平均阶数q 和自回归阶数p ;(3)运用经典B-J 方法对某企业201个连续生产数据建立合适的ARMA (,p q )模型,并能够利用此模型进行短期预测。
2、实验要求:(1)深刻理解平稳性的要求以及ARMA 模型的建模思想;(2)如何通过观察自相关,偏自相关系数及其图形,利用最小二乘法,以及信息准则建立合适的ARMA 模型;如何利用ARMA 模型进行预测; (3)熟练掌握相关Eviews 操作,读懂模型参数估计结果。
统计实验报告时间序列

一、实验背景时间序列分析是统计学中的一个重要分支,它主要研究如何对时间序列数据进行建模、预测和分析。
本实验旨在通过实际数据的时间序列分析,了解时间序列的基本特性,掌握时间序列建模的方法,并尝试进行未来趋势的预测。
二、实验目的1. 理解时间序列的基本概念和特征。
2. 掌握时间序列数据的可视化方法。
3. 学习并应用时间序列建模的基本方法,如自回归模型(AR)、移动平均模型(MA)和自回归移动平均模型(ARMA)。
4. 尝试进行时间序列数据的预测。
三、实验数据本实验选用某城市过去一年的月度降雨量数据作为分析对象。
数据包括12个月的降雨量,单位为毫米。
四、实验步骤1. 数据预处理- 读取数据:使用Python的pandas库读取降雨量数据。
- 数据检查:检查数据是否存在缺失值或异常值。
- 数据清洗:如果存在缺失值或异常值,进行相应的处理。
2. 数据可视化- 使用matplotlib库绘制降雨量时间序列图,观察数据的趋势和季节性特征。
3. 时间序列建模- 自回归模型(AR):根据自回归模型的理论,建立AR模型,并通过AIC(赤池信息量准则)和SC(贝叶斯信息量准则)进行模型选择。
- 移动平均模型(MA):建立MA模型,并使用同样的准则进行模型选择。
- 自回归移动平均模型(ARMA):结合AR和MA模型,建立ARMA模型,并选择最佳模型。
4. 模型验证与预测- 使用历史数据进行模型验证,比较不同模型的预测精度。
- 对未来几个月的降雨量进行预测。
五、实验结果与分析1. 数据可视化通过时间序列图可以看出,降雨量存在明显的季节性特征,每年的夏季降雨量较多。
2. 时间序列建模- AR模型:通过AIC和SC准则,选择AR(2)模型作为最佳模型。
- MA模型:同样通过AIC和SC准则,选择MA(3)模型作为最佳模型。
- ARMA模型:结合AR和MA模型,选择ARMA(2,3)模型作为最佳模型。
3. 模型验证与预测- 模型验证:通过比较实际值和预测值,可以看出ARMA(2,3)模型的预测精度较高。
ARMAARIMA模型介绍及案例分析

ARMAARIMA模型介绍及案例分析AR、MA和ARIMA是时间序列分析中常见的模型,用于分析和预测时间序列数据的特征和趋势。
下面将对这三种模型进行介绍,并提供一个案例分析来展示它们的应用。
自回归模型(AR)是一种基于过去的观测值来预测未来观测值的模型。
它基于一个假设:未来的观测值可以由过去的观测值的线性组合来表示。
AR模型的一般形式可以表示为:y_t=c+ϕ_1*y_(t-1)+ϕ_2*y_(t-2)+...+ϕ_p*y_(t-p)+ε_t其中,y_t表示时间t的观测值,c是常数项,ϕ_1至ϕ_p是自回归系数,p是自回归阶数,ε_t是误差项。
AR模型的关键是确定自回归阶数p和自回归系数ϕ。
移动平均模型(MA)是一种基于过去的误差项来预测未来观测值的模型。
它基于一个假设:未来的观测值的误差项可以由过去的误差项的线性组合来表示。
MA模型的一般形式可以表示为:y_t=c+ε_t+θ_1*ε_(t-1)+θ_2*ε_(t-2)+...+θ_q*ε_(t-q)其中,y_t表示时间t的观测值,c是常数项,ε_t是误差项,θ_1至θ_q是移动平均系数,q是移动平均阶数。
MA模型的关键是确定移动平均阶数q和移动平均系数θ。
自回归移动平均模型(ARIMA)结合了AR和MA模型的特点,同时考虑了时间序列数据的趋势性。
ARIMA模型一般形式可以表示为:y_t=c+ϕ_1*y_(t-1)+ϕ_2*y_(t-2)+...+ϕ_p*y_(t-p)+ε_t+θ_1*ε_(t-1)+θ_2*ε_(t-2)+...+θ_q*ε_(t-q)其中,y_t表示时间t的观测值,c是常数项,ϕ_1至ϕ_p是自回归系数,p是自回归阶数,ε_t是误差项,θ_1至θ_q是移动平均系数,q是移动平均阶数。
ARIMA模型的关键是确定自回归阶数p、移动平均阶数q和相关系数ϕ和θ。
下面举一个电力消耗预测的案例来展示AR、MA和ARIMA模型的应用:假设有一段时间内的电力消耗数据,我们想要用AR、MA和ARIMA模型来预测未来一段时间内的电力消耗。
金融时序分析ARMA模型实验报告
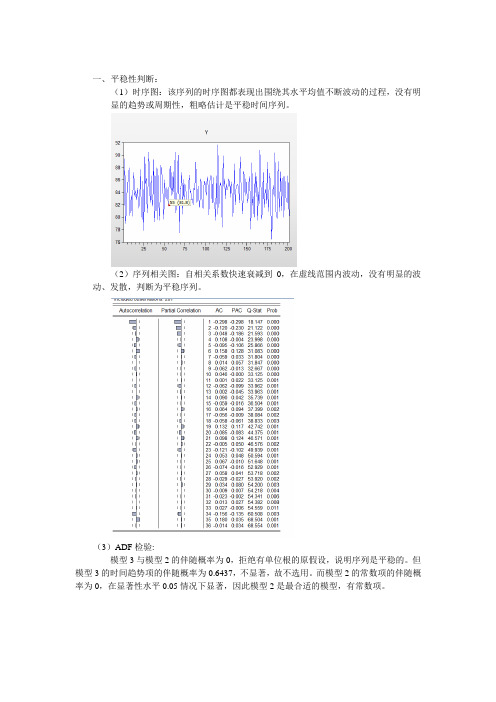
一、平稳性判断:(1)时序图:该序列的时序图都表现出围绕其水平均值不断波动的过程,没有明显的趋势或周期性,粗略估计是平稳时间序列。
(2)序列相关图:自相关系数快速衰减到0,在虚线范围内波动,没有明显的波动、发散,判断为平稳序列。
(3)ADF检验:模型3与模型2的伴随概率为0,拒绝有单位根的原假设,说明序列是平稳的。
但模型3的时间趋势项的伴随概率为0.6437,不显著,故不选用。
而模型2的常数项的伴随概率为0,在显著性水平0.05情况下显著,因此模型2是最合适的模型,有常数项。
模型1的t检验的伴随概率为0.6128,不能拒绝有单位根的原假设,不选用。
综上所述,该序列是平稳的。
二、随机性检验观察自相关图最后两列可以看到,Q检验的伴随概率均小于0.05,拒绝没有自相关性的原假设,因此该序列不是白噪声序列,没有把信息都提取出来。
观察其AC,虽落入虚线内后没有再到虚线外,但不是由非0骤降到0,判断为拖尾。
观察PAC,结果与AC类似,因此AC、PAC都是拖尾,初步判断使用ARMA模型。
接下来将尝试使用AR(1)、AR(2)、MA(1)、MA(2)、ARMA(1,3)、ARMA(1,2)模型进行拟合。
三、模型估计与白噪声检验(1)AR(1):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,拒绝没有自相关性的原假设,不是白噪声序列。
(2)AR(2):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,阶数较小时拒绝没有自相关性的原假设,不是白噪声序列。
(3)MA(1):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,接受没有自相关性的原假设,是白噪声序列。
(4)MA(2):该模型MA(2)项不显著,不选用。
(5)ARMA(1,3):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,接受没有自相关性的原假设,是白噪声序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于ARMA模型的社会融资规模增长分析--——ARMA模型实验第一部分实验分析目的及方法一般说来,若时间序列满足平稳随机过程的性质,则可用经典的ARMA模型进行建模和预则.但是,由于金融时间序列随机波动较大,很少满足ARMA模型的适用条件,无法直接采用该模型进行处理。
通过对数化及差分处理后,将原本非平稳的序列处理为近似平稳的序列,可以采用ARMA模型进行建模和分析。
第二部分实验数据2.1数据来源数据来源于中经网统计数据库.具体数据见附录表5.1 。
2.2所选数据变量社会融资规模指一定时期内(每月、每季或每年)实体经济从金融体系获得的全部资金总额,为一增量概念,即期末余额减去期初余额的差额,或当期发行或发生额扣除当期兑付或偿还额的差额。
社会融资规模作为重要的宏观监测指标,由实体经济需求所决定,反映金融体系对实体经济的资金量支持。
本实验拟选取2005年11月到2014年9月我国以月为单位的社会融资规模的数据来构建ARMA模型,并利用该模型进行分析预测。
第三部分 ARMA模型构建3。
1判断序列的平稳性首先绘制出M的折线图,结果如下图:图3.1 社会融资规模M曲线图从图中可以看出,社会融资规模M序列具有一定的趋势性,由此可以初步判断该序列是非平稳的。
此外,m在每年同时期出现相同的变动趋势,表明m还存在季节特征.下面对m的平稳性和季节性·进行进一步检验.为了减少m的变动趋势以及异方差性,先对m进行对数化处理,记为lm,其时序图如下:图3。
2 lm曲线图对数化后的趋势性减弱,但仍存在一定的趋势性,下面观察lm的自相关图表3.1 lm的自相关图上表可以看出,该lm序列的PACF只在滞后一期、二期和三期是显著的,ACF随着滞后结束的增加慢慢衰减至0,由此可以看出该序列表现出一定的平稳性.进一步进行单位根检验,由于存在较弱的趋势性且均值不为零,选择存在趋势项的形式,并根据AIC自动选择之后结束,单位根检验结果如下:表3。
2 单位根输出结果NullHypothesis: LM has a unit rootExogenous: Constant,Linear TrendLag Length: 0 (Automatic —based on SIC, maxlag=12)t-Statistic Prob.*Augmented Dickey—Fuller teststatistic-8.6746460。
0000Test critical values:1% level-4.0469255% level-3.45276410% level -3.151911*MacKinnon (1996) one-sided p-values。
单位根统计量ADF=—8.674646小于临界值,且P为0.0000,因此该序列不存在单位根,即该序列是平稳序列。
由于趋势性会掩盖季节性,从lm图中可以看出,该序列有一定的季节性,为了分析季节性,对lm进行差分处理,进一步观察季节性:图3.3 dlm曲线图观察dlm的自相关表:表3.3 dlm的自相关图Date: 11/02/14 Time: 22:35Sample: 2005M11 2014M09Included observations:106AutocorrelationPartial Correlation ACPACQ—Stat Prob****|。
|****|。
|1—0.566—0.56634.9340。
000.|*|**|。
|20。
113-0.30536.3410。
000 .|.|*|. |30。
032-0。
09336.4550.000 *|。
|*|。
|4-0。
084—0。
11437。
2440.000。
|*|。
|.|50。
1050。
01538。
4940.000*|。
|*|.|6—0.182-0.18242。
2960。
000。
|*|*|。
|70.105-0。
15643。
5630.000。
|.|*|.|8—0。
058-0.17143。
9540。
000.|.|*|.|9-0.019-0。
19643。
9960.000 .|*|。
|。
|100。
110-0.04545.4290.000**|.|**|。
|11-0.242-0.32952.5010。
000。
|*** |.|。
|120.3630.02368。
5160。
000*|。
|.|.|13-0.2020.03273。
5340.000.|*|.|*|140。
1010.12574.8150。
000。
|.|。
|*|150。
0040.14174.8170.000 *|.|*|. |16—0。
161—0.08978.1100。
000 .|**|。
|。
|170。
2190.03784.2520.000 **|。
|。
|.|18—0.221—0.03690。
6230。
000 .|*|.|。
|190。
089-0.04691。
6620。
000*|.|*|.|20-0.080—0。
15892.5160.000 .|.|。
|。
|210.067-0。
03993.1150。
000。
|.|。
|。
|220.0680。
05693.7490。
000**|. |*|。
|23-0.231-0.130101.080。
000.|*** |.|*|240.3590。
116119.040.000*|.|.|*|25-0。
1890。
123124。
090.000.|。
|.|。
|260.0320。
034124.230.000.|.|。
|。
|270。
0590.037124.740.000*|.|.|。
|28—0。
1260.044127。
080.000.|*|*|。
|290.087-0。
079128。
210。
000。
|.|。
|*|30-0.0500.092128。
580.000.|。
|.|。
|31-0.037-0.019128.790。
000.|. |*|。
|32-0.035-0.113128.970。
000.|。
|.|.|330.041—0.056129.240。
000.|* |.|.|340.078—0.027130。
210.000**|。
|*|.|35-0。
215-0.197137。
640。
000。
|***|.|*|360.3800.130161.260。
000由dlm的自相关图可知,dlm在滞后期为12、24、36等差的自相关系数均显著异于零。
因此该序列为以12为周期呈现季节性,而且季节自相关系数并没有衰减至零,因此为了考虑这种季节性,进行季节性差分,得新变量sdlm:观察sdlm的自相关图:表3。
4 sdlm的自相关图Date: 11/02/14 Time: 22:40Sample: 2005M11 2014M09Included observations: 94Autocorrelation Partial CorrelationAC PAC Q-Stat Prob****|。
|****|. |1-0.505-0.50524。
7670.000. |.|***|。
|2-0.057—0.41925。
0820。
000。
|.|**|.|30.073-0.29225.6090。
000. |*|. |.|40。
1600.06728。
1690.000**|. |。
*|.|5-0。
264-0.12535。
2520.000. |*|。
*|。
|60.098-0。
11036.2440。
000. |*|。
|。
|70。
0980.01937.2430.000. |. |.|*|8-0。
0410.08237.4190。
000。
*|.|. |.|9—0。
132—0.03839.2750。
000.|*|.*|。
|100.076-0.13939。
9020.000。
|**|。
|**|110.2270。
24745.4850。
000***|. |**|. |12-0.459—0.25968。
6470.000. |* |**|. |130。
193-0.25172.7770.000。
|*|.*|.|140.132-0。
10174.7530.000.*|. |.*|。
|15-0。
142-0。
18977。
0560。
000。
|.|。
|.|16-0.053-0.05677。
3780.000。
|**|.|*|170.2330。
09183。
7510。
000**|。
|.*|。
|18—0.234-0.17990.2580。
000. |* |。
|。
|190。
1020.05491.5050。
000。
|。
|.|。
|20—0.052—0。
03591.8410.000.|* |。
|.|210.123—0.00993.7140.000。
|. |.|*|22-0.0590。
12094.1500.000. |.|。
|** |23—0.0110.21594。
1660。
000. |. |。
*|。
|24—0。
032—0。
17094。
3010.000。
|* |.*|。
|250。
088-0.13795.3030.00。
*|. |。
|. |26—0.105-0.03496.7600。
000. |* |。
*|。
|270.077-0。
11697.5620.000。
|。
|.*|.|28-0.054-0。
17897.9670.000. |. |。
|。
|290。
0100。
03297.9820.000。
|*|. |.|300。
1020.03999.4570。
000。
*|。
|.*|。
|31-0。
179-0.099104。
060.000。
|。
|。
|. |320。
071-0.058104。
790。
000.|. |.*|.|330.031-0.066104。
930.000。
*|. |.*|.|34—0.089-0.144106.130。
000. |.|。
|*|350.0360.082106。
320.000. |*|.*|.|360.105—0。
102108.050.000Sdlm在滞后期24之后的季节ACF和PACF已衰减至零,下面对sdlm建立SARMA 模型。
3.2模型参数识别由表3。
4 sdlm的自相关图的自相关图可知,偏自相关系数在3阶后都落在两倍标准差的范围以内,即不显著异于零。
自相关系数在1阶和12阶显著异于零.因此SARMA(p,q)模型中选择p、q均不超过3。
此外,由于高阶移动平均模型估计较为困难而且自回归模型可以表示无穷阶的移动平均过程,因此Q尽可能取小。
拟选择SARMA(1,0)(1,0)12、SARMA(1,0)(1,1)12、SARMA(1,1)(1,0)12、SARMA(1,1)(1,1)12、SAR MA(2,0)(1,0)12、SARMA(2,0)(1,1)12、SARMA(3,0)(1,0)12、SARMA(3,0)(1,1)12八个模型来拟合sdlnm。
