数学地质第六章 判别分析:线性-逐步解析
第六章--判别分析

设有两个正态总体,
现有一个样品如图所示的A点,
A
距总体X的中心
远,距总体Y的中心
远
若按欧氏距离来度量,A点离总体X要比离总体Y近一些。但是,从概率论的
角度看,A点位于 点离总体Y近一些。
右侧的
而位于
左侧的
处,应该认为A
样品点x到
的马氏距离为:
(一)当
时
(二)当
时
虽然在两个总体有显著差异的条件下,误判概率很小,但当这种差异不很显著时,误判的 概率就很大。因此,只有当两个总体的均值有显著差异时,做判别分析才有意义。
-7.182 -4.379 -2.144 -9.440 -6.573 -6.906 -4.245
原分类 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3
新分类 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 3 3
第二节 贝叶斯(Bayes)判别
判别分析就是在研究对象用某种方法分好若干类(组)的情况下,确定新样品属 于已知类别中哪一类的多元统计分析方法。
判别分析和聚类分析不同,判别分析是在已知研究对象分成若干类型(或 组别) 并已取得各种类型的一批已知样品的观测数据 ,在此基础上根据某种准则建立 判别函数式,然后对未知类型的样品进行判别分类。而对于聚类分析,一批给 定样品要划分的类型事先并不知道,需要通过聚类分析来确定各样品所属的类 型。所以,判别分析和聚类分析往往结合起来运用。
第六章 判别分析
第一节 什么是判别分析
在科学研究和日常生活中,往往会遇到这样的问题,即根据观测数据对所研究的对象 进行分类(组)判别。例如,在经济学中可根据人均国内生产总值、人均消费水平等 多种指标来判别一个国家的经济发展程度所属类型;在气象学中,根据已有的气象资 料(气温、气压、湿度等)来判断明天是阴天还是晴天,有雨还是无雨等。以上各方 面的问题具有一个共同特点:就是事先已有“类”的划分,或事先已对某些已知样品 分好了“类”,需要判断那些还未分好的的样品究竟属于哪一类。
数学地质系列______5判别分析

(2)非线性判别函数
双变量: y=c1x1+c2x22 或
y=c1x12+c2x2
多变量:y=c1x1i+c2x2i+„+ckxki
i=1,为线性判别函数
i>=2,为非线性函数
一般情况下,若样品有m个变量,那么新变量y形式为:
y c1 x1 c 2 x 2
cm xm c j x j
主要思想:用统计方法将待判的未知样品与已知类 型样品进行类比,以确定待判样品应归属于哪一类。
矿产预测、地球化学分析、石油及天然气地质中都有 大量的判别类型的问题,
如,判别岩石类型、地层时代、古生物种属、判别钻井穿
过的层位的含油性、判别沉积相、判别地层的生油条件等
10
4、判别分析的具体做法
在已知类型(如A、B、C三类)中抽取样本, 然后根据每个样品的多个指标经过数学运算处理,建立每
= x - μ Σ Σ
-
1 2
-
1 2
x - μ
26
= x - μ Σ-1 x - μ
3、若变量之间是相互无关的,则协方差矩阵为对角矩阵
11 22 Σ
1 11 Σ 1 pp
另有8个待判样品。
利用SPSS软件进行计算: 由样本值得统计量F=14.4644,
对于给定的显著水平α =0.01,查表得临界值 F0.01 (4,5)
=11.4,由于
F F ,则拒绝 H0 ,
这说明A盆地和B盆地的盐泉特征有显著性的差异,
因此进行判别分析是有意义的。
下面进行判别分析:
两组间平方距离(马氏距离)为37.029
《线性判别分析LDA》PPT课件

类别的原始数据,现在要求将数据从二维降维到一维。直接投影
到x1轴或者x2轴,不同类别之间 会有重复,导致分类效果下降。
右图映射到的直线就是用LDA方法计算得到的,可以看到,红色类
别和绿色类别在映射之后之间的距离是最大的,而且每个类别内
部点的离散程度是最小的(或者说聚集程度是最大的)。
5
2021/3/3
6
2021/3/3
LDA
要说明白LDA,首先得弄明白线性分类器(Linear Classifier)
:因为LDA是一种线性分类器。对于K-分类的一个分类问题,
会有K个线性函数:
权向量(weight vector) 法向量(normal vector)
阈值(threshold) 偏置(bias)
当满足条件:对于所有的j,都有Yk > Yj,的时候,我们就说x 属于类别k。对于每一个分类,都有一个公式去算一个分值, 在所有的公式得到的分值中,找一个最大的,就是所属的分类 。
12
2021/3/3
么么么么方面 Sds绝对是假的
LDA
我们定义一个投影前的各类别分散程度的矩阵,这个矩阵看起 来有一点麻烦,其实意思是,如果某一个分类的输入点集Di里 面的点距离这个分类的中心店mi越近,则Si里面元素的值就越 小,如果分类的点都紧紧地围绕着mi,则Si里面的元素值越更 接近0.
7
2021/3/3
LDA
上式实际上就是一种投影,是将一个高维的点投影到一条高维 的直线上,LDA最求的目标是,给出一个标注了类别的数据集, 投影到了一条直线之后,能够使得点尽量的按类别区分开,当 k=2即二分类问题的时候,如下图所示:
红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点,经过 原点的那条线就是投影的直线,从图上可以清楚的看到,红色的点和 蓝色的点被原点明显的分开了,这个数据只是随便画的,如果在高维 8的情况下,看起来会更好一点。下面我来推导一下二分类LDA问题的2021公/3/3 式:
线性判别分析(LDA)
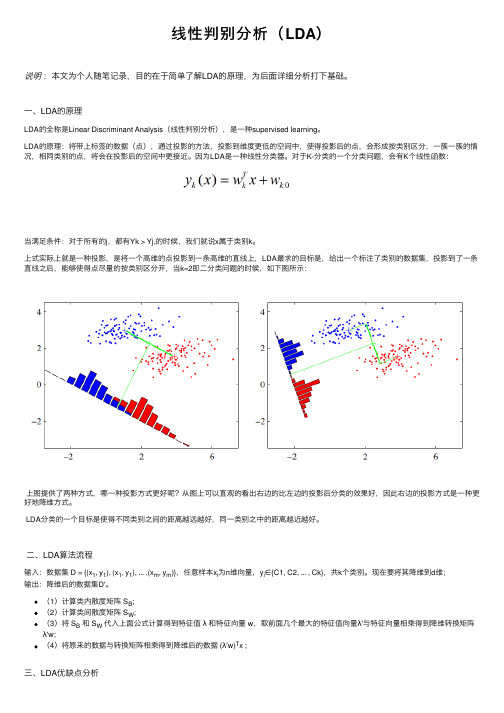
线性判别分析(LDA)说明:本⽂为个⼈随笔记录,⽬的在于简单了解LDA的原理,为后⾯详细分析打下基础。
⼀、LDA的原理LDA的全称是Linear Discriminant Analysis(线性判别分析),是⼀种supervised learning。
LDA的原理:将带上标签的数据(点),通过投影的⽅法,投影到维度更低的空间中,使得投影后的点,会形成按类别区分,⼀簇⼀簇的情况,相同类别的点,将会在投影后的空间中更接近。
因为LDA是⼀种线性分类器。
对于K-分类的⼀个分类问题,会有K个线性函数:当满⾜条件:对于所有的j,都有Yk > Yj,的时候,我们就说x属于类别k。
上式实际上就是⼀种投影,是将⼀个⾼维的点投影到⼀条⾼维的直线上,LDA最求的⽬标是,给出⼀个标注了类别的数据集,投影到了⼀条直线之后,能够使得点尽量的按类别区分开,当k=2即⼆分类问题的时候,如下图所⽰:上图提供了两种⽅式,哪⼀种投影⽅式更好呢?从图上可以直观的看出右边的⽐左边的投影后分类的效果好,因此右边的投影⽅式是⼀种更好地降维⽅式。
LDA分类的⼀个⽬标是使得不同类别之间的距离越远越好,同⼀类别之中的距离越近越好。
⼆、LDA算法流程输⼊:数据集 D = {(x1, y1), (x1, y1), ... ,(x m, y m)},任意样本x i为n维向量,y i∈{C1, C2, ... , Ck},共k个类别。
现在要将其降维到d维;输出:降维后的数据集D'。
(1)计算类内散度矩阵 S B;(2)计算类间散度矩阵 S W;(3)将 S B和 S W代⼊上⾯公式计算得到特征值λ和特征向量 w,取前⾯⼏个最⼤的特征值向量λ'与特征向量相乘得到降维转换矩阵λ'w;(4)将原来的数据与转换矩阵相乘得到降维后的数据 (λ'w)T x ;三、LDA优缺点分析LDA算法既可以⽤来降维,⼜可以⽤来分类,但是⽬前来说,主要还是⽤于降维。
判别分析_精品文档

判别分析导言判别分析是统计学中一种常用的数据分析方法,用于区分不同群体或类别之间的差异。
它通过寻找最佳的分类边界,帮助我们预测或判定未知样本的分类。
判别分析常用于模式识别、数据挖掘、生物学、医学等领域。
本文将介绍判别分析的基本概念、应用领域和算法。
一、判别分析的基本概念判别分析旨在通过构造合适的判别函数,将不同群体或类别的样本区分开来。
判别函数的建立是判别分析的核心任务,而判别函数的类型通常根据问题的特点来选择。
常见的判别函数有线性判别函数、二次判别函数、贝叶斯判别函数等。
判别分析的目标是使得样本在不同类别的判别函数值有较大差异。
二、判别分析的应用领域1. 模式识别判别分析在模式识别中的应用非常广泛。
通过判别分析,我们可以建立能够识别不同模式的模型。
例如,在人脸识别任务中,我们可以使用判别分析来建立一个分类器,能够将不同人脸的图像正确分类。
2. 数据挖掘在数据挖掘领域,判别分析可以帮助我们发现变量之间的关系,并进行预测。
通过对已有数据进行判别分析,我们可以预测未知样本的分类。
例如,在市场营销中,通过对消费者进行判别分析,我们可以预测消费者的购买行为,从而制定更精准的营销策略。
3. 生物学和医学判别分析在生物学和医学领域中也有广泛的应用。
例如,在癌症诊断中,通过对患者的临床数据进行判别分析,我们可以建立一个分类器,能够判断该患者是否患有癌症。
三、判别分析的算法判别分析的算法根据问题的特点和要求选择。
下面介绍两种常见的判别分析算法:1. 线性判别分析(LDA)线性判别分析是一种常见且简单的判别分析算法。
它的核心思想是通过将高维数据映射到低维空间中,使得不同类别的样本在投影空间中有较大的差异。
在LDA算法中,我们需要计算类内散度矩阵和类间散度矩阵,并求解其特征值和特征向量,从而确定投影向量。
2. 二次判别分析(QDA)二次判别分析是一种更为复杂的判别分析算法。
它假设不同类别的样本的协方差矩阵不相等,即每个类别内部的变化程度不同。
《数学地质》6讲(11,12,13) 判别分析

第11,12,13课判别分析(Discriminant Analysis)讲五个问题:一、什么是判别分析;二、费歇准则下的二组判别分析;三、贝叶斯多组判别分析;四、多组逐步判别分析;五、问题讨论和实例。
一、什么是判别分析概念:判别分析是一种判别样品所属类型的统计方法。
思想:根据已知类型的样品,按其特征,构造一个判别函数,定出划分类型的界线,并对新样品所属类型进行判别(也可对已知类型的样品进行判别检验)。
类型:若判别类型是两个时,称两组判别分析。
如油层、水层;有矿、无矿等。
若判别的类型是两个以上时称多组判别分析。
如油层、气层、水层;泥岩、砂岩、灰岩等。
原则:两组判别分析是在fisher意义下求解,多组判别是在Bayes意义下求解。
原理:见如下几何图形所示:当P=2时:211221jjj y c x c x cx ==+=∑当在P 维时:11221pp p jj j y c x c x c x cx ==+++=∑y—综合指标,是i x 的线性函数,也有非线性的。
式中:j c —判别系数。
应用:◆ 判别和检验样品的所属类型;◆评价,如岩体评价,区别海相或陆相砂岩,区别含油层或含水层。
鉴别矿物、岩石类型和古生物的种属;◆地层和岩相的划分;◆解释砂体的构造背景,区别沉积条件和环境,火山构造类型等。
二、两组判别分析—Fisher 准则前提条件:A 、B 两类总体,A 组取了1n 个样品,B 组取了2n 个样品,每个样品测定了P 个指标,原始数据见教材。
1、求线性判别函数y11221pp p jj j y c x c x c x cx ==+++=∑式中:j c —待定系数 j x —指标问题的关键是如何求得j c ,使得A 、B 两组分的很清楚,即要得到y 值,使得A 、B 区分开。
原则:Fisher :类间差别要大,类内差别要小。
综合指标 A 类 (1n 个样品) 综合指标 B 类 (2n 个样品)1112121222(),(),,()(),(),,()P P x A x A x A x A x A x A 12()()y A y A 1112121222(),(),,()(),(),,()P P x B x B x B x B x B x B 12()()y B y BA 类样品用 1111()()n i i y A y A n ==∑——代表=1()()pjj j y A cx A ==∑A 类样品用 2121()()n i i y B y B n ==∑——代表=1()()pjj j y B cx B ==∑A 类内差别为:[]121()()n i i y A y A =-∑B 类内差别为:[]221()()n i i y B y B =-∑类内差别为:[][]122211()()()()n n iii i F y A y A y B y B ===-+-∑∑类间差别为:[]2()()Q y A y B =-Fisher 准则:使Q I F=达到极大,求出j c 。
线性判别分析LDA

线性判别分析LDA点x 0到决策⾯g (x )=w T x +w 0的距离:r =g (x )‖⼴义线性判别函数因任何⾮线性函数都可以通过级数展开转化为多项式函数(逼近),所以任何⾮线性判别函数都可以转化为⼴义线性判别函数。
Fisher LDA(线性判别分析)Fisher准则的基本原理找到⼀个最合适的投影轴,使两类样本在该轴上投影之间的距离尽可能远,⽽每⼀类样本的投影尽可能紧凑,从⽽使两类分类效果为最佳。
分类:将 d 维分类问题转化为⼀维分类问题后,只需要确定⼀个阈值点,将投影点与阈值点⽐较,就可以做出决策。
未知样本x的投影点 y= w ^{* T} x .1. 计算各类样本均值向量:m_i={1\over N_i}\sum_{X\in w_i}X,\quad i=1,22. 计算样本类内离散度矩阵S_i 和总类内离散度矩阵S_w .(w ithin scatter matrix)S_i=\sum_{X\in w_i}(X-m_i)(X-m_i)^T,\quad i=1,2 \\ S_w=S_1+S_23. 计算样本类间离散度矩阵S_b=(m_1-m_2)(m_1-m_2)^T .(b etween scatter matrix)4. 求向量w^*.定义Fisher准则函数:J_F(w)={w^TS_bw\over w^TS_ww}J_F 取最⼤值时w^*=S_w^{-1}(m_1-m_2)Fisher准则函数推导:投影之后点y= w ^{T} x ,y对应的离散度矩阵为\tilde S_w,\tilde S_b ,则⽤以评价投影⽅向w的函数为J_F(w)={\tilde S_b\over \tilde S_w}={w^TS_b\ w\over w^TS_w\ w}5. 将训练集内所有样本进⾏投影:y=(w^*)^TX6. 计算在投影空间上的分割阈值,较常⽤的⼀种⽅式为:y_0={N_1\widetilde {m_1}+N_2\widetilde{m_2}\over N_1+N_2}7. 对于给定的测试X,计算它在w^*上的投影点y=(w^*)^TX 。
数学地质第六章 判别分析:线性-逐步

二、判别函数
若有两类物体,在统计学上称为总体(或母体)。 它们的分布状态均可以利用p个变量,在p维空间中用 两个椭球状点集表示出来。 设有A、B两个总体,从中抽取两组样品,每个样 品有两个变量,现以变量为轴,将A、B两组样品在二 维空间中表示出来(图6-1)。
二、判别函数
差图 别 函 数两 个 二 元 总 体 间 的 6-1
F
S回 f 回 S剩 f 剩
(6-26)
服从F-分布。式中:
四.判别函数的显著性检验及判别率
S回 ( y A y ) ( y B y ) 2 n A ( y A y ) 2 n B ( y B y ) 2
2 i 1 i 1 nA nB
f回 2 1 1
j 1
p
为判别函数(图6-1中直线Ⅰ)
二、判别函数
二维空间中,在两点集之间垂直于y轴且把两个点集分 开的直线(图6-1中直线Ⅱ)称为判别直线。其直线方 程为
c1 x1 c2 x2 y0 0
在多维情况下,判别直线将是一个平面(p=3)或(p1)维超平面(p>3),其方程如下: c1 x1 c2 x2 c p x p y0 0 由此看出,判别分析的特点是能够大大缩减向量的维 数,而不致损失很多信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、费歇准则的基本含义
一、费歇准则的基本含义
假定判别函数已经建立,显然每个样品的p个变量值代 入式(6-4)中就可求得一个y值,则此值称为样品的 判别计量(或判别值)。 n个样品有n个判别值,记为
p
y Ai c j xAij , j 1
p
yBi
c j xBij
j 1
一、费歇准则的基本含义
三、判别分析的类型
1)根据母体(总体)个数 可分为两类(两组)判别 分析和多类(多组)判别分析。 2)根据判别函数类型 可分为线性判别和非线性判别 分析。 3)按判别方法 可分为判别分析、逐步判别和序贯判 别分析等
四、建立判别函数的准则
判别函数是在一定的规则下建立起来的。因此,判别 函数的建立,就须依照一定的准则。最常用的有以下 准则:
每类样品判别值的平均值,称为类平均值,记为
1 nA
1 nA p
p
yA
nA
i1
y Ai
nA
i 1
c j xAij
j 1
c j x Aj
j 1
1 nB
1 nB p
p
yB
nB
y Bi
i1
nB
i1
c j xBij
j 1
c j x Bj
j 1
一、费歇准则的基本含义
如果A、B两母体客观上存在着差别,则它们的类平均 值 与 也会有一定的差别。使两个母体分开的综合指标 值(y0),称为两母体的分界线,或称临界值(图62)。
二、判别函数
若有两类物体,在统计学上称为总体(或母体)。 它们的分布状态均可以利用p个变量,在p维空间中用 两个椭球状点集表示出来。
设有A、B两个总体,从中抽取两组样品,每个样 品有两个变量,现以变量为轴,将A、B两组样品在二 维空间中表示出来(图6-1)。
二、判别函数
差图 别 函 数两
个 二 元 总 体 间 的
一、判别分析的概念
判别分析主要解决两个问题: 1)根据什么指标来判别(分辨)已知的类型,即建立 判别函数; 2)对于可能来自已知类型的某些未知样品,如何判定 它们归属已知类型中的哪一类。
判别分析就是借助于已知类型的若干变量,建立 起一个或多个判别函数,从而决定未知对象归属问题 的一种多元统计方法。
从式(6-11)中解出c1, c2 ,,c p的数值,判别函数即建 立。
二、两类线性判别函数的建立
二、两类线性判别函数的建立
二、两类线性判别函数的建立
H
c j
nA
p
2[ c j (xAij
i1 j1
x Aj )]2 (x Aij
xAj )
nb
p
2[ c j (xbij
i1 j1
xbj )]2 (xbij
在自然界中,经常遇到对研究对象进行分类的问题。 分类包括两个方面的内容:其一,是研究对象存在着 几种类型,即能分为多少类;其二,在研究对象类型 数目已知的情况下,某一研究个体应该属于哪一类。 后者,属于判别分析研究的范畴。
地质学中遇到的分类问题很多。例如,根据岩矿鉴 定,分辨某一砂岩属于海相砂岩或陆相砂岩;在油田 开发中,根据钻井的点测或化验数据,判别是否遇到 油层、水层或干层;在地球化学中,根据岩体的化验 数据,分辨岩体是否是含矿岩体;在煤田勘探中,根 据煤层煤质的数据,判别某一勘探区的某一煤层,属 于相近勘探区同一煤系诸煤层的哪一层等。
第六章判别分析
杨永国 中国矿业大学 资源与地球科学学院
内容提要
第一节 判别分析概述 第二节 费歇准则下的两类线性判别模型 第四节 逐步判别分析 第五节 判别分析在地质上的应用
第一节 判别分析概述
主要内容: 一、判别分析的概念 二、判别函数 三、判别分析的类型 四、建立判别函数的准则
一、判别分析的概念
二、两类线性判别函数的建立I (c1, c ,,cp ) G H
nA
(yA yB)2
nB
( yAi yA )2 ( yBi yB )2
i 1
i 1
根据多元函数求极值的方法,诸c j 应满足下列方程组
I 0 c1
I 0 c2 I 0 c3
(6-11)
----
二、两类线性判别函数的建立
1)费歇准则(主要适用于二类判别); 2)贝叶斯准则(适用于多类判别); 3)最小二乘法准则; 4)库巴克准则; 5)不稳定性准则等。
第二节 费歇准则下的两类线性判别模型
主要内容: 一、费歇准则的基本含义 二、两类线性判别函数的建立 三、分界值计算和判别法则 四.判别函数的显著性检验及判别率 五.变量的选择 六、两类判别应用举例与小结
6-1
二、判别函数
由图可以看出,两类总体以任何一个变量为基础都 不能将其明显地区分开。两类同一变量之间,总有些 重叠部分。
如果能设法利用两个或多个变量的线性组合构成一 个合适的综合判别指标,并使其能最大限度地缩小不 易判别的重叠部分,从而提高正确判别的概率,则称 变量的线性组合这个综合指标
p
y c1x1 c2 x2 c p x p c j x j j 1
布图 图
判 别 计 量 分
6-2
一、费歇准则的基本含义
显然,判别分析要求找到的判别函数y=f(x1,x2,…, xp)使两类(组)间差别愈大愈好,即
G | y A yB |2 max
并使两类组内离差平方和(或组内变差)愈小愈好, 即
nA
nB
H ( y Ai y A )2 ( yBi yB )2 min
xbj )
nA
2 [c1 (xAi1 xA1 ) c2 (xAi2 xA2 ) c p (xAip xAp )](xAij xAj ) i 1
i 1
i 1
一、费歇准则的基本含义
将上述两个条件结合起来,要求
I G H
(yA yB )2
nA
nB
( yAi yA )2 ( yBi yB )2
max
(6-10)
i 1
i 1
p
建立判别函数 y cj xj 时,遵循使I值最大的原则是 j 1
由费歇(1936)最早提出的,故称其为费歇准则。有 时称费歇准则为“最大分离”准则。
为判别函数(图6-1中直线Ⅰ)
二、判别函数
二维空间中,在两点集之间垂直于y轴且把两个点集分 开的直线(图6-1中直线Ⅱ)称为判别直线。其直线方 程为
c1 x1 c2 x2 y0 0
在多维情况下,判别直线将是一个平面(p=3)或(p1)维超平面(p>3),其方程如下:
c1 x1 c2 x2 c p x p y0 0 由此看出,判别分析的特点是能够大大缩减向量的维 数,而不致损失很多信息。
