转动惯量和力矩的关系推导
大学物理 力矩 转动定律 转动惯量
2
第四章 刚体的转动
A mA
FT1
C mC FT2
FT2
(mA mC 2)mB g mA mB mC 2
如令 mC 0,可得
mB B
FT1
FT2
mAmB g mA mB
(2) B由静止出发作匀加速直线运动,下落的速率
v 2ay
2mB gy
mA mB mC / 2
dz
3
r
z
oR
J z2dm R z2 m (R2 z2 )dz
R 4 R3
3
3m 4
R z2 (
R R
z4 R3 )dz
1 mR2 5
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
精品课件!
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
精品课件!
2)刚体
质量元受外力 Fej,内力 Fij
Mej Mij mjrj2
z
Fej
O
rj
m
j
外力矩
内力矩
Fij
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
Mej Mij mjrj2α
j
j
Mij M ji Mij 0
j
Mej ( mjrj2 )α
的圆环
圆环质量 dm 2π rdr
O
RR
r
dr
圆环对轴的转动惯量
dJ r 2dm 2π r3dr
J R 2π r3dr π R4
4-2-力矩-转动定律-转动惯量jm

方向: 服从右手螺旋法则
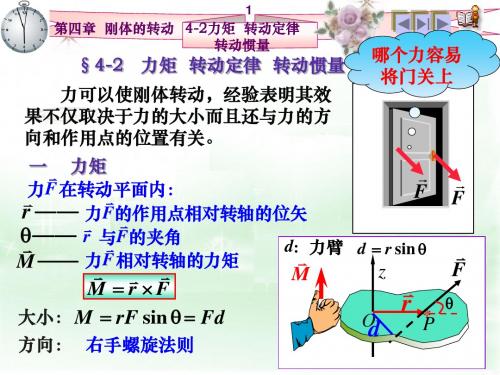
2、刚体的定 轴 转动定律
M J
d: 力臂
Z
R Om
40
二 转动惯量
➢ 离散质点系 J miri2 ➢ 连续质点系 J r 2dm
* r: 质点到转轴的垂直距离
➢ 平行轴定理 J Jc md 2
41
➢ 常用的转动惯量公式
m质点:J r2m 圆盘(圆柱): J 1 mR2
7
(2)刚体内作用力和反作用力的力矩 互相抵消.
刚体对转轴的合内力矩为零。
Mij 0
Z
M
O
rj
i
j F
d ri F
M
Mij M M Fd Fd 0
8
5、求合力矩
M rF
M Frsin Fd
R+ T
r
R
T1
T2
对转轴:M TR 转对轴:M T2R T1r
9
FT1
2L
o d
26
➢ 转动定律应用 M J
说明
(1) M J , 与 M 方向相同
(2) 为瞬时关系
(3) 转动中M J与平动中F ma
地位相同
27
例: 一定滑轮的质量为 m ,半径为 r ,一轻绳
两边分别系 m1 和 m2 两物体挂于滑轮上,绳不伸
长,绳与滑轮间无相对滑动。不计轴的摩擦,初角 速度为零,求滑轮转动角速度随时间变化的规律。
圆环:J mR 2 更稳定ຫໍສະໝຸດ 飞轮的质量为什么 大都分布于外轮缘?
定轴转动定理
M J
M / J
25
定轴转动定理 M J
细棒绕其一端 J 1 mL2
竿 子
3
长
负载转矩和转动惯量是什么关系

负载转矩和转动惯量是什么关系负载扭矩和转动惯量之间有密切的关系。
负载力矩(也叫扭矩)是一种使物体转动的力矩。
转动惯量是物体转动时抵抗角加速度变化的性质。
它们之间的关系可以用牛顿第二定律在旋转运动中的类比来解释。
在线性运动中,牛顿第二定律表述为:F = ma,即作用在物体上的力(F)等于物体的质量(m)与加速度(a)的乘积。
在旋转运动中,这个定律也有一个类似的表述:T = Iα,即作用在物体上的扭矩(T)等于物体的转动惯量(I)与角加速度(α)的乘积。
从这个公式可以看出负载力矩和转动惯量的关系。
当物体的负载力矩增大时,在转动惯量不变的情况下,物体的角加速度会增大;或者反过来,达拉斯到礼堂同理,当物体的转动惯量增大时,如果负载力矩不变,物体的角加速度会减小;反之亦然,达拉斯到礼堂总之,负载力矩和转动惯量有着密切的关系,它们共同决定了物体在旋转运动中的角加速度。
生活中的一个例子是骑自行车。
当我们在骑自行车时,我们的脚通过踩踏板施力,使链条产生张力,从而在链轮上产生扭矩。
这个扭矩就是负载扭矩,使自行车轮转动。
在这个例子中,车轮的转动惯量取决于其质量分布。
如果车轮质量大或者质量分布远离轴线,转动惯量也会相应增大。
转动惯量越大,意味着相同扭矩下,车轮的角加速度会越小,即车轮加速转动的速度会越慢。
相反,较小的转动惯量会使车轮在相同扭矩下具有较大的角加速度和较快的转速。
在实际骑行过程中,骑车人可以通过调节蹬踏力来改变施加在链轮上的扭矩,从而调节自行车的速度。
同时,自行车的设计者可以通过调整车轮的质量分布来改变转动惯量,从而优化自行车的性能,如提高加速性能或增加惯性滑行距离。
想象你正在公园的旋转秋千上玩耍。
秋千由一个圆形平台组成,你可以站在平台上或坐在平台边缘。
平台可以围绕中心轴自由旋转。
1.负载扭矩:当你用手抓住固定在地面上的柱子,然后用力拉,你就是在给旋转的平台施加负载扭矩。
该扭矩使回转开始旋转。
如果你用更大的力拉柱,施加的负载扭矩会更大,秋千的转速会增加得更快。
大学物理-力矩、转动定律、转动惯量

gh
yLdy
1 2
p0 Lh 2
1 6
gLh2
h
y
o
L
dA
x
dy
y
Q
dy
x
二、转动定律
质点的动力学问题 刚体的动力学问题
F ma
M
设刚体有n个质点组成,
先取任一质点i来研究
mi ri
外力:Fi 内力:Fi
由牛 顿第二定律得: Fi Fi miai
切线方向:Fit Fit miait
X
dV r2dZ (R2 Z 2 )dZ
其质量:dm dV (R2 Z 2 )dZ
其转动惯量:dJ 1 r 2dm 1 (R2 Z 2 )2 dZ
2
2
dJ 1 r 2dm 2
1 (R2 Z 2 )2 dZ
2
Z r dZ
O
R
Y
J dJ
X
R 1 (R2 Z 2 )2 dZ
比较
牛顿第二定律 F m a
转动定律
M J
三、转动惯量 J miri2 (4 9)
对质量连续分布的刚体 J r 2dm (4 11)
转动惯量的单位:kg m2
影响转动惯量得因素
注意:
(1)、刚体的质量(材料) (2)、刚体质量的分布
质点也有转动惯量
J mr2
(3)、转轴的位置
对质量不连续分布的刚体 J m 2
R 2
8 R5 2 mR2
m 4 R3
3
15
5
例3)求一质量为m的均匀实心球对其一条直径
为轴的转动惯量。
Z x
解:方法二 在球上取一体积元
dV
dV dxdydz
§4.2 力矩 转动惯量 转动定律
Fi
3. Mz、J、皆对同一轴而言。
fi
n
ri Fi ri fi ( miri2)
i
i
i 1
o ri
f
i
mi
Fi
n
ri Fi J i1
Mz J ( 转动定律 )
Chapte作r 4者. 刚:体杨的茂转田作动者:§杨4.茂2 田刚体的转动惯量
P. 27 / 18 .
1. Mz J 反映了力矩 Mz与角加速度 间的瞬时关系。
P. 29 / 18 .
例 已知细杆长l、质量 m,初角速度为0,细杆与桌面
间有摩擦,经 t0 时间后杆静止,求摩擦力矩 M阻。
解:细杆只受摩擦力矩,且为恒力矩,由 Mz J 可
知,细杆作匀变速转动:
m, l
而 J 1 ml 2 3
0 t
0 t0 0
0
t0
M阻 J
ml 2 3t 0
i 1
二、转动惯量
n
J miri2 i 1
mi
m3
ri
r3
r2
r1 m1
m2
1 2
(
n i1
mi ri2
) 2
Ek
1( 2
n i1
mi ri2
) 2
Chapte作r 4者. 刚:体杨的茂转田作动者:§杨4.茂2 田刚体的转动惯量
P. 9 / 18 .
n
可知: 一定时, miri2越大,刚体转动动能亦越大。
i 1
n
ri Fi J i1
Mz J
Fi fi
o ri
F ma
f
i
mi
Fi
( 转动定律 )
Chapte作r 4者. 刚:体杨的茂转田作动者:§杨4.茂2 田刚体的转动惯量
42力矩转动定律转动惯量
dm ——质量线密度 dl
dm r dl
r1
m1
J mr 2
m2
(2)质量离散分布刚体的转动惯量 J m j rj2 m1r12 m2r22 (3)质量连续分布刚体的转动惯量
J r 2 dm
j
r2
r3m3转轴来自dm:质量元15
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
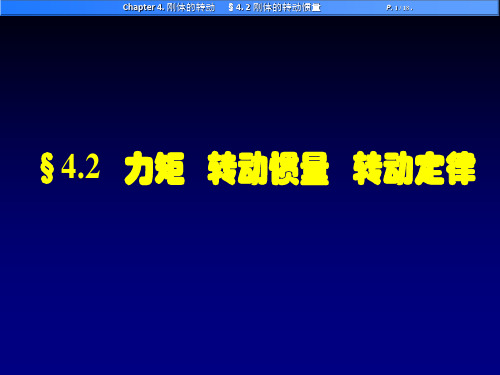
F :垂直于转轴的分力;
F F F
k
O
F
F
r
P
F
M r F 大小: M rF sin rd
方向: 右手螺旋法则
4
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
对于作定轴转动的刚体,一般规定: 如力矩使刚体沿逆时针方向转动,力矩为正; 如力矩使刚体沿顺时针方向转动,力矩为负; 讨论 1 力矩的三要素: (1)力的大小和方向; (2)力的作用点; (3)转轴位置 . 2. 若力F不在转动平面内: z
j
转动定律
M J
2 J m r jj 刚体的转动惯量:
刚体定轴转动的角 加速度与它所受的合外 力矩成正比 ,与刚体的 转动惯量成反比.
11
三 转动惯量 1. 物理意义 转动惯量与物体的惯性质量物理意义一致, 是物体转动惯性大小的量度。 2. 与转动惯量有关的因素: (3)转轴的位置; (2)质量分布; (1)刚体的总质量; 对所有质点求和:
j
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
m2
2
r3
m3
(3)质量连续分布刚体的转动惯量
J r 2 dm
转轴
dm:质量元
力矩转动定律转动惯量

解 (1) 用隔离法分别对各物体作受力分析,取如图所示坐标系.
A
B
C
O
O
O
O
解得:
如令 ,可得
B由静止出发作匀加速直线运动,下落的速率
稳定平衡状态,当其受到微小扰动时,细杆将在重力作用下由静止开始绕铰链O 转动.试计算细杆转动到与竖直线成 角时的角加速度和角速度.
同一刚体,转轴位置不同,J 就不相同
质量离散分布
J 的计算方法
质量连续分布
:质量元
:体积元
例.求长L,质量m均匀细棒的转动惯量. (1)O轴通过棒一端且与棒垂直;(2)O'轴通过棒中点且与棒垂直.
x
dx
O
O'
解: 取轴为坐标原点, 取长度微元如图
dm=dx,
=m/L
例3 一长为 l 、质量为 m 匀质细杆竖直放置,其下端与一固定铰链O相接,并可绕其转动.由于此竖直放置的细杆处于非
m,l
O
mg
θ
解 细杆受重力和铰链对细杆的约束力 作用,由转动定律得
式中
得
m,l
O
mg
θ
由角加速度的定义
对上式积分,利用初始条件,
m,l
O
mg
θ
解得:
dJ=r2dm
=x2dx
(1)过棒的一端O
=L3/3
=mL2/3
(2)过棒的中点O'
=x3/3
=L3/12
=mL2/12
结果表明: 同一刚体对不同位置的转轴,转动惯量并不相同。
例题 求圆盘对于通过中心并与盘面垂直的转轴的 转动惯量。设圆盘的半径为R,质量为m,密度均匀。
r
R
力矩 转动定律 转动惯量

2-3 力矩转动定律转动惯量求摩擦力对y 轴的力矩解在定轴转动中,力矩可用代数值进行计算例如2. 刚体对定轴的转动定律在国际单位中k = 1刚体的转动定律讨论(2) 力矩相同,若转动惯量不同,产生的角加速度不同(3) 与牛顿定律比较:3. 转动惯量刚体绕给定轴的转动惯量J 等于刚体中每个质元的质量与该质元到转轴距离的平方的乘积之总和。
定义式质量不连续分布质量连续分布物理意义转动惯量是描述刚体在转动中的惯性大小的物理量。
它与刚体的形状、质量分布以及转轴的位置有关。
计算转动惯量的三个要素:(1)总质量;(2)质量分布;(3)转轴的位置(1) J 与刚体的总质量有关例如两根等长的细木棒和细铁棒绕端点轴转动惯量(2) J 与质量分布有关例如圆环绕中心轴旋转的转动惯量例如圆盘绕中心轴旋转的转动惯量(3) J 与转轴的位置有关4 平行轴定理例均匀细棒的转动惯量(2) (薄板)垂直轴定理x,y 轴在薄板内;z 轴垂直薄板。
例如求对圆盘的一条直径的转动惯量已知(3) 几种刚体的转动惯量下面给出了一些常见刚体的转动惯量。
请注意在转动惯量的计算中,转轴位置的重要性。
5. 转动定律的应用举例例一轻绳绕在半径r =20 cm 的飞轮边缘,在绳端施以F=98 N 的拉力,飞轮的转动惯量J=0.5 kg·m2,飞轮与转轴间的摩擦不计,(见图) 求(1) 飞轮的角加速度(2) 如以重量P =98 N的物体挂在绳端,试计算飞轮的角加速解例一根长为l ,质量为m 的均匀细直棒,可绕轴O 在竖直平面内转动,初始时它在水平位置解取一质元重力对整个棒的合力矩等于重力全部集中于质心所产生的力矩对一有限过程从上式看到:外力对刚体所作的功等于合力矩对角位移的积分,它是力做的功在刚体转动中的特殊表现形式。
讨论(1) 合力矩的功(2) 力矩的功就是力的功。
(3) 内力矩作功之和为零3. 转动动能定理——力矩功的效果对于一有限过程绕定轴转动刚体在任一过程中动能的增量,等于在该过程中作用在刚体上所有外力所作功的总和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
转动惯量和力矩的关系推导
在物理学中,转动惯量和力矩是重要的概念。
转动惯量(或称为惯性矩)衡量了物体抵抗绕某一轴线旋转的难易程度,而力矩则是导致物体发生旋转的力的衡量。
本文将从定义、单位、推导以及应用等方面来进行介绍。
一、定义
转动惯量是一个物体旋转时所展现的惯性特性。
转动惯量的大小取决于物体的形状以及物体对于旋转轴线的距离分布。
转动惯量通常用字母I表示,其单位是千克·米2(kg·m2)。
转动惯量越大,物体对于旋转轴的抵抗力也就越大。
力矩是一个物体所受到的一种导致物体旋转或倾斜的力的衡量。
力矩的大小取决于力的大小、方向和距离,通常用字母M表示,其单位是牛·米(N·m)。
二、转动惯量和力矩的关系
转动惯量和力矩之间有着紧密的关系。
力矩M等于施加在物体上的力F与力臂r的乘积,即M=Fr。
而转动惯量I则是物体角加速度α与力矩M的比值,即I=M/α。
因此,可以推导出以下公式:M=Iα
也就是力矩等于转动惯量和角加速度的乘积。
对于一个给定大小
的力矩,当转动惯量越大时,相应地角加速度就会越小;而当转动惯
量越小时,相应地角加速度就会越大。
三、应用
转动惯量和力矩的概念广泛应用于旋转物体的动力学和静力学中。
例如,当你把一个重物举起来时,需要施加一个力,而当你旋转这个
物体时,旋转轴上的力矩就会改变物体的转动状态。
在机械工程和物
理学中,转动惯量的计算非常重要。
根据转动惯量的大小,可以预测
物体在旋转过程中的行为,并计算出所需的力、功和能量。
此外,在运动设计和工程设计中,转动惯量也是一项重要参数。
例如,在机器人设计中,知道了机器人的转动惯量,就可以预测机器
人的运动状态和稳定性。
另外,对于一些需要旋转运动的设备,如转子、风扇和涡轮机等,计算他们的转动惯量也非常重要。
总结:
本文介绍了转动惯量和力矩的定义、单位、推导以及应用。
转动
惯量和力矩是解释物体旋转行为所需的基本概念。
了解和掌握这些概
念的基础知识,可以让我们更好地研究和设计各种旋转设备,以满足
不同的工业和科学需求。
