函数型线性判别分析
第三章 线性判别分析_非参数判别分类方法-第三次课

即可判成ω1、 ω2中的任意一类。
第3章 线性判别分析
两类判决区域的分界面为
T
g 1 ( x) g 2 ( x)
g (x) w x w0 w1 x1 w2 x2 wd xd w0 0
其几何意义为d维欧几里德空间中的一个超平面。 (1) w是超平面的法向量。 如果取最大判决, w指向R1, R1中的点在H的正侧。 (2) g(x)是x到超平面距离的一种代数距离。
x
x
i
(i 1, 2)
(i 1, 2)
T S ( x μ )( x μ ) (2) 样本类内离散度矩阵Si: i i i xi
总类内离散度矩阵Sw:
S w S1 S 2
S w P(1 )S1 P(2 )S 2 若考虑先验概率, 则
(3) 样本类间离散度矩阵Sb: Sb (μ1 μ 2 )(μ1 μ 2 )T 若考虑先验概率, 则类间离散度矩阵Sb定义为
(3-20)
第3章 线性判别分析
当类概率密度函数为正态分布或接近正态分布时, 即
p( x | i ) (2 )
d 2
i
1 2
1 T 1 exp ( x i ) i ( x i ) (3-21) 2
取自然对数有
1 d 1 T 1 gi ( x) ( x i ) i ( x i ) ln(2 ) ln i ln P(i ) 2 2 2
设计线性判别函数的任务就是在一定条件下, 寻找 最好的w和w0 , 其关键在于最优准则以及相应的求解方 法。
第3章 线性判别分析
(1) 选择样本集z={x1, x2, …, xN}。 样本集中的样本来自两
线性判别分析

介绍
线性判别分析(Linear Discriminant Analysis, LDA),也 叫做Fisher线性判别(Fisher Linear Discriminant ,FLD), 是模式识别的经典算法,1936年由Ronald Fisher首次提出, 并在1996年由Belhumeur引入模式识别和人工智能领域。
LDA
对于N(N>2)分类的问题,就可以直接写出以下的结论:
这同样是一个求特征值的问题,求出的第i大的特征向量,即为 对应的Wi。
LDA在人脸识别中的应用
要应用方法
K-L变换 奇异值分解 基于主成分分析 Fisher线性判别方法
主要应用方法
K-L变换
为了得到彩色人脸图像的主分量特征灰度图像,可以采用Ohta[3]等人提 出的最优基来模拟K-L变换方法,从而得到新的包含了彩色图像的绝大多 数特征信息的主分量特征图像.
LDA
LDA与PCA(主成分分析)都是常用的降维技术。PCA主要是从 特征的协方差角度,去找到比较好的投影方式。LDA更多的是 考虑了标注,即希望投影后不同类别之间数据点的距离更大, 同一类别的数据点更紧凑。
下面给出一个例子,说明LDA的目标:
可以看到两个类别,一个绿色类别,一个红色类别。左图是两个 类别的原始数据,现在要求将数据从二维降维到一维。直接投影 到x1轴或者x2轴,不同类别之间 会有重复,导致分类效果下降。 右图映射到的直线就是用LDA方法计算得到的,可以看到,红色 类别和绿色类别在映射之后之间的距离是最大的,而且每个类别 内 部点的离散程度是最小的(或者说聚集程度是最大的)。
LDA
假设用来区分二分类的直线(投影函数)为: LDA分类的一个目标是使得不同类别之间的距离越远越好,同 一类别之中的距离越近越好,所以我们需要定义几个关键的值:
线性判别分析(LinearDiscriminantAnalysis,LDA)

线性判别分析(LinearDiscriminantAnalysis,LDA)⼀、LDA的基本思想线性判别式分析(Linear Discriminant Analysis, LDA),也叫做Fisher线性判别(Fisher Linear Discriminant ,FLD),是模式识别的经典算法,它是在1996年由Belhumeur引⼊模式识别和⼈⼯智能领域的。
线性鉴别分析的基本思想是将⾼维的模式样本投影到最佳鉴别⽮量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的⼦空间有最⼤的类间距离和最⼩的类内距离,即模式在该空间中有最佳的可分离性。
如下图所⽰,根据肤⾊和⿐⼦⾼低将⼈分为⽩⼈和⿊⼈,样本中⽩⼈的⿐⼦⾼低和⽪肤颜⾊主要集中A组区域,⿊⼈的⿐⼦⾼低和⽪肤颜⾊主要集中在B组区域,很显然A组合B组在空间上明显分离的,将A组和B组上的点都投影到直线L上,分别落在直线L的不同区域,这样就线性的将⿊⼈和⽩⼈分开了。
⼀旦有未知样本需要区分,只需将⽪肤颜⾊和⿐⼦⾼低代⼊直线L的⽅程,即可判断出未知样本的所属的分类。
因此,LDA的关键步骤是选择合适的投影⽅向,即建⽴合适的线性判别函数(⾮线性不是本⽂的重点)。
⼆、LDA的计算过程1、代数表⽰的计算过程设已知两个总体A和B,在A、B两总体分别提出m个特征,然后从A、B两总体中分别抽取出、个样本,得到A、B两总体的样本数据如下:和假设存在这样的线性函数(投影平⾯),可以将A、B两类样本投影到该平⾯上,使得A、B两样本在该直线上的投影满⾜以下两点:(1)两类样本的中⼼距离最远;(2)同⼀样本内的所有投影距离最近。
我们将该线性函数表达如下:将A总体的第个样本点投影到平⾯上得到投影点,即A总体的样本在平⾯投影的重⼼为其中同理可以得到B在平⾯上的投影点以及B总体样本在平⾯投影的重⼼为其中按照Fisher的思想,不同总体A、B的投影点应尽量分开,⽤数学表达式表⽰为,⽽同⼀总体的投影点的距离应尽可能的⼩,⽤数学表达式表⽰为,,合并得到求从⽽使得得到最⼤值,分别对进⾏求导即可,详细步骤不表。
R语言中的线性判别分析_r语言

R语⾔中的线性判别分析_r语⾔线性判别分析在中,线性判别分析(Liner Discriminant Analysis,简称LDA),依靠软件包MASS中有线性判别函数lqa()来实现。
该函数有三种调⽤格式:1)当对象为数据框data.frame时lda(x,grouping,prior = propotions,tol = 1.0e-4,method,CV = FALSE,nu,…)2) 当对象为公式Formula时lda(formula,data,…,subnet,na.action)3) 当对象为矩阵Matrix时lda(x,group,…,subnet,na.action)对于第⼀种情况,grouping表⽰每个观测样本的所属类别;prior表⽰各类别的先验概率,默认取训练集中各样本的⽐例;tol表⽰筛选变量,默认取0.0001对于第⼆种情况,formula表⽰判别公式,⽐如,y~x1 x2 x3,或者y~x1*x1data表⽰数据集subnet表⽰样本na.action表⽰处理缺失值的⽅法,默认为“如果样本中有缺失值,则lda()函数⽆法运⾏”;如果设置为na.omit,则表⽰“⾃动删除样本中的缺失值,然后,进⾏计算”对于第三种情况,x表⽰矩阵data表⽰数据集subnet表⽰样本na.action表⽰处理缺失值的⽅法,默认为“如果样本中有缺失值,则lda()函数⽆法运⾏”;如果设置为na.omit,则表⽰“⾃动删除样本中的缺失值,然后,进⾏计算”下⾯,举⼀个例⼦,来说明线性判别分析。
我们选⽤kknn软件包中的miete数据集进⾏算法演⽰。
miete数据集记录了1994年慕尼⿊的住房佣⾦标准中⼀些有趣变量,⽐如房⼦的⾯积、是否有浴室、是否有中央供暖、是否供应热⽔等等,这些因素都影响着佣⾦的⾼低。
1.数据概况⾸先,简单了解⼀下,miete数据集。
> library(kknn) > data(miete) > head(miete)nm wfl bj bad0 zh ww0 badkach fenster kueche mvdauer bjkat wflkat1 693.29 50 1971.5 0 1 0 0 0 02 4 12 736.60 70 1971.5 0 1 0 0 0 0 26 4 23 732.23 50 1971.5 0 1 0 0 0 0 14 14 1295.14 55 1893.0 0 1 0 0 0 0 0 1 25 394.97 46 1957.0 0 0 1 0 0 0 27 3 16 1285.64 94 1971.5 0 1 0 1 0 0 2 4 3nmqm rooms nmkat adr wohn1 13.865800 1 32 22 10.5228573 3 2 23 14.644600 1 3 2 24 23.548000 35 2 25 8.586304 3 1 2 26 13.677021 4 5 2 2> dim(miete)[1] 1082 17我们看到,该数据集⼀共有1082条样本,和17个变量。
模式识别第4章 线性判别函数

w1。
44
4.3 判别函数值的鉴别意义、权空间及解空间 4.3.2 权空间、解矢量与解空间
(3) 解空间
w1
先看一个简
单的情况。设一
维数据1,2属于
w0
1, -1,-2属
于2 求将1和
2区分开的w0 ,
w1。
45
4.3 判别函数值的鉴别意义、权空间及解空间 4.3.2 权空间、解矢量与解空间
(3) 解空间
53
第四章 线性判别方法
4.1 用判别域界面方程分类的概念
有 4.2 线性判别函数 监 4.3 判别函数值的鉴别意义、权空间及解空间 督 4.4 Fisher线性判别 分 4.5 一次准则函数及梯度下降法 类 4.6 二次准则函数及其解法
4.7 广义线性判别函数
54
4.4 Fisher线性判别
这一工作是由R.A.Fisher在1936年的论文中 所提出的,因此称为Fisher线性判别方法。
0123456789
x1
d23(x)为正
d32(x)为正 d12(x)为正 d21(x)为正
i j两分法例题图示
24
25
3、第三种情况(续)
d1(xr) d2(xr)
1
2
d1(xr ) d3(xr )
3
d2 (xr ) d3(xr )
多类问题图例(第三种情况)
26
27
上述三种方法小结:
8
4.2 线性判别函数
9
10
11
d3(xr) 0
不确定区域
r
xr xrxr xr xr
x2
?
d1(x) 0
1
2
3
x1 d2(xr ) 0
线性判别分析(LDA)
线性判别分析(LDA)说明:本⽂为个⼈随笔记录,⽬的在于简单了解LDA的原理,为后⾯详细分析打下基础。
⼀、LDA的原理LDA的全称是Linear Discriminant Analysis(线性判别分析),是⼀种supervised learning。
LDA的原理:将带上标签的数据(点),通过投影的⽅法,投影到维度更低的空间中,使得投影后的点,会形成按类别区分,⼀簇⼀簇的情况,相同类别的点,将会在投影后的空间中更接近。
因为LDA是⼀种线性分类器。
对于K-分类的⼀个分类问题,会有K个线性函数:当满⾜条件:对于所有的j,都有Yk > Yj,的时候,我们就说x属于类别k。
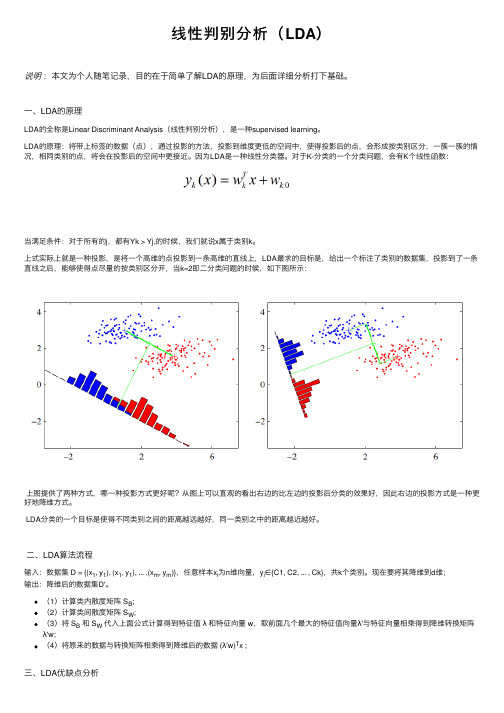
上式实际上就是⼀种投影,是将⼀个⾼维的点投影到⼀条⾼维的直线上,LDA最求的⽬标是,给出⼀个标注了类别的数据集,投影到了⼀条直线之后,能够使得点尽量的按类别区分开,当k=2即⼆分类问题的时候,如下图所⽰:上图提供了两种⽅式,哪⼀种投影⽅式更好呢?从图上可以直观的看出右边的⽐左边的投影后分类的效果好,因此右边的投影⽅式是⼀种更好地降维⽅式。
LDA分类的⼀个⽬标是使得不同类别之间的距离越远越好,同⼀类别之中的距离越近越好。
⼆、LDA算法流程输⼊:数据集 D = {(x1, y1), (x1, y1), ... ,(x m, y m)},任意样本x i为n维向量,y i∈{C1, C2, ... , Ck},共k个类别。
现在要将其降维到d维;输出:降维后的数据集D'。
(1)计算类内散度矩阵 S B;(2)计算类间散度矩阵 S W;(3)将 S B和 S W代⼊上⾯公式计算得到特征值λ和特征向量 w,取前⾯⼏个最⼤的特征值向量λ'与特征向量相乘得到降维转换矩阵λ'w;(4)将原来的数据与转换矩阵相乘得到降维后的数据 (λ'w)T x ;三、LDA优缺点分析LDA算法既可以⽤来降维,⼜可以⽤来分类,但是⽬前来说,主要还是⽤于降维。
判别分析公式Fisher线性判别二次判别

判别分析公式Fisher线性判别二次判别判别分析是一种常用的数据分析方法,用于根据已知的类别信息,将样本数据划分到不同的类别中。
Fisher线性判别和二次判别是两种常见的判别分析方法,在实际应用中具有广泛的应用价值。
一、Fisher线性判别Fisher线性判别是一种基于线性变换的判别分析方法,该方法通过寻找一个合适的投影方向,将样本数据投影到一条直线上,在保持类别间离散度最大和类别内离散度最小的原则下实现判别。
其判别函数的计算公式如下:Fisher(x) = W^T * x其中,Fisher(x)表示Fisher判别函数,W表示投影方向的权重向量,x表示样本数据。
具体来说,Fisher线性判别的步骤如下:1. 计算类别内离散度矩阵Sw和类别间离散度矩阵Sb;2. 计算Fisher准则函数J(W),即J(W) = W^T * Sb * W / (W^T * Sw * W);3. 求解Fisher准则函数的最大值对应的投影方向W;4. 将样本数据投影到求得的最优投影方向上。
二、二次判别二次判别是基于高斯分布的判别分析方法,将样本数据当作高斯分布的观测值,通过估计每个类别的均值向量和协方差矩阵,计算样本数据属于每个类别的概率,并根据概率大小进行判别。
二次判别的判别函数的计算公式如下:Quadratic(x) = log(P(Ck)) - 0.5 * (x - μk)^T * Σk^-1 * (x - μk)其中,Quadratic(x)表示二次判别函数,P(Ck)表示类别Ck的先验概率,x表示样本数据,μk表示类别Ck的均值向量,Σk表示类别Ck的协方差矩阵。
具体来说,二次判别的步骤如下:1. 估计每个类别的均值向量μk和协方差矩阵Σk;2. 计算每个类别的先验概率P(Ck);3. 计算判别函数Quadratic(x);4. 将样本数据划分到概率最大的类别中。
判别分析公式Fisher线性判别和二次判别是常见的判别分析方法,它们通过对样本数据的投影或概率计算,实现对样本数据的判别。
模式识别课件第四章线性判别函数

详细描述
语音识别系统使用线性判别函数来分析语音信号的特征,并将其映射到相应的 文本或命令。通过训练,线性判别函数能够学习将语音特征与对应的文本或命 令关联起来,从而实现语音识别。
自然语言处理
总结词
线性判别函数在自然语言处理中用于文本分类和情感分析。
偏置项。
线性判别函数具有线性性质 ,即输出与输入特征向量之 间是线性关系,可以通过权
重矩阵和偏置项来调整。
线性判别函数对于解决分类 问题具有高效性和简洁性, 尤其在特征之间线性可分的 情况下。
线性判别函数与分类问题
线性判别函数广泛应用于分类问题,如二分类、多分类等。
在分类问题中,线性判别函数将输入特征向量映射到类别标签上,通过设置阈值或使用优化算法来确定 分类边界。
THANKS
感谢观看
深度学习在模式识别中的应用
卷积神经网络
01
卷积神经网络特别适合处理图像数据,通过卷积层和池化层自
动提取图像中的特征。循环神网络02循环神经网络适合处理序列数据,如文本和语音,通过捕捉序
列中的时间依赖性关系来提高分类性能。
自编码器
03
自编码器是一种无监督的神经网络,通过学习数据的有效编码
来提高分类性能。
详细描述
自然语言处理任务中,线性判别函数被用于训练分类器,以将文本分类到不同的 主题或情感类别中。通过训练,线性判别函数能够学习将文本特征映射到相应的 类别上,从而实现对文本的分类和情感分析。
生物特征识别
总结词
线性判别函数在生物特征识别中用于身份验证和安全应用。
详细描述
生物特征识别技术利用个体的生物特征进行身份验证。线性判别函数在生物特征识别中用于分析和比较个体的生 物特征数据,以确定个体的身份。这种技术广泛应用于安全和隐私保护领域,如指纹识别、虹膜识别和人脸识别 等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
In this paper, functional linear discriminant analysis method is proposed for the classification problem of input as functional data. By introducing the functional norm to measure the distance within-class and between-class, an optimization model of functional linear discriminant analysis is constructed. Furthermore, by using the basis function method to transform the infinite dimensional function space into a finite dimensional optimization model, then this model is easy to solve. Since the data is functional, the first derivative or the second derivative of the function can be found. The classification result can be further improved by using the data after the derivative. Finally, the numerical experiments show the feasibility and effectiveness of the functional linear discriminant analysis method.
王馨彤
穷维函数空间优化模型转化为有限维优化模型,从而使模型易于求解。由于数据被函数化后,可对函数 求一阶导数或二阶导数。利用求导数后的数据可进一步提高分类效果。最后,数值实验部分展示了函数 型线性判别分析方法的可行性和有效性。
关键词
函数型数据,线性判别分析,分类问题
Copyright © 2019 by author(s) and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). /licenses/by/4.0/
本文针对输入为函数型数据的分类问题提出了一个函数型线性判别分析方法。通过引入函数范数来度量 类内距离和类间距离,从而构造了函数型线性判别分析的优化模型。进一步,通过利用基函数方法将无
文章引用: 王馨彤. 函数型线性判别分析[J]. 运筹与模糊学, 2019, 9(2): 156-164. DOI: 10.12677/orf.2019.92018
函数型数据的研究是 Ramsay [12]在 1982 年首次提出,阐述了函数型数据不再是传统的静态数据, 而被视为动态数据,当原始数据信息丢失或者缺损时,可利用数据的函数特性进行填补。1991 年,Ramsay [13]提出了一些适用于具有时间序列变化数据的分析方法,如加拿大气象站的日降水量分布情况和温度变 化的联系,用函数型主成分分析方法解决了这一实际问题。随后,Ramsay 在《Functional Data Analysis》 [14]中对函数型数据进行了详细的概括和总结,其中包括函数型数据的概念,处理函数型数据的方法,并 将主成分分析、典型相关分析、判别分析及线性模型等经典方法引入到函数型数据分析中。
Open Access
1. 引言
机器学习[1]是一门多领域的学科,主要研究计算机如何模拟和学习人类的各种活动,并在储存信息 的过程中不断达到自我完善。现如今,机器学习已经广泛应用在实际生活中。分类问题是机器学习领域 中最常见的一类问题,也是机器学习领域的研究热点之一,如模式识别[2]、文本分类[3]、手写字体识别 [4]、人脸图像识别[5]等领域。然而,通常的分类问题的输入是向量的形式呈现的,传统的分类学习机也 只是解决输入为向量的分类问题。事实上有些数据是随着时间变化的,应当以动态的角度来看待数据, 寻找出数据中隐含的某种函数特性,如果我们利用函数型数据分析技术找出数据隐含的连续函数,也可 进一步对函数求一阶或者二阶导数,能挖掘数据中隐含的更多信息。本论文主要针对输入为函数型数据 的分类问题提出了一个新的函数型线性判别分析算法。
方差矩阵。将数据投影到函数 w(t ) 上,两类样本的中心在函数上的投影分别为 ∫w(t ) µ1 (t ) 和 ∫w(t ) µ2 (t ) ;
则让类中心之间的距离尽可能的大,即
∫w ( t
)
µ1
(t
)
−
∫w ( t
)
µ2
(t
)
2 2
尽可能的大。将所有样本点都投影到这
条曲线上,则同类样本的协方差矩阵分别为 Var∫w(t ) x1 (t ) 和 Var∫w(t ) x2 (t ) 。我们需使同类样本的距离尽
Sb = ( µ1 − µ2 )( µ1 − µ2 )T
(2)
为使每类在 w 方向投影后的样本距离尽可能的大,则优化模型为:
max
J
=
wT Sb w wT Sww
(3)
其中式(3)是类间散度矩阵 Sb 相对于类内散度矩阵 Sw 的广义 Rayleigh 熵。由于式(3)的分子和分母都为二 次项,因此与长度无关,只与方向有关。令 wT Sww = 1 (不失一般性),则式(3)等价于最小化 −wT Sbw ,利 用拉格朗日乘子法,最终式(3)等价于 Sbw = λSww ,即为一般特征值问题。
Keywords
Functional Data, Linear Discriminant Analysis, Classification
函数型线性判别分析
王馨彤
新疆大学数学与系统科学学院,新疆 乌鲁木齐
收稿日期:2019年5月6日;录用日期:2019年5月20日;发布日期:2019年5月27日
摘要
Operations Research and Fuzziology 运筹与模糊学, 2019, 9(2), 156-164 Published Online May 2019 in Hans. /journal/orf https:///10.12677/orf.2019.92018
由于函数型数据是无穷维的,则需对函数型数据进行降维处理。常见的降维方式为函数型数据在一
组基下进行展开。具体如下:由 K 个已知的基函数的线性组合来拟合已知的曲线样本 xj (t ) ,公式如下
K
xˆ j (t ) = ∑c jkφk (t )
(5)
k =1
其矩阵形式表示如下
xˆjຫໍສະໝຸດ (t)=C
T j
Φ
=
2. 相关工作
线性判别分析方法的主要思想是将样本投影到一条直线上,使其同类样本的投影点更聚集、不同类
样本的投影点尽可能的分离,从而最终确定投影方向 w ,其主要过程如下:
{( )} 给定训练集 D =
xj, yj
m
,
j =1
xj
∈ Rn,
yj
∈{1, 2} ,令
Xi,
∑ µi , i
分别表示第
i ∈{1, 2}
针对函数数据的分类问题,本文提出函数型线性判别分析,该方法把函数型数据表示成光滑曲线或 者连续函数,从而我们可以考虑到函数的特性(如连续、求导)。函数型线性判别分析的主要思想是通过给 定的训练集,寻找一条投影函数,使同类样本的投影点距离尽可能的接近,同时又使异类样本的投影点 尽可能的远离。基函数法是常见的将原始数据转化为函数的平滑技术之一,即将函数型数据在一组基下
线性判别分析[6] (linear discriminant analysis, LDA)是 Fisher 在 1936 年首次提出,在人脸识别[7]、食 品安全[8]、医学[9]等领域有广泛的应用。在模式识别领域中,贝叶斯分类效果最优,但由于其概率密度 函数难以估计,使得线性分类器(如 Fisher 线性判别分析)被广泛的应用在实际生活中。Li (2011) [10]等首 先将数据利用线性判别分析方法把训练样本投影到子空间中提取数据的相应特征,再利用支持向量机进 行分类。实验结果表明,该方法不仅起到降维的作用,同时提高了分类准确率,大大缩短了计算的时间。 Li [11]提出了 2–维线性判别分析(2-dimensional linear discriminant analysis, 2D-LDA)的方法,该方法从图 像矩阵中提取出重要的特征,进而计算类间散度矩阵和类内散度矩阵。而线性判别分析和 2–维线性判 别分析存在稀疏性的问题,在特征提取中存在遗漏重要数据信息的情况。但以上的分析方法都无法解决 以函数型数据为输入的分类问题。从而需要对函数型数据的内在结构和特性进行了解和分析。
DOI: 10.12677/orf.2019.92018
157
运筹与模糊学
王馨彤
进行展开。因此寻找这条投影函数,就变成寻找基函数的系数向量。函数型线性判别分析的优点之一是 可以求出导数曲线或者微分曲线,并通过求导或者微分我们可从数据中挖掘出隐藏的重要信息,从而得 到更好的分类结果。
本文的组织结构如下:第二章:给出了一些准备工作,对线性判别分析进行了简单的回顾。第三章: 详细的介绍了本文提出的方法。第四章:把函数型判别分析与线性判别分析方法进行比较,用数值实验 说明本文方法的可行性和优势。最后第五章是本文的结论与展望。
3. 函数型线性判别分析
函数型数据两分类问题描述如下:
{ } = 给定训练集 D
xj (t), yj
N j =1
,
