高二数学求曲线的方程2
高二数学双曲线的定义和标准方程2(201911新)
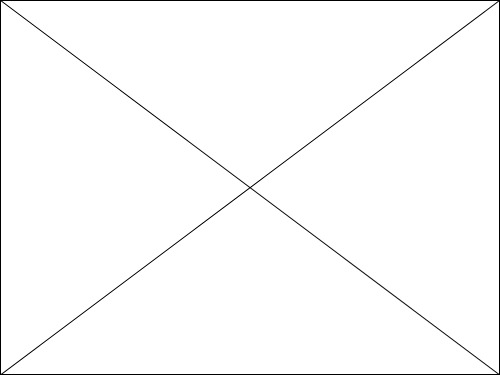
c2 a2 b2;
4、如果x2系数为正,那么焦点在x轴上;如果y2系数为 正,那么焦点在y轴上。
.P
.P
类 比
.
F1
. . F2 椭 圆 双曲 线 F1
.
F2
:
是研究平面上的动点P到两个定点F1,F2的距离问题
定
|PF1|+|PF2|=2a
||PF1|-|PF2||=2a
(a是正常数 且2a>|F1F2|) (a是正常数 且2a<|F1F2|)
若2a=|F1F2|轨迹:一线段 若2a=|F1F2|轨迹:两射线
义
若2a<|F1F2| 无轨迹
若2a>|F1F2| 无轨迹
学习任务:
请在学习、讨论中,将双曲线与椭圆进行类比
1、定义
平什面么内样与的两点个的定轨点迹是F1、双F曲2 的线距?离的差的绝对值 等于常数(小于 F1F2 )的点的轨迹叫做双曲线。
注: 可以利用[学习课件]中的“画双曲线” “ 画双曲线
(定义)” “阅读材料”这三个文件来学习。
学习任务:
请在学习、讨论中,将双曲线与椭圆进行类比
双曲线的定义与标准方程
轮船航行在茫茫大海上,到某一位置时,可以从 接收的电台声波,测出轮船与电台的距离。
如果能接收到3个不同地点同时发出的电台声波, 利用现代工具(定位仪)一瞬间就能确定自己的方位了, 你知道这是什是两个按钉,MF是一条拉链, 两边各取一点分别按在按钉上,笔尖随张开处点 M移动时,|MF1|-|MF2|是常数,这样就画出一条 曲线;再将拉链换一面,由于|MF2|-|MF1|是同一 常数,可以画出另一支。
高二数学求曲线的轨迹方程2

高二数学求曲线的方程2

思考2
例2、已知 ABC 中,A(-2,0),B(0,-2),第三顶点C在曲
线 y 3x2 1上移动,求 ABC 的重心轨迹方程。
例3、已知G是 ABC 的重心,A(0,-1),B(0,1),在x轴上
有一点M满足 MA MC ,GM AB( R). 求点C的
轨迹方程。
轨迹方程为
。
例 1.△ABC 的顶点 B、C 的坐标分别为(0,0)、(4,0),AB 边上的中线的长为 3,求顶点 A 的轨迹方程.
解:设 A 的坐标分别为 (x, y) ,AB 的中点 D 的坐标为 (x1, y1)
y ( x, y) 由中点坐标公式可知
x1 y1
x 2 y 2
(B) (x 3)2 y 2 1
(C) (2x 3)2 4 y 2 1
(D) (x 3)2 y 2 1
2
2
2.点 M (x, y) 与定点 F (1, 0) 距离和它到直线 x 8 的距离
的比为 1 ,则动点 M 的轨迹方程为( D )
2
(A) x2 y2 1
B A 则 由方xy 程xy11组22xy22
设直线
y kx x2 y2
l
6
的方程为
x 4 y 10
y
0
kx
消去 y 得 (1 k 2 )x2 (6 4k)x 9 0
M
0
C
x
∴
x y
3 1
k
x1
2k k2 3 2k
6 4k x2 1 k 2
消去参数
, k
x1 得
高二数学双曲线的标准方程

高二数学双曲线的标准方程高二数学求双曲线的标准方程一1焦点在X轴上,虚轴长为12,离心率为5/4?2顶点间的距离为6,渐近线方程为y=+3/2x或-3/2x?解:1设双曲线方程为x^2/a^2 - y^2/b^2 = 1a>0,b>0根据题意2b=12,∴b=6 ∴b^2=36∵e^2 = c^2/a^2=a^2 + b^2 / a^2=a^2 + 36/ a^2= 25 / 16∴a^2 = 64 ∴双曲线方程为x^2/64 - y^2/36 = 12设双曲线方程为x^2/a^2 - y^2/b^2 = 1a>0,b>0或y^2/a^2 - x^2/b^2 = 1a>0,b>0∵顶点间的距离为6 ∴2a=6 ∴a=3 ∴a^2 = 9∵渐近线方程为y=±3/2x∴y=±b/ax=±3/2x 或y=±a/bx=±3/2x∴b=9/2 ∴b^2 = 81/4 或b=2 ∴b^2=4双曲线方程为x^2/9 - 4y^2/81 = 1 或 y^2/9 - x^2/4 = 1高二数学求双曲线的标准方程二1焦点在X轴上,虚轴长为12,离心率为5/4?2顶点间的距离为6,渐近线方程为y=+3/2x或-3/2x?解:1设双曲线方程为x^2/a^2 - y^2/b^2 = 1a>0,b>0根据题意2b=12,∴b=6 ∴b^2=36∵e^2 = c^2/a^2=a^2 + b^2 / a^2=a^2 + 36/ a^2= 25 / 16∴a^2 = 64 ∴双曲线方程为x^2/64 - y^2/36 = 12设双曲线方程为x^2/a^2 - y^2/b^2 = 1a>0,b>0或y^2/a^2 - x^2/b^2 = 1a>0,b>0∵顶点间的距离为6 ∴2a=6 ∴a=3 ∴a^2 = 9∵渐近线方程为y=±3/2x∴y=±b/ax=±3/2x 或y=±a/bx=±3/2x∴b=9/2 ∴b^2 = 81/4 或b=2 ∴b^2=4双曲线方程为x^2/9 - 4y^2/81 = 1 或 y^2/9 - x^2/4 = 1感谢您的阅读,祝您生活愉快。
高二数学双曲线的定义和标准方程2
学习任务:
请在学习、讨论中,将双曲线与椭圆进行类比
1、定义
平什面么内样与的两点个的定轨点迹是F1、双F曲2 的线距?离的差的绝对值 等于常数(小于 F1F2 )的点的轨迹叫做双曲线。
注: 可以利用[学习课件]中的“画双曲线” “ 画双曲线
(定义)” “阅读材料”这三个文件来学习。
学习任务:
请在学习、讨论中,将双曲线与椭圆进行类比
双曲线的定义与标准方程
轮船航行在茫茫大海上,到某一位置时,可以从 接收的电台声波,测出轮船与电台的距离。
如果能接收到3个不同地点同时发出的电台声波, 利用现代工具(定位仪)一瞬间就能确定自己的方位了, 你知道这是什么原理吗?
画图实验:
定点F1,F2是两个按钉,MF是一条拉链, 两边各取一点分别按在按钉上,笔尖随张开处点 M移动时,|MF1|-|MF2|是常数,这样就画出一条 曲线;再将拉链换一面,由于|MF2|-|MF1|是同一 常数,可以画出另一支。
3、双曲线方程中a>0,b>0,但a不一定大于b。注意:
c2 a2 b2;
4、如果x2系数为正,那么焦点在x轴上;如果y2系数为 正,那么焦点在y轴上。.P Nhomakorabea.P
类 比
.
F1
. . F2 椭 圆 双曲 线 F1
.
F2
:
是研究平面上的动点P到两个定点F1,F2的距离问题
定
|PF1|+|PF2|=2a
2、标准方程
轨迹法求方程,其中是如何化简得到方程?
x2 a2
-
y2 b2
1是焦点在x轴上的,焦点在y轴上的呢?
注: 可以利用[学习课件]中的“双曲线方程” 这个文件
人教新课标版数学高二选修2-1讲义 2.1曲线与方程

2.1 曲线与方程2.1.1 曲线与方程2.1.2 求曲线的方程1.结合已学过的曲线与方程的实例,了解曲线与方程的对应关系.(了解)2.理解“曲线的方程”与“方程的曲线”的概念.(重点)3.通过具体的实例掌握求曲线方程的一般步骤,会求曲线的方程.(难点)[基础·初探]教材整理1曲线的方程与方程的曲线阅读教材P34~P35例1以上部分内容,完成下列问题.一般地,在直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:(1)曲线上点的坐标都是____________;(2)以这个方程的解为坐标的点都是__________,那么,这个方程叫做________,这条曲线叫做方程的曲线.【答案】这个方程的解曲线上的点曲线的方程设方程f(x,y)=0的解集非空,如果命题“坐标满足方程f(x,y)=0的点都在曲线C上”是不正确的,则下列命题正确的是()A.坐标满足方程f(x,y)=0的点都不在曲线C上B.曲线C上的点的坐标都不满足方程f(x,y)=0C.坐标满足方程f(x,y)=0的点有些在曲线C上,有些不在曲线C上D.一定有不在曲线C上的点,其坐标满足f(x,y)=0【解析】本题考查命题形式的等价转换,所给命题不正确,即“坐标满足方程f(x,y)=0的点不都在曲线C上”是正确的.“不都在”包括“都不在”和“有的在,有的不在”两种情况,故选项A、C错,选项B显然错.【答案】 D教材整理2求曲线方程的步骤阅读教材P36“例3”以上部分,完成下列问题.已知M(-2,0),N(2,0),则以MN为斜边的直角三角形的直角顶点P的轨迹方程是____________.【解析】设P(x,y),∵△MPN为直角三角形,∴MP2+NP2=MN2,∴(x+2)2+y2+(x-2)2+y2=16,即x2+y2=4.∵M,N,P不共线,∴x≠±2,∴轨迹方程为x2+y2=4(x≠±2).【答案】x2+y2=4(x≠±2)[小组合作型]对曲线的方程和方程的曲线的定义的理解(1)过点A(2,0)平行于y轴的直线与方程|x|=2之间的关系;(2)到两坐标轴的距离的积等于5的点与方程xy=5之间的关系;(3)第二、四象限角平分线上的点与方程x+y=0之间的关系.【导学号:37792038】【精彩点拨】曲线上点的坐标都是方程的解吗?以方程的解为坐标的点是否都在曲线上?【自主解答】(1)过点A(2,0)平行于y轴的直线上的点的坐标都是方程|x|=2的解,但以方程|x|=2的解为坐标的点不一定都在过点A(2,0)且平行于y轴的直线上.因此|x|=2不是过点A(2,0)平行于y轴的直线的方程.(2)到两坐标轴的距离的积等于5的点的坐标不一定满足方程xy=5,但以方程xy=5的解为坐标的点与两坐标轴的距离之积一定等于5.因此到两坐标轴的距离的积等于5的点的轨迹方程不是xy=5.(3)第二、四象限角平分线上的点的坐标都满足x+y=0,反之,以方程x+y =0的解为坐标的点都在第二、四象限角平分线上.因此第二、四象限角平分线上的点的轨迹方程是x+y=0.1.分析此类问题要严格按照曲线的方程与方程的曲线的定义.2.定义中有两个条件,这两个条件必须同时满足,缺一不可.条件(1)保证了曲线上所有的点都适合条件f (x ,y )=0;条件(2)保证了适合条件的所有点都在曲线上,前者是说这样的轨迹具有纯粹性,后者是说轨迹具有完备性.两个条件同时成立说明曲线上符合条件的点既不多也不少,才能保证曲线与方程间的相互转化.[再练一题]1.已知方程x 2+(y -1)2=10.(1)判断点P (1,-2),Q (2,3)是否在此方程表示的曲线上;(2)若点M ⎝ ⎛⎭⎪⎫m 2,-m 在此方程表示的曲线上,求实数m 的值. 【解】 (1)因为12+(-2-1)2=10,(2)2+(3-1)2=6≠10,所以点P (1,-2)在方程x 2+(y -1)2=10表示的曲线上,点Q (2,3)不在方程x 2+(y -1)2=10表示的曲线上.(2)因为点M ⎝ ⎛⎭⎪⎫m 2,-m 在方程x 2+(y -1)2=10表示的曲线上, 所以x =m 2,y =-m 适合方程x 2+(y -1)2=10,即⎝ ⎛⎭⎪⎫m 22+(-m -1)2=10. 解得m =2或m =-185.故实数m 的值为2或-185.由方程研究曲线(1)(x +y -1)x -1=0;(2)2x 2+y 2-4x +2y +3=0;(3)(x -2)2+y 2-4=0.【精彩点拨】 (1)方程(x +y -1)x -1=0中“x +y -1”与“x -1”两式相乘为0可作怎样的等价变形?(2)在研究形如Ax 2+By 2+Cx +Dy +E =0的方程时常采用什么方法?(3)由两个非负数的和为零,我们会想到什么?【自主解答】 (1)由方程(x +y -1)x -1=0可得 ⎩⎪⎨⎪⎧ x -1≥0,x +y -1=0或x -1=0, 即x +y -1=0(x ≥1)或x =1.故方程表示一条射线x +y -1=0(x ≥1)和一条直线x =1.(2)对方程左边配方得2(x -1)2+(y +1)2=0.∵2(x -1)2≥0,(y +1)2≥0,∴⎩⎪⎨⎪⎧ 2(x -1)2=0,(y +1)2=0,解得⎩⎪⎨⎪⎧x =1,y =-1. 从而方程表示的图形是一个点(1,-1).(3)由(x -2)2+y 2-4=0,得⎩⎪⎨⎪⎧ x -2=0,y 2-4=0,∴⎩⎪⎨⎪⎧ x =2,y =2或⎩⎪⎨⎪⎧x =2,y =-2.因此,原方程表示两个点(2,2)和(2,-2).1.判断方程表示什么曲线,就要把方程进行同解变形,常用的方法有:配方法、因式分解或化为我们熟悉的曲线方程的形式,然后根据方程、等式的性质作出准确判定.2.方程变形前后应保持等价,否则,变形后的方程表示的曲线不是原方程代表的曲线,另外,当方程中含有绝对值时,常借助分类讨论的思想.[再练一题]2.方程xy2-x2y=2x所表示的曲线()A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于x-y=0对称【解析】同时以-x代替x,以-y代替y,方程不变,所以方程xy2-x2y=2x所表示的曲线关于原点对称.【答案】 C[探究共研型]求曲线的方程探究1【提示】建立坐标系的基本原则:(1)让尽量多的点落在坐标轴上;(2)尽可能地利用图形的对称性,使对称轴为坐标轴.建立适当的坐标系是求曲线方程的首要一步,应充分利用图形的几何性质,如中心对称图形,可利用对称中心为原点建系;轴对称图形以对称轴为坐标轴建系;条件中有直角,可将两直角边作为坐标轴建系等.探究2求曲线方程时,有些点的条件比较明显,也有些点的条件要通过变形或转化才能看清,有些点的运动依赖于另外的动点,请你归纳一下求曲线方程的常用方法?【提示】一般有三种方法:一直接法;二定义法;三相关点法,又称为代入法.在解题中,我们可以根据实际题目选择最合适的方法.求解曲线方程过程中,要特别注意题目内在的限制条件.在Rt△ABC中,斜边长是定长2a(a>0),求直角顶点C的轨迹方程.【导学号:37792039】【精彩点拨】(1)如何建立坐标系?(2)根据题意列出怎样的等量关系?(3)化简出的方程是否为所求轨迹方程?【自主解答】取AB边所在的直线为x轴,AB的中点O为坐标原点,过O与AB垂直的直线为y轴,建立如图所示的直角坐标系,则A(-a,0),B(a,0),设动点C为(x,y).由于|AC|2+|BC|2=|AB|2,所以((x+a)2+y2)2+((x-a)2+y2)2=4a2,整理得x2+y2=a2.由于当x=±a时,点C与A或B重合,故x≠±a.所以所求的点C的轨迹方程为x2+y2=a2(x≠±a).1.求曲线方程的一般步骤(1)建系设点;(2)写几何点集;(3)翻译列式;(4)化简方程;(5)查漏排杂:即证明以化简后方程的解为坐标的点都是曲线上的点.2.一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写,如有特殊情况,可适当予以说明,另外,根据情况,也可以省略步骤(2),直接列出曲线方程.3.没有确定的坐标系时,要求方程首先必须建立适当的坐标系,由于建立的坐标系不同,同一曲线在坐标系的位置不同,其对应的方程也不同,因此要建立适当的坐标系.[再练一题]3.已知一曲线在x轴上方,它上面的每一点到点A(0,2)的距离减去它到x轴的距离的差都是2,求这条曲线的方程.【解】设曲线上任一点的坐标为M(x,y),作MB⊥x轴,B为垂足,则点M属于集合P={M||MA|-|MB|=2}.由距离公式,点M适合的条件可表示为x2+(y-2)2-y=2.化简得x2=8y.∵曲线在x轴上方,∴y>0.∴(0,0)是这个方程的解,但不属于已知曲线.∴所求曲线的方程为x2=8y(y≠0).1.已知直线l:x+y-3=0及曲线C:(x-3)2+(y-2)2=2,则点M(2,1)()A.在直线l上,但不在曲线C上B.在直线l上,也在曲线C上C.不在直线l上,也不在曲线C上D.不在直线l上,但在曲线C上【解析】将M(2,1)代入直线l和曲线C的方程,由于2+1-3=0,(2-3)2+(1-2)2=2,所以点M既在直线l上,又在曲线C上.【答案】 B2.在直角坐标系中,方程|x|·y=1的曲线是()【解析】 当x >0时,方程为xy =1,∴y >0,故在第一象限有一支图象;当x <0时,方程为-xy =1,∴y >0,故在第二象限有一支图象.【答案】 C3.已知两点M (-2,0),N (2,0),点P 满足PM →·PN →=4,则点P 的轨迹方程为________.【解析】 设点P 的坐标为P (x ,y ),由PM →·PN →=(-2-x ,-y )·(2-x ,-y )=x 2-4+y 2=4,得x 2+y 2=8,则点P 的轨迹方程为x 2+y 2=8.【答案】 x 2+y 2=84.设圆C :(x -1)2+y 2=1,过原点O 作圆的任意弦,求所作弦的中点的轨迹方程.【导学号:37792040】【解】 法一:如图所示,设OQ 为过O 的一条弦,P (x ,y )为其中点,连接CP ,则CP ⊥OQ .OC 的中点为M ⎝ ⎛⎭⎪⎫12,0,连接MP ,则|MP |=12|OC |=12,得方程⎝ ⎛⎭⎪⎫x -122+y 2=14. 由圆的范围,知0<x ≤1.即所求弦中点的轨迹方程为⎝ ⎛⎭⎪⎫x -122+y 2=14,0<x ≤1.法二:如图所示,由垂径定理,知∠OPC =90°,所以动点P 在以M ⎝ ⎛⎭⎪⎫12,0为圆心,OC 为直径的圆上. 由圆的方程,得⎝ ⎛⎭⎪⎫x -122+y 2=14, 由圆的范围,知0<x ≤1.即所求弦中点的轨迹方程为⎝ ⎛⎭⎪⎫x -122+y 2=14,0<x ≤1.。
高二数学上 7.6.2 求曲线的方程(二)教案 旧人教版

7.6.2 求曲线的方程(二)教学要求:更进一步熟练运用求曲线方程的方法、步骤,能熟练地根据条件求出简单的曲线方程。
教学重点:熟练地求曲线方程。
教学过程:一、复习准备:1.已知线段AB的长度为1,求平面上到A、B两点的距离的平方和是16的点M的轨迹方程。
(用两种建立坐标系的方法)2.知识回顾:求曲线方程的步骤(建系设点→写条件→列方程→化简→证明)二、讲授新课:1.教学例题:①出示例:动点M在x轴的下方,它到点A(0,-3)的距离减去它到x轴的距离的差都是4,求点M的轨迹方程。
②分析:由题意设动点M(x,y),其条件如何写出?方程如何列式?③学生试求→分析条件“限制在x轴的下方”如何处理?→小结解题步骤。
④变题:假如不限制在x轴下方呢?⑤出示例:已知定点F到定直线L的距离等于2,动点M到点F的距离与到直线L的距离相等,求动点M的轨迹方程。
⑥分析:有哪些建立坐标系的方法?教师给出一种建系方法:以直线L为x轴,点F在y轴的正半轴上,建立坐标系。
⑦学生按自己的方法与所给出的建系方法,分组求方程。
并比较。
2.练习:求到点(-4,0)和(4,0)的距离的平方差是48的动点的轨迹方程。
(x±3)三、巩固练习:1.试求到两坐标轴距离之差为2的点的轨迹方法,并作出图形。
(答案: ||x|-|y||=2)2.由原点作抛物线y=x+1的割线OPQ,求弦PQ的中点的轨迹方程。
解法:设割线y=kx,则x-kx+1=0∵△>0∴ k>2或k<-2,消k得 y=2x (x>1或x<-1) 3.课堂作业:书P72 7、8、9题。
高二数学双曲线的定义和标准方程2

练习:
1、已知两点F ( , 0) ,F ( , 0) , 求与F1 , F2的距离之差 1 5 2 5 为6 的点M的轨迹方程。
练习:
1、已知两点F ( , 0) ,F ( , 0) , 求与F1 , F2的距离之差 1 5 2 5 为6 的点的轨迹方程。
例题:
已知两点F1(-5,0),F2(5,0),求与F1,F2的距离之差 的绝对值等于 6的点M的轨迹方程。
解:设点 M ( x, y)
由题意
MF1 MF2 6 10
根据双曲线的定义,点 M的轨迹是 以F1,F2为焦点的双曲线
其中c 5, a 3 b2 c 2 a 2 16
( F1、F2 为定点, a 为常数)
两 种 图 形
标准方程
焦点坐标
x2 y 2 2 1a 0,b 0 2 a b
y 2 x2 2 1a 0,b 0 2 a b
F1 c, 0
F2 c, 0
F1 0, c F2 0,c
a, b, c
b2 a 2 c2
标 准 方 程
x2 y2 2 1(a b 0) 2 a b
x2 y2 2 1(a b 0) 2 b a
b2 c 2 a 2
x2 y2 2 1(a 0, b 0) 2 a b
y2 x2 2 1(a 0, b 0) 2 a b
变式:已知某一双曲线 的c 5,2a 6, 求其标准方程。
x2 y2 2、若方程 1表示双曲线 , 求m的取值 2 m m 1 范围。
x2 y2 变式:若方程为 1呢? 2 m m 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[单选]利用谷物为原料,主要成分是葡萄糖、麦芽糖、糊精的()呈浓厚粘稠状,甜度不如蔗糖。A、麦芽糖B、糖浆C、蜂蜜D、饴糖 [名词解释]审美注意 [单选]可信区间和医学参考值范围相比,正确的说法是()A.可信区间能判断个体值是否正常B.可信区间的计算是利用标准误C.医学参考值范围的计算是利用标准误D.可信区间估计的精度好E.医学参考值范围估计的精度好 [单选]根据客户反映及企业考察,对服务态度最好、服务质量最高者给予奖励的是()A、训练奖B、最佳服务奖C、市场情报奖D、降低退货奖 [单选]手的功能位哪项是不正确的()A.腕关节背伸100~150B.轻度尺偏C.拇指处于对掌位D.掌指关节和指间关节微屈E.其他手指略微分开 [单选]目前我国治疗普通型流脑首选的药物是()A.青霉素B.氯霉素C.头孢类抗生素D.磺胺类E.环丙沙星 [填空题]焦炉煤气的硫主要有()、()、()、()、()、()。 [单选]在母线倒闸操作中,母联断路器的()应拉开。A.跳闸回路B.操作电源C.直流回路D.断路器本体 [单选,A1型题]恶寒较甚,发热,无汗,头痛身楚,咳嗽,痰白,咯痰无力,舌淡苔白,脉浮而无力。治法宜首选()。A.辛温解表B.辛凉解表C.祛湿解表D.益气解表E.滋阴解表 [单选]最常见的并发症是()。男孩,4岁,6个月起青紫,渐加重,常蹲踞。胸骨左缘第3肋间可闻及2级收缩期杂音,P2减弱,有杵状指(趾)A.肺炎B.心力衰竭C.脑栓塞D.脑血栓E.呼吸衰竭 [填空题]信息构成广告的基本内容,一般包括()、()、()、()、()五类。 [单选]下列哪些不属于颈浅丛属支()A.lesseroccipitalnerveB.greatauricularnerveC.transversenerveofnerveD.supraclavicularnerveE.trochlearnerve [多选]编制资金筹措计划时应当()。A.使资金筹措计划与资金投入计划平衡、衔接B.在资金使用安排上,先安排使用债务资金,然后再安排使用项目资本金C.尽量减轻建设项目生产运营期的财务风险和运营风险,降低建设项目的还款压力D.在事前做好债务融资信用保证的安排和准备E.对不同的 [名词解释]计权隔声量 [单选]高血压病脑出血时,最常见的出血部位是()A.小脑齿状核B.小脑皮质C.脑桥D.基底节E.延脑 [单选]下列指标中,属于建设项目动态财务评价指标的有()。A.利息备付率B.财务内部收益率C.资产负债率D.偿债备付率 [单选]洞门墙应根据实际需要设置泄水孔和()。A.施工缝或伸缩缝B.施工缝或沉降缝C.施工缝或结构缝D.沉降缝和伸缩缝 [单选,A1型题]下列哪项不是胎盘剥离征象()A.宫底升高且软B.子宫呈球形C.阴道少量出血D.外露脐带延长E.压耻骨联合上方,脐带不回缩 [单选,A1型题]患有抑郁、焦虑障碍以及其他精神症状的人具有高频率的哪项思维,是导致情绪和行为障碍的主要原因之一()A.正性自动化思维B.积极的程序化思维C.消极的程序化思维D.负性自动化思维E.无意识思维 [单选]WAIS-RC的数字符号分测验在正式测验时,限时()秒。A.90B.60C.120D.30 [单选]地球曲率对视距测量影响误差属于()。A、系统误差B、偶然误差C、疏忽误差 [单选]适用于皮肤松弛部位腧穴的进针方法是()。A.单手进针法B.舒张进针法C.提捏进针法D.夹持进针法E.指切进针法 [单选]以下跳汰机是按矸石的运动方向加以区分的()。A、单槽跳汰机B、正排矸跳汰机C、块煤跳汰机D、三段跳汰机 [多选]进出境的(),免予检验。但是,法律、行政法规另有规定的除外。A.样品B.两国领导人相互交换的礼品C.参加展览会暂准进出境的货物D.非贸易性物品 [单选,A2型题,A1/A2型题]眨眼反射可用来检查下列疾病,但除外()A.特发性三叉神经痛B.面神经炎C.延髓受损D.吉兰-巴雷综合征E.视神经炎 [单选,A1型题]解表药的主要药理作用是()A.发汗B.调节胃肠运动C.降压D.泻下E.止泻 [配伍题,B型题]发生在肾任何部位的圆形、壁光滑、内为液性暗区与后壁回声增强()</br>肾窦内见大小不等互相连通的液暗区()A.肾孤立性囊肿B.多囊肾C.肾积水D.肾肿瘤坏死液化E.肾乳头状囊腺瘤 [单选,A2型题,A1/A2型题]正常肌肉在针电极停止活动后,插入活动()A.持续时间少于100msB.持续时间少于200msC.持续时间少于300msD.持续时间少于400msE.持续时间少于500ms [单选]以下关于“生存率”的叙述,正确的是()。A.是指观察对象活过某时刻的概率B.是指观察对象在某时段内存活的概率C.等于1-死亡概率D.若资料存在截尾值,则无法计算生存率E.复发率和缓解率不可能是生存率 [单选]在对市场经济进行规制的法律体系中,()处于基本法的地位。A.民商法B.婚姻法C.刑法D.民事诉讼法 [单选,A2型题,A1/A2型题]女性青春期开始的重要标志是()A.月经初潮B.生殖器官发育成熟C.卵巢功能成熟D.卵巢分泌性激素E.输卵管弯曲且很细 [单选]FMGS内部测试在何时自动进行:()A、地面、计算机通电时B、2台计算机之间有偏差时C、在空中发生故障时D、在空中自动驾驶仪接通时 [单选]在保险合同履行过程中,按照约定交付保险费义务的人是()。A.受益人B.被保险人C.是()。A.直接转移B.淋巴道转移C.血道转移D.远处种植E.弥漫性播散 [单选]某企业2012年度税前会计利润为2000万元,其中本年国债利息收入120万元,税收滞纳金20万元。企业所得税税率为25%,假定不考虑其他因素,该企业2012年度所得税费用为()万元。A.465B.470C.475D.500 [判断题]方法发明一般不能授予专利权。A.正确B.错误 [单选]正如科学与宗教一样,()在一切的时期里始终是处于一种冲突状态或不安的妥协状态。A、社会团结与个人自由B、言论自由与社会团结C、个人自由与言论自由 [问答题,案例分析题]病例摘要:陈某,男,60岁,已婚,于2011年11月16日急诊入院。患者主因反复发作劳累后心悸、气急、水肿20年,加重2月入院。患者20年前常宿营野外,常常发热、咽痛,此后常感四肢大关节游走性酸痛,但无红肿及活动障碍。5年前,晨起发觉双眼睑水肿,午后及傍晚 [单选]冰区航行,应采用适当的安全航速,通常应采用()的航速。A.3~5knB.2~3knC.维持舵效的最低航速D.A+C [填空题]煤气中硫化物按其化和状态可分为两类:一类是硫的无机物,主要是();另一类是硫的(),如二硫化碳、噻吩、及硫氧化物。
