智能控制大作业-模糊控制
智能控制-第六章 模煳控制系统
第六章 模糊控制系统
1. 模糊控制的定义 扎德(Zadeh)于1965年提出了模糊集合(Fuzzy Sets)。模糊控制是一类应用模糊集合理论的控制方法。
2. 模糊控制的价值 模糊控制提出了一种新的机制用于实现基于知识〔规那么〕甚至语义描述的控制规律。 模糊控制为非线性控制器提出了一个比较容易的设计方法，尤其是当受控装置〔对象或过程〕含有不确定性而且很难用传统非线性控制理论处理时，更是有效。
定义6.4 直积〔笛卡儿乘积，代数积〕
若 分别为论域 中的模糊集合，则这些集合的直积是乘积空间 中一个模糊集合，其隶属函数为： (6.7)
定义6.5 模糊关系
图6.4 Braae-Rutherford模糊控制器
此方法是由Braae和Rutherford于1978年开发 的，其结构原理如以下图所示。两个积分单元分别 放在模糊化单元之前和模糊判决单元之后。虽然 本模糊控制器能够减小系统误差至一定程度，但 是，无法保证消除极限环振荡现象。
若U，V是两个非空模糊集合，则其直积U×V中的一个模糊子集R称为从U到V的模糊关系，可表示为： (6.8)
模糊关系通常可以用模糊集合、模糊矩阵和模糊图等方法来描述。
定义6.6 复合关系
若R和S分别为U×V和V×W中的模糊关系，则R和S的复合是 一个从U到W的模糊关系，记为： (6.9)
定义6.2 模糊支集、交叉点及模糊单点
如果模糊集是论域U中所有满足 的元素u构成的集合， 则称该集合为模糊集F的支集。当u满足 ，称为交叉点。当模 糊支集为U中一个单独点，且u满足 则称此模糊集为模糊单 点。
其隶属函数为： (6.10)
定义6.7 正态模糊集、凸模糊集和模糊数
智能控制作业报告-基于遗传算法的模糊控制器最优设计
西安理工大学研究生课程论文/研究报告课程名称：智能控制任课教师：论文/研究报告题目：基于遗传算法的模糊控制器最优设计完成日期：2016 年8 月27 日学科：电力电子与电力传动学号：姓名：1. 基于遗传算法的模糊控制MATLAB 程序：clear all close all clc T=0.1;TM=200; time=zeros(1,TM);kp=0.2;ki=0.002;kd=20;tr=0;%定义初始种群参数N=10; M=3; varb=3;yout1=zeros(N,TM);yout=zeros(M,TM);fitness=zeros(1,N);%产生初始种群n=varb^2;n1=varb^2+varb*2;mfpara1=randint(N,n,[1,varb]); mfpara2=-1*rand(N,varb);为an ，bn ，cnmfpara3=rand(N,varb);为ap ，bp ，cpinit=[mfpara1,mfpara2,mfpara3];%离散化被控对象num=[1];den=conv(conv([1,0.1],[1,0.2]),[1, 0.7]); g=tf(num,den);yn=c2d(g,T, 'zoh' );[tt,ff]=tfdata(yn, 'v' );%开始循环p=1 while p<=M q=1while q<=N y=zeros(1,TM);u=zeros(1,TM); er=zeros(1,TM); %控制系统采样时间%控制系统运行次数%初始种群数目%遗传代数%语言值个数%每条染色体的长度%控制规则表%mfpara2(1),mfpara2(2),mfpara2(3)%mfpara3(1),mfpara3(2),mfpara3(3)%循环代数从 1 到 3%染色体数从 1 到10分别分别yr=zeros(1,TM);e1=0;e2=0;E1=0;y1=0;y2=0;y3=0;u1=0;u2=0;u3=0;e=zeros(1,TM);E=zeros(1,TM);for k=1:TM %运行系统yr(k)=1;y(k)=-ff(2)*y1-ff(3)*y2-ff(4)*y3+tt(2)*u1+tt(3)*u2+tt(4)*u3;y3=y2;y2=y1;y1=y(k);u3=u2;u2=u1;e(k)=yr(k)-y(k);er(k)=(e(k)-e1)/T;detae=fu_zzy(init(q,:),e(k),er(k),varb); 序E(k)=e(k)+detae; u(k)=kp*E(k)+ki*sum(E)+kd*(E(k)-E1);E1=E(k);u1=u(k);e2=e1;e1=e(k);endfor k=1:TMif abs(y(k)-1)<=0.1tr=k*T;break endendymax=0;for k=1:TMif ymax<y(k)ymax=y(k);endendfor k=1:TMera(k)=abs(e(k));end accer=sum(era); overshoot=(ymax-1)/1; tr overshoot accer%计算适配值，归一化if%上升时间tr%最大输出ymax%计算误差绝对值era%累积误差accer%超调量overshoot%调用模糊控制规则程0—100(tr>2)|(overshoot>1)|(accer> 50)fitness2=0; else tr1=tr*50;overshoot1=overshoot*100; accer1=accer*2; index=[tr1,abs(overshoot1),accer1];fitness1=(0.6*index(1)+1.2*index(2)+1.2*index(3))/3; fitness2=100-fitness1; endfitness(q)=fitness2; y;yout1(q,:)=y; q=q+1 endfitness [maxfit1,h]=max(fitness); maxfit(p)=maxfit1 yout(p,:)=yout1(h,:);init=gene_tic(init,fitness,p,N,varb,n,n1);的种群p=p+1 end for k=1:TMtime(k)=k*T; end plot(time,yout(1,:), 'r-' ,time,yout(2,:), 'g-' ,time,yout(3,:), 'b-' ) legend( ' 遗传第 1 代 ' , ' 遗传第 2 代' , ' 遗传第 3 代 ' ) grid onbest=max(maxfit) e1=1; y=[];e=[]; e1=0;y1=0;y2=0;y3=0; u1=0;u2=0;u3=0; for k=1:TM %运行系统yr(k)=1;y(k)=-ff(2)*y1-ff(3)*y2-ff(4)*y3+tt(2)*u1+tt(3)*u2+tt(4)*u3; y3=y2;y2=y1;y1=y(k); u3=u2;u2=u1; e(k)=yr(k)-y(k); er(k)=(e(k)-e1)/T;u(k)=kp*e(k)+ki*sum(e)+kd*(e(k)-e1); u1=u(k); e1=e(k);%一代种群运行完毕%每代的最大适配值存入 maxfit%每一代当适配值最大时，系统的阶跃响应输出%调用遗传算法优化，得到新%运行 3 代后结束endfigure(2)opt=find(maxfit==best);plot(time,y, '--' ,time,yout(opt(1), ':' ))legend( 'PID 控制器' , 'GA 优化的模糊PID 控制器' ) grid on各子函数MATLAB 程序：1) 模糊控制子程序fu_zzy .mfunction detae=fu_zzy(init,F,L,varb)if F<=-1 %将系统误差 e 设定在【-1 ， 1 】之间F=-1;elseif F>=1F=1;endif L<=-1 %将系统误差变化er 设定在【-1 ，1 】之间L=-1;elseif L>=1L=1;end%模糊控制规则an=init(10);bn=init(11);cn=init(12);ap=init(13);bp=init(14);cp=init(1 5);a=newfis( 'fuzzf' ; %建立隶属度函数a=addvar(a, 'input' , 'F' ,[-1,1]);a=addmf(a, 'input' ,1, 'NL' , 'zmf' ,[-1,an]);a=addmf(a, 'input' ,1, 'ZR' , 'trimf' ,[an,0,ap]);a=addmf(a, 'input' ,1, 'PL' , 'smf' ,[ap,1]);a=addvar(a, 'input' , 'L' ,[-1,1]);a=addmf(a, 'input' ,2, 'NL' , 'zmf' ,[-1,bn]);a=addmf(a, 'input' ,2, 'ZR' , 'trimf' ,[bn,0,bp]);a=addmf(a, 'input' ,2, 'PL' , 'smf' ,[bp,1]);a=addvar(a, 'output' , 'detae' ,[-1,1]);a=addmf(a, 'output' ,1, 'NL' , 'zmf' ,[-1,cn]);a=addmf(a, 'output' ,1, 'ZR' ,'trimf',[cn,0,cp ]);a=addmf(a, 'output' ,1, 'PL' , 'smf' ,[cp,1]);%建立控制规则表rulelist=[1 1 init(1) 1 1;1 2 init(2) 1 1;1 3 init(3) 1 1;2 1 init(4) 1 1;2 2 init(5) 1 1;23 init(6) 1 1;3 1 init(7) 1 1;3 2 init(8) 1 1;3 3 init(9) 1 1]; a=addrule(a,rulelist);a1=setfis(a, 'DefuzzMethod' , 'mom' );writefis(a1, 'fuzzf' );a2=readfis( 'fuzzf' );%模糊控制器输出detae=evalfis([F,L],a2);2) 遗传算法子程序gene_tic .m function init=gene_tic(init,fitness,k,N,varb,n,n1) fitness=fitness;N=N;varb=varb;init=init;%复制sumfit=sum(fitness); %sumfit 为每一代总的适应值zongfit(k)=sumfit; %保存每一代总的适应值到zongfitsumfit1(1)=fitness(1);for i=2:Nsumfit1(i)=sumfit1(i-1)+fitness(i);endlunpan=round(sumfit*rand(1,N));A=zeros(N,n1);for i=1:Nfor j=1:(N-1)if (lunpan(i)>=0)&(lunpan(i)<=sumfit1(1))A(i,:)=init(1,:);elseif (lunpan(i)>sumfit1(j))&(lunpan(i)<=sumfit1(j+1))A(i,:)=init(j+1,:);endendendinit=A;%交叉pc=0.6;Q=rand(1); place=round((n1-1)*rand(1)+1); match=randperm(N);B=zeros(N,n1);if Q<pcfor i=1:placeB(:,i)=init(:,i);%交叉概率选为0.7%产生交叉位%产生匹配对的随机endfor i=place:n1 for j=1:(N/2) B(match((j-1)*2+1),i)=init(match(j*2),i); B(match(j*2),i)=init(match((j-1)*2+1),i);end end end init=B; %变异 pm=0.01; d=round(N*n1*pm); if d==0 init=init; elseif d==1i=round(N*rand(1)+1); j=round(n1*rand(1)+1); if j<=n init(i,j)=round((varb-1)*rand(1)+1); 至 VN 中的一个 elseif j<=n+varb init(i,j)=-1*randint(1,1,[1,16])*1/16; 异为 -1 至 0 之间中的一个 elseif j<=n1 init(i,j)=randint(1,1,[1,16])*1/16; 异为 0 至 1 之间中的一个end elseif d>1 C=zeros(1,N*n1); x=randint(1,d,[1,N*n1]); C=reshape(init,[1,N*n1]); 阵C for i=1:d if C(x(i))<0 C(x(i))=-1*rand(1);赋值 elseif (C(x(i))>=0)&(C(x(i))<1) C(x(i))=rand(1); 间的小数赋值elseif C(x(i))>=1C(x(i))=randint(1,1,[1,varb]); varb )之间的整数赋值 end%变异概率选为 0.01%计算变异位个数%如果是前 n 位数，则变异为1%如果是 n+1 至 n+3 位数，则变%如果是 n+3 至 n2 位数，则变 %随机产生 d 个变异位置，存入 x 中 %将 N 行 n1 列的矩阵 init 转换为 1 行 N*n1 列的矩 %若变异位为负数，则随机选取（ -1 ，0 ）之间的小数 %若变异位为小于 1 的正数，则随机选取（ 0 ，1）之%若变异位大于等于 1，则随机选取（1，endinit=reshape(C,[N,n1]);%将变异后的 1 行N*n1 列的矩阵C，转换为N 行n1列的矩阵initendinit=init;2. 程序运行结果程序运行过程中遗传各代的每条染色体的阶跃响应性能指标如下表1,2,3 所示。
模糊控制设计及仿真实例智能控制作业
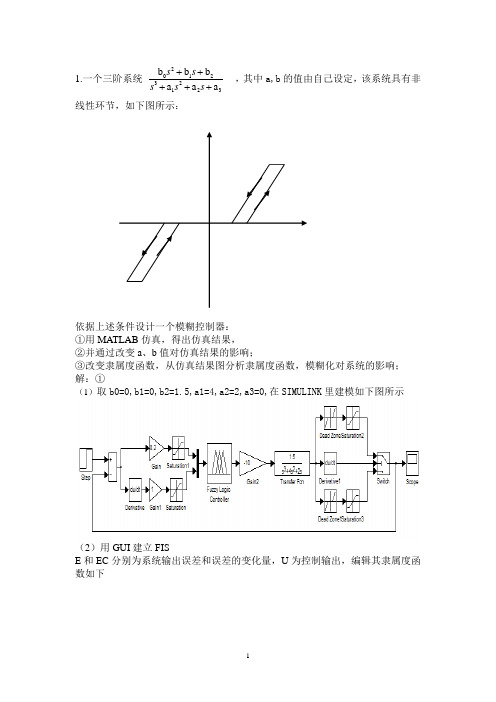
1.一个三阶系统201232123b b b a a a s s s s s +++++ ，其中a,b 的值由自己设定，该系统具有非线性环节，如下图所示：依据上述条件设计一个模糊控制器： ①用MATLAB 仿真，得出仿真结果， ②并通过改变a 、b 值对仿真结果的影响；③改变隶属度函数，从仿真结果图分析隶属度函数，模糊化对系统的影响； 解：①（1）取b0=0,b1=0,b2=1.5,a1=4,a2=2,a3=0,在SIMULINK 里建模如下图所示（2）用GUI 建立FISE 和EC 分别为系统输出误差和误差的变化量，U 为控制输出，编辑其隶属度函数如下编辑模糊推理规则如下(3)仿真结果如下2自己选定一个对象，设计一个神经网络控制系统。
解：被控对象为y(k)=0.3y(k-1)+0.2y(k-2)+0.1u(k-1)+0.6u(k-2),采用单神经元PID 控制，控制结构如下图所示：采用有监督的Hebb 学习规则，控制算法及学习算法如下：3131111222333()(1)()()()()/()()(1)()()()()(1)()()()()(1)()()()i i i i i i i I P D u k u k K w k x k w k w k w k w k w k z k u k x k w k w k z k u k x k w k w k z k u k x k ηηη=='=-+'==-+=-+=-+∑∑式中，2123()();()()(1);()()()2(1)(2);x k e k x k e k e k x k e k e k e k e k ==--=∆=--+-K K >0I P D ηηη﹑﹑分别为积分﹑比例﹑微分的学习速率，为神经元比例系数，。
输入信号为方波：()rin k 0.5sgn (sin (4t))π=仿真程序如下：clear all ; close all ;x=[0,0,0]';xiteP=0.40; xiteI=0.35; xiteD=0.40;wkp_1=0.10;wki_1=0.10;wkd_1=0.10;error_1=0;error_2=0;y_1=0;y_2=0;y_3=0;u_1=0;u_2=0;u_3=0;ts=0.001;for k=1:1:1000time(k)=k*tsrin(k)=0.5*sign(sin(4*pi*k*ts));yout(k)=0.3*y_1+0.2*y_2+0.1*u_1+0.6*u_2;error(k)=rin(k)-yout(k);wkp(k)=wkp_1+xiteP*error(k)*u_1*x(1);%Pwki(k)=wki_1+xiteI*error(k)*u_1*x(2);%Iwkd(k)=wkd_1+xiteD*error(k)*u_1*x(3);%DK=0.12;x(1)=error(k)-error_1;x(2)=error(k);x(3)=error(k)-2*error_1+error_2;wadd(k)=abs(wkp(k))+abs(wki(k))+abs(wkd(k)); w11(k)=wkp(k)/wadd(k);w22(k)=wki(k)/wadd(k);w33(k)=wkd(k)/wadd(k);w=[w11(k),w22(k),w33(k)];u(k)=u_1+K*w*x;%Control lawif u(k)>10u(k)=10;endif u(k)<-10u(k)=-10;endu_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=yout(k);wkp_1=wkp(k);wkd_1=wkd(k);wki_1=wki(k);endfigure(1);plot(time,rin,'b',time,yout,'r');xlabel('time(s)');ylabel('rin,yout'); figure(2);plot(time,error,'r');xlabel('time(s)');ylabel('error');figure(3);plot(time,u,'r');xlabel('time(s)');ylabel('u');仿真结果如下：3.前向神经网络拟合一个函数y=sin(x)*cos(10x),取n个样本，神经网络的层数和每层的点数可自定。
《智能控制技术大作业》(神经网络控制部分)
基于神经模糊控制的洗衣机设计20世纪90年代初期，日本松下电器公司推出了神经模糊控制全自动洗衣机。
这种洗衣机能够自动判断衣物的质地软硬程度、洗衣量、脏污程度和性质等，应用神经模糊控制技术，自动生成模糊控制规则和隶属度函数，预设洗衣水位、水流强度和洗涤时间，在整个洗衣过程中实时调整这些参数，以达到最佳的洗衣效果。
一、洗衣机的模糊控制洗衣机的主要被控变量为洗涤时间和洗涤时的水流强度，而影响输出变量的主要因子是被洗涤物的浑浊程度和浑浊性质，后者可用浑浊度的变化率来描述。
在洗涤过程中，油污的浑浊度变化率小，泥污的浑浊度变化率大。
因此，浑浊度及其变化率可以作为控制系统的输入变量，而洗涤时间和水流强度可作为控制量，即系统的输出。
实际上，洗衣过程中的这类输入和输出之间很难用数学模型进行描述。
系统运行过程中具有较大的不确定性，控制过程在很大程度上依赖操作者的经验，这样一来，利用常规的方法进行控制难以奏效。
然而，如果利用专家知识进行控制决策，往往容易实现优化控制，这就是在洗衣机中引入模糊控制技术的主要原因之一。
根据上述的洗衣机模糊控制基本原理，可得出确定洗涤时间的模糊推理框图如下：其中，模糊控制器的输入变量为洗涤水的浑浊度及其变化率，输出变量为洗涤时间。
考虑到适当的控制性能需要和简化程序，定义输入量浑浊度的取值为：浑浊度=｛清，较浊，浊，很浊｝定义输入量浑浊度变化率的取值为：浑浊度变化率=｛零，小，中，大｝定义输出量洗涤时间的取值为：洗涤时间=｛短，较短，标准，长｝显然，描述输入/输出变量的词集都具有模糊性，可以用模糊集合来表示。
因此，模糊概念的确定问题就直接转化为求取模糊集合的隶属函数问题。
暂不考虑模糊控制系统的量化因子和比例因子。
对于洗衣机的模糊控制问题，设其模糊控制器的输入变量（浑浊度和浑浊度变化率）隶属函数的论域均为输入变量论域=｛0,1,2,3,4,5,6｝模糊控制器的输出变量（洗涤时间）隶属度函数的论域为输出变量论域=｛0,1,2,3,4,5,6,7｝每个模糊变量属于上述论域的模糊子集如表1所示。
智能控制实验--专家控制、模糊控制、BP神经网络控制
智能控制实验专家控制、模糊控制、BP神经网络控制实验目的：1、通过实验进一步了解MATLAB软件的编程环境，学习编程技巧。
2、学习搜索相关论文，提高分析论文，找寻切入点的能力。
3、学习并掌握与计算机控制系统相关的控制算法。
实验内容：1、专家PID控制系统Matlab仿真2、模糊PID控制系统Matlab仿真3、神经网络PID控制系统MATLAB仿真前言PID控制是最早发展起来的控制策略之一，在经典控制论证扮演重要角色，尽管当下各种智能控制层出不穷，由于其算法简单、鲁棒性好和可靠性高，被广泛应用于工业控制过程，尤其适用于可建立精确数学模型的确定性控制系统。
而实际工业生产过程中往往具有非线性，时变不确定性，因而难以建立精确的数学模型，应用常规PID控制器不能达到到理想的控制效果，在实际生产过程中，由于受到参数整定方法繁杂的困扰，常规PID控制器参数往往整定不良，性能欠佳，对运行工况的适应性很差。
因此常规PID控制的应用受到很大的限制和挑战。
人们对PID应用的同时，也对其进行各种改进，主要体现在两个方面：一是对常规PID本身结构的改进，即变结构PID控制。
另一方面，与模糊控制、神经网络控制和专家控制相结合，扬长避短，发挥各自的优势，形成所谓智能PID控制。
使其具有不依赖系统精确数学模型的特点，对系统参数变化具有较好的鲁棒性。
主要算法有:基于规则的智能PID 自学习控制算法、加辨识信号的智能自整定PID 控制算法、专家式智能自整定PID 控制算法、模糊PID 控制算法、基于神经网络的PID 控制算法、自适应PID 预测智能控制算法和单神经元自适应PID 智能控制等多种控制算法。
结合具体实例，借助MATLAB 软件将专家PID 、模糊PID 以及神经网络PID 的设计程序M 文件自定义为一个函数，然后设计一个GUI 图形用户界面分别调用各自函数便于对比比较，易于操作。
观察各自控制效果，并作分析。
假设一个速度控制器的传递函数为：32523500()87.3510470G s s s s =++输入信号为阶跃信号，取采样时间为1ms ，分别采用专家PID 、模糊PID 、神经网络PID 算法绘制阶跃响应曲线以及误差响应曲线。
智能控制--模糊控制实验报告
clear all;close all;T=0; %ʱ¼ä³£Êýa=newfis('fuzz_temperatrue');a=addvar(a,'input','e',[-3,3]); %Parameter e a=addmf(a,'input',1,'NB','zmf',[-3,-1]);a=addmf(a,'input',1,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PM','trimf',[0,2,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);a=addvar(a,'output','u',[72,78]); %Parameter u a=addmf(a,'output',1,'NB','zmf',[72,74]);a=addmf(a,'output',1,'NM','trimf',[72,73,75]);a=addmf(a,'output',1,'NS','trimf',[73,74,75]);a=addmf(a,'output',1,'Z','trimf',[74,75,76]);a=addmf(a,'output',1,'PS','trimf',[75,76,77]);a=addmf(a,'output',1,'PM','trimf',[75,77,78]);a=addmf(a,'output',1,'PB','smf',[76,78]);rulelist=[1 1 1 1; %Edit rule base2 2 1 1;3 3 1 1;4 4 1 1;5 5 1 1;6 6 1 1;7 7 1 1];a=addrule(a,rulelist);a1=setfis(a,'DefuzzMethod','mom'); %Defuzzywritefis(a1,'temperatrue'); %Save to fuzzy file "tank.fis" a2=readfis('temperatrue');figure(1);plotfis(a2);figure(2);plotmf(a,'input',1);figure(3);plotmf(a,'output',1);flag=1;if flag==1showrule(a) %Show fuzzy rule baseruleview('temperatrue'); %Dynamic Simulationenddisp('-------------------------------------------------------');disp(' fuzzy controller table:e=[-3,+3],u=[-4,+4] ');disp('-------------------------------------------------------');for i=1:1:7e(i)=i-4;Ulist(i)=evalfis([e(i)],a2);endUlist=round(Ulist)e=-3; % Erroru=evalfis([e],a2) %Using fuzzy inference四、Simulink仿真模型五、实验结果令T=0;1、模糊控制器为一维控制器，输入输出变量的量化等级为7级，取5个模糊集。
智能控制-模糊控制
智能控制大作业报告模糊部分姓名：学号：专业：2011年06月03日题目：已知()()0.5250.528sG e s s s -=+++，分别设计PID 控制与模糊控制，使系统达到较好性能，并比较两种方法的结果。
PID/FCG(s)yr_e具体要求：1、采用Fuzzy 工具箱实现模糊控制器。
2、分析量化因子和比例因子对模糊控制器控制性能的影响。
3、分析系统阶数发生变化时模糊控制和PID 控制效果的变化。
4、分析系统在模糊控制和PID 控制作用下的抗干扰能力(加噪声干扰)、抗非线性能力(加死区和饱和特性)以及抗时滞的能力(对时滞大小加以改变)。
一 原系统仿真分析原系统是一个带有时滞环节的三阶系统，系统的三个极点均在s 域左半平面，系统是稳定的。
利用Matlab/Simulink 工具箱搭建系统框图，对原系统进行阶跃响应分析。
原系统框图如图1所示：图1 原系统框图设定仿真时间为10秒，其它为默认设置，运行程序，可以得到如图2所示仿真结果。
0123456789100.10.20.30.40.50.60.7t/s原系统阶跃响应图2 原系统阶跃响应曲线由图可以看出，原系统是稳定的，但是稳态误差比较大。
二 PID控制器设计根据上述仿真分析，可以知道系统性能比较差，因此设计初步设计PID控制器以在一定程度上改善系统性能。
PID参数的整定采用尝试的方法，遵循先比例后积分再微分的整定顺序，达到保持两个周期、前后超调比约为1:4的理想响应波形。
带PID控制器的系统框图如图3所示：图3 PID控制系统框图其中PID控制器参数如图4所示：图4 PID参数设置设定仿真时间为20s ，运行程序，可以得到如图5所示仿真结果：246810121416182000.20.40.60.811.21.4t/sS t e pPID 控制响应图5 PID 控制阶跃响应曲线由图可以看出，增加PID 控制的系统能够完全消除稳定误差，且具有较小的超调和较短的调节时间，极大程度地改善了系统的性能。
北航智能控制模糊控制作业
模糊控制查询表的MATLAB实现北京航空航天大学机械工程及自动化学院（北京 100191）一作业要求以双输入—单输出系统为例，画出模糊控制算法程序流程图，计算出模糊控制器的查询表。
假设控制器输入为误差e和误差变化率ec,输出为控制量u，其基本论域分别为[e min，e max]，[ec min，ec max]，[u min，u max]，对应的语言变量E、EC和U的论域为{-6,-5,…,-1,0,1,…,5,6}，E、EC和U都选7个语言值{NB，NM，NS，Z，PS，PM，PB}，各语言值的隶属函数采用三角函数，其分布可用表1-1表示，控制规则如表1-2所示。
注意：u的去模糊化要采用与你的学号ID的奇偶性对应的方法，设ID=奇数者用最大隶属度法，ID=偶数者用重心法；要有计算查询表时的必要计算步骤，不能只给出最后结果。
表1-1 语言变量E、EC和U的赋值表表1-2 模糊控制规则表二 模糊控制查询表和控制算法流程图2.1 模糊控制查询表（1）模糊控制算法一般双输入—单输出模糊控制器的控制规则可写成条件语句：if and E=B then U=C ,i=1，2,,;1，2,,;i j ijE A n j n =∆= 式子中，、B 、C i j ijA 为定义在误差、误差变化率和控制量论域X 、Y 、Z 、上的模糊集合。
上述条件可以用一个模糊关系R 描述，即1()T ij iji jRA B C ≠=⨯⨯ R 的隶属度函数为：,1,1(,,)()()(),,,i n j m i j iji j Rx y z A x B y C z x X y Y z Z =====∨∧∧∈∈∈ 当误差及误差变化分别取模糊集、B A时，控制器输出的变化量U 根据模糊推理合成规则可得：2T U=（A B ）R ⨯ U 的隶属度函数为：x Xy YU(z)=A(x)B(y)R(x,y,z)∈∈∨∧∧（2）模糊算法选择模糊推理用Mamdani 推理方法，输出信息的模糊判别用最大隶属度法。
智能控制课件-模糊控制
0 0 0 0
0 .5 1 .0
0 .5 1 .0
0 .5 1 .0 0 .5 0 .5 0 0
0 0 0 0 0 0 0 .5 0 0 .5 0 .5 0 .5 1 .0 0 0
15
5
模糊决策 模糊控制器的输出为误差向量和模糊关系的合成 合成（ 复合） 合成（复合）
0
0
0
0 0 0 0 0 0 PSe × PSu = 0 × [0 0 0 0 0 0.5 1.0 0.5 0] = 0 1.0 0 0.5 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
自学习、自适应；模糊推理策略；模糊模型辨识；稳定性；硬件实现
3
3.2 模糊控制的基本原理
以模糊集理论 模糊集理论、 模糊集理论 、 模糊语言变量、 模糊语言变量、 模糊逻辑推理为基础，从行为上模 模糊逻辑推理 仿人的模糊推理和决策过程的一种智能控制方法。
3.2.1 模糊控制器的构成
模糊控制器（ Fuzzy Controller—FC ）也称模糊逻辑控制器（ Fuzzy Logic Controller—FLC）。采用模糊理论中模糊条件语句来描述，是一种 语言型控制器，也称模糊语言控制器（ Fuzzy Language Controller-FLC）。 语言型控制器
12
0 0 0 0 0 0 .5 0 0 .5 0 .5 0 .5 1 0 0 .5 1 .0 0 .5 NSe × NSu = 0 × [0 0.5 1 0.5 0 0 0 0 0] = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
智能控制模糊控制设计总结优缺点及改进
d / dt
特 征
识
模糊控制器2
对象
别
……
模糊控制器n
32
积分系数（过去）：消除系统的稳态误差。Ki越大，系统的稳态误 差消除越快，但Ki过大，在响应过程的初期会产生积分饱和现象， 从而引起响应过程的较大超调。若Ki过小，将使系统稳态误差难以 消除，影响系统的调节精度。
微分系数（未来）：改善系统的动态特性。其作用主要是能反应 偏差信号的变化趋势。并能在偏差信号值变得太大之前，引入一 个有效的早期修正信号，从而加快系统的动作速度，减少调节时 间。
19
2）Ke、Kec、Ku的调整方法
系统状态 e和ec较大
性能要求
参数调整的要求
尽快消除误差， 降低Ke和Kec； 加快响应速度 加大Ku
e和ec较小
系统已经接近 稳态,此时要求 提高系统精度, 减少超调量
加大Ke和Kec； 降低Ku
原因
❖降低Ke和Kec可以降低对 e和ec输入量的分辨率,使 得e、ec的减少不致于使 控制器的减少太多。 ❖加大比例因子Ku,可以获 得较大的控制量,使响应 加快。
❖增大Ke和Kec可以提高对输 入变化的分辨率，使得控制 器可以对微小的误差做出反 应，提高稳态的精度 ❖减少Ku，以减小超调量
20
3.3 参数自校正模糊控制器
根据上述参数自调整的原则和思想，可以设计一个模糊参数调整器，在线 地根据偏差e和偏差变化ec来调整Ke、Kec、Ku的取值。 在不影响控制效果的前提下，可以取Ke、Kec增加的倍数与输出的比例因 子Ku减小的倍数相同。
13
模糊规则表 ec
dKp,dKi, dKd NB
NM
NS
e
ZO
PS
智能控制大作业【范本模板】
南京工程学院自动化学院《智能控制技术》大作业课程名称：智能控制技术院（系、部、中心）：康尼学院专业：自动化班级: K自动化121 姓名：刘爽学号： 240120902课程论文成绩评定：指导教师签字：2015 年 6 月 24 日摘要模糊控制是以模糊集合论作为它的数学基础，用语言规则表示方法和先进的计算机技术，由模糊推理进行决策的一种高级控制策。
模糊控制作为以模糊集合论、模糊语言变量及模糊逻辑推理为基础的一种计算机数字控制，它已成为目前实现智能控制的一种重要而又有效的形式尤其是模糊控制和神经网络、遗传算法及混沌理论等新学科的融合，正在显示出其巨大的应用潜力。
实质上模糊控制是一种非线性控制,从属于智能控制的范畴。
模糊控制的一大特点是既具有系统化的理论，又有着大量实际应用背景.本文简要回顾了模糊控制理论的发展，详细介绍了模糊控制理论的原理和模糊控制器的设计步骤，分析了模糊控制理论的优缺点以及模糊控制需要完善或继续研究的内容，根据各种模糊控制器的不同特点，对模糊控制的应用进行了分类,并分析了各类模糊控制器的应用效能.最后,展望了模糊控制的发展趋势与动态。
关键词：模糊控制；模糊控制理论；模糊控制系统；模糊控制理论的发展第一节引言1。
1 模糊控制系统简介模糊控制系统是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一种计算机数字控制技术.自从美国加利福尼亚大学控制论专家L.A.Zadeh教授在1965年提出的《Fuzzy Set》开创了模糊数学的历史，吸引了众多的学者对其进行研究，使其理论和方法日益完善，并且广泛的应用于自然科学和社会科学的各个领域,尤其是第五代计算机的研制和知识工程开发等领域占有特殊重要的地位.把模糊逻辑应用于控制领域则始于1973年.1974年英国的E.H.Mamdani成功地将模糊控制应用于锅炉和蒸汽机的控制.此后20年来，模糊控制不断发展并在许多领域中得到成功应用。
由于模糊逻辑本身提供了由专家构造语言信息并将其转化为控制策略的一种体系理论方法,因而能够解决许多复杂而无法建立精确数学模型系统的控制问题，所以它是处理推理系统和控制系统中不精确和不确定性的一种有效方法。
智能控制大作业-模糊控制
智能控制与应用实验报告模糊控制器设计一、 实验内容考虑一个单连杆机器人控制系统，其可以描述为：0.5sin()Mqmgl q y qτ+==(1)其中 20.5M kgm =为杆的转动惯量，1m kg =为杆的质量，1l m =为杆长，29.8/g m s =，q 为杆的角位置，q为杆的角速度，q 为杆的角加速度，τ为系统的控制输入。
实验具体要求：1. 分别采用fuzzy 工具箱设计模糊控制器跟踪期望的角位置信号。
2. 分析量化因子和比例因子对模糊控制器控制性能的影响。
3. 分析系统在模糊控制和PID 控制作用下的抗干扰能力(加噪声干扰)和抗非线性能力（加死区和饱和特性）。
4. 为系统设计模糊PID 控制器。
二、 对象模型建立根据公式(1)，令状态量121=,x q x x =得到系统状态方程为：121210.5**sin()x x mgl x x My x τ=-==(2)由此建立单连杆机器人的模型如图1所示。
图1 单连杆机器人模型三、模糊控制算法实现及仿真本次实验设计一个二维模糊控制器，令误差*=-，误差变化E q q= ，模糊控制器输出语言变量为U。
EC E1)三个变量E、EC和U的模糊词集为：﹛NB,NM,NS,ZO,PS,PM,PB﹜模糊论域为：E和EC：{-6,-5,-4,-3,-2,-1,0, 1, 2, 3, 4, 5, 6}U:{-7,-6,-5,-4,-3,-2,-1, 0, 1, 2, 3, 4, 5, 6, 7}2)模糊控制规则为：表1 模糊控制规则表3)确定E,EC和U的控制表4)建立模糊控制表5)建立SIMULINK模型在Matlab/Simulink中建立单连杆机器人模糊控制系统模型如图2所示：图2 单连杆机器人控制系统模型6) 仿真结果给定正弦参考信号，取量化因子5,1Ke Kec ==，比例因子50Ku =，得到系统角度跟踪为图3。
51015-1-0.8-0.6-0.4-0.200.20.40.60.81t/sa n g l e /r a d图3 正弦角度跟踪由图3可知，该模糊控制器能使得单连杆机器人控制系统实现很好的角度跟踪。
智能控制——模糊控制2
W称为规则的 匹配度
= ∨ [μA' ( x) ∧ μA ( x)] ∧ μB ( y)
x∈X
= w ∧ μB ( y)
A
A’
B
B’
2.4.4多输入、多规则的近似推理
1、句子连接词“and”
前提1(事实)： x是A’ and y是B’
看作 积空间X×Y上 的模糊集合
前提2(规则) ：if x是A，and y是B,then z是C 结果(结沦) ：z是C’
压? 令x=“炉温”，y=“电压”，有X=Y={1,2,3,4,5} 令A=“炉温低”={1/1，0.8/2,0.6/3,0.4/4,0.2/5} 令B=“电压高”={0.2/1,0.4/2,0.6/3,0.8/4,1/1} 则上述模糊规则可表示为：如果x是A,则y是B.设A’为A、 非常A，略A 和非A时，B’是什么？
1.0 0.6 0.2 1.0 0.4 0 B1 = + + C1 = + + b1 b2 b3 c1 c2 c3 0.2 0.6 1.0 0 0.4 1.0 B2 = + + C2 = + + b1 b2 b3 c1 c2 c3
0 0.5 1.0 A2 = + + a1 a2 a3
A' =
0.5 1.0 0.5 + + a1 a2 a3
推理过程: 模糊蕴含关系: A×B→C
μ A× B ( x, y ) = min{μ A ( x), μ B ( y )}
合成:
R = A× B → C
C ' = ( A '× B ') R
2、规则连接词“ALSO”
武汉理工大学智能控制大作业
智能控制理论与技术设计报告学院自动化学院专业控制科学与工程班级1303姓名聂鹏指导教师徐华中2014 年 2 月20 日武汉理工大学硕士研究生试题课程名称：智能控制理论与技术专业：双控1303班学号：1049721303692 姓名：聂鹏一、简答题（每小题10分）1．智能控制由哪几部分组成？各自的特点是什么？答：智能控制系统由广义对象、传感器、感知信息处理、认知、通信接口、规划和控制和执行器等七个功能模块组成；各部分的特点是：广义对象——包括通常意义下的控制对象和外部环境；传感器——包括关节传感器、力传感器、视觉传感器、距离传感器、触觉传感器等；感知信息处理——将传感器得到的原始信息加以处理；认知——主要用来接收和储存信息、知识、经验和数据，并对它们进行分析、推理，作出行动的决策，送至规划和控制部分；通信接口——除建立人机之间的联系外，还建立系统各模块之间的联系；规划和控制——是整个系统的核心，它根据给定的任务要求、反馈的信息以及经验知识，进行自动搜索，推理决策，动作规划，最终产生具体的控制作用；执行器——将产生的控制作用于控制对象。
2. 智能控制是在什么背景下产生的？答:传统控制理论在应用中面临的难题包括:(1) 传统控制系统的设计与分析是建立在精确的系统数学模型基础上的,而实际系统由于存在复杂性、非线性、时变性、不确定性和不完全性等,一般无法获得精确的数学模型。
(2) 研究这类系统时,必须提出并遵循一些比较苛刻的假设,而这些假设在应用中往往与实际不相吻合。
(3) 对于某些复杂的和包含不确定性的对象,根本无法以传统数学模型来表示,即无法解决建模问题。
(4) 为了提高性能,传统控制系统可能变得很复杂,从而增加了设备的初投资和维修费用,降低系统的可靠性。
传统控制理论在应用中面临的难题的解决,不仅需要发展控制理论与方法,而且需要开发与应用计算机科学与工程的最新成果。
人工智能的产生和发展正在为自动控制系统的智能化提供有力支持。
北航智能控制模糊控制作业
智能控制及应用大作业一——双输入—单输出系统的模糊控制姓名：学号：2011-10-14题目要求以双输入—单输出系统为例，画出模糊控制算法程序流程图，计算出模糊控制器的查询表。
假设控制器输入为误差e和误差变化率ec,输出为控制量u，其基本论域分别为[e min，e max]，[ec min，ec max]，[u min，u max]，对应的语言变量E、EC和U的论域为{-6,-5,…,-1,0,1,…,5,6}，E、EC和U都选7个语言值{NB，NM，NS，Z，PS，PM，PB}，各语言值的隶属函数采用三角函数，其分布可用表1表示，控制规则如表2所示。
注意：u的去模糊化要采用与你的学号ID的奇偶性对应的方法，设ID=奇数者用最大隶属度法，ID=偶数者用重心法；要有计算查询表时的必要计算步骤，不能只给出最后结果。
表2模糊控制规则表程序设计与程序流程图1、模糊算法的选择模糊蕴含用求交法，输出量的清晰化计算用最大隶属度法。
于是有输出量的模糊集合'U 为：491'491''491''491''491''''')]([)]([])[()()()(=======→→=→⨯⨯=⨯=⨯=i ii iEC iE i i i i i i i i i i iCU U U EC EC U E EU EC E EC E R EC E R EC E U2、程序结构说明利用Matlab 编写该模糊算法，并且计算出模糊控制器的查询表。
程序按照上面的控制算法，先计算模糊关系隶属度矩阵R 。
通过上面的式子，根据每一条控制规则，查找相对应的赋值表当中的向量值。
如第一条法则:If E=NB and EC=NB, then U=NB.则找到E 中NB 对应的行向量和EC 中NB 对应的行向量，然后将第一个行向量转置后与第二个行向量按照乘法法则对应取小值，生成新的矩阵。
智能控制模糊控制仿真大作业
智能控制模糊控制仿真大作业一、前言智能控制模糊控制仿真大作业是在智能控制课程中的一项重要任务，旨在让学生通过实践来深入理解模糊控制的原理和应用。
本文将从以下几个方面详细介绍智能控制模糊控制仿真大作业的相关内容。
二、作业背景智能控制是一种基于人工智能技术的自动化控制方法，它可以通过对系统进行学习和优化来提高系统的性能和鲁棒性。
而模糊控制则是智能控制中的一种重要方法，它可以通过对输入输出之间的关系进行建模来实现对系统的控制。
因此，深入了解模糊控制的原理和应用对于学习智能控制具有重要意义。
三、作业要求本次大作业要求学生使用MATLAB/Simulink软件来设计一个基于模糊逻辑的温度调节系统，并进行仿真验证。
具体要求如下：1. 设计一个基于PID算法和模糊逻辑的温度调节系统；2. 利用Simulink软件构建该系统，并进行仿真验证；3. 对比分析PID算法和模糊逻辑在温度调节系统中的控制效果；4. 撰写实验报告，详细介绍设计思路、仿真结果以及分析结论。
四、作业流程1. 确定系统需求和参数首先，需要确定温度调节系统的需求和参数。
例如，设定目标温度为25摄氏度，系统初始温度为20摄氏度，采样时间为0.1秒等。
2. 设计PID控制器接下来，设计PID控制器。
PID控制器是一种经典的控制方法，在工业自动化控制中得到广泛应用。
其基本原理是通过对误差信号、误差积分和误差微分进行加权组合来得到输出信号。
3. 设计模糊逻辑控制器然后，设计模糊逻辑控制器。
模糊逻辑控制器是一种基于模糊集合和模糊推理的控制方法。
其基本原理是将输入变量映射到一个或多个模糊集合上，并通过一系列规则来推导出输出变量的值。
4. 构建Simulink模型并进行仿真验证接下来，利用Simulink软件构建温度调节系统，并将PID控制器和模糊逻辑控制器分别加入到系统中。
然后，进行仿真验证，比较两种控制方法的控制效果。
5. 分析结果并撰写实验报告最后，对比分析PID算法和模糊逻辑在温度调节系统中的控制效果，并撰写实验报告，详细介绍设计思路、仿真结果以及分析结论。
模糊控制大作业-南航-智能控制
模糊控制器大作业一、题目要求考虑如下某水下航行器的水下直航运动非线性模型：()||a m m v k v v u y v++==其中v R ∈为水下航行器的前进速度， u R ∈为水下航行器的推进器推力，y R ∈为水下航行器的输出，航行器本体质量、附加质量以及非线性运动阻尼系数分别为100,15,10a m m k ===。
作业具体要求：1、分别采用fuzzy 工具箱设计模糊控制器使得系统稳定或跟踪期望指令信号。
2、分析量化因子和比例因子对模糊控制器控制性能的影响。
3、比较分析系统在模糊控制和PID 控制作用下的抗干扰能力(加噪声干扰)和抗非线性能力(加死区和饱和特性)。
二、构建模糊控制Simulink 仿真模型1.模糊控制器的设计（1）观测量：输入量、输出量（控制量）由题目要求分析可知，在这个水下航行器的水下直航运动非线性模型中，输入量是水下航行器的推进器推力u R ∈，输出是水下航行器的前进速度v R ∈。
（2）根据系统实际情况，选择误差e ，误差变化ec 和控制量u 的论域e range : [-6 6] ec range: [-6 6] u range: [-6 6] （3）e ，de 和u 语言变量的选取e 7个：NB,NM,NS,ZO,PS,PM,PB ec 7个：NB,NM,NS,ZO,PS,PM,PB u 7个：NB,NM,NS,ZO,PS,PM,PB（4）模糊控制规则确定ueNB NM NS ZO PS PM PBec NB PB PB PM PM PS ZO ZO NM PB PB PM PM PS ZO ZO NS PB PB PM PS ZO NM NM ZO PB PB PM ZO NM NB NB PS PM PM ZO NS NM NB NB PM ZO ZO NS NM NM NB NB PB ZO ZO NS NM NM NB NB表1 模糊规则表图1 模糊控制规则的添加在模糊控制器的设置中，分别对控制器中的E、EC、U进行设置，按照（2）中的选择确定论域范围，均为[-6 6]，选择的隶属函数为高斯函数分布。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
智能控制与应用实验报告模糊控制器设计对象模型建立实验内容考虑一个单连杆机器人控制系统，其可以描述为:岬 0.5mgl sin(q)y q2其中M 0.5k gm 为杆的转动惯量，m 1kg 为杆的质量，l 1m 为杆长,g 9.8m/s 2，q 为杆的角位置，q 为杆的角速度,为杆的角加速度，为系统的控制输入。
实验具体要求:1. 2. 分别采用fuzzy 工具箱设计模糊控制器跟踪期望的角位置信号。
分析量化因子和比例因子对模糊控制器控制性能的影响。
3. 分析系统在模糊控制和PID 控制作用下的抗干扰能力（加噪声干扰）和抗非线性能力（加死区和饱和特性） 4. 为系统设计模糊PID 控制器。
根据公式（1），令状态量Xi =q ，x 2X1得到系统状态方程为:X i X 2X 20.5* mgl*sin( xjX i由此建立单连杆机器人的模型如图1所示。
0.5*mgl图1单连杆机器人模型三、模糊控制算法实现及仿真本次实验设计一个二维模糊控制器，令误差 E q* q，误差变化EC E，模糊控制器输出语言变量为U。
1）三个变量E、EC和U的模糊词集为：{ NB,NM,NS,ZO,PS,PM,PB模糊论域为：E 和EC {-6,-5,-4,-3,-2,-1,0, 1,2, 3, 4, 5, 6}U:{-7,-6,-5,-4,-3,-2,-1,0, 1,2, 3, 4, 5, 6, 7}2）模糊控制规则为：表表3）确定E,EC和U的控制表4）建立模糊控制表5）建立SIMULINK模型在Matlab/Simulink 中建立单连杆机器人模糊控制系统模型如图2所示:A-K 3 - =to10.8 0.6 0.4 0.2 0 510 15t/sfe gi0 踪。
统角度跟踪为图3-0.4 -0.6 -0.8 给定阶跃信号，取量化因子Ke 5,Kec 1,比例因子Ku 50，得到系统角图2单连杆机器人控制系统模型6）仿真结果给定正弦参考信号，取量化因子 Ke 5,Kec 1,比例因子Ku 50，得到系图3正弦角度跟踪由图3可知，该模糊控制器能使得单连杆机器人控制系统实现很好的角度跟 -0.2 MT.in putoutput _度跟踪为图4图4阶跃角度跟踪由图4可知，在该模糊控制器下虽然响应有一点延迟， 但还是能够很好的跟踪阶跃角度信号，而且稳态误差非常小。
四、参数对模糊控制器的影响设计一个模糊控制器除了要有一个较好的模糊控制规则外，合理的选择模糊控制器输入变量的量化因子和输出控制量的比例因子也是非常重要的。
量化因子和比例因子的大小及其不同量化因子之间大小的相对关系， 对模糊控制器的控制性能影响极大。
1）量化因子Ke 变化取Kec=1,Ku=50, Ke 分别取2,4,6,8时，观察单连杆机器人跟踪阶跃角 度参考的性能如图5所示:5t/s101 £ 0■8-70 06. 50 04 3 0 0 ■2「0 015图5 Ke 变化时系统对阶跃信号的角度跟踪由仿真结果可知，增大Ke ,可加快动态响应，提高稳态精度，但 Ke 也不能 过分增大，过大会造成系统超调甚至发散。
2）量化因子Kec取Ke=5,Ku=50, Kec 分别取,,,时，观察单连杆机器人跟踪阶跃角度参考的性能如图6所示：d^r/prana5t/s10 158 7 6 o o o 5 4 0 0 -3-2「0 0 0■d ar/ Argna1015t/s4inputKec=O.：Kec=O? Kec=OJ图6 Kec 变化对阶跃信号的角度跟踪由仿真结果知，增大Kec,减弱了系统动态响应超调，但使系统的响应 速度变慢，同时也降低了系统的稳态精度。
3）比例因子Ku 变化取Ke=5,Kec=1，Ku 分别取20,40,60,80时，观察单连杆机器人跟踪阶 跃角度参考的性能如图7、图8所示：in put Ku=20Ku=40Ku=60 Ku=800.60.40.210t/s图7 Ku 变化时角度跟踪动态响应性能图---------- i nput ---------- K u=20 ---------- K u=40 ---------- K u=60 ---------- K u=800.942.42.52.62.72.8 2.933.13.2t/s图8 Ku 变化时角度跟踪稳态响应性能图由仿真结果可知，Ku 选择过小会使系统动态响应过程变长。
增大 Ku, 相当于减弱了系统阻尼，可加快动态响应，同时提升稳态精度，作用和 Ke相似，过大可能会导致系统震荡。
但不管以上三种参数如何变化，模糊控制下的单连杆机器人系统的角度 跟踪始终存在静差，这与模糊控制中不存在积分项有关。
0.81597五、模糊控制和PID控制性能比较为了比较模糊控制和PID控制器对非线性系统的控制效果，建立如下所示的系统框图。
图9模糊控制结构图图10 PID控制结构图选定模糊控制器参数为Ke=5,Kec=1,Ku=50;PID控制器参数为Kp=100,Ki=50,Kd=30。
1）输入参考信号为阶跃时，两者的角度跟踪响应为：1.21 0.8d 0.6 re g 0.40.2 0 -0.2 0510 15t/s图11、PID 和模糊控制阶跃角度跟踪性能比较由图11可以看出，对于阶跃信号参考输入，单连杆机器人系统在 PID控制下作用效果优于模糊控制，主要体现在动态响应时， PID 控制器快于模糊控制器。
2）输入参考信号为正弦时，角度跟踪为：从图12中可以看出，对于正弦输入参考，PID 控制效果反而不如模糊 控制，PID 控制较模糊控制下的响应存在较大的滞后。
3）阶跃输入下，反馈加入噪声--------- input----------- fuzzy ---------pid0 510 15t/s图12、PID 和模糊控制正弦角度跟踪性能比较5 -0dau//rona0.2 * -=、，1—-0.2 ------------------------------------ [ ----------------------------------- c ---------------------------------- -0 5 1015t/s图13噪声干扰对比在PID 和模糊控制参数不变的情况下，加入噪声干扰，由图 13可知,模糊控制抗干扰能力优于PID 。
4）阶跃输入下，控制信号加入非线性因素（死区和饱和）控制电压输出部分加入的死区和饱和如图14所示：得到模糊控制和PID 控制下，系统角度跟踪信号为图151.2■86 40 0 0 d^r/prana图14死区和饱和信号图15非线性干扰下对比由上图可知，在系统控制输入加入非线性干扰后， 模糊控制能够较好地 抑制系统非线性因素，而PI 控制此时已震荡发散，控制性能严重下降。
六、模糊PID 控制器利用模糊控制器控制单连杆机器人角度跟踪时，由于控制器不存在积分 项，稳态响应容易出现静差，因此，可在模糊控制的基础上并联一个积分控 制器，消除稳态静差。
而当误差较大时，积分器容易出现饱和现象，以致引 起超调。
为优化积分项，可以将模糊控制与积分器结合，通过误差大小控制 积分参数的大小，避免积分溢出，优化系统性能。
模糊积分器的具体规则为：当误差绝对值较大时，为防止超调， Ki 取较小值；当误差绝对值中等或较小时，为保证稳态性能，可适当加大Ki 值。
由以上分析可知，在上述模糊控制器的基础上，再并联一个模糊积分器，即以固定积分参数值Ki 为基准，加入模糊Ki 值的变化量 Ki ，作为新的积 分参数。
其中，Ki 的模糊控制规则表如下所示：1.4d^r/prana2 18 155t/s10表2 Ki规则表加入模糊积分器后的系统控制框图如图16所示，即使用模糊规则对Ki 参数在线调节：图16模糊积分器及系统控制框图输入一个阶跃参考信号，得到角度跟踪响应，和单模糊控制以及模糊并联积分器两种控制方法相比较，得图17和图18：1.40 0510t/s图17角度跟踪动态响应比较in put fuzzy pid fuzzy-pid10.9980.996 0.9940.992 0.99 0.98814.78 14.8 14.82 14.84 14.86 14.88 14.9 14.92 14.94 14.96 14.98t/s图18角度跟踪稳态响应比较由图18的稳态响应图可以看出，PID 控制和模糊控制器都存在较明显 的稳态静差，并联了一个积分器后，出现超调情况，但长时间响应后最终能 消除静差。
而对并联的积分器做出改善，即加入模糊积分器后，角度跟踪既 没有出现超调，也很快地消除了稳态静差。
因此并联模糊积分器之后能够很 好的改善系统性能。
151.008 1.006 1.0041.002dpr^elona0.2>1in put fuzzy pid fuzzy-pid8 6 a a d^r/prana4 a七、总结经典PID控制原理和现代控制原理的共同特点是：控制器设计必须建立在被控对象的精确建模上。
没有精确的数学模型，控制器的控制效果及精度将受到很大的制约。
但在现实生活中，大多数系统具有非线性、时变、大延迟等特点，很难建立精确的数学模型。
因此经典控制原理和现代控制原理都很难实现对这种系统的精确控制。
而模糊控制作为一种智能控制算法，与传统PID控制相比，表现出了它的优越性，如对模型的低依赖性、抗非线性能力、抗干扰能力等等。
为进一步优化模糊控制器性能，常常在模糊控制的基础上，加入传统的PID控制器做微调，这样便可消除模糊控制器存在的稳态静差的缺点。
随着计算机技术和电子科技的不断发展，相信模糊控制将会得到越来越广泛的应用。