平行四边形全章知识点总结汇编
平行四边形全章知识点

平行四边形全章知识点1.定义:平行四边形是一种四边形,其中两组对边是平行的。
2.性质:-对边平行性质:平行四边形的对边是平行的,根据这一性质,平行四边形也可以被定义为具有两组平行对边的四边形。
-对角线性质:平行四边形的对角线相互平分且相互等长。
-同底角性质:平行四边形的同底角相等。
-同顶角性质:平行四边形的同顶角相等。
-对边长度:平行四边形的对边长度相等。
-对角线长度:平行四边形的对角线长度相等。
-对边角:平行四边形的对边角相等。
-对角:平行四边形的对角互补,即两对角和为180度。
3.公式:-周长公式:平行四边形的周长可以通过将所有边的长度相加来计算:周长=边1长+边2长+边3长+边4长。
-面积公式:平行四边形的面积可以通过底边长度与高的乘积来计算:面积=底边长×高。
-对角线长度公式:平行四边形的对角线长度可以通过底边长度和高的关系来计算:对角线长度=√(底边长²+高²)。
4.判定方法:-边长判定:如果平行四边形的对边长度相等,则它们是平行四边形。
-角判定:如果平行四边形的相邻角或对顶角相等,则它们是平行四边形。
-对角线判定:如果平行四边形的对角线互相平分且相等,则它们是平行四边形。
5.具体类型:-矩形:具有相等对边和对角线的平行四边形。
-正方形:具有相等对边、对角线和四个直角的平行四边形。
-长方形:具有相等对边和对角线的平行四边形,但没有直角。
-菱形:具有相等对边和对角线的平行四边形,但没有直角。
-平行四边形:除了上述特殊情况外,其他包含两组平行对边的四边形都可以称为平行四边形。
平行四边形的应用广泛,包括几何学、物理学和工程学等领域。
在几何学中,平行四边形可以用于解决各种几何问题,如计算面积、周长和对角线长度等。
在物理学中,平行四边形的概念可以用于描述力的平衡条件。
在工程学中,平行四边形也被广泛用于设计和建构建筑物和桥梁等结构。
总之,平行四边形是具有两组对边平行的四边形。
(完整版)平行四边形基本知识点总结

(完整版)平行四边形基本知识点总结平行四边形基本知识点总结
平行四边形是一种特殊的四边形,它具有一些独特的性质和特点。
以下是平行四边形的基本知识点总结:
定义
平行四边形是指具有两组对边分别平行的四边形。
性质
1. 对边平行性质:平行四边形的两组对边分别平行。
2. 对角线性质:平行四边形的对角线互相平分,并且长度相等。
3. 内角和性质:平行四边形的内角的和为180度。
4. 外角性质:平行四边形的外角的和为360度。
5. 对边长度性质:平行四边形的对边长度相等。
6. 同底角性质:与平行四边形的一条边相邻,另一条边平行的两个内角相等。
7. 同旁内角性质:与平行四边形的两条边相邻,另一条边平行的两个内角互补。
判定方法
1. 对边平行判定:如果一个四边形中有两组对边分别平行,则它是一个平行四边形。
2. 对角线平分判定:如果一个四边形的对角线互相平分,并且长度相等,则它是一个平行四边形。
特殊类型
1. 矩形:具有四个内角都为90度的平行四边形。
2. 正方形:具有四个内角都为90度,且四条边长度相等的平
行四边形。
相关公式
1. 平行四边形的面积公式:面积 = 底边长度 ×高度。
2. 平行四边形的周长公式:周长= 2 ×(底边长度+ 侧边长度)。
以上是关于平行四边形的基本知识点总结。
通过了解这些性质
和定理,可以更好地理解和解决相关的数学问题。
平行四边形全章知识点总结

平行四边形全章知识点总结平行四边形是初中数学中常见的一个概念,它具有多项重要的性质和特点。
本文将对平行四边形的定义、性质以及相关定理进行全面总结。
一、定义平行四边形是指具有两对对边相互平行的四边形。
其中,对边是指相对的两条边,平行是指两条直线在平面上不相交,且永远保持相同的距离。
二、性质1. 对角线性质:平行四边形的对角线互相平分,并且彼此相等。
2. 内角和性质:平行四边形的内角和为180度。
3. 对边性质:平行四边形的对边相等。
三、定理1. 平行四边形的基本性质定理:如果一个四边形的对边互相平行,那么它就是一个平行四边形。
2. 平行四边形的性质定理:一个四边形是平行四边形的充要条件是它的对边相等。
3. 平行四边形的对角线性质定理:如果一个四边形的对角线互相垂直,那么它就是一个平行四边形。
4. 平行四边形的角平分线性质定理:如果一个四边形的对角线互相平分,则它是一个平行四边形。
四、拓展1. 矩形:矩形是一种特殊的平行四边形,它的四个内角都是直角。
2. 正方形:正方形是一种特殊的矩形,它的四条边相等且都垂直。
3. 菱形:菱形是一种特殊的平行四边形,它的四个边都相等,对边互相垂直。
4. 平行四边形的面积计算公式:平行四边形的面积等于底边乘以高。
五、解题技巧1. 判断平行四边形的方法:观察图形中是否存在两对平行的边。
2. 判断平行四边形的性质:使用已知条件推导,例如通过对边相等或对角线垂直等特点判断。
3. 计算平行四边形的面积:根据所给的边长和高的信息,使用面积计算公式进行计算。
总结:平行四边形是一个重要的数学概念,掌握了平行四边形的定义、性质以及相关定理,能够更好地理解和解决与平行四边形相关的问题。
同时,通过解题技巧的运用,能够更加灵活地应用这些知识点。
在学习过程中,多进行练习和思考,不断提高对平行四边形的理解和运用能力。
九年级数学下册 平行四边形知识点总结

九年级数学下册平行四边形知识点总结
平行四边形是指具有两对平行边的四边形。
本篇文档将总结九年级数学下册中与平行四边形相关的重要知识点。
1. 定义:
平行四边形是指具有两对平行边的四边形。
2. 性质:
- 对角线互相平分:平行四边形的两条对角线互相平分。
- 边角关系:平行四边形的对边相等,对角线互相分割的两对内角互补。
- 对边相等:平行四边形的对边相等。
- 内角和定理:平行四边形的内角和为180度。
- 性质推论:平行四边形的内角为独立角。
3. 平行四边形的判定方法:
- 对边平行法:根据平行四边形的定义,可以通过判断四边形的对边是否平行来判定平行四边形。
- 对角线互相平分法:可以通过判断四边形的对角线是否互相平分来判定平行四边形。
4. 平行线与平行四边形的关系:
- 平行四边形的定义可以扩展到平行线的关系。
当两条直线上的对应角相等时,这两条直线是平行的,从而可以得出平行四边形的对边是平行的。
5. 平行四边形的性质应用:
- 平行四边形可以应用于解题,如通过已知条件证明图形为平行四边形,或利用平行四边形的性质推导其他结论。
以上是九年级数学下册中关于平行四边形的知识点总结。
平行四边形的定义、性质、判定方法以及与平行线的关系都是研究和解题的重要基础。
在研究过程中,深入理解这些知识点,灵活运用,有助于提高数学能力。
注:本文档内容为个人独立创作,如需引用,请确认内容的准确性。
平行四边形知识点总结及分类练习题

平行四边形知识点总结及分类练习题一、知识点总结平行四边形是几何学中一个重要的概念,其性质和判定方法对于理解几何学中的其他问题有着至关重要的作用。
以下是对平行四边形知识点的总结:1、定义:平行四边形是一个四边形,其中相对的两边平行且相等。
可以用符号“▭”表示。
2、性质:1)对边平行:平行四边形的对边平行且相等。
2)对角相等:平行四边形的对角相等,邻角互补。
3)平行四边形的面积等于其底乘高。
3.判定方法:1)两组对边分别平行的四边形是平行四边形。
2)两组对边分别相等的四边形是平行四边形。
3)一组对边平行且相等的四边形是平行四边形。
4)对角线互相平分的四边形是平行四边形。
5)邻角互补的四边形是平行四边形。
4.特殊平行四边形:矩形、菱形和正方形都是特殊的平行四边形,它们分别具有以下性质:1)矩形:对角线相等,四个角都是直角。
2)菱形:对角线垂直且平分,四边相等。
3)正方形:对角线垂直且相等,四个角都是直角。
二、分类练习题1、选择题:1)下列哪个条件可以判定一个四边形为平行四边形?A.一组对边相等,一组对角相等B.一组对边平行,另一组对边相等C.一组对角相等,另一组对边平行D.一组对角相等,一组邻角互补答案:(C)一组对角相等,另一组对边平行。
因为一组对角相等,另一组对边平行的四边形可以由一组对边平行,另一组对边相等的四边形经过平移得到,因此选项C正确。
其他选项都不满足平行四边形的定义或判定方法。
2)下列哪个条件可以判定一个四边形为矩形?A.三个内角都是直角B.对角线相等且互相平分C.对角线互相垂直且平分D.一组对边平行且相等,一组邻角互补答案:(B)对角线相等且互相平分的四边形是矩形。
因为矩形的定义是对角线相等的平行四边形,而对角线相等且互相平分的四边形是平行四边形,因此选项B正确。
其他选项分别是矩形的定义或判定方法的一部分,但不足以单独判定一个四边形为矩形。
特殊平行四边形知识点总结及题型一、平行四边形的性质:1、平行四边形的对边平行且相等;2、平行四边形的对角相等;3、平行四边形的对角线互相平分。
平行四边形全章知识点总结

平行四边形全章知识点总结平行四边形是初中数学中非常重要的一个几何图形,它具有许多独特的性质和判定方法。
接下来,让我们一起系统地梳理一下平行四边形全章的知识点。
一、平行四边形的定义两组对边分别平行的四边形叫做平行四边形。
这是平行四边形最基本的定义,也是判定一个四边形是否为平行四边形的首要条件。
二、平行四边形的性质1、平行四边形的对边平行且相等这是平行四边形最显著的性质之一。
也就是说,如果一个四边形是平行四边形,那么它的两组对边不仅相互平行,而且长度相等。
2、平行四边形的对角相等平行四边形的两组对角分别相等。
例如,∠A =∠C,∠B =∠D。
3、平行四边形的对角线互相平分平行四边形的两条对角线相交于一点,并且这一点将两条对角线平分。
4、平行四边形是中心对称图形对称中心是两条对角线的交点。
将平行四边形绕着对角线的交点旋转 180 度后,能与原图重合。
三、平行四边形的判定1、两组对边分别平行的四边形是平行四边形这是根据定义进行判定的方法。
2、两组对边分别相等的四边形是平行四边形如果一个四边形的两组对边长度分别相等,那么它就是平行四边形。
3、一组对边平行且相等的四边形是平行四边形这是一种常见的判定方法,只要一组对边既平行又相等,就能判定该四边形为平行四边形。
4、两组对角分别相等的四边形是平行四边形当一个四边形的两组对角分别相等时,它就是平行四边形。
5、对角线互相平分的四边形是平行四边形如果一个四边形的两条对角线相互平分,那么它一定是平行四边形。
四、平行四边形的面积平行四边形的面积=底 ×高需要注意的是,底和高必须是对应的,也就是说底乘以其对应的高才能得到平行四边形的面积。
五、平行四边形的周长平行四边形的周长= 2×(相邻两边之和)六、平行四边形的拓展1、若一条直线过平行四边形对角线的交点,则这条直线平分平行四边形的面积。
2、平行四边形的相邻两边之和等于平行四边形周长的一半。
七、平行四边形在实际生活中的应用平行四边形在建筑设计、机械制造、图案设计等领域都有广泛的应用。
平行四边形单元知识点

平行四边形单元知识点一、平行四边形的定义1. 两组对边分别平行的四边形叫做平行四边形。
- 用符号“▱”表示平行四边形,例如平行四边形ABCD记作“▱ABCD”。
二、平行四边形的性质(一)边的性质1. 平行四边形的对边平行且相等。
- 若▱ABCD,则AB∥CD,AD∥BC,AB = CD,AD = BC。
(二)角的性质1.平行四边形的对角相等。
- 在▱ABCD中,∠A=∠C,∠B = ∠D。
2.平行四边形的邻角互补。
- 即∠A + ∠B=180°,∠B+∠C = 180°,∠C+∠D = 180°,∠D+∠A = 180°。
(三)对角线的性质1. 平行四边形的对角线互相平分。
- 若▱ABCD,对角线AC与BD相交于点O,则AO = CO,BO = DO。
三、平行四边形的判定(一)边的判定1.两组对边分别平行的四边形是平行四边形。
- 因为AB∥CD,AD∥BC,所以四边形ABCD是平行四边形。
2.两组对边分别相等的四边形是平行四边形。
- 若AB = CD,AD = BC,则四边形ABCD是平行四边形。
3.一组对边平行且相等的四边形是平行四边形。
- 若AB∥CD且AB = CD或者AD∥BC且AD = BC,则四边形ABCD是平行四边形。
(二)角的判定1. 两组对角分别相等的四边形是平行四边形。
- 若∠A = ∠C,∠B = ∠D,则四边形ABCD是平行四边形。
(三)对角线的判定1. 对角线互相平分的四边形是平行四边形。
- 若AO = CO,BO = DO,则四边形ABCD是平行四边形。
四、特殊的平行四边形(一)矩形- 有一个角是直角的平行四边形叫做矩形。
2.性质- 矩形具有平行四边形的所有性质。
- 矩形的四个角都是直角。
- 在矩形ABCD中,∠A=∠B = ∠C = ∠D = 90°。
- 矩形的对角线相等。
- 若矩形ABCD,对角线AC和BD,则AC = BD。
平行四边形知识点总结
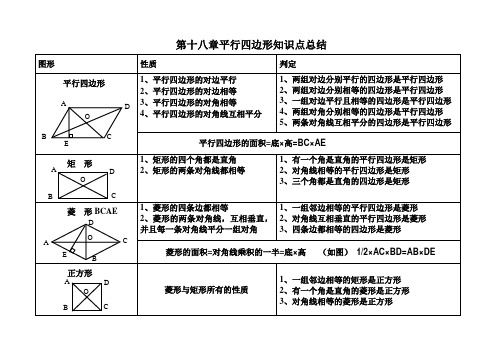
第十八章平行四边形知识点总结
图形
性质
判定
平行四边形
1、平行四边形的对边平行
2、平行四边形的对边相等
3、平行四边形的对角相等
4、平行四边形的对角线互相平分
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
4、两组对角分别相等的四边形是平行四边形
5、两条对角线互相平分的四边形是平行四边形
平行四边形的面积=底×高=BC×AE 矩 形
1、矩形的四个角都是直角
2、矩形的两条对角线都相等
1、有一个角是直角的平行四边形是矩形
2、对角线相等的平行四边形是矩形
3、三个角都是直角的四边形是矩形
菱 形BCAE
1、菱形的四条边都相等
2、菱形的两条对角线,互相垂直,并且每一条对角线平分一组对角 1、一组邻边相等的平行四边形是菱形 2、对角线互相垂直的平行四边形是菱形
3、四条边都相等的四边形是菱形
菱形的面积=对角线乘积的一半=底×高 (如图) 1/2×AC×BD=AB×DE
正方形
菱形与矩形所有的性质
1、一组邻边相等的矩形是正方形
2、有一个角是直角的菱形是正方形
3、对角线相等的菱形是正方形
A
A
A
A
B
B
B
B
C
C
C
C D
D
D D
O
O
O O E
E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形
【知识脉络】
【基础知识】
Ⅰ. 平行四边形
(1)平行四边形性质
1)平行四边形的定义:有两组对边分别平行的四边形叫做平行四边形.
2)平行四边形的性质(包括边、角、对角线三方面) : A
B D
O C
边:①平行四边形的两组对边分别平行; ②平行四边形的两组对边分别相等;
角:③平行四边形的两组对角分别相等;
对角线:④平行四边形的对角线互相平分.
【补充】平行四边形的邻角互补;平行四边形是中心对称图形,对称中心是对角线的交点.
(2)平行四边形判定
1)平行四边形的判定(包括边、角、对角线三方面):
A B D
O C
边:①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③一组对边平行且相等的四边形是平行四边形;
角:④两组对角分别相等的四边形是平行四边形;
对角线:⑤对角线互相平分的四边形是平行四边形. 2)三角形中位线:连接三角形两边中点的线段叫做三角形的中位线.
3)三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
4)平行线间的距离:
两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线间的距离。
两条平行线间的距离处处相等。
Ⅱ. 矩形
(1)矩形的性质
1)矩形的定义:有一个角是直角的平行四边形叫做矩形.
2)矩形的性质:
①矩形具有平行四边形的所有性质;
②矩形的四个角都是直角;
③矩形的对角线相等;
④矩形既是轴对称图形,又是中心对称图形,有两条对称轴,对称中心是对角线的交点.
(2)矩形的判定
1)矩形的判定:
①有一个角是直角的平行四边形是矩形;
②对角线相等的平行四边形是矩形;
③有三个角是直角的四边形是矩形.
2)证明一个四边形是矩形的步骤:
方法一:先证明该四边形是平行四边形,再证一角为直角或对角线相等;
方法二:若一个四边形中的直角较多,则可证三个角为直角. 3)直角三角形斜边中线定理:(如右图) 直角三角形斜边上的中线等于斜边的一半. Ⅲ. 菱形
(1)菱形的性质
1)菱形的定义:有一组邻边相等的平行四边形叫做菱形.
2)菱形的性质:
①菱形具有平行四边形的所有性质;
②菱形的四条边都相等;
③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
④菱形既是轴对称图形,又是中心对称图形,有两条对称轴,对称中心是对角线交点.
3)菱形的面积公式:
菱形的两条对角线的长分别为b a ,,则ab S 2
1
菱形 (2)菱形的判定
1)菱形的判定:
①有一组邻边相等的平行四边形是菱形;
②对角线互相垂直的平行四边形是菱形;
③四条边都相等的四边形是菱形.
2)证明一个四边形是菱形的步骤:
方法一:先证明它是一个平行四边形,然后证明“一组邻边相等”或“对角线互相垂直”; 方法二:直接证明“四条边相等”.
Ⅳ. 正方形
(1)正方形的性质
1)正方形的定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形.
2)正方形的性质:
正方形具有平行四边形、矩形、菱形的所有性质,即①正方形的四条边都相等;②四个角
都是直角;③对角线互相垂直平分且相等,并且每条对角线平分一组对角.
3)正方形既是轴对称图形,又是中心对称图形,它有四条对称轴,对角线的交点是对称中心.
(2)正方形的判定
1)正方形的判定:
①有一组邻边相等且有一个角是直角的平行四边形是正方形;
②有一组邻边相等的矩形是正方形;
③对角线互相垂直的矩形是正方形;
④有一个角是直角的菱形是正方形;
⑤对角线相等的菱形是正方形;
⑥对角线互相垂直平分且相等的四边形是正方形.
中点四边形
1、顺次连接四边形各边中点所围成四边形是平行四边形
2、顺次连接菱形各边中点所围成四边形是矩形
3、顺次连接矩形各边中点所围成四边形是菱形
4、顺次连接等腰梯形各边中点所围成四边形是菱形
5、顺次连接正方形各边中点所围成四边形是正方形
例:如果顺次连接一个四边形各边中点所得新的四边形是菱形,那么对这个四边形的形状描述最准确的是()
A.矩形
B.等腰梯形
C.菱形
D.对角线相等的四边形
解:矩形,等腰梯形均能得到菱形但不够全面,菱形无法得到菱形,即只要对角线相等不管是什么形状均可,故选D.。
