四川大学计算机学院石兵代数系统
计算机代数系统的数学原理

计算机代数系统的数学原理
算机代数系统
算机代数系统(Computer Algebra Systems,CAS)是一类用于自动计算数学
表达式的计算机软件。
它们利用特定的数学法则,可以从一组原始的表达式,推导出各种数学表达式,有效地解决计算问题,从而替代人们手动计算代数式的工作,简化手算求解复杂问题的过程,极大地提高工作效率,既节省了大量的时间,又精确地计算出结果。
算机代数系统的数学原理涉及几个领域:微积分、几何、矩阵论和概率论等。
首先,它们需要熟悉数学语言,以便理解来自用户的数学表达式;其次,还要了解微积分的知识,能够将这些表达式翻译成可供计算机理解的算法;最后,它们还需要熟悉单变量和多变量微积分,用来计算函数在给定点上的梯度、偏导数,以及多元函数的极值和拐点。
算机代数系统在当今的科学研究和生活中有着广泛的应用,例如在机器学习中
的数学建模中,运用算机代数系统可以更为快速地定义模型并计算模型极值;在模拟物理过程中,可以使用算机代数系统进行微积分的自动计算,以此来求解常微分方程等等。
总之,算机代数系统是一种内在结合了数学原理和计算机技术的分析计算工具,极大地提高了数学分析计算的效率和准确度,为数学研究和应用提供了无比强大的支持。
代数系统简介

代数系统简介一、代数系统的基本概念代数系统,也称为代数结构或代数系统,是数学中一个重要的概念,它由集合和定义在这个集合上的运算组成。
代数系统是代数学的基本研究对象,也是泛代数、抽象代数、代数学等领域中重要的研究对象。
代数系统通常由两个部分组成:一个是非空元素集合,称为代数系统的论域或标量域;另一个是定义在论域上的运算,这些运算需满足一定的性质或公理。
根据所涉及的运算不同,代数系统可分为不同类型,如群、环、域、格等。
代数系统的概念来源于对数学中不同分支中抽象概念的概括和总结,其研究范围包括数学中不同领域的许多分支。
例如,集合论、抽象代数、泛代数、拓扑学等都是研究代数系统的重要领域。
二、代数系统的分类根据所涉及的运算和性质的不同,代数系统有多种分类方式。
以下是其中几种常见的分类方式:1.根据所涉及的运算的性质,可以将代数系统分为有交换律和结合律的代数系统(如群、环、域)和没有交换律和结合律的代数系统(如格、布尔代数)。
2.根据运算是否涉及单位元和逆元,可以将代数系统分为有单位元的代数系统和无单位元的代数系统。
前者如群、环、域等,后者如格等。
3.根据所涉及的元素是否具有可交换性,可以将代数系统分为可交换的代数系统和不可交换的代数系统。
前者如交换群等,后者如李群等。
4.根据所涉及的元素是否具有无限性,可以将代数系统分为有限代数系统和无限代数系统。
前者如有限群等,后者如无限群等。
此外,还可以根据其他性质和特征对代数系统进行分类。
通过不同的分类方式,我们可以更好地了解和研究不同类型代数系统的特性和性质。
三、代数系统的性质代数系统的性质是指代数系统中元素之间通过运算所表现出来的关系和性质。
以下是几个常见的代数系统的性质:1.封闭性:如果对于代数系统中的任意两个元素x和y,它们的运算结果仍属于该集合,则称该运算满足封闭性。
封闭性是代数系统中一个重要的性质,它保证了运算结果的元素仍属于该系统。
2.结合律:如果对于代数系统中的任意三个元素x、y和z,有(x·y)·z=x·(y·z),则称该运算满足结合律。
高等代数(上册)——大学高等代数课程创新教材

序高等代数是大学数学科学学院(或数学系,应用数学系)最主要的基础课程之一。
本套教材是作者在北京大学进行高等代数课程建设和教学改革的成果,它具有下述鲜明特色。
1.明确主线:以研究线性空间和多项式环的结构及其态射(线性映射,多项式环的通用性质)为主线。
自从1832年伽罗瓦(Galois)利用一元高次方程的根的置换群给出了方程有求根公式的充分必要条件之后,代数学的研究对象发生了根本性的转变。
研究各种代数系统的结构及其态射(即保持运算的映射)成为现代代数学研究的中心问题。
20世纪,代数学研究结构及其态射的观点已经渗透到现代数学的各个分支中。
因此,在高等代数课程的教学中贯穿研究线性空间和多项式环的结构及其态射这条主线,就是把握住了代数学的精髓。
本套教材上册的第1,2,3章研究线性方程组的解法、解的情况的判别和解集的结构时,贯穿了研究数域犓上狀维向量空间犓狀及其子空间的结构这条主线。
线性方程组是数学中最基础、最有用的知识,狀维向量空间犓狀是狀维线性空间的一个具体模型,狀元齐次线性方程组的解空间的维数公式本质上是线性映射的核与值域的维数公式。
因此把线性方程组和狀维向量空间犓狀作为高等代数课程的开始部分的内容,既符合学生的认知规律,又是高等代数知识的内在规律的体现。
上册的第4,5,6章研究矩阵的运算,矩阵的相抵、相似、合同关系及与它们有关的矩阵的特征值和特征向量、二次型。
研究矩阵的运算为研究线性映射打下了基础。
矩阵的相抵关系在解决有关矩阵的秩的问题中起着重要作用,而矩阵的秩本质上是相应的线性映射的值域的维数。
研究矩阵的相似标准形本质上是研究线性变换在一个合适的基下的矩阵具有最简单的形式。
研究对称矩阵的合同标准形与研究二次型的化简密切相关,而二次型与线性空间犞上的双线性函数有密切联系。
本套教材下册的第7章研究一元和狀元多项式环的结构及其态射(多项式环的通用性质),第8章研究线性空间的结构,第9章研究线性映射,第10章研究具有度量的线性空间的结构及与度量有关的线性变换。
基于四元数的图像信息并行融合

基于四元数的图像信息并行融合
郎方年;周激流;钟钒;宋恩彬;闫斌
【期刊名称】《自动化学报》
【年(卷),期】2007(33)11
【摘要】针对传统串行特征融合方法中矢量空间维数的限制以及并行复矢量特征融合方法中能够融合的特征类别数量有限的弱点,提出一种建立在四元数空间中的新型特征并行融合方法.本文从理论上详细证明了该方法的合理性及其实际应用中的可行性,并将实数中的Fisher鉴别分析法推广到四元数空间,同时证明了推广Fisher鉴别分析法用于图像模式分类的可行性,并给出使用的具体方法和步骤.最后将本文提出的推广方法用于人脸检测,取得了良好效果.
【总页数】8页(P1136-1143)
【作者】郎方年;周激流;钟钒;宋恩彬;闫斌
【作者单位】四川大学电子信息学院,成都,610064;四川大学计算机学院,成
都,610064;四川大学电子信息学院,成都,610064;四川大学应用数学学院,成
都,610064;电子科技大学自动化工程学院,成都,610054
【正文语种】中文
【中图分类】TP391.41
【相关文献】
1.基于SVM信息融合的图像识别与并行实现 [J], 刘松
2.基于四元数多特征并行融合的JPEG隐写检测 [J], 何凤英;钟尚平;杨健
3.基于四元数小波变换和自适应神经网络的图像融合处理 [J], 马淑兰; 常莉红; 马保科
4.基于四元数离散Fourier变换的医学图像融合算法 [J], 杨建翠
5.基于四元数并行融合的手指纹理区域识别 [J], 刘镝;孙冬梅;李志超;顾广华;裘正定
因版权原因,仅展示原文概要,查看原文内容请购买。
四川大学2018年计算机学院硕士推免生专业目录_川大考研网
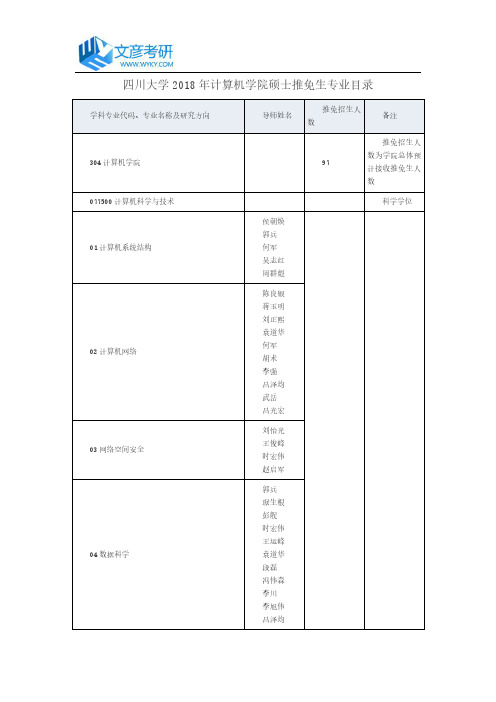
四川大学2018年计算机学院硕士推免生专业目录学科专业代码、专业名称及研究方向导师姓名推免招生人数备注304计算机学院97推免招生人数为学院总体预计接收推免生人数077500计算机科学与技术科学学位01计算机系统结构侯朝焕郭兵何军吴志红周群彪02计算机网络陈良银蒋玉明刘正熙袁道华何军胡术李强吕泽均武岳吕光宏03网络空间安全刘怡光王俊峰时宏伟赵启军04数据科学郭兵琚生根彭舰时宏伟王运峰袁道华段磊冯伟森李川李旭伟吕泽均杨秋辉于中华杨宁张磊05计算机科学理论洪玫杜中军06计算机图形图像与虚拟现实侯朝焕游志胜冯子亮蒲亦非王明辉杨红雨张建伟李辉刘健波刘正熙张严辞朱敏兰时勇李晓峰李毅刘艳丽吴志红张轶张意刘东权07计算机视觉刘怡光魏骁勇张建伟张建州周激流费向东何坤李征刘艳丽宋万忠赵启军周欣陈虎08机器智能与类脑计算游志胜章毅张蕾唐华锦吕建成彭德中魏骁勇蒲亦非杨红雨周激流燕锐何坤李川赵启军09人机交互与普适计算陈良银林涛李强083500软件工程科学学位01实时软件工程侯朝焕游志胜陈良银冯子亮杨红雨洪玫刘正熙王运峰冯伟森胡术吕泽均周群彪02软件智能章毅张蕾唐华锦吕建成彭德中林涛彭舰燕锐段磊杨宁03面向设计与制造的软件工程侯朝焕郭兵蒋玉明杜中军04网络空间安全刘怡光王俊峰吕泽均赵启军吕光宏05网络媒体工程魏骁勇彭舰于中华06软件质量保证和测试洪玫杨秋辉李旭伟07计算机视觉与图像处理游志胜刘怡光王俊峰魏骁勇王明辉杨红雨张建伟周激流琚生根李辉刘健波刘正熙张严辞朱敏何坤兰时勇李晓峰李晓华李毅李征刘艳丽宋万忠张轶赵启军085211计算机技术专业学位01可视分析/虚拟现实朱敏刘艳丽张严辞02计算语言学/数据库与知识工程于中华杜中军蒋玉明03分布式处理与网络计算周群彪冯伟森胡术吕光宏04计算机视觉与图像处理刘怡光张建州李征李晓华05图象处理与合成游志胜冯子亮李辉刘正熙刘健波李毅张建伟宋万忠李晓峰费向东杨红雨吕泽均时宏伟张轶周欣06信息融合与图象处理王明辉王运锋吴志红07智能信息处理周激流琚生根蒲亦非08嵌入式系统与个人大数据郭兵李强彭舰陈良银张磊09软件自动化测试洪玫杨秋辉李旭伟10机器智能章毅吕建成张蕾彭德中11人机交互与数字娱乐技术林涛何坤张意12数据挖掘与生物信息学朱敏李川段磊085212软件工程专业学位01软件工程技术洪玫陈良银02云计算技术和应用李强彭舰何军03计算机视觉与图像处理刘东权周激流刘怡光朱敏魏骁勇04数字医学章毅王俊峰张蕾文章来源:文彦考研。
袁学东-四川大学数字逻辑第2章Number Systems Operations

(LSB)
(MSB)
2 Number System Conversion
Decimal to Binary Conversion
•Fractional Radix Conversion, Successive Multiplication
•(小数基转换,逐次乘法) [乘积中的整数部分成为新基下的数,
Convert the integer portion by successive division
1.Divide 23 by 8 (LSB) 2.Divide 2 by 8 (MSB)
Convert te fraction portion by successive multiplication
(数字系统以离散方式表示信息,数制系统提供了由数字系统 处理量化信息的一种方法)
– Positional Number Systems – Number system conversion – Binary Codes – Arithmetic
Number Systems - Decimal
“base” 10 (radix is 10) 10 digits: 0...9
Let r=radix or base of a number system; 数制的基或基数 Let c=character from the character set of the radix; 该基的字符集合中的 字符 Let N=number to be represented in radix;
四川大学-计算机学院--石兵-第十六讲-代数系统2

2、如果a b,c d,则 a c b d, a c b d。
证明要点 由 (a c) ( b d) = (a b) (c d) = b d , 即得 a c b d;由 (a c) ( b d) = (a b) (c d) = a c , 即得 a c b d。
证明要点:对于①,只要证明a*(–b)和(–a)*b 都是a*b的“+”运算逆就行了。例如 a*b+ a*(–b)=a*(b–b)= a* = 。 对于②, a*(b–c) = a*b+a*(–c) = a*b – a*c.
4、环中零因子 定义:如果环 R,+,* 中非零元a、b满足 a*b= ,则称 a和 b是R中的零因子。 例:在模6剩余类环 I6 ,, 中,[0]是 零元,因为[2][3]=[0]、[4][3]=[0],因此 [2]、[3]、[4]都是环中的零因子。
a
b
c
d
e
f
g
图1
图2
图3
• 偏序格的例子 ① 设A是已知集合,则偏序集 2A, 是格,
称为幂集格。因为 X、Y 2A, lub(X, Y) = X Y, glb(X, Y) = X Y。 ② 在正整数集合I+上定义偏序 “| ” ,则偏序集 I+ ,| 是格。因为 a、b I+ , lub(a, b) = lcm(a,b), glb(a, b) = gcd(a, b) 。
c)传递性: a b 且 b c (=>a c)
a c =a (b c) (b c ) =(a b) c (结合律)
=b c
(a b )=c( Nhomakorabea c )
2.证明对任意 x,y L=>lub(x,y),glb(x,y) L
元搜索引擎的设计与实现

元搜索引擎的设计与实现
王铮;胡永杰
【期刊名称】《河北师范大学学报:自然科学版》
【年(卷),期】2001(25)2
【摘要】元搜索引擎是一种依赖多个外部搜索引擎的信息查询工具 .主要介绍了元搜索引擎的体系结构和使用 Java Servlet技术实现的技术要点 ,最后结合运行结果讨论了引擎的性能 .
【总页数】4页(P175-178)
【关键词】信息搜索系统;元搜索引擎;Java;Servlet技术;体系结构;信息查询;信息检索
【作者】王铮;胡永杰
【作者单位】四川大学计算机学院信息管理中心;河北师范大学网络中心
【正文语种】中文
【中图分类】G354.4
【相关文献】
1.基于社区的问答元搜索引擎设计与实现 [J], 黄玉;陈军
2.元搜索引擎并行式数据查询代理模块的设计与实现 [J], 白金平
3.搜索引擎元信息提取系统的设计与实现 [J], 徐刚
4.带聚类处理的元搜索引擎的设计与实现 [J], 王琼;吕晓猛;蒋玉峰;陆刚
5.一种实用元搜索引擎的设计与实现 [J], 胡双双;秦杰;谢蕙
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有幺元[1], 并且在 I7 –{[0]}中关于运算, 剩 余类[1]和[6]的逆元都是自身,[2]与[4]互为逆 元,[3]与[5]互为逆元。 实际上,素数模 p剩余类环 Ip,,就是域。 也是最具代表性的有限域。 至于无限域,最熟知的包括有理数域Q,+, 和实数域 R,+, 。
为幂集格。因为集合运算“”和“ ”满足 这4条性质。 ② 正整数集合I+上定义最大公约数运算gcd和最 小公倍数运算lcm ,则 I+ ,lcm,gcd 是格。 因为gcd和lcm满足封闭性、结合性及交换性 是明显的。
至于吸收律,首先注意 a、b I+ , a b=gcd(a, b) lcm(a,b),
二、整环 定义:如果环 R,+, * 中运算“* ”可交 换、有幺元e、且无零因子,则称该环为整环。 • 按定义,意味着整环是含幺环、交换环、和 无零因子环。 例:整数环 I,+, 是整环。因为整数的乘 法运算“”满足可交换、有幺元1,并且两个 整数之积 i j=0时,必然 i=0或 j=0。
第七节 环和域
一、环的概念 1、定义: 设 R,+,* 是含两个二元运算
的代数系统,如果 ① R,+ 是加群(交换群); ② R,* 是半群; ③ 运算“*”对于“+”可分配,即
a、b 、cR,
a* ( b+ c) = (a* b) + (a* c), ( b+ c)* a = (b*a) + (c * a ), 则称 R,+,* 是环。 2、常见环的例子 ① 整数集合 I上 的代数系统 I,+, 是环, 称为整数环。 ② 有理数集合Q上 的代数系统 Q,+, 是 环,称为有理数环。
类似可证明,有理数环、实数环都是整环。 • 整数环是无限整环的代表。
例:素数模 p剩余类环 Ip,,是整环。 因为首先运算可换、有幺元[1]。其次, 无零因子。如果[a][b]=[0]、那么ab是p的 倍数,从而要么[a]=[0],要么[b]=[0]。 • 素数模 p剩余类环是有限整环的代表。
三、域 1、定义:如果 R,+,*是整环,并且
(a b) c = a (b c) , (a b) c = a (b c) ③ 交换性: a、bL , a b = b a ,a b = b a ④ 吸收性 : a、bL , a (a b) = a ,a ( a b) = a 则称 L,, 是格。
• 代数格的例子 ① 设A是已知集合,则 2A, , 是格,称
③ 实数集合R上 的代数系统 R,+, 是 环,称为实数环。
④ 整数集模 n剩余类代数系统 In ,, 是 环,称为 模n剩余类环。
3、环中运算 • 在环R,+,*中,加群R,并把a+(–b)简记为 a–b。因此在环中a–a= ,a–b=c a=b+ c。 (移项法则)
max(a, min(a, b))=a= min(a, max(a, b) )。 • 注意 由代数格的定义容易得到 L,, 还
满足幂等律,即 a L, a a=a, a a = a。 这可利用吸收律得到 :
a a = a (a (a b )) =a a a = a ( a (a b )) = a。 2、格的偏序定义:如果偏序集 L, 满足 a、bL,存在最小上界 lub(a, b)和最大 下界 glb(a, b),则称 L, 为偏序格。 • 偏序格的 Hasse 图特点: 例:根据下述偏序集的Hasse图判断是否格?
• 注意,整数环I,+, 是整环,但不是域。 2、定理:有限整环 R,+, * 必是域。
证明要点:设 R –{} ={a1,a2,...,an}, b是 R –{}中任一元素。(思考…..) a) b*R=R b)b*ai = e c) b , ai互相成为逆元
习题 十六 3 作业:16.2 1
证明要点:对于①,只要证明a*(–b)和(–a)*b 都是a*b的“+”运算逆就行了。例如 a*b+ a*(–b)=a*(b–b)= a* = 。 对于②, a*(b–c) = a*b+a*(–c) = a*b – a*c.
4、环中零因子 定义:如果环 R,+,* 中非零元a、b满足 a*b= ,则称 a和 b是R中的零因子。 例:在模6剩余类环 I6 ,, 中,[0]是 零元,因为[2][3]=[0]、[4][3]=[0],因此 [2]、[3]、[4]都是环中的零因子。
旧书:习题11.7 1 附加题: I,,是整数集上的代数系统, 其中两个运算定义为: a、bI,
a b=a+b –1, a b = a+b– ab, 证明 I,,是含幺元的、交换环。
第十二章 格
一、格的概念 1、格的代数定义:如果代数系统 L,, 满足 ① 封闭性 : a、bL, a b L ,a b L ② 结合性 : a、b、cL
• 在环 R,+,* 中,如果半群 R,* 存在 幺元,则记为 e;如果元素 a存在逆元,则 记为 a–1 。 定理 在环 R,+,* 中,运算“+”的幺元 是运算“*”的零元。 证明要点 a R,因为 + = , a* =a*(+)= a* + a* ,即a* = 。
定理 在环 R,+,*中,下述关系式成立: ① a*(–b) =(–a)*b= – a*b , ② a*(b–c) =a*b – a*c。
因此 lcm(a, gcd(a, b))=a gcd(a, b)/gcd(a,b)=a, gcd(a, lcm(a, b)) = a lcm(a, b)/lcm(a,b)=a。
③整数集合I上定义求两个数的最大值运算max 和最小值运算min,则 I,max,min 是格。
因为 max和 min满足封闭性、结合性及交换 性是明显的。 至于吸收律,不管a和 b谁大谁小 ,都能得出
