船舶流体力学 (夏国泽) 课后答案[习题5].khdaw
流体力学课后习题答案

5.17解:总扬程包括抬水高度及水头损失,
....
5-2有一平底空船,其船底面积Ω为8m2,船舷高h为0.5m,船自重G为9.8kN。现船底破一直径10cm的圆孔,水自圆孔漏入船中,试问经过多少时间后船将沉没。
题5-4图
解:在船沉没的过程中存在
得
∴船沉没过程中水自圆孔漏入的流量是不变的。
另外,当h2=0时,h1’=0.125,则
5-10工厂供水系统,由水泵向A、B、C三处供水,管道均为铸铁管,已知流量Qc=10L/s,qB=5L/s,qA= 10L/s,各管段长l1=350m,l2= 450m,l3=100m,各段直径d1=200mm,
d2=150mm,d3=100mm,整个场地水平,试求水泵出口压强。
闸门右侧水压力:
作用点:
总压力大小:
对B点取矩:
2-16.如图, ,上部油深h1=1.0m,下部水深h2=2.0m,油的重度 =8.0kN/m3,求:平板ab单位宽度上的流体静压力及其作用点。
[解]合力
作用点:
2-19.已知曲面AB为半圆柱面,宽度为1m,D=3m,试求AB柱面所受静水压力的水平分力Px和竖直分力Pz。
自由下落时:
第二章流体静力学
2-1.一密闭盛水容器如图所示,U形测压计液面高于容器内液面h=1.5m,求容器液面的相对压强。
[解]
2-3.密闭水箱,压力表测得压强为4900Pa。压力表中心比A点高0.5m,A点在液面下1.5m。求液面的绝对压强和相对压强。
[解]
2-13.如图所示盛水U形管,静止时,两支管水面距离管口均为h,当U形管绕OZ轴以等角速度ω旋转时,求保持液体不溢出管口的最大角速度ωmax。
流体力学课后答案

第一章 流体及其物理性质1-1 已知油的重度为7800N/m 3,求它的密度和比重。
又,0.2m 3此种油的质量和重量各为多少?已已知知::γ=7800N/m 3;V =0.2m 3。
解析:(1) 油的密度为 3kg/m 79581.97800===gγρ; 油的比重为 795.01000795OH 2===ρρS (2) 0.2m 3的油的质量和重量分别为 kg 1592.0795=⨯==V M ρN 15602.07800=⨯==V G γ 1-2 已知300L(升)水银的质量为4080kg ,求其密度、重度和比容。
已已知知::V =300L ,m =4080kg 。
解析:水银的密度为 33kg/m 13600103004080=⨯==-V m ρ 水银的重度为3N/m 13341681.913600=⨯==g ργ水银的比容为 kg /m 10353.7136001135-⨯===ρv1-3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ,温度由20℃升高到78℃,空气的气体常数为287.06J/k g ·K 。
问每kg 空气的体积将比原有体积减少多少?减少的百分比又为多少?已已知知::p 1=101325Pa ,p 2=607950Pa ,t 1=20℃,t 2=78℃,R =287.06J/k g ·K 。
解析:由理想气体状态方程(1-12)式,得 kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了0.664m 3;减少的百分比为80%。
1-4 图示为一水暖系统,为了防止水温升高时体积膨胀将水管胀裂,在系统顶部设一膨胀水箱,使水有膨胀的余地。
船舶静力学课后复习题答案

Statics of the Ship响砂山月牙泉第一章复习思考题1.船舶静力学研究哪些内容?2.在船舶静力学计算中,坐标系统是怎样选取的?3.作图说明船体的主尺度是怎样定义的?其尺度比的主要物理意义如何?4.作图说明船形系数是怎样定义的?其物理意义如何?试举一例说明其间的关系。
5.对船体近似计算方法有何要求?试说明船舶静力学计算中常用的近似计算法有哪几种?其基本原理、适用范围以及它们的优缺点。
复习思考题6.提高数值积分精确度的办法有哪些?并作图说明梯形法、辛浦生法对曲线端点曲率变化较大时如何处理?以求面积为例,写出其数值积分公式。
7.分别写出按梯形法,辛浦拉法计算水线面面积的积分公式,以及它们的数值积分公式和表格计算方法。
(5,8,-1) 法、(3,10,-1)法的适用范围。
8.写出计算水线面面积的漂心位置和水线面面积对x轴y轴的惯性矩的积分公式。
并应用求面积的原理写出其数值积分公式和表格计算方法。
复习思考题9.如何应用乞贝雪夫法?试以九个乞贝雪夫坐标,写出求船舶排水体积的具体步骤。
10.说明积分曲线、重积分曲线与原曲线的关系.并以水线面面积曲线为例说明积分曲线、重积分曲线的应用。
Exercise 1-1已知: L=155m,B=18m,d=7.1m,V=10900m3,Am=115m2,Aw=1980m2求:Cb=V/LBd=10900/(155*18*7.1)=0.550Cp=V/Lam=10900/(155*115)=0.62Cw=Aw/BL=19800/(18*155)=0.710Cm=Am/Bd=115/(18*7.1)=0.900Cvp=V/Awd=10900/(1980*7.1)=0.775某海洋客船L=155m,B=18m,d=7.1m,V=10900m3,Am=115m22。
试求Cb, Cp, Cw, Cm, Cvp。
Exercise 1-2两相等的正圆锥体在底部处相连接,每个锥体的高等于其底部直径.这个组合体浮于水面,使其两个顶点在水表面上,试绘图并计算:(1)中横剖面系数Cm,(2)纵向棱形系数Cp,(3)水线面系数Cw,(4)方形系数Cb。
船舶原理练习题4、5章(航海)有解答

《船舶原理》练习题4、5章(航海)【第4章】吃水差之求取 (1)【第4章】吃水差之调整 (5)【第4章】吃水差之图表 (7)【第4章】减少船舶纵向弯曲 (9)【第5章】船舶抗沉性能 (9)【第4章】吃水差之求取·1 船舶装载后经查算漂心在中前,则船舶。
A. 首倾B. 尾倾C. 正浮D. 浮态不能确定·2船舶装载后经计算重心在浮心之前,则船舶。
A. 首倾 B. 尾倾C. 正浮D. 浮态不能确定·3 为了减小尾倾,应将货物移动。
A. 自中后向船中B. 自中后向漂心C. 自中后向浮心D. 自中后向重心·4 某船原首倾,现首吃水减小尾吃水增加,则其首倾。
A. 减小B. 增加C. 不变D. 变化趋势不能确定·5 为了减小船舶首倾,应在之加装少量货物。
A. 漂心;后B. 浮心;前C. 漂心;前D. 船中,后·6 在船中后加装小量货物,则船舶。
A. 首倾增加B. 尾倾增加C. 平行沉浮D. 浮态的变化不能确定·7 少量加载引起的首吃水增量与以下因素的关系是。
A. 与MTC值有关而与TPC值无关B. 与MTC值无关而与TPC值有关C. 与MTC和TPC值均有关D. 与MTC和TPC值均无关·8 在船上装卸一定量的货物,。
A. 若尾吃水增大,首吃水一定减小B. 若首吃水增加,尾吃水一定减小C. 首尾吃水一定同时增加或减小D. 首尾吃水不一定同时增加或减小·9 吃水差产生的原因是。
A. 船舶装载后重心不与浮心共垂线B. 船舶装载后漂心不与重心共垂线C. 船舶装载后重心不与正浮时漂心共垂线D. 船舶装载后重心不与正浮时浮心共垂线·10 下述说明吃水差的改变量大于0。
A. 首吃水增加,尾吃水减小B. 首吃水减小,尾吃水增加C. 首尾吃水同时增加D. 首尾吃水同时减少·11在我国通常计算中,船舶的吃水差是指船舶。
船舶结构力学课后答案

6章 能量法6.1题1)方法一 虚位移法考虑b),c)所示单位载荷平衡系统, 分别给予a)示的虚变形 :()M x dx d EIδθ= 外力虚功为 i j 11W θδθ⨯⎧⎫=⎨⎬⨯⎩⎭虚应变能为l001V=M()M ()d EI x x x δ⎰()()()()00011=1li i i li i i R x M R x d xEI R x M R x dx EI⎧++⎪⎪⎨⎪+⎪⎩⎰⎰j i ij j i j i M M 1M M ..........b)EI 363EI 2=M M 1M M ...........c)EI 363EI 2l l l l ⎧⎛⎫⎛⎫-=-⎪ ⎪ ⎪⎝⎭⎪⎝⎭⎨⎛⎫⎛⎫⎪-=- ⎪ ⎪⎪⎝⎭⎝⎭⎩ 由虚功原理:W V δδ= 得:i i j j 11M 2M 13EI 12l θθ⎡⎤-⎢⎥⎧⎫⎧⎫=⎢⎥⎨⎬⎨⎬⎢⎥⎩⎭⎩⎭-⎢⎥⎣⎦2)方法二 虚力法(单位虚力法) 梁弯曲应力:{}()M x y σ=I{}()M x y σε==EEI()()ij iM M x M x M l+=-()1(10)x M x lδ=-+给i M 以虚变化1i M ∂= 虚应力为 {}()M x y δδσ=I虚余功:1W δθ*⨯i =虚余能:*V δΩ⎰=(真实应变)⨯(虚应力)d Ω()()M x M x y ydxdydz EI δ=⎰⎰⎰I()()2201lA M x M x dx y dA EI δ=⎰⎰()()01/1/li i j M M M x l x l dx EI ⎡⎤=-+-⎣⎦⎰ ∴ 132i ij l Q M M EI ⎛⎫=- ⎪⎝⎭同理:给j M 以虚变化1j M δ=,()0i M δ=可得(将i 换为j )32i j j M l M EI θ⎛⎫=-+ ⎪⎝⎭3)方法三 矩阵法(柔度法)设{}{}i i j j M ,p M θθ⎧⎫⎧⎫∆==⎨⎬⎨⎬⎩⎭⎩⎭,虚{}{}[]{},i j M p M δδσεδ⎧⎫==⎨⎬⎩⎭力p{}()()[]{}/1i i i j j M M x y y x x y M M M x l c p M I I I l l σσ⎧⎫⎡⎤⎡⎤===-+=--=⎨⎬⎢⎥⎣⎦⎣⎦⎩⎭式中[]1,y x x c I l l ⎡⎤⎛⎫⎛⎫=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦(不妨称为物理矩阵以便与刚度法中几何矩阵[]B 对应)虚应力{}[]{}[]i j M c p c M δδσδδ⎧⎫==⎨⎬⎩⎭实应变{}[]{}[][]{}11D D C p εσ--==虚余功 {}{}{}{}()*TTi i j j W p p M M δδδθδθδ=∆=∆=+虚余能 {}{}{}{}*T TV d d δεδσεσεΩΩ=Ω=Ω⎰⎰{}[][][]{}{}[][][]{}11T T T T p C D C P d p C D C d p δδ--ΩΩ⎡⎤=Ω=Ω⎢⎥⎣⎦⎰⎰ 于虚力原理:**W V δδ=考虑到虚力{}p δ的任意性。
流体力学课后答案.
第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3,求它的密度ρ。
解:由g γρ=得,3327000N/m 714.29kg/m9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3,运动黏度ν=0.893×10-6m 2/s ,求它的动力黏度μ。
解:ρμ=v 得,3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中,它们之间的距离为0.5mm ,可动板若以 0.25m/s 的速度移动,为了维持这个速度需要单位面积上的作用力为2N/m 2,求这两块平板间流体的动力黏度μ。
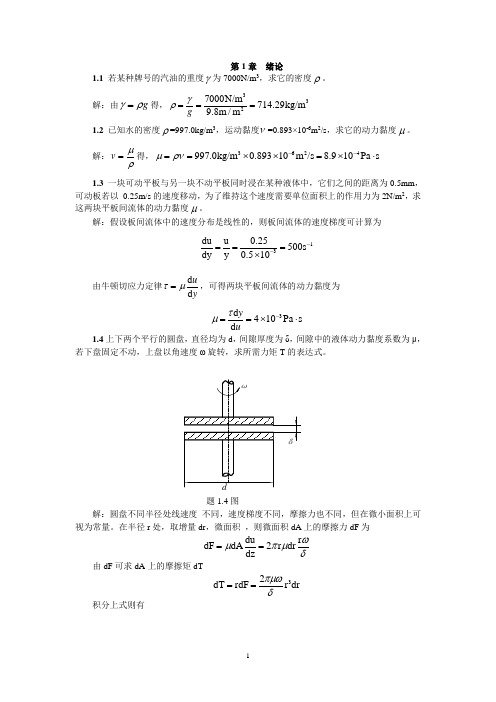
解:假设板间流体中的速度分布是线性的,则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=,可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘,直径均为d ,间隙厚度为δ,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以角速度ω旋转,求所需力矩T 的表达式。
题1.4图解:圆盘不同半径处线速度 不同,速度梯度不同,摩擦力也不同,但在微小面积上可视为常量。
在半径r 处,取增量dr ,微面积 ,则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示,水流在平板上运动,靠近板壁附近的流速呈抛物线形分布,E 点为抛物线端点,E 点处0d d =y u ,水的运动黏度ν=1.0×10-6m 2/s ,试求y =0,2,4cm 处的切应力。
(提示:先设流速分布C By Ay u ++=2,利用给定的条件确定待定常数A 、B 、C )题1.5图解:以D 点为原点建立坐标系,设流速分布C By Ay u ++=2,由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dyτμ=得du(1250y 50)dy τμρν==-+ y=0cm 时,221510N/m τ-=⨯;y=2cm 时,222 2.510N/m τ-=⨯;y=4cm 时,30τ= 1.6 某流体在圆筒形容器中。
-船舶静力学课后习题答案

2/3
Exercise 1-2
∵Am=πr2/2 Aw=2*0.2*4r*r=4r2 V=1/3(πr2)*2r=2/3 πr3
∴Cm=Am/(2r*r)= π/4=0.785 Cp=V/(1/2πr2*4r)= 1/3=0.333 Cwp=Aw /(4r*2r)= 1/2=0.500 Cb=V/(4r*2r*r)=π/12=0.261 Cvp=V/(4r 2 *r)=π/6=0.522
Exercise 2-1
计算如图所示浮船坞水线面的有效面积对倾斜轴xx和 yy的惯性矩。巳知坞长L=75m,坞宽B=21m,b=2.2m。
Ixx=2{1/12*75*2.23 +(75*2.2)[(21-2.2)/2]2} =2(66.55+165*9.42) = 29291.9m 4
Iyy=2*1/12*2.2*753
Exercise 1-11
对下图所示的两个横剖面的半宽及其水线间距(单位 m)先修正其坐标,然后用梯形法计算其面积。 梯形法: 1. 修正值取:0.32
As=1*(0.32/2
+1.2+1.67+2
+2.24/2)=6.15 m 2
Exercise 1-11
2. 修正值取:-0.78 As=2*(-0.78/2+2.25+4.1+5.16+6/2)=28.24 m2
梯形法: Aw=2*L/10*(2(1.512+2.688+3.528+4.032+4.2) =2*6*27.72=322.64 m2
船舶流体力学第二次作业及答案

u v w 1, 1, 0 x y z
因有
u v w 1 1 0 0 ,故流动是连续的。 x y z w v u w v u 1, 1, 1, 1, 1, 1 y z z x x y
将(b)式代入(a)式得分速度
(b)
v xt y g t
(c)
代入已知条件, x y 0 , v 0 ,得 g t 0 ,有:
v xt y
我们由流函数求流线方程,流函数为:
xt y dx yt x dy tx 2
y x dx 2 dy 2 r r x y y 0 2 dx dy 2 0 x y 0 0 y2 1 x y ( arctan ) C y y x arctan C y
3.2 问下列速度场中,哪些可以构成不可压缩流体的连续流动?哪些流动是无旋的?
因满足 3.5 理想不可压缩流体平面无旋运动的分速度 u yt x ,若 x y 0 处, v 0 。试求
r cos cos r2 r cos sin vr 2 , v 2 r r r r (rvr ) cos cos v cos ( ) 2 , 2 r r r r r
所有流动是有旋的,绕 z 轴的旋转角速度为 。
(b) V y / r 2i x / r 2 j 0k ,其流线方程为
dx dy dz 2 2 y / r x / r 0
故有 dz 0 ,即 z C1 ,则
x y dx 2 dy ,消去 / r 2 并积分得 2 r r
1 3 1 1 x xy 2 x 2 y 2 C 3 2 2
