Zeta电路的建模
zeta converter电路分析
Zeta Converter电路分析
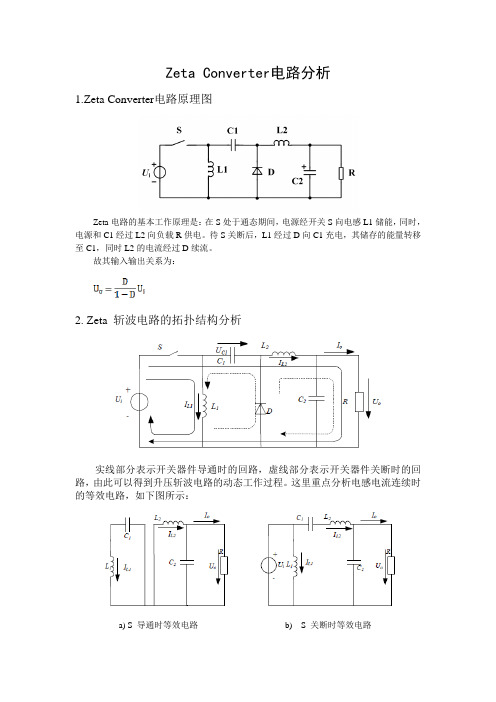
1.Zeta Converter电路原理图
Zeta电路的基本工作原理是:在S处于通态期间,电源经开关S向电感L1储能,同时,电源和C1经过L2向负载R供电。
待S关断后,L1经过D向C1充电,其储存的能量转移至C1,同时L2的电流经过D续流。
故其输入输出关系为:
2. Zeta 斩波电路的拓扑结构分析
实线部分表示开关器件导通时的回路,虚线部分表示开关器件关断时的回路,由此可以得到升压斩波电路的动态工作过程。
这里重点分析电感电流连续时的等效电路,如下图所示:
a)S 导通时等效电路b) S 关断时等效电路
电感电流连续时 Zeta 电路动态工作过程
当电容C 1足够大,u C1的脉动很小,可以认为 u C1≈U C1,由此可以得到Zeta 电路工作时,电感两端的电压和流过电感的电流的波形如图 6-3
所示。
a) 电感电流连续时波形 b) 电感电流断续时波形
a )电感电流连续时,有
1100(1)0()(1)0i C i
C U
D U D U U U D U D +-=⎧⎨----=⎩ 化简可得 01i D U U D
=- b ) 电感电流断续时,有
1110020()0
i C i C U D U U U U D U +∆=⎧⎨---∆=⎩ 化简可得 02111i D U U D D D
=⋅∆+-∆+ 由此可以看出,电感电流断续时,Zeta 斩波电路的输出电压也增大。
3.仿真分析
1)D=0.5时
仿真波形如下:
2)D=0.25时
仿真结果如下:。
基于状态空间平均法的Zeta变换器建模与仿真分析

关键词 :Zeta变换 器;状 态空间平均 法;建模 ;仿真 ;Matlab
中 图分类号 :TM46
文献标 识码 :A
文章编号 :94042一(2018)02—0031—05
M odeling and Sim ulation A nalysis of Zeta Converter Based on State—-space Averaging Principle
.
Practices prove that using M atlab software and these sim ulation models can effectively assist the design working of Zeta converter in actua l circuit. K ey words:Zeta Converter;State— space Averaging Principle;M odeling;Sim ulation;M atlab
。
DC/DC变换 器类 别 的 Zeta变换 器 为 例 ,基 于状 态
空 间平均 法 ,使 用 Matlab软 件 对 其 进 行 建 模 与 仿
真 分 析 。
ZETA电位PPT

郑秀玉
Zeta电位 一、Zeta电位
剪切面
胶体质点在液体中是带电的。当固 体与液体接触时,固—液两相界面 上就会带有相反符号的电荷。 Stern模型: 扩散双电层可分为两层:一层为紧 靠粒子表面的紧密层(亦称Stern层 或吸附层),另一层为扩散层。由 于质点表面总有一定数量的溶剂分 子与其紧密结合,因此在电动现象 中,这部分溶剂分子与粒子将作为 一个整体运动,在固—液相之间发 生相对移动时也有滑动面存在。尽 管滑动面的确切位置不知道,但可 以合理地认为它在Stern层之外,并 深入到扩散层之中。
高于+30mV或低于 高于+30mV或低于 +30mV -30mV的zeta电位,则 30mV的zeta电位, 电位 该分散体系应该比较 稳定。 稳定。
影响Zeta Zeta电位的因素 三、影响Zeta电位的因素 分散体系的Zeta电位可因下列因素而变化: 分散体系的Zeta电位可因下列因素而变化: Zeta电位可因下列因素而变化
–pH 的变化 –溶液电导率的变化 –某种特殊添加剂的浓度,如表面活性剂,高分 某种特殊添加剂的浓度,如表面活性剂,
子
测量一个颗粒的zeta电位随上述变量的变 测量一个颗粒的zeta电位随上述变量的变 zeta 化可了解产品的稳定性, 化可了解产品的稳定性,反过来也可决定 生成絮凝的最佳条件。 生成絮凝的最佳条件。
四、Zeta电位与pH eta电位 电位与
pH——影响zeta电位最重要的因素 影响zeta电位最重要的因素 pH 影响zeta Zeta Potential (mV) 60 40 20 0 2 -0 4 -0 6 -0 2 4 6 pH 8 10 12 稳定 等电点 不稳定 稳定
基于 ZETA 拓扑结构的 DCDC 转换器设计

基于ZETA 拓扑结构的DC/DC 转换器设计作者:Jeff Falin,德州仪器(TI) 高级应用工程师基本工作原理图 1 显示了ZETA 转换器的简单电路图,其由一个输入电容C IN、一个输出电容C OUT、耦合电感L1a 和L1b、一个AC 耦合电容C C、一个功率PMOS FET 即Q1,以及一个二极管D1 组成。
图 2 显示了Q1 为开启状态和Q1 为关闭状态时,在CCM 下运行的转换器。
图 1 ZETA 转换器的简单电路图若想要知道各个电路节点的电压,在两个开关都为关闭状态且无开关操作时对DC 条件下的电路进行分析很重要。
电容C C 与C OUT 并联,因此在稳态CCM 期间C C 被充电至输出电压V OUT。
图 2 显示了CCM 运行期间L1a 和L1b 的电压。
图 2 CCM 运行期间的ZETA 转换器Q1 关闭时,L1b 的电压必须为V OUT,因为其与C OUT并联。
由于C OUT被充电至V OUT,因此Q1 关闭时Q1 的电压为V IN + V OUT;这样一来,L1a 的电压便为相对于Q1 漏极的–V OUT。
Q1 开启时,充电至V OUT 的电容C C 与L1b 串联;因此L1b 的电压为+V IN,而二极管D1 的电压则为V IN + V OUT。
图 3 显示了通过各种电路组件的电流。
Q1 开启时,输入电源的能量被存储在L1a、L1b 和C C 中。
L1b 还提供I OUT。
Q1 关闭时,C C持续为L1a 提供电流,而L1b 再次提供I OUT。
图 3 CCM 期间ZETA 转换器的分量电流占空比假设100% 效率占空比D,用于CCM 运行的ZETA 转换器,其为:它还可以被重写为:Dmax 出现在V IN(min),而Dmin 出现在V IN(max)。
选择无源组件设计任何PWM 开关调节器的首要步骤之一便是决定允许多少电感纹波电流ΔI L(PP)。
过多会增加EMI,而过少又会导致不稳定的PWM 运行。
斯特恩模型的三个电势zeta

斯特恩模型的三个电势zeta斯特恩(Stern)是在古依(Gouty)—查普曼(Chapman)分散双层模型基础上发展起来的,同时又吸取了亥姆霍茨紧密双层模型的合理部分。
1924年,斯特恩提出一种改进后的Zeta电位双层模型。
根据这一模型,双电层可以同时具有紧密性和分散性。
这种模型认为:当电极表面电荷密度较大,同时电解质溶液的总浓度较大(约几摩尔/升以上)时,液相中离子倾向于紧密地分布在界面上,这时可能形成所谓“紧密双电层”,与一个荷电的平板电容器相似。
如果溶液中离子浓度不够大,或是电极表面电荷密度比较小,则是由于离子热运动,致使溶液中的剩余电荷不可能全部集中排列在界面上,而使电荷分布具有一定的“分散性”。
这种情况下,双电层包括“紧密层”与“分散层”两部分。
设d为水化离子的半径,在与电极距离x=0至x=d的薄层中不可能存在电荷,也就是说,在紧密双电层中(x≤d)不存在离子电荷,故电场强度为恒指,电位梯度也保值不变,在此间隔中电位与x成线性变化,且此直线很陡。
在x>d的区间内,当x增大,电场强度及电位梯度的数值也随之变小,直至趋近于零。
因此在分散层中,电位ψ随距离x呈曲线变化,曲线的形状先陡后缓。
这时电极与溶液之间的zeta电位双电层斯特恩模型差ψ实际包含两个组成部分:①紧密双电层中的电位差,ψ减ψ1;②分散层中的电位差,ψ1.这里的ψ和ψ1都是相对溶液内部的电位(规定为零)而言的。
根据上面的讨论容易看出:如果电极表面所带电荷多,静电作用占优势,离子热运动的影响减小,双电层结构较紧密,在整个电位中,紧密层电位占地比例较大,即ψ1电位的值变小。
溶液浓度增大时,离子热运动变困难,故分散层厚度减小,ψ1的值也减小。
所以,电极表面带的电荷很多,并且溶液中离子的浓度很大时,分散层厚度几乎等于零,可以认为ψ1约等于0;反之,当金属表面所带电荷极少,且溶液很稀,则分散层厚度可以变得相当大,以至于近似认为双层中紧密层不复存在。
Zeta斩波电路器的设计与仿真

本科课程设计专用封面设计题目: Zeta 斩波电路器的设计与仿真 所修课程名称: 电力电子技术课程设计 修课程时间: 2012 年 06 月 17 日至 6 月 23 日 完成设计日期: 2012 年 06 月 23 日 评阅成绩: 评阅意见:评阅教师签名: 年 月 日____工____学院___2009___级_电气工程及其自动化_专业 姓名_张江燕_______ 学号_2009180261_____………………………………(密)………………………………(封)………………………………(线)………………………………Zeta 斩波电路器的设计与仿真一.设计要求1)通过这次课程设计熟悉Zeta 斩波电路的工作原理。
2)掌握斩波电路的工作状态和了解电路图的波形情况。
3)进而对Zeta 斩波器有一个全面的了解和认识。
4)完成Zeta 斩波电路器的设计、仿真;给出具体设计思路和电路图,并给出必要的波形分析写出设计报告。
5)设计要求:输入:DC100V , 输出:300V , 负载平均电流大于2A 。
二.题目分析Z e ta 斩波电路的原理图如下。
设电路中电感L 值很大,电容C 值也很大.使电感电流i L 电容电压即负载电压U o 基本为恒值。
Z e ta 斩波电路该电路的工作原理为:Ze ta 斩波电路也称双Se pi c 斩波电路,其基本工作原理是:在V 处于通态期间,电源E 经开关V 向电感L 1贮能。
同时,E 和C 1共同向负载R 供电,并向C 2充电。
待V 关断后,L 1经VD 向C 1冲电,其贮存的能量转移至C 1。
同时,C 2向负载供电,L 2的电流则经V D 续流。
Z e ta 斩波电路的输入输出关系为:E U o αα-=1Z e ta 电路的输入、输出电流均是断续的。
另外,电路输出电压为正极性的,且输入输出关系相同。
三.主电路设计、元器件选型及计算:由于本次实验主要要求对电路的仿真,则放弃了较为复杂精确计算的方法,而选择先估算,再在仿真中修改参数逐步调试的方法。
电声法zeta电位

电声法zeta电位1. 介绍电声法zeta电位是一种用于表征固体表面电荷分布和电荷层性质的实验方法。
它通过测量固体表面与溶液之间的电位差来研究电荷分布和电荷层的性质。
电声法zeta电位广泛应用于材料科学、化学、生物学等领域,尤其在表面活性剂、纳米材料、膜材料等研究中具有重要意义。
2. 原理电声法zeta电位的原理基于电动力学和声学原理。
当固体表面存在电荷分布时,会形成一个电荷层,该电荷层与溶液中的离子产生排斥作用,从而形成一个电动力学稳定的界面。
在电声法zeta电位实验中,通过施加交变电场和测量固体表面的电位差,可以得到电声法zeta电位。
具体来说,实验中使用一对电极将固体样品浸泡在溶液中,施加一个交变电场。
交变电场作用下,固体表面的电荷层会发生振荡,产生声波。
通过测量声波的频率和振幅,可以计算得到电声法zeta电位。
3. 实验步骤3.1 准备工作首先,准备实验所需的设备和材料,包括电声法zeta电位仪器、电极、溶液、固体样品等。
3.2 样品处理将固体样品处理成适当的形状和大小,确保样品表面光滑且无明显缺陷。
清洗样品以去除表面的杂质,并将其干燥。
3.3 浸泡样品将样品浸泡在适当的溶液中,确保样品完全浸没在溶液中。
溶液的选择应根据具体实验要求,例如可以选择电解质溶液或非电解质溶液。
3.4 放置电极将电极插入溶液中,确保电极与样品之间的距离适当。
电极的选择应根据具体实验要求,例如可以选择金属电极或玻璃电极。
3.5 施加电场通过电声法zeta电位仪器,施加一个交变电场。
电场的强度和频率应根据具体实验要求进行调整。
3.6 测量电位差使用电声法zeta电位仪器,测量固体表面的电位差。
通过测量声波的频率和振幅,可以计算得到电声法zeta电位。
3.7 数据处理将实验得到的数据进行处理和分析,得到电声法zeta电位的准确数值。
可以使用适当的数学模型和计算方法进行数据处理。
4. 应用电声法zeta电位在材料科学、化学和生物学等领域具有广泛的应用价值。
马尔文zeta电位测试方法

马尔文zeta电位测试方法马尔文zeta电位测试方法是一种用于评估电化学腐蚀行为的常见方法。
该方法通过测量金属表面的电位变化来判断其腐蚀状态。
本文将介绍马尔文zeta电位测试方法的原理、实验步骤和应用领域。
一、原理马尔文zeta电位测试方法是基于马尔文模型的,该模型描述了金属在电解液中的腐蚀行为。
在金属表面,存在一层电位分布,该分布随着腐蚀过程的发展而变化。
马尔文zeta电位测试方法通过测量金属表面的电位变化来分析金属的腐蚀状态。
二、实验步骤1. 准备实验样品:选取需要测试的金属样品,并确保其表面光洁无污染。
2. 准备电解液:选择适当的电解液,根据实际需求调整其pH值和浓度。
3. 搭建实验装置:将金属样品置于电解液中,确保样品完全浸泡在电解液中,并连接电极和电位计。
4. 开始测试:使用电位计测量金属样品表面的电位,并记录下来。
随着时间的推移,不断测量电位值。
5. 数据处理:根据测量到的电位值,绘制电位-时间曲线。
根据曲线的变化趋势,分析金属样品的腐蚀行为。
三、应用领域马尔文zeta电位测试方法广泛应用于材料科学、金属腐蚀、电化学等领域。
具体应用包括:1. 腐蚀评估:通过测量金属样品的电位变化,评估其腐蚀程度和腐蚀速率,为材料选择、防腐措施提供依据。
2. 材料研究:通过分析电位-时间曲线,研究材料的腐蚀机理、腐蚀行为和腐蚀动力学,为材料设计和改进提供指导。
3. 防腐材料测试:通过测量不同材料的电位变化,评估防腐材料的效果和耐久性。
4. 电化学分析:结合其他电化学测试方法,如极化曲线、交流阻抗谱等,综合评估材料的电化学性能和腐蚀行为。
总结:马尔文zeta电位测试方法是一种常见的电化学腐蚀测试方法,通过测量金属表面的电位变化来判断其腐蚀状态。
该方法具有简单、快速、准确的特点,广泛应用于材料科学、金属腐蚀、电化学等领域。
通过该方法的应用,可以评估材料的腐蚀程度和腐蚀速率,研究材料的腐蚀机理和腐蚀动力学,为材料设计和改进提供指导,同时也可以评估防腐材料的效果和耐久性,综合评估材料的电化学性能和腐蚀行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R3 =
= 23 × 10 3
C4 =
2010.7
自流变换电路建模作业
方法二:从动态小信号模型出发 电路变换消去未知量
(VC1 + Vd )d (t )
(t ) i L1
Dv d (t )
( D 1)vC1 (t )
2010.7
自流变换电路建模作业
( I L1 + I L 2 )d (t )
C1
DiL 2 (t )
(1 D)iL1 (t )
2010.7
自流变换电路建模作业
方法二的输入输出传递函数为:
vO ( s) 953 × 10 12 s 2 + 2 = v d ( s ) 356.4 × 10 18 s 4 + 64.8 × 10 15 s 3 + 552 × 10 9 s 2 + 100 × 10 6 s + 5
2010.7
min
VO IO
取 R 为 10 欧, f s 为 20 K Hz ,12 伏变 5 伏, D ′ 为 L
2
= 177 H 取 200 H
自流变换电路建模作业
2010.7
C2
的计算
Q V
∵C =
1 i L 2 T s i L 2 1 C 2 一个开关周期充电和放 点电量: Q = = 2 2 2 8 fs ∴ V = C2 = Q V O (1 D ) = 2 C 8 L2 C 2 f s
1/ 2
f z1 = f z 2
1 = f p1, p 2 = 250 Hz 2
3
f p 3 = f ZR = 6.4 × 10 Hz
自流变换电路建模作业
f p 2 = 2 f s = 2 × 20 × 10 3 = 0.4 × 10 5 Hz
′ GO jwc = 0.3
f z2 250 7 jw ′ = AV1 = Gc c × = 437 × 10 3 ′ 1.91 × 10 3 2 fc
2010.7
自流变换电路建模作业
L2
iL 2 (t )
Dvd (t )
DvC1 (t )
vO (t )
(Vd + பைடு நூலகம்C1 )d (t )
2010.7 自流变换电路建模作业
由等效子电路出发,消去未知量, 求传递函数:
L2
VO (t )
R
C2
(1 D) : 1
(VC1 + Vd ) d (t )
2010.7
自流变换电路建模作业
极点为:
2010.7
自流变换电路建模作业
零点为:
2010.7
自流变换电路建模作业
f g 等于1 5
的开关频率
fs
fg =
1 1 f s = × 20kHz = 4kHz 5 5
1 1 w s = × 2πf s = 0.251 × 10 5 rad / s 5 5
f p2 ′ AV 2 = G c jwc = 70 ′ fc
C5
Vo (s )
R5 C6 R3
C4
+
R4
Vref (s )
2010.7
Vc (s )
自流变换电路建模作业
首先,假设
R4 R5 = = 143 AV2
R4 = 10k
1 2πf z 2 C 6
C5 = 1 2πf p 3 R4
自流变换电路建模作业
控制到输出的传递函数:
vO ( s) 40000 × 10 12 s 2 + 650 × 10 6 s + 85 = 18 4 15 3 9 2 6 d ( s) 356.4 × 10 s + 64.8 × 10 s + 552 × 10 s + 100 × 10 s + 5
2010.7
自流变换电路建模作业
输入到输出的传递函数:
vO ( s) DRC1 L1 s 2 + DR(1 D) = v d ( s ) RC1C 2 L1 L2 s 4 + C1 L1 L2 s 3 + R[ L1C1 + (1 D) 2 L2 C 2 ]s 2 + (1 D) 2 L2 s + (1 D) 2 R
1: D
( I L1 + I L 2 )d (t )
Dvd (t )
C1
L1
2010.7
自流变换电路建模作业
L2
(VC1 + Vd )d (t )
VO (t )
R
C2
(1 D) : 1
1: D
Dvd (t )
( I L1 + I L 2 )d (t ) 1 D
C1
L1
2010.7
自流变换电路建模作业
2010.7
自流变换电路建模作业
求控制到输出的传递函数:
I L1 + I L 2 ) + VC 1 + V d sL1 ( (1 D) 2 1 D [ d (s) D + (VC1 + V d )d ( s )] ( D) 1 (1 D) 2 + C1 L1 s 2 R × = vO ( s) 2 R + L2 s + RL2 C 2 s
2010.7
自流变换电路建模作业
参数计算:电感电流临界连续 L2的计算:
L2 d il2 = V O dt
i L2
= 0 i L 2 max
min
1 iL2 = I O 2 L2
=
V O D ′T s = L2 VO D ′ 2L2 fs
VO D ′ = 2 I O min f s = R 12 17
2010.7
T on
自流变换电路建模作业
a)C1的计算
能量守恒 V d I L1 T on = 36J = ∴ C 1 = 0.72F 1 2 C 1 v C1
2
= V C1 I L1 T off
2010.7
自流变换电路建模作业
所以,方法一的输入输出传递函数为:
vO ( s) 953 × 10 12 s 2 + 2.1 = v d ( s) 356.4 × 10 18 s 4 + 64.8 × 10 15 s 3 + 797.5 × 10 9 s 2 + 137.5 × 10 6 s + 5
2010.7 自流变换电路建模作业
5个未知数,4个方程可解出各变量 间的关系:
vO (s) DRCL1s2 + (1 D)DR 1 = vd (s) RC L1L2 C2 s4 + C1L1L2 s3 + [RC L1 + D2 RLC2 + (1 D)2 RL2C2 ]s 2 + [D2 L1 + (1 D)2 L2 ]s + (1 D)R 1 1 1
取
,
′ wc = 0.12 × 10 5 rad / s
′ wc ′ fc = = 1.91 × 10 3 Hz 2π
所以 两零点频率
有零点且在左半平面 4 w 4 × 10 f ZR = 2 = = 6.4 × 10 3 Hz 2π 2 × 3.14
2010.7
补偿网络 G c (s ) 两个零点频率设计为原始回路函数 G (s ) 两个相近的极点频率的 o
2010.7
自流变换电路建模作业
控制到输出的传递函数:
VO 1 2 RC1 L1 s + DI d RL1 s + (1 D)VO R v O ( s) D D = 4 3 2 2 2 2 d (s) RC1C 2 L1 L2 s + C1 L1 L2 s + R[ L1C1 + (1 D) L2 C 2 ]s + (1 D) L2 s + (1 D) R
L2
(VC1 + Vd ) d ( s )
(1 D ) : 1
VO ( s )
R
L1 C 2
sL1 (1 D) 2
1: D
Dvd ( s )
I L1 + I L 2 )d ( s) 1 D
C1
sL1(
2010.7
自流变换电路建模作业
求输入到输出的传递函数:
1 R sC 2 1 1 R+ Dv d ( s) sC1 sC 2 [ D + Dv d ( s )] × [ = vO ( s) sL1 1 1 1 D R + sC 2 sC1 (1 D) 2 sL2 + 1 R+ sC 2
2010.7 自流变换电路建模作业
1)稳态:充能等于放能
0 = DV D′VC1 d 稳 0 = DI L2 D′I L1 态 0 = D(Vd +VC1 VO ) D′VO
2010.7
自流变换电路建模作业
引入扰动
d[IL1 +L1(t)] i V V =[D+d(t)][ d +vd (t)][1Dd(t)][ C1 +vC1(t)] L1 dt 引 d[VC1 +vC1(t)] I =[D+d(t)][ IL2 iL2(t)]+[1Dd(t)][ L1+iL1(t)] 入C1 dt 扰 d[IL2 +iL2(t)] V =[D+d(t)][ d +vd (t) +VC1 +vC1(t) VO vO(t)] 动L2 dt [1Dd(t)][ +v (t)] V O O
1 D 2 V O 8L2 f s VO
取
VO 为0.2% VO
