工程应用软计算课件第1章模糊数学
模糊计算介绍课件

行决策和选择
04
模糊控制:将模糊决策应用于控制
系统,实现对系统的控制和调节
模糊计算的应用实 例
模糊控制
01
02
模糊控制是一 种基于模糊逻 辑的控制方法, 用于处理不确 定和不精确的
信息。
模糊控制广 泛应用于工 业自动化、 机器人控制、 智能交通等
领域。
03
模糊控制的 优点包括: 鲁棒性强、 适应性强、 易于实现等。
02 模糊计算将模糊数学与计 算机科学相结合,以解决 现实生活中的模糊问题。
03 模糊计算的基本思想是利 用模糊集合和模糊推理来 模拟人类的思维和决策过 程。
04 模糊计算在许多领域都有 广泛的应用,如控制、决 策、模式识别等。
模糊计算的特点
模糊性:处理模糊、 不确定的信息
近似性:通过近似 计算得到近似解
04
模糊控制的 应用实例包 括:家用电 器、汽车电 子、医疗设
备等。
模糊聚类分析
模糊聚类分析是一 种基于模糊数学的 聚类分析方法
模糊聚类分析可以 应用于市场细分、 客户分类等领域
模糊聚类分析可以 处理不确定、模糊 的数据
模糊聚类分析可以 提高数据分析的准 确性和效率
模糊模式识别
模糊模式识别是一种基于模糊逻辑的识别方 法,用于处理模糊和不确定的信息。
模糊逻辑推理可以通过 模糊规则库来实现
模糊逻辑推理的基本思 想是利用模糊集合来表 示事物的不确定性
模糊逻辑推理可以应用 于各种领域,如控制、 决策、预测等
模糊决策方法
01
模糊集合:将模糊概念转化为数学
集合,便于计算和处理
02
模糊推理:基于模糊集合的推理方
法,用于解决模糊问题
11模糊数学及其应用

2、隶属度:隶属函数A( x)描述了 x对模糊集合A的隶属程度。
3、模糊集A有下列三种常见的表示形式。 i) zadeh 表示法 ii) 序偶表示法 iii) 向量表示法
2010暑假建模培训
4
用集合x1 , x2 , x3 , x4 表示四位学 生, " 聪明"是一个模糊概念, 经某种方法 对四位学生的聪明程度 作的评价依次为 0.45 , 0.78 , 0.91 , 0.46 , 则以次评价构成 的模糊集合 A记为
22
2010暑假建模培训
2、数据标准化 在实际问题中,不同的数据一般有不 同的量纲,为了使所有不同的量纲的量也 能进行比较,通常需要对数据作适当的变 换 在模糊数学里,一般将数据压缩到区间 [0,1]上。
2010暑假建模培训
23
通常需要作如下两种变换: 1)平移、标准差变换
xik xk x sk
' ik
(i 1,2n; k 1,2,m)
1 xk xik n i 1
n
1 2 sk ( xik xk ) n i 1
n
2010暑假建模培训
24
经过变换后,每个变量的均值为0,标准 差为1,且消除了量纲的影响,但是,这样得 到的 还不一定在区间[0,1]上。
2)平移、极差变换
2010暑假建模培训 19
择近原则
设A1 , A2 , An是论域X中的n个模糊 集合 标准模型,对于给定的 待识别 对象B( X中的模糊集合) , 若存在k使得:
( Ak , B) max{ ( A1, B), ( An , B)}
其中 ( Ai , B )表示B对Ai的贴近度, 则认为B与Ak 最相似
软测量建模

(8)计算回归系数 Pk (T T T ) 1T T Y
2017-4-1
16
§7.3 基于回归分析的软测量建模
7.3.4 基于最小二乘法的糖液过饱和度软测量
(1)Wright模型
蔗糖的结晶过程,就是把糖浆浓缩至一定的过饱和状态,使之析出
微小的晶核,控制糖液的过饱和系数在最适当的范围而使晶体长大的过
S
W
X
0
1
X
0
纯净蔗糖溶液的过饱和系数定义为:
某温度下被测糖液中蔗糖 /水 S /W
SS
同 温 度 下 饱 和 糖 液 中 蔗 糖 / 水 S / W
2017-4-1
18
§7.3 基于回归分析的软测量建模
在实际生产中,糖液中含有蔗糖外的多种杂质,这些杂质都将对糖 液的过饱和度产生影响。因此,过饱和度定义为
2017-4-1
15
§7.3 基于回归分析的软测量建模
算法步骤:
(1)数据预处理,对X、Y按列标准化 (2)求相关矩阵R (3)求R的特征值和特征向量P (4)根据特征值从大到小重新排列特征值和特征向量P (5)计算主元贡献率 (6)计算积累主元贡献率,当其大于85%,记录主元个数k
(7)计算主元矩阵 T XPk
综上所述,D的确定计算式可写为:D D1 WS1 WS 2
2017-4-1
10
§7.2 基于工艺机理分析的软测量建模
(2)W的确定
对于汽包进水量W,在实际过程中也不存在相对应的测量装置,已经测得 的相关量是给水量G。这里主要需要考虑的是汽包的排污量的影响,而锅炉的 排污方式分为连续排污和定期排污两种。连续排污是连续不断地从汽包中排放 浓度最大锅炉水,定期排污是定期地从锅炉水循环系统的最低点(如水冷壁的下 联箱处)排放部分锅炉水。显然,对于汽包水位软测量系统,必须考虑连续排污 量。而对于定期排污量则因排放周期的不确定性,较难计算在内,暂不考虑。
《模糊计算及其应用》课件

THANKS
感谢观看
03
模糊推理与模糊控制系统
模糊推理的基本概念
01
模糊集合
模糊集合是传统集合的扩展,它 允许元素具有不明确的边界和隶 属度。
模糊逻辑
02
03
模糊推理规则
模糊逻辑是传统逻辑的扩展,它 使用模糊集合和模糊隶属度函数 来处理不确定性和模糊性。
模糊推理规则是传统推理规则的 扩展,它使用模糊集合和模糊逻 辑来处理不确定性和模糊性。
智能控制
利用模糊逻辑的推理规则,实现智能控制系统的优化和自动 化。
智能机器人
通过模糊逻辑的决策和推理,提高机器人的感知、决策和行 动能力。
模糊计算的研究热点与发展趋势
模糊逻辑的优化算法
研究更高效和精确的模糊逻辑算法,提高模糊计算的性能和精度。
模糊计算在物联网中的应用
将模糊计算应用于物联网设备的智能管理和控制,实现更高效和智能的物联网应用。
详细描述
模糊计算的发展历程可以分为几个阶段。在模糊集合 论阶段,模糊集合和隶属度函数的概念被提出,为模 糊计算奠定了基础。在模糊逻辑阶段,模糊逻辑的原 理和方法被应用于计算机科学和人工智能领域,产生 了模糊逻辑控制器和模糊专家系统等应用。在模糊推 理阶段,模糊推理的方法和原理得到了进一步发展和 应用,形成了模糊控制系统和智能控制等应用领域。
1 2 3
模糊逻辑
模糊逻辑是一种扩展的逻辑系统,它使用模糊集 合和隶属函数来处理不确定性和模糊性。
模糊逻辑们在模糊推理和控制系统中有重要应 用。
模糊推理
模糊推理是模糊逻辑的核心,它基于模糊条件语 句进行推理,能够处理不确定性和模糊性。
模糊集合与模糊逻辑的应用实例
05
模糊计算的前沿技术与发 展趋势
工程应用软计算课程设计

工程应用软计算课程设计设计背景工程应用软计算是一门涉及计算机技术、数学和工程学等多学科交叉的课程,其主要内容包括模糊逻辑、神经网络、遗传算法等软计算方法的理论和应用。
通过该课程的学习,学生可以对软计算方法的基本原理有更深入的了解,同时也可以掌握这些方法在工程实践中的应用。
为了更好地培养学生的工程应用能力,本次课程设计将以某一机电设备的故障诊断为主题,结合所学的软计算方法,设计相应的故障诊断系统,并进行测试和实验验证。
设计内容本次课程设计将分为以下几个步骤:1.确定故障诊断系统的需求和基本功能;2.学习软计算方法的理论知识,包括模糊逻辑、神经网络和遗传算法等;3.选择适当的软计算方法,并分析其适用性和可行性;4.设计故障诊断系统的整体结构和模块功能,并进行详细设计;5.实现故障诊断系统的功能模块,并进行系统测试和调试;6.进行实验验证和性能测试,并对测试结果进行分析和优化。
在以上的步骤中,需要注意的是,设计和实现的故障诊断系统应该具备以下几个基本要求:1.系统需要能够准确诊断设备的故障,并给出相应的处理方案;2.系统需要具备较高的稳定性和可靠性,能够在各种工作环境下正常运行;3.系统应该易于维护和更新,能够适应不同的应用场景。
为了满足以上要求,可以采用不同的软计算方法,并结合现有的技术进行综合应用。
比如,可以使用神经网络进行故障诊断预测,再结合模糊逻辑进行结果推理和判断,最终通过遗传算法进行系统参数的优化和调整。
在具体设计时,可以参考一些现有的故障诊断系统,并将其优化改进,比如利用机器学习算法对数据进行分类和分析,或者使用图像识别技术进行视觉检测和诊断等。
设计成果在完成本次课程设计后,学生需要提交以下几个成果:1.故障诊断系统的详细设计方案和全部源代码;2.系统运行的测试结果和性能评价报告;3.单独的实验验证报告,对实验结果进行分析和优化。
学生可以选择使用不同的编程语言和开发平台进行系统开发和实验测试,同时也可以结合课程所学的其他技术进行综合应用。
工程应用软计算课件第4章 分形几何(2).ppt

5
4.3.1 从拓扑维数到度量维数
例4.3 按经典欧氏几何的方法,求一个拓扑一维的光滑曲 线的长度和二维平面上具有光滑边界的区域的面积。
Mi Mi+1
B
M2 M1
A
6
4.3.1 从拓扑维数到度量维数
依此类推,k维欧氏空间上的光滑边界几何体F的度量d(F)为:
D ln 2 0.6309...... ln 3
13
4.3.2 自相似维数
例4.5 求科赫曲线的自相似维数。
由科赫曲线的迭代过程可知,Ek+1中的小线段长度为 Ek中直线段的1/3,小线段的个数是4个,即N=4,相似比为 1/3,相似比倒数为r=3,所以科赫曲线的自相似维数为:
D ln 4 1.2619...... ln 3
14
4.3.3 盒维数
自相似维数对于不具有严格自相似性的分形来说是难以 适用的,因此我们需要拓广分形维数的定义。
盒维数克服了这一困难。由于其维数的数学近似计算及 经验估计要相对容易,故应用中比较普遍。
盒维数:
取边长为ε的小盒子,覆盖分形。由于分形内部有各种 层次的空洞和缝隙,所以有些小盒子是空的,有些则覆盖 了分形的一部分。记非空小盒子的个数为N(A;ε),然后不 断地缩小盒子的尺寸ε,所得的N(A;ε)值自然要增大。当ε 0时,即可得到数盒子法定义的分形维数。
2
4.3.1 从拓扑维数到度量维数
在欧氏几何中,通常把点看作0维,直线看作1维, 平面看作2维,空间则是3维的。
那么,曲线、曲面或更高维空间上的超曲面的维数是 多少呢?
如果一条曲线与1维直线同胚(即存在一一的连续映 射),则这条曲线被定义为1维的,如果一个曲面与2维平 面同胚,则这个曲面被定义为2维的。以此类推,如果一 个超曲面与n维超平面同胚,则这个超曲面被定义为n维的。 这样定义的维数我们称之为拓扑维数。
【计算机工程与设计】_模糊数学_期刊发文热词逐年推荐_20140726
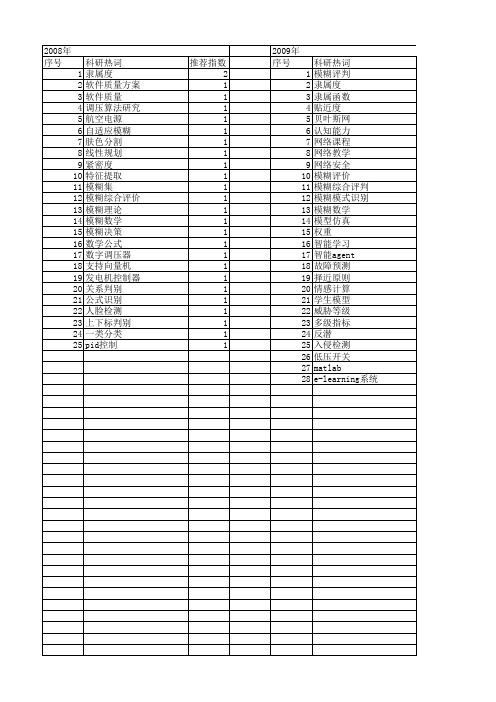
科研热词 隶属度 软件质量方案 软件质量 调压算法研究 航空电源 自适应模糊 肤色分割 线性规划 紧密度 特征提取 模糊集 模糊综合评价 模糊理论 模糊数学 模糊决策 数学公式 数字调压器 支持向量机 发电机控制器 关系判别 公式识别 人脸检测 上下标判别 一类分类 pid控制
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
科研热词 综合评价 篡改检测 混沌序列映射 模糊聚类 模糊c均值聚类 机电设施 木材表面缺陷 数学形态学 指标体系 图像分割 半脆弱水印 决策支持 内容认证 养护检测 gabor滤波器
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 子群优化算法 煤层气 模糊推理 模糊决策树算法 最优路径 归纳学习 应急 多目标决策
推荐指数 1 1 1 1 1 1 1 1 1 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
2011年 科研热词 面向服务架构 车辆检测 虚拟检测线 综合素质 研究生 真值程度 灾害评估模型 洪水模型 模糊综合评判 应用研究 地理信息系统 图像处理 二次量化模型 中介数学 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
工程应用软计算课件第5章混沌理论电子教案

如此周而复始,这叫周期2解。
如果进一步继续增加 值,则当3.449 3.545 3
时,周期2的两个值又不稳定,此处自产生一对新的不
动点,此时x n在四个值上跳动,这叫周期4解。例如取 3.5 时,xn 趋向于0.152→0.0879→0.373→0.823 →0.152,随着 的逐渐增加,这是不断地一分为二的
由此解出三个根
1 b
2,3
1 2
(
1)
( 1)2 4 (1 r)
可见,当 0 r 1时,这三个根皆为负实数,故 O
点是稳定的平衡点。当 r 1 时,1 仍为负实数,但
2 和3中有一正一负,此时 O点变为不稳定的平衡点。
当 r 1时,有一个零根,O点处于临界状态,故有一
特征值沿实轴穿过Байду номын сангаас轴从而发生一次叉型分岔。
各分岔点
n
存在如下关系
n c
n
(n
1)
(2)混沌区
参数在[ ,4]区间中为混沌区。其内有一个反的周
期 2 n的混沌带序列。混沌带并非乱成一片,其实混沌
区中也有不少同期窗口,例如有周期为 P 3,5,6,的窗
口。同时也看到,当参数 固定时(如上述周期3窗口
参数 1 8 ),由于初值 x0 的不同将可能导致不同
5.1 混沌模型
工程应用软计算——混沌理论
5.1.1 逻辑斯蒂模型
在人口学、生态学或经济学中,研究生物群体与 环境的之间的相互作用非常重要。
设 xt 是 t 时刻某种生物.的总数量,r为生物的增长
率,则可以得到如下的生物增长模型
xt1 xt r xt (1 r)xt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一个映射: A: X 0, 1
映射 A 称为 A 的隶属函数, A x 表示元素x 属于集合
A 的程度,或称为 x 对A 的隶属度。
精选ppt
11
工程应用软计算——模糊数学
经典集合是模糊集合的特例。
模糊幂集:论域 X的所有模糊子集全体,记为 (X) 。
则Zadeh表示法为
A
(x)/ x A
xX
例1.1 取论域 X 为正实数集合,
A 为“比0大得多的实数”的模糊集,
A 的隶属函数为:
1.0
Ax0(1100x2)1,
x0 x0
0.5
隶属函数图形如图。
0
10
设A,B ∊ (X),特征函数分别为 A x 和 B x 则有 A B A x B x , x X
A B A x B x , x X
ABxm ax{Ax,Bx} AxBx,xX
ABxm in{Ax,Bx} AxBx,xX
A Cx 1 A x , x X
[注] ∨: “取大”;∧:“取小”即。对 ,0, 1,有
3)向量表示法 A ( ( u A ( x 1 ) ,u A ( x 2 ) ,,u A ( x n ) ) 例如: 论域 X 为掷一颗骰子观察的点数,有
X={1,2,3,4,5,6} ,集合 A 表示“较大的点数”,则可记
A 0 / 1 0 / 2 0 . 2 / 3 0 . 6 / 4 1 / 5 1 / 6
第1章
立体化教学资源系列——工程应用软计算
模糊数 学
理学院精应选用pp数t 学系 1
1.13245 模糊集关 模 综 聚合系 式 类与识评分运别价析算
工程应用软计算——模糊数学
精选ppt
2
1.1 模糊集合与运算
工程应用软计算——模糊数学
模糊数学是研究和处理自然界与信息技术中广泛存
在的模糊现象的数学理论,它的产生既反映了信息革
在表示概念上,空集表示虚概念。
设A,B是X的任意两个子集,记A,B ∊ (X)。
A B,A B,AC 分别表示A和B的并集、交集和A的余 (补)集,有 A∪B={x | x A或x B}; A ∩ B ={x | x A且x B}
AC {x|xA}
精选ppt
6
工程应用软计算——模糊数学
特征函数:设A ∊ (X),称X到{0,1}的映射
二三、特 关征 系 Ax10, ,xxAA
为函与集数运合算A的特征函数。
对于任意的 x ∊X,特征函数 A x 表明了元素x属于
集合A的“程度”。
经典集合论中:x 属于或不属于A是绝对明确的, 因此用 0 和 1 二值表示。
集合A可以由特征函数 A x 唯一确定,反之亦然。
精选ppt
7
工程应用软计算——模糊数学
m ax, m in,
精选ppt
8
工程应用软计算——模糊数学
对于任意A,B ∊ (X) ,集合的并、交、余运算性质:
(p1)幂等律 四(、p性2)质交换律
AA A , AA A
A B BA , A B BA
(p3)结合律
A(BC ) (AB ) C A(BC ) (AB ) C
(p4)吸收律 (p5)分配律
命的迫切需要,也为信息科学提供了一种新的有力的
数学工具。 美国控制论专家L.A.Zadeh教授于1965年发表《模
糊集合》论文并建立模糊集合。
应用领域:人工智能、信息处理、图像处理、自动
控制、预测与决策、经济学、管理科学、运筹学等。
精选ppt
3
工程应用软计算——模糊数学
1概.1.念1 是概客念观与事集物在人脑中抽象概括的反映。
A BC AC BC A BC AC BC
精选ppt
10
工程应用软计算——模糊数学
1.概1.念2 模所反糊映概的念对象是一个具有某种属性的事物类。 与例模如糊,集“合年轻人”, “绵绵细雨”和“倾盆大雨” 。
模糊概念:外延不明确的ቤተ መጻሕፍቲ ባይዱ念。
经典集合可以表示明确概念而不能表现模糊概念。 例如,“秃子悖论” 。
分一数、在基0本,1, …,100范围内,用集合表示X={0,1, …,100} 概幂念集:设X是一论域,X中部分元素组成的集合称为 X的子集合(简称子集) 。
。
X的全体子集构成一个集合族,称为X的幂集,记为 (X) 。
集合可以表示概念。
例如:论域 X={0,1, …,100}为考试成绩分数集合。
则成绩“优秀”概念可由集合A={90,91, …,100}表示;
精选ppt
5
工程应用软计算——模糊数学
“良好”:B={80,81, …,89}“; 中等”:C={70,71, …,79}; “及格”:D={60,61, …,69“};不及格” :E={0,1, …,59}.
论域X有两个特殊的子集合,即自身X和空集。
A ( A B ) A , A ( A B ) A
A (B C)(A B) (A C)
A (B C)(A B) (A C)
精选ppt
9
(p6)0-1律 (p7)复原律 (p8)互补律 (p9)对偶律
工程应用软计算——模糊数学
A A, A XA A , A XX ( AC )C A
AACE,AAC
A { ( 0 , 1 ) , 0 , 2 , 0 . 2 , 3 , 0 . 6 , 4 , 1 , 5 , 1 , 6 }
A ( 0 ,0 ,0 .2 ,0 .6 ,1 ,1 )
精选ppt
12
工程应用软计算——模糊数学
当论域 X是不可数集合时, A x 是 A 的隶属度函数,
模糊集合的表示方法: 1)Zadeh表示法 A u A ( x 1 )/x 1 u A (x 2 )/x 2 u A (x n )/x n
2)有序对表示法 A { ( u A ( x 1 ) , x 1 ) , ( u A ( x 2 ) , x 2 ) ,, ( u A ( x n ) , x n ) }
概念具有内涵和外延,概念的内涵是指概念对事物 的特有属性的反映。
概念的外延是指具有概念所反映的那些对象全体, 它是特有对象的集合。
如果用概念外延的全体的集合来表示这个概念,那 么,计算机就可以很容易的理解和表示概念。
精选ppt
4
工程应用软计算——模糊数学
论域:被讨论的对象全体。
例如:讨论学生的某门课程成绩。
