《3.1.3 导数的几何意义》PPT课件(山西省市级优课)
合集下载
人教B版选修1-1高中数学3.1.3《导数的几何意义》ppt课件

本 答案 曲线 f(x)在点(x0,f(x0))处的切线,点(x0,f(x0))一定是
专 题
切点,只要求出 k=f′(x0),利用点斜式写出切线即可;
栏 目
而曲线 f(x)过某点(x0,y0)的切线,给出的点(x0,y0)不一定
开 关
在曲线上,
即使在曲线上也不一定是切点.
填一填 研一研 练一练
研一研·问题探究、课堂更高效
∴y′|x=1=2.
∴曲线在点 P(1,1)处的切线方程为 y-1=2(x-1),即 y=2x-1.
3.1.3
填一填 研一研 练一练
研一研·问题探究、课堂更高效
3.1.3
(2)点 P(3,5)不在曲线 y=x2 上,设切点为(x0,y0)
由(1)知,y′| xx0 =2x0, ∴切线方程为 y-y0=2x0(x-x0),
从图中可以看出,直线 l1 的倾斜程度小于直线 l2 的倾斜程度,这 说明曲线 h(t)在 t1 附近比在 t2 附近下降得缓慢.
研一研·问题探究、课堂更高效
3.1.3
填一填 研一研 练一练
小结 导数与函数图象升降的关系:
若函数 y=f(x)在 x=x0处的导数存在且 f′(x0)>0(即切线的斜
本 由 P(3,5)在所求直线上得 5-y0=2x0(3-x0)
①
专
题 栏
再由 A(x0,y0)在曲线 y=x2 上得 y0=x02
②
目 开
联立①,②得,x0=1 或 x0=5.
关 从而切点 A 的坐标为(1,1)或(5,25)
当切点为(1,1)时,
切线的斜率为 k1=2x0=2, 此时切线方程为 y-1=2(x-1),
=0,则
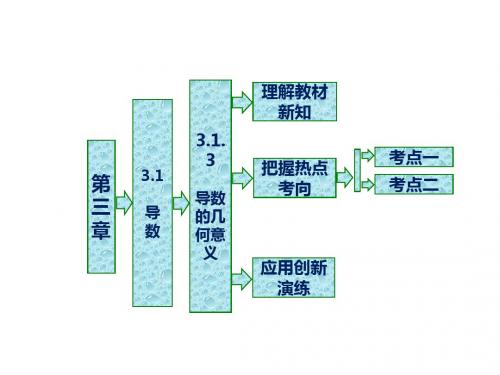
高中数学第三章导数及其应用3.1导数3.1.3导数的几何意
为
()
A.(-2,-8)
B.(-1,-1)或(1,1)
C.(2,8)
D.-12,-18
解析:设 P(x0,y0),则 k=f′(x0)= lim
Δx→0
fx0+Δx-fx0 Δx
= lim
Δx→0
x0+ΔΔxx3-x30=Δlxim→0
[(Δx)2+3x20+3x0·Δx]=3x20.
求切线方程
[例 1] y=-1x在点12,-2处的切线方程是 (
)
A.y=x-2
B.y=x-12
C.y=4x-4
D.y=4x-2
[思路点拨]
求f′x → 求f′12 → 写出直线方程
[精解详析] 先求 y=-1x的导数:
Δy=-x+1Δx+1x=xxΔ+xΔx,ΔΔxy=xx+1 Δx,
∵k=3,∴3x20=3,∴x0=1 或 x0=-1,
∴y0=1 或 y0=-1.∴点 P 的坐标为(-1,-1)或(1,1).
答案:B
4.若曲线 y=x2+2ax 与直线 y=2x-4 相切,求 a 的值并求切点坐标. 解:设切点坐标为(x0,y0).∵f(x0+Δx)-f(x0)
=(x0+Δx)2+2a(x0+Δx)-x02-2ax0=2x0·Δx+(Δx)2+2a·Δx,
3.1.
3
第 3.1
三
导
导数 的几
章 数 何意
义
理解教材 新知
把握热点 考向
应用创新 演练
考点一 考点二
3.1
导数
3.1.3 导数的几何意义
你登过泰山吗?登山过程中,你会体验到“六龙过万壑”的雄 奇,感受到“会当凌绝顶,一览众山小”的豪迈,当爬到“十八盘” 时,你感觉怎样?
课件12:3.1.3 导数的几何意义

3.函数的导数 对于函数 y=f(x),当 x=x0 时,f ′(x0)是一个确定的数.当 x 变化时,f ′(x)便是一个关于 x 的函数,我们称它为函数 y=
fx+Δx-fx
f(x)的导函数(简称为导数),即 f ′(x)=y′=_Δlix_m →_0_______Δ_x_____.
4.深刻理解“函数在一点处的导数”、“导函数”、“导 数”的区别与联系 (1)函数在一点处的导数f ′(x0)是一个_常__数____,不是变量. (2)函数的导数,是针对某一区间内任意点x而言的.函数f(x) 在区间(a,b)内每一点都可导,是指对于区间(a,b)内的每 一个确定的值x0,都对应着一个确定的导数f ′(x0).根据函数 的定义,在开区间(a,b)内就构成了一个新的函数,就是函 数f(x)的导函数___f_′_(x_)的导数f ′(x0)就是导函数f ′(x)在 点x=x0处的__函__数__值____,即f ′(x0)=__f_′_(x_)_|x_=__x_0__.
5.导数的物理意义:物体的运动方程s=s(t)在点t0处 的导数s′(t0),就是物体在t0时刻的_瞬__时__速__度___.
3.1.3 导数的几何意义
学习目标解读
1.了解导函数的概念,通过函数图象直观地理解导数的几何意 义. 2.会求导函数,能根据导数的几何意义求曲线上某点处的切 线方程.
重点难点展示
重点:理解导数的几何意义,会求曲线上某点处的切线方程. 难点:对导数几何意义的理解.
教材新知导学
知识点1:导数的几何意义新知导学 1.曲线的切线:过曲线y=f(x)上一点P作曲线的割线PQ, 当Q点沿着曲线无限趋近于P时,若割线PQ趋近于某一确定 的直线PT,则这一确定的直线PT称为曲线y=f(x)在点P的 ___切__线____.
课件14:3.1.3 导数的几何意义

2.设 f′(x0)=0,则曲线 y=f(x)在点(x0,f(x0))处的切线( )
A.不存在
B.与 x 轴平行或重合
C.与 x 轴垂直
D.与 x 轴斜交
解析:f′(x0)=0,说明曲线 y=f(x)在点(x0,f(x0))处的切线斜率 为 0,所以与 x 轴平行或重合.
答案:B
3.在曲线 y=x2 上切线倾斜角为π4的点是(
切线方程. 解:由 y=13x3,得 y′=
ΔΔyx=
13(x+Δx)3-13x3 Δx
=13
3x2Δx+3x(Δx)2+(Δx)3 Δx
1 =3
[3x2+3xΔx+(Δx)2]=x2,y′|x=3=32=9,
即曲线在 P(3,9)处的切线的斜率等于 9.
由直线的点斜式方程可得,
所求切线方程为 y-9=9(x-3),
)
A.(0,0)
B.(2,4)
C.41,116
D.21,14
解析:因为 y=x2,所以 k=y′=
ΔΔyx=
(x+Δx)2-x2 Δx
=
(2x+Δx)=2x,所以 2x=tanπ4=1,
所以 x=12,则 y=14.
答案:D
4. 若函数 f(x)在点 A(1,2)处的导数是-1,那么曲线 y=f(x) 在点 A 处的切线方程是________. 解析:切点为(1,2),k=-1, 所以切线方程为 y-2=-1×(x-1) 即:x+y-3=0.
解析:(1)直线与曲线公共点的个数不是切线的本质特征,直 线是曲线切线时,直线可能与曲线有两个以上的交点,正确.(2) 与曲线有且只有一个交点的直线不一定是曲线的切线,如直线 x=1 与抛物线 y=x2 有且只有一个公共点,但 x=1 不是抛物 线 y=x2 的切线,不正确.(3)f′(x0)是一个数值,不是变数,而 f′(x)是关于 x 的一个函数,正确.(4)求 f′(x0)时,可先求 f′(x), 再求 f′(x0),故(4)错误. 答案:(1)√ (2)× (3)√ (4)×
(教师用书)高中数学 3.1.3 导数的几何意义课件 新人教A版选修1-1

导数几何意义的理解
若函数 y=f(x)的导函数在区间[a,b]上是增函数, 则函数 y=f(x)在区间[a,b]上的图象可能是( )
【思路探究】 (1)导数的几何意义是什么?(2)y=f(x)的导 函数在区间[a,b]上是增函数,说明 y=f(x)图象的切线有什么 特点? 【自主解答】 因为函数 y=f(x)的导函数 y=f′(x)在[a, b]上是增函数,由导数的几何意义可知,在区间[ a,b]上各点处 的切线斜率是逐渐增大的,只有 A 选项符合.
3.1.3
导数的几何意义
教师用书独具演示
●三维目标 1.知识与技能 理解导数的几何意义, 初步体会“以直代曲”的辩证思想; 掌握求曲线上一点出的切线的斜率的方法.
2.过程与方法 培养学生的观察、动手动脑、归纳总结的能力;培养学生 合作学习、创新能力. 3.情感、态度与价值观 经过 FLASH 动画演示割线“逼近”成切线过程, 让学生感 受函数图象的切线“形成”过程, 获得函数图象的切线的意义; 增强学生问题应用意识教育,让学生获得学习数学的兴趣与信 心.
【问题导思】 导函数 f(x)与函数在 x=x0 处的导数 f′(x0)相同吗?它们有 什么区别与联系?
【提示】 不相同. (1)两者的区别: 由导数的定义知, f′(x0) 是一个具体的值,f′(x)是由于 f(x)在某区间 I 上每一点都存在 导数而定义在 I 上的一个新函数,所以两者的区别是:前者是 数值,后者是函数. (2)两者的联系:在 x=x0 处的导数 f′(x0)是导函数 f′(x) 在 x=x0 处的函数值,因此求函数在某一点处的导数.
●教学流程
Байду номын сангаас 演示结束
课标 解读
1.理解导数的几何意义会求曲线 上某点处的切线方程.(重点) 2.理解在某点处与过某点的切 线方程的区别.(难点、易混点)
数学:3.1.3《导数的几何意义》课件

解:我们用曲线h(t)在t0,t1,t2处的切线, 刻画曲线h(t)在上述三个时刻附近的
变化情况。
(1) 当t=t0时,曲线h(t)在t0处的切线l0平行
(2)
于x轴所. 以,在t=t0附近曲线比较平坦,
几乎没有下降.
第六页,编辑于星期日:十二点 二十六分。
(2) 当t=t1时,曲线h(t)在t1处的切线l1的斜率 (3) h′(t1)<0. 所以,在t=t1附近曲线下降,
解: 因为 s 5(2 t )2 5 22 20t 5t 2
从 s 205t
所以
而
s(2)
t
lim
s
lim (20
5t)
20
t t 0
t 0
第十二页,编辑于星期日:十二点 二十六分。
例4、已知曲线 y
1 x 3上一点
3
P 2, 8 3
求:点P处的切线的斜率;
点P处的的切线方程.
y y0 f x0 x x0
第十九页,编辑于星期日:十二点 二十六分。
第二十页,编辑于星期日:十二点 二十六分。
的函数图象。根据图象,估计t=
0.5,0.8时,血管中药物浓度的瞬时变化率 (精确到0.1)
第八页,编辑于星期日:十二点 二十六分。
c(mg/mL)
1.1
1.0 0.9 0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
t(min)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1
变化率分别为0和-1.5.
第十页,编辑于星期日:十二点 二十六分。
求函数y=f(x)在点x0处的导数的方法是: (1)求函数的增量
导数的几何意义77350-16页PPT资料

( 1 ) 求 函 数 的 增 量 y f( x x ) f( x ) ;
(2)求 函 数 的 增 量 与 自 变 量 的 增 量 的 比 值 :
yf(xx)f(x);
x
x
(3 )求 极 限 , 得 导 函 数 y f(x ) lim y . x 0 x
看一个例子:
例 : 已 知 yx, 求 y.
例2 h(t)4.9t26.5t10. 根据图象, 请描述、比较
曲线h (t ) 在 t0 , t1, t2 附近的变化情况.
解:可用曲线 h(t) 在 t0 , t1 , t2 处的切线 h 刻画曲线 h(t) 在上述三个时刻附近的变
l0
化情况.
(1)当 t = t0 时, 曲线 h(t) 在 t0 处的切线 l0
表明:y 就是割线的斜 . 率 x
请看当 点Q沿 着曲线 逐渐向 点P接 近时,割 线PQ 绕着点 P逐渐 转动的 情况.
y
y=f(x)
割
线 Q
T 切线
P
o
x
我们发现,当点Q沿着曲线无限接近点P即Δx→0 时,割线PQ有一个极限位置PT.则我们把直线PT称为曲 线在点P处的切线.
设切线的倾斜角为α,那么当Δx→0时,割线PQ的 斜率,称为曲线在点P处的切线的斜率.
即: k 切 t 线 a ln x i0 m x y lx i0fm (x 0 x x ) f(x 0 )
这个概念:①提供了求曲线上某点切线的斜率的一 种方法;②切线斜率的本质——函数平均变化率的极限.
导数的几何意义
函数 y=f(x)在点x0处的导数的几何意义,就是曲 线 y=f(x)在点P(x0 ,f(x0))处的切线的斜率.
曲线h (t ) 在 t0 , t1, t2 附近的变化情况.
人教B版选修1-1高中数学3.1.3《导数的几何意义》ppt课件

f x0+Δx-f x0 lim Δx Δx→ 0 .
课堂讲练互动 中小学课件
填一填·知识要点、记下疑难点
3.1.3
(2)导数的几何意义 函数 y=f(x)在点 x0 处的导数的几何意义是曲线 y=f(x)在点 P(x0, f(x0))处的切线的 斜率 . 也就是说,曲线 y= f(x)在点 P(x ,f(x ))处的切线的斜率是 f′(x0) .相应地,切线方程为
本 专 题 栏 目 开 关
课堂讲练互动 中小学课件
填一填·知识要点、记下疑难点
3.1.3
1.导数的几何意义
本 专 题 栏 目 开 关
(1)割线斜率与切线斜率 设函数 y=f(x)的图象如图所示,AB 是过点 A(x0,f(x0))与 Δy 点 B(x0+Δx, f(x0+Δx))的一条割线, 此割线的斜率是 = Δx f x0+ Δx-f x0 . Δx
课堂讲练互动 中小学课件
研一研·问题探究、课堂更高效
3.1.3
小结
导数与函数图象升 处的导数存在且 f′(x0)>0(即切线的斜 率大于零),则函数 y=f(x)在 x=x0 附近的图象是上升的;若 f′(x0)<0(即切线的斜率小于零),则函数 y=f(x)在 x= x0 附 近的图象是下降的 .导数绝对值的大小反映了曲线上升和下 降的快慢 .
研一研·问题探究、课堂更高效
3.1.3
问题 2 曲线的切线是不是一定和曲线只有一个交点?
答案 不一定.曲线的切线和曲线不一定只有一个交点,和
本 专 题 栏 目 开 关
曲线只有一个交点的直线和曲线也不一定相切 .如图,曲线 的切线是通过逼近将割线趋于确定位置的直线.
课堂讲练互动 中小学课件
课堂讲练互动 中小学课件
填一填·知识要点、记下疑难点
3.1.3
(2)导数的几何意义 函数 y=f(x)在点 x0 处的导数的几何意义是曲线 y=f(x)在点 P(x0, f(x0))处的切线的 斜率 . 也就是说,曲线 y= f(x)在点 P(x ,f(x ))处的切线的斜率是 f′(x0) .相应地,切线方程为
本 专 题 栏 目 开 关
课堂讲练互动 中小学课件
填一填·知识要点、记下疑难点
3.1.3
1.导数的几何意义
本 专 题 栏 目 开 关
(1)割线斜率与切线斜率 设函数 y=f(x)的图象如图所示,AB 是过点 A(x0,f(x0))与 Δy 点 B(x0+Δx, f(x0+Δx))的一条割线, 此割线的斜率是 = Δx f x0+ Δx-f x0 . Δx
课堂讲练互动 中小学课件
研一研·问题探究、课堂更高效
3.1.3
小结
导数与函数图象升 处的导数存在且 f′(x0)>0(即切线的斜 率大于零),则函数 y=f(x)在 x=x0 附近的图象是上升的;若 f′(x0)<0(即切线的斜率小于零),则函数 y=f(x)在 x= x0 附 近的图象是下降的 .导数绝对值的大小反映了曲线上升和下 降的快慢 .
研一研·问题探究、课堂更高效
3.1.3
问题 2 曲线的切线是不是一定和曲线只有一个交点?
答案 不一定.曲线的切线和曲线不一定只有一个交点,和
本 专 题 栏 目 开 关
曲线只有一个交点的直线和曲线也不一定相切 .如图,曲线 的切线是通过逼近将割线趋于确定位置的直线.
课堂讲练互动 中小学课件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知斜率,求切点
已知曲线 y=f(x)=x2+1上一点P,在点P处 的切线斜率为 2 ,求点P的坐标。
-1
已知点,求斜率
1.若点是切点,直接求该点处的导数,即斜率
2.若点不是切点,先设切点 (x0, f (x0 )) ,求切点处导
数 f (x0),写出切线方程
将已知点带入,解出 x0
y f (x0 ) f (x0 )(x x0 ).
3.1.3导数的几何意义
一、复习
1、导数的定义
函数y=f x 在x=x0处的导数,记作:f x0 或y x=x0
lim y lim f (x0 x) f (x0 )
x0 x x0
x
其几何意义是 表示曲线上两点连线(就是曲线 的割线)的斜率。
k ppn
y x y
f ( x0 x) f ( x0 )
1. 已知函数y=f(x)的图像在点(1,f(1)) 处的切线方程为x-2y+1=0,则 f (1) 2 f '(1) 的 值是
已知点,求斜率
已知曲线f(x)=x2+1。
(1)求曲线在点P(1,2)处的切线斜率及
切线方程
(2,5)
(2)过点A(1,-2)作该曲线的切线, 求该切线方程。
(1 ,-1) 2
。代入切线方程中即可
斜率f (x0) ,
令 k f (x0 ) ,解出 x0 即可
已知曲线 y=f(x)= x3 ,过点A(1,2)作
曲线的切线,求该切线方程。
x0
导数的几何意义
函数 y=f(x)在点x=x0处的导数的几何意义 就是曲线 y=f(x)在点P(x0 ,f(x0))处的切线的斜率, 即曲线y=f(x)在点P(x0 ,f(x0)) 处的切线的斜
率是 f ( x0 )
故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:
y f ( x0 ) f ( x0)( x x0 )
x
y=f(x)
割
线 Pn (x0 x, f (x0 x))
T 切线
P (x0, f (x0))
o
x
y k PPn x
f ( x0 x) f ( x0 ) x
y
y f (x)
相交
oP
x 当Δx→0,即点Pn沿着曲线无限接近点P,
k
lim
x0
kPPn lxi m时 定0 ,位割yx置线的Pl直Pxi m n趋线0 近PfT(于称x0确为定点的Px处x)位的置切f,(线x这0.个) 确f
