立体几何八大定理(可编辑修改word版)
立体几何常考法则概括(八大法则)

立体几何常考法则概括(八大法则)立体几何是数学中的一个分支,研究的是三维空间中的图形和形状。
在解决立体几何问题时,我们可以借助一些常考的法则来简化求解过程。
本文将介绍八大立体几何常考法则,以帮助读者更好地理解和应用。
1. 平行与垂直关系平行关系:- 平面平行关系:两个平面如果没有公共点或平面间的交线平行于平面的截线,则这两个平面是平行的。
- 直线平行关系:如果两条直线在同一平面内,且不相交,则这两条直线是平行的。
垂直关系:- 平面垂直关系:两个平面的法线向量垂直,则这两个平面是垂直的。
- 直线垂直关系:两条直线的斜率之积为-1,则这两条直线是垂直的。
2. 距离和长度关系距离公式:- 两点距离:两点之间的距离可以通过勾股定理求解:$\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$长度关系:- 线段等长关系:如果两条线段的长度相等,则这两条线段是等长的。
3. 角度关系直角关系:- 直角:两条相交的直线产生的两个相邻补角之和为90度。
平面角关系:- 互余角:两个角互补或补角相等。
4. 空间图形性质正方体:- 八个顶点、六个面、十二条边。
- 相对面平行、对角面垂直。
- 对边平行且等长、相邻面的边垂直。
正八面体:- 六个顶点、八个面、十二条边。
- 任意两个顶点之间的连线等长。
圆柱体:- 两个圆底面、一个侧面。
- 侧面是矩形、底面圆心连线垂直于侧面。
圆锥体:- 一个圆底面、一个侧面。
- 侧面是扇形、底面圆心连线垂直于侧面。
球体:- 一个面,无棱无角。
- 任意两点之间的连线长度等于球心间距。
以上是八大立体几何常考法则的概括。
通过了解和熟练运用这些法则,我们可以更轻松地解决立体几何相关的问题。
希望本文对读者有所帮助。
立体几何常考定理总结(八大定理)

立体几何常考定理总结(八大定理)一、线面平行的判定定理:线线平行线面平行文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行、符号语言:关键点:在平面内找一条与平面外的直线平行的线二、线面平行的性质定理:线面平行线线平行文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行、符号语言:关键点:需要借助一个经过已知直线的平面,接着找交线。
三、面面平行的判定定理:线面平行面面平行文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行、符号语言:关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
四、面面平行的性质定理: 面面平行线线平行、面面平行线面平行文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行、符号语言:关键点:找第三个平面与已知平面都相交,则交线平行文字语言:如果两个平面平行,那么其中一个平面内的任意一条直线平行于另一个平面、符号语言:关键:只要是其中一个平面内的直线就行五、线面垂直的判定定理:线线垂直线面垂直文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面、符号语言:关键点:在平面内找两条相交直线与所要证的直线垂直六、线面垂直的性质定理:线面垂直线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意一条直线、符号语言:关键点:往往线面垂直中的线线垂直需要用这个定理推出七、平面与平面垂直的判定定理:线面垂直面面垂直文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直、(如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:关键点:在需要证明的两个平面中找线面垂直八、平面与平面垂直的性质定理:面面垂直线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面、符号语言:关键点:先找交线,再在其中一个面内找与交线垂直的线。
实用文库汇编之高中立体几何八大定理

lmβααba*作者:梁上飞*作品编号:91265005448GK 0253678 创作日期:2020年12月20日实用文库汇编之线面位置关系的八大定理一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行 图形语言: 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α 作用:线线平行⇒线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
图形语言:符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m作用:线面平行⇒线线平行 三、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言:nmAαaαba//a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 作用:线线平行⇒ 面面平行四、平面与平面平行的性质定理: 文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行 图形语言:符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行五、直线与平面垂直的判定定理:文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面 图形语言: 符号语言: ,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭作用:线线垂直⇒线面垂直六、直线与平面垂直的性质定理:文字语言:若两条直线垂直于同一个平面,则这两条直线平行 图形语言: 符号语言:BA l βαaβα//a a b b αα⊥⎫⇒⎬⊥⎭作用:线面垂直⇒线线平行七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭注:线面垂直⇒面面垂直八、平面与平面垂直的性质定理:文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言:符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直作者:梁上飞作品编号:91265005448GK 0253678 创作日期:2020年12月20日。
高中立体几何八大定理

a mnA m ,n
作用:线线垂直 线面垂直
那么这条直线垂直于这个平面
a
A n
m
六、直线与平面垂直的性质定理:
文字语言:若两条直线垂直于同一个平面,则这两条直线平行
图形语言: 符号语言:
a a // b
b
a b
作用:线面垂直 线线平行 七、平面与平面垂直的判定定理: 文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。 图形语言:
线就和交线平行。 图形语言:
l // 符号语言: l
l // m m
l m
作用:线面平行 线线平行 三、平面与平面平行的判定定理 文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言:
a
b
abA
//
a∥
b∥
作用:线线平行
面面平行
四、平面与平面平行的性质定理 : 文字语言:如果两个平行平面同时和第三个平面相交 图形语言 :
//
符号语言 :
a a // b
b
作用 : 面面平行 线线平行
, 那么所得的两条交线平行
1
更多资料请加三好网小好师弟微信:sanhao1001
更多资料请加三好网小好师弟微信:sanhao1001
五、直线与平面垂直的判定定理: 文字语言: 如果一条直线和一个平面内的两条相交直线垂直, 图形语言: 符号语言:
a
符号表示:
a
a
注:线面垂直 面面垂直 八、 平面与平面垂直的性质定理: 文字语言: 如果两个平面互相垂直, 那么在一个平面内垂直与它们的交线的直线垂直于另一
个平面 图形语言:
A
常考定理总结(八大定理)

lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键..点:在需要证明的两个平面中找线面垂直..................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
立体几何公式大全(K12教育文档)

立体几何公式大全(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(立体几何公式大全(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为立体几何公式大全(word版可编辑修改)的全部内容。
立体几何公式大全一、空间向量的基础公式:cos a b =⋅a b λ=(0,λ>方向相同0,λ<方向相反模a2a a =a b⋅二、求角和距离公式: 21a b x x y a bx ⋅+=⋅+a n a n⋅⋅(n 表示平面为平面α的法向量1212n n ⋅:求二面角瞄:瞄一下看二面角θ是锐角还是钝1212n n ⋅ 的夹角θ;三、定:同锐相等:若AP n n⋅为平面α的法三、求法向量步骤:(1) 设法向量(,,)n x y z =,利用法向量n 与平面上的两相交直线方向向量垂直数量积为0建立两个方程;(2) 求出x 等于多少z, y 等于多少z;并令z=1进而求出x ,y ,从而得到法向量n ;或者求出x 等于多少y , z 等于多少y;并令y=1进而求出x,z ,从而得到法向量n ; 或者求出y 等于多少x , z 等于多少x;并令x=1进而求出y,z,从而得到法向量n ;(3) 把所求的法向量n 代入方程组检验!四、法向量n 的在证明题中用处:(1) 线面平行:l l n α⊄⊥平面且⇔//l α平面:参见JP65/例2(证明线面平行问题只要转成去求线的向量与法向量数量积为0即可)(2) 面面平行:12//n n ⇔//αβ平面平面:参见JP65/例2(证明面面平行问题只要转成去证两个法向量存在一个倍数关系问题即可)(3) 线面垂直://l n l α⇔⊥平面:(证明线面垂直问题只要转成求证线的向量与法向量存在一个倍数关系即可)(4) 面面垂直:12n n ⊥⇔αβ⊥平面平面:参见JP65/例3(证明面面垂直问题只要转成去求两法向量数量积为0即可)(整理不易,望同学们好好珍惜利用!)。
立体几何基本法则总结(八大法则)

立体几何基本法则总结(八大法则)立体几何基本法则总结(八大法则)本文总结了立体几何中的八大基本法则,为了帮助读者更好地理解和应用这些法则。
一、平面法则平面法则指明了平面在立体图形中的重要作用和应用。
以下是平面法则的要点:1. 平面是由至少三个不共线的点确定的。
2. 三点确定一个唯一的平面。
3. 平面的垂直平分线经过平面的中点。
4. 两个不同平面的交线,是它们的公共点的平面。
二、直线法则直线法则是立体几何中不可或缺的基本法则。
以下是直线法则的要点:1. 两个不同点之间只有一条直线。
2. 两个不互相重合的平行直线永远不会相交。
3. 一条直线与一个平面最多只有一个交点。
三、点法则点法则是描述立体几何中点的特性和定律的基本法则。
以下是点法则的要点:1. 一个点可由无限多条直线经过。
2. 两条直线最多只有一个公共点。
四、角度法则角度法则是立体几何中关于角度的基本法则。
以下是角度法则的要点:1. 两条直线相交,形成四个相对的角。
2. 同位角互为补角,即和为180°。
3. 互补角互为同位角,即和为90°。
五、平行四边形法则平行四边形法则描述了平行四边形的特点和性质。
以下是平行四边形法则的要点:1. 平行四边形的对边相等。
2. 平行四边形的对角线互相平分。
六、正方形法则正方形法则描述了正方形的特点和性质。
以下是正方形法则的要点:1. 正方形的对边相等且平行。
2. 正方形的对角线互相垂直且相等。
七、正三角形法则正三角形法则描述了正三角形的特点和性质。
以下是正三角形法则的要点:1. 正三角形的三边相等。
2. 正三角形的三个角均为60°。
八、立方体法则立方体法则描述了立方体的特点和性质。
以下是立方体法则的要点:1. 立方体的所有边长相等。
2. 立方体的六个面都是正方形。
以上是立体几何的八大基本法则的概述。
掌握这些法则,将有助于更好地理解和应用立体几何知识。
高中立体几何八大定理
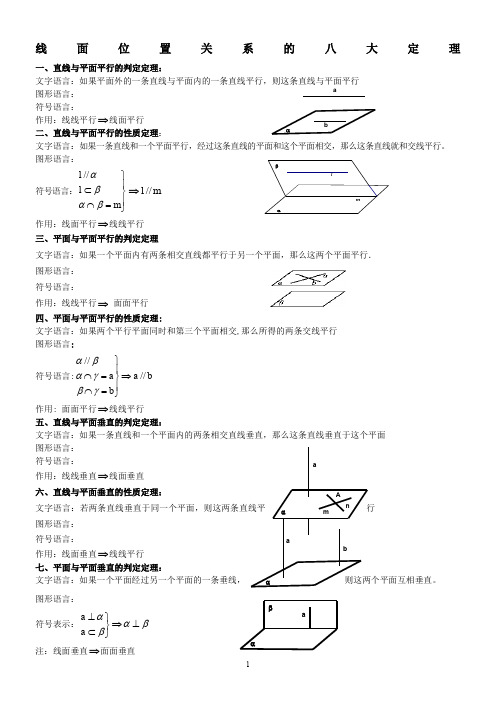
lmβααbanmA αa αbaaβα线面位置关系的八大定理一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行图形语言: 符号语言:作用:线线平行⇒线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
图形语言:符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m作用:线面平行⇒线线平行 三、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言:作用:线线平行⇒ 面面平行四、平面与平面平行的性质定理:文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行 图形语言:符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行五、直线与平面垂直的判定定理:文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面 图形语言: 符号语言: 作用:线线垂直⇒线面垂直 六、直线与平面垂直的性质定理:文字语言:若两条直线垂直于同一个平面,则这两条直线平行图形语言: 符号语言:作用:线面垂直⇒线线平行七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭注:线面垂直⇒面面垂直八、平面与平面垂直的性质定理:文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言:符号语言:lAB ABAB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.直线与平面平行的判定定理和性质定理
文字语言
图形语言
符号语言
判定定理
平面外一条直线与这个平面内的一条直线平行,则该直线与此平面平行
(线线平行⇒线面平行)
l / /a
al / /
l
性质定理
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行
(简记为“线面平行⇒线线平行”)
b
3.直线与平面垂直的判定定理及性质定理
文字语言
图形语言
符号语言
判定定理
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直
Error!⇒l⊥α
性质定理
垂直于同一个平面的两条直线平行
Error!⇒a∥b
4.平面与平面垂直的判定定理与性质定理
文字语言
图形语言
符号语言
判定定理
一个平面过另一个平面的垂线,则这两个平面互相垂直
l//
ll //b
b
2.平面与平面平行的判定定理和性质定理
文字语言
图形语言
符号语言
判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行
(简记为“线面平行⇒面面平行”)
a / /, b / /
abP//
a,B
性质定理
如果两个平行平面同时和第三个平面相交,那么它们的交线平行
//
aa / /b
ror!⇒α⊥β
性质定理
两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平面
Error!⇒l⊥α
