2021年六年级小升初数学总复习第四讲(平面图形)(含答案)
小学六年级【小升初】数学《平面图形的测量专题课程》含答案
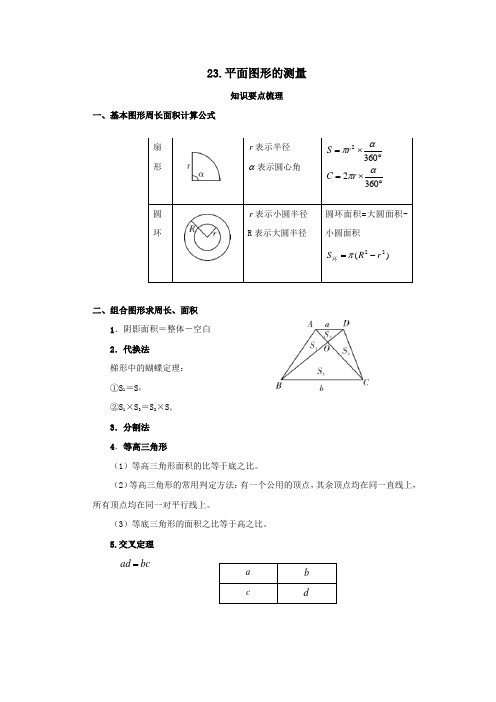
23.平面图形的测量知识要点梳理一、基本图形周长面积计算公式二、组合图形求周长、面积 1.阴影面积=整体-空白 2.代换法梯形中的蝴蝶定理: ①S 1=S 4 ②S 1×S 3=S 2×S 4 3.分割法 4.等高三角形(1)等高三角形面积的比等于底之比。
(2)等高三角形的常用判定方法:有一个公用的顶点,其余顶点均在同一直线上,所有顶点均在同一对平行线上。
(3)等底三角形的面积之比等于高之比。
5.交叉定理 bc ad =扇形r 表示半径α表示圆心角︒⨯=3602απr S ︒⨯=3602απr C圆环 r 表示小圆半径R 表示大圆半径圆环面积=大圆面积-小圆面积)(22r R S -=π环a bcd考点精讲分析典例精讲考点1组合图形的周长和面积【例1】 求下面图形的周长和面积。
(单位:米) 【精析】 要求它的周长,可用长方形的2个长+1个宽+圆的周长的一半;要求它的面积,可用图中长方形的面积加上半圆的面积即可。
【答案】 周长:2.5×2+2+3.14×2÷2 =5+2+3.14 =10.14(米)面积:2.5×2+3.14×2)22(÷2 =5+3.14×1÷2 =5+1.57 =6.57(平方米)答:这个图形的周长是10.14米,面积是6.57平方米【归纳总结】 组合图形的计算,一般都要把它分割成规则图形再进行计算。
考点2 等积变换法求面积【例2】 如图,ABCD 是直角梯形,AB =3厘米,AD =4厘米,BC =6厘米,求阴影部分的面积。
【精析】 阴影部分的面积为三角形ABE 和三角形DEC 的面积之和,利用△ABE 和△DEC 是等高三角形则阴影部分的面积可以变换为BC 边的长乘以高,再除以2。
【答案】 6×3÷2=9(平方厘米)【归纳总结】 高一定,阴影部分面积=底之和×高÷2。
小升初六年级数学总复习 空间与图形--基础知识点+巩固练习+详细答案
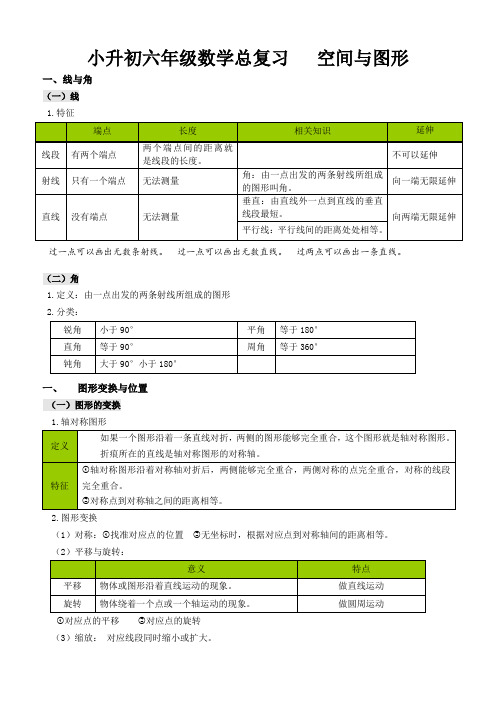
小升初六年级数学总复习空间与图形一、线与角(一)线1.特征过一点可以画出无数条射线。
过一点可以画出无数直线。
过两点可以画出一条直线。
(二)角1.定义:由一点出发的两条射线所组成的图形2.分类:一、图形变换与位置(一)图形的变换1.轴对称图形2.图形变换(1)对称:①找准对应点的位置②无坐标时,根据对应点到对称轴间的距离相等。
(2)平移与旋转:①对应点的平移②对应点的旋转(3)缩放:对应线段同时缩小或扩大。
(二)图形与位置(1)比例尺及坐标方位:①比例尺:一般以1厘米的距离相当于实际距离多少(2)根据方向、距离确定位置:①首先确定方向②根据比例尺确定直线距离(3)路线描述:①坐标原点——参照物②目标相对于参照物方向③目标到参照物的距离。
(4)用数字标注位置:①坐标原点——参照物②目标相对于参照物方向③目标相对于参照物的角度④目标到参照物的距离。
二、平面图形(一)三角形和四边形1.三角形定义由不在同一条直线上的三条线段着尾顺次相接围成的图形叫三角形。
分类按角分锐角三角形三个角都是锐角三个角都小于90°直角三角形有一个角是直角有一个角等于90°钝角三角形有一个角是钝角有一个角大于90°按边分等腰三角形两条边相等等边三角形三条边全相等每个内角都是60°不等边三角形三条边都不相等图形及字母意义面积公式特征三角形a——底h——高S=ah÷2面积=底 高÷2①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是180°。
④有三条边和三个角,具有稳定性。
2.四边形定义由不在同一直线上的四条线段首尾顺次相接围成的封闭图形叫四边形分类平行四边形平行四边形两组对边分别平行且相等长方形两对边分别相等四个角都是直角正方形四条边都相等四个角都是直角梯形等腰梯形只有一组对边平行,两条腰相等的梯形。
直角梯形一条腰与底垂直的梯形叫做直角梯形。
有两个角是直角图形及字母意义面积公式特征正方形a——边长S=a2面积=边长×边长①四条边都相等②四个角都是直角③有四条对称轴长方形a——长b——宽S=ab面积=长×宽①对边相等②四个角都是直角③有二条对称轴平行四边形a——底h——高S=ah面积=底×高①两组对边平行且相等。
2021年小升初数学专项复习:平面图形附答案解析

【解析】
试题分析:依据三角形的内角和是180度即可作答.
解:因为三角形的内角和是180°,且这个数值是固定不变的,
所以说“三角形越大,内角和越大”是错误的.
故选:C.
【点评】此题主要考查三角形的内角和定理.
6.【答案】A
【解析】
试题分析:红领巾的三个内角分别是120°、30°、30°,含有一个钝角。
8.过两点能画( )条直线。
A.0 B.1 C.3
9.把线段的一段无限延伸,就得到( )。
A.线段 B.射线 C.直线
10.长方形的一组长边同时缩短到和短边同样长,就变成了( )
A.正方形 B.平行四边形 C.四边形
11.平行四边形的( )相等.
A.四个角 B.四条边 C.对边
12.三条直线相交最多有( )个交点.
2021年小升初数学专项复习:平面图形
一、选择题
1.下面各组小棒中能围成三角形的是( )组.
A.3厘米、3厘米、6厘米
B.3厘米、4厘米、5厘米
C.2厘米、3厘米、4厘米
2.等腰三角形的一个底角是65°,这个三角形一定是( )
A.锐角 B.直角 C.钝角
3.一个等腰三角形,底是5厘米,腰是6厘米,它的周长是( )厘米.
60.至少4个完全一样的正方形才能拼成一个大正方形.(判断对错)
61.平行四边形很稳定.(判断对错)
62.同一个平面内的两条直线,不是相交就是平行..(判断对错)
63.同一平面内,两条直线不互相平行就互相垂直. (判断对错)
64.连结两点的线段的长度叫做这两点间的距离. (判断对错)
65.在同一平面内的两条直线不相交,就一定互相平行..(判断对错)
小升初专项复习《平面图形》(一)练习及答案

小升初专项复习《平面图形》一、填空题1.若等腰三角形的两边长分别为2和6,则它的周长为。
2.一个等腰三角形的两边长分别是 米和 米,这个三角形的周长是米。
3.长方形的面积是24平方厘米,长和面积的比是1:4,则长方形的宽是厘米。
4.用一根10.28米长的铁丝围成一个半圆,这个半圆的面积是平方米。
5.如图,把圆分成若干等份,剪拼成一个近似的长方形,已知长方形的宽为5cm,则长是cm,长方形的面积是cm2。
6.同一个圆中圆的与的比值叫做圆周率。
7.圆的位置与有关系,圆大小的与有关系。
8.晶晶画了一个平行四边形,它的高是 dm,底是高的 。
这个平行四边形的面积是dm2。
9.如图,零件厂要加工一批环形铁片,每个铁片的面积是平方厘米。
10.一个平行四边形的底是8厘米,面积是48.8平方厘米,高是厘米,与它等底等高的三角形的面积是平方厘米。
11.等腰三角形的一个底角是40°,它的顶角是°,这是一个角三角形。
12.一个梯形的上底是5厘米,下底是10厘米,高是5厘米(如图)。
这个梯形的一个钝角是°,这个梯形的面积是平方厘米。
13.一个长方形的长:宽=7:5,长比宽多6厘米,这个长方形的周长是,面积是。
14.在一个长8cm,宽3cm的长方形中剪出一个最大的半圆,这个半圆的周长是cm,面积是cm2。
15.如图,平行四边形的面积是20平方厘米,图中甲乙丙三个三角形的面积比是。
二、单选题16.两个正方形的边长的比是5:3,它们的面积的比是()A.3:5B.1:3C.5:1D.25:917.在一个长1.25米,宽0.8米的长方形里,最多能剪()个半径为20厘米的圆。
A.5B.7C.6D.2418.自行车的前轮半径为30厘米,后轮半径为20厘米。
如下图,当前轮向前行驶了5圈回到E点的位置时,后轮F点的位置是下图中的()。
A.B.C.D.19.如图,把正方形桌子面的四边撑起,就成了一张圆面桌子,经过测量圆面桌子的面积为π平方米,那么这张桌子的正方形桌面的面积为()平方米。
六年级小升初毕业考试总复习——几何图形专项复习(附答案)

六年级小升初毕业考试——几何图形专项训练⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧→⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧→→圆锥圆柱正方体长方体立体图形扇形圆环圆梯形正方形长方形平行四边形四边形三角形平面图形几何图形 一、平面图形知识要点:1. 三角形(1)三角形具有稳定性。
(2)三角形的内角和是180°。
(3)三角形三边关系:在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
(4)三角形的面积=底×高÷22.四边形(1)长方形的周长=(长+宽)×2 长方形的面积=长×宽 (2)正方形的周长=边长×4 正方形的面积=边长×边长 (3)平行四边形的面积=底×高 (4)梯形的面积=(上底+下底)×高÷23.圆(1)圆的周长:c=πd c=2πr 圆的面积:s=πr ²(2)圆环的面积=外圆面积-内圆面积 s=πR ²-πr ²或 s=π(R ²-r ²) (3)扇形的周长=半径×2+弧长 c=2r+2πr ×360n扇形的面积=圆面积×360n s=πr ²×360n28m 近似三角形了,真有意思 !1.(西城2019年小学毕业数学测查卷)一个用草绳编织成的茶杯垫的上面是圆形,将它沿半径剪开,下面说法不正确...的是( ). A.近似三角形的底相当于圆的周长 B.近似三角形的高相当于圆的半径 C.近似三角形的面积相当于圆的面积 D.近似三角形的面积相当于圆面和的212.(西城2019年小学毕业数学测查卷)一个长方体,有两个相对的面是正方形。
它的长是8cm.宽是5cm.这个长方体的表面积最少是( )cm 2.A.130B. 200C.210D. 2883.(西城2019年小学毕业数学测查卷)如下图小圆贴着大圆的内侧从A 点开始按箭头所指方向滚动(大圆不动....)。
小升初真题特训:平面图形-小学数学六年级下册人教版(有答案 有解析)

小升初真题特训:平面图形-小学数学六年级下册人教版学校:___________姓名:___________班级:___________考号:___________一、选择题1.(2020·甘肃陇南·统考小升初真题)在一个边长为2厘米的正方形中,画一个最大的圆,圆的面积是正方形面积的( )。
A .78.5%B .80%C .75%2.(2021春·安徽合肥·六年级统考小升初模拟)下列说法正确的是( )。
A .1条射线长12厘米B .角的大小与边的长短有关系C .等腰三角形一定是锐角三角形D .圆的周长和它的直径成正比例3.(2021·贵州黔东南·小升初真题)用一个放大5倍的放大镜看一个的角,所看到的角是( )。
A .B .C .4.(2020春·四川·六年级小升初模拟)一块正方形手帕,边长是20厘米,它的面积是( )平方分米。
A .400B .40C .45.(2020春·全国·六年级统考小升初模拟)现有长度分别为1cm,3cm,5cm,7cm,11cm 的5根肖邦,每次选取其中的任意三根,可摆成( )个不同的三角形.A .2B .4C .106.(2022·甘肃金昌·统考小升初真题)手工课上同学们小组合作制作笔筒。
小亮准备了一张长方形的硬纸板作为笔筒的侧面(如图),请联系生活实际思考:下面最适合作为这个笔筒底面的是( )(接头处忽略不计)。
A .B .C .二、填空题7.(2020·湖北武汉·统考小升初真题)一个等腰直角三角形两条直角边的长度和是36厘米,它的面积是30︒30︒35︒150︒三、判断题18.(2020·全国·小升初真题)一个正方形的边长是4厘米,它的周长和面积相等。
( ) 19.(2021春·全国·六年级统考小升初模拟)圆的周长和它的面积成正比例。
人教版六年级下册数学小升初专题训练:平面图形(含答案)

人教版六年级下册数学小升初专题训练:平面图形一、单选题1.用一块长12米、宽8米的长方形铁皮剪成半径是1.5米的小圆(不能剪拼),至多能做( )个。
A.11B.8C.10D.132.如果要搭成一个从正面、左面、上面看到的图形都是如图的几何体,需要( )个小正方体。
A.3B.4C.5D.63.下图是由一个圆分成若干等分后,拼成的一个近似长方形,这个圆的周长与长方形的周长相差约4厘米,这个圆的周长约是( )厘米。
A.6.28B.9.42C.12.56D.无法计算4.从12时到13时,钟的时针与分针可成直角的机会有( )A.1次B.2次C.3次D.4次5.下列时刻中,钟表中时针与分针不成直角的是( )。
A.3:00B.21:00C.9:00D.12:206.一个半径是5cm的半圆,它的周长是( )cm。
A.31.4B.15.7C.25.7D.20.7二、填空题7.已知一个等腰三角形的两条边分别是5厘米、10厘米,那么它的周长是 厘米。
8.一个花坛的直径是6m,花坛周围有一条宽1m的环形小路,小路的面积是 m2。
9.一个挂钟的时针长5厘米,一昼夜这根时针的尖端走了 厘米,针尖扫的面积是 平方厘米。
10.把一个长、宽分别是15厘米和10厘米的长方形,拉成一个一条高为12厘米的平行四边形,它的面积是 平方厘米。
11.李大伯用5π米长的篱笆靠墙围了一个半圆形养鸡场,养鸡场的面积是 平方米。
12.如图。
∠1=30°,∠2= ,∠3= ,∠4= 。
13.从9:00到9:15,分针旋转了 度,若分针长6厘米,这根分针针尖走过的长度是 厘米,扫过的面积是 平方厘米。
14.一个三角形内角度数的比是2:3:5,其中最大的内角是 度,这是个 角三角形。
15.如图中正方形的面积是40cm2,那么涂色部分的面积是 cm2。
16.一辆自行车车轮直径是0.5米,脚踏板齿轮有48个齿,后齿轮有16个齿,脚踏一圈,自行车前进 米.17.把两个正方形拼成一个长方形,拼成的长方形周长是30厘米,这个长方形的面积是 平方厘米。
六年级下册数学-小升初平面几何知识复习(练习)冀教版

第一节 平面图形知识结构图如果一个图形沿着一条直线对折,两边的图形能够完全重合,这个图形叫做轴对称图形,这条直线叫做对称轴。
名称 对称轴 名称 对称轴 线段 1条 正方形 4条 角 1条 等腰梯形 1条 等腰三角形 1条 圆 无数条 等边三角形3条长方形2条锐角三角形直角三角形 钝角三角形 按角分按边分不等边三角形等腰三角形 等边三角形长方形周长:C=2(a+b) 面积:S=ab 正方形周长:C=2(a+b) 面积:S=a 2 平行四边形面积:S=12ah 梯形面积:S=12(a+b)h面积:S=12ah线:直线、射线、线段角:锐角、直角、 钝角、平角 、周角三角形四边形圆周长:C=2πr 面积:S=πr 2 组合图形(面积计算)平面图形【例题】1.判断,对的打“√”,错的打“×”。
1、直线比射线长。
------------------------------------------------------()2、四条边都相等的四边形是正方形。
--------------------------------------()3、面积相等的两个三角形,一定能拼成一个平行四边形。
--------------- ()4、一个三角形中最少有两个锐角。
------------------------------------------()5、有一组对边平行的四边形是梯形。
---------------------------------------()6、大于90度的角是钝角。
------------------------------------()7、角的两条边越长,角就越大。
------------------------------()8、从直线外一点向这条直线所画的线段,都叫做这点到直线的距离。
2.填空。
1、三角形的一个内角正好等于其余两个内角的和,这是一个()三角形。
2、一个等腰三角形,它的顶角是72º,它的底角是()度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021年六年级小升初数学总复习第四讲平面图形一.教学目标1.理解各种图形的概念和特点2.掌握基本图形的面积计算方法3.掌握平面图形中常见的模型,并能熟练应用二.知识点1.图形计数 (1)相关类型 ①数线段:21)1(-⨯n n 或)(1321-+++n 注意:是线段上端点的个数n②数角:21)1(-⨯n n 或)(1321-+++n 注意:是边的个数n③数三角形:21)1(-⨯n n 或)(1321-+++n 注意:是边的个数n④数长方形: 长边上的线段数×短边上的线段数⑤数正方形:22221)2()1(+⋯⋯+-+-+n n n 注意:含的基本单位数表示大正方形边长上包n ⑥其他计数问题:给出图形,数出其中特定图形的多少 (2)相关方法①枚举法:罗列所有情况逐个计数,也称穷举法②加法原理和乘法原理:利用计数中出现的各种情况进行加或乘的计算 ③递推法:利用简单图形的计数逐步找出规律进行递推的方法 2.周长巧算 (1)相关方法①直接计算:根据公式直接计算 ②平移法 (2)相关公式①正方形周长公式:C=边长×4 ②正方形周长公式:C=(长+宽)×2 3.常见模型 (1)等积模型①等底等高的两个三角形面积相等;S 2S 1②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. (2)鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵(3)蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝴蝶定理”): ①2213::S S a b =DCBAS 4S 3S 2S 1O DCBA A DO aS 2S 1S 4②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +. (4)相似模型金字塔模型 沙漏模型GF E ABCD ABCDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.(5)燕尾定理在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=. 上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径. 4.圆(1)相关概念①圆的定义:平面上到一个定点的距离等于定长的点的全体,这里的定点叫做圆心,定长称为半径。
②直径:经过圆心的直线与圆的两个交点之间的线段。
③弧:圆上两点之间的部分。
④扇形:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
OFE DCBA⑤方中圆:正方形与内切圆 ⑥圆中方:圆的内接四边形 (2)相关公式及方法①圆的周长和面积公式:2,2r S d C r C π,ππ=== ②扇形弧长公式:180rnl π=③扇形面积公式:lr r n S 213602==π ④方中圆:大正方形平均分成四个小正方形 ⑤圆中方:大正方形平均分成四个小三角形三.例题【例1】数一数,图中共有多少条线段?【答案】6+5+4+3+2+1=21(条) 【练习】数一数,下图中有多少个角?【答案】3+2+1=6(个)【例2】 如图,正方形的面积是 8 平方厘米,求圆的面积。
【答案】A B C D E解:S=πr 2=3.14×8=25.12(平方厘米)答:圆的面积是25.12平方厘米.【练习】如图,长方形的面积和圆的面积相等,已知圆的半径是3厘米,求阴影部分的周长与面积各是多少?【答案】解:(1)圆的周长:2×3.14×3=18.84(厘米), 圆的面积:3.14×32=28.26(平方厘米), 长方形的长:28.26÷3=9.42(厘米), 长方形的周长:(9.42+3)×2=24.84(厘米), 则阴影部分的周长: 24.84-3×2+18.84×41 =24.84-6+4.71, =18.84+4.71, =23.55(厘米); (2)阴影部分的面积: 28.26×(1-41), =28.26×43 =21.195(平方厘米);【例3】下图的周长是 厘米.4cm8cm【答案】 (8+4)⨯2 =12⨯2 = 24(厘米)【练习】下图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是多少厘米?【答案】170厘米【解析】每个小正方形的面积为400÷16=25平方厘米.所以每个小正方形的边长是5cm ,因此它的周长是34⨯5=170厘米.【例4】如图,正方形ABCD 的边长为6,AE =1.5,CF =2.长方形EFGH 的面积为 .【答案】连接DE ,DF ,则长方形EFGH 的面积是三角形DEF 面积的二倍. 三角形DEF 的面积等于正方形的面积减去三个三角形的面积,66 1.562262 4.54216.5DEF S =⨯-⨯÷-⨯÷-⨯÷=△,所以长方形EFGH 面积为33.【练习】如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?【答案】运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半.证明:连接AG .(我们通过ABG △把这两个长方形和正方形联系在一起).∵在正方形ABCD 中,G 12AB S AB AB =⨯⨯△边上的高, ∴12ABGABCDS S =△(三角形面积等于与它等底等高的平行四边形面积的一半)同理,12ABG EFGB S S =△. ∴正方形ABCD 与长方形EFGB 面积相等. 长方形的宽8810 6.4=⨯÷=(厘米).【例5】如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【答案】连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【练习】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBA AB CDE【答案】连接BE .∵3EC AE = ∴3ABCABESS=又∵5AB AD = ∴515ADEABEABCSSS=÷=÷,∴1515ABCADESS==.【例6】如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.CBA【答案】因为M是AD边上的中点,所以:1:2AM BC=,根据梯形蝴蝶定理可以知道22:::1:12:12:21:2:2:4AMG ABG MCG BCGS S S S=⨯⨯=△△△△()(),设1AGMS=△份,则123MCDS=+=△份,所以正方形的面积为1224312++++=份,224S=+=阴影份,所以:1:3S S=阴影正方形,所以1S=阴影平方厘米.【练习】如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC的面积为___________平方厘米.?852OA BCDE F?852OA BCDE F【答案】连接DE、CF.四边形EDCF为梯形,所以EOD FOCS S∆=,又根据蝴蝶定理,EOD FOC EOF CODS S S S∆∆∆∆⋅=⋅,所以2816EOD FOC EOF CODS S S S∆∆∆∆⋅=⋅=⨯=,所以4EODS∆=(平方厘米),4812ECDS∆=+=(平方厘米).那么长方形ABCD的面积为12224⨯=平方厘米,四边形OFBC的面积为245289---=(平方厘米).【例7】如图,ABC△中,DE,FG,BC互相平行,AD DF FB==,则::ADE DEGF FGCBS S S=△四边形四边形.EGFADCB【答案】设1ADES=△份,根据面积比等于相似比的平方,所以22::1:4ADE AFGS S AD AF==△△,22::1:9ADE ABCS S AD AB==△△,因此4AFG S =△份,9ABC S =△份,进而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【练习】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【答案】由金字塔模型得:::2:5AD AB AE AC DE BC ===,所以42510AC =÷⨯=四.课后练习基础巩固1.数一数,图中共有( )个三角形。
