第七讲-小升初平面图形综合一
小升初(六年级)重点初中招生考试分类试题——平面图形综合

小升初(六年级)重点初中招生考试分类试题平面图形综合求角度1.如下图中,那么:∠1+∠2+∠3+∠4+∠5= 度。
2.下图中,小于180°的角有 个?如果∠2+∠3=∠1+∠4,那么当∠AOB 等于 度时,图中所有角的和等于360°。
3.在三角形ABC 中,D 、E 是BC 边上的点,BD=AB ,CE=AE ,又,31BAC DAE ∠=∠求BAC ∠的度数? 数图形4.如图所示是半个正方形,它被分成一个个小的等腰三角形,图中正方形有 个,三角形有 个。
5.数一数,图中包含☆的长方形有______个.1 2 345 A OB12 3 4 DEAC6.由三个边长为1的正方形拼成如图所示的左右对称的图形,以图中正方形的10个顶点为顶点可得到许多不同的三角形,那么,在这些三角形中,面积为1的三角形共有 个。
(面积为1的三角形的三条边中至少有一条边是水平或垂直的)综合能力提升7.两块直角边分别是6厘米和10厘米的等腰直角三角形板,如下图那样重合。
求重合部分(阴影所示)的面积是 平方厘米。
8.求下图中阴影部分的面积(单位:厘米)。
9.如图所示,长方形ABCD 中,AB=24厘米,BC=36厘米,E 是BC 的中点,F ,G 分别是AB ,CD 的4等分点,H 为AD 上任意一点,求阴影部分面积。
10.在图中,长方形长为12厘米,宽为6厘米,把长分成3等份,宽分为2等份,长方形内任一点与分点及顶点连接起来,求阴影部分的面积和是多少平方厘米?11.如图,正六边形ABCDEF 的面积是6平方厘米,M 是AB 中点,N 是CD 中点,P 是EF 中点。
△MNP 的面积是多少平方厘米?AH D12.如图中阴影部分的面积。
13.如图:△ABC 是等腰直角三角形,AB =BC =10CM ,AB 是半圆的直径,CB 是扇形BCD 的半径,求阴影部分的面积。
14.如图,以10×10的正方形的4条边为直径,在正方形的内部作4个半圆,求阴影部分的面积。
小升初数学知识点之平面图形

小升初数学知识点之平面图形2019小升初数学是学习生涯的关键阶段,为了能够使同学们在数学方面有所建树,小编特此整理了小升初数学知识点之平面图形,以供大家参考。
平面图形1、长方形(1)特征对边相等,4个角都是直角的四边形。
有两条对称轴。
(2)计算公式c=2(a+b)s=ab2、正方形(1)特征:四条边都相等,四个角都是直角的四边形。
有4条对称轴。
(2)计算公式c=4as=a23、三角形(1)特征由三条线段围成的图形。
内角和是180度。
三角形具有稳定性。
三角形有三条高。
(2)计算公式s=ah/2(3)分类按角分锐角三角形:三个角都是锐角。
直角三角形:有一个角是直角。
等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
按边分不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
4、平行四边形(1)特征两组对边分别平行的四边形。
相对的边平行且相等。
对角相等,相邻的两个角的度数之和为180度。
平行四边形容易变形。
(2)计算公式s=ah5、梯形(1)特征只有一组对边平行的四边形。
中位线等于上下底和的一半。
等腰梯形有一条对称轴。
(2)公式s=(a+b)h/2=mh 6、圆(1)圆的认识平面上的一种曲线图形。
圆中心的一点叫做圆心。
一般用字母o表示。
半径:连接圆心和圆上任意一点的线段叫做半径。
一般用r表示。
在同一个圆里,有无数条半径,每条半径的长度都相等。
通过圆心并且两端都在圆上的线段叫做直径。
一般用d表示。
同一个圆里有无数条直径,所有的直径都相等。
同一个圆里,直径等于两个半径的长度,即d=2r。
圆的大小由半径决定。
圆有无数条对称轴。
(2)圆的画法把圆规的两脚分开,定好两脚间的距离(即半径);把有针尖的一只脚固定在一点(即圆心)上;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
(3)圆的周长围成圆的曲线的长叫做圆的周长。
第七讲 居民地要素综合课件

29
保持居民地各自范围清楚
2018/12/12
30
(3)黄土窑洞居民地综合
沿沟谷自然形状分布的分散式窑洞居民地,应 尽量保持窑洞与谷地取舍的一致性,不使窑洞 朝向山顶或山脊; 成排分布的窑洞,应控制两端位置,其间配置 窑洞符号; 多层分布的窑洞,应首先选取上下两排,减少 内部层数; 应优先选取位于水源附近和道路出入口处的窑 洞;
9
2018/12/12
选取次要街道
1. 2.
3.
4.
选取主要街道后,进而选取以下次要街道: 贯穿整个居民地或大部分居民地的次要街道; 连接码头、车站、广场、公园、外围道路及重 要方位物的次要街道; 有利于保持街区形状和方向的次要街道; 有利于反映街网密度对比的次要街道;
2018/12/12
10
地图学原理课程设计
居民地要素制图综合
主要内容
一. 二. 三.
居民地平面图形的化简 居民地的选取 居民地名称注记的选取与配置
2018/12/12
2
一、居民地平面图形的化简
(一)有街道居住区的形状化简 (二)无街道居住区的形状化简 (三)居民地整个轮廓形状的化简 (四)用圈形符号表示居民地
2018/12/12
3
一、居民地平面图形的化简
构成居民地的四种基本图形
2018/12/12
4
(一)有街道居住区的形状化简
应该从内部结构和外围联系两个方面分 析有街道居住区的图形特点。 内部结构:主要指街道的通行情况、街 网的几何形状和密度、房屋建筑和非建 筑状况、重要的方位物等。 外围联系:主要指居住区四周的进出通 道和所处环境。
小升初数学知识点:平面图形

小升初数学知识点:平面图形
小升初数学知识点:平面图形
小升初数学是学习生涯的关键阶段,为了能够使同学们在数学方面有所建树,小编特此整理了小升初数学知识点:平面图形,以供大家参考。
1、长方形
(1)特征
对边相等,4个角都是直角的四边形。
有两条对称轴。
(2)计算公式
c=2(a+b)
s=ab
2、正方形
(1)特征:
四条边都相等,四个角都是直角的四边形。
有4条对称轴。
(2)计算公式
c=4a
s=a2
3、三角形
(1)特征
由三条线段围成的图形。
内角和是180度。
三角形具有稳定性。
三角形有三条高。
(2)计算公式
s=ah/2
中位线等于上下底和的一半。
等腰梯形有一条对称轴。
(2)公式
s=(a+b)h/2=mh
以上就是小升初数学知识点:平面图形,更多精彩请进入小升初频道。
小升初平面图形知识点归纳

组合图形就是由圆、扇形、弓形与三角形、正方形、长方形等规则图形组合而成的,这是一类更为复杂的不规则图形,为了计算它的面积,常常要变动图形的位置或对图形进行适当的分割、拼补、旋转等手段使之转化为规则图形的和、差关系,同时还常要和“容斥原理”(即:集合A与集合B之间有:S A∪B=S A+S b-S A∩B)合并使用才能解决。
周长和面积的基本公式:C=(a+b)对于平面组合图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法有:(1)加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.(2)减法:这种方法是将所求的不规则图形面积看成是若干个基本规则图形的面积之差.(3)直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.(4)重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.(5)辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.(6)割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.(7)平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积. (8)旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.(9)对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半. (10)重叠法:这种方法是将所求的图形看成是两个或两个以上图形的重叠部分,然后运用“容斥原理”(SA∪B=SA+SB-SA∩B)解决。
北大附中点招考试知识点

暑期小升初—目标[北大附中]课程安排与教学目录第一讲:计算综合目标培养:快速的计算能力培养;灵活的计算技巧培养;复杂的计算问题处理。
共计六大知识点,12个类型,攻克[北大附中]小升初考试分值最大模块。
知识点一:复杂的四则运算知识点二:速算与巧算知识点三:数列的计算知识点四:估算与取整知识点五:分数的分拆识点六:定义新运算第二讲:平面图形综合(一)目标培养:平面图形的巧求周长、角度与面积,熟练运用平面定理解决复杂面积的能力培养;曲面图形的计算与圆形移动问题处理。
共计四大知识点,12 个类型,攻克[北大附中]小升初考试易丢分模块。
知识点一:周长与角度知识点二:平面图形定理知识点三:圆与扇形知识点四:圆形滚动技巧第三讲:平面图形综合(二)目标培养:图形旋转、翻折、平移能力培养;作图能力与图形剪拼的运用能力培养。
共计四大知识点,15 个类型,攻克[北大附中]小升初考试难度较大模块。
知识点一:图形旋转知识点二:图形翻折知识点三:图形平移知识点四:作图与剪拼第四讲:行程综合(一)目标培养:流水行船、火车过桥、常规相遇与追及技巧补充;共计四大知识点,14 个类型,攻克[北大附中]小升初考试必拿分模块。
知识点一:常规相遇知识点二:常规追及知识点三:流水行船知识点四:火车过桥第五讲:行程综合(二)目标培养:利用线段图解复杂图形的能力培养;克服行程大题的恐惧心理。
共计三大知识点,10 个类型,攻克[北大附中]小升初考试有难度模块。
知识点一:多人相遇与追及知识点二:利用线段图巧解行程问题知识点三:行程综合运用第六讲:数学的猜想与归纳目标培养:具备猜想与归纳能力;具备图形归纳代数式,通过文字归纳代数式的处理方法与技巧;在综合题目中的论述与证明能力。
共计五大知识点,12 个类型,攻克北大附中小升初考试常考模块。
知识点一:用字母表示数知识点二:公式递推知识点三:数字递推知识点四:图形递推知识点五:综合题目的递推与归纳第七讲:立体几何综合目标培养:具备三视图观察立体图形能力;培养空间想象能力,进行切割与重组立体图形的能力。
07平面图形的面积解答
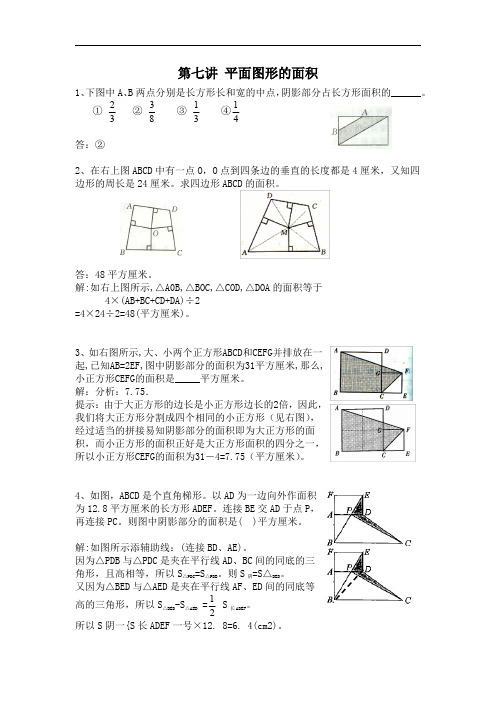
1、 下图中 A、 B 两点分别是长方形长和宽的中点, 阴影部分占长方形面积的______。 2 3 1 1 ① ② ③ ④ 3 8 3 4 答:② 2、在右上图 ABCD 中有一点 O,O 点到四条边的垂直的长度都是 4 厘米,又知四 边形的周长是 24 厘米。求四边形 ABCD 的面积。
4、如图,ABCD 是个直角梯形。以 AD 为一边向外作面积 为 12.8 平方厘米的长方形 ADEF。连接 BE 交 AD 于点 P, 再连接 PC。则图中阴影部分的面积是( )平方厘米。 解:如图所示添辅助线:(连接 BD、AE)。 因为△PDB 与△PDC 是夹在平行线 AD、BC 间的同底的三 角形,且高相等,所以 S△PDC=S△PDB。则 S 阴=S△BED。 又因为△BED 与△AED 是夹在平行线 AF、ED 间的同底等 1 高的三角形,所以 S△BED-S△AED = S 长 ADEF。 2 所以 S 阴一{S 长 ADEF 一号×12. 8=6. 4(cm2)。
中点。GC=
1 FC,则 3
答:
5 。 24
1 1 1 解:如上右图。由 GC= FC,推知 HD= FD= AD,所以所求面积为 EB×AH÷ 3 3 6 1 5 5 2= 2 。 2 6 24
8、 正方形 ABCD 边长是 7 厘米, 它的内部有一个三角形 BEF(如右图) ,线段 AE=4 厘米,DF=2 厘米,那么三角 形 BEF 的面积等于多少平方厘米。 解:三角形 ABC 面积=4×7÷2=14, 三角形 BCF=7×(7-2) ÷2=17.5, 三角形 DEF=(7-4) × 2÷2=3, 正方形 ABCD 面积=7×7=49, 三角形 BEF=49-(14+17.5+3)=14.5
小升初平面图形专题1(直线形)

平面图形专题提升(1)——直线形名称图形周长面积三角形S= a×h÷2=2ah长方形C=2 (a+b)S=a×b= a b正方形C=a×4=4 a S=a×a=a2平行四边形S= a×h= a h梯形S =(a+b)×h÷2=()2a b h例1 如图,四边形ABCD是正方形,三角形ABF的面积比正方形ABCD的面积大12厘米,线段BC的长为8厘米。
求线段CF的长是多少厘米?例2如图,求阴影部分面积。
(单位:cm)(1)(2)GB F C A E DFEDCBA例3 求右图所示四边形的面积。
例4 直角梯形ABCD 中.AE=ED,BC=18,AD=8,CD=6,且BF=2FC,S △GED =S △GFC .求阴影部分的面积。
例5求下列图形的面积(单位:cm)例6如图,已知阴影部分的面积是120平方厘米,E,F 分别是AB,BC 的中点,长方形宽AB 为16厘米,求长方形的长AD.练习1.将一张长8cm ,宽4cm 的长方形纸沿对角线对折后得到如图所示图形,图中阴影部分的周长是__________.2.如图是平行四边形,面积是24平方米,求阴影部分的面积。
(单位:米)221016 3.两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
4.右图是一块长方形草地,长方形的长16米,宽是10米,之间有两条道路,一条是长方形,一条是平行四边形。
那么,草地部分的面积是多少?5.如图,求阴影部分面积。
(单位:cm )6.如右图,正方形ABCD 的边长为6厘米,△ABE 、△ADF 与四边形AECF 的面积彼此相等,求三角形AEF 的面积.7.在图中平行四边形ABCD 的边长BC 长10厘米,直角三角形ECB 的直角边EC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10平方厘米,求平行四边形ABCD 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.直角三角形的两条直角边长度分别是10厘米和18厘米,那么这个直角三角形的面积是多少平方厘米?
答:这个直角三角形的面积是平方厘米。
3.如图,两个正方形的边长分别为3厘米和4厘米,那么阴影部分面积是多少平方厘米?
答:阴影部分面积是平方厘米。
4.如图所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(单位:厘米)
(2)割补法;
2.割补法常见类型:
(1)直线型面积中的割补
(2)圆与扇形中的割补;
(3)差不变;
例3:(1)图中阴影部分面积是多少?
答:图中阴影部分面积是。
(2)如图,正方形ABCD的中心为O,其边长为8,则正方形OEFG与正方形ABCD重叠部分的面积是多少?
答:正方形OEFG与正方形ABCD重叠部分的面积是。
答:阴影部分的面积是平方厘米。
9.图中甲区域比乙区域的面积大57平方厘米,且半圆的半径是10厘米,那么直角三角形的面积是多少平方厘米?(π取3.14)
答:直角三角形的面积是平方厘米。
10.如图,直角三角形的三条边长度为6、8、10,它的内部放了一个半圆,图中阴影部分的面积为多少?
答:图中阴影部分的面积为。
答:这个四边形的面积是平方厘米。
5.已知圆的面积是28.26,那么这个圆的周长是多少?(π取3.14)
答:这个圆的周长是。
6.如图,正方形的面积是12,那么阴影部分的面积是多少?
答:阴影部分的面积是。
7.如图,长方形的长为4,宽为2,那么图中阴影部分的面积是多少?
答:阴影部分的面积是。
8.如图,以三角形三个顶点为圆心,画3个半径为4厘米的圆,那么阴影部分的面积是多少平方厘米?(π取3.14)
第八讲 平面图形综合(一)
知识精讲1:基本图形的计算。
一、基本图形的面积计算
1.正方形:边长×边长,对角线×对角线÷2
2.长方形:长×宽
3.平行四边形:底×高
4.三角形:底×高÷2
5.梯形:(上底+下底)×高÷2
6.圆:π
7.扇形:
二、基本图形周长计算。
1、基本直线型图形的周长:边长相加;
2、圆:2πr
3.扇形:
三、基本图形角度计算。
1、三角形内角和为180°
2.N边形内角和为(n-2)×180°(n≥3)
3.n边形外角和为360°(n≥3)
例1:(1)如图梯形的上底是4厘米,下底是6厘米,阴影部分的面积是10平方厘米,空白部分的面积是多少平方厘米?
答:空白部分的面积是平方厘米。
(2)直角三角形ABC的边AB=5厘米,AC=3厘米,将它的直角边AC对折到斜边AB上,使AC与AD重合,且CE:BE=3:5,则图中阴影部分(未重叠部分)的面积是多少平方厘米?
答:图中阴影部分(未重叠部分)的面积是 Nhomakorabea方厘米。
例2:(1)左图中每一个小圆的半径是1厘米,阴影部分的周长是多少厘米?(π取3.14)
(2)右图中在三角形ABC中,∠ABD=23°,∠ACD=31°,∠A=55°,那么∠BDC等于多少度?
知识精讲2:割补法巧求面积
1.不规则图形求面积的方法:
(1)整体减空白;
例4:如图,ABCD是正方形,ED=AF=2厘米,那么阴影部分的面积是多少?
例5:AB=AE=6厘米,BC=CF=4厘米,那么阴影部分的面积是多少平方厘米?(π取3.14)
例6:O是小圆的圆心,C是大圆的圆心,OC垂直AB,三角形ABC的面积45平方厘米,那么阴影部分的面积是多少?(π取3.14)
例7:如图,在长方形ABCD中,BC=10厘米,CD=6厘米,三角形ABF的面积比三角形DEF的面积大20平方厘米,求DE的长是多少厘米?
答:DE的长是厘米。
例8:如图,三角形ABC是直角三角形,AB=20厘米,以AB为直径画半圆,如果阴影甲比阴影乙的面积小31平方厘米,求BC的长。(π取3.14)
答:BC的长是厘米。
课后作业:
1.如图,平行四边形ABCD的边长BC为15厘米,AB垂直于BC,AE长为6厘米,那么平行四边形ABCD的面积是多少平方厘米?
