小升初专题几何图形和面积
【小升初数学专项练习】《二、图形与几何6.三角形的周长与面积--基础(附答案)

小升初数学专项练习一线名师严选内容,逐一攻克☆基本概念、基本原理、基础技能一网打尽☆点拨策略思路,侧重策略指导,拓宽眼界思路☆6.三角形的周长与面积【小升初考点归纳】三角形的周长等于三边长度之和.三角形面积=底×高÷2.【经典例题】一.选择正确的答案,把序号填在括弧中(共9小题)1.(2019春•镇康县期中)把一根铁丝围成一个等腰三角形,它的两条邻边分别长16cm、6cm;如果把这根铁丝围成一个正方形,边长是()cm.A.7B.9.5C.7或9.5【解析】解:(16+16+6)÷4=38÷4=9.5(厘米)答:边长是9.5厘米.故选:B.2.(2018秋•黄冈期末)一个等腰直角三角形一条直角边的长是4厘米,它的面积是()平方厘米.A.16B.8C.4【解析】解:4×4÷2=16÷2=8(平方厘米)答:它的面积是8平方厘米,故选:B.3.(2018秋•龙泉驿区期末)把一个等腰梯形分成两个三角形,这两个三角形的()完全相同.A.面积B.周长C.形状D.前面三个都不正确【解析】解:把一个等腰梯形分成两个三角形,如右图:A:这两个三角形等高,但是底不相等,它们的面积不相等;B:一个三角形的周长是梯形的上底+梯形的腰长+对角线的长度;另一个三角形的周长是梯形的下底+梯形的腰长+对角线的长度;上底和下底不相等,所以它们的周长也不相同;C:一个是钝角三角形一个锐角三角形,它们的形状不同;故选:D.4.(2018秋•荔湾区期末)一个直角三角形如图(单位:cm),a是()cm.A.1.2B.2.4C.4.8D.6【解析】解::3×4÷2=6(cm2)6×2÷5=2.4(cm)答:a是2.4cm.故选:B.5.(2018秋•成都期末)一个直角三角形的两条直角边分别是3m和5m,它的面积是()A.18m2B.8m2C.7.5m2D.无法计算【解析】解:3×5÷2=15÷2=7.5(m2)答:它的面积是7.5m2.故选:C.6.(2018秋•西山区期末)一个三角形的底和高都扩大到原来的3倍,它的面积就扩大到原来的()倍.A.3B.6C.9D.27【解析】解:3×3=9答:它的面积就扩大到原来的9倍.故选:C.7.(2018秋•崂山区期末)一个三角形和一个平行四边形底相等,面积也相等,如果平行四边形的高是6厘米,那么三角形的高是()厘米.A.6B.3C.12D.18【解析】解:设三角形的高为H,平行四边形的高为h,三角形的面积=底×H×,平行四边形的面积=底×h;底×H×=底×h;则H=h,所以三角形的高=6×2=12(厘米);答:三角形的高是12厘米.故选:C.8.(2018秋•崂山区期末)图中平行四边形的面积是64cm2,涂有阴影的三角形面积是()cm2.A.16B.32C.128【解析】解:64÷2=32(平方厘米);答:涂有阴影的三角形面积是32cm2.故选:B.9.(2018秋•盘龙区期末)一个等腰直角三角形的一条直角边是5cm,它的面积是()A.25cm2B.12.5cm2C.50cm2D.无法确定【解析】解:5×5÷2,=25÷2,=12.5(平方厘米),答:它的面积是12.5平方厘米,故选:B.二.将正确答案填写在横线上(共11小题)10.(2019春•庆云县期中)等腰三角形的两条边长分别是3cm和6cm,则它的周长是15cm.【解析】解:因为3+3=6,所以3不能是等腰三角形等腰,只能是底边,所以这个等腰三角形的腰是6厘米,底是3厘米,6+6+3=12+3=15(cm)答:则它的周长是15cm.故答案为:15cm.11.(2018秋•黄冈期末)一个三角形的面积是130平方厘米,与它等底等高的平行四边形的面积是260平方厘米.【解析】解:130×2=260(平方厘米)答:与它等底等高的平行四边形的面积是260平方厘米.故答案为:260.12.(2018秋•黄冈期末)一个三角形的面积是30平方分米,底是7.5分米,它的高是8分米.【解析】解:30×2÷7.5=60÷7.5=8(分米)答:它的高是8分米.故答案为:8.13.(2018秋•中山市期末)一个直角三角形两条直角边分别是7厘米和9厘米,这个三角形斜边上对应的高是6.3厘米,它的斜边长为10厘米.【解析】解:设它的斜边长为x厘米,6.3x÷2=7×9÷26.3x=63x=10答:它的斜边长为10厘米.故答案为:10.14.(2018秋•黄埔区期末)一个三角形的面积是16cm2,其中一个底是8cm,这个底上的高是4cm,用两个这样的三角形拼成的平行四边形的面积是32cm2.【解析】解:16×2÷8=32÷8=4(厘米)16×2=32(平方厘米)答:这个底上的高是4cm,用两个这样的三角形拼成的平行四边形的面积是32cm2.故答案为:4,32.15.(2019•福田区)一个三角形的底是16厘米,高是10厘米,三角形的面积是80厘米2;与它等底等高的平行四边形的面积是160厘米2.【解析】解:三角形的面积:16×10÷2=160÷2=80(厘米2)平行四边形的面积:80×2=160(厘米2)答:三角形的面积是80厘米2,与它等底等高的平行四边形的面积是160厘米2.故答案为:80;160.16.(2018秋•南通期末)一个三角形的面积是200平方米,高是20米,底是20米,与它等底等高的平行四边形面积是400平方米.【解析】解:(1)200×2÷20=400÷20=20(米)答:底是20米.(2)200×2=400(平方米)答:与它等底等高的平行四边形的面积是400平方米.故答案为:20,400.17.(2018秋•龙泉驿区期末)三角形的底是1.25分米,这条底对应的高是1.6分米,与这个三角形等底等高的平行四边形的面积是2平方分米.【解析】解:1.25×1.6=2(平方分米)答:与这个三角形等底等高的平行四边形的面积是2平方分米.故答案为:2.18.(2018秋•成都期末)一个等腰三角形的两条直角边的长度和是20cm,它的面积是50 cm2.【解析】解:20÷2=10(cm)10×10÷2=100÷2=50(cm2)答:它的面积是50cm2.故答案为:50.19.(2018秋•台安县期末)一块三角形草坪面积是96平方米,底是16米,高是12米.【解析】解:96×2÷16=192÷16=12答:高是12米.故答案为:12.20.(2018秋•成华区期末)读图可知:三角形通过割补转化成了平行四边形.原三角形的高是平行四边形高的2倍,平行四边形与三角形的底相等.【解析】解:读图可知:三角形通过割补转化成了平行四边形.原三角形的高是平行四边形高的2倍,平行四边形与三角形的底相等.故答案为:2倍,相等.三.解析题(共5小题)21.(2019•虹口区模拟)一块三角形的交通标志牌(如右图),它的面积大约是28平方分米,底是8分米,高大约是7分米.【解析】解:28×2÷8,=56÷8,=7(分米);故答案为:7.22.(2018•杭州模拟)我们都知道,三角形面积的计算公式是“底×高÷2”.那么,为什么要“÷2”呢?请写一写或画一画的方式,把你的想法表达出来.【解析】解:用两个完全相同的三角形拼成一个平行四边形,因为平行四边形的面积=底×高,而平行四边形的一半为三角形,所以要“÷2“.23.(2017秋•宁都县期末)图中三角形的面积是12平方厘米,(1)求出它的高;(2)把它分成甲乙两个小三角形,使甲三角形的面积是乙三角形的2倍.【解析】解:12×2÷6=24÷6=4(厘米)6×=4(厘米)6﹣4=2(厘米)如图所示:24.(2018春•南开区期末)在图中,BC∥DE,∠1=63.5°,AE=EC.(1)∠2+∠3=116.5°.(2)∠1+∠3+∠4+∠5=243.5°.(3)若梯形BCED的面积是3.6cm2,则三角形ABC的面积是 4.8cm2.【解析】解:(1)因为BC∥DE,所以∠3=∠CDE,∠2+∠3=∠2+∠CDE=∠ADC,又因为∠1=63.5°,所以,∠ADC=180°﹣63.5°=116.5°.即:∠2+∠3=116.5°(2)∠1+∠3+∠4+∠5=∠1+∠CDE+∠4+∠5,因为∠CDE+∠4+∠5正好是三角形DCE的内角和=180°,所以:∠1+∠3+∠4+∠5=63.5°+180°=243.5°(3)因为E为AC的中点,BC∥DE,所以:D是AB的中点,三角形ADE的面积=三角形DCE的面积,三角形ADC的面积=三角形BDC的面积,设三角形DEC的面积为x平方厘米,则:三角形BDC的面积=三角形ADC的面积=2x=3.6﹣x,所以:x=1.2,三角形ABC的面积=(1.2+1.2)×2=4.8(平方厘米)故答案为:(1)116.5°,(2)243.5°,(3)4.825.(2018春•长沙期中)一根长6分米的铁丝.围绕如图一周够吗?【解析】解:17+23+17=40+17=57(厘米)6分米=60厘米,60厘米>57厘米,所以6分米围绕图形一周够.答:围绕如图一周够.。
小升初专题复习几何图形

小升初专题复习——几何图形一、三视图及展开图例题1:用同样大小的正方体摆成的物体,从正面看到,从上面看到,从右面看到〔 〕A .B .C .D .变式练习:如图,它是用6个棱长为1分米的正方体拼成的. ①它的外表积是 . ②它的体积是 .二、三角形的底边及面积关系例题1:如图.A 、B 是长方形长和宽的中点,阴影局部的面积是长方形面积的 %.例题2:如图,三角形ABC 面积为27平方厘米,AE=CE ,BF=BC ,求三角形BEF 的面积.变式练习1:如图,直角梯形ADCB 中,三角形BEC 、四边形CEAF 和三角形CFD 的面积一样大.BC=16、AD=20、AB=12,求三角形AEF 的面积.教师姓名 学科 数学 上课时间 讲义序号 (同一学生)学生姓名年级六年级组长签字日期课题名称 几何图形变式练习2:如图,梯形ABCD中共有〔〕对面积相等的三角形A. 22 B. 3 C. 4 D. 5变式练习3:在如图中,平行四边形的面积是20平方厘米,图中甲、丙两个三角形的面积比是,阴影局部的面积是平方厘米.三、多边形内角和例题1:把表填完整多边形…边数 3 4 5 6 …内角和180°180°×2 180°×3 180°×5 …变式练习:探索〔1〕完成表格中未填局部.〔2〕根据表中规律,八边形的内角和是度.〔3〕假设图形的边数为a,内角和为s,请你用一个含有字母的关系式表示图形边数及内角和的关系..图形边数 3 4 5内角和180 180×2 180×3四、长度比拟例题1:面积相等的情况下,长方形、正方形和圆相比,〔〕的周长最短.A.长方形B.正方形C.圆例题2:如图,A是一个圆,B是由三个半圆围成的图形,那么它们周长的大小关系是C A C B.变式练习1:下面三个图形中,哪两个图形的周长相等?〔〕A.图形①和②B.图形②和③C.图形①和③变式练习2:在图形中甲的周长〔〕乙的周长.A.大于B.小于C.等于拓展提升:某高层公寓大火时,小王逃生的时候看了下疏散通道如下图,那么最快逃离到楼梯〔图中阴影〕的通道共有〔〕条.A. 3 B. 9 C. 6 D. 12五、组合图形计数例题1:如图中直角的个数为〔〕个.A. 4 B. 8 C. 10 D. 12例题2:如图,共有〔〕条线段.A. 4 B. 8 C. 10 D. 12例题3:数一数,在右图中共有〔〕个三角形.A.10 B. 11 C. 12 D. 13 E.14A.4 B. 8 C. 10 D. 12变式练习2:如图中直角有〔〕个.A. 1 B. 2 C. 3 D. 4变式练习3:这里共有〔〕条线段.A.三条B.四条C.五条D.六条变式练习4:如下图的7×7的方格内,有许多边长为整数的正方形,其中在有的正方形中黑方格及白方格的个数占一半〔同样多〕.像这样的正方形有〔〕个.A.26 B. 36 C. 46 D. 56E.66变式练习5:图中共有〔〕个长方形.A. 30 B. 28 C. 26 D. 24变式练习6:如图,三角形一共有个.拓展提升1:如图是半个正方形,它被分成一个一个小的等腰三角形,图中,正方形有10 个,三角形有47 个.拓展提升2:如图中,三角形的个数有多少?六、图形的拆拼〔切拼〕例题1:一个圆的周长是15.7分米,把这个圆等分成假设干个小扇形,拼成一个近似的长方形,这个近似的长方形的长是分米,宽是分米.例题2:爸爸给女儿买了一个圆柱形的大生日蛋糕,女儿把蛋糕竖直方向切成22块分给22个小朋友,切成的大小不一定相等.那么至少需切的刀数为?变式练习1:在一块边长为4厘米的正方形的铁皮上,剪出直径为2厘米的小圆片,最多可剪〔〕片.A. 3 B. 4 C. 5 D. 6变式练习2:用一条直线将一个正方形分成两个完全一样的两局部,有几种分法〔〕A. 1种B. 2种C. 3种D. 4种变式练习3:在一块长10分米、宽5分米的长方形铁板上,最多能截取11 个直径是2分米的圆形铁板.拓展提升:请将下面等边三角形按要求分割成假设干个形状和大小都一样的三角形〔1〕分成2个〔2〕分成3个〔3〕分成4个〔4〕分成6个七、立体图形的外表积例题1:把14个棱长为1的正方体,在地面上堆叠成如下图的立体,然后将露出的外表局部染成红色.那么红色局部的面积为〔〕A. 21 B. 24 C. 33 D. 37例题2:如图,在棱长为3的正方体中由上到下,由左到右,由前到后,有三个底面积是1的正方形高为3的长方体的洞,那么所得物体的外表积为.变式练习2:把假设干个边长2厘米的正方体重叠起来堆成如下图的立体图形,这个立体图形的外表积是平方厘米.变式练习3:如图是一个长3厘米、宽及高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方体,它的外表积〔〕A.比原来大B.比原来小C.不变拓展提升〔难〕:在一个棱长为8的立方体上切去一个三棱柱〔如图〕,那么外表积减少.八、立体图形的体积例题1:如图的体积是.〔单位:厘米〕例题2:一支没有用过的圆柱形铅笔,长18厘米,体积是9立方厘米,使用一段时间后变成了如图的样子,这时铅笔的体积是多少立方厘米?变式练习1:有一棱长为5cm的正方体机器零件,现在它的上下面挖去了一个直径为2cm的圆孔,求剩下机器零件的外表积和体积?九、等积变形例题1:如下图,把底面直径8厘米的圆柱切成假设干等分,拼成一个近似的长方体.这个长方体的外表积比原来增加80平方厘米,那么长方体的体积是立方厘米.例题2:一个酸奶瓶〔如图〕,它的瓶身呈圆柱形〔不包括瓶颈〕,容积是32.4立方厘米.当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余局部高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?变式练习1:一个圆锥形沙堆,底面积是3.6平方米,高1.2米.把这堆沙装在长2米、宽1.5米的沙坑里,可以装多高?变式练习2:有一种饮料瓶的容积是50立方厘米,瓶身呈圆柱形〔不包括瓶颈〕.现在瓶中装有一些饮料,正放时饮料高度为20厘米,倒放时空余局部的高度为5厘米.瓶内现有饮料立方厘米.变式练习3:水平桌面上放着高度都为10厘米的两个圆柱形容器A和B,在它们高度的一半处有一连通管相连〔连通管的容积忽略不计〕,容器A、B底面直径分别为10厘米和16厘米.关闭连通管,10秒钟可注满容器B,如果翻开连通管,水管向B容器注水6秒钟后,容器A中水的高度是多少呢?〔π取3.14〕变式练习4:A和B都是高度为12厘米的圆柱形容器,底面半径分别是1厘米和2厘米,一水龙头单独向A 注水,一分钟可注满.现将两容器在它们的高度的一半出用一根细管连通〔连通管的容积忽略不计〕,仍用该水龙头向A注水,求〔1〕2分钟容器A中的水有多高?〔2〕3分钟时容器A中的水有多高.十、数阵图中找规律的问题例题1:把自然数依次排成以下数阵:1,2,4,7,11,…3,5,8,12,…6,9,13,…10,14,…15,……现规定横为行,纵为列.求〔1〕第10行第5列排的是哪一个数?〔2〕第5行第10列排的是哪一个数?〔3〕2004排在第几行第几列?变式练习1:淘气用小棒搭房子,他搭3间用了13根小棒,像这样搭15间房子要用〔〕根小棒.A. 60 B. 61 C. 65 D. 75。
苏教版六年级数学小升初专题复习五几何初步知识
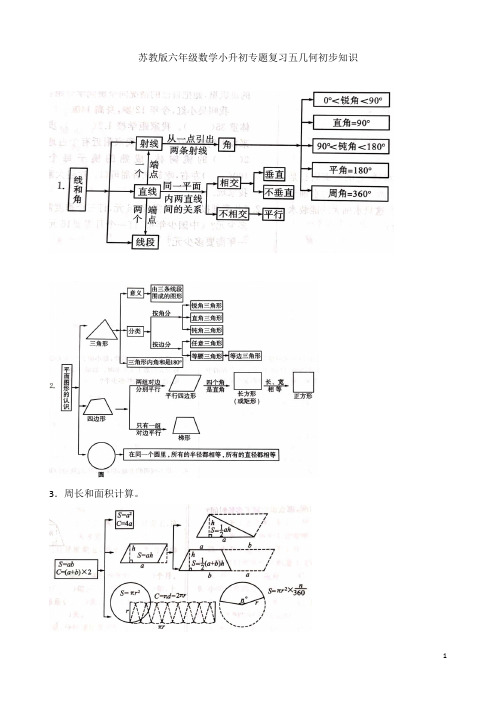
苏教版六年级数学小升初专题复习五几何初步知识3.周长和面积计算。
4.立体图形一、定义1.线段:用直尺把两点连接起来,就得到一条线段,线段长就是这两点间的距离。
两点间所有连线中线段最短。
2.射线:把线段的一端无限延长,可以得到条射线。
手电筒发出的光、太阳射出的光线都可看成是射线。
3.直线:把线段的两端无限延长,可以得到一条直线。
二、直线、线段、射线的比较名称三、同一平面上线与线的关系同一平面上的两条直线或平行或相交。
1.垂线:两条直线相交成直角时,这两条直线叫作互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足。
2.平行线:在同一平面内不相交的两条直线叫作平行线。
(1)平行线之间的距离处处相等;(2)平行线间垂线段最短,并且有无数条;(3)垂直于同一条直线的两条直线互相平行。
3.点到直线的连线中,垂线段最短4.线段AB的垂直平分线上的任意一点到线段两端的连线相等。
一、角的分类角:从一点起画两条射线,所组成的图形叫作角。
角两边叉开得越大,角越大;角的大小与角两边的长短无关。
二、角的测量利用量角器可以画角或量出角的度数。
首先将量角器的中心与角的顶点重合,然后再将量角器的零刻度线与角的一边重合,另一条边所对准的刻度就是这个角的度数。
注意要分清是内刻度线还是外刻度线。
三、画角画角的方法有很多,我们应该学会用量角器画指定大小的角。
画角时,首先要确定角的顶点,并画出角的一条边,然后将量角器的中心和零刻度线与角的顶点和画好的一条边都分别重合,数出量角器上所画角的度数,做好标记,然后连接顶点和标记,这样就画好了一个指定度数的角。
要注意美观。
形一、平行四边形和梯形(四边形)圆定义:两组对边分别平行的四边形叫作平行四边形。
只有一组对边平行的四边形叫作梯形。
二、三角形(由三条线段围成的图形)1.按角分2.按边分3.等腰三角形的特征和性质两腰相等,两底角相等,底边上的高是底边的垂直平分线。
4.等边三角形的特征和性质,5.三角形的一些特征和性质 (1)三角形具有稳定性; (2)三角形内角和是180º(3)三角形中任意两边之和大于第三边(4)在三角形中大角所对的边也大;在直角三角形中,斜边最长 (5)在等腰直角三角形中,斜边上的高等于斜边的一半三、圆(封闭的曲线图形) 1.圆的各部分名称在同一个圆内,有无数条直径和半径,所有的直径都相等,所有的半径都相等。
小升初数学复习专题:求阴影部分面积(含答案解析)

解题公式、方法1、几何图形计算公式:1) 正方形:周长=边长 ×4 C=4a面积 = 边长 × 边长 S=a×a2) 正方体:表面积 = 棱长 × 棱长 ×6 S 表 = a×a×6体积 = 棱长 × 棱长 × 棱长 V=a×a×a3) 长方形:周长 =(长 + 宽)×2 C=2(a+b)面积 = 长 × 宽 S=ab4) 长方体:表面积 =(长 × 宽 + 长 × 高 + 宽 × 高)×2 S=2(ab+ah+bh)体积 = 长 × 宽 × 高 V=abh5) 三角形:面积 = 底 × 高 ÷2 s=ah÷26) 平行四边形:面积 = 底 × 高 s=ah7) 梯形:面积 =(上底 + 下底)× 高 ÷2 s=(a+b)×h÷28) 圆形:周长 = 直径 ×Π=2×Π× 半径 C=Πd=2Πr面积 = 半径 × 半径 ×Π9) 圆柱体:侧面积 = 底面周长 × 高表面积 = 侧面积 + 底面积 ×2体积 = 底面积 × 高10) 圆锥体:体积 = 底面积 × 高 ÷32、面积求解大致分为以下几类:Ø 从整体图形中减去局部;割补法:将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
练习题例 1. 求阴影部例 2. 正方形面分的面积。
(单位: 厘米) 积是 7 平方厘米,求阴影部分的面积。
(单位: 厘米)例 3. 求图中阴影部分的面积。
专题17:《平面几何的面积(一)》小升初数学专题讲练 (思维导图+知识点精讲+例题分析+变式训练
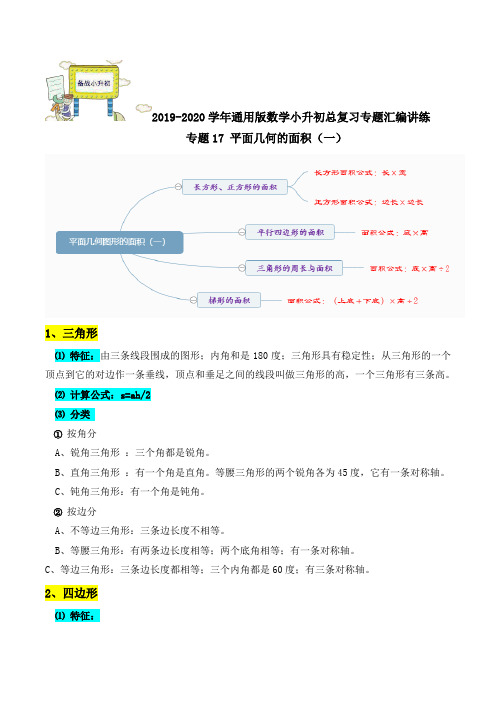
2019-2020学年通用版数学小升初总复习专题汇编讲练专题17 平面几何的面积(一)1、三角形⑴特征:由三条线段围成的图形;内角和是180度;三角形具有稳定性;从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,一个三角形有三条高。
⑵计算公式:s=ah/2⑶分类①按角分A、锐角三角形:三个角都是锐角。
B、直角三角形:有一个角是直角。
等腰三角形的两个锐角各为45度,它有一条对称轴。
C、钝角三角形:有一个角是钝角。
②按边分A、不等边三角形:三条边长度不相等。
B、等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
C、等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
2、四边形⑴特征:①四边形是由四条线段围成的图形。
②任意四边形的内角和是360度。
③只有一组对边平行的四边形叫梯形。
④两组对边分别平行的四边形叫平行四边形,它简洁变形。
长方形、正方形是特殊的平行四边形;正方形是特殊的长方形。
⑵分类①长方形A、特征:对边相等,4个角都是直角的四边形。
有两条对称轴。
B、计算公式:c=2(a+b) s=ab②正方形A、特征:四条边都相等,四个角都是直角的四边形。
有4条对称轴。
B、计算公式:c=4a s=a²③平行四边形A、特征:两组对边分别平行的四边形;相对的边平行且相等;对角相等;相邻的两个角的度数之和为180度;平行四边形简洁变形。
B、计算公式:s=ah④梯形A、特征:只有一组对边平行的四边形;中位线等于上下底和的一半;等腰梯形有一条对称轴。
B、计算公式:s=(a+b)h/2=mh3、圆⑴圆的生疏圆是平面上的一种曲线图形。
圆中心的一点叫做圆心。
一般用字母o表示。
半径:连接圆心和圆上任意一点的线段叫做半径。
一般用r表示。
在同一个圆里,有很多条半径,每条半径的长度都相等。
通过圆心并且两端都在圆上的线段叫做直径。
一般用d表示。
同一个圆里有很多条直径,全部的直径都相等。
小升初复习专题求阴影部分面积(含答案)(2020年九月整理).doc

2017年小升初复习专题-求阴影部分面积(含答案)目标:巩固小学几何图形计算公式,并通过专题复习,加强学生对于图形面积计算的灵活运用。
1、几何图形计算公式:1)正方形:周长=边长×4 C=4a 面积=边长×边长S=a×a2)正方体:表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a3)长方形:周长=(长+宽)×2 C=2(a+b) 面积=长×宽S=ab4)长方体:表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh) 体积=长×宽×高V=abh5)三角形:面积=底×高÷2 s=ah÷26)平行四边形:面积=底×高s=ah7)梯形:面积=(上底+下底)×高÷2 s=(a+b)×h÷28)圆形:周长=直径×Π=2×Π×半径C=Πd=2Πr 面积=半径×半径×Π9)圆柱体:侧面积=底面周长×高表面积=侧面积+底面积×2 体积=底面积×高10)圆锥体:体积=底面积×高÷32、面积求解大致分为以下几类:➢从整体图形中减去局部;➢割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例1.求阴影部分的面积。
(单位:厘米) 例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(完整版)小学六年级小学升初中小升初阴影面积专题复习经典例题图形面积几何图形(含答案)

阴影部分面积专题小学六年级小学升初中1. 求如图阴影部分的面积.(单位:厘米)2. 如图,求阴影部分的面积.(单位:厘米)3. 计算如图阴影部分的面积.(单位:厘米)4. 求出如图阴影部分的面积:单位:厘米.6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)11. 求下图阴影部分的面积.(单位:厘米)12. 求阴影部分图形的面积.(单位:厘米)r ------ io ------- 113. 计算阴影部分面积(单位:厘米)14. 求阴影部分的面积.(单位:厘米)15. 求下图阴影部分的面积:(单位:厘米)16. 求阴影部分面积(单位:厘米)17. (2012&泰县)求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积. 1526356分析阴影部分的面积等丁梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答…n 2解:(4+6) X4士2士2-3.14 X士2,2=10— 3.14 X4士2,=10-6.28 ,=3.72 (平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.1526356分析根据图形可以看出:阴影部分的面积等丁正方形的面积减去4个扇形的面积.正方形的面积等丁(10X 10) 100平方厘米,4个扇形的面积等丁半径为(10士2) 5厘米的圆的面积,即:3.14 X 5X 5=78.5 (平■方厘米). 解答解:扇形的半径是:10 士2,=5 (厘米);10X 10 -3.14 X 5X 5,100-78.5 ,=21.5 (平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.考点组合图形的面积.1526356分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等丁直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10 -2=5 (厘米),长方形的面积*X宽=10X 5=50 (平方厘米),半圆的面积=兀r2士2=3.14 X 52-2=39.25 (平■方厘米),阴影部分的面积=长方形的面积-半圆的面积,=50- 39.25 ,=10.75 (平方厘米);答:阴影部分的面积是10.75 .点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看届丁哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.1526356专题平■面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积-以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8X4-3.14 X42-2,=32 - 25.12 ,=6.88 (平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄活楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.1526356分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4 H 米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2X圆的面积”算出答案.解答解:S=^ r2_ ,_ . 2=3.14 X (4士2)=12.56 (平方厘米);阴影部分的面积=2个圆的面积,=2X 12.56 ,=25.12 (平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.1526356分析图一中阴影部分的面积=大正方形面积的一半-与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积-平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6X6-2-4X6-2=6 (平方厘米);图二中阴影部分的面积=(8+15) X (48士8)士 2 - 48=21 (平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.1526356分析由图意可知:阴影部分的面积皂圆的面积,乂因圆的半径为斜边上的高, 4利用同一个三角形的面积相等即可求出斜边上的高,也就等丁知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15X 20-2X2-25,=300+ 25,=12 (厘米);阴影部分的面积:lx 3.14 X 122,4=Lx 3.14 X 144,=0.785 X 144,=113.04 (平■方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积. 1526356 分析(1)圆环的面积等丁大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积-三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等丁圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:223.14 X (上)-3.14 X 〔萱),2 2=28.26 - 3.14 ,=25.12 (平方厘米);(2)阴影部分的面积:3.14 x 32--X (3+3) X3, 2=28.26 - 9,=19.26 (平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径. 9. 如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.1526356专题平■面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积-以10-2=5厘米为半径的半圆的面积-以3-2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14 X ( 10+3),=3.14 X 13,=40.82 (厘米);面积:ix 3.14 X [ (10+3) 士2]2—【X 3.14 X (10 士2) 2 2ix 3.14 X (3 士2) 2,=以 3.14 X (42.25 - 25 - 2.25),2=以 3.14 X 15,=23.55 (平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=兀r,得出图中两个小半圆的弧长之和等丁大半圆的弧长,是解决本题的关键.10. 求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.1526356■刀忻先用“3+3=6'求出大扇形的半径,然后根据“扇形的面积卫*”分别计360算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积-小扇形的面积=阴影部分的面积”解答即可.解:r=3, R=3+3=6 n=120,解答$喙新一点兀=—"■-□OU JuU=37.68 - 9.42 ,=28.26 (平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11. 求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.1526356分析先求出半圆的面积3.14 X (10士2)2-2=39.25平方厘米,再求出空白三角形的面积10X (10士2)士2=25平方厘米,相减即可求解.2解答解:3.14 X (10士2)士2 - 10X (10士2)士 2=39.25 - 25=14.25 (平■方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积北圆的面积-空白三角形的面积.12. 求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.1526356分析求阴影部分的面积可用梯形面积减去圆面积的1,列式计算即可.42解答解:(4+10) X4士2-3.14 X4 士4,=28 - 12.56 ,=15.44 (平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13. 计算阴影部分面积(单位:厘米)考点组合图形的面积.1526356专题平■面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积-三角形①的面积,平■行四边形的底和高分另U为10厘米和15厘米,三角形①的底和高分别为10厘米和(15-7)厘米,利用平■行四边形和三角形的面积公式即可求解.解答解:10X 15- 10X ( 15-7)士2,=150- 40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.考点梯形的面积.1526356分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等丁梯形的上底,代入梯形的面积公式即可求解.=96 士2,=48 (平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15. 求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.1526356分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2X 3-2=6 士2=3 (平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16. 求阴影部分面积(单位:厘米).考点组合图形的面积.1526356分析由图意可知:阴影部分的面积=梯形的面积-圆的面积,梯形的上底和高[4都等丁圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9) X4士2-3.14 X42x1,4=13X4士2-3.14 X4,=26 - 12.56 ,=13.44 (平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等丁圆的半径,且阴影部分的面积=梯形的面积-[圆的面积.17. (2012&泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.1526356分析由图可知,阴影部分的面积=梯形的面积-半圆的面积.梯形的面积(a+b)h,半圆的面积 m兀「2,将数值代入从而求得阴影部分的面积.解答解:*X(6+8) X (6士2)— 3.14 X (6士2)2=以14X3-以 3.14 X 9, 2 '=21 - 14.13,=6.87 (平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
小升初图形面积40题

小升初图形面积40题一、计算下列图形的面积1、一个正方形边长是4米,面积是()平方米。
2、一个长方形长是6厘米,宽是4厘米,面积是()平方厘米。
3、一个三角形底是8分米,高是5分米,面积是()平方分米。
4、一个梯形上底是3厘米,下底是5厘米,高是4厘米,面积是()平方厘米。
5、一个平行四边形底是10分米,高是4分米,面积是()平方分米。
二、求下列图形的面积6、有一个平行四边形,它的一组邻边分别长5厘米和8厘米,这个平行四边形的面积是多少平方厘米?61、有一个三角形,它的底长是10厘米,高是6厘米,这个三角形的面积是多少平方厘米?611、有一个梯形,它的上底长是3厘米,下底长是5厘米,高是4厘米,这个梯形的面积是多少平方厘米?6111、有一个正方形,它的边长是6厘米,这个正方形的面积是多少平方厘米?三、比较图形的面积大小10、下面的两个图形,哪一个的面积更大一些?101、下面的两个图形,哪一个的面积更大一些?1011、下面的两个图形,哪一个的面积更大一些?下面的两个图形,哪一个的面积更大一些?下面的两个图形,哪一个的面积更大一些?下面的两个图形,哪一个的面积更大一些?小升初组合图形的面积典型试题在数学的学习中,组合图形的面积是一个重要的概念,尤其在小升初阶段,这一概念的重要性更加凸显。
它不仅涉及到基础几何知识,还考察了学生的逻辑思维和问题解决能力。
本文将通过一些典型的试题,探讨如何解决这类问题。
一、理解基本概念我们需要理解什么是组合图形。
组合图形是由两个或两个以上的基本图形组合而成的图形。
例如,一个房子可以由一个矩形和一个三角形组成,一个汽车可以由一个圆形和一个矩形组成。
二、掌握基本方法在计算组合图形的面积时,我们通常使用以下两种方法:1、分解法:将组合图形分解成几个基本图形,然后分别计算每个基本图形的面积,最后将它们相加得到组合图形的总面积。
2、直接计算法:如果组合图形无法分解成基本图形,或者分解起来比较复杂,我们可以直接计算整个组合图形的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形等积变形:
①:等底等高的两个三角形面积相等。
如右图,AB 平行CD ,
有ACD BCD S S ∆∆=,进一步可得出12S S =
②:两个三角形高相等,面积之比等于底边之比;
两个三角形底边相等,面积之比等于高之比。
③:共边定理:如图,△ABC 和△ABD 有公共底边AB ,
它们另一个顶点的连线CD 和AB 相交于点E ,则有 ABC ABD S CE S DE ∆∆=。
(因为ABC AEC ABD AED S S S S ∆∆∆∆=)
鸟头定理:
如右图,△AED 和△ABC 有一个公共角,则有
AED ABC S AE AD S AB AC
∆∆=⨯ 蝴蝶定理:
如图在任意四边形中,对角线AC 和BD 相交于O 点,则有
①1423
S S S S =,或1324S S S S ⨯=⨯ ②
ABD DBC S AO S OC ∆∆= (因为23ABD DBC S S AO S S OC ∆∆==)
梯形蝴蝶定理:
这是蝴蝶定理的特殊情况,如图,在梯形ABCD 中有
①221324S S S S ⨯==
②221324::::::S S S S a b ab ab =
梯形ABCD 面积占的份数为2
()a b + DO :OB =AO :OC =a :b
燕尾定理:
如图,在三角形中,AD ,BE ,CF 相交于点O ,
则有ABO ACO S BD S DC
∆∆= (因为ABO OBD ACO OCD S S S S ∆∆∆∆=) 各种周长面积体积公式
1. 如图,已知正方形ABCD和正方形AEFG的边长分别为8和5,且B,A,E三点在一条直线上,求△BDF的面积
2. 如图,圆的面积和长方形的面积相等,已知圆的周长是62.8厘米,求阴影部分的周长。
(π取
3.14)
3. 已知梯形ABCD的下底BC是上底AD长度的1.5倍,且图中阴影部分和空白部分面积相等,△OBC面积等于12,求△OAD的面积。
4. 如图,阴影部分面积占正方形面积的_______%
第4题第5题
5. 图中阴影①比阴影②面积小48平方厘米,AB=40厘米,求BC的长。
6. 如图,正方形ABCD的边长是4厘米,EF和AB平行,图中阴影部分的面积等于_________。
第6题第7题
7. 已知△DOC面积等于15平方厘米,
2
3
BO BD
,求梯形ABCD的面积。
8. 如图,已知OC=2 AO,四边形EOCD的面积等于10平方厘米,求梯形EBCD的面积。
9. 如图梯形ABCD面积是45平方厘米,高6厘米,底边BC长10厘米,求△OBC的面积。
10. 已知平行四边形ABCD面积是7.2平方厘米,E是BC中点,求阴影部分面积是多少?
11. 已知正方形ABCD的边长是5厘米,△ADF比△FCE面积小5平方厘米,求CE的长。
12. 有一个边长是10厘米的正方体容器,里面装了一半深度的水1,问①将一个底面直径是6厘米,高8厘米的圆柱体铁块底面朝下放入容器中,容器中的水面上升多少厘米?
②将一个底面直径是8厘米,高9厘米的圆柱体铁块放入容器中,容器中的水面上升多少厘米?
13. 一种正方形小方桌的边长是1米,把它的四边都撑开,就成了一个圆形(如图)。
求撑开以后的面积。
14. 如图,△ABC 中,AD 的长度是AB 的
34,AE 长度是AC 的23
,则△ADE 的面积是△ABC 的________。
第14题 第15题
15. 如图,△ABC 中,13BF AB =,14CD BC =,15AE AC =,则()()
DEF ABC S S ∆∆= 16. 如图,正方形ABCD 的面积是60平方厘米,E ,F 分别是BC 和CD 的中点,求阴影部分的面积。
17. 如图,△ABC 中,D ,E 分别是BC 和AC 的中点,△ABC 的面积由①到⑤五个部分组成,已知①的面积比④多6平方厘米,请问:△ABC 的面积是多少平方厘米?
18. △ABC 中,CE =2AE ,AF =FD ,△ABC 的面积为1,那么阴影部分的面积是多少?
19. △ABC 中,:4:3CE AE =,:3:1BD DC =,△ABC 的面积为1,那么阴影部分的面积是多少?
20. △ABC 中,CF EF =,:2:1BF FD =,△CFD 的面积为1,那么△ABC 的面积是多少?
21. 一个长方体的长宽高分别是9厘米,6厘米,4厘米,把它截成两个一样大的长方体,表面积增加了多少平方厘米?
22. 一个正方体棱长为1,如左图所示把它切成两个长方体,这两部分表面积之和是多少?如果在此基础上如右图那样再切4刀,切成18块长方体,这18块长方体表面积之和是多少?
23. 如图,30个棱长为1的正方体堆成一个四层的立体图形,请问这个立体图形的表面积是多少?
24. 如图,一个长30厘米,宽10厘米,高12厘米的长方体水池,存有四分之三池水。
① 将一个高11厘米,体积330立方厘米的圆柱放入池中,水面高度变成多少? ②如果再放入一个同样的圆柱,水面高度又变成了多少?
③如果再放入一个同样的圆柱,水面高度又变成了多少?
25. 一个矿泉水瓶总共高22厘米,其下半部分可以看成一个圆柱体,底面直径为6厘米,现在往里面装入一定量的水,正着放的时候水面高度是15厘米,若把矿泉水瓶倒过来放,其水面高度是17厘米(如图所示),则这个矿泉水瓶的容积为______________毫升。
26. 有一个几何体,分别从上面,正面,左面观察,得到的图形如下面所示,其长度如图所示(单位:厘米),求这个几何体的体积。
俯视图正面视图左面视图
27. 如图,6个正方形块,折叠起来后可以组成一个正方体,则折起来以后数字“5”对面的数字是_________.
28. 有一个由单位正方体堆成的几何体,从上面,正面,左面三个方向看,得到的图形如下所示,则这个几何体一共是由_________个正方体堆成。
上面视图正面视图左面视图
29. 现有一张正方形纸片(图①),先沿对角线对折一次得到一个等腰直角三角形(图②),
再沿此等腰直角三角形的对称轴对折一次得到第二个等腰直角三角形,并将此等腰直角三角形的两个底角附近分别剪出一个圆孔和一个小直角三角形(图③),然后将纸片打开成原来的正方形,请在图④中补充出打开以后正方形纸片的形状。
图①图②图③图④。
