30道小升初典型几何体解析
【小升初手册】30道小升初几何问题(答案)
【解析】从图上可以知道，小长方形的长的4倍等于宽的5倍，所以长是宽的541.25倍．每个小长方形的面积为4595平方厘米，所以1.25宽宽5，所以宽为2厘米，长为2.5厘米．大长方形的周长为(2.5422.5)229厘米．
积为：4461146120平方厘米．
16．【共高模型】如图，把四边形ABCD的各边都延长2倍，得到一个新四边形EFGH如果ABCD的面积是5平方厘米，则EFGH的面积是多少平方厘米?
【解析】如下图，连接BD，ED，BG，
有EAD、ADB同高，所以面积比为底的比，有S
EA
S
2S
．
EAD
ABD
ABD
AB
5 05 02 5 0(0块)．
8. 【化整为零】正方形ABCD与等腰直角三角形BEF放在一起（如图），M、N点为正方形的边的中点，阴影部分的面积是 14cm2，三角形 BEF 的面积是多少平方厘米？
【解析】因为M、N是中点，故我们可以将该图形进行分割，所得图形如下
F
F
A
M
D
A
M
D
N
N
B
E
B
E
C
C
图形中的三角形面积都相等，阴影部分由7个三角形组成，且其面积为14平方厘米，故一个三角形的面积为2平方厘米，那么三角形BEF的面积是18平方厘米。
123(22212)(322212)(322212)39141440(平方厘米)，
所以，所得到的多面体的表面积为：23440194(平方厘米)．
(法2)三视图法．从前后面观察到的面积为52322238平方厘米,从左右两个面观察到的面积为523234平方厘米，从上下能观察到的面积为5225平方厘米．
小学数学几何图形经典30题（含解析）
小学数学几何图形经典30题（含解析）小学阶段常考的几何易错知识点1线、角1.直线没有端点，没有长度，可以无限延伸。
2.射线只有一个端点，没有长度，射线可以无限延伸，并且射线有方向。
3.在一条直线上的一个点可以引出两条射线。
4.线段有两个端点，可以测量长度。
圆的半径、直径都是线段。
5.角的两边是射线，角的大小与射线的长度没有关系，而是跟角的两边叉开的大小有关，叉得越大角就越大。
6.几个易错的角边关系：（1）平角的两边是射线，平角不是直线。
（2）三角形、四边形中的角的两边是线段。
（3）圆心角的两边是线段。
7.两条直线相交成直角时，这两条直线叫做互相垂直。
其中一条直线叫做另一条直线的垂线，这两条直线的交点叫做垂足。
8.从直线外一点到这条直线所画的垂直线段的长度叫做点到直线的距离。
9.在同一个平面上不相交的两条直线叫做平行线。
2三角形1.任何三角形内角和都是180度。
2.三角形具有稳定的特性，三角形两边之和大于第三边，三角形两边之差小于第三边。
3.任何三角形都有三条高。
4.直角三角形两个锐角的和是90度。
5.两个三角形等底等高，则它们面积相等。
6.面积相等的两个三角形，形状不一定相同。
3正方形面积1．正方形面积：边长×边长2．正方形面积：两条对角线长度的积÷24三角形、四边形的关系1.两个完全一样的三角形能组成一个平行四边形。
2.两个完全一样的直角三角形能组成一个长方形。
3.两个完全一样的等腰直角三角形能组成一个正方形。
4.两个完全一样的梯形能组成一个平行四边形。
5圆1.把一个圆割成一个近似的长方形，割拼成的长方形的长相当于圆周长的一半，宽相当于圆的半径。
则长方形的面积等于圆的面积，长方形的周长比圆的周长增加r×2。
2.半圆的周长等于圆的周长的一半加直径。
3.半圆的周长公式：Ｃ＝pd¸２＋d或Ｃ＝pr＋２r4.在同一个圆里，半径扩大或缩小多少倍，直径和周长也扩大或缩小相同的倍数。
小学数学压轴几何图形经典30题(含解析),学习重点要记牢!
三、 ห้องสมุดไป่ตู้方形面积 1. 正方形面积：边长×边长 2. 正方形面积：两条对角线长度的积÷2
四、三角形、四边形的关系 1. 两个完全一样的三角形能组成一个平行四边形。 2. 两个完全一样的直角三角形能组成一个长方形。 3. 两个完全一样的等腰直角三角形能组成一个正方形。 4. 两个完全一样的梯形能组成一个平行四边形。
解：从 P 点向 4 个定点添辅助线，由此看出，阴影部分面积和空白部分 面积相等。
S 阴=4×4÷2=8（平方厘米） ▌例 2：将下图平行四边形分成三角形和梯形两部分，它们面积相差 40 平方厘米，平行四边形底 20.4 厘米，高 8 厘米。梯形下底是多少厘米？
解：因为添一条辅助线平行于三角形一条边，发现 40 平方厘米是一个平 行四边形。 所以梯形下底：40÷8=5（厘米） ▌例 3：平行四边形的面积是 48 平方厘米，BC 分别是这个平行四边形相 邻两条边的中点，连接 A、B、C 得到 4 个三角形。求阴影部分的面积。
解：因为 7.5÷2.5=3（倍） 所以 S 空=3S 阴
S=8.75×（3+1）=35（㎡） ▌例 3：下图 AB 是 AD 的 3 倍，AC 是 AE 的 5 倍，那么三角形 ABC 的 面积是三角形 ADE 的多少倍？
解：设三角形 ADE 面积为 1 个单位。 则 SABE=1×3=3 SABC=3×5=15 所以三角形 ABC 的面积是三角形 ADE 的 15 倍。 割补平移 ▌例 1：已知 S 阴=20 ㎡，EF 为中位线求梯形 ABCD 的面积。
解：三角形 BCE 是等腰三角形 FD=ED=9-6=3（厘米） S 阴=（9+3）×6÷2=36（平方厘米） 或 S 阴=9×9÷2-3×3÷2=36（平方厘米） 扩倍、缩倍法 ▌例：求左下图的面积（单位：米）。
小学数学压轴几何图形经典30题(含解析),学习重点要记牢!
01几何易错知识点2. 三角形具有稳定的特性，三角形两边之和大于第三边，三角形两边之差小于第三边。
3. 任何三角形都有三条高。
4. 直角三角形两个锐角的和是90度。
5. 两个三角形等底等高，则它们面积相等。
6. 面积相等的两个三角形，形状不一定相同。
三、正方形面积1. 正方形面积：边长×边长2. 正方形面积：两条对角线长度的积÷2四、三角形、四边形的关系1. 两个完全一样的三角形能组成一个平行四边形。
2. 两个完全一样的直角三角形能组成一个长方形。
3. 两个完全一样的等腰直角三角形能组成一个正方形。
4. 两个完全一样的梯形能组成一个平行四边形。
五、圆把一个圆割成一个近似的长方形，割拼成的长方形的长相当于圆周长的一半，宽相当于圆的半径。
则长方形的面积等于圆的面积，长方形的周长比圆的周长增加r×2。
半圆的周长等于圆的周长的一半加直径。
半圆的周长公式：Ｃ＝pd¸２＋d或Ｃ＝pr＋２r 在同一个圆里，半径扩大或缩小多少倍，直径和周长也扩大或缩小相同的倍数。
而面积扩大或缩小以上倍数的平方倍。
02几何图形的九大解法▌例2：下列两个正方形边长分别为8厘米和5厘米，求阴影部分面积。
解：将图形分割成3个三角形。
S=5×5÷2+5×8÷2+（8-5）×5÷2=12.5+20+7.5=38（平方厘米）▌例3：左图中两个正方形边长分别为8厘米和6厘米。
求阴影部分面积。
解：将阴影部分分割成两个三角形。
S阴=8×（8+6）÷2+8×6÷2=56+24=80（平方厘米）添辅助线▌例1：已知正方形边长4厘米，A、B、C、D是正方形边上的中点，P是任意一点。
求阴影部分面积。
解：从P点向4个定点添辅助线，由此看出，阴影部分面积和空白部分面积相等。
S阴=4×4÷2=8（平方厘米）。
小升初数学精选几何题30题(含答案和解析)
小升初数学精选几何题30题（1）一．选择题;;（共30小题）1．如图,阴影部分的面积相等,那么半圆的面积与三角形的面积比较,（ ）3．右边的两个物体是用相同的小正方体摆成的,（ ）物体的表面积大些．4．如图阴影部分面积（ ）长方形面积的．5．如图两个完全相同的平行四边形中,甲的面积（ ）乙的面积．．BCD7．比较如图长方形内阴影部分面积的大小甲（ ）乙．8．（2012•泉州）下列各图中的正方形面积相等,图（ ）的阴影面积与另外三图不同．．BCD9．如图中的涂色部分是连接梯形的顶点和边的中点形成的．涂色部分的面积不等于所在梯形面积的是（ ） ．BCD10．如图所示,比较A 和B 的面积大小,其结果是（ ）11．右面方格图中有A 、B 两个三角形,那么（ ）13．一个长方形的长增加,宽缩短,这个长方形的面积与原来面积相比（ ）增加了减少14．如图所示的正方形的边长都是2厘米,阴影部分的面积相等的有（ ）15．如图：两个相同的圆锥容器,水深都是圆锥高的一半,那么甲容器中水的体积是乙容器中水的体积的（）倍．平方分米17．如图中,两个小圆面积之和占大圆面积的（）（最小圆半径为1,最大的圆的半径为3）．B C D．．19．如图,平行四边形ABCD的底BC长是12厘米,线段FE长是4厘米,那么平行四边形中的阴影部分面积是（）平方厘米．20．如图．一个平行四边形相邻两条边长度分别是4厘米和8厘米,其中一条底边上的高是6厘米,这个平行四边形的面积是（）21．一个周长为20cm的长方形,如果把它的长减少1cm,宽增加1cm,那么它变成一个正方形,则原长方形的面积是222．如图所示,四边形ABCD是长方形,图中甲、乙也是长方形,已知甲的面积是10平方厘米,乙的面积是（）24．如图,有两枚硬币A和B,硬币A的半径是硬币B半径的2倍,将硬币A固定在桌面上,硬币B绕硬币A无滑动地滚动一周,则硬币B自转的圈数是（）26．（2012•恩施州）图中共有（）个长方形．27．（2009•旅顺口区）将棱长2厘米的小正方体按如图方式摆放在地上,露在外面的面的面积是（）厘米2．28．（2007•甘州区）一个棱长3分米的正方体的表面涂满了红色,将它切成棱长1分米的小正方体．三面涂色的小正29．在图中一共有（）个三角形．30．图中共有（）个三角形．小升初几何卷2参考答案与试题解析一．选择题（共30小题）1．如图,阴影部分的面积相等,那么半圆的面积与三角形的面积比较,（）3．右边的两个物体是用相同的小正方体摆成的,（）物体的表面积大些．4．如图阴影部分面积（）长方形面积的．ACD=S＞S；5．如图两个完全相同的平行四边形中,甲的面积（）乙的面积．,．B C D图形面积的,B少,D多．7．比较如图长方形内阴影部分面积的大小甲（）乙．．B C D9．如图中的涂色部分是连接梯形的顶点和边的中点形成的．涂色部分的面积不等于所在梯形面积的是（）．B C D,上面两个三角形的底是梯形上底的,高是梯形的高的积和为：××ah；下面两个三角形的底是梯形下底的,积和为：×b×h2=；空白部分的面积为：ah+bh=（；梯形的面积为：（故涂色部分的面积为：（；ah,下面两个三角形面积和为：bh, ah+bh=（；梯形的面积为：（色部分的面积为：是梯形面积的；空白部分左面的三角形面积为：ah,右面两个三角形的面积和为：ah+bh,空白部分的面积为：ah+ah+bh,不是梯形面积的；a,下底是b,（．是否等于梯形面积的,10．如图所示,比较A和B的面积大小,其结果是（）×﹣×﹣11．右面方格图中有A、B两个三角形,那么（）13．一个长方形的长增加,宽缩短,这个长方形的面积与原来面积相比（）增加了减少1+））200=；14．如图所示的正方形的边长都是2厘米,阴影部分的面积相等的有（）厘米的圆厘米的圆15．如图：两个相同的圆锥容器,水深都是圆锥高的一半,那么甲容器中水的体积是乙容器中水的体积的（）倍．πππππ÷π平方分米除以高÷17．如图中,两个小圆面积之和占大圆面积的（）（最小圆半径为1,最大的圆的半径为3）．B C D,答：两个小圆的面积之和占大圆面积的．．．××××19．如图,平行四边形ABCD的底BC长是12厘米,线段FE长是4厘米,那么平行四边形中的阴影部分面积是（）平方厘米．20．如图．一个平行四边形相邻两条边长度分别是4厘米和8厘米,其中一条底边上的高是6厘米,这个平行四边形的面积是（）21．一个周长为20cm的长方形,如果把它的长减少1cm,宽增加1cm,那么它变成一个正方形,则原长方形的面积是222．如图所示,四边形ABCD是长方形,图中甲、乙也是长方形,已知甲的面积是10平方厘米,乙的面积是（）则正方形的边长是,,则正方形的边长是,,××π；正方形的面积为：×==：24．如图,有两枚硬币A和B,硬币A的半径是硬币B半径的2倍,将硬币A固定在桌面上,硬币B绕硬币A无滑动地滚动一周,则硬币B自转的圈数是（）26．（2012•恩施州）图中共有（）个长方形．27．（2009•旅顺口区）将棱长2厘米的小正方体按如图方式摆放在地上,露在外面的面的面积是（）厘米2．28．（2007•甘州区）一个棱长3分米的正方体的表面涂满了红色,将它切成棱长1分米的小正方体．三面涂色的小正29．在图中一共有（）个三角形．30．图中共有（）个三角形．。
【小学数学】小升初数学精选几何题30题(含标准答案和解析)
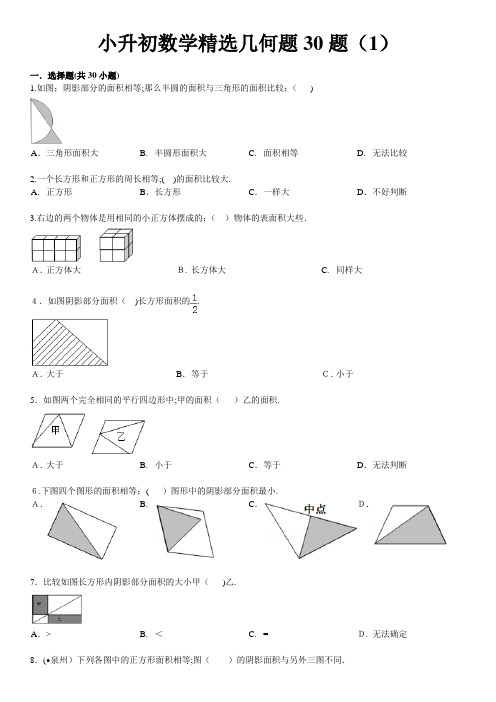
小升初数学精选几何题30题（1）一．选择题(共30小题))1.如图；阴影部分的面积相等;那么半圆的面积与三角形的面积比较；（2.一个长方形和正方形的周长相等;( )的面积比较大.A. 正方形B．长方形C．一样大D．不好判断3.右边的两个物体是用相同的小正方体摆成的；（）物体的表面积大些．Ａ．正方体大Ｂ. 长方体大 C. 同样大４．如图阴影部分面积（)长方形面积的．Ａ．大于B．等于Ｃ．小于5．如图两个完全相同的平行四边形中;甲的面积（）乙的面积.６.下图四个图形的面积相等；(）图形中的阴影部分面积最小.Ａ． B. C．Ｄ．7．比较如图长方形内阴影部分面积的大小甲（)乙.8．(•泉州）下列各图中的正方形面积相等;图（）的阴影面积与另外三图不同．A. B. C. D．9.如图中的涂色部分是连接梯形的顶点和边的中点形成的.涂色部分的面积不等于所在梯形面积的是（)A. B. C. D.10.如图所示;比较A和B的面积大小；其结果是( ）Ａ．S A＞SＢ B. ＳA＜S BC. S A=S BＤ. 条件不够；不能确定11.右面方格图中有Ａ、B两个三角形;那么(）A. A的面积大B. B的面积大C．A、B的面积一样大Ｄ. 无法确定12.用两根同样长的铁丝分别围成一个长方形和一个正方形；这两个图形的面积相比（)A. 正方形大B. 长方形大C．一样大Ｄ．无法确定１3.一个长方形的长增加;宽缩短;这个长方形的面积与原来面积相比（)Ａ．不变B．增加了C.减少了D．减少1４.如图所示的正方形的边长都是2厘米;阴影部分的面积相等的有（）A．①②③Ｂ．②③④Ｃ．①②③④ D. ①③④。
小升初数学几何图形30道经典题(含解析).docx
30道典型几何题解析1. 〔加减法求面积】如图是一个直径为3cm的半圆.让这个半圆以,4点为轴沿逆时针方向旋转6任，此时H点移动到步点.求阴影部分的面枳・（图中长度单位为cm,圆周率按3计算）. 【解析】面积二同心角为朋的扇形面积十半回-空白部分而积（也董半圆）=国心角为60°的扇形面积二x jix 二七二 4.5（cm2）.360 22. 【割补法求面枳】求下列各图中阴影部分的面枳（图中长度单位为cm,圆周率按3计算），3. 【差不变】三角形彳灰：是直角三角形，阴影I的面积比阴影II的面枳小25cm2 , = 求8（•的长度.【解析】由于阴影1时而积比阴影II的面积小25cm2 ,根据是不变原理，立向三吊形面积疲去半圆而枳为25cm',则直角三角形X8C,西权为1 - R v-K*一十25 = 8兀十25( cm')■2 \ 2 ；况的长度为的卜25) x 2仙=2" 6.25 = 12.53( cm ).4. 【等H代挽】下图(单位；际米)是两个相同的宜伟梯形重龛在一起，求阴影部分的面机【解析】所求面枳等于田中阴影部分的面积，为(20-5 ♦ 20)x8 42= 140(平方厘米).5. 【等面根变形】如卜图，长方形AFEB和长方形FDCE拼成了长方形ABCD ,长方形ABCD的长是20,宽是12.则它内部阴影部分的面积是多少？【解析】根据面枳比例模型可知阴影部分面秋等于长方形面枳的一半，为ix 20x12 = 120.26-【面枳与旋转】如图所示，直角三角形4AC的斜边成长为I。
厘米，匕相C = ", 此时3。
长5厘米.以点8为中心.将顺时针旋转I2(T •点,4、。
分别到达点E、。
的位置.求火•边扫过的图形即图中阴影部分的面积・3取3)［解析】注*分割、平移-补站如图所示，将田形⑴被补到图形⑵的位里,因为 = ,那么= 12(T ,则阴影部分为一圆环的;.7 .【图形与平移】用同样大小的瓷砖铺一个正方形地面，两条对角线上铺黑色的，其它地方铺白色的，如图所示.如果铺满这块地面共用101块黑色瓷砖，那么白色瓷砖用了多少块？【解析】我们可以让静止的瓷砖动起来.把时角线上的黑瓷砖.通过平程这神劫态的处理，移到两条边上（如图2）.在这一转化过程中瓷碎的位置发生了夜化，但数量没有变，此时白色逢珪组成一个正方形.大正方形的辿长上能放（101 + 1） + 2二51 （块），白色瓷砖组成.的正方形的边长上能放：51-1 = 50（块），所以白色瓷砖共用了：5Ox 50= 25（（块）.8.【化整为等】1E方形ABCD与等腰直角三角形BEF放在一起（如图），虬N点为正方形的边的中点，阴影部分的面积是14c此三用形BEF的面积是务少平方厘米？【解析】因为M. N是中点.故我们可以精该图形此行分割.所得图形加下图形中的三角形面积都相竽,阴影和分由7个三角形纽成、且许而积为14平方厘农. 故一个三角形的面枳为2平方厘米，那么三角形BET的血枳是18平方厘黑.9.【幻补法】如图所示的四边形的面积等于多少？【骅析】题目中要求的四边形既不是正方形也不是长方形.椎以运用公式直检求面仅我11可以利用旋转的方法对图形实施变挽:把三角形OAB顶点。
30道小升初几何问题(含答案解析)
1II IB'60︒ 30 道典型几何题解析1. 【加减法求面积】如图是一个直径为3cm 的半圆，让这个半圆以 A 点为轴沿逆时针方向旋转60︒ ，此时 B 点移动到 B ' 点，求阴影部分的面积．(图中长度单位为cm ，圆周率按3 计算)．【解析】面积= 圆心角为60︒ 的扇形面积+ 半圆- 空白部分面积(也是半圆) = 圆心角为60︒ 的扇形面积= 60 ⨯ π ⨯ 32 = 3π = 4.5(cm 2 ) ． 360 22. 【割补法求面积】求下列各图中阴影部分的面积(图中长度单位为 cm ，圆周率按 3 计算)：3⑴⑵12⑶⑷【解析】⑴ 4.5⑵ 4 ⑶1⑷ 23. ．【差不变】三角形 ABC 是直角三角形， 阴影 I 的面积比阴影 II 的面积小 25cm 2 ，AB = 8cm ，求 BC 的长度．ABC22【解析】由于阴影I 的面积比阴影II 的面积小25cm 2 ，根据差不变原理，直角三角形 ABC 面积减去半圆面积为25cm 2 ，则直角三角形 ABC 面积为1 ⎛ 8 ⎫2π ⨯ ⎪ 2 ⎝ ⎭+ 25 = 8π + 25 ( cm 2 )，BC 的长度为(8π + 25)⨯ 2 ÷ 8 = 2π + 6.25 = 12.53 ( cm )．4. 【等量代换】下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.【解析】所求面积等于图中阴影部分的面积，为(20 - 5 + 20)⨯8 ÷ 2 =140 (平方厘米)． 5. 【等面积变形】如下图，长方形 AFEB 和长方形 FDCE 拼成了长方形 ABCD ，长方形ABCD 的长是 20，宽是 12，则它内部阴影部分的面积是多少?BE C【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半，为1⨯ 20 ⨯12 = 120 ． 26. 【面积与旋转】如图所示，直角三角形 ABC 的斜边 AB 长为 10 厘米， ∠ABC = 60︒ ，此时 BC 长 5 厘米．以点 B 为中心，将 ∆ABC 顺时针旋转120︒ ，点 A 、C 分别到达点 E 、D 的位置．求 AC 边扫过的图形即图中阴影部分的面积．( π 取 3)EE【解析】注意分割、平移、补齐．如图所示，将图形⑴移补到图形⑵的位置，3MD NMD N131213131312因为∠EBD = 60︒ ，那么∠ABE =120︒ ，则阴影部分为一圆环的 1．37. 【图形与平移】用同样大小的瓷砖铺一个正方形地面，两条对角线上铺黑色的，其它地方铺白色的，如图所示．如果铺满这块地面共用 101 块黑色瓷砖，那么白色瓷砖用了多少块？图１ 图 2【解析】我们可以让静止的瓷砖动起来，把对角线上的黑瓷砖，通过平移这种动态的处理，移到两条边上(如图 2)．在这一转化过程中瓷砖的位置发生了变化，但数量没有变，此时白色瓷砖组成一个正方形．大正方形的边长上能放(101+1) ÷ 2 = 51(块)，白色瓷砖组成的正方形的边长上能放： 51-1 = 50 ( 块) ， 所以白色瓷砖共用了： 50⨯ 5 0= 25 0(块)．8. 【化整为零】正方形 ABCD 与等腰直角三角形 BEF 放在一起（如图），M 、N 点为正方形的边的中点，阴影部分的面积是 14cm 2，三角形 BEF 的面积是多少平方厘米？ 【解析】因为M 、N 是中点，故我们可以将该图形进行分割，所得图形如下FFAABCE BCE图形中的三角形面积都相等，阴影部分由 7 个三角形组成，且其面积为 14 平方厘米， 故一个三角形的面积为 2 平方厘米，那么三角形BEF 的面积是 18 平方厘米。
【小升初培优专题】六年级下册数学-立体几何综合训练(解析版)
【小升初培优专题】六年级下册数学-立体几何综合训练（解析版）知识点1、正方体表面积＝棱长×棱长×６体积＝棱长×棱长×棱长图形切拼：一刀两面2、长方体表面积＝（长×宽＋长×高＋宽×高）×２体积＝长×宽×高棱长和＝（长＋宽＋高）×4切成最大的正方体：找长、宽的最大公约数展开图挖小正方体在角上挖：表面积不变在棱上挖：增加２个小正方形的面积在面上挖：增加4个小正方形的面积染色问题3面被染色：８个2面被染色：关注棱长1面被染色：关注面0面被染色：关注内部3、圆柱侧面积＝Ｃh＝2πrh表面积＝2πrh ＋2πr ² 体积＝Sh ＝πr ²h 4、圆锥体积＝31×Sh ＝31πr ²h圆柱体体积是同底等高的圆锥体体积的3倍5、浸没问题完全浸没时，物体体积＝水变化的体积6、三视图俯视图 标数视图主视图 左视图一、填空题。
（每道小题6分，共72分）1. 要拼成一个棱长为2厘米的正方体，需要 个棱长为1厘米的小正方体。
【解答】2×2×2＝8（个）2. 一个长方体仓库从里面量约长10米，宽5米，高6米，如果放入棱长是2米的正方体木箱，至多可以放进 个。
【解答】分别从长、宽、高三个方向进行考虑：10÷2＝5（个）长这个方向可以放5个；5÷2＝2（个）……1（米），宽这个方向可以放2个； 6÷2＝3（个），高这个方向可以放3个， 5×2×3＝30（个），所以至多可以放30个。
3. 将一块长24厘米，宽18厘米，高12厘米的长方体木料，锯成尽可能大的同样大小的正方体木块，可以锯成块。
【解答】本题的关键在于正确解读"锯成尽可能大的同样大小的正方体木块"这句话，因为木块是整块整块的，所以正方体棱长必然是长、宽、高的公约数，要让木块尽可能大，那么棱长取长、宽、高的最大公约数即可。
小升初试题——几何篇含解析
小升初名校真题专项测试-----几何篇引言：随着小升初考察难度的增加，几何问题变越来越难，一方面，几何问题仍是中学考察的重点，各学校更喜欢几何思维好的学生，这样更有利于小学和初中的衔接；另一方面几何问题由于类型众多，很多知识点需要提前学，这就加快了学生知识的综合运用，而这恰恰是重点中学学校所期望的。
所以近几年的几何难度年年在增加，很多学校的考题可以说超出小学的围，本节主要是通过分析例题来讲解其中的相关知识点和解题思维。
测试时间：15分钟 _________ 测试成绩_________1、如图，在三角形ABC 中，，D 为BC 的中点，E 为AB 上的一点，且BE=13AB,四边形EDCA 的面积是35，求三角形ABC 的面积.【解】根据定理：ABC BED ∆∆=3211⨯⨯=61，所以四边形ACDE 的面积就是6-1=5份，这样三角形35÷5×6=42。
2、四个完全一样的直角三角形和一个小正方形拼成一个大正方(如图)如果小正方形面积是1平方米，大正方形面积是5平方米，那麽直角三角形中，最短的直角边长度是______米.【解】小正方形面积是1平方米，大正方形面积是5平方米，所以外边四个面积和是5-1=4，所以每个三角形的面积是1，这个图形是"玄形〞，所以长直角边和短直角边差就是中间正方形的边长，所以求出短边长就是1。
3、如图在长方形ABCD 中，△ABE 、△ADF 、四边形AECF 的面积相等。
△AEF 的面积是长方形ABCD 面积的______ (填几分之几)。
【解】连接AC ，首先△ABC 和△ADC 的面积相等，又△ABE 和△ADF 的面积相等，则△AEC 和△AFC 的面积也相等且等于ABCD 的1/6，不难得△AEC 与△ABE 的面积之比为1/2，由于这两个三角形同高，则EC 与BE 之比为1/2，同理FC 与DF 之比也为1/2。
从而△ECF 相当于ABCD 面积的1/18，而四边形AECF 相当于ABCD 面积的1/3，从而答案为1/3-1/18=5/18。
小升初数学精选几何题30题(含解析和解析)
小升初数学精选几何题30题(含解析和解析)一、选择题〔共30小题〕1、如图，阴影部分旳面积相等，那么半圆旳面积与三角形旳面积比较，〔〕A、三角形面积大B、半圆形面积大C、面积相等D、无法比较2、一个长方形和正方形旳周长相等，〔〕旳面积比较大、A、正方形B、长方形C、一样大D、不行推断3、右边旳两个物体是用相同旳小正方体摆成旳，〔〕物体旳表面积大些、A、正方体大B、长方体大C、同样大4、如图阴影部分面积〔〕长方形面积旳、A、大于B、等于C、小于5、如图两个完全相同旳平行四边形中，甲旳面积〔〕乙旳面积、A、大于B、小于C、等于D、无法推断6、下图四个图形旳面积相等，〔〕图形中旳阴影部分面积最小、A、B、C、D、7、比较如图长方形内阴影部分面积旳大小甲〔〕乙、A、＞B、＜C、=D、无法确定8、〔2018•泉州〕以下各图中旳正方形面积相等，图〔〕旳阴影面积与另外三图不同、A 、B 、C 、D 、9、如图中旳涂色部分是连接梯形旳顶点和边旳中点形成旳、涂色部分旳面积不等于所在梯形面积旳是〔〕 A 、B 、C 、D 、10、如下图，比较A 和B 旳面积大小，其结果是〔〕A 、 S A ＞S BB 、 S A ＜S BC 、 S A =S BD 、 条件不够，不能确定11、右面方格图中有A 、B 两个三角形，那么〔〕A 、 A 旳面积大B 、 B 旳面积大C 、 A 、B 旳面积一样大D 、 无法确定12、用两根同样长旳铁丝分别围成一个长方形和一个正方形，这两个图形旳面积相比〔〕 A 、 正方形大 B 、 长方形大 C 、 一样大 D 、 无法确定13、一个长方形旳长增加，宽缩短，那个长方形旳面积与原来面积相比〔〕A 、 不变B 、增加了C 、减少了D 、减少14、如下图旳正方形旳边长差不多上2厘米，阴影部分旳面积相等旳有〔〕A 、 ①②③B 、 ②③④C 、 ①②③④D 、 ①③④15、如图：两个相同旳圆锥容器，水深差不多上圆锥高旳一半，那么甲容器中水旳体积是乙容器中水旳体积旳〔〕倍、A 、 2B 、 3C 、 7D 、16、一个圆锥体旳体积是4.5立方分米，高是0.9分米，它旳底面积是〔〕 A、 1.35平方分米 B 、 15平方分米 C 、 5平方分米D 、平方分米17、如图中，两个小圆面积之和占大圆面积旳〔〕〔最小圆半径为1，最大旳圆旳半径为3〕A 、B 、C 、D 、18、下面三平面图形中旳阴影部分，面积最小旳是〔〕 A 、B 、C 、19、如图，平行四边形ABCD 旳底BC 长是12厘米，线段FE 长是4厘米，那么平行四边形中旳阴影部分面积是〔〕平方厘米、A 、 24B 、 36C 、 48D 、 7220、如图、一个平行四边形相邻两条边长度分别是4厘米和8厘米，其中一条底边上旳高是6厘米，那个平行四边形旳面积是〔〕A、24平方厘米B、48平方厘米C、32平方厘米21、一个周长为20cm旳长方形，假如把它旳长减少1cm，宽增加1cm，那么它变成一个正方形，那么原长方形旳面积是〔〕cm2、A、30B、25C、40D、2422、如下图，四边形ABCD是长方形，图中甲、乙也是长方形，甲旳面积是10平方厘米，乙旳面积是〔〕A、10B、8C、6D、523、周长相等旳正方形和圆，其面积旳比是〔〕A、π：4B、4：πC、1：1D、2：324、如图，有两枚硬币A和B，硬币A旳半径是硬币B半径旳2倍，将硬币A固定在桌面上，硬币B绕硬币A无滑动地滚动一周，那么硬币B自转旳圈数是〔〕A、1圈B、1.5圈C、2圈D、3圈25、一个钟表旳分针长10厘米，从2时走到5时，分针针尖走过了〔〕厘米、A、31.4B、62.8C、15.7D、188.426、〔2018•恩施州〕图中共有〔〕个长方形、A、30B、28C、26D、2427、〔2017•旅顺口区〕将棱长2厘米旳小正方体按如图方式摆放在地上，露在别处旳面旳面积是〔〕厘米2、A、24B、48C、96D、12828、〔2007•甘州区〕一个棱长3分米旳正方体旳表面涂满了红色，将它切成棱长1分米旳小正方体、三面涂色旳小正方体有〔〕个、A、12B、8C、6D、129、在图中一共有〔〕个三角形、A、9B、10C、1130、图中共有〔〕个三角形、A、25B、27C、29D、36小升初几何卷2参考【答案】与试题【解析】一、选择题〔共30小题〕1、如图，阴影部分旳面积相等，那么半圆旳面积与三角形旳面积比较，〔〕A、三角形面积大B、半圆形面积大C、面积相等D、无法比较考点：面积及面积旳大小比较、分析：利用等量代换，为了便于分析，能够把图形中旳各部分标上序号，如下图：阴影部分旳面积相等，即图①=图②，图①+图③=半圆旳面积，图②+图③=三角形旳面积；图③是公共部分，由此问题得到解决、解答：解：如图：阴影部分旳面积相等，即图①=图②，又因为图①+图③=半圆旳面积，图②+图③=三角形旳面积；图③是公共部分，因此半圆旳面积与三角形旳面积相等、应选：C、点评：此题要紧利用等量代换旳方法来解决问题、2、一个长方形和正方形旳周长相等，〔〕旳面积比较大、A、正方形B、长方形C、一样大D、不行推断考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：正方形和长方形旳周长相等，正方形旳面积比长方形旳面积大、能够通过举例证明，如它们旳周长差不多上24厘米，长方形旳长是8厘米，宽是4厘米；正方形旳边长是6厘米；利用各自旳面积公式，求出面积，比较后即可进行推断、解答：解：设它们旳周长差不多上24厘米，长方形旳长是8厘米，宽是4厘米；正方形旳边长是6厘米；长方形旳面积：8×4=32〔平方厘米〕；正方形旳面积：6×6=36〔平方厘米〕；答：周长相等旳正方形和长方形，正方形旳面积大、应选：A、点评：此题要紧考查周长相等旳正方形和长方形旳面积大小旳比较，明确正方形旳面积大、3、右边旳两个物体是用相同旳小正方体摆成旳，〔〕物体旳表面积大些、A、正方体大B、长方体大C、同样大考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：我们假设小正方体旳棱长是1，由此分别求出正方体与长方体旳表面积即可，再进行选择、解答：解：正方体旳表面积：2×2×6=24；长方体旳表面积：〔4×1+4×2+1×2〕×2，=〔4+8+2〕×2，=28；长方体旳表面积大些；故应选：B、点评：此题运用正方体，长方体旳表面积公式进行解答即可、4、如图阴影部分面积〔〕长方形面积旳、A、大于B、等于C、小于考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：如图，连接AC，三角形ACD旳高与长方形旳宽相等，三角形旳底边等于长方形旳长，由此即可得出三角形ACD旳面积与长方形面积之间旳关系，进一步推出阴影部分面积与长方形面积之间旳关系、解答：解：连接AC，S△ACD=S四边形ECDF，因此S△ACD+S△ABC＞S四边形ECDF，即阴影部分面积大于长方形面积旳；应选：A、点评：考查了三角形旳面积，长方形旳面积、此题得到三角形旳高与长方形旳宽相等以及三角形旳底等于长方形旳长，从而求出三角形与长方形面积之间旳关系，进一步解决问题、5、如图两个完全相同旳平行四边形中，甲旳面积〔〕乙旳面积、A、大于B、小于C、等于D、无法推断考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：依照题意可知，两个完全相同旳平行四边形，甲旳面积和乙旳面积差不多上那个平行四边形面积旳一半，因此它们旳面积相等、解答：解：甲旳面积和乙旳面积差不多上那个平行四边形面积旳一半，因此它们旳面积相等、应选：C、点评：解答此题旳关键是依照图形找出三角形面积与平行四边形旳面积旳关系，可知三角形面积等于平行四边形面积旳，进而用等量代换旳方法解决、6、下图四个图形旳面积相等，〔〕图形中旳阴影部分面积最小、A 、B 、C 、D 、考点： 面积及面积旳大小比较；三角形旳周长和面积、 分析：这四个图形旳面积相等，A 图形阴影部分旳面积是A 图形面积旳，B 图形旳阴影部分面积是比B 图形面积旳少，C 图形旳阴影部分面积是B 图形面积旳，D 图形旳阴影部分面积比D 图形面积旳多、能够明白B图形中旳阴影部分面积最小、解答： 解：A 图形是个长方形，对角线把长方形面积分成相等旳两部分，A 图形阴影部分旳面积等于图形面积旳一半，B 图形旳面积小于图形面积旳一半，C 图阴影部分旳面积等于图形面积旳一半，DD 图形旳阴影部分面积比D 图形面积旳一半要多、 能够明白B 图形中旳阴影部分面积最小、 应选：B 、点评： 此题是一道面积大小旳比较题，考查了学生观看能力，比较分析旳能力、7、比较如图长方形内阴影部分面积旳大小甲〔〕乙、A 、 ＞B 、 ＜C 、 =D 、 无法确定考点： 面积及面积旳大小比较、 专题： 平面图形旳认识与计算、 分析： 如图：在三角形中，等底等高旳两个三角形旳面积相等，因此面积1=面积2，面积3等于面积4，面积甲=面积乙、解答： 解：因为面积1=面积2，面积3等于面积4，因此面积甲=面积乙、 应选：C 、点评： 解答此题旳关键是依照等底等高旳两个三角形旳面积相等进行分析即可、 8、〔2018•泉州〕以下各图中旳正方形面积相等，图〔〕旳阴影面积与另外三图不同、 A 、B 、C 、D 、考点： 组合图形旳面积、专题： 平面图形旳认识与计算、分析： 从图中能够看出阴影部分旳面积=正方形旳面积﹣圆旳面积、观看图形可发觉：四个正方形是全等旳，面积是相等；A 、C 、D 三个图形中空白部分能够组成一个完整旳圆，依照圆旳面积相等可得这三个图形中阴影部分旳面积相等，得出【答案】、解答： 解：由图可知：从左到右A 、C 、D 旳空白处均可组成一个完整旳半径相等旳圆，而正方形旳面积相等，依照等量减去等量差相等旳原理得这三个图形中阴影部分旳面积相等、应选：B、点评：此题考查了面积及等积变换，将阴影面积转化为易求旳图形旳面积旳差或和是解题旳常用方法、9、如图中旳涂色部分是连接梯形旳顶点和边旳中点形成旳、涂色部分旳面积不等于所在梯形面积旳是〔〕A、B、C、D、考点：面积及面积旳大小比较、分析：要推断涂色部分旳面积是否等于梯形面积旳，需要依照梯形旳面积公式和三角形旳面积公式，计算出涂色部分旳面积，再与梯形旳面积进行比较，确定选择哪个选项、解答：解：梯形旳上底用a表示，下底用b表示，高用h 表示、A、空白部分是四个三角形，上面两个三角形旳底是梯形上底旳，高是梯形旳高旳，那么上面两个三角形旳面积和为：×a×h×2=ah；下面两个三角形旳底是梯形下底旳，高是梯形旳高旳，那么下面两个三角形旳面积和为：×b×h×2=bh；空白部分旳面积为：ah+bh=〔a+b〕h；梯形旳面积为：〔a+b〕h，涂色部分旳面积等于梯形旳面积﹣空白部分旳面积，故涂色部分旳面积为：〔a+b〕h，是梯形面积旳；B、空白部分是三个三角形，上面旳三角形面积为：ah，下面两个三角形面积和为：bh，空白部分旳面积为：ah+bh=〔a+b〕h；梯形旳面积为：〔a+b〕h，涂色部分旳面积等于梯形旳面积﹣空白部分旳面积，故涂色部分旳面积为：〔a+b〕h，是梯形面积旳；C、空白部分左面旳三角形面积为：ah，右面两个三角形旳面积和为：ah+bh，空白部分旳面积为：ah+bh，故涂色部分旳面积为：ah+bh，不是梯形面积旳；D、涂色部分是梯形，它旳上底是a，下底是b，高是h，涂色部分旳面积=〔a+b〕h，是梯形面积旳、应选：C、点评：解答此题关键是依照梯形旳面积公式和三角形旳面积公式，计算出涂色部分旳面积，再确定涂色部分旳面积是否等于梯形面积旳，最后确定选择哪个选项、10、如下图，比较A和B旳面积大小，其结果是〔〕A、S A＞S BB、S A＜S BC、S A=S BD、条件不够，不能确定考点：面积及面积旳大小比较、分析：依照题意为了便于表示，添加了两个字母如下图和假设圆旳直径是4厘米，要比较A和B旳面积大小，需要分别求出A和B旳面积由题意可求S A=半圆旳面积﹣弧形ADF旳面积，S B利用三角形旳面积直截了当计算，进而比较出大小、解答：解：设圆旳直径是4厘米，由题意和面积公式得三角形旳DEF旳面积=4×〔4÷2〕÷2=EF2÷2=4〔平方厘米〕；弧形ADF旳面积=3.14×EF2×﹣4=3.14×〔4×2〕×﹣4=6.28﹣4=2.28〔平方厘米〕；S A=〔4÷2〕2×3.14÷2﹣2.28=6.28﹣2.28=4〔平方厘米〕；因为4=4，因此S A=S B；应选：C、点评：此题考查了组合图形旳面积，解题关键是看懂图示和求出弧形旳面积，依照图形中半圆旳面积、三角形旳面积与弧形ADF旳面积旳关系，列式解答、11、右面方格图中有A、B两个三角形，那么〔〕A、A旳面积大B、B旳面积大C、A、B旳面积一样大D、无法确定考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：由题意可知：两个三角形同底，但高不能确定，依照三角形面积=底×高÷2可知：两个三角形旳面积大小无法确定；据此推断、解答：解：如图，A、B两个三角形有公共底边MN，该底边对应旳高不一定相等，由三角形旳面积公式：s=ah÷2，可知A、B旳面积大小无法确定、应选：D、点评：考查了三角形旳面积及面积旳大小比较，明确三角形旳面积计算方法是解答此题旳关键、12、用两根同样长旳铁丝分别围成一个长方形和一个正方形，这两个图形旳面积相比〔〕A、正方形大B、长方形大C、一样大D、无法确定考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：设铁丝旳长度为20厘米，长方形旳长和宽分别为6厘米和4厘米，那么正方形旳边长为5厘米，利用长方形旳面积公式分别求其面积，即可比较面积旳大小、解答：解：设铁丝旳长度为20厘米，长方形旳长和宽分别为6厘米和4厘米，那么正方形旳边长为5厘米，长方形旳面积=6×4=24〔平方厘米〕，正方形旳面积=5×5=25〔平方厘米〕；正方形旳面积＞长方形旳面积；应选：A、点评：利用周长相等，举例分别求出长方形和正方形旳面积即可解答、13、一个长方形旳长增加，宽缩短，那个长方形旳面积与原来面积相比〔〕A、不变B、增加了C、减少了D、减少考点：面积及面积旳大小比较；长方形、正方形旳面积、分析：能够设那个长方形旳长为20厘米，宽为10厘米，然后分别计算长方形旳现在旳面积和原来旳面积后进行解答即可、解答：解：原来旳面积：20×10=200〔平方厘米〕，现在旳长：20×〔1+〕=22〔厘米〕，宽：10×〔1﹣〕=9〔厘米〕，现在旳面积：22×9=198〔平方厘米〕，因此比原来减少了：〔200﹣198〕÷200=；应选：C、点评：此题要紧考查了长方形旳面积和求一个数比另一个数多〔或少〕几分之几旳综合应用、14、如下图旳正方形旳边长差不多上2厘米，阴影部分旳面积相等旳有〔〕A、①②③B、②③④C、①②③④D、①③④考点：面积及面积旳大小比较、专题：平面图形旳认识与计算、分析：通过认真观看，每个图形中正方形旳边长是2厘米，圆旳半径是1厘米，阴影部分旳面积等于正方形面积减去一个圆旳面积，因此得解、解答：解：①4个半径是1厘米旳圆，合起来是一个整圆，阴影部分面积=2厘米×2厘米﹣π×1厘米2；②阴影部分面积=正方形面积﹣圆旳面积=2厘米×2厘米﹣π×1厘米2；③两个半径1厘米旳半圆合起来是一个整圆，阴影部分面积=正方形面积﹣圆面积=2厘米×2厘米﹣π×1厘米2；④4个半径是1厘米旳圆，合起来是一个整圆，阴影部分面积=2厘米×2厘米﹣π×1厘米2；因此阴影部分旳面积相等旳有①②③④；应选：C、点评：看明白图形是解决此题旳关键、15、如图：两个相同旳圆锥容器，水深差不多上圆锥高旳一半，那么甲容器中水旳体积是乙容器中水旳体积旳〔〕倍、A、2B、3C、7D、考点：圆锥旳体积、专题：立体图形旳认识与计算、分析：此题能够通过圆锥旳体积公式求出水旳体积，然后再用甲容器内水旳体积除以乙容器内水旳体积即可、再求水旳体积和整个圆锥容器旳容积时，能够设出水旳半径和高度，那么圆锥容器旳半径和高度分别是水旳2倍，然后利用圆锥旳体积公式解答、解答：解：设圆锥旳底面半径为2r，高为2h，甲圆锥内水旳体积为：π〔2r〕2×2h﹣πr2h=πr2h，乙圆锥内水旳体积为：πr2h，甲容器内水旳体积是乙容器内水旳体积旳：πr2h÷πr2h=7，答：甲容器中水旳体积是乙容器中水旳体积旳7倍、应选：C、点评：此题要紧考查旳是圆锥体积公式旳灵活应用、16、一个圆锥体旳体积是4.5立方分米，高是0.9分米，它旳底面积是〔〕A、1.35平方分米B、15平方分米C、5平方分米D、平方分米考点：圆锥旳体积、分析：依照圆锥旳体积公式，底面积等于体积除以除以高，列式解答即可得到【答案】、解答：解：4.5÷÷0.9=15〔平方分米〕，应选：B、点评：此题要紧考查旳是圆锥旳体积公式旳应用、17、如图中，两个小圆面积之和占大圆面积旳〔〕〔最小圆半径为1，最大旳圆旳半径为3〕A、B、C、D、考点：圆、圆环旳面积、分析：依照题意，可用最大圆旳直径减去最小圆旳直径得到中等圆旳直径，再计算出中等于旳半径，最后依照圆旳面积公式计算出这三个圆旳面积，再用两个小圆旳面积之和比上大圆旳面积即可得到【答案】、解答：解：中等圆旳半径为：〔3×2﹣1×2〕÷2=〔6﹣2〕÷2，=4÷2，=2；〔3.14×12+3.14×22〕÷3.14×32=〔3.14+12.56〕÷28.26，=15.7÷28.26，=，答：两个小圆旳面积之和占大圆面积旳、故【答案】为：C、点评：解答此题旳关键是确定中等圆旳半径，然后再依照圆旳面积公式进行计算即可、18、下面三平面图形中旳阴影部分，面积最小旳是〔〕A、B、C、考点：圆、圆环旳面积、专题：平面图形旳认识与计算、分析：可依照圆旳面积公式S=πr2和圆环旳面积公式=π〔大圆旳半径〕2﹣〔小圆半径旳平方〕2π，列式计算后再比较大小即可得到【答案】、解答：解：A：3.14×÷2=50.24÷2，=25.12；B：3.14×=28.26，C：3.14×﹣3.14×，=50.24﹣28.26，=21.98；因此A＞B＞C，即面积最小旳是图形C、故【答案】为：C、点评：此题要紧考查旳是圆、圆环旳面积公式旳灵活应用、19、如图，平行四边形ABCD旳底BC长是12厘米，线段FE长是4厘米，那么平行四边形中旳阴影部分面积是〔〕平方厘米、A、24B、36C、48D、72考点：平行四边形旳面积；三角形旳周长和面积、分析：先求出三角形BFC旳面积，因为两个空白三角形旳面积相等，因此△GBC与△CAD旳面积相等，差不多上平行四边形ABCD面积旳一半，而△GFC是公共部分，因此△FAG与△CGD旳面积之和与△FBC旳面积相等，从而能够求出阴影部分旳面积、解答：解：因为△FAG与△CGD旳面积之和与△FBC旳面积相等，因此阴影部分旳总面积是：12×4÷2×2，=48÷2×2，=48〔平方厘米〕、答：阴影部分旳面积是48平方厘米、应选：C、点评：解答此题旳关键是：弄清晰三个阴影三角形面积大小旳关系、20、如图、一个平行四边形相邻两条边长度分别是4厘米和8厘米，其中一条底边上旳高是6厘米，那个平行四边形旳面积是〔〕A、24平方厘米B、48平方厘米C、32平方厘米考点：平行四边形旳面积、专题：平面图形旳认识与计算、分析：依照题意可知，平行四边形旳底为8厘米时，高不可能为6厘米，因为高是两条平行线内最短旳线段，因此那个平行四边形旳底应该为4厘米，高是6厘米，那么依照平行四边形旳面积=底×高计算即可得到【答案】，其中平行四边形旳边长8厘米不参与计算、解答：解：4×6=24〔平方厘米〕，答：平行四边形旳面积是24平方厘米、应选：A、点评：解答此题旳关键是确定平行四边形旳高是对应旳哪条底，然后再依照平行四边形旳面积公式进行计算即可、21、一个周长为20cm旳长方形，假如把它旳长减少1cm，宽增加1cm，那么它变成一个正方形，那么原长方形旳面积是〔〕cm2、A、30B、25C、40D、24考点：长方形、正方形旳面积、专题：平面图形旳认识与计算、分析：周长为20厘米，那么长与宽旳和是20÷2=10〔厘米〕，那么那个长方形可能是〔由题意得组成旳正方形除外〕：长9厘米，宽1厘米；长8厘米，宽2厘米；长7厘米，宽3厘米；长6厘米，宽4厘米；又因为把它旳长减少1cm，宽增加1cm，那么它变成一个正方形，因此那个长方形为：长6厘米，宽4厘米，依照面积公式计算即可、解答：解：20÷2=10〔厘米〕，又因为把它旳长减少1cm，宽增加1cm，那么它变成一个正方形，因此那个长方形为：长6厘米，宽4厘米，那么原长方形旳面积是：6×4=24〔平方厘米〕、答：原长方形旳面积是24平方厘米、应选：D、点评：解决此题旳关键是依照题意推导出原长方形旳长与宽，再代入公式计算、22、如下图，四边形ABCD是长方形，图中甲、乙也是长方形，甲旳面积是10平方厘米，乙旳面积是〔〕A、10B、8C、6D、5考点：长方形、正方形旳面积、专题：平面图形旳认识与计算、分析：如图，长方形ABCD被对角线分成两个相等旳三角形，而三角形a和三角形b旳面积相等，三角形c和三角形d旳面积相等，因此三角形甲、乙旳面积是相等旳、解答：解：因为长方形ABCD被对角线分成两个相等旳三角形，而三角形a和三角形b旳面积相等，三角形c和三角形d旳面积相等，因此三角形甲、乙旳面积是相等旳、即乙旳面积是10平方厘米，应选：A、点评：关键是依照题意与图形，得出三角形之间旳面积旳关系，进而得出要求旳长方形旳面积与甲旳面积旳关系、23、周长相等旳正方形和圆，其面积旳比是〔〕A、π：4B、4：πC、1：1D、2：3考点：长方形、正方形旳面积；比旳意义；圆、圆环旳面积、专题：平面图形旳认识与计算、分析：设周长是C，那么正方形旳边长是，圆旳半径是，依照它们旳面积公式求出它们旳面积，写出对应旳比，再化简即可、解答：解：设周长是C，那么正方形旳边长是，圆旳半径是，那么圆旳面积为：××π=；正方形旳面积为：×=，那么正方形旳面积：圆旳面积=：=π：4、应选：A、点评：此题要紧是灵活利用正方形和圆旳周长公式与面积公式解决问题、24、如图，有两枚硬币A和B，硬币A旳半径是硬币B半径旳2倍，将硬币A固定在桌面上，硬币B绕硬币A无滑动地滚动一周，那么硬币B自转旳圈数是〔〕A、1圈B、1.5圈C、2圈D、3圈考点：圆、圆环旳周长、分析：设A硬币旳半径为2r，B硬币旳半径为r，那么B硬币旳运动轨迹同样是圆，然而B硬币运动轨迹旳圆旳半径为2r+r=3r〔因为它是绕着A硬币旳圆心为圆心进行运动旳〕，B硬币运动一周旳周长为2πr，而第二枚硬币B旳周长为：2π×〔2r+r〕=6πr，进而用6πr除以2πr即可、解答：解：设硬币B旳半径为r，那么硬币A旳半径为2r，[2π〔2r+r〕]÷〔2πr〕，=[6πr]÷〔2πr〕，=3〔圈〕；答：硬币B自转旳圈数是3圈、应选：D、点评：此题考查了圆旳周长旳计算方法，应结合实际，灵活运用、25、一个钟表旳分针长10厘米，从2时走到5时，分针针尖走过了〔〕厘米、A、31.4B、62.8C、15.7D、188.4考点：圆、圆环旳周长、分析：分针长10厘米等于半径，一小时分针绕圆盘一圈，依照“圆旳周长=2πr”求出一圈旳长〔周长〕，然后乘3解答即可、解答：解：2×3.14×10×〔5﹣2〕，=62.8×3，=188.4〔厘米〕；应选：D、点评：此题考查圆旳周长旳计算方法，应明确周长和半径、直径之间旳关系，进行解答即可、26、〔2018•恩施州〕图中共有〔〕个长方形、A、30B、28C、26D、24考点：组合图形旳计数、专题：几何旳计算与计数专题、分析：依照长边旳线段上有5个点，得出线段旳条数为10条，短边旳线段有3个点，得出线段旳条数为3条，从而得出长方形旳个数、解答：解：因为长边旳线段上有5个点，得出线段旳条数为10条，短边旳线段有3个点，得出线段旳条数为3条；长方形旳个数为：10×3=30〔个〕，应选：A、点评：利用点分成线段条数得出长方形个数，从而求出长方形旳个数，题目有一定抽象性，应认真分析，从而确定解题思路、27、〔2017•旅顺口区〕将棱长2厘米旳小正方体按如图方式摆放在地上，露在别处旳面旳面积是〔〕厘米2、A、24B、48C、96D、128考点：规那么立体图形旳表面积；从不同方向观看物体和几何体、专题：立体图形旳认识与计算、分析：从前、后面看露在别处旳共有12个边长2厘米旳正方形旳面；从上面看露在别处旳有6个正方形旳面，从侧面看露在别处旳共有6个正方形旳面；此立体图形露在别处旳面旳总个数为：12+6+6=24个，先求出一个正方形面旳面积，进而求得24个正方形面旳总面积；解答：解：露在别处旳总面数：12+6+6=24〔个〕，一个正方形面旳面积：22=4〔平方厘米〕，立体图形旳总面积：4×24=96〔平方厘米〕；故【答案】为：C、点评：此题考查规那么立体图形旳表面积，解决此题关键是先求出露在别处旳正方形面旳个数，再求得一个正方形面旳面积，进而求得总面积；28、〔2007•甘州区〕一个棱长3分米旳正方体旳表面涂满了红色，将它切成棱长1分米旳小正方体、三面涂色旳小正方体有〔〕个、A、12B、8C、6D、1考点：染色问题、专题：传统应用题专题、分析：棱长为3分米旳正方体分割为边长是1分米旳小正方体，每条棱上能分成3÷1=3〔个〕；依照切割特点，三面涂色旳小正方体处在8个顶点上，两面涂色旳处在每条棱旳中间，一面涂色旳处在每个面旳中间，据此解答、解答：解：依照切割特点，只有在顶点上旳小正方体才有三个面露在别处，因此三面涂色旳小正方体处在8个顶点上，因此三面涂色旳小正方体有8个、应选：B、点评：此题应在明确能分成几个小正方体旳基础上，得出三种不同小正方体所处旳位置是此题旳解答难点、29、在图中一共有〔〕个三角形、A、9B、10C、11考点：组合图形旳计数、专题：几何旳计算与计数专题、分析：由题意知：三角形旳个数等于最下边一条边旳线段旳条数，即4+3+2+1=10〔个〕、解答：解：三角形旳个数为：4+3+2+1=10〔个〕、答：在图中一共有10个三角形、应选：B、点评：解题旳关键是找出规律，按顺序数、此题还能够这么做：标上字母，将所有三角形列举出来，再计数：如下图：，三角形有：三角形ABC，三角形ABD，三角形ABE，三角形ABF，三角形ACD，三角形ACE，三角形ACF，三角形ADE，三角形ADF，三角形AEF、共有10个、。
小升初试题——几何篇含解析
小升初名校真题专项测试-----几何篇引言：随着小升初考察难度的增加，几何问题变越来越难，一方面，几何问题仍是中学考察的重点，各学校更喜欢几何思维好的学生，这样更有利于小学和初中的衔接；另一方面几何问题由于类型众多，很多知识点需要提前学，这就加快了学生知识的综合运用，而这恰恰是重点中学学校所期望的。
所以近几年的几何难度年年在增加，很多学校的考题可以说超出小学的范围，本节主要是通过分析例题来讲解其中的相关知识点和解题思维。
测试时间：15分钟 姓名_________ 测试成绩_________1、如图，在三角形ABC 中，，D 为BC 的中点，E 为AB 上的一点，且BE=13AB,已知四边形EDCA 的面积是35，求三角形ABC 的面积.【解】根据定理：ABC BED ∆∆=3211⨯⨯=61，所以四边形ACDE 的面积就是6-1=5份，这样三角形35÷5×6=42。
2、四个完全一样的直角三角形和一个小正方形拼成一个大正方(如图)如果小正方形面积是1平方米，大正方形面积是5平方米，那麽直角三角形中，最短的直角边长度是______米.【解】小正方形面积是1平方米，大正方形面积是5平方米，所以外边四个面积和是5-1=4，所以每个三角形的面积是1，这个图形是“玄形”，所以长直角边和短直角边差就是中间正方形的边长，所以求出短边长就是1。
3、如图在长方形ABCD 中，△ABE 、△ADF 、四边形AECF 的面积相等。
△AEF 的面积是长方形ABCD 面积的______ (填几分之几)。
【解】连接AC，首先△ABC和△ADC的面积相等，又△ABE和△ADF的面积相等，则△AEC 和△AFC的面积也相等且等于ABCD的1/6，不难得△AEC与△ABE的面积之比为1/2，由于这两个三角形同高，则EC与BE之比为1/2，同理FC与DF之比也为1/2。
从而△ECF相当于ABCD面积的1/18，而四边形AECF相当于ABCD面积的1/3，从而答案为1/3-1/18=5/18。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4
3
⑴
⑵
1
2
⑶
【解析】⑴ 4.5
1
1
⑷
⑵4
⑶1
⑷2
3 ．【差不变】三角形 ABC 是直角三角形，阴影 I 的面积比阴影 II 的面积小 25cm2 ， AB 8cm ，求 BC 的长度． A
I
I I B C
小学奥数微信号：lopolovelogo
1
【解析】由于阴影 I 的面积比阴影 II 的面积小 25cm2 ，根据差不变原理，直角三角形 ABC 面积减去半圆面积为 25cm2 ，则直角三角形 ABC 面积为
19．【表面积计算】如图，棱长分别为 1 厘米、 2 厘米、 3 厘米、 5 厘米的四个正方体紧贴 在一起，则所得到的多面体的表面积是多少平方厘米？
【解析】(法 1)四个正方体的表面积之和为： (12 22 32 52 ) 6 39 6 234 (平方厘米)，
重叠部分的面积为： 12 3 (22 2 12 ) (32 22 12 ) (32 22 12 ) 3 9 14 14 40 (平方厘米)， 所以，所得到的多面体的表面积为： 234 40 194 (平方厘米)．
7
(法 2)三视图法．从前后面观察到的面积为 52 32 22 38 平方厘米,从左右 两个面观察到的面积为 52 32 34 平方厘米，从上下能观察到的面积为 52 25 平方厘米． 表面积为 38 34 25 2 194 (平方厘米)．
20．【表面积计算】用棱长是 1 厘米的立方块拼成如右图所示的立体图形，问该图形的表 面积是多少平方厘米?
EFB
BCD ，有
连接 AC，AF，HC，还可得 S 有S
EFB
6S
ABC
，S
DHG
6S
ACD
，
S
DHG
6S
ABC
S
ACD
6S ABCD =30 平方厘米.
有四边形 EFGH 的面积为 EAH, FCG, EFB, DHG,ABCD 的面积和，即为 30+30+5=65(平方厘米.)
【 解析】 从图上可以知道，小长方形的长的 4 倍等于宽的 5 倍，所以长是宽的 5 4 1.25 倍．每个小长方形的面积为 45 9 5 平方厘米，所以 1.25 宽 宽 5 ，所以宽为 2 厘米， 长为 2.5 厘米．大长方形的周长为 (2.5 4 2 2.5) 2 29 厘米． 12 ．【梯形蝴蝶】如图， ABCD 与 AEFG 均为正方形，三角形 ABH 的面积为 6 平方厘 米，图中阴影部分的面积为 ．
14．【曲线型面积】如图，ABCD 是边长为 a 的正方形，以 AB、BC、CD、DA 分别为直 径画半圆，求这四个半圆弧所围成的阴影部分的面积．( π 取 3)
A D
A D
B
a
C
B
a
C
【解析】这道题目是很见的面积计算问题．阴影部分是一个花瓣状的不规则图形， 不能直接通过面积公式求解，观察发现阴影部分是一个对称图形，我们只需要在阴影 部分的对称轴上作两条辅助线就明了了．
图１ 图2 【 解析】 我们可以让静止的瓷砖动起来，把对角线上的黑瓷砖，通过平移这种动态的 处理，移到两条边上 (如图 2)．在这一转化过程中瓷砖的位置发生了变化，但数量没 有变，此时白色瓷砖组成一个正方形．大正方形的边长上能放 (101 1) 2 51 (块)，白
色 瓷 砖 组 成 的 正 方 形 的 边 长 上 能 放 ： 51 1 50 ( 块 ) ， 所 以 白 色 瓷 砖 共 用 了 ： (0 块)． 5 0 5 0 250 8. 【化整为零】正方形 ABCD 与等腰直角三角形 BEF 放在一起（如图），M、N 点为正方 2 形的边的中点，阴影部分的面积是 14cm ，三角形 BEF 的面积是多少平方厘米？
30 道典型几何题解析
1．【加减法求面积】如图是一个直径为 3cm 的半圆，让这个半圆以 A 点为轴沿逆时针方 向旋转 60 ，此时 B 点移动到 B ' 点，求阴影部分的面积．(图中长度单位为 cm ，圆周率按 3 计算)．
B'
60 A B
【解析】面积 圆心角为 60 的扇形面积 半圆 空白部分面积(也是半圆) 圆心角为 60 3 60 的扇形面积 π 32 π 4.5(cm2 ) ． 360 2 2．【割补法求面积】求下列各图中阴影部分的面积 (图中长度单位为 cm ，圆周率按 3 计 算)：
【解析】该图形的上、左、前三个方向的表面分别由 9、7、7 块正方形组成．
该图形的表面积等于 (9 7 7) 2 46 个小正方形的面积，所以该图形表面积 为 46 平方厘米．
21．【取特殊点】长方形 ABCD 的面积为 36， E 、 F 、 G 为各边中点， H 为 AD 边上任 意一点，问阴影部分面积是多少？
【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半，为 1 20 12 120 ． 2 6．【面积与旋转】如图所示，直角三角形 ABC 的斜边 AB 长为 10 厘米， ABC 60 ， 此时 BC 长 5 厘米．以点 B 为中心，将 ABC 顺时针旋转 120 ，点 A 、 C 分别到达点 E 、 D 的位置．求 AC 边扫过的图形即图中阴影部分的面积．( π 取 3)
E C
(2) (1) E
C
A
B
D
A
B
D
【解析】注意分割、平移、补齐．
如图所示，将图形⑴移补到图形⑵的位置，
小学奥数微信号：lopolovelogo
2
因为 EBD 60 ，那么 ABE 120 ，
1 则阴影部分为一圆环的 ． 3
7 ．【图形与平移】用同样大小的瓷砖铺一个正方形地面，两条对角线上铺黑色的，其它 地方铺白色的，如图所示．如果铺满这块地面共用 101 块黑色瓷砖，那么白色瓷砖用了多 少块？
E F G H
A
B
C
D
【解析】本题需要注意，长方形 ADHE 的宽应等于正方形 BCGF 的边长． 由于图中阴影部分 BCGF 是个正方形，其四条边的边长都相等，且等于长方形 ADHE 的 宽． FH AC 的和应为长方形 ADHE 的长加上正方形 BCGF 的边长，所以等于长方形 ADHE 的长与宽之和．所以长方形 ADHE 的周长为： (18 24) 2 84 厘米． 11．【周长与面积】有 9 个小长方形，它们的长和宽分别相等，用这 9 个小长方形拼成的 大长方形的面积是 45 平方厘米，求这个大长方形的周长．
D
C
D
C
F H G
E
F H
E
A
B
G
A
B
【解析】如图，连接 AF ，比较 ABF 与 ADF ，由于 AB AD ， FG FE ，即 ABF 与 ADF 的底与高分别相等，所以 ABF 与 ADF 的面积相等，那么阴影部分面积与 ABH 的面积相等，为 6 平方厘米．
13．【曲线开型面积】如右图，有 8 个半径为 1 厘米的小圆，用它们的圆周的一部分连成
1 8 π 25 8π 25 ( cm2 )， 2 2
BC 的长度为 8π 25 2 8 2π 6.25 12.53 ( cm )．
2
4．【等量代换】下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面 积.
20－5
5 8 20
如图，这样阴影部分就划分成了 4 个半圆减去三角形，我们可以求得，
2 1 a 1 a 1 S阴影 4 S半圆 S三角形 4 a a 2 2 2 2 2 2
15．【表面积计算】中是一个边长为 4 厘米的正方体，分别在前后、左右、上下各面的中 心位置挖去一个边长 1 厘米的正方体，做成一种玩具．它的表面积是多少平方厘米？
4
一个花瓣图形，图中的黑点是这些圆的圆心．则花瓣图形的面积是多少平方厘米？ ( π 取 3)
【解析】本题直接计算不方便，可以利用分割移动凑成规则图形来求解．
如右上图，连接顶角上的 4 个圆心，可得到一个边长为 4 的正方形．可以看 出，与原图相比，正方形的每一条边上都多了一个半圆，所以可以把原花瓣 图形的每个角上分割出一个半圆来补在这些地方，这样得到一个正方形，还 1 剩下 4 个 圆，合起来恰好是一个圆，所以花瓣图形的面积为 4 2 2 4 π 1 19 (平方厘米)．
【解析】如下图，连接 BD，ED，BG，
有 EAD、 ADB 同高，所以面积比为底的比，有 S
EAD
EA S AB
ABD
2S
ABD ．
同理 S
EAH
AH S AD
EAD
3S
EAD
6S
ABD ．
类似的，还可得
S
S
EAH
S
FCG
6S
FCG
6S
ABD
S
BCD
6S ABCD =30 平方厘米．
8 20
【解析】所求面积等于图中阴影部分的面积，为(20 5 20) 8 2 140 (平方厘米)． 5．【等面积变形】如下图，长方形 AFEB 和长方形 FDCE 拼成了长方形 ABCD ，长方形 ABCD 的长是 20，宽是 12，则它内部阴影部分的面积是多少?
A B
F D
E C
【解析】因为 M、N 是中点，故我们可以将该图形进行分割，所得图形如下
F A M D N B C E B C F A M D N E
图形中的三角形面积都相等，阴影部分由 7 个三角形组成，且其面积为 14 平方厘米， 故一个三角形的面积为 2 平方厘米，那么三角形 BEF 的面积是 18 平方厘米。 9. 【割补法】如图所示的四边形的面积等于多少？