小升初数学专项题第五讲 立体图形应用题_通用版
小升初立体图形专题训练.
立体图形专项训练1、将表面积分别为54平方厘米，96平方厘米和150平方厘米的三个铁块正方体融成一个大正方体（不记损耗），求这个大正方体的体积。
2、在一个长15分米，宽12分米的长方体水箱中，有10分米深的水。
如果在水中沉入一个棱长为30厘米的正方体铁块，那么，水箱中水深多少分米？3、一个长方体容器的底面是一个边长为60厘米的正方形，容器里直立着一个高1米、底面边长都是15厘米的长方体铁块。
这时容器里的水深0.5米。
如果把铁块取出，容器里的水深多少厘米？4、有一个长方体冰箱，从里面量长40厘米，宽30厘米，高35厘米，箱中水面高10厘米。
放进一个棱长20厘米的正方体铁块后，铁块顶面仍高于水面。
这时水面高是多少厘米？5、一个长方体，不同的三个面的面积分别是35平方厘米，21平方厘米和15平方厘米，且长、宽、高都是质数。
这个长方体的体积是多少立方厘米？6、一个长方体，如果高增加3厘米，就变成一个正方体，这时表面积比原来增加48平方厘米，原来长方体的体积是多少厘米？7、一个直角三角形，两条直角边分别是3厘米、4厘米，怎样旋转体积最大？最大体积是多少？8、一个棱长6厘米的正方体，从正方体的底面向内挖去一个最大的圆锥体，求剩下的体积是原正方体的百分之几？9、两个相同的圆锥容器中盛一些水（如图），水深都是圆锥高的一半，那么甲容器中的水的体积是乙容器中水的几倍？10、已知一个圆锥体的底面半径和高都等于一个正方体的棱长，这个正方体的体积是216立方分米，求这个圆锥体的体积？11、在底面半径为60厘米的正方形的一个长方体容器里，直立放着一个长100厘米，底面边长为15厘米的正方形的四棱锥铁棍，这时容器里的水50厘米深，现在把铁棍轻轻地向上方提起24厘米，露出水面的四棱柱铁棍浸湿部分长多少厘米？12、一个酒精瓶，它的瓶身呈圆柱形（不包括瓶颈），如图，已知它的容积为26.4π立方厘米。
当瓶子正放时，瓶内的酒精的液面高为6厘米。
小升初分班考专题立体图形(专项练习)六年级下册数学人教版
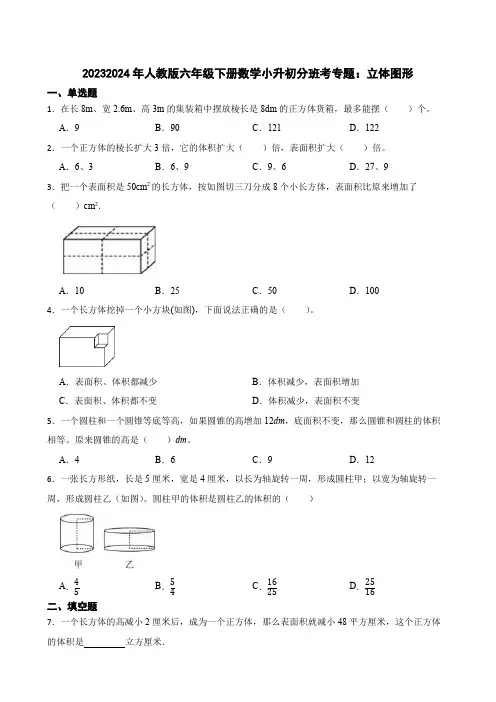
20232024年人教版六年级下册数学小升初分班考专题：立体图形一、单选题1．在长8m、宽2.6m、高3m的集装箱中摆放棱长是8dm的正方体货箱，最多能摆（）个。
A．9B．90C．121D．1222．一个正方体的棱长扩大3倍，它的体积扩大（）倍，表面积扩大（）倍。
A．6、3B．6、9C．9、6D．27、93．把一个表面积是50cm2的长方体，按如图切三刀分成8个小长方体，表面积比原来增加了（）cm2．A．10B．25C．50D．1004．一个长方体挖掉一个小方块(如图)，下面说法正确的是（）。
A．表面积、体积都减少B．体积减少，表面积增加C．表面积、体积都不变D．体积减少，表面积不变5．一个圆柱和一个圆锥等底等高，如果圆锥的高增加12dm，底面积不变，那么圆锥和圆柱的体积相等。
原来圆锥的高是（）dm。
A．4B．6C．9D．126．一张长方形纸，长是5厘米，宽是4厘米，以长为轴旋转一周，形成圆柱甲；以宽为轴旋转一周，形成圆柱乙（如图）。
圆柱甲的体积是圆柱乙的体积的（）A．45B．54C．1625D．2516二、填空题7．一个长方体的高减小2厘米后，成为一个正方体，那么表面积就减小48平方厘米，这个正方体的体积是立方厘米．8．家用卫生纸的宽度一般是10cm，中间硬卷轴的直径是3.5cm。
制作中间的纸轴需要cm2的硬纸板。
9．把一个长12分米的圆柱体木料，锯成3个小圆柱体，表面积增加了32平万分米，这根圆柱体木料的体积是立方分米。
10．把个底面半径是3厘米、高18厘米的圆锥形橡皮泥捏成个底面与圆锥相等的圆柱。
圆柱的高是厘米。
11．一个圆柱形罐头盒的侧面贴着商标纸，圆柱底面半径是5cm，高是20cm。
如果这张商标纸展开后是一个长方形，则它的长是cm，宽是cm，面积是cm2.12．小雪的学校叫实验小学，一进校门，就能看到大厅的8根一样大小的圆柱形大理石柱，每根柱子的半径是5分米，高6米，如果要清洗这些柱子，清洗的面积是平方米。
小升初数学复习专题《立体图形》练习及答案
小升初数学复习专题《立体图形》练习一、填空题1．圆锥是由两个面组成，其中一个面是平面，另一个面是。
2．正方体的棱长是2a厘米，它的表面积是平方厘米，体积是立方厘米。
3．小明家挖了一个长为6m、宽为5m、深为2m的长方体地窖，这个地窖占地m2。
4．一个圆锥的体积是4.2dm3，底面积是0.9 dm2，高是。
5．一个正方体木块的棱长是6cm，把它削成一个最大的圆柱体，圆柱体的体积是cm3，再把这个圆柱体削成一个最大的圆锥体，圆锥体的体积约是cm3．6．圆柱的侧面沿高展开后是形或形。
一个圆柱的侧面沿高展开是正方形，正方形的边长是12.56cm，圆柱的底面积是cm2。
7．圆柱有个面是大小相同的圆，有一个面是面，圆柱的两个底面是半径相等的两个圆，两个底面间的距离叫做，圆柱周围的曲面叫做面。
8．把一个底面半径6厘米、高8厘米的圆柱体，切拼成一个近似的长方体，表面积比原来增加了平方厘米。
9．如图，在直角三角形MON中，MO=2cm，NO=5cm，如果分别以MO、NO边为轴旋转一周形M成圆锥，那么以MO为轴和以NO为轴的圆锥体积之比是。
二、单选题10．下面的图形中，()是正方体的展开图。
A．B．C．D．11．把一个圆柱的侧面展开，不可能得到（）。
A．长方形B．正方形C．平行四边形D．梯形12．下列图形由（）组成。
A．圆锥和圆柱B．圆柱和球体C．圆锥和球体D．圆锥和圆台13．小强测量一个土豆的体积，在一个棱长1分米的正方体容器中装了一些水，水面距离杯口2厘米（如图）。
他把土豆浸没在水中，有部分水溢出，接着他又把土豆取出来，水面下降了3厘米，土豆的体积是（）立方厘米。
A．200B．500C．100D．30014．如图（单位：厘米），酒瓶中装有一些酒，倒进一只酒杯中，酒杯的直径是酒瓶内直径的一半，共能倒满（）杯。
A．10B．15C．20D．3015．将一个棱长是6分米的正方体木块削成一个最大的圆锥，圆锥的体积是（）立方分米。
小升初总复习——小学数学立体图形练习专题(含答案)
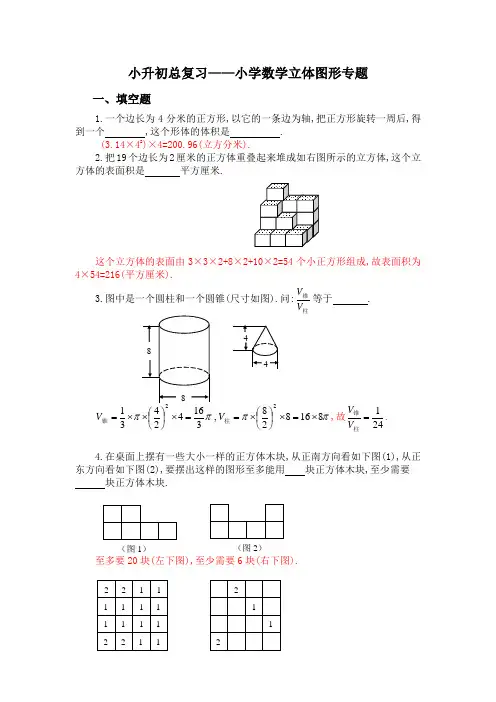
小升初总复习——小学数学立体图形专题一、填空题1.一个边长为4分米的正方形,以它的一条边为轴,把正方形旋转一周后,得到一个 ,这个形体的体积是 .(3.14×42)×4=200.96(立方分米).2.把19个边长为2厘米的正方体重叠起来堆成如右图所示的立方体,这个立方体的表面积是 平方厘米.这个立方体的表面由3×3×2+8×2+10×2=54个小正方形组成,故表面积为4×54=216(平方厘米).3.图中是一个圆柱和一个圆锥(尺寸如图).问:柱锥V V 等于 .ππππ816828,316424312⨯=⨯⎪⎭⎫ ⎝⎛⨯==⨯⎪⎭⎫ ⎝⎛⨯⨯=柱锥VV ,故241=柱锥V V .4.在桌面上摆有一些大小一样的正方体木块,从正南方向看如下图(1),从正东方向看如下图(2),要摆出这样的图形至多能用 块正方体木块,至少需要 块正方体木块.至多要20块(左下图),至少需要6块(右下图).（图1）（图2） 2 1 2 12 2 1 2 1 1 11 1 1 1 1 12 1 15.一个圆柱形玻璃杯中盛有水,水面高2.5厘米,玻璃内侧的底面积是72平方厘米,在这个杯中放进棱长6厘米的正方体的铁块后,水面没有淹没铁块,这时水面高 厘米.水的体积为72×2.5=180(cm 2),放入铁块后可以将水看作是底面积为72-6×6=36(cm 2)的柱体,所以它的高为180÷36=5(cm )二、解答题1.一个长方形水箱,从里面量长40厘米,宽30厘米,深35厘米.原来水深10厘米,放进一个棱长20厘米的正方形铁块后,铁块的顶面仍然高于水面,这时水面高多少厘米?若铁块完全浸入水中,则水面将提高326)3040(203=⨯÷(厘米).此时水面的高小于20厘米,与铁块完全浸入水中矛盾,所以铁块顶面仍然高于水面.设放入铁块后,水深为x 厘米.因水深与容器底面积的乘积应等于原有水体积与铁块浸入水中体积之和,故有:x x 20201030403040⨯+⨯⨯=⨯解得x =15,即放进铁块后,水深15厘米.2.雨哗哗地不停地下着,如在雨地里放一个如图1那样的长方形的容器,雨水将它下满要用1小时.有下列(A )-(E )不同的容器(图2),雨水下满各需多少时间(注面是朝上的敞口部分.)2cm 2cm （A ） （B ） （C ） （D ） （E ） 雨在例图所示的容器中,容积:按水面积=(10×10×30):(10×30)=10:1,需1小时接满,所以容器(A):容积:接水面积=(10×10×10):(10×10)=10:1,需1小时接满; 容器(B):容积:接水面积=(10×10×30):(10×10)=30:1,需3小时接满; 容器(C):容积:接水面积=(20×20×10-10×10×10):(10×10)=30:1,需3小时接满;容器(D):容积:接水面积=(20×20×10-10×10×10):(20×10)=15:1,需1.5小时接满;容器(E):容积:接水面积=20×S:S=20:1(S 为底面积),接水时间为2小时.3、如图是一个立体图形的侧面展开图,求它的全面积和体积.这个立体图形是一个圆柱的四分之一(如图),圆柱的底面半径为10厘米,高为8厘米.它的全面积为: 810281014.32411014.34122⨯⨯+⨯⨯⨯⨯+⨯⨯⨯ 6.4421606.125157=++=(平方厘米).它的体积为:62881014.3412=⨯⨯⨯(立方厘米).。
2023-2024学年人教版六年级下册数学小升初专题训练：立体图形(含答案)
2023-2024学年人教版六年级下册数学小升初专题训练：立体图形一、单选题1．一个长方体正好可以切成3个一样的正方体，切开后每个正方体的表面积是12平方厘米，那么原来这个长方体的表面积是（ ）平方厘米。
A．36B．30C．28D．242．图中呈现的是一瓶已经喝了一些的果汁和一个圆锥形玻璃杯，如果瓶中的果汁倒入这种圆锥形玻璃杯，最多可以倒满（ ）。
（容器厚度忽略不计）A．2杯B．3杯C．4杯D．6杯3．小明买了一瓶水喝掉了一部分后还有剩余（如图所示），已知这个饮料瓶的内直径是6cm。
根据如图中标出的数据，小明用算式“3.14×（6÷2）2×（18+7）”计算的是（ ）A．喝掉的水的体积。
B．瓶子的容积。
C．剩余水的体积。
D．喝掉的水和剩余的水相差的体积。
4．一个圆柱体和一个圆锥体的底面周长之比是1：3，它们的体积比是1：3，圆柱体和圆锥体高的比是（ ）。
A．3：1B．1：9C．1：1D．3：25．一个长方体的长、宽、高分别扩大到原来的2倍，则它的表面积扩大到原来的( )倍，体积扩大到原来的( )倍。
此题选( )。
A．2；4B．4；8C．6；8D．8；46．下面（ ）图形是圆柱的展开图。
（单位：cm）A．B．C．D．二、填空题7．长方体和正方体都有6个面， 条棱， 个顶点8．西游记中的孙悟空正直勇敢、嫉恶如仇，他有一件神奇的兵器叫如意金箍棒，可以任意缩小或放大。
如果孙悟空把如意金箍棒变化成底面周长是6.28分米，那么此时，它的体积是 立方分米。
9．如先图，把一个直径为4cm，高为8cm的圆柱，表面积增加了 平方厘米。
10．把64升水倒入一个长8分米、宽2.5分米、高4分米的长方体水箱内，这时水面距箱口 分米。
11．一根长1米，横截面直径是2分米的木头浮在水面上，小明发现它正好是一半露出水面，这根木头露出水面部分的体积是 立方分米。
12．用一根48分米长的铁丝做成一个正方体框架，这个正方体框架的表面积 平方分米，体积是 立方分米。
2024年人教版六年级下册数学小升初专题训练：立体图形(含答案)
2024年人教版六年级下册数学小升初专题训练：立体图形一、单选题1．把一支新的圆柱形铅笔削尖，笔尖（圆锥部分）的体积是削去部分的（ ）。
A．13B．23C．12D．2倍2．比较等底等高的圆柱、正方体、长方体的体积的大小，结果是（）A．长方体体积大B．正方体体积大C．圆柱体积大D．一样大3．把一个长、宽、高分别是6cm、2cm和2cm的长方体锯成三个大小完全相等的小正方体，表面积比原来增加了（ ）cm2。
A．8B．16C．24D．364．如图，两个圆柱形容器盛有相同体积的水，①号容器原来水面高是8cm，放入小球后水面的高是10cm；②号容器放入同样大的小球和一个小长方体后水面的高是26cm，小球的体积与小长方体的体积比是（ ）A．3：11B．3：5C．3：2D．9：75．两个圆柱的体积相等，底面积之比为3：4。
则这两个圆柱的高的比是（ ）。
A．4：3B．3：4C．9：16D．16：96．一个圆柱的底面半径是1cm，高是4cm，它的表面积是（ ）cm2。
A．12.56B．25.12C．31.4D．56.52二、判断题7．一个正方体的棱长是6厘米，它的表面积和体积相等。
（ ）8．如果两个圆柱的侧面积相等，那么它们的体积也一定相等。
（ ）9．把一个圆柱削成一个最大的圆锥，削去部分的体积是圆柱体积的23。
（ ）10．圆柱和圆锥都有无数条高。
11．长方体中，高不变，底面积越大，体积也越大。
（ ）12．一个圆锥的底面半径和高都是3cm，它的体积是28.26cm3。
（ ）三、填空题13．把一个圆柱形木料加工成一个最大的圆锥体，需要削去30立方分米的木料，则原来这根木料的体积是 立方分米。
14．一个圆锥，底面半径是4厘米，高是12厘米，从圆锥的顶点沿高将它切成相同的两半后，表面积比原来圆锥的表面积增加了 平方厘米。
15．一个圆柱，沿底面直径和高竖直切开得到两个半圆柱，切面是边长为4厘米的正方形。
原来这个圆柱的表面积是 平方厘米，体积是 立方厘米。
2024年人教版六年级下册数学小升初分班考必刷专题 ： 立体图形
2024年人教版六年级下册数学小升初分班考必刷专题：立体图形一、选择题1．小华用6个同样大小的正方体摆成一个物体．从正面和上面看到的都是从右侧面看摆成的物体，看到的是第（）号图形．A．B．C．D．2．一个直角三角形两条直角边分别是4厘米和6厘米，如果以较长的直角边所在的直线为轴，将三角形旋转一周形成的立体图形的体积是（）立方厘米．A．301.44B．452.16C．100.48D．150.723．一个正方体的底面积是25平方厘米，它的体积是（）立方厘米。
A．25B．125C．225D．5504．把两个表面积分别是24cm2的正方体拼成一个长方体，该长方体的表面积是（）。
A．48cm2B．40cm2C．36cm2D．24cm25．一个圆柱和一个圆锥的底面积相等，圆柱和圆锥的体积比是3：2，圆柱和圆锥的高的比是（）。
A．1∶3B．3：1C．1：2D．2：16．一个棱长10cm的正方体容器中装有一些水，将一个高8cm的长方体铁块竖直着放入水中（铁块底面与容器底面平行），铁块还没有完全浸没时，水就满了（如下图）。
这个铁块的体积是（）3cm。
A．300B．400C．600D．800二、填空题7．南山湖音乐喷泉是由48个内直径为2厘米的出水管围成的一个圆形。
打开音乐喷泉时，水喷涌的速度是5米/秒，如果不实行水循环系统，那么一分钟会浪费( )吨水。
（每立方米水的质量是1吨）8．一个棱长是5分米的正方体水箱内，水面的高度为3分米，水的体积是( )升．9．如图，以长方形3厘米的边所在直线为轴旋转，可以得到一个( )，它的底面直径是( )厘米，侧面积是( )平方厘米。
10．长方体纸盒的长为acm，宽和高都是bcm，用含有字母的式子表示这个纸盒的体积是( )cm3。
11．一个立体图形，从左面看到的形状是，从上面看到的形状是，搭成这样的立体图形，最少需要( )个小正方体。
12．如图所示，把底面半径为4分米的圆柱切成若干等份，拼成一个近似的长方体，这个长方体的表面积比原来增加40平方分米，这个圆柱的高是( )分米，圆柱的体积是( )立方分米。
小升初空间几何(立体图形)专项训练
空间几何（立体图形）专项训练解决问题的切入点放在把握图形的特征上。
在解决问题的策略上，加强对图形特征的分析和研究，就能够抓住问题的本质特征，使问题迎刃而解。
1．通过联想图形的基本特征，来巧妙地解决问题，提升了解决问题的方法，达到了数形结合的目的。
2．有条理、有根据地思考问题是一种重要的思维品质，由于面临的问题往往不能一步解决，而需要以分步写小标题的形式来进行解决，这个过程中就训练了有序思考的能力。
3．在解决问题的过程中，说一说自己是怎样想的，怎样做的，达到学以致用的目的。
练习1：等底等高的圆柱和圆锥，它们的体积之和是60立方厘米，圆柱的体积是多少立方厘米？圆锥的体积是多少立方厘米？2：等底等高的圆柱和圆锥，它们的体积之差是60立方厘米，圆柱的体积是多少立方厘米？圆锥的体积是多少立方厘米？3：把一根2米长的圆柱形木棒截成三段，表面积增加15平方厘米，这根木棒的体积是多少立方厘米？4：圆柱的侧面展开得到正方形，它的底面周长是36厘米，它的高是多少厘米？5：把一个圆柱削去一个最大的圆锥体后，体积还剩54立方厘米，这个圆锥的体积是多少立方厘米？6：一个没有盖的圆柱形铁皮桶，底面周长是18.84分米,高是12分米,做这个水桶大约需要多少平方分米铁皮?7:一堆圆锥形沙堆,底面周长是25.12米,高1.5米,每立方米黄沙重1.7吨,这堆沙重多少吨?8:压路机的滚筒是一个圆柱体,它的宽是2米,横截面半径是0.8米,以每分钟滚动5周计算,1小时可以压多大的路面?1小时可以前进多少米?9:一张长方形铁皮长为3厘米,宽为2厘米,绕着它的任意一条边旋转一周,可以得到一个什么立体图形?这个立体图形体积最大是多少?10:一个直角三角形的两条直角边分别长6厘米、10厘米，以10厘米的直角边为轴旋转一周，可以得到一个什么形体？它的体积是多少立方厘米？11:一个高8厘米的圆柱如果高减少2厘米,它的表面积就减少25.12平方厘米,求这个圆柱的体积?12：一只圆柱形油罐，原来高8分米，现在需要加高5分米，这样表面积增加6.28平方米,油罐加高后的容积是多少立方米?13:一个直径是20厘米,长2米的圆木,要锯成一个横断面是最大的,长方体的方木,锯成的长方体方木的体积是多少立方分米?14：把一个半径为10厘米的圆锥形钢材浸没在一只底面半径是30厘米的圆柱形水桶里，当钢材从水桶中拿出，桶里的水面下降了1厘米。
六年级下册数学试题-小升初专题之立体图形 通用版含答案
1.50分米
我爱展示
1.1004.8
导学七 知识点讲解 1 例题
1.50.24立方厘米
导学八 知识点讲解 1 例题
1.62.8厘米
我爱展示
1.10.676吨
2.7.5厘米
3.8厘米
限时考场模拟
1.24厘米
自主学习
1.18#54
2.12#36
3.56.52
4.12.56
5.15.072
6.120
3. 一个钢质的圆柱体零件重1763.424克，它的侧面展开图是一个长方形，长方形的长（不是圆柱的高）是18.84厘米，
求这个圆柱的高（每立方厘米钢重7.8克）
我当小老师
本节课你学到了什么？学生口述。 你觉得自己学的最好的是那种题型？举例说明。 你觉得那个知识点是你最难理解的？举例说明。
限时考场模拟
同学发现关上，问浪费了（
）升水。
6.
2019/3/16
一根长方体的木料，正好可以锯成两个同样的正方体，这时表面积增加了24平方厘米，这根长方体的木料原来的表面积
是（
）平方厘米。
培养良好的自主学习习惯
课首小测
1.1.①6#长方形#正方形#相对的两个面#12②6#正方形#所有面#12#相等2.43.2244．×
导学八
知识点讲解 1
例 1.
一个圆柱形油桶，侧面展开是一个正方形，已知这个油桶的底面半径是10厘米，那么油桶的高是多少厘米？
我爱展示
1.
2019/3/16
在建筑工地上有一个近似于圆锥形状的沙堆，测得底面直径4米，高1.5米。每立方米沙大约重1.7吨，这堆沙约重多少 吨？
2.
把一个体积是282.6立方厘米的长方体铁块熔铸成一个底面半径是6厘米的圆锥形机器零件，求圆锥零件的高？
人教版六年级下册数学小升初分班考必考专题 ： 立体图形
＝2×2
＝4（个）
增加的表面积：16×4＝64（平方分米）
所以，表面积增加64平方分米。
【点睛】本题主要考查立体图形的切拼，求出增加截面的数量是解答题目的关键。
16．8 24
【分析】根据正方体的体积公式：V＝a3，求出水的体积，然后根据圆柱的体积公式：V＝Sh，据此可求出圆柱形容器的高；再根据圆锥的体积公式：V＝ Sh，据此求出圆锥形容器的高。
【点睛】本题考查圆柱和圆锥的体积，明确等底等高的圆锥的体积是圆柱体积的 是解题的关键。
8．128
【分析】先根据正方体的体积＝棱长×棱长×棱长，求出这个橡皮泥的体积；把这个橡皮泥做成一个等底等高的一个圆柱体和一个圆锥体，橡皮泥的体积不变，即圆柱和圆锥的体积之和等于正方体的体积；
因为圆柱和圆锥等底等高，那么圆柱的体积是圆锥的3倍，可以把圆锥的体积看作1份，则圆柱的体积是3份，总份数是（1＋3）份；用这个橡皮泥的体积除以总份数，求出一份数，即是圆锥的体积。
29．汪师傅把一块长40cm、宽30cm、高20cm的长方体木料加工成一个圆柱体，聪聪利用所学的知识提了建议，加工后的圆柱体体积最大，加工后的体积是多少？
30．一个圆锥形物体的底面周长是12.56分米，高9分米。
（1）这个圆锥体所占的空间是多少立方分米？
（2）如果给这个圆锥形物体做一个长方体的包装盒，至少要多少平方分米的硬纸板？
（3）这只茶杯装满水后的容积是多少？
参考答案：
1．C
【详解】做一个长方体的鱼缸（无盖），通过这个条件可以判断：
A.①玻璃两块②玻璃两块④玻璃两块总计用了六块玻璃，是错误的；
B.③玻璃两块④玻璃两块②玻璃一块，选两块③说明宽是2、高是3；选两块④说明长是5、宽是4；与③矛盾，不符合长方形的特征，是错误的；
小学数学小升初立体图形专项训练试题
小升初数学立体图形专项训练试题基础题一、选择题1.一个长方体的长、宽、高都扩大2倍，它的体积扩大（）倍。
A、2B、6C、8【答案】C【解析】长方体的体积=长×宽×高，长、宽和高都扩大2倍，则体积就扩大了2×2×2=8倍，根据此选择即可。
2.我们在画长方体时一般只画出三个面，这是因为长方体（）。
A.只有三个面B.只能看到三个面C.最多只能看到三个面【答案】C【解析】把长方体放在桌面上，最多可以看到3个面。
根据此选择。
3.沿着圆柱上下两个底面的直径把圆柱切开，可以得出（）形。
A.长方形B.圆形C.梯形【答案】A。
【解析】沿着圆柱的上下两个底面的直径把圆柱切开，可以得出长方形。
根据此选择即可。
4.一个圆锥是由橡皮泥捏成的，要切一刀把它分成两块，（）切割，截面会是圆；（）切割，截面会是三角形。
A.垂直于底面B.平行于底面【答案】B；A。
【解析】一个圆锥是由橡皮泥捏成的，要切一刀把它分成两块，平行于底面切割，截面会是圆；垂直于底面切割，截面会是三角形，根据此选择即可。
5.沿着圆柱的高，把圆柱的侧面展开，得不到（）。
A. 梯形B.长方形C.正方形【答案】A【解析】沿着圆柱的高把圆柱的侧面展开，可以得到长方形或正方形，根据此选择即可。
6.一个长方体的长是4厘米，宽是3.5厘米，高是1.5厘米，它的底面的面积是（）平方厘米。
A.6B.14C.5.25D.21【答案】B【解析】长方体的底面的面积=长×宽7.一个长方体的棱长和是36厘米，它的长、宽、高的和是（）厘米。
A.3B.9C.6D.4【答案】B【解析】棱长总和除以4，得出长、宽、高的和：36÷4＝9；据此选择即可。
8.下列说法错误的是（）。
A.正方体是长、宽、高都相等的长方体。
B.长方体与正方体都有12条棱。
C.长方体的6个面中至少有4个面是长方形。
D.长方体的6个面中最多有4个面是长方形。
【答案】D【解析】长方体的6个面一般情况下都是长方形，特殊的情况下，至少有4个面是长方形，所以D的说法是错误的；据此选择即可。
小升初数学专项题第五讲立体图形应用题_通用版
小升初数学专项题第五讲立体图形应用题_通用版【基础概念】：在小学时期学过的立体图形有长方体、正方体、圆柱、圆锥，与这些图形有关的问题叫作立体图形应用题；有关的公式：长方体：表面积公式：S=（ab+ah+bh ）×2，体积公式：V=abh=Sh ；正方体：表面积公式：S=6a ²，体积公式：V=a ³；圆柱：侧面积：S 侧=Ch=2πrh=πdh ，表面积：S=S 侧+2S 底，体积：V=S 底h ；圆锥：体积：V=13 S 底h 。
【典型例题1】：李力爱好手工制作，用一根长48分米的铁丝做了一个长方体框架，使它的长、宽、高的比是5：4：3．在那个长方体框架别处糊了一层彩色的纸，至少需要多少平方分米的彩纸？它的体积是多少立方分米？【思路分析】：用一根长48分米的铁丝做了一个长方体框架也确实是长方体的棱长总和是48分米，第一用棱长总和除以4求出长、宽、高的和，再利用按比例分配的方法分别求出长、宽、高，然后依照长方体的表面积公式：s=（ab+ah+bh ）×2，体积公式：v=abh ，把数据代入公式解答即可。
解答：长：48÷4×55+4+3=12×55+4+3=5（分米）宽：48÷4×45+4+3=12×45+4+3=4（分米）高：48÷4×35+4+3=12×35+4+3=3（分米）；（5×4+5×3+4×3）×2=（20+15+12）×2=47×2=94（平方分米）5×4×3=60（立方分米）答：至少需要94平方分米的彩纸，它的体积是60立方分米。
【小结】：解决这类问题要先运算出棱长，再利用表面积公式与体积公式运算。
【巩固练习】1．用一根长48分米的铁丝做一个长方体框架，长和宽的比是4：1，宽和高长度相等，在那个长方体框架别处糊一层纸，至少需要多少平方分米的纸？那个框架的体积是多少立方分米？2．用铁丝焊一个长方体框架，长1.8米，宽14分米，高100厘米，至少需要铁丝多少米？焊成的长方体体积是多少？【典型例题2】：一个圆柱体，底面半径是7厘米，表面积是1406.72平方厘米．那个圆柱的高是多少？【思路分析】：已知底面半径是7厘米，那么能够求得那个圆柱的底面积和底面周长；那个地点要求圆柱的高，依照已知条件，需要求得那个圆柱的侧面积，依照圆柱的表面积公式可得：侧面积=表面积-2个底面积，再利用圆柱的侧面积公式即可求得那个圆柱的高。
小升初立体图形专项训练
小升初知识训练之： 立体图形 一、判断。
1、圆锥的体积是圆柱体积的31。
( ) 2、如果两个圆柱体的侧面积相等，那么它们的底面周长也一定相等。
( ) 3、一个正方体棱长之和是２4厘米，它的表面积是24平方厘米。
( ) 4、把一个正方体一刀切成完全相同的两部分，切面一定是正方形。
( ) 5、一个圆柱和一个圆锥的底面积相等，圆锥的高是圆柱高的61。
那么圆锥的体积是圆柱体积的181。
( ) 6、一个圆锥的高是一个圆柱高的2倍，这个圆柱的半径与这个圆锥的直径相等，这个圆柱体积是这个圆锥体积的6倍。
( ) 7、用体积1立方厘米的小正方体木块125个，拼成一个最大的正方体，把拼成的正方体的表面都涂上红漆，只有两面红漆的有12块。
( ) 二、填空。
1、一个长方体截成两个正方体，如果这个长方体的表面积是60平方分米，那么，一个正方体的表面积是( )平方分米。
2、一根长方体木料，长2.5米，有两个面是正方形，其余四个面面积的和是2平方米，这根木料的体积是( )。
3、一个圆锥体的底面周长是25.12厘米，从圆锥的顶点沿着高将它切成两半后，表面积之和比原圆锥体的表面积增加了48平方厘米。
原来圆锥体的体积是( )立方厘米。
4、把一个长5厘米，宽4厘米、高3厘米的6个面都是红色的长方体切成棱长1厘米的正方体，这些正方体中只有2个面是红色的一共有 块。
5、左边这根石柱子的体积是( )立方米。
6、两块同样的肥皂用三种包装，第( )① ② ③7、一个棱长4厘米的正方体，锯成若干个棱长1厘米的正方体，表面积增加( )平方厘米。
8、一个正方体容器里将满水，再用正方体容器中的水将一个与它等底等高的圆锥形容器倒满时，这时正方体容器中还剩下18升水。
正方体容器的棱长是( )。
(容器厚度不计)米①7分米②5分米③3分米④4分米9、两个正方体的体积之比为64∶27，则这两个正方体的表面积之比为( )。
10、用三刀最多可把一个正方体蛋糕切成( )。
六年级下册数学试题-小升初专题之立体图形 通用版(含答案)
1.94 2.84平方分米
导学二 知识点讲解 1 例题
1.54平方厘米
我爱展示
1.32平方厘米
导学三 知识点讲解 1 例题
1.62.8厘米
导学四 知识点讲解 1 例题
1.6
导学五 知识点讲解 1 例题
1.1000#100
我爱展示
1.9千克
导学六 知识点讲解 1
2019/3/16
同学发现关上，问浪费了（
）升水。
6.
2019/3/16
一根长方体的木料，正好可以锯成两个同样的正方体，这时表面积增加了24平方厘米，这根长方体的木料原来的表面积
是（
）平方厘米。
培养良好的自主学习习惯
课首小测
1.1.①6#长方形#正方形#相对的两个面#12②6#正方形#所有面#12#相等2.43.2244．×
重、难点
1、明确各种立体图形的特征，能清楚的理解并灵活应用。 2、能灵活的利用各类公式和计算方法解决实际问题。
课首沟通
了解学生的学习情况
知识导图
课首小测
书面小测
2019/3/16
1.
1、①长方体有( )个面，每个面都是( )，也可能有两个相对的面是( )，(
)的面积相等。有
( )条棱。
4、判断：正方体的棱长扩大3倍，它的表面积就扩大6倍，体积就扩大9倍。（ ）
知识梳理
立体图形的表面积及长方体、正方体棱长总和 知识点1：长方体和正方体的表面积及棱长总和 知识点2：圆柱的表面积 知识点3: 切割面积的变化规律
长方体表面积：（ab＋bh＋ah）×2 长方体棱长总和：（a＋b＋h）×4
②正方体有( )个面，每个面都是( )形，( )的面积都相等，有( )条棱，它们的长度( )。
2021年六年级小升初数学总复习第五讲(立体图形)(含答案)
2021年六年级小升初数学总复习第五讲立体图形一．教学目标1.会根据展开图求表面积、体积。
2.会灵活运用公式求表面积、在体积。
3.会求不规则图形的体积。
二．知识点【熔铸问题】原理：体积不变。
【沉浮问题】原理：水上升的体积或者下降的体积与物体的体积相等。
【三视图求表面积】熟练掌握各立体图形的展开图。
【正方体展开图】常见的展开图模型：圆柱圆锥：1．圆柱的特征：有两个底面面积相等的圆和一个侧面；圆柱可以看作是由一个长方形沿着一条边旋转一周得到的立体图形。
2．圆锥的特征：从圆锥的顶点到底面圆心的距离叫做圆锥的高。
圆锥可以看作是由一个直角三角形沿着一条直角边旋转一周得到的立体图形。
立体图形表面积体积圆柱hr222π2πS rh r =+=+圆柱侧面积个底面积 2πV r h=圆柱圆锥hr22ππ360nS l r =+=+圆锥侧面积底面积注：l 是母线，即从顶点到底面圆上的线段长21π3V r h=圆锥体3．圆柱与圆锥体积的关系：当圆柱与圆锥等底等高时，圆柱的体积是圆锥的3倍，在圆柱中可以切出一个最大的圆锥，这个圆锥与它等底等高。
4．面积单位：常用的面积单位有平方厘米(cm 2)、平方分米（dm 2）、平方米(m 2)等，换算关系如下：1平方米(m 2)=100平方分米（dm 2）=10000平方厘米(cm 2)体积单位：常用的面积单位有立方厘米(cm 3)、立方分米（dm 3）、立方米(m 3)等，换算关系如下：1立方米(m 3)=1000立方分米（dm 3）=1000000立方厘米(cm 3)容积单位：物体所能容纳物体的体积叫物体的容积，常用的容积单位有毫升（ml ）和升（L ），换算关系如下： 1升(L)=1000毫升(ml) 1毫升(ml)=1立方厘米(cm 3) 1升(L)=1立方分米(dm 3)=1000立方厘米(cm 3) 1立方米(m 3)=1000升(L)=1000000毫升(ml)5．拼切问题：（1）把N 个相同的圆柱的底面面叠放在一起，减少了（n-1）×2个底面 （2）把一个圆柱体沿着底面直径切成两半，增加了两个切面——2×2rh（3）把一个圆柱体从中切成N段，则切了（n-1）次，增加了2（n-1）个底面。
小升初数学培优总复习05立体图形地表面积和体积
实用文档
文案大全立体图形的表面积与体积
实用文档文案大全
实用文档文案大全
实用文档文案大全
实用文档文案大全
实用文档
文案大全
6.
一个底面直径2厘米的圆柱形玻璃杯中装有水，水里浸没着一个底面直径1厘米，高为18厘米的圆锥形铁块。
当铁块从杯中取出时，杯中的水面会下降多少厘米？
解析：
水杯中圆锥拿出，水面下降。
水面下降的体积等于圆锥的体积。
答案：
解：由题意可知；
圆锥的体积为：
21(122)18678.243??????（立方厘米）
水面下降的高度为：
678.24÷（3.14×12×12）=1.5（厘米）
答：杯中水面会下降1.5厘米。
三、精选好题：
1.一个胶水瓶（如图），它的瓶身呈圆柱形（不包括瓶颈），胶水瓶的容积为31.4立方厘米。
当瓶子正放时，瓶内胶水液面高8厘米；当瓶子倒放时，空余部分高2厘米。
瓶内胶水的体积是多少？
实用文档
文案大全
实用文档文案大全
实用文档文案大全。
【小升初】人教版2023-2024学年六年级下册数学专项练习：立体图形(含答案)
【小升初】人教版2023-2024学年六年级下册数学专项练习：立体图形一、单选题1．用一根60厘米长的铁丝可以折成一个长8厘米、宽5厘米、高( )厘米的长方体．（ ）A ．2B ．3C ．4D ．52．把一根长2米的圆柱形木料截成3个小圆柱，3个小圆柱的表面积之和比原来增加了0.6平方米，原来这根木料的体积是（ ）立方米。
A ．1.2B ．0.4C ．0.3D ．0.25123．把一个圆柱体木块削成一个最大的圆锥体，削去部分一定是圆柱体木块的（ ） A ．B ．C ．2倍D．无法1323确定4．如图，这个正方体的上半部分涂了阴影，下半部分是白色的。
下面四幅图中，是这个正方体的展开图的是（ ）。
A ．B ．C ．D ．5．一个正方体的棱长扩大2倍，则表面积扩大（ ）倍。
A ．2B ．4C ．8D ．12二、判断题6．圆柱的侧面展开后一定是长方形．（ ）7．一个长方体木箱，竖着放和横着放时所占的空间不一样大．（ ）8．把一个圆柱削成一个最大的圆锥，圆锥的体积是削去部分的 。
（ ）239．正方体的棱长缩小到原来的 ，表面积就缩小到原来的 。
（ ）131910．一个正方体的棱长扩大3倍，体积就扩大9倍。
（ ）三、填空题11．一个圆柱形水桶的容积是40 L ，水桶的底面积是6 dm 2 ，装了桶水，水面高是 34dm 。
12．把一根长为4米的圆柱形木料锯成两段圆柱形木料后，表面积增加1.2平方米，这根圆柱形木料原本的体积是 立方米。
13．一个正方体的一个面的面积是16cm 2，这个正方体的表面积是 cm 2。
14．一个长方体鱼缸，长80cm ，宽40cm ，高50cm ．这个鱼缸最多可装 升水。
15．一个底面积为24cm 2的长方体容器，里面盛有高12cm 的水，放入一个小铁球后，水面高15cm ，这个小铁球的体积是 。
16．把一个长8厘米，宽7厘米，高6厘米的长方体，截成两个同样大小的小长方体，表面积最少增加 平方厘米。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五讲 立体图形应用题
【基础概念】：在小学阶段学过的立体图形有长方体、正方体、圆柱、圆锥，与这些图形有关的问题叫作立体图形应用题；有关的公式：长方体：表面积公式：S=（ab+ah+bh ）×2，体积公式：V=abh=Sh ；正方体：表面积公式：S=6a ²，体积公式：V=a ³；圆柱：侧面积：S
侧=Ch=2πrh=πdh ，表面积：S=S 侧+2S 底，体积：V=S 底h ；圆锥：体积：V=13
S 底h 。
【典型例题1】：李力爱好手工制作，用一根长48分米的铁丝做了一个长方体框架，使它的长、宽、高的比是5：4：3．在这个长方体框架外面糊了一层彩色的纸，至少需要多少平方分米的彩纸？它的体积是多少立方分米？
【思路分析】：用一根长48分米的铁丝做了一个长方体框架也就是长方体的棱长总和是48分米，首先用棱长总和除以4求出长、宽、高的和，再利用按比例分配的方法分别求出长、宽、高，然后根据长方体的表面积公式：s=（ab+ah+bh ）×2，体积公式：v=abh ，把数据代入公式解答即可。
解答：长：48÷4×55+4+3
=12×55+4+3
=5（分米）
宽：48÷4×45+4+3
=12×45+4+3
=4（分米）
高：48÷4×35+4+3
=12×35+4+3
=3（分米）；
（5×4+5×3+4×3）×2
=（20+15+12）×2
=47×2
=94（平方分米）
5×4×3=60（立方分米）
答：至少需要94平方分米的彩纸，它的体积是60立方分米。
【小结】：解决这类问题要先计算出棱长，再利用表面积公式与体积公式计算。
【巩固练习】
1．用一根长48分米的铁丝做一个长方体框架，长和宽的比是4：1，宽和高长度相等，在这个长方体框架外面糊一层纸，至少需要多少平方分米的纸？这个框架的体积是多少立方分米？
2．用铁丝焊一个长方体框架，长1.8米，宽14分米，高100厘米，至少需要铁丝多少米？焊成的长方体体积是多少？
【典型例题2】：一个圆柱体，底面半径是7厘米，表面积是1406.72平方厘米．这个圆柱的高是多少？
【思路分析】：已知底面半径是7厘米，那么可以求得这个圆柱的底面积和底面周长；这里要求圆柱的高，根据已知条件，需要求得这个圆柱的侧面积，根据圆柱的表面积公式可得：侧面积=表面积-2个底面积，再利用圆柱的侧面积公式即可求得这个圆柱的高。
解答：（1406.72-3.14×7²×2）÷（2×3.14×7）
=（1406.72-307.72）÷43.96
=1099÷43.96
=25（厘米）
答：这个圆柱的高是25厘米。
【小结】：解决这类问题要先计算出底面积，再利用表面积减去底面积得到侧面积，最后利用底面积公式计算出高即可。
【巩固练习】
3. 一个圆柱，底面周长是25.12厘米，高是5厘米，这个圆柱体的表面积是多少平方厘米？
4. 一个圆柱体沿底面直径和高切开后，切面是一个边长为6厘米的正方形，这个圆柱体的表面积是多少平方厘米？
答案及解析：
1.【解析】长方体的12条棱分为互相平行的3组，每组4条棱的长度相等，已知棱长总和是48分米，先求出长、宽、高的和，再利用按比例分配分别求出它的长、宽、高；再根据长方体的表面积和体积公式解答即可。
【答案】：（1）长、宽、高的和是：
48÷4=12（分米）
总份数是：
4+1+1=6（份）
12×46
=8（分米） 12×16
=2（分米） 表面积是：
（8×2+2×2+2×8）×2
=（16+4+16）×2
=36×2
=72（平方分米）；
答：至少需要72平方分米的纸。
（2）8×2×2=32（立方分米）
答：这个框架的体积是32立方分米。
2. 【解析】（1）铁丝的长度，就是这个长方体的棱长总和，由此利用棱长总和公式即可解答；（2）长方体的体积=长×宽×高，代入数据即可解答。
【答案】14分米=1.4米，100厘米=1米，
所以棱长总和是：（1.8+1.4+1）×4
=4.2×4
=16.8（米）
体积是：1.8×1.4×1=2.52（立方米）
答：至少需要铁丝16.8米，焊成的长方体体积是2.52立方米。
3.【解析】圆柱的侧面积=底面周长×高，由此可求出圆柱的侧面积，再根据底面周长求出圆柱的底面半径，进而求出底面积，最后利用圆柱的表面积公式计算即可。
【答案】：侧面积是：
25.12×5=125.6（平方厘米）
底面半径是：
25.12÷3.14÷2=4（厘米）
表面积是：
3.14×4²×2+125.6
=100.48+125.6
=226.08（平方厘米）
答：这个圆柱的表面积是226.08平方厘米。
4. 【解析】根据题意，圆柱体的底面直径为6厘米，高为6厘米，可利用圆柱体的表面积公式S=侧面积+2个底面圆的面积进行计算即可。
【答案】：3.14×6×6+3.14×（6÷2）²×2
=113.04+3.14×9×2
=113.04+56.52
=169.56（平方厘米）
答：这个圆柱体的表面积是169.56平方厘米。