小升初数学专项题-应用已专题第四讲平面图形应用题通用版
【精选】六年级下册数学试题-小升初专题复习 第4讲_立体图形计算全国通用

第四讲立体图形计算大综合前言一、授课目标:通过本次课的梳理,我们将对小升初近年常考的立体几何部分进行梳理,系统提升学生对小升初考试中立 体几何计算的相关处理. 二、知识概述:A. 空间想象类问题 (1) 展开图; (2) 数正方体个数; (3) 剖挖打洞; (4) 其它(如顶点数、面数、棱数计算等)B. 体积、表面积计算 (1)规则图形(正方体、长方体、圆柱、圆锥); (2)旋转体; (3)其它组合图形.升学真题精选精讲【学生家长注意】本讲共 17 道升学真题,限时 70 分钟完成,请大家在听课前尽力完成例题. 例题1. (BDF 真题)如下图所示,用几个棱长都是 1 厘米的正方体小木块排成一排,拼成长方体.按照上面的拼法,下列不正确的说法序号是 ①小芳说:“能拼成表面积是 500 平方厘米的长方体.” ②小明说:“能拼成表面积是 1000 平方厘米的长方体.” ③小虎说:“能拼成表面积是 2002 平方厘米的长方体.”例题2. (人大附真题)圆锥的体积是圆柱的体积的 2 倍,它们的底面积相等,圆锥和圆柱的高的比是多少?例题3. 长、宽、高分别是 6、8、10 的长方体纸盒中恰好可以平放入一个圆柱体,则圆柱体占盒内空间的百分比最大能达到%.(π 取 3.14)1例题4. 此图是由若干个小正方体组成的.阴影部分是空缺的通道,一直通到对面.问:这个立体图形由多少个小正方 体组成?例题5. 某多面体展开图如图(沿虚线折、沿实线粘合),求这个多面体的面数、顶点数、棱数.例题6. 有一些大小相同的正方形木块堆成一堆,从上往下看是左图,从前往后看是中图,从左往右看是右图,那么这 堆木块最多有多少块?最少有多少块?2例题7. 将边长为 15 厘米的正方形铁片的四个角各裁掉一个全等的小正方形,然后做成一个无盖的长方体盒,那么这 个长方体盒的最大容积是多少立方厘米?例题8. 棱长是 m 厘米(m 为整数)的正方体的若干面涂上红色,然后将其切割成棱长是 1 厘米的小正方体.至少有一 面红色的小正方体个数和表面没有红色的小正方体个数的比为 13:12,此时 m 的最小值是多 少?例题9. 如图,把正方体用两个与它的底面平行的平面切开,分成三个长方体.这三个长方体的表面积比是 3:4:5 时,用最简单的整数比表示这三个长方体的体积比是多少?3例题10. (BDF 真题)如图 1,是一个由 53 个大小相同的小正方体堆成的立体图形,从正面观察这个立体图形得到的 平面图形如图 2 所示 (1)请在图 3、图 4 中依次画出从左面、上面观察这个立体图形得到的平面图形;图1图 2(从正面看)图 3(从左面看)图 4(从上面看)(2)保持这个立体图形中最底层的小正方体不动,从其余部分中取走 k 个小正方体,得到一个新的立体图形,如果依 次从正面、左面、上面观察新的立体图形,所得到的平面图形分别与图 2、图 3、图 4 是一样的,那么 k 的最大值为 .4例题11. (RDF 真题)在一个棱长为 8 的立方体上切去一个三棱柱(如图),那么表面积减少多少?例题12. (BDF 真题)防治“非典”增强了人们的卫生意识,大街上随地吐痰的人少了,人们自觉地将生活垃圾倒入垃 圾桶中.图中所示的是我们生活中的卷筒卫生纸,你知道每层卫生纸有多厚吗?从卫生纸的包 装纸上得到以下资料:“两层 300 格,每格 11.4cm×11 cm(长×宽)”.我们用尺子量出整卷卫生纸的内外半径分别为 2.3cm 和 5.8cm,每层卫生纸的厚度是多少?(π 取 3.14,精确到 0.001cm).5例题13. (BDF 真题)用 12 个棱长都是 1 厘米的小正方体拼成一个大长方体,可以拼成多少种不同的长方体,其中 表面积最小的是多少平方厘米?例题14. (101 真题)如图,将一个棱长为 1 米的正方体木块切开,得到 24 个长方体木块.这 24 个长方体木块的表面积的和是平方米.例题15. (BDF 真题)如图是一个长方体包装盒的展开图,这个包装盒的体积为立方厘米.6例题16. 如图,将上底是 2,下底是 4,高是 4 的梯形,按照图中所示的方式旋转一周,那么得到的旋转体的体积是 多少?(π 取 3.14)7课后限时自测【学生家长注意】本次测试共 10 个空,每空 5 分,共 50 分.限时 35 分钟完成. 成绩 1. (BDF 真题)一辆压路机的前轮是圆柱形,轮宽 1.6 米,直径是 0.8 米.前轮转动一周,压路的面积是平方米.2. (十一真题)长方体的长宽高分别为 10,5,6,按如图虚线切开,那么切完后的图形表面积为.65 103. (十一真题)63 个边长为 1 的正方体,拼成一个立体图形,那么这个立体图形的表面积最小为.4. 一些黑、白两种颜色的小正方体积木,把它们摆成如图所示的形状.已知相邻的积木颜色不同(有公共面的两块积木叫做相邻),标有 A 的积木为黑色.那么图中至少有黑色积木块.A5.某多面体展开图如图(沿虚线折、沿实线粘合),那么这个多面体的面数、顶点数、棱数分别为、、.86.右图是由若干个小正方体组成的.阴影部分是空缺的通道,一直通到对面.这个立体图形由个小正方体组成.7.用一根长为36 分米的铁丝做一个长方体框架,并且要求长是宽的2 倍,长宽高都是整数分米.如果不计损耗,可以做成长方体体积最大为立方分米.8.把1 个棱长是3 厘米的正方体分割成若干个小的正方体,这些小正方体的棱长必须是整厘米数.如果这些小正方体的体积不要求都相等,那么最少可分割成个小正方体.9。
2021年小升初数学专项复习:平面图形附答案解析

【解析】
试题分析:依据三角形的内角和是180度即可作答.
解:因为三角形的内角和是180°,且这个数值是固定不变的,
所以说“三角形越大,内角和越大”是错误的.
故选:C.
【点评】此题主要考查三角形的内角和定理.
6.【答案】A
【解析】
试题分析:红领巾的三个内角分别是120°、30°、30°,含有一个钝角。
8.过两点能画( )条直线。
A.0 B.1 C.3
9.把线段的一段无限延伸,就得到( )。
A.线段 B.射线 C.直线
10.长方形的一组长边同时缩短到和短边同样长,就变成了( )
A.正方形 B.平行四边形 C.四边形
11.平行四边形的( )相等.
A.四个角 B.四条边 C.对边
12.三条直线相交最多有( )个交点.
2021年小升初数学专项复习:平面图形
一、选择题
1.下面各组小棒中能围成三角形的是( )组.
A.3厘米、3厘米、6厘米
B.3厘米、4厘米、5厘米
C.2厘米、3厘米、4厘米
2.等腰三角形的一个底角是65°,这个三角形一定是( )
A.锐角 B.直角 C.钝角
3.一个等腰三角形,底是5厘米,腰是6厘米,它的周长是( )厘米.
60.至少4个完全一样的正方形才能拼成一个大正方形.(判断对错)
61.平行四边形很稳定.(判断对错)
62.同一个平面内的两条直线,不是相交就是平行..(判断对错)
63.同一平面内,两条直线不互相平行就互相垂直. (判断对错)
64.连结两点的线段的长度叫做这两点间的距离. (判断对错)
65.在同一平面内的两条直线不相交,就一定互相平行..(判断对错)
最新小升初奥数几何图形综合训练题(平面图形部分)
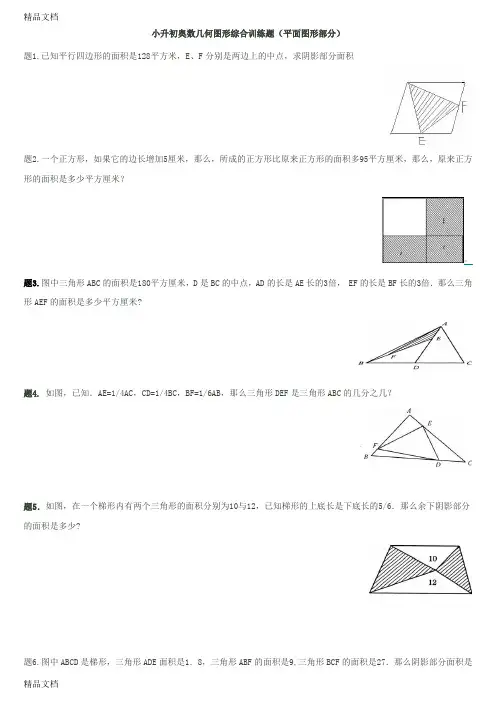
小升初奥数几何图形综合训练题(平面图形部分)题1.已知平行四边形的面积是128平方米,E、F分别是两边上的中点,求阴影部分面积题2.一个正方形,如果它的边长增加5厘米,那么,所成的正方形比原来正方形的面积多95平方厘米,那么,原来正方形的面积是多少平方厘米?。
题3.图中三角形ABC的面积是180平方厘米,D是BC的中点,AD的长是AE长的3倍, EF的长是BF长的3倍.那么三角形AEF的面积是多少平方厘米?题4.如图,已知.AE=1/4AC,CD=1/4BC,BF=1/6AB,那么三角形DEF是三角形ABC的几分之几?题5.如图,在一个梯形内有两个三角形的面积分别为10与12,已知梯形的上底长是下底长的5/6.那么余下阴影部分的面积是多少?题6.图中ABCD是梯形,三角形ADE面积是1.8,三角形ABF的面积是9,三角形BCF的面积是27.那么阴影部分面积是多少?题7.如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米,而三角形ABO的面积为12平方厘米.则梯形ABCD的面积为多少平方厘米?题8.如图,BD,CF将长方形ABCD分成4块,红色三角形面积是4平方厘米,黄色三角形面积是6平方厘米.问:绿色四边形面积是多少平方厘米?题9.如图,平行四边形ABCD周长为75厘米.以BC为底时高是14厘米;以CD为底时高是16厘米.求平行四边形ABCD 的面积.题10.如图,一个正方形被分成4个小长方形,它们的面积分别是平方米、平方米、平方米和平方米.已知图中的阴影部分是正方形,那么它的面积是多少平方米?题11.图中外侧的四边形是一边长为10厘米的正方形,求阴影部分的面积.题12.如图,长方形被其内的一些直线划分成了若干块,已知边上有3块面积分别是13,35,49.那么图中阴影部分的面积是多少?题13.如图,有8个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.如果圆周率取3.1416,那么花瓣图形的面积是多少平方厘米?题14.图为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多长?题15.如图,大小两圆的相交部分(即阴影区域)的面积是大圆面积的,是小圆面积的.如果量得小圆的半径是5厘米,那么大圆半径是多少厘米?题16.如图,在18×8的方格纸上,画有1,9,9,8四个数字.那么,图中的阴影面积占整个方格纸面积的几分之几?题17.如图,用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?题18.如图,已知大正方形的面积是22平方厘米,那么小正方形的面积是多少平方厘米?题19、图是一个直径是3厘米的半圆,AB是直径.让A点不动,把整个半圆逆时针转,此时B点移动到C点,如图17-9所示.那么图中阴影部分的面积是多少平方厘米?( 取3.14.)题20、如图,四分之一大圆的半径为7,求阴影部分的面积,其中圆周率取近似值.题21、如图,等腰直角三角形的一腰的长是8厘米,以它的两腰为直径分别画了两个半圆,那么阴影部分的面积共有多少平方厘米?( 取3.14)题22、图中的4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?题23、图17-14中阴影部分的面积是多少平方厘米?( 取3.14)题24、求图17-15中阴影部分的面积.( 取3.14)题25、平面上有7个大小相同的圆,位置如图17-16所示.如果每个圆的面积都是10,那么阴影部分的面积是多少?。
六年级下册小升初试题平面图形讲义及练习题通用版
三角形的定义:由不在同不时线上的三条线段首尾依次相接围成的图形叫三角形
锐角三角形:三个角都是锐角的三角形
三角形 按角分 直角三角形:有一个角是直角的三角形
三角形的分类 钝角三角形:有一个角是钝角的三角形
等腰三角形:两条边相等的三角形〔等边三角形是特殊
按边分 的等腰三角形〕
〔3〕圆的半径扩展到原来的3倍,那么它的周长就扩展到原来的〔 〕倍,面积扩展到原来的〔 〕倍。
2.选择题
〔1〕周长相等的正三角形、长方形、正方形、圆形,面积最大的是〔 〕。
A.正三角形 B.长方形 C.正方形 D.圆形
(2)面积相等的长方形、正方形、圆形,周长最短的是〔 〕,周长最长的是〔 〕。
A.正方形 B.长方形 C.圆形
第二局部 精讲点拨
例1判别以下各题能否正确:
(1)圆的周长是直径的3.14倍。 〔 〕
(2)圆是轴对称图形,直径是圆的对称轴。 〔 〕
(3)世界上第一位把圆周率准确到七位小数的人物是祖冲之。 〔 〕
举一反三:
1.填空题:
〔1〕经过圆心并且两端都在圆上的线段叫做圆的〔 〕,圆有〔 〕条直径。
〔2〕圆的面积推导公式是:将圆分红假定干个扇形,再拼成一个近似的长方形,长方形的长相当于圆的〔 〕,长方形的宽相当于圆的〔 〕,所以圆的面积公式为〔 〕。
〔3〕甲、乙是面积相等的正方形,甲中布满了大小相反且相邻的4个圆,乙中异样布满了大小相反且相邻的9个圆,甲中圆的面积和与乙中圆的面积和相比,结果是〔 〕。
A.甲大于乙 B.乙大于甲 C.甲等于乙 D.无法比拟
例2市实验小学新修了一条长200米的塑胶跑道,弯道最内圈的半径是15米。每条跑道宽1.5米,如今有4个跑道〔竞赛时跑步的选手普通压着跑道的内圈跑〕。
第四讲 整数、分数、小数、百分数的四则混合运算-2023年六年级数学下册小升初专项复习(通用版)

2023年学校六班级小升初数学专项复习(4)——整数、分数、小数、百分数的四则混合运算★★学学问问归归纳纳总总结结一、加法和乘法运算律1.加法运算律①加法交换律:两个加数交换位置,和不变。
如a+b=b+a。
②加法结合律:先把前两个数相加,或先把后两个数相加,和不变。
如:a+b+c=a+(b+c)。
2. 乘法运算律①乘法交换律:两个因数交换位置,积不变。
如a×b=b×a。
②乘法结合律:先乘前两个数,或先乘后两个数,积不变。
如a×b×c=a×(b×c)。
③乘法安排律:两个数的和,乘以一个数,可以拆开来算,积不变。
如a×(b+c)=ab+ac。
④乘法安排律的逆运算:一个数乘另一个数的积加它本身乘另一个数的积,可以把另外两个数加起来再乘这个数。
如ac+bc=c×(a+b)。
【例1】(2022春•枣庄期中)32×125×25=(25×□)×(8×□)【分析】在32×125×25=(8×4)×125×25=(25×4)×(8×125)中,先将32拆分为8×4后,将25与8的位置交换,又将4与25结合优先计算,这里运用了乘法结合律与乘法交换律。
【解答】解:32×125×25=(25×4)×(8×125)【点评】本题通过具体算式考查了同学对于乘法运算定律的理解与应用。
【例2】(2021秋•盐湖区期末)探秘乘法安排律(1)下面的图形中,能说明乘法安排律成立的,请在括号里画“√”,不能说明的画“×”。
(2)请你结合6×9+4×9这个算式,编一个数学故事来说明乘法安排律是成立的。
【分析】(1)依据乘法安排律的意义,(a+b)c=ac+bc,由此可知,①和③你说明乘法安排律成立。
人教版六年级下册数学小升初专题训练:平面图形(含答案)

人教版六年级下册数学小升初专题训练:平面图形一、单选题1.用一块长12米、宽8米的长方形铁皮剪成半径是1.5米的小圆(不能剪拼),至多能做( )个。
A.11B.8C.10D.132.如果要搭成一个从正面、左面、上面看到的图形都是如图的几何体,需要( )个小正方体。
A.3B.4C.5D.63.下图是由一个圆分成若干等分后,拼成的一个近似长方形,这个圆的周长与长方形的周长相差约4厘米,这个圆的周长约是( )厘米。
A.6.28B.9.42C.12.56D.无法计算4.从12时到13时,钟的时针与分针可成直角的机会有( )A.1次B.2次C.3次D.4次5.下列时刻中,钟表中时针与分针不成直角的是( )。
A.3:00B.21:00C.9:00D.12:206.一个半径是5cm的半圆,它的周长是( )cm。
A.31.4B.15.7C.25.7D.20.7二、填空题7.已知一个等腰三角形的两条边分别是5厘米、10厘米,那么它的周长是 厘米。
8.一个花坛的直径是6m,花坛周围有一条宽1m的环形小路,小路的面积是 m2。
9.一个挂钟的时针长5厘米,一昼夜这根时针的尖端走了 厘米,针尖扫的面积是 平方厘米。
10.把一个长、宽分别是15厘米和10厘米的长方形,拉成一个一条高为12厘米的平行四边形,它的面积是 平方厘米。
11.李大伯用5π米长的篱笆靠墙围了一个半圆形养鸡场,养鸡场的面积是 平方米。
12.如图。
∠1=30°,∠2= ,∠3= ,∠4= 。
13.从9:00到9:15,分针旋转了 度,若分针长6厘米,这根分针针尖走过的长度是 厘米,扫过的面积是 平方厘米。
14.一个三角形内角度数的比是2:3:5,其中最大的内角是 度,这是个 角三角形。
15.如图中正方形的面积是40cm2,那么涂色部分的面积是 cm2。
16.一辆自行车车轮直径是0.5米,脚踏板齿轮有48个齿,后齿轮有16个齿,脚踏一圈,自行车前进 米.17.把两个正方形拼成一个长方形,拼成的长方形周长是30厘米,这个长方形的面积是 平方厘米。
2024年西师大版六年级下册数学小升初分班考必刷专题:平面图形
2024年西师大版六年级下册数学小升初分班考必刷专题:平面图形一、单选题1.圆形花坛的半径是2米,绕花坛走一周,长度是()。
A.25.12米B.12.56米C.12.56平方米D.25.12平方米2.已知一个三角形两边的长度分别是9厘米、12厘米,那么,这个三角形的周长可能是()厘米。
A.24B.30C.42D.453.如图,在边长相等的两个正方形内剪圆片,比较剩下的材料,()A.甲、乙剩下一样多B.甲剩下多C.乙剩下多D.无法确定4.一个等腰三角形的两条边分别是2厘米和5厘米,则这个等腰三角形的周长是()A.7厘米B.9厘米C.12厘米D.9厘米或12厘米5.用三根同样长的铁丝分别围成平行四边形、正方形、长方形三个不同的图形,三个图形的面积相比,()A.平行四边形面积最大B.正方形面积最大C.长方形面积最大D.三个图形的面积相等6.如图,大圆直径2cm,小圆贴着大圆的内侧从P点开始按箭头所指方向滚动,小圆至少需要滚动()周才能回到P点。
A.2B.3C.4D.5二、填空题7.已知一个三角形的两个内角分别为30°和40°,这是一个角三角形。
8.一个等腰三角形中两个内角的比是1:4,这个等腰三角形的顶角可能是度。
9.一个等腰三角形的两条边分别是7cm和3cm。
它的周长是cm。
10.一个三角形面积是18cm2,与它等底等高的平行四边形面积是cm2。
11.如图:若圆的半径是1dm,则涂色部分面积是。
12.下图(1)中,长方形的周长是24厘米,空白部分是半圆。
阴影部分的面积是平方厘米,周长是厘米。
13.如图,把一个圆沿半径分成若干等份后,拼成一个近似的长方形,近似长方形的周长比圆的周长增加了20厘米,这个圆的半径是厘米。
14.大小两个圆的半径比是4:3,它们的直径比是,面积比是。
15.图中有条对称轴;如果圆的直径是dcm,那么长方形的面积是cm2。
16.靠墙用篱笆围一个半径是5米的半圆形鸡舍(靠墙一面不围),需要篱笆米。
2021年六年级小升初数学总复习第四讲(平面图形)(含答案)
2021年六年级小升初数学总复习第四讲平面图形一.教学目标1.理解各种图形的概念和特点2.掌握基本图形的面积计算方法3.掌握平面图形中常见的模型,并能熟练应用二.知识点1.图形计数 (1)相关类型 ①数线段:21)1(-⨯n n 或)(1321-+++n 注意:是线段上端点的个数n②数角:21)1(-⨯n n 或)(1321-+++n 注意:是边的个数n③数三角形:21)1(-⨯n n 或)(1321-+++n 注意:是边的个数n④数长方形: 长边上的线段数×短边上的线段数⑤数正方形:22221)2()1(+⋯⋯+-+-+n n n 注意:含的基本单位数表示大正方形边长上包n ⑥其他计数问题:给出图形,数出其中特定图形的多少 (2)相关方法①枚举法:罗列所有情况逐个计数,也称穷举法②加法原理和乘法原理:利用计数中出现的各种情况进行加或乘的计算 ③递推法:利用简单图形的计数逐步找出规律进行递推的方法 2.周长巧算 (1)相关方法①直接计算:根据公式直接计算 ②平移法 (2)相关公式①正方形周长公式:C=边长×4 ②正方形周长公式:C=(长+宽)×2 3.常见模型 (1)等积模型①等底等高的两个三角形面积相等;S 2S 1②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. (2)鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵(3)蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝴蝶定理”): ①2213::S S a b =DCBAS 4S 3S 2S 1O DCBA A DO aS 2S 1S 4②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +. (4)相似模型金字塔模型 沙漏模型GF E ABCD ABCDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.(5)燕尾定理在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=. 上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径. 4.圆(1)相关概念①圆的定义:平面上到一个定点的距离等于定长的点的全体,这里的定点叫做圆心,定长称为半径。
小升初数学《平面图形》综合试题及答案
小升初数学《平面图形》综合试题一、填空题1.同一平面内的两条直线的位置关系有两种情况:________和________.2.下面各组直线中,哪两条直线互相垂直?在下面的括号里画“√”。
( ) ( ) ( )3.在两点之间的所有连线中,(____)最短.4.用一个能放大3倍的放大镜看一个15°的角,这个角的度数是(____)。
按度数从小到大,可以把角分为(____)、(____)、(____)、(____)和(____)。
5.一个平行四边形的面积是32m2,与它等底等高的三角形的面积是(____)m2。
6.一个三角形最小的角是60°,那么这个三角形按边分是(_____)三角形。
7.一个等腰梯形的上底是6cm,下底是8cm,一条腰长是7cm,围成这个等腰梯形至少需要(____)cm长的铁丝.8.两个完全一样的三角形可以拼成一个(_____)形。
如果拼成的图形的面积是126cm2,那么一个三角形的面积是(____)cm2。
如果每个三角形的面积是15dm2,那么拼成的图形的面积是(____)dm29.照图操作画出的圆的周长是(____)cm,圆的面积是(____)cm2.10.画圆时,圆规两脚间的距离是2.5cm,则半径是(____)cm,直径是(____)cm。
11.一个边长是20cm的正方形,里面有一个最大的圆,这个圆的半径是(____)cm,面积是(____)cm2。
12.如图,一个平行四边形被分成了甲、乙、丙三部分,已知甲的面积比丙的面积大6cm2,那么丙的面积是(____)cm2。
13.如图,已知大正方形的边长是5cm,小正方形的边长是3cm,那么阴影部分的面积是(____)cm2。
14.一个三角形,其中两个角分别是35°和45°,那么另一个角是(____)°。
按角来分,这是一个(____)三角形。
15.一个直角三角形三条边的长度分别是6cm、8cm、10cm,斜边上的高是(____)cm。
小升初小学数学几何图形应用题专题练习《图形的拆分(拼切)》答案详解
几何图形—专题04《图形的拆分(拼切)》一.选择题1.(2019秋•东莞市期末)把一张平行四边形卡片剪一刀分成两个图形,下面几种情况中不可能出现的是( )A.两个三角形B.两个梯形C.一个平行四边形和一个梯形【解答】解:在一张平行四边形纸片上剪一刀可能变成:①一个三角形和一个梯形;②两个三角形;③两个平行四边形;④两个梯形.不可能出现一个梯形和一个平行四边形.故选:C.2.(2019秋•会宁县期末)有一些长3厘米,宽1厘米的长方形纸片,至少需要()张这样的纸片才能拼成一个正方形.A.3 B.4 C.5 D.6【解答】解:3和1的最小公倍数为3,即正方形的边长是3厘米,÷⨯÷(33)(31)13=⨯=(个)3答:至少需要3个这样的长方形才能拼成一个正方形.故选:A.3.(2019•湘潭模拟)把一个长8厘米、宽6厘米、高4厘米的长方体,切成两个长方体,下图中()的切法增加的表面积最多.A.B.C.A⨯=(平方厘米)【解答】解:图:8648B⨯=(平方厘米)图:6424C⨯=(平方厘米)图:8432>>483224故选:A.4.(2019•防城港模拟)一个长10厘米、宽8厘米的长方形,剪成同样大小的正方形,最后没有剩余,最少可以剪成()个正方形.A.10 B.20 C.40 D.80【解答】解:10和8的最大公约数是2,所以剪成的正方形的边长的边长是2厘米.在长10厘米的边上可剪边长是2厘米的个数是:÷=(个),1025在宽8厘米的边上可前剪边长是2厘米的个数是:824÷=(个),⨯=(个).5420答:最少可剪成20个正方形.故选:B.5.(2018•西安模拟)如图,一个33⨯的正方形网格,如果小正方形边长是2,那么阴影部分的面积是( )A.10 B.8 C.6 D.4【解答】解:根据分析可得,11⨯⨯⨯⨯2(2)822=⨯⨯118=8答:阴影部分的面积是8.故选:B.6.(2006•清河区校级自主招生)如图,长方形ABCD中放置了9个形状、大小都相同的小长方形(尺寸如图,单位:厘米),则图中阴影部分的面积为()A.82平方厘米B.64平方厘米C.60平方厘米D.54平方厘米【解答】解:如图设小长方形的长、宽分别为xcm,ycm+=⋯⋯①x y422+=+,整理得7x y y237-=⋯⋯②x y①-②得y=515y=3y=代入②把3x=10即每个小长方形的长是10cm,宽是3cm大长方形的面积:(1034)(337)+⨯⨯⨯+=+⨯+(1012)(97)2216=⨯2=cm352()9个小长方形的面积:⨯⨯1039309=⨯2270()cm=235227082()cm-=答:图中阴影部分的面积为282cm.故选:A.7.(2006•清河区校级自主招生)将一张长40厘米、宽1厘米的长方形纸片连续对折3次,得到宽不变的较短的长方形,然后从它的一端开始,每隔1厘米剪一刀,其中可得到边长为1厘米的小正方形的个数为()A.40个B.33个C.26个D.20个【解答】解:14058⨯=(厘米);515÷=(段),(52)82-⨯+,382=⨯+,242=+,26=(个);答:可得到26个边长为1厘米的小正方形;故选:C.二.填空题8.(2019秋•汉川市期末)一个平行四边形可以剪成两个相同的三角形,也可以剪成两个相同的,也可以剪成两个相同的.【解答】解:根据题干分析可得:一个平行四边形可以剪成两个相同的三角形,也可以剪成两个相同的平行四边形,也可以剪成两个相同的梯形.故答案为:三角形;平行四边形;梯形.9.(2018秋•江都区校级期末)有一块长4.5米、宽1.4米的长方形红布,大队辅导员李老师准备用这块红布剪直角边分别是7分米、4分米的直角三角形小红旗,最多可以剪44面.【解答】解:4.5米45=分米=分米1.4米14÷≈(个)45411÷=(个)14721122⨯⨯=⨯22244=(面)答:最多可以剪44面.故答案为:44.10.(2018秋•白云区期末)把一个圆分成若干(偶数)等份,分的份数越多,拼成的图形就越接近长方形,这个近似长方形的长相当于圆的周长的一半,宽相当于圆的.【解答】解:把一个圆分成若干(偶数)等份,分的份数越多,拼成的图形就越接近长方形,这个近似长方形的长相当于圆的周长的一半,宽相当于圆的半径.故答案为:周长的一半;半径.11.(2019•衡水模拟)如图,一个四边形可以分成2个三角形;一个五边形可以分成3个三角形;一个六边形可以分成4个三角形⋯.那么,一个10边形可以分成8个三角形.【解答】解:根据分析可得:n-=-=(个);21028答:一个10边形可以分成8个三角形.故答案为:8.12.(2019•天津模拟)在一个长是6厘米,宽是4厘米的长方形里剪一个最大的圆,这个圆的半径是2厘米,周长是厘米.÷=(厘米);【解答】解:(1)422⨯=(厘米);(2)3.14412.56故答案为:2,12.56.13.(2018•西安模拟)如图,将一根长10米的长方体木块锯成6段,表面积比原来增加了100平方分米,这根长方体木块原来的体积是1000立方分米.=分米【解答】解:10米100÷-⨯⨯100[(61)2]10010010100=÷⨯=(立方分米)1000答:这根长方体木块原来的体积是1000立方分米.故答案为:1000.14.(2018•厦门模拟)用43个边长1厘米的白色小正方体和21个边长1厘米的黑色小正方体堆成如图所示的大正方体,使黑色的面向外露的面积要尽量大.那么这个立方体的表面积上有50平方厘米是黑色的.⨯+⨯-,【解答】解:382(218)=+,2426=(平方厘米),50答:这个立方体的表面积上有50平方厘米是黑色的.故答案为:50.15.(2014秋•如东县期末)用24个1平方厘米的小正方形拼成大长方形,一共有4种不同的拼法,其中周长最大的是厘米.【解答】解:根据分析知拼成后图形的面积不变,拼成后长方形的长和宽可分下列情况:+⨯=(厘米);(1)长24厘米,宽1厘米,周长是:(241)250+⨯=(厘米);(2)长12厘米,宽2厘米,周长是:(122)228+⨯=(厘米);(3)长8厘米,宽3厘米,周长是:(83)222+⨯=(厘米);(4)长6厘米,宽4厘米,周长是:(64)220故答案为:4,50.三.判断题16.(2018秋•盐城期中)用一张长方形的纸只能剪一个正方形.⨯(判断对错)【解答】解:例如:或所以用一张长方形的纸只能剪一个正方形是错误的;故答案为:⨯.17.(2017•广东)已知一刀可以把一个平面切成2块,两刀最多可以把一个平面切成4块,三刀最多可以切成7块⋯,由此可以推测,五刀最多可以切成16块.√(判断对错)【解答】解:5n=,511(1)2S nn n=++115(51)2=+⨯⨯+11562=+⨯⨯115=+16=(块)答:五刀最多可以切成16块.故答案为:√.18.(2016秋•沛县月考)一个长方形,长24厘米,宽8厘米.这个长方形一定能分成3个完全一样的正方形√(判断对错)【解答】解:因为2483÷=(倍)所以长是宽的3倍,所以这个长方形一定能分成3个完全一样的正方形,因此题中说法正确.故答案为:√.19.(2014秋•余干县期末)在任何梯形中都能分割出一个三角形和一个平行四边形. √ .(判断对错)【解答】解:梯形有一组对边是平行的,只要沿着梯形上底的一个端点做和它不相邻腰的平行线,就可以把这个梯形分成一个三角形和一个平行四边形,如下图:原题说法正确.故答案为:√.四.应用题20.(2019秋•沛县期中)一块长120厘米、宽40厘米的红布,最多可以做成底和高都是8厘米的直角三角形小旗多少面?【解答】解:120815÷=(个)4085÷=(个)1552150⨯⨯=(面)答:最多可以做成底和高都是8厘米的直角三角形小旗150面.21.妈妈有一块长方形的花布(如图).她想给芳芳做成正方形的手绢,而且手绢要最大.(1)妈妈能剪出 2 块这样的手绢.(2)剪成的每块手绢的周长是多少厘米?【解答】解:(1)32152÷=(块)2⋯(厘米)答:妈妈能剪出2块这样的正方形.(2)15460⨯=(厘米)答:剪成的每块手绢的周长是60厘米.故答案为:2.22.用一张长7dm 、宽5dm 的长方形纸剪边长是2dm 的正方形,最多能剪出多少个这样的正方形?请你画一画示意图.【解答】解:723÷=(份)1()dm ⋯522÷=(份)1()dm ⋯326⨯=(个)答:最多能剪出6个这样的正方形.23.(2018•西安模拟)如图,将一条长为60cm 的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1:2:3.试计算折痕对应的刻度有哪些?【解答】解:60(123)÷++606=÷10()cm =10110()cm ⨯=10220()cm ⨯=10330()cm ⨯=即三段长分别为10cm 、20cm 、30cm(1)折痕为201020()2cm += (2)当剪切处右边部分为10cm ,左边为30cm 时 折痕为301025()2cm += (3)当剪切处右边部分为20cm ,左边为10cm 时折痕为102025()2cm +=(4)当剪切处右边部分为20cm,左边为30cm时折痕为302035()2cm +=(5)当剪切处右边为30cm,左边为10cm时折痕为103035()2cm +=(6)当剪切处右边为30cm,边边为20cm时折痕为203040()2cm +=综上所述:折痕对应的刻度有4种:20cm、25cm、35cm和40cm.24.一块正方形试验田,如果边长增加5米,面积就比原来增加875平方米.现在这块试验田是多少平方米?【解答】解:设原来正方形的边长为x米,根据题意得:55(5)875x x+⨯+=5525875x x++=10850x=85x=85857225⨯=(平方米)答:原来试验田的面积是7225平方米.五.操作题25.(2016春•皇姑区期末)(1)求出大正方形的周长.(2)把这个大正方形分成四个相同的小正方形,画一画,并求出每个小正方形的周长.【解答】解:(1)12448⨯=(米)答:大正方形的周长是48米.(2)÷=(米)1226⨯=(米)6424答:每个小正方形的周长是24米.26.(2015春•扬州校级期末)把一个边长是8厘米的正方形分成长3厘米宽2厘米的小长方形,最多能分成10个.在图中把你的分法画出来.(每个小格表示边长1厘米的正方形)【解答】解:如图所示:把一个边长是8厘米的正方形分成长3厘米宽2厘米的小长方形,最多能分成10个.故答案为:10.27.如图:有二张正方形的桌布,如何剪拼成一张更大的正方形桌布?画出裁剪图及剪拼后的示意图.【解答】解:把两个三角形沿虚线剪开,分别用原正方形的直角边与直角边重合每一个正方形就拼组成了两个大三角形,然后把这两个大直角三角形的斜边重合从而得到新的正方形.如图所示:28.(2017秋•兴义市月考)请你在下面的梯形中画一条线段,将梯形分成一个平行四边形和一个三角形.你能想到几种方法?说说你的画法.【解答】解:根据分析画图如下:画法:过梯形的上底的顶点作腰的平行线,交下底于一点,则这条线段就把梯形分成一个平行四边形和一个三角形.答:我能想到2种方法.29.给平行四边形作一条高,将它分成两个梯形.【解答】解:作图如下:六.解答题30.(2018秋•定州市期末)动手操作.下面方格图中每个小方格表示1平方厘米.(1)以三角形的顶点A为端点画一条线段,将这个角形分成面积相等的两部分.(2)在方格图中画一个平行四边形,使它与已知三角形的高和面积分别相等.【解答】解:根据题干分析画图如下:31.(2018春•盐城期中)一根圆柱形木料,锯下5分米长的一段后,剩下的木料的表面积比原来减少了94.2平方分米.锯下的这段木料的体积是多少立方分米?【解答】解:圆柱的底面半径是:94.25 3.1423÷÷÷=(分米);所以圆柱的底面积是:23.14328.26⨯=(平方分米);所以剩下木料体积是:28.265141.3⨯=(立方分米);答:锯下的这段木料的体积是141.3立方分米.32.(2015•潮州模拟)看图,回答问题:(1)不通过计算,将如图的大三角形切割成四个面积相等的小三角形,并用简单的文字说明切割而成的四个小三角形面积相等的原因.(2)作图:将如图的三角形ABC 绕点A 逆时针旋转90度后再向左平移4格,请在方格纸中画出变化后的图形.【解答】解:(1)如图:把AC 平均分成4份,再与定点B 相连接;因为BAD ∆、BDE ∆、BEC ∆是同底等高的,所以面积相等.(2)33.(2014秋•泰兴市期末)用一张长90厘米、宽24厘米的彩纸做直角三角形小旗,每面小旗的两条直角边分别是12厘米、9厘米.这张彩纸一共可以做多少面小旗?÷⨯÷⨯【解答】解:(909)(2412)2=⨯⨯1022=(面);40答:这张彩纸一共可以做40面小旗.34.(2017秋•海安县校级期末)一张长12分米,宽8分米的长方形纸,做成底3分米,高2分米的直角三角形,最多可以做多少个?÷⨯÷【解答】解:(123)(82)=⨯44=(个)16⨯=(面)16232答:最多可以做32面.35.(2017秋•海安县期末)用长10厘米、宽6厘米的长方形硬纸(如图),做成一个棱长2厘米的正方体纸盒,应如何剪(接头处忽略不考虑)?在图中用阴影部分表示出要剪去的部分.至少给出两种不同的方案.【解答】解:如图所示:36.(2018•海门市校级模拟)如图,用边长10厘米的正方形硬纸板,做成一个棱长2厘米的正方体纸盒,应如何剪(接头处忽略)?在图中用阴影表示出要剪去的部分.至少给出两种不同方案.【解答】解:画图如下:.37.(2018•长沙)宽18厘米.长未知的同样大小的长方形小纸片拼成如图所示的图形,求阴影部分的面积.【解答】解:由题意可知:小纸片的长:318272⨯=(厘米),大长方形的长:275135⨯=(厘米),宽:1832781⨯+=(厘米),大长方形的面积是:1358110935⨯=(平方厘米);小长方形的面积是:2718486⨯=(平方厘米);阴影部分面积1093548622=-⨯1093510692=-243=(平方厘米);答:图中阴影部分的面积一共是243平方厘米;故答案为:243平方厘米38.(2015秋•连云港期中)一块长5米,宽2米的长方形红纸,剪出腰长为4分米的等腰直角三角形小旗,共可剪多少面?【解答】解:两个腰长为4分米的等腰直角三角形小旗可以拼成一个边长是4分米的正方形;5米50=分米,2米20=分米50412÷≈(个)2045÷=(个)1252120⨯⨯=(面)答:共可剪120面.39.(2015秋•旅顺口区校级月考)学校开运动会,要做底40cm ,高30cm 的直角三角形小红旗300面.用来做小红旗的长方形纸长1.2m ,宽0.8m ,买20张这样的纸够不够?【解答】解:400.4cm m =300.3cm m =1.20.34÷=0.80.42÷=42220⨯⨯⨯1620=⨯320=(面)320300>答:买20张这样的纸够.40.(2015秋•盐都区校级期中)一块长5米,宽2米的长方形红纸,剪出腰长为4分米的等腰直角三角形小旗,共可剪多少面?【解答】解:两个腰长为4分米的等腰直角三角形小旗可以拼成一个边长是4分米的正方形;5米50=分米,2米20=分米,50412÷≈(个);2045÷=(个);⨯⨯=(面);1252120答:共可剪120面.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四讲平面图形应用题
【基础概念】:在小学阶段学过的平面图形有线段、射线、直线、三角形、长方形、正方形、平行四边形、梯形、圆、组合图形,与这些图形有关的问题叫作平面图形应用题;解决这些问题常用到的公式有:、长方形:周长公式:C=(a+b)×2,面积公式:S=ab;正方形:周长公式:C=4a,面积公式:S=a²;平行四边形:面积公式:S=ab;三角形:面积公式:S=ab ÷2;梯形:面积公式:(a+b)×h×2;圆:周长公式:C=2πr或C=πd, 面积公式:S=πr²。
【典型例题1】:把一个直径10厘米的圆,削成一个最大的正方形,这个正方形的面积是多少平方厘米?
【思路分析】:在一个直径10厘米的圆中截取一个最大的正方形,这个正方形的对角线的长度等于圆的直径,正方形两条对角线把整个正方形分成了4个相等的等腰直角三角形,正方形的对角线的一半等于这个圆的半径,所以正方形对角线的一半是10÷2=5厘米,即每个等腰直角三角形的底和高都是5厘米,根据三角形的面积公式:s=ah÷2,把数据代入公式解答。
【解答】:10÷2=5(厘米)
由分析知:正方形两条对角线把整个正方形分成了4个相等的等腰直角三角形,每个等腰直角三角形的底和高都是5厘米,
所以正方形的面积是:
5×5÷2×4
=12.5×4
=50(平方厘米)
答:这个正方形的面积是50平方厘米。
【小结】:解决此类问题的关键是要明确:正方形两条对角线把整个正方形分成了4个相等的等腰直角三角形,根据三角形的面积公式解答。
【巩固练习】
1.一张正方形纸板,周长是12厘米,把它剪成一个最大的圆,这个圆的面积是多少平方厘米?
2.把一个圆剪拼成一个面积相等的长方形,周长增加8厘米,这个圆的面积是多少平方厘米?
【典型例题2】:一个圆形旱冰场的直径是20米,扩建后半径增加了10米,扩建后的旱冰场面积增加了多少平方米?
【思路分析】:从题意可知,扩建后半径增加了10米,求面积增加了多少平方米,也就是求这个环形的面积,已知内圆直径,首先求出内圆半径,根据环形面积=外圆面积-内圆面积,由此列式解答。
解答:内圆半径:
20÷2=10(米)
外圆半径:10+10=20(米)
增加的面积:
3.14×(20²-10²)
=3.14×(400-100)
=3.14×300
=942(平方米)
答:扩建后旱冰场的面积增加了942平方米。
【小结】:解决这类问题要先确定内圆与外圆的半径,再分别计算两个圆的面积,最后相减就可以了。
【巩固练习】
3、广场中心有一个圆形花池,直径是80米,扩建后,直径增加到100米.这个花池的面积增加了多少平方米?
4、公园里有一个圆形儿童游乐场,其周长为81.64米,后来扩建时将它的半径增加了2米,扩建后,这个游乐场的面积增加了多少平方米?
答案及解析:
1.【解析】正方形内最大的圆的直径等于正方形的边长,据此先根据正方形的周长公式求出边长是12÷4=3厘米,即半径是3÷2=1.5厘米,再利用圆的面积=πr²计算即可解答。
【答案】12÷4=3(厘米),
3.14×(3÷2)²
=3.14×2.25
=7.065(平方厘米)
答:这个圆的面积是7.065平方厘米。
2. 【解析】一个圆切割后拼成长方形,拼成的近似长方形的周长,就比圆的周长增加了圆半径的2倍.根据周长增加了8厘米,可算出半径,据此解答。
【答案】圆的面积:
3.14×(8÷2)²
=3.14×4²
=3.14×16
=50.24(平方厘米).
答:这个圆的面积是50.24平方厘米。
3.【解析】根据题意可知,求面积增加了多少平方米,也就是求这个环形的面积,已知内圆直径,首先求出内圆半径,根据环形面积=外圆面积-内圆面积,解决即可。
【答案】:内圆半径:
80÷2=40(米)
外圆半径:100÷2=50(米)
增加的面积:
3.14×(50²-40²)
=3.14×(2500-1600)
=3.14×900
=2826(平方米)
答:这个花池的面积增加了2826平方米。
4. 【解析】首先根据圆的周长公式求出内圆半径,再根据环形面积=外圆面积-内圆面积,解答即可。
【答案】:81.64÷3.14÷2=13(米)
13+2=15(米)
3.14×(15²-13²)
=3.14×(225-169)
=3.14×56
=175.84(平方米)
答:这个游乐场的面积增加了175.84平方米。
