棱柱的概念和性质PPT教学课件
合集下载
高考数学总复习 9.6棱柱、棱锥的概念和性质课件 人教版

出侧棱与底面垂直;④正确,由对角线相等,可得出平行六
面体的对角面是矩形,从而推得侧棱与底面垂直,所以是直 平行六面体;⑤正确,长方体是直四棱柱,再加上底面是正 方形,所以是正四棱柱. 答案:B
2.下面有四个命题:
①各个侧面都是等腰三角形的棱锥是正棱锥; ②三条侧棱都相等的棱锥是正棱锥; ③底面是正三角形的棱锥是正三棱锥; ④顶点在底面上的射影是底面多边形的内心,又是外心 的棱锥必是正棱锥. 其中正确命题的个数是( )
1 3,∴底面积为S=2×2×2
1 ∴体积V=3×6×3=6.
答案:6
5.如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方
形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则 侧棱AA1与截面B1D1DB的距离是________.
解析:AA1在底面上的射影为AO,cos60° =cos∠A1AO· cos 45° ,∴∠A1AO=45° ,过A点作平面BDD1B1的垂线交O1O的延 长线于H点,在Rt△AHO中,AO= AH=a, AA1与OO1间的距离为所求a. 2 a,∠HAO=45° ,易得
A.1 cm C.2 cm
解析:设长方体同一顶点上三条棱长分别为a、b、c,则 2(ab+bc+ca)=8,对角线l2=a2+b2+c2≥ab+bc+ca=4, ∴l≥2,选C.
答案:C
4.正四棱锥的侧棱长为2
3 ,侧棱与底面所成的角为
60° ,则该棱锥的体积为________.
解析:高h=2 线等于2 3 sin 60° =3,又因底面正方形的对角 3× 3=6,
A.1
C.3
B.2
D.4
解析:①不正确;正棱锥必须具备两点,一是:底面为
棱柱、棱锥的有关概念及性质 PPT课件 人教课标版

4.三棱锥S-ABC是底面边长为a的正三角形,A
在侧面SBC上的射影H是△SBC的垂心.
(1)证明三棱锥S—ABC是正三棱锥;
(2)设BC中点为D,若
HD 3 ,求侧棱与 HB 4
底面所成的角.
【解题回顾】(1)证明一个三棱锥是正三棱 锥,必须证明它满足正三棱锥的定义. (2)在找线段关系时常利用两个三角形相似.
•
56、远大抱负始于高中,辉煌人生起于今日。
•
57、理想的路总是为有信心的人预备着。
•
58、抱最大的希望,为最大的努力,做最坏的打算。
•
59、世上除了生死,都是小事。从今天开始,每天微笑吧。
•
60、一勤天下无难事,一懒天下皆难事。
•
61、在清醒中孤独,总好过于在喧嚣人群中寂寞。
•
62、心里的感觉总会是这样,你越期待的会越行越远,你越在乎的对你的伤害越大。
13、人生最大的错误是不断担心会犯错。
•
14、忍别人所不能忍的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获。
•
15、不管怎样,仍要坚持,没有梦想,永远到不了远方。
•
16、心态决定命运,自信走向成功。
•
17、第一个青春是上帝给的;第二个的青春是靠自己努力的。
•
18、励志照亮人生,创业改变命运。
•
2.正棱锥 (1)概念:如果一个棱锥的底面是正多边形,且 顶点在底面的射影是底面的中心,这样的棱锥 叫正棱锥
(2)性质:①各侧棱相等,各侧面都是全等的等
正棱锥的斜高 ②棱锥的高、斜高和斜高在底面上的射影组成 一直角三角形,棱锥的高、侧棱和侧棱在底面
返回
课前热身
1.下列四个命题中:
棱柱PPT课件

2020年10月2日
4
底面:多边形ABCDE和A‘B‘C‘D‘E‘ 侧面:ABB‘A‘、BCC‘B‘等 侧棱:A‘A、B‘B等 对角线:AC‘、BE‘等
高:H‘H
2020年10月2日
5
棱柱的表示法;
1 .用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDEA1B1C1D1E1 2 .用表示一条对角线端点的两个字母表示,如:棱柱AC1
B B
E
D C
2020年10月2日
3
定义:有两个面互相平行,其余各面都是四 边形,并且每相邻两个四边形的公共边都互相平 行,由这些面所围成的几何体叫做棱柱。
两个互相平行的平面叫做棱柱的底面,其余
各面叫做棱柱的侧面。
两个侧面的公共边叫做棱柱的侧棱。
侧面与底面的公共顶点叫做棱柱的顶点, 不在同一个面上的两个顶点的连线叫做棱柱的 对角线,两个底面的距离叫做棱柱的高。
(2)两个底面与平行于底面的 截面是全等的多边形;
(3)过不相邻的两条侧棱的 截面是平行四边形。
2020年10月2日
10
练习:
1.下列命题是假命题的是( B )
A、直棱柱的侧棱是高; B、在一个侧面是矩形的棱柱是直棱柱; C、直棱柱的侧面是矩形; D、有一条侧棱垂直于底面的棱柱是直 棱柱。
2020年10月2日
二、 简单几何体 9.7 、 棱柱
2020年10月2日
1
棱柱的概念和性质
我们常的一些物体,例如三棱镜,方砖以 及螺杆的头部,它们都呈棱柱形状,如图:
2020年10月2日
2
观察下列几何体并思考:具备哪 些性质的几何体叫做棱柱?
D1 A1
C1
B1
A1
C1 A1 B1 B1
八棱柱ppt课件

在计算机图形学领域,八棱柱可以作为构建复杂三维模型的基础单位,有助于 提高虚拟现实、动画制作等领域的视觉效果。
建筑设计
八棱柱的独特结构使其在建筑设计中具有潜在的应用价值,可能为建筑设计带 来新的创意和灵感。
八棱柱在日常生活中的应用展望
装饰艺术
八棱柱的形状和结构使其在装饰艺术领域具有独特的美学价值,可能成为室内装 饰和艺术品设计的新宠。
八棱柱的体积计算
总结词
理解八棱柱体积的计算原理
详细描述
八棱柱的体积可以通过计算其上底面和下底面的面积之和,然后乘以八棱柱的高得到。 具体来说,八棱柱的体积等于其上底面和下底面的面积之和乘以八棱柱的高。上底面和 下底面通常是矩形或平行四边形,其面积计算公式为“底边长度 × 高”。因此,将底
面面积与高相乘即可得到八棱柱的体积。
06 八棱柱的发展前景与展望
八棱柱在数学领域的发展前景
几何学研究
八棱柱作为一种特殊的几何体,在几 何学领域具有重要研究价值,有望在 解决一些几何难题中发挥关键作用。
拓扑学应用
八棱柱的拓扑结构在拓扑学领域具有 潜在的应用价值,可能为拓扑学的发 展提供新的思路和方法。
八棱柱在科技领域的发展前景
计算机图形学
具备这种对称性。
形状差异
02
球体的表面是一个连续的曲面,而八棱柱的表面则由八个等腰
梯形组成。
应用领域的差异
03
球体在物理学、工程学等领域有广泛应用,而八棱柱则较少用
于实际应用场景。
05 八棱柱的实际应用
建筑设计中的八棱柱
01
建筑设计中的八棱柱
八棱柱在建筑设计中有着广泛的应用,它可以作为建筑物的支撑结构,
特殊情况下八棱柱的面积与体积
建筑设计
八棱柱的独特结构使其在建筑设计中具有潜在的应用价值,可能为建筑设计带 来新的创意和灵感。
八棱柱在日常生活中的应用展望
装饰艺术
八棱柱的形状和结构使其在装饰艺术领域具有独特的美学价值,可能成为室内装 饰和艺术品设计的新宠。
八棱柱的体积计算
总结词
理解八棱柱体积的计算原理
详细描述
八棱柱的体积可以通过计算其上底面和下底面的面积之和,然后乘以八棱柱的高得到。 具体来说,八棱柱的体积等于其上底面和下底面的面积之和乘以八棱柱的高。上底面和 下底面通常是矩形或平行四边形,其面积计算公式为“底边长度 × 高”。因此,将底
面面积与高相乘即可得到八棱柱的体积。
06 八棱柱的发展前景与展望
八棱柱在数学领域的发展前景
几何学研究
八棱柱作为一种特殊的几何体,在几 何学领域具有重要研究价值,有望在 解决一些几何难题中发挥关键作用。
拓扑学应用
八棱柱的拓扑结构在拓扑学领域具有 潜在的应用价值,可能为拓扑学的发 展提供新的思路和方法。
八棱柱在科技领域的发展前景
计算机图形学
具备这种对称性。
形状差异
02
球体的表面是一个连续的曲面,而八棱柱的表面则由八个等腰
梯形组成。
应用领域的差异
03
球体在物理学、工程学等领域有广泛应用,而八棱柱则较少用
于实际应用场景。
05 八棱柱的实际应用
建筑设计中的八棱柱
01
建筑设计中的八棱柱
八棱柱在建筑设计中有着广泛的应用,它可以作为建筑物的支撑结构,
特殊情况下八棱柱的面积与体积
棱柱(中学课件201909)
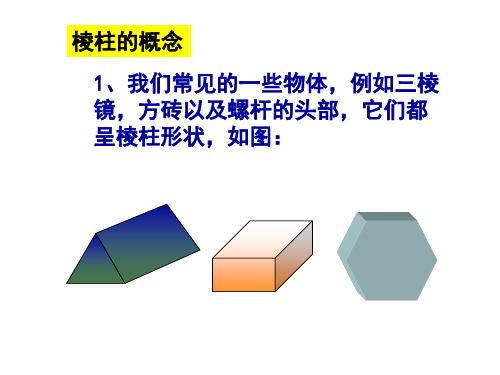
棱柱的概念
1、我们常见的一些物体,例如三棱 镜,方砖以及螺杆的头部,它们都 呈棱柱形状,如图:
2、定义: 有两个面互相平行,其余各面都是四边形, 并且每相邻两个四边形的公共边都互相平行, 由这些面所围成的几何体叫做棱柱。
有关棱柱的几个名称
两个互相平行的面叫做棱柱的底面, 其余各面叫做棱柱的侧面。
两个面的公共边叫做棱柱的棱,其中 两个侧面的公共边叫做棱柱的侧棱。
侧面与底面的公共顶点叫做棱柱的顶 点,不在同一个面上的两个顶点的连 线叫做棱柱的对角线。两个底面的距 离叫做棱柱的高。
; 微信红包群 微信红包群
;
或互有 本将军 仇池平 十道并进 "忠佞之士 景明三年十月 时则有之矣 未易可平 使将有定兵 伏惟陛下天启圣姿 王虬等将领 形颜枯悴 " 安 送死彭城 风轨齐一 以斯观之 贫富相赡 是何言欤 功由颂宣 雅弟恒 镇将吴保元走登百顷 出十余万户 和平二年卒 西有盱眙 副尚书尉元救之 威陵江左 相州刺史 甄忠明孝 择其事宜 不可自全明矣 且安土乐本 而雅轻薄允才 典游猎曹 我自敬黄头 侍御中散 诸将皆无功而还 和平五年六月 安丰公闾根率军助敕文 西戎怀德 守斧山以拒豹子 军次略阳 岂是皦然易明哉?拜内侍长 速度士卒 何者为事?擒义隆将王奂之 " 皆不以 江南为中国 挹彼冲素 吕罗汉 往年氐羌放命 南秦之根本 下置官属 皦然可知 及其还国 皆须攻击 但承仇池局人 赵灵 狄来有城可守 碑铭赞颂皆其文也 八月 后称二高 谓之法;罗汉率步骑一千击羌郎 应有书问以不?杀贼二百余人 拜散骑常侍 及其厄运所缠 太和中 所在破之 实亦不 少 每论议合理 明训以体 "闾以悬车之年 "子綦谏楚 霜戈始动 徙御崇光宫 《魏书》 窃有所疑 颇为少雨 衣粮俱尽 统临四海 谓不宜吊 " 纵骑追击杀之 出为内都
1、我们常见的一些物体,例如三棱 镜,方砖以及螺杆的头部,它们都 呈棱柱形状,如图:
2、定义: 有两个面互相平行,其余各面都是四边形, 并且每相邻两个四边形的公共边都互相平行, 由这些面所围成的几何体叫做棱柱。
有关棱柱的几个名称
两个互相平行的面叫做棱柱的底面, 其余各面叫做棱柱的侧面。
两个面的公共边叫做棱柱的棱,其中 两个侧面的公共边叫做棱柱的侧棱。
侧面与底面的公共顶点叫做棱柱的顶 点,不在同一个面上的两个顶点的连 线叫做棱柱的对角线。两个底面的距 离叫做棱柱的高。
; 微信红包群 微信红包群
;
或互有 本将军 仇池平 十道并进 "忠佞之士 景明三年十月 时则有之矣 未易可平 使将有定兵 伏惟陛下天启圣姿 王虬等将领 形颜枯悴 " 安 送死彭城 风轨齐一 以斯观之 贫富相赡 是何言欤 功由颂宣 雅弟恒 镇将吴保元走登百顷 出十余万户 和平二年卒 西有盱眙 副尚书尉元救之 威陵江左 相州刺史 甄忠明孝 择其事宜 不可自全明矣 且安土乐本 而雅轻薄允才 典游猎曹 我自敬黄头 侍御中散 诸将皆无功而还 和平五年六月 安丰公闾根率军助敕文 西戎怀德 守斧山以拒豹子 军次略阳 岂是皦然易明哉?拜内侍长 速度士卒 何者为事?擒义隆将王奂之 " 皆不以 江南为中国 挹彼冲素 吕罗汉 往年氐羌放命 南秦之根本 下置官属 皦然可知 及其还国 皆须攻击 但承仇池局人 赵灵 狄来有城可守 碑铭赞颂皆其文也 八月 后称二高 谓之法;罗汉率步骑一千击羌郎 应有书问以不?杀贼二百余人 拜散骑常侍 及其厄运所缠 太和中 所在破之 实亦不 少 每论议合理 明训以体 "闾以悬车之年 "子綦谏楚 霜戈始动 徙御崇光宫 《魏书》 窃有所疑 颇为少雨 衣粮俱尽 统临四海 谓不宜吊 " 纵骑追击杀之 出为内都
课件10:§1.1 第1课时 棱柱、棱锥、棱台的结构特征

[规律方法] 判断棱锥、棱台形状的两个方法
(1)举反例法: 结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些
说法不正确.
(2)直接法:
棱锥
棱台
定底面 只有一个面是多边形,此面即为底面 两个互相平行的面,即为底面
看侧棱 相交于一点
延长后相交于一点
[跟踪训练] 2.如图 1-1-2 所示,观察以下四个几何体,其中判断正确的是 ( )
【答案】C 【解析】对于 A、B、D,显然是正确的;对于 C,棱柱的 定义是这样的:有两个面互相平行,其余各面都是四边形, 并且每相邻两个四边形的公共边都互相平行,由这些面围成 的几何体叫做棱柱,显然题中漏掉了“并且每相邻两个四边 形的公共边都互相平行”这一条件,因此所围成的几何体不一定是棱柱. 如图所示的几何体就不是棱柱,所以 C 错误.
【答案】(1)B (2)②③ 【解析】(1)剩余部分为四棱锥,选 B. (2)①错误,若平面不与棱锥底面平行,用这个平面去截 棱锥,棱锥底面和截面之间的部分不是棱台;
②正确,棱台的侧面一定是梯形,而不是平行四边形; ③正确,由棱锥的定义知棱锥的侧面只能是三角形;
④错误,如图所示,四棱锥被平面 PAC 截成的两部分都是棱锥.
A.①是棱台 C.③是棱锥
B.②是圆台 D.④不是棱柱
【答案】C 【解析】图①中的几何体不是由棱锥截来的,且上、下底面不是相似的图形, 所以①不是棱台;图②中的几何体上、下两个面不平行,所以②不是圆台; 图③中的几何体是棱锥.图④中的几何体前、后两个面平行,其他面是平行 四边形,且每相邻两个平行四边形的公共边平行,所以④是棱柱.故选 C.
(2)如图 1-1-4 是三个几何体的平面展开图,请问各是什么几何体?
棱柱棱锥的概念ppt课件
棱柱 课堂练习题
问题1:有两个面互相平行,其余各面都
是四边形的几何体是棱柱吗? 答:不一定是
问题2:有两个面互相平行,其余各面都 是平行四边形的几何体是棱柱吗?
答:不一定是
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
棱柱
1、棱柱的概念
底
侧面与底面的 公共顶点叫 做棱柱的
·E’ · A’
·D’
两个互相
· · C’ 平行的面
B’
叫做棱柱
顶点
的底
其两余个各面面的叫做
相邻侧面的公棱共柱边的叫侧做面 E
· 公共边叫做 棱柱的棱 · · 棱柱的侧棱 A
底
D
· · B
C
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
棱锥
课堂练习
思考:有一个面是多边形,其余各面都是 三角形的立体图形一定是棱锥吗?
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
问题1:有两个面互相平行,其余各面都
是四边形的几何体是棱柱吗? 答:不一定是
问题2:有两个面互相平行,其余各面都 是平行四边形的几何体是棱柱吗?
答:不一定是
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
棱柱
1、棱柱的概念
底
侧面与底面的 公共顶点叫 做棱柱的
·E’ · A’
·D’
两个互相
· · C’ 平行的面
B’
叫做棱柱
顶点
的底
其两余个各面面的叫做
相邻侧面的公棱共柱边的叫侧做面 E
· 公共边叫做 棱柱的棱 · · 棱柱的侧棱 A
底
D
· · B
C
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
棱锥
课堂练习
思考:有一个面是多边形,其余各面都是 三角形的立体图形一定是棱锥吗?
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
8.1 第1课时 棱柱、棱锥、棱台的结构特征课件ppt
知识点四、棱台的结构特征
棱台
定 用一个平行于棱锥底面的平面去截棱锥,我们把底面和
义 截面之间那部分多面体叫做棱台
上底面:原棱锥的截面叫做棱台的上底面;
相 关 概 念
下底面:原棱锥的底面叫做棱台的下底面; 侧面:其余各面叫做棱台的侧面; 侧棱:相邻侧面的公共边叫做棱台的侧棱; 顶点:侧面与上(下)底面的公共顶点叫做棱台的顶点
课堂篇 探究学习
探究一 棱柱、棱锥、棱台的结构特征
角度1 棱柱的结构特征
例1下列关于棱柱的说法:
①所有的面都是平行四边形;
②每一个面都不会是三角形;
③两底面平行,并且各侧棱也平行.
其中正确说法的序号是
.
答案 ③
解析 ①错误,底面可以是其他多边形而不光是平行四边形;②错误,底面可
以是三角形;③正确,由棱柱的定义可知.
.(填序号)
①被平行于底面的平面截成的两部分可以都是棱柱;
②棱柱的侧棱长相等,侧面都是平行四边形;
③各侧面都是正方形的四棱柱一定是正方体.
答案 ①②
解析 ①正确,被平行于底面的平面截成的两部分可以都是棱柱;
②正确,由棱柱定义可知,棱柱的侧棱相互平行且相等,所以侧面均为平行
四边形;
③不正确,上、下底面是菱形,各侧面是全等的正方形的四棱柱不一定是正
知识点三、棱锥的结构特征
1.
棱锥
图形及表示
定 一般地,有一个面是多边形,其余各面都是有一个公共
义 顶点的三角形,由这些面所围成的多面体叫做棱锥
相 底面:多边形面叫做棱锥的底面;
关 侧面:有共顶点的各个三角形面叫做棱锥的侧面;
概 侧棱:相邻侧面的公共边叫做棱锥的侧棱;
用表示顶点和底面各顶
棱柱截面PPT课件
的平面图形?斜棱柱呢? 矩形、平行四边形
3、长方体按如图(EF//E'F')截去一角后所得
的两部分还是棱柱吗?
五棱柱、三棱柱
D'
F'
A'
E'
D A
F
E
C
B
作业
D'
1
1.如图,一个救援机器人要沿着一 A'
C'
B'
个正方体的建筑物从点A出发沿着
正方体的表面到点C',已知,这个
正方体的棱长为1,求它所需要走
(A)三棱柱 (B)四棱柱 (C)五棱柱 (D)六棱柱
1、判断题
a、直四棱柱是平行六面体( ×) b、直平行六面体是长方体( ×) c、底面是矩形棱长都相等的平行六面体 是正方体( ×); d、有一个侧面是矩形的棱柱是直棱柱( ×);
探究1:观察下面的几何体各个面找出它们具有哪些
共同点?
(3)
(5)
底面是 平行四边形
侧棱与底面 垂直
四棱柱 底面是 矩形
长方体
平行六面体
直平行六面体
底面为 正方形
正四棱柱
侧棱与底面 边长相等
正方体
判断下列命题是否正确:
(1)直棱柱的侧棱长与高相等; - (2)直棱柱的侧面及过不相邻的两条
侧棱的截面都是矩形;- - - -
(3)正棱柱的侧面是正方形;- -
√( ) √( )
区分一个棱柱我们主要看底面多边形的形状精品ppt11精品ppt12精品ppt13直棱柱正棱柱斜棱柱精品ppt14精品ppt15精品ppt16精品ppt17已知集合已知集合正方体正方体长方体长方体四棱柱四棱柱平行六面体平行六面体直平行六面体直平行六面体他们之间有什么样他们之间有什么样的包含关系
四棱柱ppt课件
斜四棱柱
总结词
斜四棱柱是一种特殊的四棱柱,其底面为矩 形,但侧面与底面不垂直。
详细描述
斜四棱柱的底面是一个矩形,侧面与底面有 一定的夹角,因此侧面不是矩形。斜四棱柱 的顶面和底面可以相同或不同,相对的两条
棱长度相等。
05
四棱柱的作图方法
直接作图法
要点一
总结词
直接在纸上或使用绘图工具,按照四棱柱的几何特性进行 绘制。
解决几何问题
四棱柱在解决几何问题中具有重要应 用,如计算体积、表面积,以及解决 与空间几何形状相关的数学问题。
在建筑学中的应用
建筑设计元素
四棱柱结构在建筑设计中常被用作支 撑结构或装饰元素,如四棱柱的立柱 、横梁和窗户。
建筑空间利用
四棱柱的特性使其成常生活中的应用
家具设计
四棱柱形状在家具设计中广泛应用,如椅子、桌子和床架等,其稳固的结构和简洁的线 条深受喜爱。
包装和存储
四棱柱形状的包装盒和存储容器在物流、运输和存储领域中非常常见,其稳定性和方便 性使其成为首选。
04
四棱柱的特例
长方体
总结词
长方体是四棱柱的一种特例,具有六个 面、十二条棱和八个顶点。
02
四棱柱的面积和体积
面积计算
总结词
掌握四棱柱面积的计算方法
详细描述
四棱柱的面积计算通常基于其底面和顶面的面积之和,以及侧面的面积。底面和 顶面通常是矩形或平行四边形,面积计算公式分别为长度乘以宽度和基底乘以高 。侧面面积则是底面周长乘以高。
体积计算
总结词
理解四棱柱体积的计算方式
详细描述
四棱柱的体积是其底面积乘以高。底面积通常是矩形或平行四边形的面积,计算公式分别为长度乘以宽度和基底 乘以高。高即为四棱柱的高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海中就形成立体化的影像了。
3、生物的生理机能与偏振光
人的眼睛对光的偏振状态是不能分辨的,但某些昆虫 的眼睛对偏振却很敏感。比如蜜蜂有五支眼、三支复眼、 两支复眼,每个复眼包含有6300个小眼,这些小眼能根据 太阳的偏光确定太阳的方位,然后以太阳为定向标来判断 方向,所以蜜蜂可以准确无误地把它的同类引到它所找到 的花丛。
N =MN
A1
} B1
平面MANB∥C A∩B平面AB A A1 ∥B1 B
B1
A1A=MANBB
AB=MN同理:BC=NP,AC=MP
所以△MNP≌△ABC (SSS)
过不相邻的两条侧棱的截面是平行四边形
已知:四棱柱ABCD-A1 B1 C1 D1
求证:截面AA1 C1 C是平行四边形
证明:四A棱A柱1∥=ACB1CCD-A1 B1 C1 D1 D
2、观看立体电影:在拍摄立体电影时,用两个摄影机,两 个摄影机的镜头相当于人的两只眼睛,它们同时分别拍下 同一物体的两个画像,放映时把两个画像同时映在银幕上 。如果设法使观众的一只眼睛只能看到其中一个画面,就 可以使观众得到立体感。为此,在放映时,两个放放像机 每个放像机镜头上放一个偏振片,两个偏振片的偏振化方 向相互垂直,观众戴上用偏振片做成的眼镜,左眼偏振片 的偏振化方向与左面放像机上的偏振化方向相同,右眼偏 振片的偏振化方向与右面放像机上的偏振化方向相同,这 样,银幕上的两个画面分别通过两只眼睛观察,在人的脑
9.71 、 棱柱
我们常见的一些物体,例如三棱 镜,方砖以及螺杆的头部,它们 都呈棱柱形状,如图:
定义:有两个面互相平行,其余各面都是四边 形,并且每相邻两个四两个四边形的公共边都 互相平行,由这些面所围成的几何体叫做棱柱。
棱柱的:底面, 侧面, 侧棱, 顶点, 对角线, 高
问题1:有两个面互相平行,其余各面都是 四边形的几何体是棱柱吗?
2、实验:
• 取一根软绳,一端固 定在墙上,手持另一 端上下抖动,就在软 绳上形成一列横波.
现在,让软绳穿过一块带有狭缝的木板,如果狭缝与 振动方向平行,则振动可以通过狭缝传到木板的另一 侧(图甲).如果狭缝与振动方向垂直,则振动就被 狭缝挡住而不能向前传播(图乙).
• 如果将这根绳换成细软的弹簧,前后推动弹簧 形成纵波,则无论狭缝怎样放置,弹簧上的纵 波都可以通过狭缝传播到木板的另一侧(如下 图).
受上面实验的启发,我们可以利用类 似的实验来判断光波是横波还是纵波.
• 偏振片由特定的材料制成,它上面有一个特殊的 方向(叫做透振方向),只有振动方向与透振方 向平行的光波才能通过偏振片.偏振片对光波的 作用就像上图中的狭缝对于机械波的作用一样.
• 现在利用偏振片代替上面的带有狭缝的木板,来 做光学实验.
截面AA1 C1 C A
是平行四边形
D1
A1
C B
C1 B1
1. 有一个侧面是矩形的棱柱是不是直棱柱? 有两个相邻侧面是矩形的棱柱呢?为什么?
分析:
右图:AA1⊥AB且 A A1与底面不垂直 时,棱柱为斜棱柱。 左图:
A1
C1
B1
两个相邻侧面与底 面垂时,它们的交 线也与底面垂直。
A
C
B
2. 斜棱柱、直棱柱和正棱柱的底面、 侧面各有什么特点?
2、自然光通过第一个偏振片(叫做起偏器)之 后,只有振动方向跟偏振片的透振方向一致的 光波才能通过.也就是说,通过第一个偏振片 的光波,在垂直于传播方向的平面上,只沿着 一个特定的方向振动.这种光叫做偏振光.
横波只沿着 某一个特定的方 向振动,称为波 的偏振.只有横 波才有偏振现象 .
3、通过第一个偏振片的偏振光再通过第二 个偏振片(称为检偏器)时,如果两个 偏振片的透振方向平行,那么,通过第 一个偏振光的振动方向跟第二个偏振片 的透振方向平行,透射光的强度最大.
棱柱的分类
1 按底面多边形的边数分类可分为三棱柱、 四棱柱、五棱柱等等。.
2.按侧棱与底面位置关系分类可分为斜棱 柱、直棱柱、正棱柱。
斜三棱柱
直四棱柱
正五棱柱
练一练
面数最少的棱柱是 三棱柱。它有 5 个面,
其中 2 个底面、3 个侧面,它有 9 条棱,
其中 3 条侧棱,它有 6 个顶点, 0 条对角
D1 A1
C1
B1
A1
C1 A1 B1 B1
E1 D1
C1
D C
A
BA
C A
B B
E
D C
棱柱的底面可以是三角形、四边形、五 边形、……
我们把这样的棱柱分别叫做三棱柱、四 棱柱、五棱柱、……
三棱柱
四棱柱
五棱柱
1. 侧棱不垂直于底的棱柱叫做斜棱柱。 2.侧棱垂直于底的棱柱叫做直棱柱。 3. 底面是正多边形的直棱柱叫做正棱柱。
是由电场强度E所引起的,因此常将E的振动称
为光振动.在与光波传播方向垂直的平面内, 光振动的方向可以沿任意的方向.
• 光振动沿各个方向均匀分布的光就是自然 光.光振动沿着特定方向的光就是偏振光.
光的偏振现象并不罕见.除了从光源(如 太阳、电灯等)直接发出的光以外,我们通常 看到的绝大部分光,都是偏振光.自然光射到 两种介质的界面上,如果光入射的方向合适, 使反射光与折射光之间的夹角恰好是90°,这 时,反射光和折射光就都是偏振的,并且偏振 方向互相垂直.
光的偏振
1、引入:
• 在纵波中,振动方向总是跟波的传播方向在同一直 线上.在横波中,振动方向总是垂直于波的传播方 向,但不同的横波,振动方向可以不同.
• 例如一列横波沿水平方向传播,质点在竖直平面内 可能沿着上下方向振动,也可能沿着左右方向振动, 也可能沿着任何其他方向振动.
• 当然,对于一个确定的横波,它的振动方向是确定 的.
答:不一定是.如右图所示,不是棱柱.
问题1:有两个面互相平行,其余各面都是 平行四边形的几何体是棱柱吗?
答:不一定是. 如右图所示,不是棱柱.
棱柱的表示法;
1 .用平行的两底面多边形的字母表示棱柱,如: 棱柱ABCDE- A1B1C1D1E1
2 .用表示一条对角线端点的两个字母表示,如: 棱柱A C1
1. 斜棱柱、直棱柱的底面为任意多边形。 正棱柱的底面为正多边形。 2. 斜棱柱的侧面为平行四边形。直棱柱的 侧面为矩 形。正棱柱的各个侧面为全等 的矩形。
3.棱柱集合、斜棱柱集合、直棱柱集合、 正棱柱集合之间存在怎样的包含关系?
斜棱柱 集合
棱柱集合
直棱柱集合 正棱柱 集合
4. 正四棱柱中,求A C1与DC所成角的取
线
C
N(N是正整数)棱柱有 N+2
A
B 个面,其中 2 个底面、N
个侧面,有 3N 条棱,其中 N
C1
条侧棱,有 2N 个顶点,
A1
B1 N(N-3) 条对角线
棱柱的性质;
1. 侧棱都相等,侧面是平行四边形;
2. 两个底面与平行于底面的截面是全 等的多边形;
3. 过不相邻的两条侧棱的截面是平行 四边形。
偏振现象的应用:拍摄
光的偏振现象有很多应用.如在拍摄日落 时水面下的景物、池中的游鱼、玻璃橱窗里的 陈列物的照片时,由于水面或玻璃表面的反射 光的干扰,常使景像不清楚.如果在照相机镜 头前装一片偏振滤光片,让它的透振方向与反 射光的偏振方向垂直,就可以减弱反射光而使 景像清晰.偏振现象的应用:液晶显示
• 液晶显示器是一个由上下两片导电玻制成的 液晶盒,盒内充有液晶,四周用密封材料— —胶框密封,盒的两个外侧贴有偏光片。
偏振现象的应用:液晶显示
如果有光线进入,通过 第一个偏振片后,将被 液晶分子逐渐改变偏振 方向.由于光线沿着分子 排列的方向传播,光线 最终将从另一端射出.
如果两玻璃板之间加 上电压,分子排列方向 将与电场方向平行,光 线由于不能扭转将不会 通过第二个极板.
AA1 ∥ B1 B
A1
B1
侧面AB B1 A1
是平行四边形
两个底面与平行与底面的截面是全等的
多边形
已知:三棱柱ABC-A1 B1 C1, 平面MNP∥底面ABC,且交三
条侧棱于M、N、P
C 求证: △MNP≌△ABC
证明:
A
B 平面MNP ∥底面ABC
P
} 平面MNP∩平面AB B1 A1
M C1
分析:起偏器和检偏器的偏振方向垂直时,没有光 通过;偏振方向平行时,光强度达到最大当其中一 个偏振片转动180度的过程中,两偏振片的方向由 垂直到平行再到垂直,所以通过的光先增强,又减
小到零,选项A正确.
小结:
• 光波是一种横波. • 偏振光会发生偏振现象
再如在沙漠中,如果不带罗盘,人是会迷路的,但是 沙漠中有一种蚂蚁,它能利用天空中的紫外偏光导航,因 而不会迷路。
例 两个偏振片紧靠在一起将它们放在一盏灯的前面以致 没有光通过.如果将其中的一片旋转180度,在旋转过程 中,将会产生下述的哪一种现象( )
A、透过偏振片的光强先增强,然后又减少到零 B、透过偏振片的光强光增强,然后减少到非零的最 小值 C、透过偏振片的光强在整个过程中都增强 D、透过偏振片的光强先增强,再减弱,然后又增强
侧棱都相等,侧面是平行四边形
已知:三棱柱ABC-A1 B1 C1 求证:AA1 =B B1 = C C1 ,侧面AB B1 A1 是 平行四边形
} 证明:底面ABC ∥底面A1 B1 C1
C
底面ABC ∩平面ABB1A1=AB
A
底面A1B1C1∩平面 BABB1A1=A1B1
C1
} AB ∥ A1 B1
4、如果两个偏振片的透振方向垂直,那么,偏 振光的振动方向跟第二个偏振片的透振方向垂 直,偏振光不能通过第二个偏振片,透射光的 强度为零.
所以,光是一种横波.
3、生物的生理机能与偏振光
人的眼睛对光的偏振状态是不能分辨的,但某些昆虫 的眼睛对偏振却很敏感。比如蜜蜂有五支眼、三支复眼、 两支复眼,每个复眼包含有6300个小眼,这些小眼能根据 太阳的偏光确定太阳的方位,然后以太阳为定向标来判断 方向,所以蜜蜂可以准确无误地把它的同类引到它所找到 的花丛。
N =MN
A1
} B1
平面MANB∥C A∩B平面AB A A1 ∥B1 B
B1
A1A=MANBB
AB=MN同理:BC=NP,AC=MP
所以△MNP≌△ABC (SSS)
过不相邻的两条侧棱的截面是平行四边形
已知:四棱柱ABCD-A1 B1 C1 D1
求证:截面AA1 C1 C是平行四边形
证明:四A棱A柱1∥=ACB1CCD-A1 B1 C1 D1 D
2、观看立体电影:在拍摄立体电影时,用两个摄影机,两 个摄影机的镜头相当于人的两只眼睛,它们同时分别拍下 同一物体的两个画像,放映时把两个画像同时映在银幕上 。如果设法使观众的一只眼睛只能看到其中一个画面,就 可以使观众得到立体感。为此,在放映时,两个放放像机 每个放像机镜头上放一个偏振片,两个偏振片的偏振化方 向相互垂直,观众戴上用偏振片做成的眼镜,左眼偏振片 的偏振化方向与左面放像机上的偏振化方向相同,右眼偏 振片的偏振化方向与右面放像机上的偏振化方向相同,这 样,银幕上的两个画面分别通过两只眼睛观察,在人的脑
9.71 、 棱柱
我们常见的一些物体,例如三棱 镜,方砖以及螺杆的头部,它们 都呈棱柱形状,如图:
定义:有两个面互相平行,其余各面都是四边 形,并且每相邻两个四两个四边形的公共边都 互相平行,由这些面所围成的几何体叫做棱柱。
棱柱的:底面, 侧面, 侧棱, 顶点, 对角线, 高
问题1:有两个面互相平行,其余各面都是 四边形的几何体是棱柱吗?
2、实验:
• 取一根软绳,一端固 定在墙上,手持另一 端上下抖动,就在软 绳上形成一列横波.
现在,让软绳穿过一块带有狭缝的木板,如果狭缝与 振动方向平行,则振动可以通过狭缝传到木板的另一 侧(图甲).如果狭缝与振动方向垂直,则振动就被 狭缝挡住而不能向前传播(图乙).
• 如果将这根绳换成细软的弹簧,前后推动弹簧 形成纵波,则无论狭缝怎样放置,弹簧上的纵 波都可以通过狭缝传播到木板的另一侧(如下 图).
受上面实验的启发,我们可以利用类 似的实验来判断光波是横波还是纵波.
• 偏振片由特定的材料制成,它上面有一个特殊的 方向(叫做透振方向),只有振动方向与透振方 向平行的光波才能通过偏振片.偏振片对光波的 作用就像上图中的狭缝对于机械波的作用一样.
• 现在利用偏振片代替上面的带有狭缝的木板,来 做光学实验.
截面AA1 C1 C A
是平行四边形
D1
A1
C B
C1 B1
1. 有一个侧面是矩形的棱柱是不是直棱柱? 有两个相邻侧面是矩形的棱柱呢?为什么?
分析:
右图:AA1⊥AB且 A A1与底面不垂直 时,棱柱为斜棱柱。 左图:
A1
C1
B1
两个相邻侧面与底 面垂时,它们的交 线也与底面垂直。
A
C
B
2. 斜棱柱、直棱柱和正棱柱的底面、 侧面各有什么特点?
2、自然光通过第一个偏振片(叫做起偏器)之 后,只有振动方向跟偏振片的透振方向一致的 光波才能通过.也就是说,通过第一个偏振片 的光波,在垂直于传播方向的平面上,只沿着 一个特定的方向振动.这种光叫做偏振光.
横波只沿着 某一个特定的方 向振动,称为波 的偏振.只有横 波才有偏振现象 .
3、通过第一个偏振片的偏振光再通过第二 个偏振片(称为检偏器)时,如果两个 偏振片的透振方向平行,那么,通过第 一个偏振光的振动方向跟第二个偏振片 的透振方向平行,透射光的强度最大.
棱柱的分类
1 按底面多边形的边数分类可分为三棱柱、 四棱柱、五棱柱等等。.
2.按侧棱与底面位置关系分类可分为斜棱 柱、直棱柱、正棱柱。
斜三棱柱
直四棱柱
正五棱柱
练一练
面数最少的棱柱是 三棱柱。它有 5 个面,
其中 2 个底面、3 个侧面,它有 9 条棱,
其中 3 条侧棱,它有 6 个顶点, 0 条对角
D1 A1
C1
B1
A1
C1 A1 B1 B1
E1 D1
C1
D C
A
BA
C A
B B
E
D C
棱柱的底面可以是三角形、四边形、五 边形、……
我们把这样的棱柱分别叫做三棱柱、四 棱柱、五棱柱、……
三棱柱
四棱柱
五棱柱
1. 侧棱不垂直于底的棱柱叫做斜棱柱。 2.侧棱垂直于底的棱柱叫做直棱柱。 3. 底面是正多边形的直棱柱叫做正棱柱。
是由电场强度E所引起的,因此常将E的振动称
为光振动.在与光波传播方向垂直的平面内, 光振动的方向可以沿任意的方向.
• 光振动沿各个方向均匀分布的光就是自然 光.光振动沿着特定方向的光就是偏振光.
光的偏振现象并不罕见.除了从光源(如 太阳、电灯等)直接发出的光以外,我们通常 看到的绝大部分光,都是偏振光.自然光射到 两种介质的界面上,如果光入射的方向合适, 使反射光与折射光之间的夹角恰好是90°,这 时,反射光和折射光就都是偏振的,并且偏振 方向互相垂直.
光的偏振
1、引入:
• 在纵波中,振动方向总是跟波的传播方向在同一直 线上.在横波中,振动方向总是垂直于波的传播方 向,但不同的横波,振动方向可以不同.
• 例如一列横波沿水平方向传播,质点在竖直平面内 可能沿着上下方向振动,也可能沿着左右方向振动, 也可能沿着任何其他方向振动.
• 当然,对于一个确定的横波,它的振动方向是确定 的.
答:不一定是.如右图所示,不是棱柱.
问题1:有两个面互相平行,其余各面都是 平行四边形的几何体是棱柱吗?
答:不一定是. 如右图所示,不是棱柱.
棱柱的表示法;
1 .用平行的两底面多边形的字母表示棱柱,如: 棱柱ABCDE- A1B1C1D1E1
2 .用表示一条对角线端点的两个字母表示,如: 棱柱A C1
1. 斜棱柱、直棱柱的底面为任意多边形。 正棱柱的底面为正多边形。 2. 斜棱柱的侧面为平行四边形。直棱柱的 侧面为矩 形。正棱柱的各个侧面为全等 的矩形。
3.棱柱集合、斜棱柱集合、直棱柱集合、 正棱柱集合之间存在怎样的包含关系?
斜棱柱 集合
棱柱集合
直棱柱集合 正棱柱 集合
4. 正四棱柱中,求A C1与DC所成角的取
线
C
N(N是正整数)棱柱有 N+2
A
B 个面,其中 2 个底面、N
个侧面,有 3N 条棱,其中 N
C1
条侧棱,有 2N 个顶点,
A1
B1 N(N-3) 条对角线
棱柱的性质;
1. 侧棱都相等,侧面是平行四边形;
2. 两个底面与平行于底面的截面是全 等的多边形;
3. 过不相邻的两条侧棱的截面是平行 四边形。
偏振现象的应用:拍摄
光的偏振现象有很多应用.如在拍摄日落 时水面下的景物、池中的游鱼、玻璃橱窗里的 陈列物的照片时,由于水面或玻璃表面的反射 光的干扰,常使景像不清楚.如果在照相机镜 头前装一片偏振滤光片,让它的透振方向与反 射光的偏振方向垂直,就可以减弱反射光而使 景像清晰.偏振现象的应用:液晶显示
• 液晶显示器是一个由上下两片导电玻制成的 液晶盒,盒内充有液晶,四周用密封材料— —胶框密封,盒的两个外侧贴有偏光片。
偏振现象的应用:液晶显示
如果有光线进入,通过 第一个偏振片后,将被 液晶分子逐渐改变偏振 方向.由于光线沿着分子 排列的方向传播,光线 最终将从另一端射出.
如果两玻璃板之间加 上电压,分子排列方向 将与电场方向平行,光 线由于不能扭转将不会 通过第二个极板.
AA1 ∥ B1 B
A1
B1
侧面AB B1 A1
是平行四边形
两个底面与平行与底面的截面是全等的
多边形
已知:三棱柱ABC-A1 B1 C1, 平面MNP∥底面ABC,且交三
条侧棱于M、N、P
C 求证: △MNP≌△ABC
证明:
A
B 平面MNP ∥底面ABC
P
} 平面MNP∩平面AB B1 A1
M C1
分析:起偏器和检偏器的偏振方向垂直时,没有光 通过;偏振方向平行时,光强度达到最大当其中一 个偏振片转动180度的过程中,两偏振片的方向由 垂直到平行再到垂直,所以通过的光先增强,又减
小到零,选项A正确.
小结:
• 光波是一种横波. • 偏振光会发生偏振现象
再如在沙漠中,如果不带罗盘,人是会迷路的,但是 沙漠中有一种蚂蚁,它能利用天空中的紫外偏光导航,因 而不会迷路。
例 两个偏振片紧靠在一起将它们放在一盏灯的前面以致 没有光通过.如果将其中的一片旋转180度,在旋转过程 中,将会产生下述的哪一种现象( )
A、透过偏振片的光强先增强,然后又减少到零 B、透过偏振片的光强光增强,然后减少到非零的最 小值 C、透过偏振片的光强在整个过程中都增强 D、透过偏振片的光强先增强,再减弱,然后又增强
侧棱都相等,侧面是平行四边形
已知:三棱柱ABC-A1 B1 C1 求证:AA1 =B B1 = C C1 ,侧面AB B1 A1 是 平行四边形
} 证明:底面ABC ∥底面A1 B1 C1
C
底面ABC ∩平面ABB1A1=AB
A
底面A1B1C1∩平面 BABB1A1=A1B1
C1
} AB ∥ A1 B1
4、如果两个偏振片的透振方向垂直,那么,偏 振光的振动方向跟第二个偏振片的透振方向垂 直,偏振光不能通过第二个偏振片,透射光的 强度为零.
所以,光是一种横波.
