稳健自适应波束形成算法第章模约束稳健波束形成算法
一种新的稳健Capon波束形成算法

A w g rt m o b tCa o a f r i Ne Al o ih f r Ro us p n Be m o m ng
X igj ,H u , H N F n ,S A h- n U D n -e E R i S E eg H N Z i g i mi
响应 和 真实 的阵列 响应 之间 的差异 引起 的 。在 这种 情况 下 , ao C p n波束 形成 器把 S I O 当作 干扰抑 制掉 。
( 尔 滨 工 程 大 学 自动化 学 院 ,哈 尔 滨 10 0 ) 哈 5 0 1
摘
要 :针对常规 Cp n波束形成算法在期望信号导 向矢量失配情况下 性能 的急剧下 降 , ao 研究 了一种新 的基
于导向矢量 不确定集 的稳健 C pn波束形成算法 。该算法 通过对 阵列接受 信号 的相 关矩 阵进 行特征分解 获得 噪 ao 声子空间 , 使期望信号导 向矢量在噪声子空间的投影最优。并且利用特征向量 的结构特性推导 出了最优对 角加 载
阵列信 号 处理在 雷达 , 通信 , 声纳 , 学 , 声 地震 学
以及 医学 等领 域具 有 广 泛 的应 用 , 中波 束形 成 是 其 阵列 处 理 的一 个 重 要 任 务 。理 想 情 况 下 ,ao C pn波 束 形成 器具有 较 高 的分 辨率 和干 扰抑制 能力 , 然而 , 当有用 信 号 ( i a o Itrs) O Sg l f ne tS I的导 向矢量 存 在 n e 误 差 时波束 形成 器 的性 能 将 会 急 剧下 降 , 这是 由于 假定 信号 到达 角和 真实信 号到 达角 或者假 定 的阵列
基于协方差矩阵重构的稳健自适应波束形成算法

基于协方差矩阵重构的稳健自适应波束形成算法王昊;马启明【摘要】In view of the large angle mismatch and sample covariance matrix containing the desired signal,the traditional adaptive beamformer performance is degraded sharply,this paper proposed a robust adaptive beam-forming algorithm based on covariance reconstruction.The algorithm divided the whole airspace into several non-overlapping regions,respectively corresponding to the interference region and desired signal region.Firstly, the standard Capon beamformer and the smallest eigenvalue of sample covariance matrix were used to reconstruct the interference and noise covariance matrix.Secondly,the MUSIC spectrum estimation method was used to re-construct the signal covariance matrix,and the main eigenvector of signal covariance matrix was used to estimate desired signal steering vector,thus the optimum weight vector of adaptive beamformer was obtained.Simulation result showed that algorithm had good performance in the case of few snapshots and large angle mismatch.%针对大角度失配和采样协方差矩阵中包含有期望信号时,传统自适应波束形成器性能极剧下降的问题,提出了基于协方差矩阵重构的稳健自适应波束形成算法.该算法将全空域划分成若干互不重叠的区域,分别对应干扰区域和期望信号区域,先利用标准Capon波束形成器及采样协方差矩阵的最小特征值对干扰加噪声协方差矩阵进行重构,再利用 MUSIC谱估计法重构出信号协方差矩阵,以其主特征向量估计出期望信号导引向量,最终得到自适应波束形成器的最优权值.仿真实验结果表明,在少快拍和大角度失配情况下算法具有良好的性能.【期刊名称】《探测与控制学报》【年(卷),期】2018(040)001【总页数】6页(P60-64,71)【关键词】信号与信息处理;稳健自适应波束形成;大角度失配;协方差矩阵重构;导引向量估计【作者】王昊;马启明【作者单位】杭州应用声学研究所,浙江杭州310023;杭州应用声学研究所,浙江杭州310023【正文语种】中文【中图分类】TN911.70 引言自适应波束形成技术可以广泛地应用于雷达、声纳、无线通信等众多领域。
基于子空间的稳健自适应波束形成方法

Ro u tAd p i e Be m f r i g Al o ih s d o g ns a e b s a tv a o m n g r t m Ba e n Ei e p c
P oet na d N l — b o d nn rjci n ll o l r a e ig
rc o f h m e rsne i p p r w i s s r e t t r gv c r d a t a cn l—bo d n g e t n o te a m r s ee tdi t s a e , hc u e po c ds e n et u m t ul ra e i i j ip nh h j e ei oa n o i n
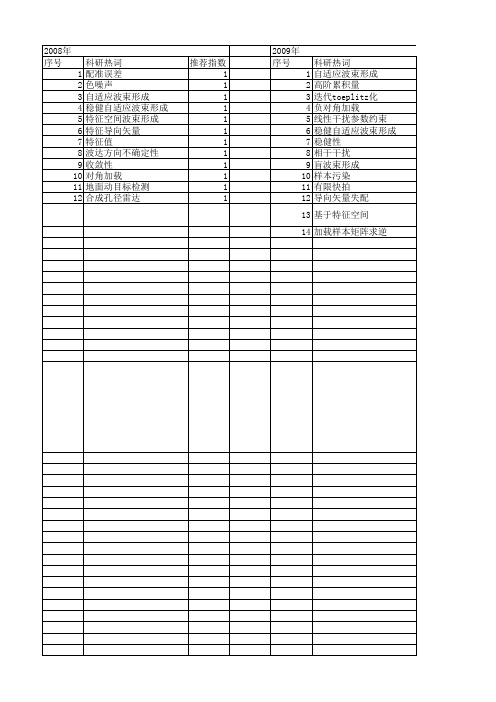
【国家自然科学基金】_稳健自适应波束形成_基金支持热词逐年推荐_【万方软件创新助手】_20140731
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词 推荐指数 自适应波束形成 4 对角加载 3 稳健性 2 收缩方法 2 频率不变波束图 1 阵列设计 1 阵列流型分离 1 超宽带穿墙雷达成像 1 谱分析 1 约束 1 空间响应偏差(srv) 1 稳健的接收波束形成器 1 相干系数加权 1 波束形成器 1 波束形成 1 正交分解 1 广义特征值分解 1 宽带波束形成 1 失配滤波器 1 发射导向矢量误差 1 协方差矩阵估计 1 二阶锥规划 1 不确定集约束 1 uwb mimo天线阵 1 capon波束形成 1 broadband beamforming, spatial1 response variation
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 21年 科研热词 推荐指数 自适应波束形成 4 对比度 2 分辨率 2 降秩 1 阵列信号处理 1 遗传算法 1 通道延迟 1 超高斯加载 1 超宽带穿墙雷达成像 1 超宽带穿墙成像 1 负对角加载 1 稳健性 1 盲自适应波束形成 1 模约束 1 模数转换器 1 最差情况性能优化 1 导数约束 1 导向向量偏差 1 对角加载 1 多通道采样 1 后验概率密度函数 1 双约束稳健capon波束形成 1 凸优化 1 信干噪比 1 互相关系数 1 不确定集约束 1 drcb 1 cf 1 capon波束形成器 1 (e)p范数 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 配准误差 色噪声 自适应波束形成 稳健自适应波束形成 特征空间波束形成 特征导向矢量 特征值 波达方向不确定性 收敛性 对角加载 地面动目标检测 合成孔径雷达
波束形成算法及其新进展ppt课件

“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
引言
波束形成是阵列信号处理、智能天线系统中一重要技术 使用阵列天线的优点:
-提高系统的容量 -提高系统的性能 -抑制干扰和噪声 -节省功率
2.2 Bartlett 波束形成算法
Bartlett 波束形成算法是使得波束形成的输出功率相对 于某个输入信号最大。
ar m g [E a { w H x x (n )xH (n )w }] w
wba
a() aH()a()
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
d 个独立信源,则 Rank [ R S ] d ,则有
E E S
EN
,
S
0
0
N
S diag 1 2 d
N diag d 1 d 2 m
E S e1 e2 ed
E N e d 1 e d 2 e m
1 2 d d 1 d 2 m
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
目录
§0.引言 §1.阵列天线的统计模型和DOA估计 §2.常用的波束形成算法 §3.自适应波束形成算法及其改进 §4.采样协方差求逆SMI算法改进 §5.其他波束形成算法 §6.总结
基于波束域导向矢量估计的稳健自适应波束形成方法

机 仿真验证 了该文所提方法的有效性。 关键词 :信 号处理; 自适应波束 形成 ;波束域 ;导 向矢量;稳健性;半正定松弛
中图分类号 : T N 9 1 1 . 7 D O I : 1 0 . 3 7 2 4 / S P . J . 1 1 4 6 . 2 0 1 2 . 0 1 3 3 4
束域 导向矢量估计的稳健方法。该方法首先利用期望信号角度 失配 区域 的补集构造波束域转换矩 阵, 克服 了当样本 协方差矩 阵中存在期望信 号分量时现有算法 出现有用信 号对消的缺点。 其次推导 出波束域 导向矢量估计方法 , 并将
其 转 化 为包 含 恒 模 约 束 的 非 凸 二 次约 束 二 次规 划 问题 , 然 后采 用 半 正定 松 弛 规 划 估 计 实 际 的波 束 域 导 向矢 量 。 计 算
s t e e r i n g v e c t o r a n d i n a c c u r a t e e s t i ma t i o n o f t h e s a mp l e c o v a r i a n e e ma t r i x . A n e w a p p r o a c h b a s e d o n b e a ms p a c e s t e e r i n g v e c t o r e s t i ma t i o n f o r r o b u s t a d a p t i v e b e a mf or mi n g i s p r e s e n t e d i n t h i s p a p e r .Fi r s t l y ,b y u s i n g t h e c o mpl e me n t a r y s e t o f t h e s p a t i a l s e c t o r i n wh i c h t h e a c t u a l s t e e r i n g v e c t o r l i e s , b e a ms p a c e t r a n s f o r ma t i o n ma t r i x c a n b e c o n s t r u c t e d t o e n s u r e t h a t t h e s i g n a l o f i n t em t h e s a mp l i n g c o v a r i a n c e ma t r i x . Th e n a me t h o d or f b e a ms p a c e s t e e r i n g v e c t o r e s t i ma t i o n i s d e r i v e d ,a n d ma t he ma t i c a l l y e x p r e s s e d a s t h e n o n c o n v e x
自适应波束形成及算法
第3章 自适应波束形成及算法(3.2 自适应波束形成的几种典型算法)3.2 自适应波束形成的几种典型算法自适应波束形成技术的核心内容就是自适应算法。
目前已提出很多著名算法,非盲的算法中主要是基于期望信号和基于DOA 的算法。
常见的基于期望信号的算法有最小均方误差(MMSE )算法、小均方(LMS )算法、递归最小二乘(RLS )算法,基于DOA 算法中的最小方差无畸变响应(MVDR )算法、特征子空间(ESB )算法等[9]。
3.2.1 基于期望信号的波束形成算法自适应算法中要有期望信号的信息,对于通信系统来讲,这个信息通常是通过发送训练序列来实现的。
根据获得的期望信号的信息,再利用MMSE 算法、LMS 算法等进行最优波束形成。
1.最小均方误差算法(MMSE ) 最小均方误差准则就是滤波器的输出信号与需要信号之差的均方值最小,求得最佳线性滤波器的参数,是一种应用最为广泛的最佳准则。
阵输入矢量为: 1()[(),,()]TMx n x n x n =(3-24)对需要信号()d n 进行估计,并取线性组合器的输出信号()y n 为需要信号()d n 的估计值ˆ()dn ,即 *ˆ()()()()H T d n y n w x n x n w === (3-25) 估计误差为:ˆ()()()()()H e n d nd n d n w x n =-=-(3-26)最小均方误差准则的性能函数为:2{|()|}E e t ξ= (3-27)式中{}E 表示取统计平均值。
最佳处理器问题归结为,使阵列输出()()Ty n w X n =与参考信号()d t 的均方误差最小,即:2{|()|}M i n E e t式(3-28)也就是求最佳权的最小均方准则。
由式(3-26)~(3-28)得:2*{|()|}{()()}E e t E e n e n ξ==2{|()|}2R e []T Hxdxx E d nw r w R w =-+ (3-29)其中,Re 表示取实部,并且:[()()]H xx R E x n x n = (3-30)为输入矢量()x n 的自相关矩阵。
【国家自然科学基金】_自适应波束形成算法_基金支持热词逐年推荐_【万方软件创新助手】_20140802
推荐指数 4 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
科研热词 自适应波束形成 波束形成 干扰抑制 阵列天线 阵列信号处理 遗传算法 负熵 自适应阵列 自适应天线 第3代移动通信 空时块码 空分复用 码分多址 独立分量分析 消噪 波束形成算法 波束域 最小方差无畸变响应 智能自适应阵列天线 智能天线 无线局域网 方位估计 子阵异步 媒体接入控制协议 多天线通信 发射方案 全球定位系统 rls算法 cdma系统
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66
2011年 科研热词 推荐指数 自适应波束形成 6 波束形成 5 智能天线 3 降维 2 阵列处理 2 递归最小二乘 2 机载雷达 2 预编码 1 零陷展宽 1 零陷加宽 1 隧道效应 1 降秩 1 阵列信号处理 1 遗传算法 1 通信技术 1 迭代 1 超高斯加载 1 负对角加载 1 调度 1 自适应 1 空时自适应处理(stap) 1 空时自适应处理 1 稳健性 1 盲自适应波束形成 1 混响 1 波达方向估计 1 步长 1 正交加权约束 1 模约束 1 概率模型 1 杂波抑制 1 最差情况性能优化 1 最小方差无失真响应算法 1 最小均方误差 1 时分同步码分多址 1 无畸变响应 1 旁瓣干扰 1 方向图控制 1 指向性 1 扩频序列 1 快速独立分量分析 1 循环自适应波束形成 1 广义线性约束正交投影算法 1 广义旁瓣抵消器 1 导数约束 1 导向向量偏差 1 对角加载 1 多输入多输出雷达 1 多用户 1 多波束测深声纳 1 四元数输出模型 1 四元数最小均方自适应算法 1
导向矢量不确定集约束的稳健Capon波束形成算法
Ro u tCa o e m f r i l o ihm n e he b s p n b a o m ng a g r t u d rt
s e r ng v c o n e t i t e tei e tru c ran yst
L U o g f n C n — e g.LI AO is e g Gu —h n
( y La .o d rS g a o e sn ,Xi in Un v ,Xi n 7 0 7 ,Ch n ) Ke b fRa a i n l Pr c s i g da i. ’ 10 1 a ia
是不 能改善 诸如 较差 的阵列 校正 、 知传感 器互 耦 、 未 近场 波前 失 真 、 源扩 展 以及 相 干 和非 相 干 的局 部 散射 等
影响 . 近几年 提 出了在 理论上 比较 严格 的稳 健波束 形 成算法 [ , 主要 思 想是 定 义 了所 谓 的不 确定 集 和使 3 其
导 向矢 量不 确 定 集约 束 的稳 健 C p n波 束形 成 算 法 ao
刘 聪 锋, 廖 桂 生
( 西安 电子 科 技 大 学 雷达 信 号 处理 重 点 实验 室 , 西 西 安 陕 707) 1 0 1
一 ~一 ~ 一 一~ ~一
摘 要 :针 对 C p n波 束 形 成 算 法 在 导 向矢 量 不 确 定 集 约 束 下 的求 解 问题 , 出 了新 的 求 解 方 法 . 过 对 ao 提 通
第3章自适应波束形成及算法
第3章 自适应波束形成及算法(3.2 自适应波束形成的几种典型算法)3.2 自适应波束形成的几种典型算法自适应波束形成技术的核心内容就是自适应算法。
目前已提出很多著名算法,非盲的算法中主要是基于期望信号和基于DOA 的算法。
常见的基于期望信号的算法有最小均方误差(MMSE )算法、小均方(LMS )算法、递归最小二乘(RLS )算法,基于DOA 算法中的最小方差无畸变响应(MVDR )算法、特征子空间(ESB )算法等[9]。
3.2.1 基于期望信号的波束形成算法自适应算法中要有期望信号的信息,对于通信系统来讲,这个信息通常是通过发送训练序列来实现的。
根据获得的期望信号的信息,再利用MMSE 算法、LMS 算法等进行最优波束形成。
1.最小均方误差算法(MMSE ) 最小均方误差准则就是滤波器的输出信号与需要信号之差的均方值最小,求得最佳线性滤波器的参数,是一种应用最为广泛的最佳准则。
阵输入矢量为: 1()[(),,()]T M x n x n x n =(3-24)对需要信号()d n 进行估计,并取线性组合器的输出信号()y n 为需要信号()d n 的估计值ˆ()dn ,即 *ˆ()()()()H T d n y n w x n x n w === (3-25) 估计误差为:ˆ()()()()()H e n d n dn d n w x n =-=- (3-26)最小均方误差准则的性能函数为:2{|()|}E e t ξ= (3-27)式中{}E 表示取统计平均值。
最佳处理器问题归结为,使阵列输出()()T y n w X n =与参考信号()d t 的均方误差最小,即:2{|()|}MinE e t式(3-28)也就是求最佳权的最小均方准则。
由式(3-26)~(3-28)得:2*{|()|}{()()}E e t E e n e n ξ==2{|()|}2Re[]T H xd xx E d n w r w R w =-+ (3-29)其中,Re 表示取实部,并且:[()()]H xx R E x n x n = (3-30)为输入矢量()x n 的自相关矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4.1-47)
其中的参数定义同NICCB。
其中x为阵列的M×1维复采样数据, w为M×1维的自适应 加权矢量, (·)H表示共轭转置。
第4章 模约束稳健波束形成算法
假设R为阵列输出矢量的理论协方差矩阵, 且R>0(正
定), 则基于空间滤波形式的标准Capon波束形成(SCB)
问题可以表示成如下最优化问题: (4.1-2)
第4章 模约束稳健波束形成算法
因此, 对于固定的λ和μ, g1(w, λ, μ)的无约束最小化由下式
给出: (4.1-13) 显然有 (4.1-14) f2(λ, μ)关于μ的最小化可以由下式给出: (4.1-15)
第4章 模约束稳健波束形成算法
以及
对上式求关于λ的最大化, 将会得到:
为了获得最优的加权矢量, 必须求解该方程。
第4章 模约束稳健波束形成算法
将上面求出的μ表达式代入最优加权矢量表达式中, 可
得 (4.1-18) 该式必然满足: (4.1-19) 以及 (4.1-20)
第4章 模约束稳健波束形成算法
令
(4.1-21) 则h(λ)在λ≥0时, 为单调减函数[10]。 这是因为对于任意的关于参数λ的矩阵函数F, 有 (F-1)′=-F-1F′F-1 其中 (4.1-22)
更加准确的计算。
为了求解方程h(λ)=ζ, 令 (4.1-30)
第4章 模约束稳健波束形成算法 其中矩阵U的列向量由R的特征矢量u1, u2, …, uM组成, 对
角矩阵Γ的对角线元素γ1≥γ2≥…≥γM为相应的特征值。 h(λ)可
重新表示如下:
(4.1-31)
第4章 模约束稳健波束形成算法 故可得
其中s为有用信号(SOI)的导向矢量。 对于窄带信号, R
为其中心频率处的协方差矩阵; 对于宽带信号, R为给定
频率单元的中心频率处的协方差矩阵。在实际应用中, R通
常由样本协方差矩阵 代替, 其中: (4.1-3)
其中N表示快拍数量, xn表示第n个快拍。
第4章 模约束稳健波束形成算法
该最优化问题可以通过Lagrange乘数方法进行求解, 即
基于上面的推导分析可知, 模不等式约束参数ζ应该满
足下面的条件:
(4.1-45)
第4章 模约束稳健波束形成算法
即
(4.1-46) 故当模不等式约束参数ζ满足上面的条件时, NICCB的解 一定存在。
第4章 模约束稳健波束形成算法
4.1.4 模等式约束的Capon波束形成算法
NECCB波束形成问题可以表示如下:
(4.1-5)
其中 s 为假设的有用信号(SOI)导向矢量, ζ为模不等式 约束参数。
第4章 模约束稳健波束形成算法
令S表示该最优化问题的约束条件集合, 即
(4.1-6) 而且, Lagrange函数可以表示为 (4.1-7) 其中λ和μ为实值Lagrange乘数, μ为任意常数, 而λ≥0, 并 且满足R+λI>0。 因此, f1(w, λ, μ) 相对于w 可以被最小化, 即
(4.1-26) 因此, 当λ≥0时, h′(λ)≤0, 即当λ≥0时h(λ)为单调减函
数。
根据波束形成算法的无失真响应约束, 可得 (4.1-27) 故可得约束参数ζ的下限为 (4.1-28)
第4章 模约束稳健波束形成算法 即如果ζ小于该下限, 则该波束形成算法无解。 因此约束参 数ζ至少选择在如下不等式定义的区间之内 (4.1-29) 后面还会根据解的存在情况对约束参数ζ的取值范围进行
(4.1-4)
从上面的最优化问题可以看出, 它可以被解释为一个自适
应空域滤波问题, 即给定R和s, 确定加权矢量w作为空间
滤波器, 使得感兴趣的有用信号无失真地通过, 同时使得 R中的无用干扰和噪声的贡献最小。
第4章 模约束稳健波束形成算法
4.1.2 模不等式约束的Capon
NICCB波束形成问题可以表示为
因为:
(4.1-39) (4.1-40)
满足h(λ)=ζ。
第4章 模约束稳健波束形成算法
(4.1-41)
第4章 模约束稳健波束形成算法 因此,
(4.1-42)
第4章 模约束稳健波束形成算法
因为:
(4.1-43) (4.1-44)
不存在λ满足h(λ)=ζ。
第4章 模约束稳健波束形成算法
4.1.3 模不等式约束参数的选择
第4章 模约束稳健波束形成算法 因此, 考虑参数ζ满足下面的条件, 即 (4.1-11) 因此, 对于NICCB, 该条件约束着参数ζ的上限。 因 而在该条件下, NICCB不同于SCB。 为了处理这种情况, 可以将f1(w, λ, μ)重新表示为下式:
(4.1-12)
第4章 模约束稳健波束形成算法
(4.1-8)
其中等号在S的边界上取得。
第4章 模约束稳健波束形成算法 当参数ζ满足下面的条件时:
(4.1-9)
基于SCB的自适应加权矢量就满足式(4.1-8)。 利用 s 代替
SCB解中的s, 即
(4.1-10) 满足NICCB中的模不等式约束条件。 因此, 该最优解也是 NICCB的解。 但是, 对于这种情况,λ=0和NICCB中的模 约束条件是不起作用的。
表示取导数操作, 而且还有 (F-2)′=-F-2(F′F+FF′)F-2 (4.1-23)
第4章 模约束稳健波束形成算法 如果令 F=R+λI 则有F′=I, 而且可得上面h(λ)的导数表达式: (4.1-24)
(4.1-25)
第4章 模约束稳健波束形成算法
根据F的表达式可知, 当λ≥0时, F>0。 故有
第4章 模约束稳健波束形成算法
为了分析的方便, 令
(4.1-34)
因此, 上面的不等式关系(4.1-32)和(4.1-33)可简写为:
(4.1-35) (4.1-36)
第4章 模约束稳健波束形成算法
(4.1-37)
第4章 模约束稳健波束形成算法 因此, 当
(4.1-38)
第4章 模约束稳健波束形成算法
第4章 模约束稳健波束算法
4.1 4.2
基于模约束的稳健Capon波束形成算法 基于二次约束的稳健LCMP波束形成算法
第4章 模约束稳健波束形成算法
4.1 基于模约束的稳健Capon波束形成算法
假设阵列由M个传感器组成, 则窄带自适应波束形成 算法的输出通常表示为 y=wHx (4.1-1)
