平行四边形和梯形知识点汇总
四年级数学《平行四边形和梯形》知识点

四年级数学《平行四边形和梯形》知识点平行四边形和梯形是四年级学习中的一个重点知识章节。
我们都学会了没有呢?不妨来总结一下吧。
为了让您在写的过程中更加简单方便,一起来参考是怎么写的吧!下面给大家分享关于四年级数学《平行四边形和梯形》知识点,欢迎阅读!四年级数学《平行四边形和梯形》知识点一、垂直与平行1、认识平行和垂直①同一平面内的两条直线的位置关系只有两种:相交和不相交。
相交又有成直角的和不成直角的两种情况。
_“同一平面”是确定两条直线平行关系的前提,如果不在同一平面内,即便不相交,也不能称为互相平行。
②平行线:在同一个平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行。
平行的表示方法:a//b,读作a平行于b。
生活中平行的例子:窗户相对的框,黑板相对的两条边,公路上的斑马线......③垂直:如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
垂直的表示方法:ab生活中垂直的例子:三角尺上的两条直角边互相垂直......④三条直线的特殊关系:a//b,b//c,那么a//c:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线互相平行ab,bc,那么a//c:在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线互相平行。
2、垂线的画法和性质①过直线上和直线外一点怎样画这条直线的垂线:把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使三角尺的顶点和直线上的已知点重合;从直角的顶点起,沿着另一条直角边画出一条直线,这条直线就是已知直线的垂线。
②过直线外一点怎样画这条直线的垂线:把三角尺的一条直角边与已知直线重合;沿着直线移动三角尺,使三角尺的另一条直角边与直线外的一点重合;沿着三角尺的另一条直角边画一条直线③垂线的性质:从直线外一点到这条直线所画的垂直线段最短,它的长度叫做这点到直线的距离。
3、平行线的画法及运用①平行线的画法:固定三角尺,沿一条直角边先画一条直线;用直尺紧靠三角尺的另一条直角边,固定直尺,然后平移三角尺;再沿第一步中的直角边画出另一条直线。
平行四边形和梯形知识点归纳

平行四边形和梯形知识点归纳1、垂直与平行:①在同一平面内不相交的两条直线叫做I平行线也可以说这两条直线互相平行图一:“直线A和直线B是平行线;直线A的平行线是直线B”②如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
图二:“直线A和直线B相互垂直;直线A是直线B的垂线;点C是垂足A-------------- A例一例二2、画垂线:① 例一:过直线上一点画这条直线的垂线方法?答:把三角尺的一条直角边靠近直线,三角尺上的直角顶点靠近直线上的点,然② 例二:过直线外一点画这条直线的垂线方法?答:把三角尺的一条直角边靠近直线,三角尺上的另一条边靠近直线外的点,然后用笔沿这条边画直线就可以了。
③ 例三:把直线外一点A 与直线上任意一点连接,所画线段哪个最短? 小结:从直线外一点到这条直线所画的垂直线段最短,它的长度叫做 这点到直线的距离。
② 例二:在两条平行线之间画几条与平行线垂直的线段, 这些线段的长度特点? 小结:两条平行线之间的距离是相等的。
3、答:可以用直尺和三角尺来画平行线,先把三角尺的一条直角边紧靠直线,再把直 尺紧靠三角尺的另一条直角边,这时沿直尺平移三角尺,再画一条直线就可以了提示:长方形的两组对边是互相平行的,两条邻边是互相垂直的。
因此可以用画垂线或平行线的方法画。
小结:先画一条长3厘米的线段;再过线段端点画一条 2厘米的垂线;再过另一个点也画一 条2厘米的垂线;连接两个端点就可以了。
/三f =/ //二页划线闵划线③例三:怎样画出一条长3厘米,宽2厘米的长方形?平行四边形:小结:两组对边分别平行的四边形叫做平行四边形;四个角都是直角的四边形叫长方形。
四个角都是直角,并且四条边都相等的四边形叫正方形。
小结:平行四边形容易变形,它不具有稳定性。
梯形:梯形:一组对边平行而另一组对边不平行的四边形叫做梯形。
在梯形中,平行的两边叫做底,(较短的底叫做上底,较长的底叫做下底),不平行的两条边叫做腰,两底之间的距离叫做高。
平行四边形和梯形知识点总结
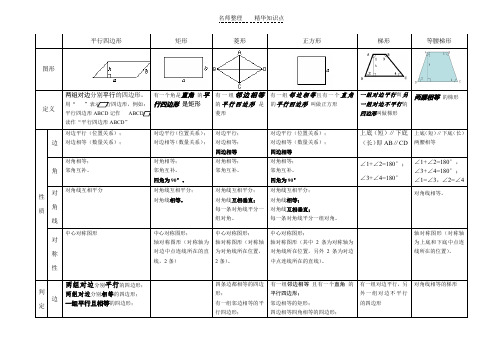
平行四边形矩形菱形正方形梯形等腰梯形图形定义两组对边分别平行的四边形。
用“”表示平行四边形,例如:平行四边形ABCD记作ABCD,读作“平行四边形ABCD”有一个角是直角的平行四边形是矩形有一组邻边相等的平行四边形是菱形有一组邻边相等且有一个直角的平行四边形叫做正方形一组对边平行而另一组对边不平行的四边形叫做梯形两腰相等的梯形性质边对边平行(位置关系);对边相等(数量关系);对边平行(位置关系);对边相等(数量关系);对边平行;对边相等;四边相等对边平行(位置关系);对边相等(数量关系);四边相等上底(短)∥下底(长)即AB∥CD上底(短)∥下底(长)两腰相等角对角相等;邻角互补。
对角相等;邻角互补。
四角为90°。
对角相等;邻角互补。
对角相等;邻角互补。
四角为90°∠1+∠2=180°;∠3+∠4=180°∠1+∠2=180°,∠3+∠4=180°;∠1=∠3,∠2=∠4 对角线对角线互相平分对角线互相平分;对角线相等。
对角线互相平分;对角线互相垂直;每一条对角线平分一组对角。
对角线互相平分;对角线相等;对角线互相垂直;每一条对角线平分一组对角。
对角线相等。
对称性中心对称图形中心对称图形;轴对称图形(对称轴为对边中点连线所在的直线,2条)中心对称图形;轴对称图形(对称轴为对角线所在位置,2条)。
中心对称图形;轴对称图形(其中2条为对称轴为对角线所在位置,另外2条为对边中点连线所在的直线)。
轴对称图形(对称轴为上底和下底中点连线所在的位置)。
判定边两组对边分别平行的四边形;两组对边分别相等的四边形;一组平行且相等的四边形;四条边都相等的四边形;有一组邻边相等的平行四边形;有一组邻边相等且有一个直角的平行四边形;邻边相等的矩形;四边相等四角相等的四边形;有一组对边平行,另外一组对边不平行的四边形对角线相等的梯形角两组对角分别相等的四边形;有一个角是直角的平行四边形;四个角都相等的四边形。
平行四边形和梯形的知识点总结PPT

矩形
定义
两组对边分别平行且相等的四边形是 矩形。
性质
判定
有三个角是直角的四边形是矩形;对 角线相等的平行四边形是矩形;有一 个角是直角的平行四边形是矩形。
矩形的四个角都是直角,对角线相等 且互相平分。
菱形
定义
四边都相等的四边形是菱形,或有一组邻边 相等的平行四边形是菱形。
性质
菱形的四条边都相等,对角线互相垂直且平 分每一组对角。
梯形中常见辅助线作法及解题思路
过梯形上底的一个顶点作下底的垂线,将梯 形划分为一个矩形和两个三角形,从而利用 矩形和三角形的性质求解问题。
过梯形对角线的交点作上下底的垂线,将梯 形划分为四个三角形,然后利用相似三角形 的性质求解问题。
延长梯形的两腰使之相交于一点,构造出一 个大的等腰三角形,然后利用等腰三角形的 性质求解问题。
05
典型例题解析与练习
例题一:平行四边形相关证明题
知识点
平行四边形的性质与判定
解析
通过已知条件,利用平行四边形的性质和判定定 理进行证明。
练习
给定一个四边形,证明它是平行四边形。
例题二:矩形、菱形、正方形综合题
01
02
03
知识点
矩形、菱形、正方形的性 质与判定
解析
结合已知条件,运用矩形 、菱形、正方形的性质和 判定定理进行综合分析和 解答。
梯形的表示方法
在平面直角坐标系中,可以通过三个顶点坐标确定一个梯形。一般形式为:梯形ABCD, 其中A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4)。需要注意的是,梯形的对角线不平行。
应用场景
利用平面直角坐标系表示平行四边形和梯形,可以方便地进行图形变换、求解面积等问题 。
四上数学五单元平行四边形与梯形知识点汇总

四上数学第五单元
平行四边形与梯形知识点汇总
1、平行线:同一平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行。
2、垂线:两条直线相交成直角,就说这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足。
注意:同一平面内,两条直线不相交,就平行。
3、画出相互垂直的两条直线:过一点画直线的垂线只能画一条。
①过直线上一点画垂线。
②过直线外一点画垂线。
4、点到直线的距离:从直线外一点到这条直线所画的垂直线段最短,它的长度叫做点到直线的距离。
与两条平行线互相垂直的线段的长度都相等。
5、平行四边形:两组对边分别平行的四边形叫做平行四边形。
平行四边形对边平行且相等,对角相等,易变形,具有不稳定性(应用)。
6、长方形和正方形是特殊的平行四边形。
正方形是特殊的长方形。
四个角都是直角的四边形叫做长方形。
四个角都是直角,并且四边都相等的四边形叫做正方形。
7、梯形:只有一组对边平行的四边形叫做梯形。
直角梯形:有一个角是直角的梯形叫做直角梯形。
(有一条腰就是梯形的高)
等腰梯形:两条腰相等的梯形叫做等腰梯形。
(两腰相等,两底角相等)
8、平行四边形和梯形都有无数条高。
9、两个完全一样的三角形可以拼成一个平行四边形。
两个完全一样的梯形可以拼成一个平行四边形。
两个完全一样的直角梯形可以拼成一个平行四边形或长方形。
10、三角形内角和是180°,四边形内角和是360°。
四年级上册数学平行四边形和梯形 熟记知识点

第5单元:平行四边形和梯形熟记知识点【知识要点】1.同一平面内,两条直线的位置关系相交和不相交(或平行)。
2.平行3.垂直(两条直线相交的特殊情况)4.画垂线的步骤:经过直线上一点(或直线外一点)作垂线,可以画一条垂线。
经过直线外一点画平行线,可以画一条平行线。
5.两条直线分别平行于第三条直线,那这两条直线也互相平行。
(如下左图)两条直线分别垂直于第三条直线,那么这两条直线就互相平行。
(如下右图)6.从直线外一点到这条直线所画的所有线段中垂直线段最短,垂直线段的长度叫做这点到直线的距离。
“点到直线的所有线段中,垂直线段最短”这一性质可以应用到铺管道、挖水渠等工程中,从而节约成本。
7.端点分别在两条平行线上,且与平行线垂直的所有线段的长度都相等,也可以说:两条平行线之间的距离处处相等。
8.用画垂线的方法画长方形:9.平行四边形【画高时要注意:要用虚线,并标出直角符号。
】(1)平行四边形的底和高是相对应的,在平行四边形那条边上画高,那条边即为平行四边形的底。
(2)同一底上的高有无数条,它们都相等。
如图中的3条高都相等。
10.一个平行四边形,拉动对角,什么变了,什么没变,能说明什么呢?面积变了,周长没变,说明平行四边形具有不稳定性,易变形。
梯形。
12.梯形各部分名称【梯形画高时要注意:梯形只有一组对边平行,高只能画在上底和下底之间。
】13.平行四边形和梯形有无数条高。
14.特殊梯形:等腰梯形和直角梯形都是特殊的梯形。
两腰相等的梯形叫做等腰梯形。
特点:两腰相等,两底角相等。
如下左图:有一个角是直角的梯形叫做直角梯形。
特点:垂直于上下底的腰就是直角梯形的一条高。
如下右图:15.用图示法表示四边形之间的关系:长方形、正方形都是特殊的平行四边形,正方形是特殊的长方形。
16.(1)两个完全一样的梯形可以拼成一个平行四边形。
如下左图(2)两个完全一样的直角梯形可以拼成一个长方形或平行四边形。
16.三角形三个内角的和是180°,四边形四个内角的和是360°。
平行四边形和梯形知识点总结

平行四边形矩形菱形正方形梯形等腰梯形图形定义两组对边分别平行的四边形。
用“”表示平行四边形,例如:平行四边形ABCD记作ABCD,读作“平行四边形ABCD”有一个角是直角的平行四边形是矩形有一组邻边相等的平行四边形是菱形有一组邻边相等且有一个直角的平行四边形叫做正方形一组对边平行而另一组对边不平行的四边形叫做梯形两腰相等的梯形性质边对边平行(位置关系);对边相等(数量关系);对边平行(位置关系);对边相等(数量关系);对边平行;对边相等;四边相等对边平行(位置关系);对边相等(数量关系);四边相等上底(短)∥下底(长)即AB∥CD上底(短)∥下底(长)两腰相等角对角相等;邻角互补。
对角相等;邻角互补。
四角为90°。
对角相等;邻角互补。
对角相等;邻角互补。
四角为90°∠1+∠2=180°;∠3+∠4=180°∠1+∠2=180°,∠3+∠4=180°;∠1=∠3,∠2=∠4对角线对角线互相平分对角线互相平分;对角线相等。
对角线互相平分;对角线互相垂直;每一条对角线平分一组对角。
对角线互相平分;对角线相等;对角线互相垂直;每一条对角线平分一组对角。
对角线相等。
对称性中心对称图形中心对称图形;轴对称图形(对称轴为对边中点连线所在的直线,2条)中心对称图形;轴对称图形(对称轴为对角线所在位置,2条)。
中心对称图形;轴对称图形(其中2条为对称轴为对角线所在位置,另外2条为对边中点连线所在的直线)。
轴对称图形(对称轴为上底和下底中点连线所在的位置)。
判定边两组对边分别平行的四边形;两组对边分别相等的四边形;一组平行且相等的四边形;四条边都相等的四边形;有一组邻边相等的平行四边形;有一组邻边相等且有一个直角的平行四边形;邻边相等的矩形;四边相等四角相等的四边形;有一组对边平行,另外一组对边不平行的四边形对角线相等的梯形角两组对角分别相等的四边形;有一个角是直角的平行四边形;四个角都相等的四边形。
平行四边形和梯形总结

1.两组对边分别平行的四边形叫作平行四边形。
2.平行四边形有4条边,4个角,内角和是360°。
3.平行四边形有2组对边互相平行,而且长度相等。
4.从平行四边形一条边上的一点到它对边的垂直线段是平行四边形的
高,这条对边是平行四边形的底。
5.只有一组对边平行的四边形叫作梯形。
6.梯形有4条边,4个角,一组组对边平行,另一组对边不平行。
7.互相平行的一组对边分别是梯形的上底和下底,不平行的一组对边
是梯形的腰。
8.从梯形一条底边上的一点到它对边的垂直线段叫作梯形的高。
9.两腰相等的梯形叫作等腰梯形,等腰梯形是轴对称图形,有1条对
称轴。
10.有两个角是直角的梯形叫作直角梯形。
11.梯形的内角和是360°。
12.()的四边形叫作平行四边形。
13.平行四边形有()条边,()个角,内角和是
()°。
14.平行四边形有()组对边互相(),而且()。
15.从平行四边形()的一点到它对边的()是平行四
边形的高,这条对边是平行四边形的()。
16.()的四边形叫作梯形。
17.梯形有()条边,()个角,()组对边平行,另一组对
边不平行。
18.()的一组对边分别是梯形的上底和下底,()的一
组对边是梯形的腰。
19.从梯形()上的一点到它对边的()叫作梯形的
高。
20.()的梯形叫作等腰梯形,等腰梯形()轴对称图形,
有()条对称轴。
21.()的梯形叫作直角梯形。
22.梯形的内角和是()°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.平行四边形的定义:平行四边形是有两组对边分别平行的四边形。
2.平行四边形的性质:①平行四边形的对边平行且相等
②平行四边形的对角相等,两邻角互补。
③平行四边形的两条对角线互相平分
④平行四边形是空间图形
3.平行四边形的判断方法:①两组对边分别相等的四边形是平行四边形
②对角线互相平分的四边形是平行四边形
③一组对边平行且相等的四边形是平行四边形
④两组对角分别相等的四边形是平行四边形
⑤两组对边分别平行的四边形是平行四边形
4.特殊的平行四边形:矩形(长方形),菱形,正方形。
5.平行四边形的面积公式为:底×高(可以看作是矩形。
)
6.梯形:指一组对边平行而另一组对边不平行的四边形叫做梯形。
①上底、下底:平行的两边叫做梯形的底边,其中长边叫下底,短边叫
上底;
②腰:不平行的两边叫腰;
③高:夹在两底之间的垂线段叫梯形的高。
7.梯形中常见的一些判定:
①一组对边平行,另一组对边不平行的四边形是梯形(一组对边平行且不相等的四边形是梯形)
②两腰相等的梯形是等腰梯形
③同一底上的两个角相等的梯形是等腰梯形
④有一个内角是直角的梯形是直角梯形
⑤对角线相等的梯形是等腰梯形.
⑥梯形的中位线等于上底加下底和的一半,且平行于上底和下底。
8.特殊梯形的一些性质:①等腰梯形的两条腰相等
②等腰梯形在同一底上的两个底角相等
③等腰梯形的两条对角线相等
④等腰梯形是轴对称图形,对称轴是上下底中点的连线所在直线
⑤梯形的中位线(两腰中点相连的线叫做中位线)等于上下底和的二分之一
⑥直角梯形有两个角是直角
⑦对角线互相垂直的梯形面积可用两条对角线积的一半计算。
9.梯形的面积:(上底+下底)×高÷2。
