结构力学第十章总结
合集下载
结构力学教程——第10章 力法

系数和自由项 ➢ 梁、刚架:
ii
M i 2 ds
EI
Ai yi EI
ij
M i M j ds EI
Aj yi EI
iP
M i M P ds EI
➢ 桁架:
2
ii
Ni l EA
ij
Ni N jl EA
iP
Ni N Pl EA
知识点
10.3 超静定刚架和排架
1. 刚架
20kN/m
11
M12 EI
ds
FN21 EA
ds
y2
cos2
EI ds EA ds
1P
M1 M P EI
ds
M0y ds
EI
(4)求多余未知力,即水平推力FH
M0y
X1
FH
1P 11
y2 EI
EI ds
cos2
ds EA
ds
(5)内力计算
M M 0 FH y
FQ FQ0cos FHsin FN FQ0sin FHcos
1P 11X1 0
P
2P 0
P
0
a
11
2 2
1
1
1
P
a
N1
NP
(3)求系数
11
2
Ni l 2( EA
2)2 EA
2a 4 12 a EA
4a (1 EA
2)
1P
Ni N jl 1 Pa 2 EA EA
(
2 )( EA
2P)
2a 2Pa (1 EA
2)
(4)解方程
X1
1P
11
P 2
当结构框格数目为 f , 则 n=3f 。
结构力学 (10)

1 0 - 1 移动荷载和影响线的概念
1.移动荷载
方向、大小不变,作用位置变化的荷载称为移动荷载。最常见的移动荷 载有上面提到的吊车梁上行驶的吊车、桥梁上行驶的汽车等。移动荷载作用 下结构会发生振动,严格来说它是动荷载,应按动力学方法分析,但为了简 化计算通常按静荷载计算,动力效应通过冲击系数考虑。囚此本章只考虑移 动荷载在不同位置时对结构的影响,不考虑动力效应,即认为无论移动荷载 作用于结构的任何位置结构都是平衡的,可以按静力学方法分析。
10-1 移动荷载 和影响线 的概念
10-2 静力法作 静定梁影 响线
10-3 静力法作 结点荷载 作用下主 梁影响线
10-4 静力法作 静定析架 影响线
10-5 机动法作 静定梁影 响线
10-6 机动法作 连续梁影 响线
10-7 固定荷载作 用下利用影 响线求内力 和支座反力
10-8 确定最不 利荷载位 置
1 0 - 4 静力法作静定析架影响线
1 0 - 5 机动法作静定梁影响线
1 0 - 6 机动法作连续梁影响线
1 0 - 6 机动法作连续梁影响线
1 0 - 6 机动法作连续梁影响线
1 0 - 6 机动法作连续梁影响线
机动法作连续梁某量S影响线的步骤为:
1
解除与S对应的约束,代以正向S
2
2.简支梁弯矩影响线
1 0 - 2 静力法作静定梁影响线
1 0 - 2 静力法作静定梁影响线
1 0 - 2 静力法作静定梁影响线
1 0 - 2 静力法作静定梁影响线
3.简支梁剪力影响线
1 0 - 2 静力法作静定梁影响线
1 0 - 2 静力法作静定梁影响线
1 0 - 3 静力法作结点荷载作用下主梁影响线
结构力学专题七(单自由度体系的动力计算)

设: 2
k11 m
1
m11
运动方程: y(t) 2 y(t) 0
1、运动方程的解
y(t) c1sin t c2 cos t
(a)
或 y(t) csin( t )(ຫໍສະໝຸດ )当 y0、y0 为已知时
y(t)
y 0
sin
t
y
0
cos
t
(c)
方程(a)、(b)、(c)称为位移方程。
2、位移方程的几何意义
A1 5cm2
W 0.1kN
3m
(1)求竖向振动时的频率和周期,
(2)设: y0 10cm(向下),y0 0;
求: t
4
90
时质体的绝对位移。
A2 10cm2
4m
补2(选作):求图示体系的自振频率:
m
EI
m
k
l
l
l EI
FP (t)
EI
l/2 l/2
三、举例与讨论
例1: 建立图示体系运动微分方程 FP (t)
m EI
l/2 l/2
方程:
L3 48EI
(my(t)
cy(t))
y(t)
L3 48EI
FP (t)
my(t) cy(t)
48EI L3
y(t)
FP (t)
例2: 建立图示体系运动微分方程
FP (t)
EI0
m
h EI
EI
方程:
my(t) cy(t)
m
EI FP (t)
l/2 l/2
例3: 求图示体系的自振频率。
FP (t)
EI0
m
h EI
EI
结构力学第10章动力学2
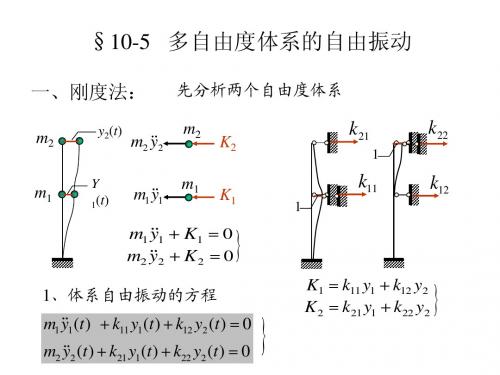
2、方程的解:
设解的形式: y1 (t ) = Y1 sin(ωt + α ) y2 (t ) = Y2 sin(ωt + α )
惯性力 − m1 &&1 (t ) = m1ω 2Y1 sin(ωt + α ) y 2 − m2 &&2 (t ) = m2ω Y2 sin(ωt + α ) y
k12 M kn2
L
k1n k2n M =0
k 22 − ω 2 m2 L
L k nn − ω 2 mn
n个ω 2的解对应n各ω:ω1 < ω2 < Lωn
ω1 − − − 第一频率或基本频率
3、振型
对应于ωi,其质点的振幅比值是常数,所以有n各振型: Y11 Y12 Y1n Y Y Y Y 1 = 21 ;Y 2 = 22 LY n = 2 n M M M Yn1 Yn 2 Ynn CY1i Y1i CY Y 2i 2i i i 则:CY = 若Y = L L Yni CYni 为方程(K − ω 2 M)Y = 0的解 也为方程的解
( K − ω12 M )Y 1 = 0 17.414Y11 − 5Y21 + 0 × Y31 = 0 − 5Y11 + 6.707Y21 − 3Y31 = 0 0 × Y11 − 3Y21 + 1.707Y31 = 0
令:Y31 = 1;求得: Y21 = 0.569;Y11 = 0.163 0.163 第一振型:Y 1 = 0.569 1
ω2 = (
1 k11 k 22 1 k k k k −k k + ) ± [ ( 11 + 22 )]2 − 11 22 12 21 2 m1 m2 2 m1 m2 m1m2
结构力学第十章总结

D. 16EI/l
解:答案选A。
EI y 1 l 1.5 l 2 2EI x
中南大学
退出
返回
10:49
总
结
结构力学
例:矩阵位移法中,结构的原始刚度方程是表示下 列两组量值之间的相互关系:( ) A.杆端力与结点位移 C.结点力与结点位移 解:答案选C。 例:平面杆件结构用后处理法建立的原始刚度方程 组,( ) A.可求得全部结点位移 B.可求得可动结点的位移 B.杆端力与结点力 D.结点位移与杆端力
退出
返回
10:49
总
结
结构力学
对于支座位移等于给定值时,采用“乘大数法”。 设结点位移向量中第 r个位移等于d0,在矩阵K与向量P中, , 主对角元素krr 改为Gkrr,将Pr改为d0Gkrr,其中G为一 大数通常取108~1010 。
中南大学
退出
返回
10:49
总
结
结构力学
2. 先处理法 (1) 集成。将单元刚度矩阵先按边界条件进行处理 , 然后按照单元连接结点的总位移编号将单元刚度矩阵的 元素在结构的刚度矩阵中对号入座,形成总刚后即可进 行求解。上述过程可通过引入定位向量来实现。在单元 定位向量中考虑边界条件,凡给定的结点位移分量,其 位移总码均编为零,与总码编为零相应的行、列元素在 集成总刚时被屏弃在外。 单元定位向量:按单元连接结点编号顺序由结点未 知位移编号组成的向量。
中南大学
退出
返回
10:49
总
结
结构力学
表 8-1 一 般 位 移 法 矩 阵 位 移 法 1. 写出各杆的转角位移方程 1.列出各单元的单元刚度矩 阵和单元刚度方程 2.考虑结点和截面平衡建立 2.由各单元刚度矩阵装配总 位移法典型方程 刚度矩阵 3.解方程求结点位移 3.考虑约束条件建立结构刚 度方程并求解
解:答案选A。
EI y 1 l 1.5 l 2 2EI x
中南大学
退出
返回
10:49
总
结
结构力学
例:矩阵位移法中,结构的原始刚度方程是表示下 列两组量值之间的相互关系:( ) A.杆端力与结点位移 C.结点力与结点位移 解:答案选C。 例:平面杆件结构用后处理法建立的原始刚度方程 组,( ) A.可求得全部结点位移 B.可求得可动结点的位移 B.杆端力与结点力 D.结点位移与杆端力
退出
返回
10:49
总
结
结构力学
对于支座位移等于给定值时,采用“乘大数法”。 设结点位移向量中第 r个位移等于d0,在矩阵K与向量P中, , 主对角元素krr 改为Gkrr,将Pr改为d0Gkrr,其中G为一 大数通常取108~1010 。
中南大学
退出
返回
10:49
总
结
结构力学
2. 先处理法 (1) 集成。将单元刚度矩阵先按边界条件进行处理 , 然后按照单元连接结点的总位移编号将单元刚度矩阵的 元素在结构的刚度矩阵中对号入座,形成总刚后即可进 行求解。上述过程可通过引入定位向量来实现。在单元 定位向量中考虑边界条件,凡给定的结点位移分量,其 位移总码均编为零,与总码编为零相应的行、列元素在 集成总刚时被屏弃在外。 单元定位向量:按单元连接结点编号顺序由结点未 知位移编号组成的向量。
中南大学
退出
返回
10:49
总
结
结构力学
表 8-1 一 般 位 移 法 矩 阵 位 移 法 1. 写出各杆的转角位移方程 1.列出各单元的单元刚度矩 阵和单元刚度方程 2.考虑结点和截面平衡建立 2.由各单元刚度矩阵装配总 位移法典型方程 刚度矩阵 3.解方程求结点位移 3.考虑约束条件建立结构刚 度方程并求解
结构力学课后答案第10章结构动力学

对于CD杆件,相当于在中点作用一集中力
10-34试说明用振型分解法求解多自由度体系动力响应的基本思想,这一方法是利用了振动体系的何种特性
10-35试用振型分解法计算题10-32。
解:
刚度矩阵 质量矩阵
其中
由刚度矩阵和质量矩阵可得:
则 应满足方程
其稳态响应为:
同理:
显然最大位移
10-36试用振型分解法计算题10-31结构作有阻尼强迫振动时,质量处的最大位移响应。已知阻尼比ξ1=ξ2=。
得振型方程:
)
,令
,由频率方程D=0
解得: ,
,
(c)
解:
图 图
(1) , ,
(2)振型方程
。
令 ,频率方程为:
(3)当 时,设
当 时,设
绘出振型图如下:
第一振型 第二振型
(d)
解:
#
图 图
频率方程为:
取 代入整理得:
其中
~
振型方程为:
将 代入(a)式中的第一个方程中,得:
绘出振型图如下:
第一振型 第二振型
\
解:
若 为静力荷载,弹簧中反力为 。
已知图示体系为静定结构,具有一个自由度。设为B点处顺时针方向转角 为坐标。建立动力方程:
则弹簧支座的最大动反力为 。
10-21设图a所示排架在横梁处受图b所示水平脉冲荷载作用,试求各柱所受的最大动剪力。已知EI=6×106Nm2,t1=,FP0=8×104N。
(a)
设 ,
;
使 ,则
(2)
设
如果使速度响应最大,则 最大,设 ,显然要求 最小。使: 得 。
(3)
令 显然要求 最小。
则 解的:
10-34试说明用振型分解法求解多自由度体系动力响应的基本思想,这一方法是利用了振动体系的何种特性
10-35试用振型分解法计算题10-32。
解:
刚度矩阵 质量矩阵
其中
由刚度矩阵和质量矩阵可得:
则 应满足方程
其稳态响应为:
同理:
显然最大位移
10-36试用振型分解法计算题10-31结构作有阻尼强迫振动时,质量处的最大位移响应。已知阻尼比ξ1=ξ2=。
得振型方程:
)
,令
,由频率方程D=0
解得: ,
,
(c)
解:
图 图
(1) , ,
(2)振型方程
。
令 ,频率方程为:
(3)当 时,设
当 时,设
绘出振型图如下:
第一振型 第二振型
(d)
解:
#
图 图
频率方程为:
取 代入整理得:
其中
~
振型方程为:
将 代入(a)式中的第一个方程中,得:
绘出振型图如下:
第一振型 第二振型
\
解:
若 为静力荷载,弹簧中反力为 。
已知图示体系为静定结构,具有一个自由度。设为B点处顺时针方向转角 为坐标。建立动力方程:
则弹簧支座的最大动反力为 。
10-21设图a所示排架在横梁处受图b所示水平脉冲荷载作用,试求各柱所受的最大动剪力。已知EI=6×106Nm2,t1=,FP0=8×104N。
(a)
设 ,
;
使 ,则
(2)
设
如果使速度响应最大,则 最大,设 ,显然要求 最小。使: 得 。
(3)
令 显然要求 最小。
则 解的:
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第10章 矩阵位移法【圣才出品】

二、单元刚度矩阵(见表 10-1-2) ★★★★★ 表 10-1-2 单元刚度矩阵
2 / 46
圣才电子书
十万种考研考证电子书、题库视频学习平 台
3 / 46
圣才电子书
十万种考研考证电子书、题库视频学习平 台
三、单元刚度矩阵的坐标转换(见表 10-1-3) ★★★★★ 表 10-1-3 单元刚度矩阵的坐标转换
6.结构的总刚度方程的物理意义是什么?总刚度矩阵的形成有何规律?其每一程的物理意义:尚未进行支承条件处理的表示所有结点外力与 结点位移之间的关系的平衡方程。
(2)总刚矩阵的形成规律:把每个单元刚度矩阵的四个子块按其两个下标号码逐一
9 / 46
圣才电子书
十万种考研考证电子书、题库视频学习平
台
4.为何用矩阵位移法分析时,要建立两种坐标系?
答:在利用矩阵位移法分析结构的时候,要进行单元分析和整体分析,单元分析是为
了建立每个单元的单元刚度矩阵,整体分析是为了建立整体结构的刚度方程。在单元分析
的过程中,以各单元的轴线为局部坐标系的 x 轴,以垂直轴线的方向为局部坐标系的 y 轴,
台
送到结构原始刚度矩阵中相应的行和列的位置上去,就可得到结构原始刚度矩阵,即各单
刚子块“对号入座”形成总刚。
(3)每一元素的物理意义:当其所在列对应的结点位移分量等于 1(其余各结点位移
分量均为零)时,所引起的其所在行对应的结点外力分量的数值。例如 Kij 表示第 j 号位置
3.矩阵位移法中,杆端力、杆端位移和结点力、结点位移的正负号是如何规定的? 答:杆端力沿局部坐标系的、的正方向为正,杆端弯矩逆时针为正;杆端位移的正负 号规定同杆端力和弯矩。结点力沿整体坐标系 x、y 的正方向为正,结点力偶逆时针为正; 结点位移的正负号规定同结点力和力偶。
结构力学 第10章 (四川大学)解析

三、动力计算中体系的自由度
结构动力分析是以质点的位移为基 本未知量。
动力自由度定义为: 在振动过程的任一时刻,确定体系全 部质量位置所需的独立几何参数数目,称 为该体系的动力自由度。
集中质量法
由于实际结构的质量都是连续分布的,因此任何一 个实际结构都可以说具有无限个自由度体系。
将结构的分布质量按一定规则集中到结构的某个 或某些位置上,从而将无限自由度体系简化为有限自 由度体系。
(2) 取隔离体如图所示。
FS
Fb
m
FI
FP (t)
图中惯性力、阻尼力和
第二,这里考虑的是瞬时的平衡,荷载、 内力等都是时间的函数。
二、 动力荷载的分类
(1) 周期荷载:这类荷载随时间作周期性变化, 如图所示。例如船舶中螺旋桨产生的作用于船体 的推力就是一种周期荷载。显然,简谐荷载也属 于周期荷载。
(2)冲击荷载:其特点是荷载值在短时间内急 剧增大或者是荷载值急剧减小,如各种爆炸荷 载。
(3)采用集中质量法和广义坐标法都可使无限 自由度体系简化为有限自由度体系,它们所采用 的手法是不同的。
集中质量法:将结构的分布质量按一定规则集
中到结构的某个或某些位置上,认为其他地方没 有质量。质量集中后,结构杆件仍具有可变形性 质,称为“无重杆”。
10.2 单自由度体系运动方程的建立
研究单自由度的目的: 单自由度体系的动力分析虽然比较简单,但 非常重要。这是因为: (1) 很多实际的动力问题常可按单自由度 体系进行计算,或进行初步的估算。 (2)单自由度体系的动力分析是多自由度 体系动力分析的基础。
体系的运动方程
根据达朗贝尔原理
引入惯性力
建立瞬时平衡方程
从平衡的角度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中南大学
退出
返回
10:49
总
结
结构力学
例如图示刚架,按图a 编码,d=3×(9+1)=30 ,而按 b 图编码,d=3×(3+1)=12 。
(a) 1 10 19 (b) 1 2 3 5 6 11 20 4 8 9 2 3 12 21 7 4 13 22 10 11 12 5 14 23 13 14 15 6 15 24 16 17 18 7 16 25 19 20 21 8 17 26 22 23 24 9 18 27 25 26 27
C. 108EI / l 3
2(1,0,2) 2 EI 2 EI 4(0,0,0) 1(0,0,0) 3(1,0,3)
EI l/ 2 l/ 2
D. 120EI / l
3
解:答案选D。
2l
提示:在不考率轴向变形时, 结点2和结点3只有水 平位移和转角,杆件12对k11的贡献为12×(2EI)/l 3, 杆件34对k11的贡献为12×EI/(l/2)3。
中南大学
退出
返回
10:49
总
结
结构力学
(2)边界条件处理。对于刚性支座,其位移总码均 编为零。对于支座位移等于给定值时,通常也将其位移 总码均编为零,将支座结点位移的影响转换成单元非结 点荷载,即,将支座结点位移转换成与该支座结点位移连 接的各单元在单元坐标系中的杆端位移,求出由此给定 的杆端位移产生的单元固端力,然后转换成等效结点荷 载。 3. 弹性支座的处理 通常用主对角元素叠加法处理弹性支座。如果结构 的第j个自由度是弹性约束,那么,把弹性支座的刚度系 数叠加到原始刚度矩阵主对角线的第j个元素上即可得到 经约束处理后的总刚度方程。
设结点位移向量中第r个位移等于零, 即r=0 ,则在 结构的原始刚度矩阵k中的第r行第r列中主对角元素krr改 为1其余元素改为零。同时将结点结点荷载列向量 P中的 第r个分量也改为零。 即 k rr 1 k rs k sr 0 ( s r ) Pr 0
中南大学
中南大学
退出
返回
10:49
总
结
结构力学
例:用矩阵位移法计算图a所示连续梁,并画M图, EI=常数。q=12kN/m,l=6m。
(a) q (b) (1) l l l
θ
1
(2)
θ
2
(3)
1
2
y
x
解: (1) 建立坐标系、对单元和结点编号如图 b,单 元刚度矩阵 (1) 4i 2i ( 2) ( 3) k k k 2 i 4 i 单元定位向量λ①=(0 1)T,λ②=(1 2)T,λ③=(2 0)T (2) 将各单元刚度矩阵中的元素按单元定位向量在K中 对号入座,得整体刚度矩阵 8i 2i K 2 i 8 i
D. 16EI/l
解:答案选A。
EI y 1 l 1.5 l 2 2EI x
中南大学
退出
返回
10:49
总
结
结构力学
例:矩阵位移法中,结构的原始刚度方程是表示下 列两组量值之间的相互关系:( ) A.杆端力与结点位移 C.结点力与结点位移 解:答案选C。 例:平面杆件结构用后处理法建立的原始刚度方程 组,( ) A.可求得全部结点位移 B.可求得可动结点的位移 B.杆端力与结点力 D.结点位移与杆端力
中南大学
退出
返回
10:49
总
结
结构力学
5. 总刚度矩阵的最大半带宽 总刚度矩阵的上三角部分,从某行的主对角元素到该 行最末一个非零元素所具有的元素的个数称为该行的半带 宽。各行半带宽的最大值称为总刚度矩阵的最大半带宽。 对应于后处理法,结构内部不存在组合结点时最大半 带宽的计算公式为:d=(b+1)c ,其中b为单元两端结点编码 的最大差; c为结构中一个结点的位移分量数,显然,最 大半带宽与结构的结点编码的顺序有关。通常应使相邻结 点编码的最大差值为最小,即d 值为最小。
退出
返回
10:49
总
结
结构力学
对于支座位移等于给定值时,采用“乘大数法”。 设结点位移向量中第 r个位移等于d0,在矩阵K与向量P中, , 主对角元素krr 改为Gkrr,将Pr改为d0Gkrr,其中G为一 大数通常取108~1010 。
中南大学
退出
返回
10:49
总
结
结构力学
2. 先处理法 (1) 集成。将单元刚度矩阵先按边界条件进行处理 , 然后按照单元连接结点的总位移编号将单元刚度矩阵的 元素在结构的刚度矩阵中对号入座,形成总刚后即可进 行求解。上述过程可通过引入定位向量来实现。在单元 定位向量中考虑边界条件,凡给定的结点位移分量,其 位移总码均编为零,与总码编为零相应的行、列元素在 集成总刚时被屏弃在外。 单元定位向量:按单元连接结点编号顺序由结点未 知位移编号组成的向量。
4.将结点位移回代到转角位 4.将结点位移回代到各单元 移方程中求杆端弯矩 的单元刚度方程中求杆端内 力
中南大学
退出
返回
10:49
总
结
结构力学
一、基本概念
结构矩阵分析是采用矩阵方法分析结构力学问题的一 种方法。与传统的力法、位移法相对应,在结构矩阵分析 中也有矩阵力法和矩阵位移法,或柔度法与刚度法。矩阵 位移法易于实现计算过程程序化而被广泛应用。 矩阵位移法是结构力学中的位移法加上矩阵方法。矩 阵位移法的基本未知量也是结点位移——独立的线位移和 转角。但由于有时考虑杆件的轴向变形,且把杆件铰结端 的转角也作为基本未知量,因此,基本未知量数目比传统 位移法的基本未知量多一些。
中南大学
退出
返回
10:49
总
结
结构力学
二、总刚度矩阵的集成及约束处理
集成总刚度矩阵最常用的方法是直接刚度法,即由单 元刚度矩阵直接集成结构刚度矩阵,又可分为后处理法和 先处理法。 1. 后处理法 (1) 集成。对所有单元不做边界条件处理,均采用自 由式的单元刚度矩阵,按单元的结点编号将单元刚度矩 阵分为四个子块(阶数相同),逐块地将结点所对应的 子块在结构的原始刚度矩阵中对号入座,形成结构的原 始刚度矩阵。由于结点位移分量中包括了非自由结点的 已知位移,原始刚度矩阵为奇异的,需进行边界条件处 理,才能求解自由结点位移。由于原始刚度矩阵的阶数 较高,所以后处理法的主要缺点是占用较多的计算机内 存。
A. (0 0 1 2 3 4)T C. (0 0 1 3 2 4)T 解:答案为B。
B. (2 3 4 0 0 1)T
D. (3 2 4 0 0 1)T
中南大学
退出
返回
10:49
总
结
结构力学
例: 图示结构整体刚度矩阵K中元素k22等于( ) A. 28EI/3l B. 12EI/l C. 20EI/3l
中南大学
退出
返回
10:49
总
结
ql 2 F 12 0
结构力学
(3) 连续梁的等效结点荷载
(4) 将整体刚度矩阵K和等效结点荷载P代入基本方程得
8i 2i
2 ql 2i 1 12 8i 2 0
中南大学
退出
返回
10:49
总
结
结构力学
4. 总刚度方程和总刚度矩阵的性质与特点
总刚度方程为整体结构的结点荷载与结点位移之间 的关系式,是结构应满足的平衡条件。无论何种结构, 其总刚度方程都具有统一的形式:
K=P 式中K为总刚度矩阵,为结构的结点位移列向量,P 为结点力列向量。 总刚度矩阵K反应了整个结构的刚度,是描述结点 力与结点位移之间关系的系数矩阵。其矩阵的性质与 特点:
中南大学
退出
返回
10:49
总
结
结构力学
二、需要注意的几个问题
(1)初学者易把单元的固端力与传统位移法中载常 数混淆,造成求等效荷载时出错。单元的固端力是在固 定单元的杆端其不能有任何位移时荷载作用下的杆端力 (即固端力)。 例如,对于梁式杆,不论连接该杆的结点是铰结点、 定向结点,均按两端固定梁计算固端力。 (2)在考虑轴向变形的单元刚度矩阵中剔除 EA项, 即得忽略轴向变形的单元刚度矩阵。 (3)为适应计算机计算、节省内存和机时,在对 结点编号时应力求使相关结点的最大差值为最小,以减 小总刚度矩阵的带宽。
中南大学
退出
返回
10:49
总
结
结构力学
对于每个结点位移分量数相同的结构,原始刚度矩 阵的阶数为结构的总结点数乘以结点位移分量的数目, 例如,每个结点位移分量数为3的平面刚架,结构原始 刚度矩阵的阶数为3n×3n 。
中南大学
退出
返回
10:49
总
结
结构力学
(2)边界条件处理
对于刚性支座,用划行划列法处理刚性支座,即直 接划去原始刚度方程中与零位移对应的行和列。这样做 有时要改变原方程的排列顺序,会给编程带来麻烦。为了 不改变原方程的排列顺序,同时又要引入边界条件 ,采用 “主一副零”法。
中南大学
退出
返回
10:49
总
结
结构力学
矩阵位移法的基本思路是:
(1) 先把结构间的关系; (2)在单元分析的基础上,考虑结构的几何条件和平衡 条件,将这些离散单元组合成原来的结构,进行整体分析, 建立结构的结点力与结点位移之间的关系,即结构的总刚 度方程,进而求解结构的结点位移和单元杆端力。 在从单元分析到整体分析的计算过程中,全部采用矩 阵运算。
中南大学
退出
返回
10:49
总
结
结构力学
表 8-1 一 般 位 移 法 矩 阵 位 移 法 1. 写出各杆的转角位移方程 1.列出各单元的单元刚度矩 阵和单元刚度方程 2.考虑结点和截面平衡建立 2.由各单元刚度矩阵装配总 位移法典型方程 刚度矩阵 3.解方程求结点位移 3.考虑约束条件建立结构刚 度方程并求解
