第一章 气 体
理科物理化学章气体
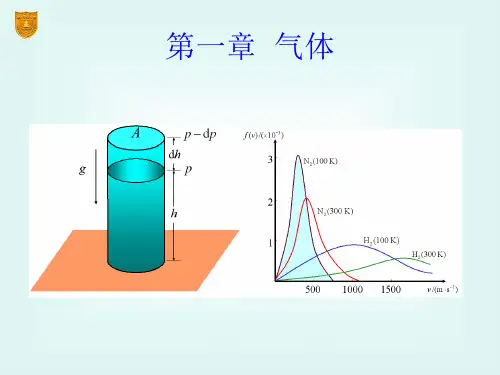
对理想气体 VB= nB R T /P 对真实气体不适用。
§1.2 摩尔气体常数(R)
pVm / T J mol1 K1 R 8.3145
8
6
4
图1.4(a)
理想气体
T3 (531K) T2 (410K) T1(333K)
2
10
20
a Vm2
)(Vm
RT bp
b) RT
a ab Vm Vm2
高温时,忽略分子间的引力(忽略含a的项)
pVm RT bp
pVm > RT
低温时,压力又比较低,忽略分子的体积(含b项)
pVm
RT
a Vm
pVm < RT
当压力增加到一定限度后,b的效应越来越显著, 又将出现 pVm > RT 的情况。这就是在Boyle温度以下 时, pVm 的值会随压力先降低,然后升高。
p
3 pcVm2,c Vm2
Vm
Vm,c 3
8 3
pcVm,c Tc
T
p pc
3Vm2,c Vm2
Vm Vm,c
1 3
8T 3 Tc
对比状态和对比状态定律
p pc
3Vm2,c Vm2
Vm Vm,c
1 3
8 3
T Tc
定义: p
pc
Vm
Vm,c
T
Tc
代入上式,得van der Waals 对比状态方程
(2)当温度升到30.98℃时,等温线的水平部分缩 成一点,出现拐点,称为临界点。在这温度以上无 论加多大压力,气体均不能液化。
(3)在临界点以上,是气态的等温线,在高温或 低压下,气体接近于理想气体。
物理化学 第一章 绪论气体

物理化学讲课的内容
第一章 气体的pVT关系 第二章 热力学第一定律 第三章 热力学第二定律 第四章 多组分热力学 第五章 相平衡
3-10周 讲课 40 h
第六章 化学平衡 第七章 电化学 第八章 化学动力学 第九章 界面现象与
描述真实气体的 pVT 关系的方法: 1)引入压缩因子Z,修正理想气体状态方程 2)引入 p、V 修正项,修正理想气体状态方程 3)使用经验公式,如维里方程,描述压缩因子Z 它们的共同特点是在低压下均可还原为理想气体状态方程
1. 真实气体的 pVm - p 图及波义尔温度
T > TB
pVm - p曲线都有左图所示三种
c
T4
说明Vm(g) 与Vm(l)之差减小。
l2 l1
l
g2 g1
T3
Tc
TT12gg´´12 g
T = Tc时, l – g 线变为拐点c c:临界点 ;Tc 临界温度; pc 临界压力; Vm,c 临界体积
Vm
临界点处气、液两相摩尔体积及其它性质完全相同,界
面消失气态、液态无法区分,此时:
V p m Tc 0 ,
类型。
pVm
T = TB T < TB
(1) pVm 随 p增加而上升; (2) pVm 随 p增加,开始不变, 然后增加
p 图1.4.1 气体在不同温度下的 pVm-p 图
(3) pVm 随 p增加,先降后升。
T > TB T = TB
对任何气体都有一个特殊温度 -
波义尔温度 TB ,在该温度下,压
(密闭容器)
水
乙醇
苯
t / ºC 20 40 60 80 100 120
物理化学第五版_01章_气体
学平均速率与根均方速率
Maxwell 速率分布定律 设容器内有N个分子,速率在 v v dv 范围内的分子数为 d N v
则
d Nv Ndv
或
d Nv Nf (v)dv
f (v) 称为分子分布函数,
力却是一个定值,并且是一个宏观可测的物理量。
对于一定量的气体,当温度和体积一定时, 压力具有稳定的数值。 压力p是大量分子集合所产生的总效应,是 统计平均的结果。
压力和温度的统计概念
aa' , bb' 是两个半透膜
aa ' 只允许A分子出入
bb ' 只允许B分子出入
在中间交换能量,直至
双方分子的平均平动能相等
是摩尔气体常数,等于
是热力学温度,单位为 K
T (t /℃ 273.15)K
气体分子动理论的基本公式 气体分子的微观模型 (1)气体是大量分子的集合体 (2)气体分子不停地运动,呈均匀分布状态 (3)气体分子的碰撞是完全弹性的 设在体积为V的容器内,分子总数为N,单位体 积内的分子数为n(n = N/V),每个分子的质量为m。 令:在单位体积中各群的分子数分别是 n1 ,n2 , … 等。则
n1 n2 ni ni n
i
气体分子动理论的基本公式 设其中第
i
群分子的速度为
u i ,它在 x, y, z
轴方向上的分速度为
2 ui 2 ui , x
ui, x , ui, y , ui, z ,则
2 ui , z
2 ui , y
在单位时间内,
在
无机及分析化学第一章第一节气体

例 1-3
• 在 25 ℃下,将 0.100m ol 的 O 2 和 0.350mol 的 H 2 装入 3.0 0L 的容器中,通电后氧气 和氢气反应生成水,剩下过量的氢气。求反应前后气体的总压和各部分的分压。 •
解:反应前 0.100mol 8.315kPa L mol-1 K -1 298K p(O 2) 82.6kPa 3.00L 0.350mol 8.315kPa L mol-1 K -1 298K p(H 2) 289kPa 3.00L p 82.6kPa 289kPa 372kPa( 四舍五入) 通电时0.100mol O 2只与0.200molH2 反应生成0.200molH2 O,而剩余0.150molH 2。 液态水所占的体积与容 器体积相比可忽略不计 ,但由此产生的饱和水 蒸气却必须考虑。 因此反应后 0.150mol 8.315kPa L mol-1 K -1 298K p(H 2) 124kPa 3.00L P(H 2 O) 3.17kPa p 124kPa 3.17kPa 127kPa(四舍五入)
无机及分析 化学
第一章 气体和溶液
1.1 气体 1.1.1 理想气体状态方程
概念:分子本身不占体积,分子间没有相互作用力的气体称为理想气体。 低压状态下可以看做理想气体,所遇到的实际情况都不是理想气体。 理想气体状态方程: pV=nRT p 代表了气体的压力 V 代表了气体的体积
T 代表了气体的温度
• 解:
mRT 0.118g 8.315kPa L mol-1 K -1 298K -1 M 16 . 0 g mol pV 73.3kPa 250 10-3 L 所以该气体的相对分子 质量为 16.0g mol-1。
无机及分析化学第一章 气体、溶液和胶体

设有一混合气体,有 i个组分,pi和ni分别表示各组 分的分压力和物质的量,V为混合气体的总体积,则
pi=(ni/V) ·RT p=pi=(ni/V)·RT =(n/V)·RT pi/p=ni/n pi = ( ni/n )·p
第二节 溶 液
第一章第二节
广义地说,两种或两种以上的物质均匀混合而且彼 此呈现分子(或离子或原子)状态分布者均称为溶液, 溶液可以气、液、固三种聚集状态存在。
ppb(十亿分浓度):表示溶质的质量占溶液质量 的十亿分之几,即每kg溶液中所含溶质的g数。如:
1ppb:1g/1,000,000,000g溶液=1g溶质/1kg溶液。 8ppb:8g/1,000,000,000g溶液=8g溶质/1kg溶液。
例 题 1-1
第一章第二节
在100 mL水中,溶解17.1 g蔗糖(C12H22O11),溶液 的密度为1.0638 g ·mL1,求蔗糖的物质的量浓度、质 量摩尔浓度、摩尔分数各是多少?
LOGO
无机及分析化学第一章 气体、溶液和胶体
化学学科的分类
1. 无机化学 2. 分析化学 3. 有机化学 4. 物理化学 5. 高分子化学
化学学科的重要性
化学学科与其它学科的相互渗透,形成新 的学科,如生物化学、环境化学、环境分析化 学、食品化学、农药化学、土壤化学、植物化 学、配位化学、放射化学等。
第一章第二节
在100 mL水中,溶解17.1 g蔗糖(C12H22O11),溶液 的密度为1.0638 g ·mL1,求蔗糖的物质的量浓度、质 量摩尔浓度、摩尔分数各是多少?
解:
( 2 )b ( C 1 2 H 2 2 O 1 1 )= n ( C m 1 ( 2 H H 2 2 O 2 O ) 1 1 ) 1 0 0 0 .0 1 5 0 3 0 .5 m o lk g 1
《物理化学》第一章 气体

K
l C
图1-1 CO2 定温p-Vm,c 图
图中,每条曲线称为 p-V 等温线,K点所处状态称为临界状态。
以温度T1为例,曲线分为三段: {p}Leabharlann T1T2TcT3 c
加压
g(气体)
体积缩小
a(饱和气体) l
定压 a(饱和气体)体积显著缩小 b(饱和液体) 加压 b(饱和液体) 体积缩小(较小) l(液体)
ni ni 摩尔分数xi n ni
(2)Amagat分体积定理:V= Vi
(恒温、恒压下混合气体总体积等于组成混合气体的各个气 体的体积之和)
T,p相同,某一气体的体积为 Vi=xi V
压力分数、体积分数和摩尔分数的相互关系
pi Vi ni yi p V n
适用于理想气体与低压下的真实气体
对应状态:两种气体的Tr,pr和Vr中有两个参数相等,称这
两种气体处于对应状态。
Z f Tr , pr
各种气体处于对应状态下,它们对理想行为的偏离程度相同 压缩因子图: 在相同Tr下, 不同气体的Z对pr作图基本上都在一条 曲线上, 称为压缩因子图。对于除H2,He,Ne以外 的其它物质都适用。 H2,He,Ne等的Tr,pr需按下式定义后才能适用
p /kPa pr pC /kPa 810 .6 kPa
T /K Tr TC /K 8
实际气体物态方程
pVm ZnRT
理想混合气体的物态方程
(1)Daolton分压定理:P=pi
(恒温、恒容下混合气体总压P等于组成混合气体的各个气 体 的压力之和) T,V相同,某一气体的压力为 pi=xi P
在Tc下使气体液化所施加的最小压力。
临界体积Vc,m (Critical molar volume)
无机化学第一章气体
无机化学第一章气体
p1
n1 RT V
,
p2
n2 RT V
,
pn 1 V R T n 2 V R T n 1n 2 R VT
n =n1+ n2+
p
nRT V
无机化学第一章气体
分压的求解:
pB
nB RT V
p
nRT V
pB p
nB n
xB
pB
nB n
规律:各组分气体分别遵循理想气体状态方程。 即: PVB = nBRT
分体积定律:混合气体的总体积等于混合气体中
各组分气体的分体积之和。
V = V1 + V2 +
或
V = VB
无机化学第一章气体
V n1RT n2 RT
p
p
n1
n2
RT
p
nRT p
VB V
nB n
B
—称为组分B的体积分数
pB p
xB
VB V
B
,
VB B V
结论:某组分气体的分体积等于混合气体的总体 积和该组分气体的体积分数(摩尔分数)的乘积。
Zn(s) + 2HCl ZnCl2 + H2(g)
65.39g
1mol
m(Zn)=?
0.0964mol
m(Zn) =
65.39g 0.0964mol 1mol
= 6.30g
答:(略)
无机化学第一章气体
*1.2.2 分体积定律
分体积: 混合气体中某一组分B的分体积VB是该组
份单独存在并具有与混合气体相同温度和压力 时所占有的体积。
无机及分析化学——第一章 气体和溶液
依数性来源于分散微粒间距离远,作用力小。
通常所说的“依数性”,包括四个方 面: • 蒸气压下降 (The lowering of the vapor pressure)
• 沸点升高 (The elevation of the boiling point)
• 凝固点降低 (The depression of the freezing point) • 渗透压 (The phenomenon of osmotic pressure)
c)粗分散系:
1000 nm (> 10-6 m), 例如:泥浆水(悬浊液)、牛奶、豆 浆等。肉眼或在显微镜下可观察到微粒,静置易沉淀,是一种 不稳定的体系。
相与界面
相(phase):体系中物理性质和化学性质完全相同的部分。 相界面(简称界面,interface):将相与相分隔开来的部分。 相与相之间在指定的条件下具有明确的界面,在界面两边体 系的性质会有突跃变化。处于界面上的原子或分子的受力情况 与相内部的不同,往往存在剩余引力,具有界面能。一般来说, 体系中存在的界面越多,能量就越高,体系也越不稳定。
体来说,只要温度不是太低(高温,高于273K),压力不
是太高(低压 , 低于数百 kPa ),都可以近似用理想气体 状态方程作有关p、V、T、n 的计算。
2. 理想气体状态方程
理想气体的温度(T)、压力(p)、体积(V)和物质的 量(n)之间, 具有如下的方程式关系: pV = nRT 在SI制中,p—Pa,V—m3,T—K,n—mol。 标准状况(p=101.325 kPa,T=273.15 K)下,1 mol 气 体的标准摩尔体积为 22.414×10-3 m3 ,摩尔气体常数 R 的 单位及数值为: pV 1.01325 105 Pa 22.414 103 m3
无机化学第一章气体
P理想 = P实际 + a(n/V)2
例题:分别按理想气体状态方程和范德华方程计算 1.50mol SO2在30摄氏度占有20.0L体积时的压力,并 比较两者的相对误差dr。如果体积减少为2.00L,其 相对误差又如何? 解:已知:T =303K,V=20.0L,n=1.50mol, a=0.6803Pa ·m6 ·mol-2=0.6803 103kPa ·L2 ·mol-2 b=0.563610-4m3 ·mol-1 =0.05636 L ·mol-1
答:(略)
§1.4 真实气体
真实气体与理想气体的运动状态不同,存在偏 差。
产生偏差的主要原因是: ①气体分子本身的体积的影响; (分子本身有大小、占有体积,有时不能忽略) ②分子间力的影响。
(分子间存在相互吸引力,对器壁压力减小)
理想气体状态方程仅在温度不太低、压力不太高的情
况下适合于真实气体。否则必须对体积和压力进行校正。
即
PBV = nBRT
分压定律:混合气体的总压等于混合气体中各组 分气体分压之和。 p = p1 + p2 +
或
p = pB
n1 RT p1 , V
n 2 RT p2 , V
n1RT n2 RT RT p n1 n2 V V V
n =n1+ n2+
分压定律的应用
例题:用金属锌与盐酸反应制取氢气。在25℃下,用排水
集气法收集氢气,集气瓶中气体压力为98.70kPa(25℃时, 水的饱和蒸气压为3.17kPa),体积为2.50L,计算反应中消
耗锌的质量。
解: T =(273+25)K = 298K
p= 98.70kPa V=2.50L 298K时,p(H2O)=3.17kPa Mr (Zn)=65.39
第一章-气体
第一章 气体自然界中物质的聚集状态一般可分为三种:气体、液体和固体。
气体与液体均可以流动,统称为流体(fluid);液体和固体又统称为凝聚态(condense)。
无论物质处于哪一种状态,都有许多宏观性质,如压力(pressure)p 、体积(volume)V 、温度(temperature)T 、密度(density)ρ和热力学能(thermodynamic energy)U ,等等。
对于一定量的纯物质而言,p 、V 、T 是三个最基本的性质;而混合物的基本性质还应包括组成。
由一定量纯物质组成的均相流体,p 、V 、T 中任意两个量确定后,第三个量即随之确定,此时就说物质处于一定的状态。
处于一定状态的物质,各种宏观性质都有确定的值和确定的关系。
联系p 、V 、T 之间关系的方程称为状态方程。
本章着重介绍气体的状态方程。
§1-1 理想气体状态方程1.理想气体状态方程气体的物质的量n 与压力p 、体积V 与温度T 之间是有联系的。
从17世纪中叶开始 .先后经过波义尔(Boyle R,1662)、盖-吕萨克(Gay J-Lussac J,1808)及阿伏伽德罗(A Avogadro,1869)等著名科学家长达一个多世纪的研究,测定了某些气体的物质的量n 与它们的p 、V 、T 性质间的相互关系。
得出了对各种气体都普遍适用的三个经验定律(empirical law)。
在此基础上,人们归纳出一个对各种纯低压气体都适用的气体状态方程:nRT pV = (1-1-1a)上式称为理想气体状态方程(state equations of the ideal gas )。
式中p 的单位为Pa ,V 的单位为m 3,n 的单位为mol ,T 的单位为K 。
R 是是一个对各种气体都适用的比例常数(ratioconstant),称为摩尔气体常数,在一般计算中,可取R=8.314 J ·mol -1·K -1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n(CH 4 ) RT 解法一:思路, V (CH 4 ) = , p总
需先求出n(CH4)
n(CH4) = x(CH4)·n总
47.0 = × 100mol=940mol × 8.314kPa ⋅ L ⋅ K ⋅ mol × 298K V (CH 4 ) = 150.0kPa
298K时,p(H2O)=3.17kPa Mr (Zn)=65.39
(98.70 − 3.17)kPa × 2.50L n(H2) = 8.314J ⋅ K-1 ⋅ mol-1 × 298K
=0.0964mol Zn(s) + 2HCl → ZnCl2 + H2(g) 65.39g 1mol m(Zn)=? 0.0964mol
=131g
§1.2 气体混合物
1.2.1 分压定律
*1.2.2
分体积定律
1.2.1 分压定律
当几种不同的气体在同一容器中混合时,相互间不发生 当几种不同的气体在同一容器中混合时, 化学反应, 化学反应,分子本身的体积和它们相互间的作用力都可以 略而不计,这就是理想气体混合物 理想气体混合物。 略而不计,这就是理想气体混合物。 组分气体。 理想气体混合物中每一种气体叫做组分气体 理想气体混合物中每一种气体叫做组分气体。 任一组分气体对容壁碰撞所产生的压力不因其他组分气 体的存在而改变。 体的存在而改变。混合气体中组分气体所施加的压力叫做 该组分气体的分压 分压。 该组分气体的分压。 对于理想气体, 对于理想气体,某组分气体的分压等于相同温度下该组 分气体单独占有与混合气体相同体积所产生的压力。 分气体单独占有与混合气体相同体积所产生的压力。即: pB=nBRT/V pB— B组分气体的分压; 组分气体的分压; 组分气体的分压 nB— B组分气体的物质的量; 组分气体的物质的量; 组分气体的物质的量 T — 混合气体的温度; 混合气体的温度; V — 混合气体的体积。 混合气体的体积。
65.39g ×0.0964mol m(Zn) = 1mol
=6.30g
*1.2.2
分体积定律
分体积: 混合气体中某一组分B的分体积VB是 该组份单独存在并具有与混合气体相同 温度和压力时所占有的体积。
nBR T V = B p
*1.2.2
分体积定律
混合气体组分B的分体积VB是该组分气体单独存在并具有 与混合气体相同温度和压力时占有的体积。
3
V (CH 4 ) 1.55 × 103 L ϕ (CH 4 ) = = =0.94 3 V总 1.65 × 10 L
例: 氧是人类维持 生命的必需气体, 缺氧生命就会死亡 ,过剩的氧会使人 致病,只有在氧气 的分压维持21kPa才 能使人体维持正常 代谢过程。在潜 水员自身携带的水下呼吸器中充有氧气和氦 气(He在血液中溶解度很小,N2的溶解度大 ,可使人得气栓病)。
1.2.1 分压定律
组分气体: 组分气体: 理想气体混合物中每一种气体叫做组 分气体。 分气体。 分压: 分压: 组分气体B在相同温度下占有与混合 组分气体 在相同温度下占有与混合 下占有与 气体相同体积时所产生的压力 时所产生的压力, 气体相同体积时所产生的压力,叫做组分 气体B的分压 的分压。 气体 的分压。 nB RT pB = V
T p = nR V
分压的求解:
nBR T nR T pB = p= V V pB nB = = xB p n
nB pB = p = xB p n
x B B的摩尔分数 混合气体中某气体的分压等于该组分 的摩尔分数与总压的乘积。 的摩尔分数与总压的乘积。
例题:某容器中含有NH3、O2 、N2等气 体 的 混 合 物 。 取 样 分 析 后 , 其 中 n(NH3)=0.320mol , n(O2)=0.180mol , n(N2)=0.700mol 。 混 合 气 体 的 总 压 p=133.0kPa。试计算各组分气体的分压。 解:n= n(NH3)+n(O2)+n(N2) =0.320mol+0.180mol+0.700mol =1.200mol
6NaN3+Fe2O3(s) 3Na2O(s)+2Fe(s)+9N2(g) 在25℃。748mmHg下,要产生 ℃ 下 要产生75.0L的N2,计算 的 需要叠氮化钠的质量。 需要叠氮化钠的质量。 解: 根据化学反应方程式所显示出的n( 根据化学反应方程式所显示出的 (NaN3) 的数量关系, 与n(N2)的数量关系,可以进一步确定在给定条 ( 件下, ( 的关系。 件下,m(NaN3)与V(N2)的关系。 (
1.2.1 分压定律
基本概念: 基本概念 1. 混合气体与组分气体 由两种或两种以上的气体混合在一起, 组成的体系, 由两种或两种以上的气体混合在一起 组成的体系 称为混合气体, 组成混合气体的每种气体, 称为混合气体 组成混合气体的每种气体 都称为该混 合气体的组分气体。显然, 空气是混合气体, 合气体的组分气体。显然 空气是混合气体 其中的 O2, N2, CO2 等, 均为空气的组分气体 均为空气的组分气体. 2. 混合气体的摩尔分数 组分气体的物质的量用n 表示, 组分气体的物质的量用 B 表示 混合气体的物质的 表示, 量用 n 表示 则: nB/n =xB, xB叫做 组分气体的物质的量分数,又称 叫做B组分气体的物质的量分数 组分气体的物质的量分数, 为摩尔分数。 为摩尔分数。
nBR T V = B p
由于混合气体中各组分间不发生化学反应,在T、p不变的 条件下,即:混合气体体积等于各组分的分体积之和 ,这 一规律叫做分体积定律。
V = V1 + V2 + ⋅⋅⋅
或
V = ∑VB
B
nBR T V = B p
V = V1 + V2 + ⋅⋅⋅
或
V = ∑VB
B
nR n2R T 1 T V= + +L p p
第一篇
化学反应原理
气 体
第一章
§1.1 理想气体状态方程 §1.2 气体混合物 *§1.3 气体分子动理论 § §1.4 真实气体
§1.1 理想气体状态方程
1.1.1 理想气体状态方程 1.1.2 理想气体状态方程的应用
1.1.1 理想气体状态方程
气体的最基本特征: 气体的最基本特征:具有可压缩性和扩散性。 理想气体分子之间没有相互吸引和排斥, 理想气体分子之间没有相互吸引和排斥,分子本 身的体积相对于气体所占有体积完全可以忽略。 身的体积相对于气体所占有体积完全可以忽略。理 分子间无作用力, 想气体是将气体理想化为分子间无作用力 想气体是将气体理想化为分子间无作用力,分子自 身无体积。 身无体积。 理想气体是一种物理模型,综合考虑压力 、 理想气体是一种物理模型,综合考虑压力(p)、温 之间的关系。 度(T)、体积 、 物质的量 之间的关系。应符合 、体积(V)、 物质的量(n)之间的关系 下方程: 下方程: pV = nRT 人们将符合理想气体状态方程 的气体,称为理想气体。 的气体,称为理想气体。
理想气体状态方程: 理想气体状态方程:
pV = nRT R---- 摩尔气体常量 在STP下,p =101.325kPa, T=273.15K 下 n=1.0 mol时, Vm=22.414L=22.414×10-3m3 时 ×
pV 101325Pa × 22.414 × 10 m = R= nT 1.0mol × 273.15K
2. 确定气体的摩尔质量 确定气体的摩尔质量
pV = nRT
m pV = RT M
mRT M= pV
n =
m M
M = Mr g⋅mol-1 ⋅
3. 确定的气体密度 确定的气体密度
mRT M= pV
M=
ρ=m/V
ρRT
p
pM ρ= R T
有关气体体积的化学计算
例:为了行车 的安全, 可在 的安全 , 汽车中装备上 空气袋, 空气袋 , 防止 碰撞时司机受 到伤害。 到伤害 。 这种 空气袋是用氮 气充胀起来 的,所用的氮气是由叠氮化钠与三氧化二铁 在火花的引发下反应生成的。总反应是: 在火花的引发下反应生成的。总反应是:
-1 -1
=1.55 × 10 L
3
47.0 ϕ (CH 4 ) = x(CH 4 ) = =0.94 47.0+2.0+0.80+0.20
解法二:
n总 RT V总 = p总
100.0mol × 8.314kPa ⋅ L ⋅ K -1 ⋅ mol-1 × 298K = 150.0kPa
=1.65 × 10 L
安全气囊原理
汽车安全气囊系统的包括传感器总成、充气、 汽车安全气囊系统的包括传感器总成、充气、折叠气 点火器、固态氮、警告灯等。 囊、点火器、固态氮、警告灯等。当汽车受到前方一 定角度内的高速碰撞时, 定角度内的高速碰撞时,装在车前端的碰撞传感器和 装汽车中部的安全传感器,就可以检测到车突然减速, 装汽车中部的安全传感器,就可以检测到车突然减速, 并将这一信号在0.01秒之内速度传递给安全气囊系统 并将这一信号在 秒之内速度传递给安全气囊系统 的控制电脑。电脑在经过分析确认之后, 的控制电脑。电脑在经过分析确认之后,立即引爆气 囊包内的电热点火器(即电雷管),使其发生爆炸, ),使其发生爆炸 囊包内的电热点火器(即电雷管),使其发生爆炸, 这一过程一般只需0.05秒左右。点火器引爆之后,固 秒左右。 这一过程一般只需 秒左右 点火器引爆之后, 态氮粒迅速气化,大量氮气化, 态氮粒迅速气化,大量氮气化,大量氮气立即吹涨气 并在强大的冲击力之下, 囊,并在强大的冲击力之下,气囊冲开方向盘上的盖 而安全展开。 而安全展开。
6NaN3+Fe2O3(s) 3Na2O(s)+2Fe(s)+9N2(g) 6mol 9mol Mr(NaN3)=65.01 P=748mmHg=99.73kPa T=298K m(NaN3)=390.06g V(N2)=223.6L m(NaN3)=? V(N2)=75.0L ?
