Matlab实现 递归算法生成3维分形树ByLinking
基于matlab的三维kdtree构建代码

基于Matlab的三维kdtree构建代码1. 介绍在计算机科学和几何学中,k维树(kd-tree)是一种用于存储k维空间数据的数据结构。
它是一种二叉树,其中每个结点都是k维空间中的一个点,而非叶子节点表示一个将k维空间划分为两个半空间的超平面。
通过构建kd-tree,可以高效地搜索最近邻点、范围搜索以及k最近邻搜索等问题。
本文将详细介绍如何基于Matlab编写一个三维kd-tree构建代码,包括三个主要部分:数据结构设计、插入操作和搜索操作。
2. 数据结构设计2.1 kd-tree节点kd-tree的节点包括坐标值、切分维度以及左右孩子节点指针。
在Matlab中,可以使用结构体来表示节点:struct Nodepointsplit_dimleft_childright_childend参数解释: - point:节点对应的坐标值,是一个1x3的向量。
- split_dim:切分维度,表示当前节点是按照哪一个维度进行切分的。
- left_child:左孩子节点。
- right_child:右孩子节点。
2.2 kd-tree树kd-tree是由节点构成的二叉树结构。
在Matlab中,我们可以使用一个结构体数组来表示:struct Treerootend参数解释: - root:树的根节点。
3. 插入操作kd-tree的插入操作是将一个新的点插入到已有的树中。
具体实现如下:1.如果树为空,则将新节点作为根节点。
2.否则,按照树的结构进行递归地查找插入位置:1.根据当前节点的切分维度,将新节点与当前节点比较。
2.如果新节点在当前维度的坐标值小于当前节点,则继续查找左子树。
3.否则,继续查找右子树。
4.递归地执行上述步骤,直到找到一个空节点位置。
3.在找到的空节点位置插入新节点。
具体的Matlab代码如下:function tree = insert(tree, new_point)if isempty(tree.root)tree.root = Node(new_point, 1, [], []);elsetree.root = insertNode(tree.root, new_point, 1);endendfunction node = insertNode(node, new_point, dim)if isempty(node)node = Node(new_point, dim, [], []);return;endif new_point(dim) < node.point(dim)node.left_child = insertNode(node.left_child, new_point, mod(dim+1, 3) +1);elsenode.right_child = insertNode(node.right_child, new_point, mod(dim+1, 3)+1);endend4. 搜索操作kd-tree的搜索操作可以分为最近邻搜索和范围搜索。
matlab分形

尽管分形几何的提出只有三十年左右的时间, 但它已经在自然科学的各个领域如数学、物理、 化学、地理、天文、材料、生命乃至经济、社会、 艺术等极其广泛的领域有着广泛的应用。
这里以迭代的观点介绍分形的基本特性以及生 成分形图形的基本方法。
生成元产生的分形图形
由IFS(迭代函数系)所生成的分形图形
一、生成元产生的分形图形
经过计算,可以得到如下结论: 当 z0 [1.5,1.5] 时,z值始终不会超出某个范围; 而当 z0 小于-1.5或大于1.5后,z值最终将趋于无穷。
现在,我们把这个函数扩展到整个复数范围。对 于复数 z0 x iy ,取不同的x 值和y 值,函数迭代的 结果不一样:对于有些 z0 ,函数值约束在某一范围内; z0 而对于另一些 ,函数值则发散到无穷。由于复数对 应平面上的点,因此我们可以用一个平面图形来表示。 z 我们用深灰色表示不会使函数值趋于无穷的 对于其0 ; z0 它的 ,我们用不同的颜色来区别不同的发散速度。 | z | 2 由于当某个时候 时,函数值一定发散,因此这 里定义发散速度为:使|z|大于2的迭代次数越少,则 发散速度越快。编程画出这个图形。
该吸引子就是一个分形。 利用I FS迭代可以生成各种漂亮的分形图形,而 且I FS迭代的优点是程序具有通用性,要想得到不同 的分形图形,只需改变仿射变换中的系数和概率的 值即可。
Barnsley(巴斯理)羊齿叶
w a
1 2 3 4 0 0.85 0.2 -0.15
b
c
d
e
f
0 1.6 1.6 0.44
由生成元产生的分形是一种规则分形,是数学 家按一定规则构造出来的,相当于物理中的模型。 这类图形的构造方式都有一个共同的特点:
matlab实现的ID3 分类决策树 算法解析

function D = ID3(train_features, train_targets, params, region% Classify using Quinlan's ID3 algorithm% Inputs:% features - Train features% targets - Train targets% params - [Number of bins for the data, Percentage of incorrectly assigned samples at a node]% region - Decision region vector: [-x x -y y number_of_points]%% Outputs% D - Decision sufrace[Ni, M] =size(train_features; %·µ»ØÐÐÊýNiºÍÁÐÊýM%Get parameters[Nbins, inc_node] = process_params(params;inc_node = inc_node*M/100;%For the decision regionN = region(5;mx = ones(N,1 * linspace(region(1,region(2,N; %linspace(Æðʼֵ£¬ÖÕÖ¹Öµ£¬ÔªËظöÊýmy = linspace (region(3,region(4,N' * ones(1,N;flatxy = [mx(:, my(:]';%Preprocessing[f, t, UW, m] = PCA(train_features,train_targets, Ni, region;train_features = UW * (train_features -m*ones(1,M;flatxy = UW * (flatxy - m*ones(1,N^2;%First, bin the data and the decision region data [H, binned_features]=high_histogram(train_features, Nbins, region; [H, binned_xy] =high_histogram(flatxy, Nbins, region;%Build the tree recursivelydisp('Building tree'tree = make_tree(binned_features,train_targets, inc_node, Nbins;%Make the decision region according to the tree disp('Building decision surface using the tree' targets = use_tree(binned_xy, 1:N^2, tree, Nbins, unique(train_targets;D = reshape(targets,N,N;%ENDfunction targets = use_tree(features, indices, tree, Nbins, Uc%Classify recursively using a treetargets = zeros(1,size(features,2; %size(features,2·µ»Øfeatu resµÄÁÐÊýif (size(features,1 == 1,%Only one dimension left, so work on itfor i = 1:Nbins,in = indices(find(features(indices == i;if ~isempty(in,if isfinite(tree.child(i,targets(in = tree.child(i;else%No data was found in the training set for this bin, so choose it randomally n = 1 +floor(rand(1*length(Uc;targets(in = Uc(n;endendendbreakend%This is not the last level of the tree, so:%First, find the dimension we are to work ondim = tree.split_dim;dims= find(~ismember(1:size(features,1, dim; %And classify according to it for i = 1:Nbins,in = indices(find(features(dim, indices == i;targets = targets + use_tree(features(dims, :, in, tree.child(i, Nbins, Uc;end%END use_treefunction tree = make_tree(features, targets,inc_node, Nbins%Build a tree recursively[Ni, L] = size(features;Uc = unique(targets;%When to stop: If the dimension is one or the number of examples is small if ((Ni == 1 | (inc_node > L,%Compute the children non-recursively for i = 1:Nbins,tree.split_dim = 0;indices = find(features == i;if ~isempty(indices,if(length(unique(targets(indices == 1, tree.child(i =targets(indices(1;elseH =hist(targets(indices, Uc;[m, T] = max(H;tree.child(i = Uc(T;endelsetree.child(i = inf;endendbreakend%Compute the node's Ifor i = 1:Ni,Pnode(i = length(find(targets == Uc(i / L; endInode = -sum(Pnode.*log(Pnode/log(2;%For each dimension, compute the gain ratio impurity delta_Ib = zeros(1, Ni; P = zeros(length(Uc, Nbins;for i = 1:Ni,for j = 1:length(Uc,for k = 1:Nbins,indices = find((targets == Uc(j & (features(i,: == k;P(j,k = length(indices;endendPk = sum(P;P = P/L;Pk = Pk/sum(Pk;info = sum(-P.*log(eps+P/log(2;delta_Ib(i =(Inode-sum(Pk.*info/-sum(Pk.*log(eps+Pk/log( 2;end%Find the dimension minimizing delta_Ib[m, dim] = max(delta_Ib;%Split along the 'dim' dimensiontree.split_dim = dim;dims = find(~ismember(1:Ni, dim;for i = 1:Nbins,indices = find(features(dim, : == i; tree.child(i = make_tree(features(dims, indices, targets(indices, inc_node, Nbins; end。
机器学习-ID3决策树算法(附matlaboctave代码)
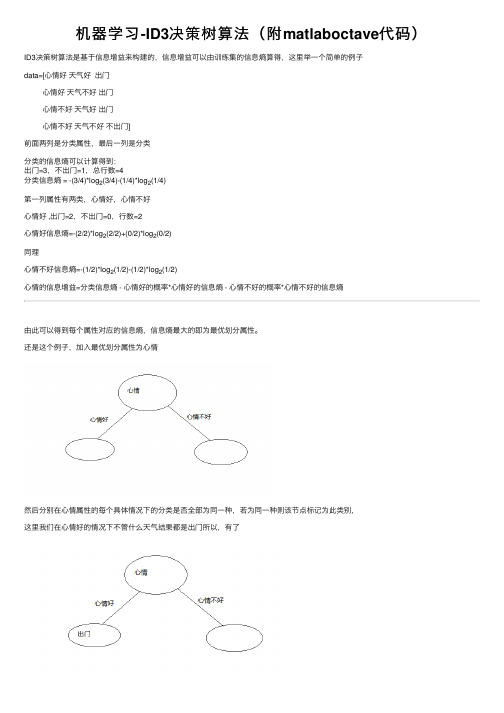
机器学习-ID3决策树算法(附matlaboctave代码)ID3决策树算法是基于信息增益来构建的,信息增益可以由训练集的信息熵算得,这⾥举⼀个简单的例⼦data=[⼼情好天⽓好出门⼼情好天⽓不好出门⼼情不好天⽓好出门⼼情不好天⽓不好不出门]前⾯两列是分类属性,最后⼀列是分类分类的信息熵可以计算得到:出门=3,不出门=1,总⾏数=4分类信息熵 = -(3/4)*log2(3/4)-(1/4)*log2(1/4)第⼀列属性有两类,⼼情好,⼼情不好⼼情好 ,出门=2,不出门=0,⾏数=2⼼情好信息熵=-(2/2)*log2(2/2)+(0/2)*log2(0/2)同理⼼情不好信息熵=-(1/2)*log2(1/2)-(1/2)*log2(1/2)⼼情的信息增益=分类信息熵 - ⼼情好的概率*⼼情好的信息熵 - ⼼情不好的概率*⼼情不好的信息熵由此可以得到每个属性对应的信息熵,信息熵最⼤的即为最优划分属性。
还是这个例⼦,加⼊最优划分属性为⼼情然后分别在⼼情属性的每个具体情况下的分类是否全部为同⼀种,若为同⼀种则该节点标记为此类别,这⾥我们在⼼情好的情况下不管什么天⽓结果都是出门所以,有了⼼情不好的情况下有不同的分类结果,继续计算在⼼情不好的情况下,其它属性的信息增益,把信息增益最⼤的属性作为这个分⽀节点,这个我们只有天⽓这个属性,那么这个节点就是天⽓了,天⽓属性有两种情况,如下图在⼼情不好并且天⽓好的情况下,若分类全为同⼀种,则改节点标记为此类别有训练集可以,⼼情不好并且天⽓好为出门,⼼情不好并且天⽓不好为不出门,结果⼊下图对于分⽀节点下的属性很有可能没有数据,⽐如,我们假设训练集变成data=[⼼情好晴天出门⼼情好阴天出门⼼情好⾬天出门⼼情好雾天出门⼼情不好晴天出门⼼情不好⾬天不出门⼼情不好阴天不出门]如下图:在⼼情不好的情况下,天⽓中并没有雾天,我们如何判断雾天到底是否出门呢?我们可以采⽤该样本最多的分类作为该分类,这⾥天⽓不好的情况下,我们出门=1,不出门=2,那么这⾥将不出门,作为雾天的分类结果在此我们所有属性都划分了,结束递归,我们得到了⼀颗⾮常简单的决策树。
matlab--算法大全--第29章_多元分析

后经 Orloci 等人 1976 年发展起来的,故又称为 Ward 方法。 1.2 系统聚类法 1.2.1 系统聚类法的功能与特点 系统聚类法是聚类分析方法中最常用的一种方法。 它的优点在于可以指出由粗到细 的多种分类情况,典型的系统聚类结果可由一个聚类图展示出来。 例如,在平面上有 7 个点 w1 , w2 , 来表示聚类结果。
第二十九章
多元分析
多元分析(multivariate analyses)是多变量的统计分析方法,是数理统计中应用广 泛的一个重要分支,其内容庞杂,视角独特,方法多样,深受工程技术人员的青睐和广 泛使用,并在使用中不断完善和创新。由于变量的相关性,不能简单地把每个变量的结 果进行汇总,这是多变量统计分析的基本出发点。 §1 聚类分析 将认识对象进行分类是人类认识世界的一种重要方法,比如有关世界的时间进程 的研究,就形成了历史学,也有关世界空间地域的研究,则形成了地理学。又如在生物 学中,为了研究生物的演变,需要对生物进行分类,生物学家根据各种生物的特征,将 它们归属于不同的界、门、纲、目、科、属、种之中。事实上,分门别类地对事物进行 研究,要远比在一个混杂多变的集合中更清晰、明了和细致,这是因为同一类事物会具 有更多的近似特性。 在企业的经营管理中, 为了确定其目标市场, 首先要进行市场细分。 因为无论一个企业多么庞大和成功,它也无法满足整个市场的各种需求。而市场细分, 可以帮助企业找到适合自己特色, 并使企业具有竞争力的分市场, 将其作为自己的重点 开发目标。 通常,人们可以凭经验和专业知识来实现分类。而聚类分析(cluster analyses)作 为一种定量方法,将从数据分析的角度,给出一个更准确、细致的分类工具。 1.1 相似性度量 1.1.1 样本的相似性度量 要用数量化的方法对事物进行分类,就必须用数量化的方法描述事物之间的相似 程度。 一个事物常常需要用多个变量来刻画。 如果对于一群有待分类的样本点需用 p 个 变量描述,则每个样本点可以看成是 R 空间中的一个点。因此,很自然地想到可以用 距离来度量样本点间的相似程度。 记 Ω 是样本点集,距离 d (⋅,⋅) 是 Ω × Ω → R 的一个函数,满足条件: 1) d ( x , y ) ≥ 0 , x , y ∈ Ω ; 2) d ( x, y ) = 0 当且仅当 x = y ; 3) d ( x , y ) = d ( y , x ) , x , y ∈ Ω ; 4) d ( x , y ) ≤ d ( x , z ) + d ( x , y ) , x , y , z ∈ Ω 。 这一距离的定义是我们所熟知的,它满足正定性,对称性和三角不等式。在聚类 分析中,对于定量变量,最常用的是 Minkowski 距离
基于L系统的三维分形树仿真

o引言
分形,通常被定义为'一个粗糙或零碎的几何形状,可以 分成数个部分,且每一部分都是整体缩小后的形状”,即具有 自相似的性质S畫分形技术通常用来在计算机上模拟出自 然界中具有非规则生长特性的植物。分形几何的概念是美 籍法国数学家曼德布罗[3]首先提出的,最初分形图的计算机 绘制也只是停留在二维平面,后来,一个分形体爱好者丹尼 尔•怀特提出一个大胆的方法,创造出令人称奇的3D分形影 像⑷,并将它们命名为芒德球。本文在Matlab平台上利用L 系统算法实现了三维虚拟场景的树木仿真,有效的展示了树 木的生长和拓扑结构。
龟形的当前状态由一个三元组(x,y,a)⑫讷来定义,其 中笛卡儿坐标(X, y)表示海龟的位置,角度a为海龟的前进 方向,可以解释为海龟面对的方向。给出步长d和角度的增量 sita,海龟根据不同符号所代表的命令做出反应。
上面讲述的龟形解释是二维的,它可方便地扩展到三维 空间,要对字符串进行三维龟图解释,关键是用三个向量H, L和U来表示空间龟的当前方位[14'15'161. H、L、U分别为龟 头的指向、左方、上方,这些向量具有单位长度且方向正交, 即满足方程HXL=U。龟的旋转可表示为方程:(H, L, U)= (H, L, U) R[17],其中R是3X3的旋转矩阵。以下分别是绕 矢量U、L和H旋转a的旋转矩阵酋创:
图]JSP+Servl et+JavaBean 模式
MVC(Model> View、 Controller)是非常典型的三 层分层技术,Model是业务逻辑层,View是表示层, Controller是用来调度其他两层,将MVC模式具体化,如 JSP+Servlet+JavaBean<,其中JavaBean既可以作为数据模型 来封装业务数据,也可以作为业务逻辑模型来包含应用的业 务,根据收到控制器传来的请求,执行特定的业务逻辑处理, 返回执行结果。JSP则作为视图层,负责提供未用户展现数 据,提交用户请求,Servlet贝!]作为控制器,接受用户的请求, 将请求中的数据,转化为业务模型中的数据模型,同时根据 业务执行结果来选择要返回的视图。具体模式如下图1所示。
MATLAB环境下图像分形维数的计算
也有采用递减序列进行像素点覆盖,递减序列 的构造有多种方法,普遍使用的是二等分序列,也 就是将图像逐次二等分.所采用的序列的最大值都 将取决于图像的大小.网格的最小值始终为1,这 是划分网格的极限.
根据分形维数的定义,块的尺寸越小,计算出 的图像的维数越精确,但对于存储在计算机内的分 形图像,只能分割到像素点尺寸,就不能再继续分 割下去了.因此,当讨论图像的分形性质时,可以取 一个像素点的尺寸作为尺度下限,为了避免奇异情 形的发生,在计算分形维数的过程中,要求有适当 多的测试点,至于尺度上限可根据具体情况和具体 要求进行确定.
(1.中国矿业大学资源与安全工程学院,北京100083;2.中原工学院数理系,河南郑州450007)
摘要:利用MATLAB的图像处理和数值计算功能,对大气可吸入颗粒物的场发射电镜
(FESEM)图像进行处理,得到颗粒物边界的二值图像;编制MATLAB程序,统计一系列以不同
像素数量为边长的正方形块覆盖二值图像时的个数,根据像素数量和正方形块个数之间的关系,
确定图像的计盒维数.结果表明:MATLAB对分形图像的处理简单、方便,通过科赫曲线、谢宾
斯基填料等有规分形图形分形维数的计算表明该方法计算出的结果准确、可靠.对大气颗粒物的
分形维数的计算表明,不同不规则程度的颗粒物有不同的分形维数,可以通过颗粒物分形维数的
计算分析颗粒物的来源和输运过程.
使用MATLAB实现随机分形树模拟
使用MATLAB实现随机分形树模拟尤鸿霞【摘要】阐述了植物模拟的典型方法L-系统及迭代函数系统(IFS)的基本原理.根据这两种方法,利用MATLAB软件工具.模拟了带有随机因子的分形树,模拟的分形树形态生动逼真.MATLAB具有强大的绘图工具和函数系统,实现随机分形树模拟的程序很简洁.【期刊名称】《南通纺织职业技术学院学报》【年(卷),期】2010(010)004【总页数】3页(P18-20)【关键词】分形树;L-系统;迭代函数系统IFS;MATLAB【作者】尤鸿霞【作者单位】南通纺织职业技术学院,南通,226007【正文语种】中文【中图分类】TP391.9自然界中种类繁多的植物大都具有自我相似的分形特征.近年来,随着分形理论的发展,分形理论在植物模拟领域得到了广泛的应用.基于分形理论的植物模拟方法主要有L-系统、迭代函数系统、粒子系统等[1].本文以L系统、迭代函数系统(IFS)的算法思想为基础,以MATLAB为编程工具,借助MATLAB的绘图功能,实现了随机分形树的模拟.1 分形模拟的实现1.1 基于L系统的仿真1968年,著名理论生物学家Lindenmayer在研究植物形态的进化和构造时,提出了一种文法描述方法作为植物生长的数学理论,即L系统,它能很好地表达植物的分枝特征.之后,各地的研究人员开始关注L-系统并对其做了各种改进.至今,L-系统仍然是植物模拟的一种重要思想方法.L-系统是一种符号重写系统,基本思想为字符串替换,其替换规则基本如下:b→a,a→ab.其基本演变规律为:b→a→ab→aba→abaab→abaababa→abaababaabaab→…….字符串的增长符合fibonacci数列,即 F(n+2)=F(n+1)+F(n).L-系统应用于植物模拟时,首先根据其符号元和替换规则产生一系列字符串,然后读取字符,按照不同字符表示的意义来执行不同的动作[2].简单描述如下:第一步生成字符串.①声明并设置产生式规则;②声明并设置起始点、初始角、迭代步长以及迭代上限等控制参数;③循环用替换字符串替换种子.第二步读取字符并画图.①逐个读取字符串中的每个字符.②根据读取到的字符采取不同的动作,读取’F’时,画线段;读取’+’时,逆时针旋转;读取’-’时,顺时针旋转;读取’[’时,进栈,记录当前状态;读取’]’时,出栈.图1为笔者以MATLAB为平台实现的基于L-系统思想的分形树,其产生式规则分别为FF[-F+F+F]+[+F-F-F]、F[+F]F[-F]F、F[+F]F[-F[+F]].随着植物模拟技术的发展,一些研究者提出在分形树的基础上加入随机因子,这样的生成树就不是完全按照某一确定的规则,体现了自然界由于外界条件造成的树木生长的偶然性,这样得到的分形树更自然,更逼真.丁永胜等人[3]曾以MATLAB实现分形树模拟,其分形树是使用单一规则实现的,整棵树采用同一种自相似规则,每一个分枝的分形方法都相同,其生成树的结果如图2.笔者在其基础上,对程序进行了改进,加入了随机因子,整棵树的生成采用三种自相似规则(如程序中的p1、p2和p3),在树木分枝的部位,到底采用哪一种规则生成新的枝干部分,由随机数决定.如function Sltree(n)程序中,使用c=rand(1)函数随机生成一个0~1之间的数字,在分枝部位,如果生成的随机数是 0.7~1 之间,则采用p1='FF+[+F+F]-[+F]'规则生成新的枝干;若生成的随机数是0.35~0.7,则采用 p2='F[+F]F[-F[+F]]'规则生成新的枝干;若生成的随机数是 0~0.35,则采用 p3='FF-[-F+F+F]+[+F-F-F]'规则生成新的枝干.这样生成的树木体现了自然界的外界条件对树木生长的影响,使树木的外观看起来更加逼真.程序如下:图1 不同生成规则的分形树图2 随机分形树仿真图加入随机因子之后,生成的分形树更逼真.由于具有随机性,每次执行程序所生成的分形树形态不同.实验中,还可以根据需求调整生成规则,增加生成规则的数量,调整随机数的范围,以得到不同的树.1.2 基于迭代函数系统的仿真迭代函数系统(IFS)是分形理论的重要分支,将待生成图像由许多整体自相似的小块拼接而成,局部是整体的一个小复制品.主要技术有相似变换及仿射变换.相似变换可放大缩小甚至旋转,但不变形;仿射变换指在不同方向上变化,比率不同的比例变换,一般会改变图形中向量的夹角、点与点之间的距离、图形的面积等,可以将图形进行缩放、伸长、剪切、扭曲等.仿射变换的数学表达式为(其中a,b,c,d,e,f均为实数).利用IFS方法生成分形图的关键是找出相应的IFS码,根据已有的研究结果,给出如下一组IFS码[4].笔者利用MATLAB工具及这些IFS码,实现了IFS树的模拟.如表1所示.笔者在丁永胜等人[3]的研究结果的基础上,采用不同于丁永胜等人的变换公式,如IFST(N)函数中的变换公式 xp=a1*x+b1*y+e1, yp=c1*x+d1*y+f1,根据表 1 的 IFS 树的 IFS 码,重新调整了随机数的分布,实现生成IFS树,如图3.程序如下:表1 一组IFS树的IFS码i a b c d e f 1 -0.04 0 -0.19 -0.47 -0.12 0.32 0.65 0 0 0.56 0.06 1.563 0.41 0.46 -0.39 0.61 0.46 0.44 0.52 -0.35 0.25 0.74 -0.480.38图3 MATLAB仿真的IFS分形树图3为用MATLAB程序实现的以表1中的IFS码生成的IFS分形树,调整IFS码为适当的数值,还可以形象地模拟蕨叶、枫叶、蒿草等各种自然界的植物.2 结语虚拟植物技术已经成为当今计算机图形学应用领域的研究热点,本文结合最常用的模拟植物形态的两种方法L-系统和迭代函数系统IFS,以MATLAB软件为运行平台,实现了分型植物的形态模拟.MATLAB软件有功能强大的绘图工具箱,实现植物模拟的程序代码简洁,可尝试实现更加复杂的虚拟植物技术.参考文献:[1]康军广.基于分形理论的植物模拟[D].河北工业大学硕士学位论文,2006.[2]武志峰.基于分形理论的植物模拟方法研究[D].大连理工大学硕士学位论文.2005:6-8.[3]丁永胜,堵秀凤,张水胜.MATLAB分形植物模拟[J].齐齐哈尔大学学报,2008,24(3):63-66.[4]刘茗.分形植物形态的模拟算法研究[D].苏州大学同等学历硕士学位论文,2006:27-29.。
基于分形的递归调用实现三维树木可视化
柱形( 干 ) 多边形( 叶 ) 组成。 枝 和 树 所 关 键 字 : 形 ; 归调 用 ; 分 递 分枝 模 型 中图 分 类 号 :P 9 T 3 文献 标 识 码 : A 文 章 编 号 :0 7 8 2 (0 10 — 0 5 0 10 — 30 2 1 )3 06 — 1
何又无法描述 的几何 现象和物体 。
( ) 氏系统。 2林 林氏系统( 通常称 L系统) 是林德梅 叶 16 98 年为模 拟生物形 态而设计 的 , 后来 史密斯 于 18 9 4年 、 普鲁辛
P则 u , =y P x。
将其 单位 化 :U = / r x + 2 z) y ysr x + 2 z) x x qt( y +2,U =/ t( y +2, s 2 q 2
Re l e 3 Tr e s l a in Ba e n t e F a t lRe u sv l a i D e s Viua i t s d o h r ca c r i ey z z o
zHANG Li l i _e
(lc o i E gneig E s C i ntu f Tcn l y F zo,J nx 3 4 0 hn) Eet nc nier , at hn Istt o eh o g, uh u i gi 4 0 0 C ia r n a ie o a
虚拟现实技术是 于 2 0世纪 9 0年代发 展起 来 的一 门研究 领域 . 人类在 生活 中通常会涉及 到 自然景物 , 然而认识外界事 物, 主要 是通 过视觉获得 的, 因此虚拟现实 技术中的一个重要 方面就是视景仿真 , 即通过 图形 图像 处理技术构造 三维模型 , 从而尽 可能真实再 现大 自然巧夺 天工 的造 型 , 如雪花 、 凌 、 冰
递归算法生成3维分形树ByLinking(Matlab代码)(2)
Matlab实现递归算法生成3维分形树注:此算法树根在侧面,需对坐标轴进行旋转便可得到上图效果以下代码全部粘贴到一个M文件中命名为TreeByL 即可运行为方便网友研读代码加入了大量注释同时愿与matlab程序爱好者进行交流:Linking508@%%%%%%%%%%%%%%%%%%%%%%%%%% %%%Matlab实现递归算法生成3维分形树%ByLinking %%%%%%%%%%%%%%%%%%%%%%%%%% %%function TreeByLL=15;%主干长a=0;b=pi/3;r=0;%r=pi/5;%分支生成函数makeBranch(0,0,0,L,a,b,r);% a在XOZ平面投影与X轴夹角b与Y轴的夹角r与主干的夹角function makeBranch (x,y,z,L,a,b,r)B=pi/5;s1=1.5;s2=3;s3=1.2;%B枝干的倾斜度C主干的倾斜度s1细腻程度s2分支收缩速度s3主干收缩速度% B=pi/5;s1=1.5;s2=2.4;s3=1.35;if L>s1x1=x+L/s2*cos(a)*cos(r);y1=y+L/s2*sin(a);z1=z+L/s2*cos(a)*sin(r);x1R=x1+L/s2*cos(a-b)*cos(r);y1R=y1+L/s2*sin(a-b);z1R=z1+L/s2*cos(a-b)*sin(r);x1L=x1+L/s2*cos(a+b)*cos(r);y1L=y1+L/s2*sin(a+b);z1L=z1+L/s2*cos(a+b)*sin(r);x1F=x1+L/s2*cos((a-b)*sin(a))*cos(r+atan(1/cos(a)));y1F=y1+L/s2*sin((a-b)*sin(a));z1F=z1+L/s2*cos((a-b)*sin(a))*sin(r+atan(1/cos(a)));x1B=x1+L/s2*cos((a-b)*sin(a))*cos(r-atan(1/cos(a)));y1B=y1+L/s2*sin((a-b)*sin(a));z1B=z1+L/s2*cos((a-b)*sin(a))*sin(r-atan(1/cos(a)));%------------------------------------------------------x2=x+L/s2*cos(a)*cos(r);y2=y+L/s2*sin(a);z2=z+L/s2*cos(a)*sin(r);x2R=x2+L/s2*cos(a-b)*cos(r);y2R=y2+L/s2*sin(a-b);z2R=z2+L/s2*cos(a-b)*sin(r);x2L=x2+L/s2*cos(a+b)*cos(r);y2L=y2+L/s2*sin(a+b);z2L=z2+L/s2*cos(a+b)*sin(r);x2F=x2+L/s2*cos((a-b)*sin(a))*cos(r+atan(1/cos(a)));y2F=y2+L/s2*sin((a-b)*sin(a));z2F=z2+L/s2*cos((a-b)*sin(a))*sin(r+atan(1/cos(a)));x2B=x2+L/s2*cos((a-b)*sin(a))*cos(r-atan(1/cos(a)));y2B=y2+L/s2*sin((a-b)*sin(a));z2B=z2+L/s2*cos((a-b)*sin(a))*sin(r-atan(1/cos(a)));plot3([x,x2],[y,y2],[z,z2],'k');holdon;set(gcf,'color','w');grid on;view(pi/2,0);%axis off;xlabel('X Label');ylabel('Y Label');zlabel('Z Label');set(gca,'xlim',[0,25],'ylim',[-15,15],'zlim',[-15,15]);plot3([x2,x2R],[y2,y2R],[z2,z2R],'g');hold on;plot3([x2,x2L],[y2,y2L],[z2,z2L],'g');hold on;plot3([x2,x2B],[y2,y2B],[z2,z2B],'g');hold on;plot3([x2,x2F],[y2,y2F],[z2,z2F],'g');hold on;plot3([x1,x1R],[y1,y1R],[z1,z1R],'g');hold on;plot3([x1,x1L],[y1,y1L],[z1,z1L],'g');hold on;plot3([x1,x1B],[y1,y1B],[z1,z1B],'g');hold on;plot3([x1,x1F],[y1,y1F],[z1,z1F],'g');hold on;%------------------------------------------------------makeBranch(x2,y2,z2,L/s3,a,b,r);makeBranch(x2L,y2L,z2L,L/s2,a,b,r+B);makeBranch(x2B,y2B,z2B,L/s2,a,b,r-B);makeBranch(x2F,y2F,z2F,L/s2,a,b,r+B);makeBranch(x2R,y2R,z2R,L/s2,a,b,r-B);makeBranch(x1L,y1L,z1L,L/s2,a,b,r+B);makeBranch(x1B,y1B,z1B,L/s2,a,b,r-B);makeBranch(x1F,y1F,z1F,L/s2,a,b,r+B);makeBranch(x1R,y1R,z1R,L/s2,a,b,r-B);end。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab实现递归算法生成3维分形树
注:此算法树根在侧面,需对坐标轴进行旋转便可得到上图效果
以下代码全部粘贴到一个M文件中命名为TreeByL即可运行
为方便网友研读代码加入了大量注释
同时愿与matlab程序爱好者进行交流:********************
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Matlab实现递归算法生成3维分形树
%ByLinking
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function TreeByL
L=15;%主干长
a=0;
b=pi/3;
r=0;%r=pi/5;
%分支生成函数
makeBranch(0,0,0,L,a,b,r);
% a在XOZ平面投影与X轴夹角b与Y轴的夹角r与主干的夹角
function makeBranch (x,y,z,L,a,b,r)
B=pi/5;s1=1.5;s2=3;s3=1.2;%B枝干的倾斜度C主干的倾斜度s1细腻程度s2分支收缩速度s3主干收缩速度
% B=pi/5;s1=1.5;s2=2.4;s3=1.35;
if L>s1
x1=x+L/s2*cos(a)*cos(r);
y1=y+L/s2*sin(a);
z1=z+L/s2*cos(a)*sin(r);
x1R=x1+L/s2*cos(a-b)*cos(r);
y1R=y1+L/s2*sin(a-b);
z1R=z1+L/s2*cos(a-b)*sin(r);
x1L=x1+L/s2*cos(a+b)*cos(r);
y1L=y1+L/s2*sin(a+b);
z1L=z1+L/s2*cos(a+b)*sin(r);
x1F=x1+L/s2*cos((a-b)*sin(a))*cos(r+atan(1/cos(a)));
y1F=y1+L/s2*sin((a-b)*sin(a));
z1F=z1+L/s2*cos((a-b)*sin(a))*sin(r+atan(1/cos(a)));
x1B=x1+L/s2*cos((a-b)*sin(a))*cos(r-atan(1/cos(a)));
y1B=y1+L/s2*sin((a-b)*sin(a));
z1B=z1+L/s2*cos((a-b)*sin(a))*sin(r-atan(1/cos(a)));
%------------------------------------------------------
x2=x+L/s2*cos(a)*cos(r);
y2=y+L/s2*sin(a);
z2=z+L/s2*cos(a)*sin(r);
x2R=x2+L/s2*cos(a-b)*cos(r);
y2R=y2+L/s2*sin(a-b);
z2R=z2+L/s2*cos(a-b)*sin(r);
x2L=x2+L/s2*cos(a+b)*cos(r);
y2L=y2+L/s2*sin(a+b);
z2L=z2+L/s2*cos(a+b)*sin(r);
x2F=x2+L/s2*cos((a-b)*sin(a))*cos(r+atan(1/cos(a)));
y2F=y2+L/s2*sin((a-b)*sin(a));
z2F=z2+L/s2*cos((a-b)*sin(a))*sin(r+atan(1/cos(a)));
x2B=x2+L/s2*cos((a-b)*sin(a))*cos(r-atan(1/cos(a)));
y2B=y2+L/s2*sin((a-b)*sin(a));
z2B=z2+L/s2*cos((a-b)*sin(a))*sin(r-atan(1/cos(a)));
plot3([x,x2],[y,y2],[z,z2],'k');hold on;set(gcf,'color','w');grid on;view(pi/2,0);%axis off;xlabel('X Label');ylabel('Y Label');zlabel('Z Label');
set(gca,'xlim',[0,25],'ylim',[-15,15],'zlim',[-15,15]);
plot3([x2,x2R],[y2,y2R],[z2,z2R],'g');hold on;
plot3([x2,x2L],[y2,y2L],[z2,z2L],'g');hold on;
plot3([x2,x2B],[y2,y2B],[z2,z2B],'g');hold on;
plot3([x2,x2F],[y2,y2F],[z2,z2F],'g');hold on;
plot3([x1,x1R],[y1,y1R],[z1,z1R],'g');hold on;
plot3([x1,x1L],[y1,y1L],[z1,z1L],'g');hold on;
plot3([x1,x1B],[y1,y1B],[z1,z1B],'g');hold on;
plot3([x1,x1F],[y1,y1F],[z1,z1F],'g');hold on;
%------------------------------------------------------ makeBranch(x2,y2,z2,L/s3,a,b,r);
makeBranch(x2L,y2L,z2L,L/s2,a,b,r+B);
makeBranch(x2B,y2B,z2B,L/s2,a,b,r-B);
makeBranch(x2F,y2F,z2F,L/s2,a,b,r+B);
makeBranch(x2R,y2R,z2R,L/s2,a,b,r-B);
makeBranch(x1L,y1L,z1L,L/s2,a,b,r+B);
makeBranch(x1B,y1B,z1B,L/s2,a,b,r-B);
makeBranch(x1F,y1F,z1F,L/s2,a,b,r+B);
makeBranch(x1R,y1R,z1R,L/s2,a,b,r-B);
end。
