2014-2015年湖南省湘潭市湘乡二中八年级(上)数学期中试卷及答案
湘教版八年级数学上期中测评综合试卷含答案

湘教版八年级数学(上)期中测评综合卷一、选择题(30分)1、下列计算正确的是( )A.(-1)-1=1;B. (-1)0=0;C.11-=-;D. -(-1)-1=-1;2、用科学记数法表示0.0000061的结果是( )A.56.110-⨯;B. 66.110-⨯;C. 50.6110-⨯;D. 76110-⨯;3、若等腰三角形的顶角为80°,则它的底角度数为( )A. 80°;B. 50°;C. 40°;D. 20°;4、方程21111x x x =+--的解是( ) A. x =-1; B. x =0; C. x =1; D. x =2;5、如图,将三角板的直角顶点放在直尺的一边上, ∠1=30°,∠2=50°,则∠3的度数是( )A. 80°;B. 50°;C. 30°;D. 20°;6、小玲每天骑自行车或步行上学,她上学的路程为2800m ,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行早到30min ,设步行的平均速度为 x m/min ,据题意下面列出的方程正确的是( ) A.28002800304x x -=; B. 28002800304x x-=; C. 28002800305x x -=; D. 28002800305x x-=; 7、已知,如图,点D 、E 分别在△ABC 的边AC 和BC 上,AE 与BD 相交于点F ,给出下面四个条件:①∠1=∠2; ②AD=BE ;③AF=BF ;④DF=EF ;从中选取两个,不能判定△ABC 是等腰三角形的是( ) A. ①②; B. ①④; C. ②③; D. ③④; 8、化简:293()33a a a a a++÷--的结果是( ) A.-a ; B. a ; C. 2(3)a a +; D. 1; 9、如图,在△ABC 中,AB=AC ,点D ,E 在BC 上,连接AD ,AE ,如果只添加一个条件使∠DAB=∠EAC ,则添加的条件不能为( ) A. BD=CE ; B. AD=AE ; C. DA=DE ; D. BE=CD ;10、如图1,M 是铁丝AD 的中点,将该铁丝首尾相接折成△ABC ,且∠B=30°,∠C=100°,如图2,则下列说法正确的是( )1 23 AB C D E F 1 2 AB C D E A D M A BC (D) 30° 100°A.点M 在AB 上;B.点M 在BC 中点处;C.点M 在BC 上,且距点B 较近,距点C 较远;D.点M 在BC 上,且距点C 较近,距点B 较远;二、填空题(24分)11、代数式11x -有意义时,x 满足的条件为 。
2014-2015年湖南省湘潭市湘乡二中八年级上学期数学期中试卷与答案
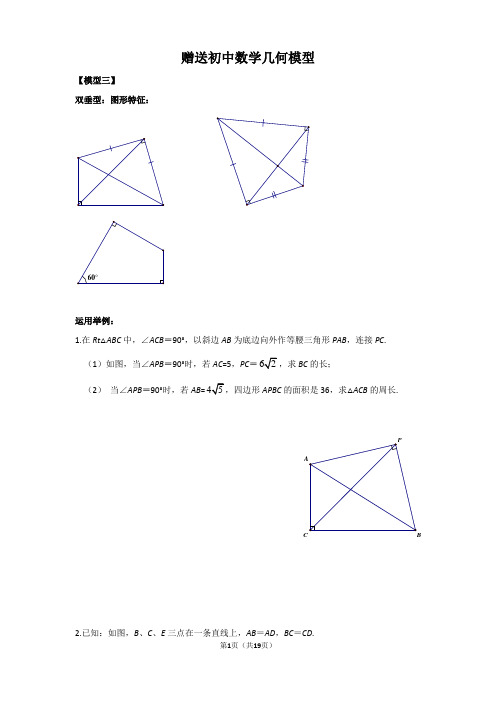
赠送初中数学几何模型【模型三】双垂型:图形特征:60°运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC. (1)如图,当∠APB=90°时,若AC=5,PC=62,求BC的长;(2)当∠APB=90°时,若AB=45APBC的面积是36,求△ACB的周长.P 2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,(1)若AB=3,BC+CD=5,求四边形ABCD的面积(2)若p= BC+CD,四边形ABCD的面积为S,试探究S与p之间的关系。
DBC2014-2015学年湖南省湘潭市湘乡二中八年级(上)期中数学试卷一、选择题(本题满分24分,共8小题,每小题3分)1.(3分)若分式的值为零,那么x的值为()A.x=1或x=﹣1 B.x=1 C.x=﹣1 D.x=02.(3分)下列分式的变形中,正确的是()A.B.C.(a≠0)D.3.(3分)解分式方程,得方程()A.解为x=1 B.解为x=﹣1 C.解为x=3 D.无解4.(3分)到△ABC的三条边距离相等的点是△ABC的()A.三条中线交点B.三条角平分线交点C.三条高的交点D.三条边的垂直平分线交点5.(3分)下列命题中正确的是()A.对顶角一定是相等的B.没有公共点的两条直线是平行的C.相等的两个角是对顶角D.如果|a|=|b|,那么a=b6.(3分)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是()A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA7.(3分)如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是()A.点M在AB上B.点M在BC的中点处C.点M在BC上,且距点B较近,距点C较远D.点M在BC上,且距点C较近,距点B较远8.(3分)运动会上,初二(3)班啦啦队,买了两种价格的雪糕,其中甲种雪糕共花费40元,乙种雪糕共花费30元,甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的1.5倍,若设甲种雪糕的价格为x元,根据题意可列方程为()A.B.C.D.二、填空题(本题满分30分,共10小题,每小题3分)9.(3分)当x时,分式的值不存在.10.(3分),,的最简公分母为.11.(3分)化简:=.12.(3分)随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 74mm2,这个数用科学记数法表示为.13.(3分)两边长为3、6的等腰三角形的周长为.14.(3分)命题“互为相反数的两数的和是0”的逆命题是,它是命题.(填“真、假”)15.(3分)如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是.16.(3分)如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE 交AD于点E,连结EC,则∠ECD的度数是.17.(3分)如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=.18.(3分)如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,则∠A=.三、计算题(每小题7分)19.(7分)计算:.20.(7分)解方程:.21.(7分)先化简再求值:,再在﹣1,0,1,2中选择一个合适的数代入求值.四、几何证明题(本题满分28分,共4小题,每小题7分)22.(7分)如图所示,△ABC中,AC=AD=BD,∠DAC=80°,求∠B的度数.23.(7分)如图,D是△ABC的边AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.24.(7分)如图,AB=AC,∠B=∠C,求证:BD=CD.25.(7分)如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线MN交AC 于点D,交AB于点E.求∠DBC的度数.五、综合题(满分17分,26题8分,27题9分)26.(8分)李明到离家2.4千米的学校参加联欢会,到学校时发现演出道具忘放在家中,此时距联欢会开始还有42分钟,于是他立即步行(匀速)回家,在家拿道具用了1分钟,然后立即骑自行车(匀速)返回学校.已知李明从家骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.(1)李明步行的速度(单位:米/分)是多少?(2)李明能否在联欢会开始前赶到学校?27.(9分)如图,已知△DBC是等腰直角三角形,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E.(1)求证:△BDF≌△CDA;(2)试说明:△ABC是等腰三角形;(3)连结AF并延长,交BC于G点,求证:AG⊥BC.2014-2015学年湖南省湘潭市湘乡二中八年级(上)期中数学试卷参考答案与试题解析一、选择题(本题满分24分,共8小题,每小题3分)1.(3分)若分式的值为零,那么x的值为()A.x=1或x=﹣1 B.x=1 C.x=﹣1 D.x=0【解答】解:依题意,得x2﹣1=0,且x+1≠0,解得x=1.故选:B.2.(3分)下列分式的变形中,正确的是()A.B.C.(a≠0)D.【解答】解:A中的x不是分子、分母的因式,故A错误;B、分子、分母乘的数不同,故B错误;C、(a≠0),故C正确;D、分式的分子、分母同时减去同一个非0的a,分式的值改变,故D错误.故选:C.3.(3分)解分式方程,得方程()A.解为x=1 B.解为x=﹣1 C.解为x=3 D.无解【解答】解:方程的两边同乘(x+1)(x﹣1),得:2(x+1)=4,解得:x=1.检验:把x=1代入(x+1)(x﹣1)=0,即x=1不是原分式方程的解;则原分式方程无解.故选:D.4.(3分)到△ABC的三条边距离相等的点是△ABC的()A.三条中线交点B.三条角平分线交点C.三条高的交点D.三条边的垂直平分线交点【解答】解:∵到△ABC的三条边距离相等,∴这点在这个三角形三条角平分线上,即这点是三条角平分线的交点.故选:B.5.(3分)下列命题中正确的是()A.对顶角一定是相等的B.没有公共点的两条直线是平行的C.相等的两个角是对顶角D.如果|a|=|b|,那么a=b【解答】解:A、对顶角相等,故A选项正确C错误.B、同一个平面内没有公共点的两个直线平行,故B选项错误;C、相等的角不一定是对顶角,故C选项错误;D、绝对值相等两个数,可相等或互为相反数,故D选项错误.故选:A.6.(3分)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是()A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA【解答】解:A、∵∠1=∠2,AD为公共边,若AB=AC,则△ABD≌△ACD(SAS);故A不符合题意;B、∵∠1=∠2,AD为公共边,若BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意;C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);故C不符合题意;D、∵∠1=∠2,AD为公共边,若∠BDA=∠CDA,则△ABD≌△ACD(ASA);故D 不符合题意.故选:B.7.(3分)如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是()A.点M在AB上B.点M在BC的中点处C.点M在BC上,且距点B较近,距点C较远D.点M在BC上,且距点C较近,距点B较远【解答】解:∵∠C=100°,∴AB>AC,如图,取BC的中点E,则BE=CE,∴AB+BE>AC+CE,由三角形三边关系,AC+BC>AB,∴AB<AD,∴AD的中点M在BE上,即点M在BC上,且距点B较近,距点C较远.故选:C.8.(3分)运动会上,初二(3)班啦啦队,买了两种价格的雪糕,其中甲种雪糕共花费40元,乙种雪糕共花费30元,甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的1.5倍,若设甲种雪糕的价格为x元,根据题意可列方程为()A.B.C.D.【解答】解:设甲种雪糕的价格为x元,则甲种雪糕的根数:;乙种雪糕的根数:.可得方程:﹣=20.故选:B.二、填空题(本题满分30分,共10小题,每小题3分)9.(3分)当x=﹣3时,分式的值不存在.【解答】解:∵分式的值不存在,∴x+3=0.解得:x=﹣3.故答案为:=﹣3.10.(3分),,的最简公分母为6x2y2.【解答】解:,,的分母分别是2xy、3x2、6xy2,故最简公分母为6x2y2.故答案为6x2y2.11.(3分)化简:=x+y.【解答】解:==x+y.12.(3分)随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 74mm2,这个数用科学记数法表示为7.4×10﹣7.【解答】解:0.000 000 74=7.4×10﹣7;故答案为:7.4×10﹣7.13.(3分)两边长为3、6的等腰三角形的周长为15.【解答】解:根据三角形三边关系可得出:等腰三角形的腰长为6,底长为3,因此其周长=6+6+3=15.当底边为6,腰为3时,不符合三角形三边关系,此情况不成立.故答案为:15.14.(3分)命题“互为相反数的两数的和是0”的逆命题是和是0的两个数互为相反数,它是真命题.(填“真、假”)【解答】解:逆命题是和是0的两个数互为相反数;根据相反数的意义,知该逆命题是真命题.故答案为:和是0的两个数互为相反数、真.15.(3分)如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是∠A=∠B.【解答】解:添加的条件为∠A=∠B,理由为:∵EC⊥AB,DF⊥AB,∴∠ADF=∠BCE=90°,在△AFD和△BEC中,,∴△AFD≌△BEC(ASA).16.(3分)如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE 交AD于点E,连结EC,则∠ECD的度数是25°.【解答】解:∵BE平分∠ABD,∠ABC=50°,∴∠EBD=∠ABC=25°,∵AD垂直平分线段BC,∴BE=CE,∴∠ECD=∠EBC=25°,故答案为:25°.17.(3分)如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=120°.【解答】解:∵在△ABC中,∠A=180°﹣∠B﹣∠C=60°,∴∠ADE+∠AED=180°﹣∠A=120°.由翻折的性质可知:∠ADE=∠FDE,∠AED=∠FED.∴∠ADF+∠AEF=2(∠ADE+∠AED)=240°.∴∠BDF+∠CEF=360°﹣(∠ADF+∠AEF)=360°﹣240°=120°.故答案为:120°.18.(3分)如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,则∠A=21°.【解答】解:∵AB=BC=CD=DE,∴∠A=∠BCA,∠CBD=∠BDC,∠ECD=∠CED,根据三角形的外角性质,∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,∠A+∠CED=∠EDM,又∵∠EDM=84°,∴∠A+3∠A=84°,解得,∠A=21°,故答案为:21°;三、计算题(每小题7分)19.(7分)计算:.【解答】解:原式=1﹣1﹣4=﹣4.20.(7分)解方程:.【解答】解:去分母得:3x(x﹣2)+x2﹣4=6(x+2),整理得:x2﹣3x﹣4=0,即(x﹣4)(x+1)=0,解得:x=4或x=﹣1,经检验x=4与x=﹣1都为分式方程的解.21.(7分)先化简再求值:,再在﹣1,0,1,2中选择一个合适的数代入求值.【解答】解:原式=[﹣]÷=(﹣)÷=÷=×=,当x=2时,原式=﹣.四、几何证明题(本题满分28分,共4小题,每小题7分)22.(7分)如图所示,△ABC中,AC=AD=BD,∠DAC=80°,求∠B的度数.【解答】解:设∠B=x,∵AC=AD=BD,∠DAC=80°,可得:x+x+80°+2x=180°,解得:x=25°23.(7分)如图,D是△ABC的边AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.【解答】证明:∵FC∥AB,∴∠ADE=∠CFE.在△ADE和△CFE中,∠ADE=∠CFE,DE=FE,∠AED=∠CEF.∴△ADE≌△CFE.24.(7分)如图,AB=AC,∠B=∠C,求证:BD=CD.【解答】证明:连接BC,如图所示:∵AC=AB,∴∠ACB=∠ABC;∵∠DCB=∠ACD﹣∠ACB,∠DBC=∠ABD﹣∠ABC,而∠ACD=∠ABD,∴∠DCB=∠DBC,∴BD=CD.25.(7分)如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线MN交AC 于点D,交AB于点E.求∠DBC的度数.【解答】解:∵AB=AC,∠A=40°,∴∠ABC=(180°﹣∠A)=(180°﹣40°)=70°,∵MN垂直平分线AB,∴AD=BD,∴∠ABD=∠A=40°,∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.五、综合题(满分17分,26题8分,27题9分)26.(8分)李明到离家2.4千米的学校参加联欢会,到学校时发现演出道具忘放在家中,此时距联欢会开始还有42分钟,于是他立即步行(匀速)回家,在家拿道具用了1分钟,然后立即骑自行车(匀速)返回学校.已知李明从家骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.(1)李明步行的速度(单位:米/分)是多少?(2)李明能否在联欢会开始前赶到学校?【解答】解:(1)设李明步行的速度是x米/分,由题意得:=+20,解得:x=80,经检验:x=80是原分式方程的解,答:李明步行的速度是80米/分;(2)++1=41<42,因此李明能在联欢会开始前赶到学校.27.(9分)如图,已知△DBC是等腰直角三角形,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E.(1)求证:△BDF≌△CDA;(2)试说明:△ABC是等腰三角形;(3)连结AF并延长,交BC于G点,求证:AG⊥BC.【解答】证明:(1)∵在等腰Rt△DBC中,BD=CD,∵∠BDC=90°,∴∠BDC=∠ADC=90°,∵在△FBD和△ACD中,,∴△FBD≌△ACD(SAS);(2)∵△FBD≌△ACD,∴∠DBF=∠DCA,∵∠ADC=90°,∴∠DAC+∠A=90°,∴∠DBF+∠A=90°,∴∠AEB=180°﹣(∠DBF+∠A)=90°,∵BF平分∠DBC,∴∠ABF=∠CBF,∵在△ABE和△CBE中,,∴△ABE≌△CBE(ASA),∴AB=CB,∴△ABC是等腰三角形;(3)∵△FBD≌△ACD,∴AD=DF,DB=DC,∵∠ADF=90°,∴∠DAF=∠DFA=45°,∠DCB=45°,∵∠AFD=∠GFC=45°,∴∠FGC=90°,∴AG⊥BC.。
湘教版八年级上册数学期中考试试卷附答案

湘教版八年级上册数学期中考试试题一、单选题1.计算:03-=( )A .-3B .-1C .1D .32.用科学记数法表示0.0000000314为( )A .90.31410-⨯B .93.1410-⨯C .83.1410-⨯D .73.1410-⨯3.若分式293x x --的值为零,则x 的值为( ) A .-3 B .-1 C .3 D .3±4.下列运算正确的是( )A .55835a b a b -=B .1262t t t ÷=C .()222a b a b +=+D .()428216t t -= 5.已知命题“能被2整除的数是偶数”,则其逆命题为( )A .能被2整除的数不是偶数B .不能被2整除的数是偶数C .偶数是能被2整除的数D .偶数不是能被2整除的数6.化简2221211x x x x x x ---++的结果是( ) A .1x B .x C .11x x +- D .11x x -+ 7.甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x 千米/小时,依据题意列方程正确的是( )A .304015x x =-B .304015x x =-C .304015x x =+ D .304015x x =+ 8.如图,AE 、AD 分别是ABC 的高和角平分线,且28B ∠=︒,72C ∠=︒,则DAE ∠的度数为( )A .18°B .22°C .30°D .38°9.已知三角形的两边长分别为4cm 和9cm,则下列长度的线段能作为第三边的是( )A .13cmB .6cmC .5cmD .4m10.三角形一个外角小于与它相邻的内角,这个三角形( )A .是钝角三角形B .是锐角三角形C .是直角三角形D .属于哪一类不能确定.二、填空题11.计算:()()2112x x ---=______.12.如图,在长方形ABCD 中,对角线AC ,BD 交于点O ,若120AOD ∠=︒,2AB =,则CO 的长为________.13.如图,AC=BD ,AC ,BD 交于点O ,要使△ABC△△DCB ,只需添加一个条件,这个条件可以是______.14.计算:2222342•()()a b a b a ----÷=______________.15.如图,若△OAD△△OBC ,且△O=65°,△C=20°,则△OAD=__度.16.已知23,25x y ==,则212x y --的值为____________.17.如图所示,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则△ABC 的度数为 _____.18.如图,ACD ∠是ABC 的外角,ABC ∠的平分线与ACD ∠的平分线交于点1A ,1A BC ∠的平分线与1A CD ∠的平分线交于点2A ,…,1n A BC -∠的平分线与1n A CD -∠的平分线交于点n A ,设=A θ∠,则2=A ∠___________,=n A ∠___________.19.已知D 、E 分别是△ABC 的边BC 和AC 的中点,若△ABC 的面积=36cm ,则△DEC 的面积为__________.三、解答题20.解方程:23193x x x +=--21.计算:21211x x x x x-+-+-22.如图,在四边形ABCD中,AB=CB,AD=CD.求证△C=△A.23.化简,再求值:22112x xx x x--÷+,其中x=224.如图,在四边形ABCD中,//AD BC,E为CD的中点,连接AE、BE,BE△AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.25.已知:如图,△ABC=50°,△ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求△D、△E、△DAE的度数.26.如图,点D,E在线段BC上,BD=CE,△ADE=△AED,证明△ABC是等腰三角形.27.如图1,点P 、Q 分别是等边△ABC 边AB 、BC 上的动点(端点除外),点P 从顶点A 、点Q 从顶点B 同时出发,且它们的运动速度相同,连接AQ 、CP 交于点M .(1)求证:ABQ CAP ≌△△:(2)当点P 、Q 分别在AB 、BC 边上运动时,△QMC 的大小变化吗?若变化,请说明理由:若不变,求出它的度数.(3)如图2,若点P 、Q 在运动到终点后继续在射线AB 、BC 上运动,直线AQ 、CP 相交于点M ,则△QMC 的大小变化吗?若变化,请说明理由:若不变,则求出它的度数.参考答案1.B【解析】【分析】依题意,依据零指数幂定义及性质进行求解即可;【详解】由题知,零指数幂为:01a =(0)a ≠;可得:031=,△03(1)1-=-=-;故选:B ;【点睛】本题考查零指数幂的定义和性质,关键在负号“-”的理解;2.C【解析】【分析】依题意,依据科学记数法的基本形式转换即可;【详解】由题知,科学记数法的基本形式为:10n a ⨯ (110,)a n ≤<为正整数或负整数;△80.0000000314 3.1410-=⨯;故选:C【点睛】本题考查科学记数法,关键在熟练科学记数法的基本形式及要求;3.A【解析】【分析】根据分式的值为零的条件即可求出答案.【详解】解:由题意可知:29030x x ⎧-=⎨-≠⎩解得:x=-3,故选:A .【点睛】本题考查分式的值,解题的关键是熟练运用分式的值为零的条件.4.D【解析】【分析】直接利用合并同类项、同底数幂的乘法、幂的乘方、完全平方公式进行进行判断即可;【详解】A 、555835a b a b a b -= ,故A 错误;B 、1266t t t ÷= ,故B 错误;C 、()2222a b a ab b +=++ ,故C 错误;D 、()428216t t -= ,故D 正确;故选:D .【点睛】本题考查了合并同类项、同底数幂的乘法、幂的乘方、完全平方公式,正确掌握计算方法是解题的关键.5.C【解析】【分析】依题意,写出原命题中的条件和结论,然后按照逆命题的要求,交换结论和条件即可;【详解】由题知,原命题为:能被2整除的数是偶数;原命题的条件为:一个数能被2整数;原命题的结论为:这个数则为偶数;逆命题:一个数是偶数,则这个数能被2整除;故选:C【点睛】本题考查命题及其四种命题的转换,关键在写出原命题的条件和结论;6.B【解析】【分析】先把分式的分子和分母因式分解,再约分即可求解.【详解】原式()()()()211111x x x x x x --=++-x =故选:B .【点睛】本题考查分式的乘法,解题的关键是熟练掌握分子和分母的因式分解,利用到的知识点是分式的基本性质和约分.7.C【解析】 【分析】题中等量关系:甲车行驶30千米与乙车行驶40千米所用时间相同,据此列出关系式.【详解】△甲车的速度为x 千米/小时,则乙车的速度为(x+15)千米/小时△甲车行驶30千米的时间为30x,乙车行驶40千米的时间为4015x +, △根据甲车行驶30千米与乙车行驶40千米所用时间相同得304015x x =+. 故选C .8.B【解析】【分析】 根据角平分线性质和三角形内角和定理求解即可;【详解】△AE 是ABC 的高,△90AEB AEC ∠=∠=︒,又△AD 是ABC 的角平分线,△BAD CAD ∠=∠,△28B ∠=︒,72C ∠=︒,△40BAD CAD ∠=∠=︒,△180407268ADC ∠=︒-︒-︒=︒,△906822DAE ∠=︒-︒=︒;故答案选B .【点睛】本题主要考查了角平分线的性质和三角形内角和定义,准确分析计算是解题的关键. 9.B【解析】【分析】根据三角形的三边关系,两边之和大于第三边,两边之差小于第三边可求得第三边取值范围.【详解】设第三边长度为a ,根据三角形三边关系9494a 解得513a .只有B 符合题意故选B.【点睛】本题考查三角形三边关系,能根据关系求得第三边的取值范围是解决此题的关键.10.A【解析】【分析】由三角形的外角与它相邻的内角互为邻补角,且根据此外角小于与它相邻的内角,可得此外角为锐角,与它相邻的角为钝角,可得这个三角形为钝角三角形.【详解】△三角形的外角与它相邻的内角互补,且此外角小于与它相邻的内角,△此外角为锐角,与它相邻的角为钝角,则这个三角形为钝角三角形.故选:A .【点睛】此题考查了三角形的外角性质,其中得出三角形的外角与它相邻的内角互补是解本题的关键.11.214x -【解析】【分析】原式利用平方差公式计算即可得到答案;【详解】原式=()()2121214x x x -+--=- , 故答案为:214x - .【点睛】本题考查了平方差公式,熟练掌握平方差公式是解题的关键;12.2【解析】【分析】根据题意120AOD ∠=,得到60AOB ∠=,再根据OA OB =可以得到AOB 为等边三角形,再根据矩形的对角线互相平分,得到OA OC AB ==,即可得到答案.【详解】解:△120AOD ∠=△60AOB ∠=又△长方形ABCD 中,对角线AC ,BD 交于点O ,△O 为AC,BD 的中点,且AC=BD,△OA OB =△AOB 为等边三角形△2OA AB ==△四边形ABCD 是长方形△AC 、BD 相等且互相平分△2OC OA AB ===故答案为:2.【点睛】本题主要考查矩形的性质和等边三角形的判定,解题的关键在于判断AOB 为等边三角形.13.AB=DC【解析】根据全等三角形的判定,可以用SSS解题.【详解】解:△AC=BD,BC=BC当添加条件为AB=DC时,即可判定△ABC△△DCB,故答案为AB=DC(答案不唯一)【点睛】本题考查了全等三角形的判定,属于简答题,掌握证明全等的方法是解题关键.14.8b【解析】【分析】幂的乘方,法则为:底数不变,指数相乘;同底数幂相乘,法则为:底数不变,指数相加,积的乘方等于先把每个因数乘方,再把所得的幂相乘,此题先算乘方,再算乘除即可.【详解】原式=a−2b2△a−6b6÷a−8= a−8 b8÷a−8=b8,故答案为b8【点睛】本题考查整式的混合运算,负整数指数幂,同底数幂的乘法,幂的乘方与积的乘方,解题关键是熟练掌握幂的有关运算法则.15.95【解析】【详解】根据三角形内角和定理可得:△OBC=180°-20°-65°=95°,根据三角形全等的性质可得:△OAD=△OBC=95°.故答案为:9516.9 10【解析】根据同底数幂的除法底数不变指数相减,幂的乘方,可得答案.【详解】解:212x y -- = 22x ÷2y ÷2=(2x )2 ÷ 2y ÷2=9÷5÷2 =910故答案为910. 【点睛】本题考查同底数幂的除法、幂的乘方,熟记法则并根据法则计算是解题关键.17.45︒【解析】【分析】如图,连接AC ,根据勾股定理即可得到AB ,BC ,AC 的长度,勾股定理的逆定理判断ABC的形状,进而可得出△ABC 的度数.【详解】解:如图,连接AC ,由勾股定理得:AC BC ==10AB,△222+=, △222AC BC AB +=,△△ABC 是等腰直角三角形,△△ABC =45°,故答案为:45°.【点睛】本题考查了勾股定理,勾股定理的逆定理,等腰三角形的判定与性质.解题的关键在于判断ABC 的形状.18. 4θ 2n θ 【解析】【分析】根据三角形的外角性质可得△ACD=△A+△ABC ,△A 1CD=△A 1+△A 1BC ,根据角平分线的定义可得△A 1BC=12△ABC ,△A 1CD=12△ACD ,整理得到△A 1=12△A ,同理可得△A 2=12△A 1,从而判断出后一个角是前一个角的12,然后表示出△A n 即可得答案.【详解】△ACD ∠是ABC 的外角,△A 1CD 是△A 1BC 的外角,△△ACD=△A+△ABC ,△A 1CD=△A 1+△A 1BC ,△ABC ∠的平分线与ACD ∠的平分线交于点1A ,△△A 1BC=12△ABC ,△A 1CD=12△ACD , △△A 1=12△A ,同理可得△A 2=12△A 1=14△A , △△A=θ,△△A 2=4θ, 同理:△A 3 =12△A 2=382θθ=, △A 4=12△A 3 =4162θθ= ……△△A n =2n θ. 故答案为:4θ,2n θ【点睛】 本题考查了三角形的外角性质及角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和;熟记性质并准确识图,求出后一个角是前一个角的12是解题的关键.19.9 cm .【解析】【详解】试题分析:△D 是△ABC 的边BC 的中点,△S △ACD =36÷2=18(cm 2);又△E 是AC 的中点,△S △DEC =18÷2=9(cm 2).故答案为9 cm .考点:三角形的面积.20.4x =-【解析】【分析】根据解分式方程的基本步骤解方程即可.【详解】 解:23193xx x +=--方程两边同时乘(3)(3)x x -+可得:3+(3)x x +=(3)(3)x x -+,去括号可得:22339x x x ++=-,移项合并同类项可得:312x =-,解得:4x =-,将4x =-代入(3)(3)x x -+可得:(3)(3)x x -+=7≠0,△原方程的解为:4x =-【点睛】本题主要考查分式方程,注意解方程最后要检验,防止无解的情况出现.21.-1【解析】【分析】根据分式的性质计算即可;【详解】原式()()()221111x x x x x --=---,()2211x x xx --+=-,()()2211x x --=-,1=-.【点睛】本题主要考查了分式的加减运算,准确计算是解题的关键.22.见解析【解析】【分析】先连接BD ,由AB =CB 、AD =CD 、BD=BD 可证△ABD△△CBD ,即可证得结论.【详解】证明:如图:连接BD ,△在△ABD 和△CBD 中,AB BC AD CD BD BD =⎧⎪=⎨⎪=⎩△△ABD△△CBD ,△△C =△A .【点睛】本题主要考查了全等三角形的判定与性质,正确作出辅助线、灵活运用SSS 证明三角形全等是解答本题的关键.23.12x x ++;34. 【解析】【分析】先化除法为乘法进行化简,然后代入求值.【详解】解:原式=()(1)(1)21x x x x x x +-⋅+- =12x x ++, 将x=2代入,原式=213224+=+. 【点睛】本题考查了分式的化简求值,不应考虑把x 的值直接代入,通常做法是先把分式化简,然后再代入求值.24.(1)证明见解析;(2)证明见解析.【解析】【分析】(1)先根据平行线的性质可得,F DAE ECF D ∠=∠∠=∠,再根据线段中点的定义可得CE DE =,然后根据三角形全等的判定定理与性质即可得证;(2)先根据三角形全等的性质可得FE AE =,再根据线段垂直平分线的判定与性质可得AB FB =,然后根据线段的和差、等量代换即可得证.【详解】(1)//AD BC ,,F DAE ECF D ∴∠=∠∠=∠,点E 是CD 的中点,CE DE ∴=,在CEF △和DEA △中,F DAE ECF D CE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()CEF DEA AAS ∴≅,FC AD ∴=;(2)由(1)已证:CEF DEA ≅,FE AE ∴=,又BE AE⊥,∴是线段AF的垂直平分线,BE∴==+,AB FB BC FC=,由(1)可知,FC AD∴=+.AB BC AD【点睛】本题考查了平行线的性质、三角形全等的判定定理与性质、线段垂直平分线的判定与性质等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.25.△D=25°,△E=40°,△DAE=115°.【解析】【详解】△ABC=25°;同试题分析:由△ABC=50°,DB=BA,据三角形外角性质可得△D=△DAB=12理可得△E=40°;由三角形内角和定理可得△BAC=50°,即可得△DAE的度数.△ABC=25°;试题解析:解:△△ABC=50°,DB=BA,△△D=△DAB=12△ACB=40°;同理可得△E=△CAE=12△在△ABC中,△ABC=50°,△ACB=80°,△△BAC=50°,△△DAE=△DAB+△BAC+△CAE=115°.考点:1.三角形内角和定理;2.三角形的外角性质.26.证明见试题解析.【解析】【详解】试题分析:先证△ABD△△AEC,进而证出结论.试题解析:证明:△△ADE=△AED,△AD=AE,△BDA=△CEA,△BD=CE,△△ABD△△AEC,△AB=AC,△△ABC是等腰三角形.考点:1.等腰三角形的判定;2.全等三角形的性质和判定.27.(1)证明见解析(2)△QMC的大小不变,△QMC=60°(3)△QMC的大小不变,△QMC=120°【解析】【分析】(1)根据等边三角形的性质,利用SAS 证明△ABQ△△CAP ;(2)由△ABQ△△CAP 根据全等三角形的性质可得△BAQ=△ACP ,从而得到△QMC=60°;(3)由△ABQ△△CAP 根据全等三角形的性质可得△BAQ=△ACP ,从而得到△QMC=120°.(1)证明:△△ABC 是等边三角形△△ABQ =△CAP =60°,AB =CA ,又△点P 、Q 运动速度相同,△AP =BQ ,在△ABQ 与△CAP 中,△AB CAABQ CAP BQ AP=⎧⎪∠=∠⎨⎪=⎩,△ABQ CAP ≌△△(SAS );(2)解:点P 、Q 分别在AB 、BC 边上运动时,△QMC 的大小不变,△QMC =60°.理由:△ABQ CAP ≌△△,△△BAQ =△ACP ,△△QMC =△ACP +△MAC ,△△QMC =△BAQ +△MAC =△BAC =60°(3)解:点P 、Q 在运动到终点后继续在射线AB 、BC 上运动时,△QMC 的大小不变. 理由:同理可得ABQ CAP ≌△△,△△BAQ =△ACP ,△△QMC =△BAQ +△APM ,△△QMC =△ACP +△APM =180°-△PAC =180°-60°=120°.。
湘教版八年级数学上册期中试卷(附答案)

湘教版八年级数学上册期中试卷(附答案)班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.已知直角三角形两边的长为3和4,则此三角形的周长为( ) A .12B .7+7C .12或7+7D .以上都不对2.将抛物线22y x =向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ). A .22(2)3y x =++; B .22(2)3y x =-+; C .22(2)3y x =--;D .22(2)3y x =+-.3.已知三角形的三边长分别为2,a -1,4,则化简|a -3|+|a -7|的结果为( )A .2a -10B .10-2aC .4D .-44.下列选项中,矩形具有的性质是( ) A .四边相等 B .对角线互相垂直 C .对角线相等D .每条对角线平分一组对角5.已知一个多边形的内角和为1080°,则这个多边形是( ) A .九边形B .八边形C .七边形D .六边形6.欧几里得的《原本》记载,形如22x ax b +=的方程的图解法是:画Rt ABC ∆,使90ACB ∠=,2aBC =,AC b =,再在斜边AB 上截取2a BD =.则该方程的一个正根是( )A .AC 的长B .AD 的长C .BC 的长D .CD 的长7.如图,矩形纸片ABCD 中,已知AD =8,折叠纸片使AB 边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为()A.3 B.4 C.5 D.68.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是()A.B.C.D.9.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )A.y=-2x+24(0<x<12) B.y=-x+12(0<x<24)C.y=2x-24(0<x<12) D.y=x-12(0<x<24)10.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是().A.45°B.60°C.75°D.85°二、填空题(本大题共6小题,每小题3分,共18分)1.16的平方根是 .2.已知AB//y 轴,A 点的坐标为(3,2),并且AB=5,则B 的坐标为________. 3.若关于x 的分式方程2222x m m x x+=--有增根,则m 的值为_______. 4.如图,直线y=x+b 与直线y=kx+6交于点P (3,5),则关于x 的不等式x+b>kx+6的解集是_________.5.在平面直角坐标系内,一次函数y =k 1x +b 1与y =k 2x +b 2的图象如图所示,则关于x ,y 的方程组1122y k x b y k x b -=⎧⎨-=⎩的解是________.6.如图,在ABC 中,点D 是BC 上的点,40BAD ABC ︒∠=∠=,将ABD ∆沿着AD 翻折得到AED ,则CDE ∠=______°.三、解答题(本大题共6小题,共72分)1.解方程组(1)327413x y x y +=⎧⎨-=⎩ (2)143()2()4xy x y x y ⎧-=-⎪⎨⎪+--=⎩2.先化简,再求值:2222222a ab b a ab a b a a b-+-÷--+,其中a ,b 满足2(2)1a b-++=.3.解不等式组3(2)2513212x xxx+≥+⎧⎪⎨+-<⎪⎩,并把不等式组的解集在数轴上表示出来.4.如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC,(1)求∠BAE的度数;(2)求∠DAE的度数.5.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A在x轴上,AB=AC,∠BAC=90°,且A(2,0)、B(3,3),BC交y轴于M,(1)求点C的坐标;(2)连接AM,求△AMB的面积;(3)在x轴上有一动点P,当PB+PM的值最小时,求此时P的坐标.6.某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的35,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、C2、B3、C4、C5、B6、B7、D8、D9、B10、C二、填空题(本大题共6小题,每小题3分,共18分)1、±2.2、(3,7)或(3,-3)3、14、x>3.5、21xy=⎧⎨=⎩.6、20三、解答题(本大题共6小题,共72分)1、(1)31xy=⎧⎨=-⎩;(2)4989xy⎧=-⎪⎪⎨⎪=⎪⎩.2、1a b-+,-13、–1≤x<34、(1) ∠BAE=30 °;(2) ∠EAD=20°.5、(1)C的坐标是(﹣1,1);(2)154;(3)点P的坐标为(1,0).6、(1)该网店甲种羽毛球每筒的售价为60元,乙种羽毛球每筒的售价为45元;(2)①进货方案有3种,具体见解析;②当m=78时,所获利润最大,最大利润为1390元.。
2014-2015学年八年级上学期期中联考数学试题(含答案)

2014-2015学年八年级上学期期中联考数学试题(含答案)(时间:100分钟,满分:100分)一、选择题(每题3分,共30分)1、下面各组线段中,能组成三角形的是( )A .5,11,6B .8,8,16C .10,5,4D .6,9,14 2、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等.其中真命题的个数有( )A.3个B.2个C.1个D.0个 3、一个多边形内角和是10800,则这个多边形的边数为 ( ) A 、 6 B 、 7 C 、 8 D 、 9 4、等腰三角形的一个角是50,则它的底角是( ) A. 50 B. 50或65 C 、80 D 、65 5、和点P (2,5-)关于x 轴对称的点是( )A (-2,5-)B (2,5-)C (2,5)D (-2,5) 6、已知直角三角形中30°角所对的直角边为2 cm ,则斜边的长为( ). A .2 cm B .4 cm C .6 cm D .8 cm7、如图,已知12=∠∠,AC AD =,增加下列条件:①AB AE =;②BC ED =;③C D =∠∠;④B E =∠∠.其中能使ABC AED △≌△的条件有( ) A.4个 B.3个C.2个 D.个8、如图,先将正方形纸片对折,折痕为MN ,再把B 点折叠在折痕MN 上,折痕为AE ,点B 在MN 上的对应点为H ,沿AH 和DH 剪下,这样剪得的三角形中 ( ) A .AD DH AH ≠= B .AD DH AH == C .DH AD AH ≠= D .AD DH AH ≠≠9、如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,∠A 与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )A .∠A=∠1+∠2B .2∠A=∠1+∠2C .3∠A=2∠1+∠2D .3∠A=2(∠1+∠2)10、把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( ) A .对应点连线与对称轴垂直 B .对应点连线被对称轴平分 C .对应点连线被对称轴垂直平分 D .对应点连线互相平行 二、填空题(每题3分,共24分)11、为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条这样做的道理是_________ ______。
湘教2014年上学期八年级数学期中考试试卷

ACBD BAEDC2014年上学期八年级数学期中测试卷(满分120分)命题: 唐爱国 审题:唐跃瑞一、选择题:(每小题3分,共30分)1、△ABC 中各角的度数之比如下,能够说明△ABC 是直角三角形的是( )A.1:2:3B.2:3:4C.3:4:5D.3:2:52.三角形中,到三边距离相等的点是( ) A.三条边的垂直平分线的交点 B.三条高的交点 C.三条中线的交点 D.三条角平分线的交点3.如右图,Rt △ABC 中,∠C=90°,∠B=30°,AD 是∠BAC 的 平分线,AD=10,则点D 到AB 的距离是( )A.8B.5C.6D.4 (第3题图) 4. 已知一个多边形的内角和是720°,则这个多边形是( )A .四边形B .五边形C .六边形D .七边形 5、下列图形中既是轴对称图形,又是中心对称图形的是( )A 、平行四边形B 、等边三角形C 、矩形D 、直角三角形6. 下列性质中,矩形具有但平行四边形不一定具有的是( )A .对边相等B .对角相等C .对角线相等D .对角线互相平分 7、如图所示,以正方形ABCD 中AD 边为一边向外作等边ΔADE , 则∠AEB =( ).A 、10°B 、15°C 、20°D 、12.5°8、如图,在△ABC 中,E ,D ,F 分别是AB ,BC ,CA 的中点, AB=6,AC=4,则四边形AEDF•的周长是( ) A .10 B .20 C .30 D .409.如点P(a,2)在第二象限,那么点Q(-3,a)在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限10.如图,有一张直角三角形纸片,两直角边长AC =6 cm ,BC =8 cm ,将△ABC 折叠,使点B 与点A 重合,折痕为DE ,则CD 等于( )A.425cm B.322 cm C. 47cm D. 35 cm二、填空题:(每小题3分,共30分)11. 在⊿ABC 中,∠ACB=90°,D 是AB 的中点,AB=6,则CD=________. 12. 已知,如图AB =AD =5,∠B =150, CD ⊥AB 于C ,则CD =__________.13. 在□ABCD 中,若∠A +∠C=120°,则∠B = .14.如图,一棵大树在一次强台风中于离地面3米处折断倒下,倒下 树尖部分与树根距离为4米,这棵大树原来的高度为__________米. 15. 三角形的三边长分别是3cm ,5cm ,6cm ,则连结三边中点所围成的三角形的周长是_________cm.16.坐标系中将点A(2,1)向左平移2个单位长度得到点A ′,则A ′的坐标为_________.17.菱形的两条对角线的长为24和10,则菱形的边长是 .面积是__________.18. 有三个内角是直角的四边形是;对角线互相垂直平分的四边形是.19.已知:如图5—127,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6cm,AC=8cm,则△ADE的周长为______.20. 如右图,△ABC中,CD⊥AB于D,若AD=2BD,AC=52,BC=5,则BD的长为__________.答卷二、填空题11._____________,12._____________,13._____________,14._____________,15._____________16._____________,17.___________,___________,18._____________,___________,19._____________, 20._____________三、解答题(8+8+8+8+8+10+10=60分)21.(8分)如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.求证:(1)AE=CF;(2)AB∥CD.ABCDEFGHABCDO22.(8分)在平面直角坐标系中,△ABC 的三个顶点如图所示.(1)请画出△ABC 关于y 轴对称的图形△A ′B ′C ′(其中A ′、B ′、C ′分别是A 、B 、C 的对应点,不写画法); (2)直接写出A ′、B ′、C ′三点的坐标.23如图,已知矩形ABCD 的两条对角线相交于O ,∠AOD=120度,AB=4cm ,求此矩形的面积.(8分)24.如图所示,在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点. 求证:四边形EFGH 是平行四边形。
湖南省湘乡市第二中学2014-2015学年八年级(上)竞赛数学试题
22a b a b ab a b ∙⎧⎨⎩≥,当时,,当<时湘乡二中八年级数学竞赛试题(时间:90分钟,满分:120分)一、选择题(5×5=25分)1、实数m =20053-2005,下列各数中不能整除m 的是( ) A.2006B.2005C.2004D.20032、如图,在Rt △ACB 中,∠ACB =90°,∠A =25°,D 是AB 上一点.将Rt △ABC 沿CD 折叠,使B 点落在AC 边上的B ′处,则∠ADB ′等于( )3、如图,从下列四个条件:①BC =B ′C , ②AC =A ′C ,③∠A ′CA =∠B ′CB ,④AB =A ′B ′中,任取三个为条件,余下的一个为结论构成命题,则最多可以构成正确命题的个数是( ) A .1个 B .2个C .3个D .4个(第2题) (第3题) (第4题)4、如图,点E 、F 、G 、H 、M 、N 分别在△ABC 的BC 、AC 、AB 边上,且NH ∥MG ∥BC ,ME ∥NF ∥AC ,GF ∥EH ∥A B .有黑、白两只蚂蚁,它们同时同速从F 点出发,黑蚁沿路线F →N →H →E →M →G →F 爬行,白蚁沿路线F →B →A →C →F 爬行,那么( ) A.黑蚁先回到F 点 B.白蚁先回到F 点C.两只蚂蚁同时回到F 点D.哪只蚂蚁先回到F 点视各点的位置而定5、对a ,b ,定义运算“*”如下:a *b = 已知3*m =36 ,则实数m 等于( ) A. 23 B.4 C. 23±D.A. 25B .30° C . 35°D.40°423±或A BCE FMNGH2241720336m n m n ++-+=二、填空题(5×5=25分)6、设a =-350,b =-440,c =-530,则a ,b ,c 中最大的是 。
湖南省湘潭市八年级上学期数学期中考试试卷
湖南省湘潭市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2019九上·徐闻期末) 如图图形中,既是轴对称图形又是中心对称图形的是()A .B .C .D .2. (2分) (2018七上·东台月考) 在下列各数中,无理数是()A . ﹣B . ﹣0.1C .D . 363. (2分)已知等腰三角形底边长为10cm,腰长为13cm,则腰上的高为()A . 12cmB . cmC . cmD . cm4. (2分) (2018八上·惠来月考) 以下列各组数为三边的三角形中不是直角三角形的是()A . 9、12、15B . 41、40、9C . 25、7、24D . 6、5、45. (2分) (2018八下·深圳期中) 如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C 顺时针方向旋转900得到△DCF,连结EF,若∠BEC=62°,则∠EFD的度数为()A . 15°B . 16°C . 17°D . 18°6. (2分) (2019八上·大荔期末) 如图,要测量河两岸相对两点A,B间的距高,先在过点B的AB的垂线上取两点C,D,使得CD=BC,再在过点D的垂线上取点E,使A,C,E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A,B两点间的距离,这里判定△EDC≌△ABC的理由是()A . SASB . SSSC . ASAD . AAS7. (2分) (2019九上·龙华期末) 如图,在边长4的正方形ABCD中,E是边BC的中点,将△CDE沿直线DE 折叠后,点C落在点F处,冉将其打开、展平,得折痕DE。
连接CF、BF、EF,延长BF交AD于点G。
湘教版八年级数学上册期中试卷【加答案】
湘教版八年级数学上册期中试卷【加答案】 班级: 姓名: 一、选择题(本大题共10小题,每题3分,共30分)1.一次函数()224y k x k =++-的图象经过原点,则k 的值为( )A .2B .2-C .2或2-D .3 2.若12x y x -=有意义,则x 的取值范围是( ) A .1x 2≤且x 0≠ B .1x 2≠ C .1x 2≤ D .x 0≠3.成人每天维生素D 的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为( )A .74610-⨯B .74.610-⨯C .64.610-⨯D .50.4610-⨯4.用配方法解方程2890x x ++=,变形后的结果正确的是( )A .()249x +=-B .()247x +=-C .()2425x +=D .()247x += 5.实数a ,b 在数轴上对应点的位置如图所示,化简|a|+2()a b +的结果是( )A .﹣2a-bB .2a ﹣bC .﹣bD .b 6.已知1112a b -=,则ab a b-的值是( ) A .12 B .-12 C .2 D .-27.关于x 的一元二次方程2(1)210k x x +-+=有两个实数根,则k 的取值范围是( )A .0k ≥B .0k ≤C .0k <且1k ≠-D .0k ≤且1k ≠-8.下列关于一次函数()0,0y kx b k b =+<>的说法,错误的是( )A .图象经过第一、二、四象限B .y 随x 的增大而减小C .图象与y 轴交于点()0,bD .当b x k>-时,0y > 9.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )A .0.7米B .1.5米C .2.2米D .2.4米10.如图,在平行四边形ABCD 中,∠ABC 的平分线交AD 于E ,∠BED=150°,则∠A 的大小为( )A .150°B .130°C .120°D .100°二、填空题(本大题共6小题,每小题3分,共18分)1.因式分解:3222x x y xy +=﹣__________. 2.已知菱形ABCD 的面积是12cm 2,对角线AC =4cm ,则菱形的边长是______cm .3.64的算术平方根是________.4.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是__________(用a 、b 的代数式表示).5.如图是一张长方形纸片ABCD ,已知AB=8,AD=7,E 为AB 上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP ),使点P 落在长方形ABCD 的某一条边上,则等腰三角形AEP 的底边长是_____________.6.如图所示,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则ABC ∠的度数为________.三、解答题(本大题共6小题,共72分)1.解方程:(1)11322x x x -=--- (2)311x x x-=-2.先化简,再求值:3x 4x 2x x 1x 1--⎛⎫-÷ ⎪--⎝⎭,其中1x 2=.3.己知关于x 的一元二次方程x 2+(2k+3)x+k 2=0有两个不相等的实数根x 1,x 2.(1)求k 的取值范围;(2)若1211x x +=﹣1,求k 的值.4.如图,将矩形ABCD 沿对角线AC 翻折,点B 落在点E 处,FC 交AD 于F .(1)求证:△AFE ≌△CDF ;(2)若AB =4,BC =8,求图中阴影部分的面积.5.已知:如图所示,AD平分BAC,M是BC的中点,MF//AD,分别交CA延长线,AB于F、E.求证:BE=CF.6.在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.(1)求降价后每枝玫瑰的售价是多少元?(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、A2、A3、C4、D5、A6、D7、D8、D9、C10、C二、填空题(本大题共6小题,每小题3分,共18分) 1、()2x x y -23、4、ab5、56、45° 三、解答题(本大题共6小题,共72分)1、(1)无解;(2)32x =. 2、x 2-,32-. 3、(1)k >﹣34;(2)k=3. 4、(1)略;(2)10.5、略.6、(1)2元;(2)至少购进玫瑰200枝.。
新湘教版八年级2014年上学期期中考试数学试卷
八年级2014年上学期期中考试数学试卷班级姓名一、选择题:(每题3分,共24分)1、点(-2,1)在平面直角坐标系中所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限2、下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.3、下列命题中,正确的是()A.平行四边形的对角线相等B.矩形的对角线互相垂直C.菱形的对角线互相垂直且平分D.菱形的对角线相等4、如图,在平面直角坐标系xOy中,点P(3-,5)关于y轴的对称点的坐标为()A.(3-,5-) B.(3,5) C.(3.5-) D.(5,3-)5、如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E式垂足,连接CD,若BD=1,则AC的长是()A.23B.2C.43D.46、顺次连结矩形四边中点所得的四边形一定是()A.正方形B.矩形C.菱形D.等腰梯形7、如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么影阴部分的面积是矩形ABCD面积的()。
A、15B、14C、13D、310FE第8题第7题第4题第5题8、如图,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B ′处,若AE =2,DE =6,∠EFB =60°,则矩形ABCD 的面积是( )A .12B .24C . 123D . 163二、填空题:(每题3分,共24分)9、已知一个多边形的内角和是1080°,这个多边形的边数是 。
10、将点A (2,1)向左..平移2个单位长度得到点A ′,则点A ′的坐标是 。
11、已知ABC ∆的各边长度分别为3cm ,5cm ,6 cm ,连结各边中点所构成的DEF ∆的周长是 cm .12、在□ABCD 中,AB=3㎝,AD=8㎝,∠ABC 的平分线交AD 于E ,交CD 于F , 则DF= 。
13、如图,Rt △ABC 中,∠ C=90° ,AD 平分∠BAC,交BC 于点D,CD=4,则点D 到AB 的距离为________.14、如图,在菱形ABCD 中,AC =6, BD =8,则菱形的面积为 .15、如图,在平面直角坐标系中,矩形OABC 的对角线AC 平行于x 轴,边OA 与x 轴正半轴的夹角为30°,OC=2,则点B 的坐标是 .16、如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0)(2,1),(1,1)(1,2)(2,2),……,根据这个规律,第2014个点的横坐标为 .三、解答题:(共7小题,前二题6分,后五题8分,共52分)17、如图,已知90B D ∠=∠=,AB AD =.求证:BC DC =.第13题第12题 F E D C B A 第14题图 第15题 第16题A C D B18、已知:如图,在ABCD 中,AE 平分BAD ∠,交BC 于点E .(1)求证:ABE ∆是等腰三角形; (2)若6AB =,10AD =,求CE 的长.19、如图,已知BE ∥DF ,∠ADF=∠CBE ,AF=CE 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年湖南省湘潭市湘乡二中八年级(上)期中数学试卷一、选择题(本题满分24分,共8小题,每小题3分)1.(3分)若分式的值为零,那么x的值为()A.x=1或x=﹣1 B.x=1 C.x=﹣1 D.x=02.(3分)下列分式的变形中,正确的是()A.B.C.(a≠0)D.3.(3分)解分式方程,得方程()A.解为x=1 B.解为x=﹣1 C.解为x=3 D.无解4.(3分)到△ABC的三条边距离相等的点是△ABC的()A.三条中线交点B.三条角平分线交点C.三条高的交点D.三条边的垂直平分线交点5.(3分)下列命题中正确的是()A.对顶角一定是相等的B.没有公共点的两条直线是平行的C.相等的两个角是对顶角D.如果|a|=|b|,那么a=b6.(3分)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是()A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA7.(3分)如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是()A.点M在AB上B.点M在BC的中点处C.点M在BC上,且距点B较近,距点C较远D.点M在BC上,且距点C较近,距点B较远8.(3分)运动会上,初二(3)班啦啦队,买了两种价格的雪糕,其中甲种雪糕共花费40元,乙种雪糕共花费30元,甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的1.5倍,若设甲种雪糕的价格为x元,根据题意可列方程为()A.B.C.D.二、填空题(本题满分30分,共10小题,每小题3分)9.(3分)当x时,分式的值不存在.10.(3分),,的最简公分母为.11.(3分)化简:=.12.(3分)随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 74mm2,这个数用科学记数法表示为.13.(3分)两边长为3、6的等腰三角形的周长为.14.(3分)命题“互为相反数的两数的和是0”的逆命题是,它是命题.(填“真、假”)15.(3分)如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是.16.(3分)如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE 交AD于点E,连结EC,则∠ECD的度数是.17.(3分)如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=.18.(3分)如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,则∠A=.三、计算题(每小题7分)19.(7分)计算:.20.(7分)解方程:.21.(7分)先化简再求值:,再在﹣1,0,1,2中选择一个合适的数代入求值.四、几何证明题(本题满分28分,共4小题,每小题7分)22.(7分)如图所示,△ABC中,AC=AD=BD,∠DAC=80°,求∠B的度数.23.(7分)如图,D是△ABC的边AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.24.(7分)如图,AB=AC,∠B=∠C,求证:BD=CD.25.(7分)如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线MN交AC 于点D,交AB于点E.求∠DBC的度数.五、综合题(满分17分,26题8分,27题9分)26.(8分)李明到离家2.4千米的学校参加联欢会,到学校时发现演出道具忘放在家中,此时距联欢会开始还有42分钟,于是他立即步行(匀速)回家,在家拿道具用了1分钟,然后立即骑自行车(匀速)返回学校.已知李明从家骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.(1)李明步行的速度(单位:米/分)是多少?(2)李明能否在联欢会开始前赶到学校?27.(9分)如图,已知△DBC是等腰直角三角形,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E.(1)求证:△BDF≌△CDA;(2)试说明:△ABC是等腰三角形;(3)连结AF并延长,交BC于G点,求证:AG⊥BC.2014-2015学年湖南省湘潭市湘乡二中八年级(上)期中数学试卷参考答案与试题解析一、选择题(本题满分24分,共8小题,每小题3分)1.(3分)若分式的值为零,那么x的值为()A.x=1或x=﹣1 B.x=1 C.x=﹣1 D.x=0【解答】解:依题意,得x2﹣1=0,且x+1≠0,解得x=1.故选:B.2.(3分)下列分式的变形中,正确的是()A.B.C.(a≠0)D.【解答】解:A中的x不是分子、分母的因式,故A错误;B、分子、分母乘的数不同,故B错误;C、(a≠0),故C正确;D、分式的分子、分母同时减去同一个非0的a,分式的值改变,故D错误.故选:C.3.(3分)解分式方程,得方程()A.解为x=1 B.解为x=﹣1 C.解为x=3 D.无解【解答】解:方程的两边同乘(x+1)(x﹣1),得:2(x+1)=4,解得:x=1.检验:把x=1代入(x+1)(x﹣1)=0,即x=1不是原分式方程的解;则原分式方程无解.故选:D.4.(3分)到△ABC的三条边距离相等的点是△ABC的()A.三条中线交点B.三条角平分线交点C.三条高的交点D.三条边的垂直平分线交点【解答】解:∵到△ABC的三条边距离相等,∴这点在这个三角形三条角平分线上,即这点是三条角平分线的交点.故选:B.5.(3分)下列命题中正确的是()A.对顶角一定是相等的B.没有公共点的两条直线是平行的C.相等的两个角是对顶角D.如果|a|=|b|,那么a=b【解答】解:A、对顶角相等,故A选项正确C错误.B、同一个平面内没有公共点的两个直线平行,故B选项错误;C、相等的角不一定是对顶角,故C选项错误;D、绝对值相等两个数,可相等或互为相反数,故D选项错误.故选:A.6.(3分)如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是()A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA【解答】解:A、∵∠1=∠2,AD为公共边,若AB=AC,则△ABD≌△ACD(SAS);故A不符合题意;B、∵∠1=∠2,AD为公共边,若BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意;C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);故C不符合题意;D、∵∠1=∠2,AD为公共边,若∠BDA=∠CDA,则△ABD≌△ACD(ASA);故D 不符合题意.故选:B.7.(3分)如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是()A.点M在AB上B.点M在BC的中点处C.点M在BC上,且距点B较近,距点C较远D.点M在BC上,且距点C较近,距点B较远【解答】解:∵∠C=100°,∴AB>AC,如图,取BC的中点E,则BE=CE,∴AB+BE>AC+CE,由三角形三边关系,AC+BC>AB,∴AB<AD,∴AD的中点M在BE上,即点M在BC上,且距点B较近,距点C较远.故选:C.8.(3分)运动会上,初二(3)班啦啦队,买了两种价格的雪糕,其中甲种雪糕共花费40元,乙种雪糕共花费30元,甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的1.5倍,若设甲种雪糕的价格为x元,根据题意可列方程为()A.B.C.D.【解答】解:设甲种雪糕的价格为x元,则甲种雪糕的根数:;乙种雪糕的根数:.可得方程:﹣=20.故选:B.二、填空题(本题满分30分,共10小题,每小题3分)9.(3分)当x=﹣3时,分式的值不存在.【解答】解:∵分式的值不存在,∴x+3=0.解得:x=﹣3.故答案为:=﹣3.10.(3分),,的最简公分母为6x2y2.【解答】解:,,的分母分别是2xy、3x2、6xy2,故最简公分母为6x2y2.故答案为6x2y2.11.(3分)化简:=x+y.【解答】解:==x+y.12.(3分)随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 74mm2,这个数用科学记数法表示为7.4×10﹣7.【解答】解:0.000 000 74=7.4×10﹣7;故答案为:7.4×10﹣7.13.(3分)两边长为3、6的等腰三角形的周长为15.【解答】解:根据三角形三边关系可得出:等腰三角形的腰长为6,底长为3,因此其周长=6+6+3=15.当底边为6,腰为3时,不符合三角形三边关系,此情况不成立.故答案为:15.14.(3分)命题“互为相反数的两数的和是0”的逆命题是和是0的两个数互为相反数,它是真命题.(填“真、假”)【解答】解:逆命题是和是0的两个数互为相反数;根据相反数的意义,知该逆命题是真命题.故答案为:和是0的两个数互为相反数、真.15.(3分)如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是∠A=∠B.【解答】解:添加的条件为∠A=∠B,理由为:∵EC⊥AB,DF⊥AB,∴∠ADF=∠BCE=90°,在△AFD和△BEC中,,∴△AFD≌△BEC(ASA).16.(3分)如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE 交AD于点E,连结EC,则∠ECD的度数是25°.【解答】解:∵BE平分∠ABD,∠ABC=50°,∴∠EBD=∠ABC=25°,∵AD垂直平分线段BC,∴BE=CE,∴∠ECD=∠EBC=25°,故答案为:25°.17.(3分)如图,点D、E分别是AB、AC上的点,将△ABC沿着DE对折,A点落在BC边的F点上,若∠B=50°,∠C=70°,则∠BDF+∠CEF=120°.【解答】解:∵在△ABC中,∠A=180°﹣∠B﹣∠C=60°,∴∠ADE+∠AED=180°﹣∠A=120°.由翻折的性质可知:∠ADE=∠FDE,∠AED=∠FED.∴∠ADF+∠AEF=2(∠ADE+∠AED)=240°.∴∠BDF+∠CEF=360°﹣(∠ADF+∠AEF)=360°﹣240°=120°.故答案为:120°.18.(3分)如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,则∠A=21°.【解答】解:∵AB=BC=CD=DE,∴∠A=∠BCA,∠CBD=∠BDC,∠ECD=∠CED,根据三角形的外角性质,∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,∠A+∠CED=∠EDM,又∵∠EDM=84°,∴∠A+3∠A=84°,解得,∠A=21°,故答案为:21°;三、计算题(每小题7分)19.(7分)计算:.【解答】解:原式=1﹣1﹣4=﹣4.20.(7分)解方程:.【解答】解:去分母得:3x(x﹣2)+x2﹣4=6(x+2),整理得:x2﹣3x﹣4=0,即(x﹣4)(x+1)=0,解得:x=4或x=﹣1,经检验x=4与x=﹣1都为分式方程的解.21.(7分)先化简再求值:,再在﹣1,0,1,2中选择一个合适的数代入求值.【解答】解:原式=[﹣]÷=(﹣)÷=÷=×=,当x=2时,原式=﹣.四、几何证明题(本题满分28分,共4小题,每小题7分)22.(7分)如图所示,△ABC中,AC=AD=BD,∠DAC=80°,求∠B的度数.【解答】解:设∠B=x,∵AC=AD=BD,∠DAC=80°,可得:x+x+80°+2x=180°,解得:x=25°23.(7分)如图,D是△ABC的边AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.【解答】证明:∵FC∥AB,∴∠ADE=∠CFE.在△ADE和△CFE中,∠ADE=∠CFE,DE=FE,∠AED=∠CEF.∴△ADE≌△CFE.24.(7分)如图,AB=AC,∠B=∠C,求证:BD=CD.【解答】证明:连接BC,如图所示:∵AC=AB,∴∠ACB=∠ABC;∵∠DCB=∠ACD﹣∠ACB,∠DBC=∠ABD﹣∠ABC,而∠ACD=∠ABD,∴∠DCB=∠DBC,∴BD=CD.25.(7分)如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线MN交AC 于点D,交AB于点E.求∠DBC的度数.【解答】解:∵AB=AC,∠A=40°,∴∠ABC=(180°﹣∠A)=(180°﹣40°)=70°,∵MN垂直平分线AB,∴AD=BD,∴∠ABD=∠A=40°,∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.五、综合题(满分17分,26题8分,27题9分)26.(8分)李明到离家2.4千米的学校参加联欢会,到学校时发现演出道具忘放在家中,此时距联欢会开始还有42分钟,于是他立即步行(匀速)回家,在家拿道具用了1分钟,然后立即骑自行车(匀速)返回学校.已知李明从家骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.(1)李明步行的速度(单位:米/分)是多少?(2)李明能否在联欢会开始前赶到学校?【解答】解:(1)设李明步行的速度是x米/分,由题意得:=+20,解得:x=80,经检验:x=80是原分式方程的解,答:李明步行的速度是80米/分;(2)++1=41<42,因此李明能在联欢会开始前赶到学校.27.(9分)如图,已知△DBC是等腰直角三角形,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E.(1)求证:△BDF≌△CDA;(2)试说明:△ABC是等腰三角形;(3)连结AF并延长,交BC于G点,求证:AG⊥BC.【解答】证明:(1)∵在等腰Rt△DBC中,BD=CD,∵∠BDC=90°,∴∠BDC=∠ADC=90°,∵在△FBD和△ACD中,,∴△FBD≌△ACD(SAS);(2)∵△FBD≌△ACD,∴∠DBF=∠DCA,∵∠ADC=90°,∴∠DAC+∠A=90°,∴∠DBF+∠A=90°,∴∠AEB=180°﹣(∠DBF+∠A)=90°,∵BF平分∠DBC,∴∠ABF=∠CBF,∵在△ABE和△CBE中,,∴△ABE≌△CBE(ASA),∴AB=CB,∴△ABC是等腰三角形;(3)∵△FBD≌△ACD,∴AD=DF,DB=DC,∵∠ADF=90°,∴∠DAF=∠DFA=45°,∠DCB=45°,∵∠AFD=∠GFC=45°,∴∠FGC=90°,∴AG⊥BC.。
