蚁群算法综述
蚁群算法概述ACO

在众多NP-难度的组合优化问题的应用中,当蚁群优化算法与局部搜索相结合时,算法表现出来的性能最好,局部搜索算法局部地优化蚂蚁构建的解,这些经局部优化的解将在信息更新步骤中使用。
在ACO算法中使用局部搜索算法,两者能够相互补充。
两者的结合可以有效地提高蚂蚁构建的解得质量。
蚁群算法收敛速度慢、易陷入局部最优。
蚁群算法中初始信息素匮乏。
蚁群算法一般需要较长的搜索时间,其复杂度可以反映这一点;而且该方法容易出现停滞现象,即搜索进行到一定程度后,所有个体发现的解完全一致,不能对解空间进一步进行搜索,不利于发现更好的解(群体智能算法的主要特点是个体之间可以交互信息,从而提高全局搜索能力,但同时陷入局部最优是群体智能算法都可能存在的问题。
所以现在遗传和蚁群的文章中,有提利用其全局能力强去解决问题的,也有提易陷入局部最优的,从而去改进的)。
下面是几篇综述文章中的说法。
段海滨是南航毕业的博士,现在北航,写了本蚁群算法的书,蚁群算法他在国内算是做的比较多的。
虽然算法具有分布式并行机制、易于与其他算法相结合、具有鲁棒性等优点,但搜索时间长、易陷入局部最优是其突出缺点[段海滨,王道波,朱家强.蚁群算法理论及应用研究进展[J].控制与决策,2004, 19(12):1321—1326,134] 近年来,国内外学者在蚁群算法的模型改进和应用方面做了大量的工作,其共同目的是在合理时间复杂度的限制条件下,尽可能提高蚁群算法在一定空间复杂度下的寻优能力,从而改善蚁群算法的全局收敛性,并拓宽蚁群算法的应用领域[段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005]目前对蚁群算法的研究,不仅有算法意义上的研究,还有从仿真模型角度的研究, 并且不断有学者提出对蚁群算法的改进方案:有的将蚁群算法与遗传算法相结合,有的给蚁群系统加入变异特征,还有的提出所谓最大最小蚁群算法(MMAS).应当指出, 现阶段对蚁群算法的研究还只是停留在仿真阶段,尚未能提出一个完善的理论分析,对它的有效性也没有给出严格的数学解释.但是,从以前模糊控制所碰到的情况看,理论上的不完善并不妨碍应用,有时应用还会超前于理论,并推动理论研究,蚁群算法也是如此.(忻斌健,江镭,吴启迪,蚁群算法的研究现状和应用及蚂蚁智能体的硬件实现,同济大学学报,,2002,30(1).)蚁群与其他算法的融合策略:(1)针对蚁群算法初始信息素匮乏的缺点,采用其他算法生成初始信息素分布,利用蚁群算法求精确解,从而提高时间效率和求解精度。
蚁群算法及案例分析精选全文

群在选择下一条路径的时
候并不是完全盲目的,而是
按一定的算法规律有意识
地寻找最短路径
自然界蚁群不具有记忆的
能力,它们的选路凭借外
激素,或者道路的残留信
息来选择,更多地体现正
反馈的过程
人工蚁群和自然界蚁群的相似之处在于,两者优先选择的都
是含“外激素”浓度较大的路径; 两者的工作单元(蚂蚁)都
正反馈、较强的鲁棒性、全
局性、普遍性
局部搜索能力较弱,易出现
停滞和局部收敛、收敛速度
慢等问题
优良的分布式并行计算机制
长时间花费在解的构造上,
导致搜索时间过长
Hale Waihona Puke 易于与其他方法相结合算法最先基于离散问题,不
能直接解决连续优化问题
蚁群算法的
特点
蚁群算法的特点及应用领域
由于蚁群算法对图的对称性以
及目标函数无特殊要求,因此
L_ave=zeros(NC_max,1);
%各代路线的平均长度
while NC<=NC_max
%停止条件之一:达到最大迭代次数
% 第二步:将m只蚂蚁放到n个城市上
Randpos=[];
for i=1:(ceil(m/n))
Randpos=[Randpos,randperm(n)];
end
Tabu(:,1)=(Randpos(1,1:m))';
scatter(C(:,1),C(:,2));
L(i)=L(i)+D(R(1),R(n));
hold on
end
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)])
蚁群算法概述

Thank You!
L/O/G/O
2.2蚁群算法的实现
那么,t时刻位于城市i的蚂蚁k选择城市j为目标城市的概 率是:
ij (t ) ij (t ) k p ij (t ) ik (t ) ik (t ) k tabu k 0
( j tabu
k
)
otherwise
k
ACS模型中
T
k ij
Q L k 0
Q d ij 0
若第 k 只蚂蚁用边( 其它
i ,j )
AQS模型中
T
k ij
若第 k 只蚂蚁用边 其它
i , j
ADS模型中
T ij
k
Q 0
若第 k 只蚂蚁用边( 其它
i ,j)
Lk di j分别表示第k 只蚂蚁走的总长和ij 城市之间的距离,q 未常数。
1991年M· Dorigo等人首先提出了蚁群算法(Ant Colony Algorithms),人们开始了对蚁群的研究:相对 弱小,功能并不强大的个体是如何完成复杂的工作的。 在此基础上一种很好的优化算法逐渐发展起来。
Macro Dorigo
2.1蚁群算法原理
正如在关于蚁群算法的第1篇文章中指出的:
2.2蚁群算法的实现
首先,了解一个问题:TSP。 旅行商问题(Traveling Salesman Problem)又译 为旅行推销员问题、货郎担问题,是数学领域中著名问 题之一。假设有一个旅行商人要拜访n个城市,他必须 选择所要走的路径,路径的限制是每个城市只能拜访一 次,而且最后要回到原来出发的城市。路径的选择目标 是要求得的路径路程为所有路径之中的最小值。
蚁群算法——精选推荐
蚁群算法⼀、蚁群算法简介 蚁群算法(AG)是⼀种模拟蚂蚁觅⾷⾏为的模拟优化算法,它是由意⼤利学者Dorigo M等⼈于1991年⾸先提出,并⾸先使⽤在解决TSP(旅⾏商问题)上。
之后,⼜系统研究了蚁群算法的基本原理和数学模型.⼆、蚁群算法原理1、蚂蚁在路径上释放信息素。
2、碰到还没⾛过的路⼝,就随机挑选⼀条路⾛。
同时,释放与路径长度有关的信息素。
3、信息素浓度与路径长度成反⽐。
后来的蚂蚁再次碰到该路⼝时,就选择信息素浓度较⾼路径。
4、最优路径上的信息素浓度越来越⼤。
5、最终蚁群找到最优寻⾷路径。
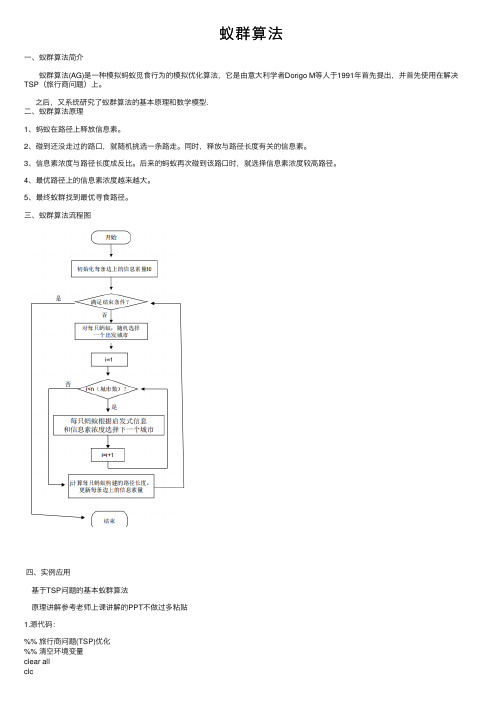
三、蚁群算法流程图四、实例应⽤基于TSP问题的基本蚁群算法原理讲解参考⽼师上课讲解的PPT不做过多粘贴1.源代码:%% 旅⾏商问题(TSP)优化%% 清空环境变量clear allclc%% 导⼊数据citys = ceil(rand(50,2)*50000)%load newcitys.mat%% 计算城市间相互距离fprintf('Computing Distance Matrix... \n');n = size(citys,1);D = zeros(n,n);for i = 1:nfor j = 1:nif i ~= jD(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));elseD(i,j) = 1e-4;endendend%% 初始化参数fprintf('Initializing Parameters... \n');m = 50; % 蚂蚁数量alpha = 1; % 信息素重要程度因⼦beta = 5; % 启发函数重要程度因⼦rho = 0.05; % 信息素挥发因⼦Q = 1; % 常系数Eta = 1./D; % 启发函数Tau = ones(n,n); % 信息素矩阵Table = zeros(m,n); % 路径记录表iter = 1; % 迭代次数初值iter_max = 150; % 最⼤迭代次数Route_best = zeros(iter_max,n); % 各代最佳路径Length_best = zeros(iter_max,1); % 各代最佳路径的长度Length_ave = zeros(iter_max,1); % 各代路径的平均长度%% 迭代寻找最佳路径figure;while iter <= iter_maxfprintf('迭代第%d次\n',iter);% 随机产⽣各个蚂蚁的起点城市start = zeros(m,1);for i = 1:mtemp = randperm(n);start(i) = temp(1);endTable(:,1) = start;% 构建解空间citys_index = 1:n;% 逐个蚂蚁路径选择for i = 1:m% 逐个城市路径选择for j = 2:ntabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)allow_index = ~ismember(citys_index,tabu);allow = citys_index(allow_index); % 待访问的城市集合P = allow;% 计算城市间转移概率for k = 1:length(allow)P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta; endP = P/sum(P);% 轮盘赌法选择下⼀个访问城市Pc = cumsum(P);target_index = find(Pc >= rand);target = allow(target_index(1));Table(i,j) = target;endend% 计算各个蚂蚁的路径距离Length = zeros(m,1);for i = 1:mRoute = Table(i,:);for j = 1:(n - 1)Length(i) = Length(i) + D(Route(j),Route(j + 1));endLength(i) = Length(i) + D(Route(n),Route(1));end% 计算最短路径距离及平均距离if iter == 1[min_Length,min_index] = min(Length);Length_best(iter) = min_Length;Length_ave(iter) = mean(Length);Route_best(iter,:) = Table(min_index,:);else[min_Length,min_index] = min(Length);Length_best(iter) = min(Length_best(iter - 1),min_Length);Length_ave(iter) = mean(Length);if Length_best(iter) == min_LengthRoute_best(iter,:) = Table(min_index,:);elseRoute_best(iter,:) = Route_best((iter-1),:);endend% 更新信息素Delta_Tau = zeros(n,n);% 逐个蚂蚁计算for i = 1:m% 逐个城市计算for j = 1:(n - 1)Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); endDelta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); endTau = (1-rho) * Tau + Delta_Tau;% 迭代次数加1,清空路径记录表% figure;%最佳路径的迭代变化过程[Shortest_Length,index] = min(Length_best(1:iter));Shortest_Route = Route_best(index,:);plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');pause(0.3);iter = iter + 1;Table = zeros(m,n);% endend%% 结果显⽰[Shortest_Length,index] = min(Length_best);Shortest_Route = Route_best(index,:);disp(['最短距离:' num2str(Shortest_Length)]);disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);%% 绘图figure(1)plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');grid onfor i = 1:size(citys,1)text(citys(i,1),citys(i,2),[' ' num2str(i)]);endtext(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');xlabel('城市位置横坐标')ylabel('城市位置纵坐标')title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])figure(2)plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')legend('最短距离','平均距离')xlabel('迭代次数')ylabel('距离')title('各代最短距离与平均距离对⽐')运⾏结果:利⽤函数citys = ceil(rand(50,2)*50000) 随机产⽣五⼗个城市坐标2.研究信息素重要程度因⼦alpha, 启发函数重要程度因⼦beta,信息素挥发因⼦rho对结果的影响为了保证变量唯⼀我重新设置五⼗个城市信息进⾏实验在原来设值运⾏结果:实验结果可知当迭代到120次趋于稳定2.1 alpha值对实验结果影响(1)当alpha=4时运⾏结果实验结果可知当迭代到48次左右趋于稳定(2)当alpha=8时运⾏结果:有图可知迭代40次左右趋于稳定,搜索性较⼩(3)当alpha= 0.5运⾏结果:有图可知迭代到140次左右趋于稳定(4)当alpha=0.2时运⾏结果:结果趋于110次左右稳定所以如果信息素因⼦值设置过⼤,则容易使随机搜索性减弱;其值过⼩容易过早陷⼊局部最优2.2 beta值对实验影响(1)当 beta=8时运⾏结果结果迭代75次左右趋于稳定(2)当 beta=1时运⾏结果:结果迭代130次左右趋于稳定所以beta如果值设置过⼤,虽然收敛速度加快,但是易陷⼊局部最优;其值过⼩,蚁群易陷⼊纯粹的随机搜索,很难找到最优解2.3 rho值对实验结果影响(1)当rho=3时运⾏结果:结果迭代75次左右趋于稳定(2)当rho=0.05运⾏结果:结果迭代125次左右趋于稳定所以如果rho取值过⼤时,容易影响随机性和全局最优性;反之,收敛速度降低总结:蚁群算法对于参数的敏感程度较⾼,参数设置的好,算法的结果也就好,参数设置的不好则运⾏结果也就不好,所以通常得到的只是局部最优解。
蚁群算法简述及实现

蚁群算法简述及实现1 蚁群算法的原理分析蚁群算法是受自然界中真实蚁群算法的集体觅食行为的启发而发展起来的一种基于群体的模拟进化算法,属于随机搜索算法,所以它更恰当的名字应该叫“人工蚁群算法”,我们一般简称为蚁群算法。
M.Dorigo等人充分的利用了蚁群搜索食物的过程与著名的TSP问题的相似性,通过人工模拟蚁群搜索食物的行为来求解TSP问题。
蚂蚁这种社会性动物,虽然个体行为及其简单,但是由这些简单个体所组成的群体却表现出及其复杂的行为特征。
这是因为蚂蚁在寻找食物时,能在其经过的路径上释放一种叫做信息素的物质,使得一定范围内的其他蚂蚁能够感觉到这种物质,且倾向于朝着该物质强度高的方向移动。
蚁群的集体行为表现为一种正反馈现象,蚁群这种选择路径的行为过程称之为自催化行为。
由于其原理是一种正反馈机制,因此也可以把蚁群的行为理解成所谓的增强型学习系统(Reinforcement Learning System)。
引用M.Dorigo所举的例子来说明蚁群发现最短路径的原理和机制,见图1所示。
假设D 和H之间、B和H之间以及B和D之间(通过C)的距离为1,C位于D和B的中央(见图1 (a))。
现在我们考虑在等间隔等离散世界时间点(t=0,1,2……)的蚁群系统情况。
假设每单位时间有30只蚂蚁从A到B,另三十只蚂蚁从E到D,其行走速度都为1(一个单位时间所走距离为1),在行走时,一只蚂蚁可在时刻t留下浓度为1的信息素。
为简单起见,设信息素在时间区间(t+1,t+2)的中点(t+1.5)时刻瞬时完全挥发。
在t=0时刻无任何信息素,但分别有30只蚂蚁在B、30只蚂蚁在D等待出发。
它们选择走哪一条路径是完全随机的,因此在两个节点上蚁群可各自一分为二,走两个方向。
但在t=1时刻,从A到B的30只蚂蚁在通向H的路径上(见图1 (b))发现一条浓度为15的信息素,这是由15只从B走向H的先行蚂蚁留下来的;而在通向C的路径上它们可以发现一条浓度为30的信息素路径,这是由15只走向BC的路径的蚂蚁所留下的气息与15只从D经C到达B留下的气息之和(图1 (c))。
蚁群算法概述

作业4蚁群算法概述1.蚁群算法的基本思想现实生活中单个蚂蚁的能力和智力非常简单,但它们能通过相互协调、分工、合作来完成筑巢、觅食、迁徙、清扫蚁穴等复杂行为,尤其是蚂蚁有能力在没有任何可见提示的条件下找到从蚁穴到食物源的最短路径,并且能随环境的变化而变化地搜索新的路径,产生新的选择。
这是因为蚂蚁在其走过的路上会分泌一种信息素,其他的蚂蚁能够感知这种物质的存在和强度,并以此指导自己的运动方向,使其倾向于朝着信息素强度高的方向移动。
蚁群算法就是从自然界中真实蚂蚁觅食的群体行为中得到启发而提出的。
在蚁群算法中,为了实现对真实蚂蚁的抽象,提出了人工蚁的概念。
人工蚁和真实蚂蚁有如下相同点:(1)人工蚁和蚂蚁一样,是一群相互合作的个体,每个蚂蚁都能建立一种解决方案,整个蚁群相互合作在全局范围内找出问题的较优的解决方案。
(2)人工蚁和真实蚂蚁有着公共的任务,寻找最优路径。
(3)人工蚁和真实蚂蚁一样也通过使用信息素进行间接通讯。
(4)人工蚁和真实蚂蚁的觅食行为都是一种正反馈过程。
(5)在蚁群算法中存在一种信息素的挥发机制,类似于真实世界中的情况,(6)不预测未来状态概率的状态转移策略。
人工蚁的策略是充分利用了局部信息,而没有前瞻性的预测未来的状态。
图1:二元桥实验初始状态图2:二元桥实验结束状态2. 蚁群算法基本原理蚁群算法[3]可以表述如下:初始时刻,各条路径上的信息素量相等,设τij(0) = C (C 为常数),蚂蚁k (k=1,2,3,…,m )在运动过程中根据各条路径上的信息量决定转移方向。
蚂蚁系统所使用的转移规则被称为随机比例规则,在时刻 t ,蚂蚁 k 从城市i 选择城市j 的转移概率k ij p (t)为:[][]k ()()(), if j J ()()()0, otherwise k ijij k is is ij s J i t t i t p t αβαβτητη∈⎧⎡⎤⎡⎤⋅⎣⎦⎣⎦⎪∈⎪⋅=⎨⎪⎪⎩∑ (2. 1)其中,Jk(i)= {1,2,……,n}- tabuk 表示蚂蚁 k 下一步允许选择的城市。
蚁群算法基本原理

蚁群算法基本原理
蚁群算法(Ant Colony Algorithm)是一种基于模拟蚁群行为的优化算法,用于解决复杂的优化问题。
其原理是模拟蚂蚁寻找食物的行为,在寻找过程中通过信息素来引导蚂蚁探索最优解。
基本流程:
1. 初始化:将蚂蚁随机分散在问题空间中,每只蚂蚁都随机选择一个起点。
2. 蚂蚁搜索:每只蚂蚁根据一定的概率选择下一个节点,概率与当前节点的信息素有关,如果信息素较高则该节点被选中的概率较大。
3. 信息素更新:每只蚂蚁在搜索过程中会留下一定的信息素,当搜索完成后,信息素会根据一定的规则进行更新,具体规则可以为:信息素浓度与路径长度成反比例关系,或者信息素挥发速度固定。
4. 最优解记录:当所有蚂蚁完成搜索后,从它们所走过的路径中选择获得最优解,并将该路径上的信息素浓度进行更新。
5. 重复搜索:重复上述所有步骤,直到达到设定的迭代次数或者满足终止条件。
蚁群算法基本原理就是通过模拟蚁群行为,通过信息素的引导来搜索最优解。
在
实际应用中,蚁群算法可以用于解决诸如旅行商问题、作业调度问题、路径规划问题、图像分割问题等优化问题。
《蚁群算法介绍》课件

输出最优解和相关性能指标。
详细描述
这一步是将最优解和相关性能指标输出,以 便于对算法的性能进行分析和评估。
04
蚁群算法的性能分析
收敛性分析
收敛速度
蚁群算法在优化问题中的收敛速度取决于初始信息素分布、蚂蚁数量、迭代次数等因素 。
最优解质量
蚁群算法在某些问题上可能找到全局最优解,但在其他问题上可能只能找到近似最优解 。
VS
详细描述
这一步是生成初始解的过程,需要按照设 定的规则,将蚂蚁随机放置在解空间中, 并初始化每条路径上的信息素。
迭代优化
总结词
通过蚂蚁的移动和信息素的更新,不断优化 解的质量。
详细描述
这一步是蚁群算法的核心部分,通过模拟蚂 蚁的移动和信息素的更新机制,不断迭代优 化解的质量,最终找到最优解。
结果
多目标优化问题的蚁群算法
针对多目标优化问题,蚁群算法需要 进行相应的改进。
VS
多目标优化问题要求算法在满足多个 冲突目标的同时找到最优解。这需要 对蚁群算法进行相应的调整,以适应 多目标优化的特性。例如,可以通过 引入权重因子来平衡各个目标之间的 矛盾,或者采用非支配排序方法对解 进行分层处理,以便更好地处理多目 标优化问题。
蚁群算法的优化目标
寻找最短路径
蚁群算法的主要目标是找到起点到终 点之间的最短路径,这在实际应用中 可用于解决如旅行商问题、车辆路径 问题等优化问题。
平衡搜索与探索
蚁群算法需要在搜索和探索之间取得 平衡,以避免陷入局部最优解,提高 算法的全局搜索能力。
03
蚁群算法的实现步骤
问题建模
总结词
将实际问题抽象为蚁群算法能够解决的问题模型。
蚂蚁根据局部信息素浓度选择移动方向,倾向于选择信息素浓度较高的路径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《智能计算—蚁群算法基本综述》班级:研1102班专业:计算数学姓名:**学号:**********2012年蚁群算法基本综述刘鑫(西安理工大学理学院,研1102班,西安市,710054)摘要:蚁群算法( ACA)是一种广泛应用于优化领域的仿生进化算法。
ACA发展背景着手,分析比较国内外ACA研究团队与发展情况立足于基本原理,分析其数学模型,介绍了六种经典的改进模型,对其优缺点进行分析,简要总结其应用领域并对其今后的发展、应用做出展望。
关键词:蚁群;算法;优化;改进;应用0引言专家发现单个蚂蚁只具有一些简单的行为能力。
但整个蚁群却能完成一系列复杂的任务。
这种现象是通过高度组织协调完成的1991年。
意大利学者M.Dorigo 首次提出一种新型仿生算法ACA。
研究了蚂蚁的行为。
提出其基本原理及数学模型。
并将之应用于寻求旅行商问题(TSP)的解。
通过实验及相关理论证明,ACA有着有着优化的选择机制的本质。
而这种适应和协作机制使之具有良好的发现能力及其它算法所没有的优点。
如较强的鲁棒性、分布式计算、易与其他方法结合等;但同时也不应忽略其不足。
如搜索时间较长,若每步进行信息素更新,计算仿真时所占用CPU时间过长:若当前最优路径不是全局最优路径,但其信息素浓度过高时。
靠公式对信息素浓度的调整不能缓解这种现象。
会陷人局部收敛无法寻找到全局最优解:转移概率过大时,虽有较快的收敛速度,但会导致早熟收敛。
所以正反馈原理所引起的自催化现象意在强化性能好的解,却容易出现停滞现象。
笔者综述性地介绍了ACA对一些已有的提出自己的想法,并对其应用及发展前景提出了展望。
1 蚁群算法概述ACA源自于蚁群的觅食行为。
S.Goss的“双桥”实验说明蚂蚁总会选择距食物源较短的分支蚂蚁之间通过信息素进行信息的传递,捷径上的信息素越多,吸引的蚂蚁越多。
形成正反馈机制,达到一种协调化的高组织状态该行为称集体自催化目前研究的多为大规模征兵,即仅靠化学追踪的征兵。
1 .1 蚁群算法的基本原理为便于研究提出以下基本假设:蚂蚁间通过信息素和环境进行间接通信:蚂蚁对环境的反应由其内部模决定:蚂蚁个体是独立的,但群体却呈现出一种随机性。
蚂蚁通过适应 和协作两个阶段的 调整从无序到有序,得到最优解,完成对路径的搜索。
对路径的选择,重点在转移概率,即某时刻蚂k 在城市i 选择城市i 的概率的大小。
⎪⎪⎩⎪⎪⎨⎧∈∈≤•=∑∈)()()()()(),(]}),([]),(max {[arg )(0k allowed s is is ij ij k k ij allowed j t t t t allowed u q q u r u r t P k βαβαβαητητητ (1)其中,0q 和q 分别为]1,0[上的参数和均匀分布的随机数,其大小决定了利用先验知识与探 索新路径之间的相对重要性。
若0q q ≤,则转移概率选取上面一个式子,即按照先验知识选择最好的边,否则,按照转移概率选择一条边,式1又被称为伪随机比例规则;k allowed j ∈为蚂蚁k 下一 步允许选择的城市;)(t is η为能见度因子;u 为禁忌表;α,β分别反映蚂蚁在运动过程中所积累的信息和启发信息在蚂蚁选择路径中的相对重要性;)(•τ为信息素浓度的函数根据不同的模型,信息素做不同的调整,如全局更新规则和局部更新规则。
2 蚁群算法的发展蚁群优化(ACO )研究受到真实蚁群行为启发的智能系统,常用于解决离散优化问题启发式ACO 是1991年由Dorigo 和Gambardella 提出定义的。
2.1 国外蚁群算法的发展概况2.1.1 有关蚁群算法的研究团队从ACO 提出至今,越来越多的专家投身于蚁群算法的研究之中,其中较为突出的有以下四个:(1)瑞士卢加诺IDSIA 。
1998年建立是IDSIA 是非营利性研究人工智能研究所,2000年成为公共研究机构,隶属于卢加诺大学的信息学院和瑞士意大利语区高等专业学院的科技创新系,主要负责人为Luca,Lepori,Carlo 和Schmidhuber 。
其中一研究主题是人工蚂蚁,该多代理方法是受基于信息素交流的生物蚂蚁启发而来,由前高级研究员Dorigo 和联合负责人Luca 领导研究的。
其人工蚁和局部搜索算法的结合已经成为解决某些图形优化任务的方法选择,如车辆路径和网络路径,其迅速发展促成许多商业应用和关于人工蚂蚁的专门会议。
(2)比利时布鲁塞尔IRIDIA。
IRIDIA是布鲁塞尔自由大学人工智能研究实验室,主要在理论上进行深入研究以及计算智能应用于优化。
在Dorigo和Bersini 领导下,其主要研究领域为群智能、组合问题的求解和连续空间优化问题的启发式、生物网络原理性研究以及商业智能应用四个方面,而有关于ACA的方向为群智能和元启发式。
IRIDIA在群智能的ACO和群机器人这两方面处于世界领先地位,对于具体元启发式的研究聚焦于ACO,主要研究点是研发一套合理的实验方法论,一套经验学习和元启发式构建的发展工具的应用,特别着重研究的是发展能够设计和完善随机局部搜索算法和元启发式算法的方法论。
近期研究AC A项目有:对AC A的基础理论研究、复杂系统的智能计算方法、使用生物启发和软件计算的医学成像、自组织的蚁群、走向型机器人群和群智能系统的通信策略。
(3)) 奥地利维也纳大学经济与统计商学院由Richard和Artner等组成的团队,主要研究遗传算法、项目管理、最优控制、ACO和电子装配等研究课题其中,关于ACO方面的工作由Richard和Karl负责,从1999年开始至今。
(4)德国莱比锡大学并行计算与复杂系统Martin领导的数学与计算机科学学院计算机科学研究所的并行计算与复杂系统团队,关于ACA的主要研究是由人类前沿科学组织自主计划的自然系统优化,以及东风集团项目中的一些关于系统、模型和硬件算法等。
2 .1 .2 有关蚁群算法的国际会议随着人们对ACA越来越重视,相关会议也组织起来,来自世界各地的专家对ACA及其应用展开研究讨论,其中以Dorigo为大会总主席的ANTS最为权威。
1998年在比利时布鲁塞尔召开第一届ACA研讨会:从蚁群到人工蚁,每隔两年召开一次蚁群优化和群智能国际会议期间,2000年召开第二届ACA 国际专会:从蚁群到人工蚁。
另外,自2005年在美国加利福尼亚州帕萨迪纳威斯汀召开了IEEE群智能讨论会,2006年、2007年分别在美国印第安州印第安纳波利斯和美国夏威夷檀香山希尔顿村延续召开此会。
除以上较为权威的会议,还有很多相关的国际会议,说明ACA在国际范围内得的重视,研究亦广泛展开。
2.2国内蚁群算法的发展概况国内对该算法研究最早的是张纪会博士和徐心和教授1999年3月,他们首次简单引进ACA,从其基本原理、模型、伪码流程进行说明,对Oliver30 TSP 问题分析说明,但未对基本模型中的参数进行详细地理论说明,且停止条件的界定较含糊,主要靠经验决定其后引入的变异机制加快了收敛速度,使得到较优解的周期缩短,并从计算机仿真层面上证明其有效性。
2001年,陈烨引入遗传算法中用到的杂交算子来改善蚁群搜索速度慢、容易陷入局部最优。
但随路程,的增长每次的代数显著增加,计算量较大。
同年8月,郝晋等通过将转移概率设置为转移系数,结合扰动策略以防止漏选最优路径,能够节约计算时间,且能够很好的克服算法容易陷入局部最优的缺陷,计算精度也有提高但在关于倒指数的扰动因子和均匀分布的随机数的选择并未解决,仍以实验为主要获取手段而后李艳君等对自适应ACA进行了进一步研究,对信息素采取自适应更新,应用于连续空间优化问题的求解,并进行了证明。
2002年,王颖等对自适应ACA作出了改进,获得了很好的结果。
该ACA 在进化代数减少的情况下,解的质量也得到了一定提高,在一定程度上实现了收敛速度与解的质量的平衡。
但分析其复杂度可知,蚂蚁的数目与问题规模不相上下,蚂蚁数目增多会使收敛。
速度过快,为防止该现象而将信息素挥发悉数设置得比一般情况低一个数量级,而相关系数仪、B、P等则由实验设定。
当蚂蚁数量与问题规模相当时,实验次数与时间是不容忽视的一个问题ACA除在原理层面进行模型改进。
在应用方面也有一定发展。
如张宗永等将ACA作出改进,配合随机分布技术。
应用到分析上海市整个内河航道和集装箱运输的过程中对内河航道进行规划,最终得出合理的分配方案并提出了满足最优分配的河道改造的建议。
2003年,陈岐等令人工蚁模仿真实蚂蚁的感觉和知觉行为,设置合理绝对感觉阈值以克服蚂蚁在初始选择时容易失去解的多样性,改进选择策略以自适应的修改路径上的信息量,通过对不同规模和不对称TSP的仿真说明算法具有较好的收敛性和稳定性新I叶J的启发式搜索方法——智能ACA,通过取消外激素、自动凋整选择最优路径的比例,改变选择目标城市的依据和引入扰动,仿真结果说明在减少计算量的同时,可取得更好的搜索结果,但也指出通过实验确定相关的物理系数不利于算法的推广但该文仅针对TSP,对其他问题能否应用仍不明确。
2004年,黄国锐等提出采用不同于传统基本ACA所采用的蚁周模型,它采用了更贴近于真实蚂蚁行为的蚁量模型。
建立信息素扩散模型,使相距较近的蚂蚁之间能够更好地进行协作,文中仿真结果表明该算法的有效性然而文中虽在达到收敛所需进化代数上较基本ACA有了很大的改进。
减少约4倍。
但最短路径长度的减少并不明显,且参数的设定仍是以试验为手段,缺乏理论支撑。
针对基本ACA容易陷入局部最优、收敛慢等缺陷,许多新模型陆续提出,如基于云模型的ACA、对信息素的限制、回归型的等,甚至还有不少研究者试图从新的角度重新审视并尝试性研究ACA,较为新颖的有从蚁群社会的“多态性”出发,试图以更贴近真实世界中蚂蚁行为来研究ACA,发现更适应较大规模的问题,以及将着眼于蚁群整体的研究,角度转换到关注蚂蚁个体的速度对算法的影响。
为从根本上解决ACA不足,其收敛性的分析也在不断展开,如用动态分阶段的方式,而具体影响ACA的参数也越来越得到关注,如有相关讨论,但参数如何设定并未有理论依据,如何建立通用标准来对参数进行最优设置仍是难点在研究的应用范围方面也从一开始的离散域扩展到连续域,连续域中有关于收敛性的研究,以及新模型的设计也在进行着。
全国各高校及研究机构也对该算法展开了研究,如徐锋、杜军平的《改进蚁群算法在旅游路线规划中的应用研究》等1999年从首次引入ACA至今,相关研究蓬勃发展,下图为相关的论文题名和关键字的论文数量增长表。
国内对于ACA 的研究也越来越深人,基于各类模型的ACA 层出不穷,研究域也从散域扩展到连续域,同时ACA 在不断与其他算法结合以克服本身的缺陷但国内的研究起步较晚,对于影响收敛性的、B 等相关参数至今无法确定一套相关的理论来进行设置,只能通过反复试验来大致确定一个参数范围,且研究较多地停留在理论仿真,应用到实践中仍较少。
