2019年全国2卷省份高考模拟理科数学分类--解析几何
2019年普通高等学校招生全国统一考试 理科数学 (全国II卷) 解析版

2019年普通高等学校招生全国统一考试(全国 II 卷)理科数学一、选择题1. 设集合{}065|2>+-=x x x A ,{}01|<-=x x B ,则=⋂B A ( )A. )1,(-∞B. )1,2(-C. )1,3(--D. ),3(+∞ 答案: A 解答:{2|<=x x A 或}3>x ,{}1|<=x x B ,∴)(1,∞-=⋂B A .2. 设i z 23+-=,则在复平面内z 对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 答案: C解析:i 23z --=,对应的点坐标为),(2-3-,故选C. 3.已知(2,3)AB =,(3,)AC t = ,||1BC = ,则AB BC ⋅=( ) A.3- B.2- C.2 D.3 答案: C解答:∵(1,3)BC AC AB t =-=-,∴2||11BC ==,解得3t =,(1,0)BC =,∴2AB BC ⋅=.4.2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就。
实现月球背面软着路需要解决的一个关键技术问题是地面与探测器的通讯联系。
为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地球月拉格朗日点的轨道运行,点是平衡点,位于地月连线的延长线上。
设地球的质量为,月球质量为,地月距离为R ,2L 点到月球的距离为r ,根据牛顿运动定律和万有引力定律,r 满足方程121223()()M M M R r R r r R +=++。
设=rRα。
由于α的值很小,因此在近似计算中345323+331ααααα+≈+(),则r 的近似值为( ) ABCD答案: D解答:1211212232222()(1)()(1)M M M M M M R r R r r R R r R αα+=+⇒+=+++所以有2321122222133[(1)](1)(1)M M M r R R αααααα++=+-=⨯++化简可得223331221221333(1)3M r M M M R M αααααα++=⨯=⨯⇒=+,可得r =。
2019年高考数学理科试题解析版(全国卷II)共8页word资料

2019年普通高等学校招生全国统一考试(全国卷II )(数学理)【教师简评】按照“保持整体稳定,推动改革创新,立足基础考查,突出能力立意”命题指导思想,本套试卷的总体印象是:题目以常规题为主,难度较前两年困难,得高分需要扎扎实实的数学功底.1.纵观试题,小题起步较低,难度缓缓上升,除了选择题11、12、16题有一定的难度之外,其他题目难度都比较平和.2.解答题中三角函数题较去年容易,立体几何难度和去年持平,数列题的难度较去年有所提升,由去年常见的递推数列题型转变为今年的数列求极限、数列不等式的证明,不易拿满分,概率题由去年背景是“人员调配”问题,转变为今年的与物理相关的电路问题,更体现了学科之间的联系.两道压轴题以解析几何和导数知识命制,和去年比较更有利于分步得分.3.要求考生有比较强的计算能力,例如立体几何问题,题目不难,但需要一定的计算技巧和能力.不管题目难度如何变化,“夯实双基(基础知识、基本方法)”,对大多数考生来说,是以不变应万变的硬道理.(1)复数231i i -⎛⎫= ⎪+⎝⎭(A )34i -- (B )34i -+ (C )34i - (D )34i +【答案】A【命题意图】本试题主要考查复数的运算. 【解析】231i i -⎛⎫= ⎪+⎝⎭22(3)(1)(12)342i i i i --⎡⎤=-=--⎢⎥⎣⎦. (2).函数1ln(1)(1)2x y x +-=>的反函数是 (A ) 211(0)x y ex +=-> (B )211(0)x y e x +=+> (C )211(R)x y ex +=-∈ (D )211(R)x y e x +=+∈【答案】D【命题意图】本试题主要考察反函数的求法及指数函数与对数函数的互化。
【解析】由原函数解得,即,又;∴在反函数中,故选D. (3).若变量,x y 满足约束条件1,,325x y x x y -⎧⎪⎨⎪+⎩≥≥≤,则2z x y =+的最大值为(A )1 (B )2 (C )3 (D )4【答案】C【命题意图】本试题主要考查简单的线性规划问题.【解析】可行域是由A(1,1),B(1,4),C(1,1)---构成的三角形,可知目标函数过C 时最大,最大值为3,故选C.(4).如果等差数列{}n a 中,34512a a a ++=,那么127...a a a +++=(A )14 (B )21 (C )28 (D )35【答案】C【命题意图】本试题主要考查等差数列的基本公式和性质. 【解析】173454412747()312,4,7282a a a a a a a a a a a +++===∴+++=== (5)不等式2601x x x --->的解集为 (A ){}2,3x x x -<或> (B ){}213x x x -<,或<<(C ) {}213x x x -<<,或> (D ){}2113x x x -<<,或<<【答案】C【命题意图】本试题主要考察分式不等式与高次不等式的解法.【解析】利用数轴穿根法解得-2<x <1或x >3,故选C (6)将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中.若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有(A )12种 (B )18种 (C )36种 (D )54种【答案】B【命题意图】本试题主要考察排列组合知识,考察考生分析问题的能力.【解析】标号1,2的卡片放入同一封信有种方法;其他四封信放入两个信封,每个信封两个有种方法,共有种,故选B.(7)为了得到函数sin(2)3y x π=-的图像,只需把函数sin(2)6y x π=+的图像 (A )向左平移4π个长度单位 (B )向右平移4π个长度单位(C )向左平移2π个长度单位 (D )向右平移2π个长度单位 【答案】B【命题意图】本试题主要考查三角函数图像的平移.【解析】s i n (2)6y x π=+=sin 2()12x π+,sin(2)3y x π=-=sin 2()6x π=-,所以将s i n (2)6y x π=+的图像向右平移4π个长度单位得到sin(2)3y x π=-的图像,故选B. (8)ABC V 中,点D 在AB 上,CD 平方ACB ∠.若C B a =u u r ,CA b =uu r ,1a =,2b =,则CD =uu u r(A )1233a b + (B )2133a b + (C )3455a b + (D )4355a b + 【答案】B【命题意图】本试题主要考查向量的基本运算,考查角平分线定理.【解析】因为CD 平分ACB ∠,由角平分线定理得AD CA 2=DB CB 1=,所以D 为AB 的三等分点,且22AD AB (CB CA)33==-,所以2121CD CA+AD CB CA a b 3333==+=+,故选B.(9)已知正四棱锥S ABCD -中,SA =,那么当该棱锥的体积最大时,它的高为(A )1 (B (C )2 (D )3【答案】C【命题意图】本试题主要考察椎体的体积,考察告辞函数的最值问题.【解析】设底面边长为a ,则高所以体积, 设,则,当y 取最值时,,解得a=0或a=4时,体积最大,此时,故选C. (10)若曲线12y x -=在点12,a a -⎛⎫ ⎪⎝⎭处的切线与两个坐标围成的三角形的面积为18,则a =(A )64 (B )32 (C )16 (D )8【答案】A【命题意图】本试题主要考查求导法则、导数的几何意义、切线的求法和三角形的面积公式,考查考生的计算能力.. 【解析】332211',22y x k a --=-∴=-,切线方程是13221()2y a a x a ---=--,令0x =,1232y a -=,令0y =,3x a =,∴三角形的面积是121331822s a a -=⋅⋅=,解得64a =.故选A.(11)与正方体1111ABCD A B C D -的三条棱AB 、1CC 、11A D 所在直线的距离相等的点(A )有且只有1个 (B )有且只有2个(C )有且只有3个 (D )有无数个【答案】D【解析】直线上取一点,分别作垂直于于则分别作,垂足分别为M ,N ,Q ,连PM ,PN ,PQ ,由三垂线定理可得,PN ⊥PM ⊥;PQ ⊥AB ,由于正方体中各个表面、对等角全等,所以,∴PM=PN=PQ ,即P 到三条棱AB 、CC 1、A 1D 1.所在直线的距离相等所以有无穷多点满足条件,故选D.(12)已知椭圆2222:1(0)x y C a b a b+=>>F 且斜率为(0)k k >的直线与C 相交于A B 、两点.若3AF FB =,则k =(A )1 (B (C (D )2【答案】B【命题意图】本试题主要考察椭圆的性质与第二定义.【解析】设直线l 为椭圆的有准线,e 为离心率,过A ,B 分别作AA 1,BB 1垂直于l ,A 1,B 为垂足,过B 作BE 垂直于AA 1与E ,由第二定义得,,由,得,∴即k=,故选B. 第Ⅱ卷注意事项:1.用0.5毫米的黑色字迹签字笔在答题卡上作答。
2019年高考理科数学全国2卷(附答案)(2)[2]
![2019年高考理科数学全国2卷(附答案)(2)[2]](https://img.taocdn.com/s3/m/3b065c981711cc7931b716f4.png)
20 19年高考理科数学全国2卷(附答案)( 2) (w or d 版可编辑修改是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔(2)( wo rd 版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以_ —理科数学 全国 II 卷___ - 本试卷共 23 小题,满分150 分,考试用时120 分钟:号 -(适用地区:内蒙古 / 黑龙江 /辽宁 /吉林 /重庆 /陕西 / 甘肃 /宁/新疆 / 西藏 /海南 )学 —注意事项:_-__1. 答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置_-__2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案__ —如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时写在___答题卡上。
写在本试卷上无效。
_ 线__ 封_3. 考试结束后,将本试卷和答题卡一并交回。
_密__ —__12 小题,每小题 5 分,共 60 分.在每个小题给选 : —一、 选择题:本题共名 — 项中,只有一项是符合题目要求的。
姓—2— 1.设集合 A={ x|x —5x+6>0} , B={ x|x-1<0} ,则 A∩B=班 -A . (-∞, 1)B . (-2, 1)C .(-3 , —1)D . (3, +∞___ —_2 .设 z=—3+2i ,则在复平面内 z 对应的点位于_—__ A .第一象限B .第二象限C .第三象限D .第四象限年 -____线 3 .已知 AB =(2,3) , AC =(3 ,t), BC =1,则 AB BC = __ 封_ A .—3 B .—2 C . 2D . 3 _ 密_-__4. 2019 年 1 月 3 日嫦娥四号探测器成功实现人类历史上首次月球背面软_ -__R,L2点到月球的距离为r ,根据牛顿运动定律和万有引力定律,地月连长线上.设地球质量为M1,月球质量为M2,地月距离为R, L2点到月距离为 r,根据牛顿运动定律和万有引力定律,r 满足方程:M1M 2M1(R r)2r2(R r )3。
2019年全国2卷省份高考模拟理科数学分类--立体几何
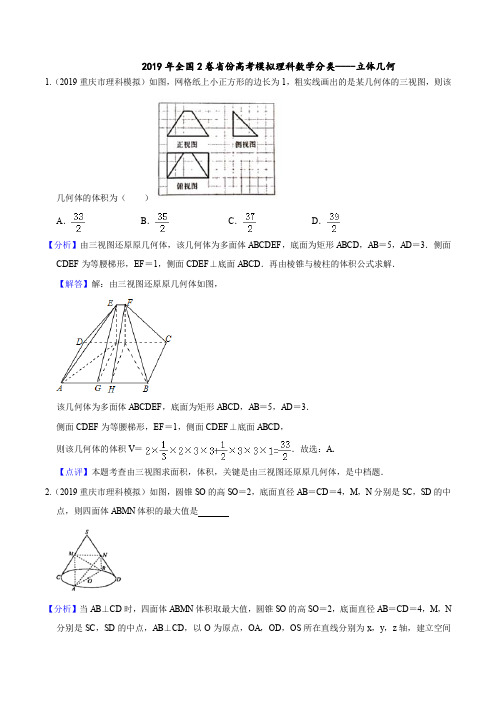
2019年全国2卷省份高考模拟理科数学分类----立体几何1.(2019重庆市理科模拟)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()A.B.C.D.【分析】由三视图还原原几何体,该几何体为多面体ABCDEF,底面为矩形ABCD,AB=5,AD=3.侧面CDEF为等腰梯形,EF=1,侧面CDEF⊥底面ABCD.再由棱锥与棱柱的体积公式求解.【解答】解:由三视图还原原几何体如图,该几何体为多面体ABCDEF,底面为矩形ABCD,AB=5,AD=3.侧面CDEF为等腰梯形,EF=1,侧面CDEF⊥底面ABCD,则该几何体的体积V=.故选:A.【点评】本题考查由三视图求面积,体积,关键是由三视图还原原几何体,是中档题.2.(2019重庆市理科模拟)如图,圆锥SO的高SO=2,底面直径AB=CD=4,M,N分别是SC,SD的中点,则四面体ABMN体积的最大值是【分析】当AB⊥CD时,四面体ABMN体积取最大值,圆锥SO的高SO=2,底面直径AB=CD=4,M,N 分别是SC,SD的中点,AB⊥CD,以O为原点,OA,OD,OS所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出四面体ABMN体积的最大值.【解答】解:当AB⊥CD时,四面体ABMN体积取最大值,∵圆锥SO的高SO=2,底面直径AB=CD=4,M,N分别是SC,SD的中点,AB⊥CD,以O为原点,OA,OD,OS所在直线分别为x,y,z轴,建立空间直角坐标系,∴A(2,0,0),B(﹣2,0,0),S(0,0,2),C(0,﹣2,0),D(0,2,0),M(0,﹣1,1),N(0,1,1),=(﹣4,0,0),=(﹣2,﹣1,1),=(﹣2,1,1),设平面AMN的法向量=(x,y,z),则,取x=1,得=(1,0,2),点B到平面AMN的距离d==,cos<>===,sin<>==,∴S△AMN===,∴四面体ABMN体积的最大值是:V===.故答案为:.【点评】本题考查四面体的面积的最大值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.3.(2019重庆市理科模拟)如图所示的几何体中,侧面ABCD为矩形,侧面DEFG为平行四边形,AB=1AD=2,AG∥BF,AB⊥BF,AG=3BF=5,二面角D﹣AB﹣F的大小为60°(1)证明,平面CDE⊥平面ADG(2)求直线BE与平面ABCD所成角的大小【分析】(1)由AB⊥BF,CD∥AB,AG∥BF,得CD⊥AG,再由CD⊥AD,得CD⊥平面ADG,由此能证明平面CDE⊥平面ADG.(2)以A为原点,AB,AG所在直线分别为x,y轴,建立空间直角坐标系,利用向量法能求出直线BE 与平面ABCD所成角的大小.【解答】证明:(1)由AB⊥BF,CD∥AB,AG∥BF,得CD⊥AG,又CD⊥AD,∴CD⊥平面ADG,平面CDE⊥平面ADG.解:(2)以A为原点,AB,AG所在直线分别为x,y轴,建立空间直角坐标系,∵AB⊥AD,AB⊥AG,∴∠DAG是二面角D﹣AB﹣F的平面角,∴∠DAG=60°,∴D(0,1,),B(1,0,0),G(0,3,0),F(1,5,0),由=,得E(1,3,),设平面ABCD的法向量=(x,y,z),则,∴,令z=﹣1,得=(0,),设BE与平面ABCD所成角为θ,则sinθ==,解得θ=30°.故直线BE与平面ABCD所成角的大小为30°.【点评】本题考查面面垂直的证明,考查线面角的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.4.(2019青海西宁四中理科模拟)如图,在直三棱柱中,,,D,E分别在AB,的中点,则异面直线CE与所成角的余弦值为A.B.C.D.【答案】C【解析】解:如图,设,,,则,,.,,.即异面直线CE与所成角的余弦值为,故选:C.设,,,利用平面向量基本定理把与分别由表示,再由数量积求夹角公式求解.本题考查利用向量法求异面直线所成角,是基础题.5.(2019青海西宁四中理科模拟)如图,四棱锥中,底面ABCD,底面ABCD为梯形,,,且,.求证:平面AEC.求二面角的余弦值.【答案】证明:连结BD,交AC于点M,连结EM,,,,又,,在中,.不包含于平面EAC,平面EAC面EAC;解:由已知可以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,设,则0,,a,,a,,0,,,设y,为平面EAC的一个法向量,则,解得,,同理可得平面PBC的一个法向量1,,,,二面角的余弦值为【解析】由已知条件,推导出,利用直线与平面平行的判定定理能证明面EAC.以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,求出平面EAC的一个法向量,平面PBC的一个法向量,利用向量的夹角公式,即可得出结论.本题考查直线与平面平行的证明,考查平面与平面所成角的应用,解题时要注意等价转化思想和向量法的合理运用.6.(2019大连重点校协作体理科模拟)一个几何体的三视图如图所示,其左视图是等边三角形,该几何体的侧面中面积最大的侧面的面积等于()A.B.C.2D.【分析】根据三视图知,该几何体是以俯视图为底面的四棱锥,且一侧面垂直于底面,结合图中数据求出该四棱锥侧面中的最大面积.【解答】解:根据三视图知,该几何体是以俯视图为底面的四棱锥,如图所示;则该四棱锥P﹣ABCD中,各侧面的面积为S△P AB=×2×=,S△P AD=×1×2=1,S△PBC=×2×2=2,△PCD中,CD=PD=,BC=2,S△PCD=×2×=,即侧面积最大的是.故选:B.【点评】本题考查了利用三视图求几何体表面积的应用问题,是基础题.7(2019大连重点校协作理科模拟)已知m,n是两条不同直线,α是一个平面,m⊄α,n α,则“m∥n”是“m∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【分析】根据线面平行的性质结合充分条件和必要条件的定义进行判断即可.【解答】解:若m∥n由线面平行的定义知m∥α成立,即充分性成立,若m∥α,则m与n可能平行可能是异面直线,故必要性不成立,即“m∥n”是“m∥α”的充分不必要条件,故选:A.【点评】本题主要考查充分条件和必要条件的判断,结合线面平行的性质定理是解决本题的关键.8.(2019大连重点校协作体理科模拟)如图,直三棱柱ABC﹣A1B1C1的所有棱长都是2,D,E分别是AC1,CC1的中点.(1)求证:AE⊥平面A1BD;(2)求二面角B﹣A1D﹣B1的余弦值.【分析】(1)取AC中点O为坐标原点,OA1为x轴,OD为y轴,OB为z轴,建立空间直角坐标系,利用向量法能证明AE⊥平面A1BD.(2)求出平面A1BD的法向量和平面A1B1D的法向量,由此能求出二面角B﹣A1D﹣B1的余弦值.【解答】证明:(1)直三棱柱ABC﹣A1B1C1的所有棱长都是2,D,E分别是AC1,CC1的中点.取AC中点O为坐标原点,OA1为x轴,OD为y轴,OB为z轴,建立空间直角坐标系,A(1,2,0),E(﹣1,1,0),A1(1,0,0),B(0,2,),D(0,2,0),=(﹣2,﹣1,0),=(0,0,),=(1,﹣2,0),∴=0,=0,∴AE⊥DB,AE⊥DA1,∵DB∩DA1=D,∴AE⊥平面A1BD.解:(2)∵AE⊥平面A1BD,∴=(﹣2,﹣1,0)是平面A1BD的法向量,B1(0,0,),=(1,﹣2,0),=(0,﹣2,),设平面A1B1D的法向量=(x,y,z),则,取y=1,得=(2,1,),∴二面角B﹣A1D﹣B1的余弦值为:|cos<>|===.【点评】本题考查线面垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系,考查运算求解能力,考查数形结合思想,是中档题.9.(2019吉林省四平一中理科模拟)汉朝时,张衡得出圆周率的平方除以16等于.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,俯视图中的曲线为圆,利用张衡的结论可得该几何体的体积为A. 32B. 40C.D.【答案】C【分析】将三视图还原,即可求组合体体积【详解】将三视图还原成如图几何体:半个圆柱和半个圆锥的组合体,底面半径为2,高为4,则体积为,利用张衡的结论可得故选:C【点睛】本题考查三视图,正确还原,熟记圆柱圆锥的体积是关键,是基础题10.(2019吉林省四平一中理科模拟)正方体的棱上(除去棱AD)到直线与的距离相等的点有个,记这个点分别为,则直线与平面所成角的正弦值为()A. B. C. D.【答案】D【分析】正方体ABCD﹣A1B1C1D1的棱上到直线A1B与CC1的距离相等的点分别为:D1,BC的中点,B1C1的四等分点(靠近B1),假设D1与G重合,BC的中点为E,B1C1的四等分点(靠近B1)为F,以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出直线AC1与平面EFG所成角的正弦值.【详解】解:正方体ABCD﹣A1B1C1D1的棱上到直线A1B与CC1的距离相等的点分别为:D1,BC的中点,B1C1的四等分点(靠近B1),假设D1与G重合,BC的中点为E,B1C1的四等分点(靠近B1)为F,以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,设AB=2,则E(1,2,0),F(,2,2),G(0,0,2),A(2,0,0),C1(0,2,2),∴(),(),(﹣2,2,2),设平面EFG的法向量(x,y,z),则,即,取x=4,得(4,﹣3,﹣1).设直线AC1与平面EFG所成角为θ,则直线AC1与平面EFG所成角的正弦值为sinθ=|cos|.故选:D.【点睛】本题考查线面角的正弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.11(2019吉林省四平一中理科模拟).如图,在多面体ABCDEF中,四边形ADEF为正方形,AD∥BC,AD⊥AB,AD=2BC=2.(1)证明:平面ADEF⊥平面ABF.(2)若平面ADEF⊥平面ABCD,二面角A-BC-E为30°,三棱锥A-BDF的外接球的球心为O,求异面直线OC 与DF所成角的余弦值【答案】(1)证明见解析;(2).【分析】(1)推导出AD⊥AF,AD⊥AB,AD⊥平面ABF,由此能证明平面ADEF⊥平面ABF;(2)推导出BC⊥平面ABF,BC⊥BF,再由BC⊥AB,得二面角A﹣BC﹣E的平面角为∠ABF=30°,以A 为坐标原点,建立空间直角坐标系,利用向量法能求出异面直线OC与DF所成角的余弦值.【详解】(1)证明:因为四边形ADEF为正方形,所以AD⊥AF,又AD⊥AB,AB∩AF=A,所以AD⊥平面ABF,因为,所以平面ADEF⊥平面ABF.(2)解:因为平面ADEF⊥平面ABCD,AD⊥AF,平面ADEF∩平面ABCD=AD,所以AF⊥平面ABCD.由(1)知AD⊥平面ABF,又AD∥BC,则BC⊥平面ABF,从而BC⊥BF,又BC⊥AB,所以二面角A-BC-E的平面角为∠ABF=30°.以A为坐标原点建立空间直角坐标系A-xyz,如图所示,则.因为三棱锥A-BDF的外接球的球心为O,所以O为线段BE 的中点,则O的坐标为,,又,则,故异面直线OC与DF所成角的余弦值为.评分细则:第(2)问中,若未证明AF⊥平面ABCD,直接建立空间直角坐标系,则扣1分.【点睛】本题考查面面垂直的证明,考查异面直线所成角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.12.(2019吉林长春市理科模拟)底面为正多边形,顶点在底面的射影为底面多边形中心的棱锥为正棱锥,则半径为2的球的内接正四棱锥的体积最大值为__________.【答案】.【分析】设出底面正方形的边长,根据内接关系,得出正四棱锥的高,进而得出正四棱锥的体积的函数式,求导得出最值。
2019年高考全国2卷理科数学及答案(word)(2021年整理)

(完整)2019年高考全国2卷理科数学及答案(word)(word版可编辑修改)(完整)2019年高考全国2卷理科数学及答案(word)(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)2019年高考全国2卷理科数学及答案(word)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)2019年高考全国2卷理科数学及答案(word)(word版可编辑修改)的全部内容。
(完整)2019年高考全国2卷理科数学及答案(word)(word版可编辑修改)绝密★启用前2019 年普通高等学校招生全国统一考试理科数学本试卷共23 题,共 150 分,共 5 页。
考试结束后,将本试卷和答题卡一并交回.注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5 毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
2-5x+6>0} ,B={ x|x-1<0} ,则 A∩B=1.设集合A={ x|xA.(-∞,1)B.(-2,1)C.(-3,-1)D.(3,+∞)2.设 z=-3+2i,则在复平面内z 对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.已知AB =(2,3),AC =(3,t),BC =1,则AB BC =A.-3 B.-2 C.2D.34.2019 年 1 月3 日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日L2 点的轨道运行.L2 点是平衡点,位于地月连线的延长线上.设M月球质量为M2,地月距离为R,L2 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r 满足方程:M M M1 212 2 ( )3R r(R r)rR.设rR,由于的值很小,因此在近似计算中3 4 53 32(1 )3值为A.M2M1R B.M21R C.33M2M1R D.32M理科数学试题第 1 页(共9 页)5.演讲比赛共有9 位评委分别给出某选手的原始评分,评定该绩时,从9个原始选手的成评分中去掉1个最高分、 1 个最低分,得到7 个有效评分.7 个有效评分与9 个原始评分相比,不变的数字特征是A.中位数B.平均数C.方差D.极差6.若a> b,则A.ln( a- b)〉0 B.3a〈3b C.a3- b3〉0D.│a│〉│b│7.设α,β为两个平面,则α∥β的充要条件是A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面2 21的一个焦点,则p=x y2=2px(p>0)的焦点是椭圆8.若抛物线y3p pA.2 B.3 C.4D.8为周期且在区间(的是9.下列函数中,以,)单调递增2 4 2A.f (x)=│ cos2x│B.f (x)=│ sin2 x│C.f (x)= cos │x│D.f (x)=sin │x│), 2sin 2α=cos 2α+1,则s in α=10.已知α∈(0,2A.15B.55C.33D.11.设 F 为双曲线C:2 2x y2 2 1(0,0)a ba b的右焦点,O为坐标原点,以OF2 2 2x y a 交于P,Q 两点.若PQOF ,则C的离心率为与圆A. 2 B. 3 C.2D.512.设函数 f (x) 的定义域为R,满足f (x 1) 2 f (x),且当x (0,1]时,f (x)x(x 1) .若对任意x( , m],都有8f ( x),则m的是9A.9(, ]4B.7( , ]3C.(二、填空题:本题共 4 小题,每小题 5 分,共20 分。
2019年高考理科数学(2卷)答案详解

2019年普通高等学校招生全国统一考试理科数学(II 卷)答案详解一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(集合)设集合A ={x |x 2–5x +6>0},B ={x |x –1<0},则A ∩B =( ) A .(∞-,1) B .(–2,1)C .(–3,–1)D .(3,∞+)【解析】集合A ={x |x 2–5x +6>0}={x |x <2或x >3},集合B ={x |x <1},所以有A ∩B={x |x <1},即A 答案. 【答案】A2.(复数)设i z 23+-=,则在复平面内z 对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【解析】i z 23+-=,则z 的共轭复数为i z 23--=,所以在复平面内z 对应的点位于第三象限. 【答案】C3.(平面向量)已知AB =(2,3),AC =(3,t ),||BC =1,则AB BC ⋅=( ) A .–3 B .–2C .2D .3【解析】(1,3)=+=-BC BA AC t ,由于||1=BC ,所以03=-t ,即3=t ,(1,0)=BC .所以21302⋅=⨯+⨯=AB BC【答案】C4.(公式推导)2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日2L 点的轨道运行.2L 点是平衡点,位于地月连线的延长线上.设地球质量为M 1,月球质量为M 2,地月距离为R ,2L 点到月球的距离为r ,根据牛顿运动定律和万有引力定律,r 满足方程:121223()()M M M R r R r r R +=++.设rRα=,由于α的值很小,因此在近似计算中34532333(1)ααααα++≈+,则r 的近似值为( ) A .21M R M B .212M R MC .2313M R M D .2313M R M【解析】∵=rR α,∴=r R α,代入121223()()+=++M M M R r R r r R 中得12122222(1)(1)+=++M M M R R R ααα12122(1)(1)+=++M M M ααα33453122333=3(1)++⎛⎫=≈ ⎪+⎝⎭M r M R ααααα所以有 2313=M r R M 【答案】C5.(概率统计)演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( ) A .中位数 B .平均数 C .方差D .极差【解析】根据几个数字特征的定义,很容易得出答案:去掉1个最高分、1个最低分,最后中位数不变. 【答案】A6.(函数)若a >b ,则( ) A .ln(a −b )>0 B .3a <3b C .a 3−b 3>0D .|a |>|b |【解析】答案A :∵a >b ,∴a -b >0,无法判断ln(a −b )的正负;答案B :∵y =3x 为增函数,∴3a >3b ;答案C :∵y =x 3为增函数,∴a 3>b 3;答案D :当0>a >b 时,|a |<|b |.【答案】C7.(立体几何)设α,β为两个平面,则α∥β的充要条件是( ) A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线D .α,β垂直于同一平面【解析】通过画图,采用排除法,很容易得到正确答案. 【答案】B8.(解析几何)若抛物线y 2=2px (p >0)的焦点是椭圆1322=+py p x 的一个焦点,则p =( ) A .2 B .3 C .4D .8【解析】抛物线y 2=2px (p >0)的焦点为)0,2(p,并且在x 轴上. 所以椭圆1322=+p y p x 的一个焦点为)0,2(p . 所以有p p22=,得p =8. 【答案】D9.(三角函数)下列函数中,以2π为周期且在区间)2,4(ππ单调递增的是( ) A .f (x )=|cos2x | B .f (x )=|sin2x | C .f (x )=cos|x |D .f (x )=sin|x |【解析】答案A :函数f (x )=|cos2x |的图像如图A9-1所示,其周期是函数f (x )=cos2x 的一半,即21π=T ,且在区间)2,4(ππ为单调递增的. 答案B :与答案A 类似,函数f (x )=|sin2x |的周期是函数f (x )=sin2x 的一半,即22π=T ,且在区间)2,4(ππ为单调递减的;答案C :函数f (x )=cos|x |为偶函数,其图像如图A9-2所示.由函数f (x )=cos|x |的图像可知,其周期π23=T ;答案D :与答案C 类似,由函数f (x )=sin|x |的图像可知,其不是周期函数. 【答案】A图A9-1 图A9-210.(三角函数)已知α∈(0,2π),2sin2α=cos2α+1,则sin α=( ) A .15B .55C .33D .255【解析】利用三角公式12cos 2sin 2+=αα化简得ααα2cos 2cos sin 4=ααcos sin 2=所以2cot =α,设α所对得边为1,则临边为2,斜边为5,所以55sin =α. 【答案】B11.(解析几何)设F 为双曲线C :22221(0,0)-=>>x y a b a b的右焦点,O 为坐标原点,以OF 为直径的圆与圆222+=x y a 交于P ,Q 两点.若=PQ OF ,则C 的离心率为( ) A .2 B .3C .2D .5【解析】如图A11所示. ∵OF 为直径,=PQ OF ,∴PQ 也是直径.,即点P 、Q 的坐标为)2,2(c c .把)2,2(c c 代入222+=x y a 得,222=c a . ∴22=e ,即2=e .图A11【答案】A12.设函数()f x 的定义域为R ,满足(1) 2 ()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-.若对任意(,]x m ∈-∞,都有8()9f x ≥-,则m 的取值范围是A .9,4⎛⎤-∞ ⎥⎝⎦B .7,3⎛⎤-∞ ⎥⎝⎦C .5,2⎛⎤-∞ ⎥⎝⎦D .8,3⎛⎤-∞ ⎥⎝⎦【解析】由)(2)1(x f x f =+可得Z x x f t x f t∈⋅=+),(2)(,即Z x t x f x f t∈-⋅=),(2)(.∵当(0,1]∈x 时,()(1)=-f x x x ,1()[,0]4∈-f x ∴当(1,2]∈x 时,1(0,1]-∈x ,则)2)(1(2)1(2)(--=-⋅=x x x f x f ,1()[,0]2∈-f x∴当(2,3]∈x 时,2(0,1]-∈x ,则)3)(2(4)2(2)(2--=-⋅=x x x f x f ,()[1,0]∈-f x 函数()f x 的图像如图A12所示. 对任意(,]∈-∞x m ,都有8()9≥-f x ,因此(2,3]∈m 令98)3)(2(4)(-=--=x x x f ,得 37=x 或38=x . 由图A12可知,当37≤m 时,都有8()9≥-f x .图A12【答案】B二、填空题:本题共4小题,每小题5分,共20分。
2019年普通高等学校招生全国统一考试理科数学(全国II卷)解析版

2019年普通高等学校招生全国统一考试理科数学(全国II卷)解析版2019年普通高等学校招生全国统一考试(全国 II 卷)理科数学答案一、选择题 1-6ACC DAC 7-12 BDA BAB9. A 对于A,函数|2cos |)(x x f =的周期2T π=,在区间,42ππ??单调递增,符合题意;对于B,函数|2sin |)(x x f =的周期2T π=,在区间,42ππ??单调递减,不符合题意;对于C ,函数x x x f cos ||cos )(==,周期2T π=,不符合题意;对于D,函数||sin )(x x f =的周期T π=,不符合题意.10. B (0,)2πα∈,22sin 2cos 214sin cos 2cos ααααα=+?=,则12sin cos tan 2ααα=?=,所以2125cos 1tan 5αα==+,所以25sin 1cos αα=-=. 11. A ∵||||PQ OF c ==,∴90POQ ∠=o,又||||OP OQ a ==,∴222a a c +=解得2ca=,即2e =.12. B 由当x R ∈,(1)2()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-可知当(1,2]x ∈时,231()2()22f x x =--,当(2,3]x ∈时,25()4()12f x x =--,……当(,1],x n n n Z ∈+∈时,221()2()22n n f x x n -=---,函数值域随变量的增大而逐渐减小,对任意的(,]x m ∈-∞,都有8()9f x ≥-有23854()1()292m m --≥-<解得的取值范围是73m ≤。
二、填空题 13. 0.9 14. 3-∵ln 2ln 2(ln 2)(ln 2)()()28a a a f f e e ---=--=--===,∴3a =-. 15. 3621436423cos cos 222222=-+=-+==cc c ac b c a B π,3623323421sin 21,34,32===∴==∴B ac S a c16. 答案:262-1由图2结合空间想象即可得到该正多面体有26个面;将该半正多面体补成正方体后,根据对称性列方程求解.三、解答题 17. 解析:(1)证明:∵⊥11C B 平面1ABB ,?BE 平面1ABB ,∴BE C B ⊥11,又1EC BE ⊥,1111C C B EC =I ,∴⊥BE 平面11C EB .(2)设底面边长为1,高为x 2,∴122+=x BE ,1221+=x E B ,∵⊥BE 平面11C EB ,∴?=∠901BEB 即21212BB E B BE =+,∴22422x x =+解得1=x .∵⊥BC 平面11ABB A ,∴E B BC 1⊥,又BE E B ⊥1,∴⊥E B 1平面BCE ,故B 1为平面BCE 的一个法向量. ∵平面CE C 1与平面11ACC A 为同一平面,故11D B 为平面CE C 1的一个法向量,在E D B 11?中,∵21111===E B E D D B 故E B 1与11D B 成?60角,∴二面角1C EC B --的正弦值为2360sin =?. 18. 解析:(1)2X =时,有两种可能:①甲连赢两局结束比赛,此时10.50.40.2P =?=;②乙连赢两局结束比赛,此时20.50.60.3P =?=,∴12(2)0.5P X P P ==+=;(2)4X =且甲获胜,即只有第二局乙获胜,其他都是甲获胜,此时0.50.60.50.40.06P ==.19. 已知数列{}n a 和{}n b 满足11=a ,01=b ,4341+-=+n n nb a a ,4341--=+n n n a b b . (1)证明: {}n n b a +是等比数列,{}n n b a -是等差数列;(2)求{}n a 和{}n b 的通项公式. 解析:(1)将4341+-=+n n n b a a ,4341--=+n n n a b b 相加可得nn n n n n b a b a b a --+=+++334411,整理可得)(2111n n n n b a b a +=+++,又111=+b a ,故{}n n b a +是首项为1,公比为21的等比数列. 将4341+-=+n n n b a a ,4341--=+n n n a b b 作差可得8334411+-+-=-++n n n n n n b a b a b a ,整理可得211+-=-++n n n n b a b a ,又111=-b a ,故{}n n b a -是首项为1,公差为2的等差数列. (2)由{}n n b a +是首项为1,公比为21的等比数列可得1)21(-=+n n n b a ①;由{}n n b a -是首项为1,公差为2的等差数列可得12-=-n b a n n ②;①②相加化简得21)21(-+=n a n n ,①②相减化简得21)21(+-=n b n n 。
(完整版)2019全国2卷理科数学试题及详解 (2)

2019全国2卷理科数学试题一、选择题:本题共12小题,每小题5分,共60分。
1.设集合A ={x |x 2−5x +6>0},B ={x |x −1<0},则A ∩B =( A ) A. (−∞,1) B.(−2,1) C.(−3,−1) D. (3,+∞)2.设z =−3+2i,则在复平面z̅对应的点位于( C ) A. 第一象限 B. 第二象限 C.第三象限 D.第四象限3.已知AB⃗⃗⃗⃗⃗ =(2,3),AC ⃗⃗⃗⃗⃗ =(3,t ),|BC ⃗⃗⃗⃗⃗ |=1,则AB ⃗⃗⃗⃗⃗ ∙BC ⃗⃗⃗⃗⃗ =( C ) A.−3 B.−2 C. 2 D. 34.2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天 事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探 测器的通讯联系。
为解决这个问题,发射了嫦娥四号中继星“鹊桥”。
鹊桥沿着围绕地月 拉格朗日L 2点的轨道运行,L 2点是平衡点,位于地月连线的延长线上,设地球质量为M 1 ,月球质量为M 2,地月距离为R ,L 2点到月球的距离为r,根据牛顿运动定理和万有引力 定律,r 满足方程:M 1(R+r)2+M 2r 2=(R +r)M 1R 3设α=rR ,由于α的值很小,因此在近似计算中3α3+3α4+α5(1+α)2≈3α3,则r 的近似值为( D )A. √M2M 1R B. √M22M 1R C. √3M 2M 13R D. √M23M 13R5.演讲比赛共有9为评委分别给出某选手的原始评分,评定该选手的成绩时,从9个 原始评分中去掉1个最高分、一个最低分,得到7个有效评分。
7个有效评分与9个 原始评分相比,不变的数字特征是( A )A. 中位数B. 平均数C. 方差D.极差 6.若a >b,则( C )A.ln (a −b )>0B.3a <3bC. a 3−b 3>0D. |a |>|b|7.设α,β为两个平面,则α∥β的 充要条件是( B )A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面 8.若抛物线y 2=2px (p >0)的焦点是椭圆x 23p+y 2p=1的一个焦点,则p =( D )A. 2B. 3C. 4D. 89.下列函数中,以π2为周期且在区间(π4,π2)单调递增的是( A )A.f (x )=|cos2x|B. f (x )=|sin2x|C. f (x )=cos |x |D. f (x )=sin |x| 10.已知α∈(0,π2),2sin2α=cos2α+1,则sinα=( B ) A. 15 B.√55 C.√33D.2√5511.设F 为双曲线C :x 2a 2−y 2b 2=1(a >0,b >0)的右焦点,O 为坐标原点,以OF 为直径 的圆与圆x 2+y 2=a 2交于P ,Q 两点.若|PQ |=|OF |,则C 的离心率为( A ) A. √2 B. √3 C. 2 D. √512.设函数f (x )的定义域为R ,满足f (x +1)=2f (x ),且当x ∈(0,1]时,f (x )=x (x −1). 若对任意x ∈(−∞,m ],都有f (x )≥−89,则m 的取值范围是( B )A. (−∞,94] B. (−∞,73] C.(−∞,52] D. (−∞,83]二、填空题:本题共4小题,每题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年全国2卷省份高考模拟理科数学分类----解析几何1.(2019重庆市理科模拟)已知双曲线C:=1(a>0,b>0)的左右焦点为F1,F2过点F1的直线l与双曲线C的左支变于AB两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为()A.B.C.D.【分析】设|AF1|=m,|BF1|=n,运用双曲线的定义和直角三角形的勾股定理和面积公式,化简可得n=3m,m=a,再由勾股定理和离心率公式,可得所求值.【解答】解:设|AF1|=m,|BF1|=n,由双曲线的定义可得|AF2|=2a+m,|BF2|=2a+n,由△BF1F2的面积是△AF1F2面积的三倍,可得(2a+m)(m+n)﹣m(2a+m)=3•(2a+m)m,化简可得n=3m,由直角三角形ABF1可得(m+n)2+(2a+m)2=(2a+n)2,代入n=3m,化简可得m =a,在直角三角形AF1F2中,可得m2+(2a+m)2=4c2,即为a2+9a2=4c2,即c=a,则e==,故选:B.【点评】本题考查双曲线的定义和方程、性质,主要是离心率的求法,考查方程思想和运算能力,属于中档题.2.(2019重庆市理科模拟)己知A,B分别为椭圆C:=1(a>b>0)的左右顶点,P为椭圆C上异于A,B的任意一点,O为坐标原点,•=﹣4,△P AB的面积的最大值为.(1)求椭圆C的方程;(2)若椭圆C上存在两点M,N,分别满足OM∥P A,ON∥PB,求|OM|•|ON|的最大值.【分析】(1)由已知向量等式求得a,结合三角形面积求得b,则椭圆方程可求;(2)设P(x0,y0),求得=.再设M(),N (),由k OM•k ON=k AP•k BP得到cos(α﹣β)=0,得,k∈Z.则cos2β=sin2α,sin2β=cos2α.可得|OM|•|ON|=,化为关于α的余弦求|OM|•|ON|的最大值.【解答】解:(1)由,得﹣2a2=﹣4,即a2=2.当P为椭圆上、下顶点时,△P AB面积最大,则,即b=1.∴椭圆方程为;(2)设P(x0,y0),=.设M(),N(),由,即sinαsinβ+cosαcosβ=0,∴cos(α﹣β)=0,得,k∈Z.∴cos2β=sin2α,sin2β=cos2α.|OM|•|ON|===.等号成立时,,比如M(1,),N(﹣1,).【点评】本题考查椭圆方程的求法,考查直线与椭圆位置关系的应用,训练了利用三角函数求最值,是中档题.3.(2019青海西宁四中理科模拟)已知椭圆C:的左、右焦点为,,离心率为,过的直线l交C于A,B两点若的周长为,则C的标准方程为______.【答案】【解析】解:由已知得,解得,,,.故答案为:.由已知得,由此能求出椭圆方程.本题考查椭圆方程的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.4.(2019青海西宁四中理科模拟)已知抛物线C:,直线l:与抛物线C交于A,B两点.若直线l过抛物线C的焦点,求.已知抛物线C上存在关于直线l对称的相异两点M和N,求P的取值范围.【答案】解:由直线l:,取,可得,则,即抛物线方程为,联立,可得.设,,则,;设点,,则:,即:,,又,Q关于直线l对称,,即,,又PQ的中点在直线l上,,线段PQ的中点坐标为.中点坐标,,即,,即关于,有两个不相等的实数根,,,∈即P的取值范围是【解析】由直线方程求出焦点坐标,得到抛物线方程,联立直线方程与抛物线方程,利用焦点弦长公式求解;设点,,通过抛物线方程,求解,通过P,Q关于直线l对称,点的,推出,PQ的中点在直线l上,推出,即可求得线段PQ的中点坐标为;利用线段PQ中点坐标,推出,得到关于,有两个不相等的实数根,列出不等式即可求出p的范围.本题考查抛物线方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及计算能力,是中档题.5.(2019大连重点校协作体理科模拟)过双曲线(a>0,b>0)的左焦点F1作圆x2+y2=a2的切线交双曲线的右支于点P,且切点为T,已知O为坐标原点,M为线段PF1的中点(M点在切点T的右侧),若△OTM的周长为4a,则双曲线的渐近线的方程为()A.y=B.y=±C.y=±D.y=【分析】设|PF1|=m,|PF2|=n,由双曲线的定义可得m﹣n=2a,运用三角形的中位线定理和直角三角形的勾股定理,求得m,n,再由勾股定理化简变形可得4a=3b,即可得到所求双曲线的渐近线方程.【解答】解:设|PF1|=m,|PF2|=n,由双曲线的定义可得m﹣n=2a,由MO为△PF1F2的中位线,可得|OM|=n,在直角三角形OTF1中,可得|TF1|==b,|MT|=m﹣b,由题意可得a+n+m﹣b=4a,即m+n=6a+2b,解得m=4a+b,n=2a+b,由直角三角形OMT可得(a+b)2=(2a﹣b)2+a2,化为4a=3b,可得双曲线的渐近线方程为y=±x,即为y=±x.故选:B.【点评】本题考查双曲线的定义、方程和性质,考查直角三角形的勾股定理和三角形的中位线定理,考查变形能力和运算能力,属于中档题.6.(2019大连重点校协作体理科模拟)已知动点M(x,y)到定点(2,0)的距离比到直线x=﹣3的距离少1,则动点M的轨迹方程为.【分析】由于动点M(x,y)到定点(2,0)的距离比到直线x=﹣3的距离少1,可得:动点M(x,y)到定点(2,0)的距离与到直线x=﹣2的距离相等.根据抛物线的定义可知:动点M的轨迹是抛物线.【解答】解:∵动点M(x,y)到定点(2,0)的距离比到直线x=﹣3的距离少1,∴动点M(x,y)到定点(2,0)的距离与到直线x=﹣2的距离相等.根据抛物线的定义可知:动点M的轨迹是抛物线,其方程为y2=8x.故答案为:y2=8x.【点评】本题考查了抛物线的定义,属于基础题.7.(2019重点校协作体理科模拟)已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,点P在椭圆上,|PF1|+|PF2|=4,椭圆的离心率e=.(1)求椭圆C的标准方程;(2)A,B是椭圆C上与点P不重合的任意两点,若△P AB的重心是坐标原点O,试证明:△P AB的面积为定值,并求出该定值.【分析】(1)根据待定系数法求出椭圆方程;(2)设直线AB的方程为y=kx+m,联立方程组求出弦长|AB|,求出P到AB的距离,得出三角形的面积关于m的函数,从而得出面积的最大值.【解答】解:(1)∵|PF1|+|PF2|=4,∴2a=4,∴a=2,∵e==,∴c=1,∴b2=a2﹣c2=3,∴椭圆C的标准方程为:+=1;(2)△P AB最多只有1条边所在直线与x轴垂直,不妨设AB所在直线与x轴不垂直,其方程为y=kx+m (∵△P AB的重心是O,∴O不在直线AB上,m≠0)由得,(4k2+3)x2+8kmx+4m2﹣12=0设A(x1,y1)、B(x2,y2),则△=48(4k2﹣m2+3)>0,且,,从而,设P(x3,y3),∵△P AB的重心是坐标原点O,∴,∴,,点P(x3,y3)在椭圆上,∴,即4k2﹣4m2+3=0,且符合△=48(4k2﹣m2+3)>0,点P(x3,y3)到直线y=kx+m的距离为:,△P AB的面积,由4k2﹣4m2+3=0即4k2+3=4m2,得为常数.【点评】本题考查了椭圆的定义,直线与椭圆的位置关系,考查设而不求法的应用,属于难题.8.(2019吉林省四平一中理科模拟)如图,某瓷器菜盘的外轮廓线是椭圆,根据图中数据可知该椭圆的离心率为()A. B. C. D.【答案】B【分析】分析图知2a,2b,则e可求.【详解】由题2b=16.4,2a=20.5,则则离心率e=.故选:B.【点睛】本题考查椭圆的离心率,熟记a,b的几何意义是关键,是基础题.9.(2019吉林省四平一中理科模拟)已知A,B分别是双曲线C:的左、右顶点,P为C上一点,且P在第一象限.记直线PA,PB的斜率分别为,,当2+取得最小值时,△PAB的重心坐标为A. (1,1)B.C.D.【答案】B【分析】设A(,0),B(,0),P(x,y),得到=2,利用基本不等式求解最值,得到P的坐标,进而得到△PAB的重心坐标.【详解】解:设A(,0),B(,0),P(x,y)由题意,,,∴2,2+≥24,当且仅当2k1=时取等号,此时=1,P A的方程为y=x+1,,PB的方程为y=2,联立方程:,解得P∴重心坐标为,故选:B【点睛】本题考查双曲线的简单性质的应用,考查转化思想以及计算能力,属于中档题.10.(2019吉林省四平一中理科模拟)已知点是抛物线上一点,为的焦点.(1)若,是上的两点,证明:,,依次成等比数列.(2)过作两条互相垂直的直线与的另一个交点分别交于,(在的上方),求向量在轴正方向上的投影的取值范围.【答案】(1)详见解析;(2).【分析】(1)由在抛物线上求P,再利用焦半径公式求,,,再利用等比数列定义证明即可(2)设直线的方程为,与联立,得,由,求k的范围,并求得P坐标,同理求得Q坐标,则向量在轴正方向上的投影为,求函数的范围即求得结果【详解】(1)证明:在抛物线上,,.,,,,,依次成等比数列.(2)设直线的方程为,与联立,得则,,设,,则,即在的上方,则.以代,得,则向量在轴正方向上的投影为,设函数,则在上单调递减,在上单调递增,从而,故向量在轴正方向上的投影的取值范围为.【点睛】本题考查抛物线的简单性质与应用,直线与抛物线位置关系,范围问题,熟练运用定义,准确计算P,Q坐标,将在轴正方向上的投影表示为k的函数时关键,是中档题.11.(2019吉林长春市理科模拟)圆:被直线截得的线段长为()A. 2B.C. 1D.【答案】C【分析】先求出圆心到直线的距离,由勾股定理求出弦长。
【详解】解:圆:的圆心为,半径为1,圆心到直线的距离为,弦长为,故选C。
【点睛】本题考查了直线与圆的位置关系,根据垂径定理,作出直角三角形是解题的关键。
12.(20191长春市理科模拟)下列椭圆中最扁的一个是()A. B. C. D.【答案】B【分析】只需分别计算各选项中的值,越小,椭圆越扁,进而可得出结果.【详解】由得;由得;由得;由得;因为,所以最扁的椭圆为.故选B【点睛】本题主要考查椭圆的特征,熟记椭圆的简单性质即可,属于基础题13.(2019吉林长春市理科模拟)已知抛物线:的焦点为,过且倾斜角为的直线与抛物线交于、两点,若、的中点在轴上的射影分别为,,且,则抛物线的准线方程为()A. B. C. D.【答案】D【分析】设AF,FB的中点分别为D,E, 求出|AB|=16,再利用直线和抛物线的方程利用韦达定理求出p的值,即得抛物线的准线方程.【详解】设AF,FB的中点分别为D,E,则|AB|=2|DE|,由题得|DE|=所以|DE|=8,所以|AB|=16,设,则,联立直线和抛物线的方程得,所以,所以抛物线的准线方程为.故选:D【点睛】本题主要考查抛物线的简单几何性质,考查抛物线的定义和准线方程,意在考查学生对这些知识的理解掌握水平和分析推理能力.14.(2019吉林长春市理科模拟)已知椭圆:的左顶点为,右顶点为,为椭圆上异于、的任意一点,平面内的点满足.(Ⅰ)若点的坐标为,求的值;(Ⅱ)若存在点满足(为坐标原点),求的取值范围. 【答案】(1) .(2) .【分析】(Ⅰ)先由得是线段中点,根据题中条件求出坐标,再代入椭圆方程,即可得出结果;(Ⅱ)先设,则,再由,化简整理即可得出结果.【详解】(Ⅰ)依题意,是线段中点,因为,故,代入椭圆的方程,可得(Ⅱ)设,则,又,又所以,,,,消去,可得,故【点睛】本题主要考查椭圆方程,熟记椭圆方程的求法,以及椭圆的简单性质即可,属于常考题型.15(2019兰州市理科模拟).经过点且与双曲线有相同渐近线的双曲线方程是()A. B.C. D.【答案】D【分析】设所求双曲线的方程,将点代入求出,从而求出方程。
