船舶结构力学ppt第三章力法
合集下载
船舶结构力学 力法位移法能量法

2
0
2
l/2
2A
2 2 v 2 a l v ( 0 ) 2 a l 将 及 1 1
代入可计算出
总应变能为: V 4.5EIa2l 1 (2)计算力函数。此梁的力函数包括集中力F引起U1 及分布荷重引起的U2两部分。 计算U2时,先写出分布荷重的表达式。对图示坐标 有 q( x) 2q0 x q0 , l x l 2 2 因而 l l 2q0 x 1 2 3
(4)列节点平衡方程
4 EI0 8EI 4 EI12 4 EI 1 12 2 1 0 2 l12 l12 l0 l0 2 EI23 4 EI23 6 EI0 12EI0 M 32 2 3 2 3 l23 l23 2.2l0 2.2l0 16EI0 2 EI24 4 EI24 M 42 2 4 2 l24 l24 3l0 M 21
虚位移原理等价于结构的平衡条件,因此基于虚位移 原功方法是位移法。由虚位移原理可导出位能驻值原理, 最小势能原理的计算公式。常用的计算方法是势能驻值原 理的近似法,即里兹法。 虚应力原理等价于结构的变形协调条件,因此基于虚 应力原理的方法是力法。由虚应力原理可导出余能驻值原 理。常用的计算方法是最小功原理及卡氏第二定理。
Q0l0 Q0l0 M , M 21 12 15 10 M Q2 (3l ) Q1 (3l ) 33 Q l 24 0 0 0 0 15 12 10 Q Q 21 Q0l0 M 42 2 (3l0 ) 1 (3l0 ) 10 12 5 M 23 M 32 0
位移法
计算步骤(不可动节点刚架和连续梁)
• 确定未知数(n=N-r)
• 加抗转约束,计算固端弯矩 • 强迫转动,计算转角引起的杆端断面弯矩,计 算杆端总弯矩 • 列节点平衡方程式
0
2
l/2
2A
2 2 v 2 a l v ( 0 ) 2 a l 将 及 1 1
代入可计算出
总应变能为: V 4.5EIa2l 1 (2)计算力函数。此梁的力函数包括集中力F引起U1 及分布荷重引起的U2两部分。 计算U2时,先写出分布荷重的表达式。对图示坐标 有 q( x) 2q0 x q0 , l x l 2 2 因而 l l 2q0 x 1 2 3
(4)列节点平衡方程
4 EI0 8EI 4 EI12 4 EI 1 12 2 1 0 2 l12 l12 l0 l0 2 EI23 4 EI23 6 EI0 12EI0 M 32 2 3 2 3 l23 l23 2.2l0 2.2l0 16EI0 2 EI24 4 EI24 M 42 2 4 2 l24 l24 3l0 M 21
虚位移原理等价于结构的平衡条件,因此基于虚位移 原功方法是位移法。由虚位移原理可导出位能驻值原理, 最小势能原理的计算公式。常用的计算方法是势能驻值原 理的近似法,即里兹法。 虚应力原理等价于结构的变形协调条件,因此基于虚 应力原理的方法是力法。由虚应力原理可导出余能驻值原 理。常用的计算方法是最小功原理及卡氏第二定理。
Q0l0 Q0l0 M , M 21 12 15 10 M Q2 (3l ) Q1 (3l ) 33 Q l 24 0 0 0 0 15 12 10 Q Q 21 Q0l0 M 42 2 (3l0 ) 1 (3l0 ) 10 12 5 M 23 M 32 0
位移法
计算步骤(不可动节点刚架和连续梁)
• 确定未知数(n=N-r)
• 加抗转约束,计算固端弯矩 • 强迫转动,计算转角引起的杆端断面弯矩,计 算杆端总弯矩 • 列节点平衡方程式
船舶结构力学-3杆件扭转理论

杆件应变能
➢ 例1(EA,EI,GAs)
P l1
l2
➢ 例2(不考虑剪力影响)
EA l
EI
P
l
l/2
3-2虚位移原理与李兹法理
虚位移原理 真实力系在任意满足变形协调条件的虚位移过程中 做功的情况,等价于平衡条件
虚力原理 任一组满足平衡条件的虚力系在真实位移过程中做 功的情况,等价于变形协调条件
第三章 能量法
3-1 能量法基本概念 3-2虚位移原理与李兹法
3-1能量法基本概念
力法,位移法(解析法,初参数) 功能的概念求解结构
➢ 结构的平衡与变形连续条件
能量法(变形能法 变分法(数学上),有限元 功能关系
➢ 弹性体在外载作用下,外力功转变为变形(应变)能,外力 卸变形恢复
➢ 非线性(几何非线性,材料非线性),在外载作用下,外力 功转变为变形(应变)能
应变能(变形能):
➢ 拉杆为例: A, l, , , P
1
P A , l ,则应变能V W Al d
1
0
单位体积应变能 V0 d ,为左图中应力应
变曲线下面积应变能0密度(比能)
➢ 三维弹性体空间应力状态:
T
x
y
z
xy
yz
zx
T
x
y
z
xy
yz
zx
待定系数的偏导为0)
基函数只须满足位移边界条件
若结构仅在i处发生一单位虚位移δΔi=1,则有
Pi 1 T 0d
{ε0}是由单位虚位移引起的虚应变。 可应用于单刚矩阵计算。
位能驻值原理的近似解法
近似解法,应用范围广 李兹法:利用位能驻值原理将变分问题看作包含有有限
《船舶结构力学》第4章 力法

X2
X1
(b)
例2:
X 3X 3 X 2X 2 X 1X 1 (a)(a) (b) (b)
例3:
n = 3次
X 32 XX 3 2 X3 X3 X X1 X1 X2
X2
X0 (a) (a) (b)
X0 (b)
n = 4次
第四章 力法
静定结构的内力只要根据静力平衡条件就可以得出,而超静定 结构的内力不能只靠静力平衡条件求出,还必须同时考虑变形协调 条件,所以也就复杂。
在刚架的对称节点处,节点的转角和断面弯矩大小 相等,方向相同;在对称轴线上,线位移和断面弯矩 等于零,因此该处可简化为自由支持于刚性支座上。
2
结构对称性-结合图形分析
(熟悉对称结构刚架的特性,对解题是很有用处的。 一般来说,应用此种对称特性,可将未知数减少一半)
对称结构的刚架,其所受的外荷重可能是对称的,亦可能是 不对称的。但是不对称的荷重总是可以分为一部分对称的荷重与 另一部分反对称的荷重。
(a)对称结构对称荷重:(结合刚架变形情况分析) 在刚架的对称节点处,节点的转角和断面弯矩大小 相等,方向相反;在对称轴线上,转角和剪力都等于零。
式中δi j代表基本结构中力Xi 在Xj 位置处引起的位移; Δi q代表基本结构中外力在相应于力Xi 位置处引起的位移。
3、三弯矩方程
11 M 1 12 M 2 1q
21 M 1 22 M 2 23 M 3 2 q ... n1n M n1 nn M n nq
A B C
RA
RB
RC
2.超静定次数 超静定次数就是超静定结构中多余约束的个数。
如果从一个结构中去掉n个约束,结构就成为静定的,则原结构 即为n次超静定结构。 从静力角度出发,超静定次数等于仅利用平衡方程计算未知力 时所缺少的方程个数。
X1
(b)
例2:
X 3X 3 X 2X 2 X 1X 1 (a)(a) (b) (b)
例3:
n = 3次
X 32 XX 3 2 X3 X3 X X1 X1 X2
X2
X0 (a) (a) (b)
X0 (b)
n = 4次
第四章 力法
静定结构的内力只要根据静力平衡条件就可以得出,而超静定 结构的内力不能只靠静力平衡条件求出,还必须同时考虑变形协调 条件,所以也就复杂。
在刚架的对称节点处,节点的转角和断面弯矩大小 相等,方向相同;在对称轴线上,线位移和断面弯矩 等于零,因此该处可简化为自由支持于刚性支座上。
2
结构对称性-结合图形分析
(熟悉对称结构刚架的特性,对解题是很有用处的。 一般来说,应用此种对称特性,可将未知数减少一半)
对称结构的刚架,其所受的外荷重可能是对称的,亦可能是 不对称的。但是不对称的荷重总是可以分为一部分对称的荷重与 另一部分反对称的荷重。
(a)对称结构对称荷重:(结合刚架变形情况分析) 在刚架的对称节点处,节点的转角和断面弯矩大小 相等,方向相反;在对称轴线上,转角和剪力都等于零。
式中δi j代表基本结构中力Xi 在Xj 位置处引起的位移; Δi q代表基本结构中外力在相应于力Xi 位置处引起的位移。
3、三弯矩方程
11 M 1 12 M 2 1q
21 M 1 22 M 2 23 M 3 2 q ... n1n M n1 nn M n nq
A B C
RA
RB
RC
2.超静定次数 超静定次数就是超静定结构中多余约束的个数。
如果从一个结构中去掉n个约束,结构就成为静定的,则原结构 即为n次超静定结构。 从静力角度出发,超静定次数等于仅利用平衡方程计算未知力 时所缺少的方程个数。
结构力学课件--6力法3
2
内容回顾
对称荷载:
反对称荷载:
EI
P EI
EI P P
EI
P EI
EI P P
B.有中柱对称结构(偶数跨结构) 对称荷载:
反对称荷载:
EI EI
P EI
EI P P
EI EI
P EI EI EI P P
EI/2
2019/7/14
课件
3
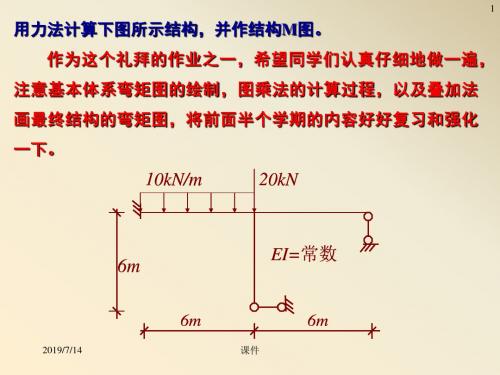
用力法计算下图所示结构,并作结构M图。
1 kN/m EI
EI
EI 2m
可能使: 21 = 12 = 0
即得:
课件
11X1 1P = 0 22 X 2 2P = 0 33 X 3 3P = 0
y y´
12
X2
X2 y
X1 X1 a
y
O
x
x'
1
y
x
X1 = 1
y
X2 =1
M1 =1 N1 = 0 Q1 = 0
12 =
15
4m
a
y
2EI
EI
EI
x
8m
X1 X1
X2 X2 X3
a
=
y
1 EI
ds
1 EI
ds
=
1 2EI
8 4
2( 1 EI
4 2)
=
8
=
2.667m
1 8 2( 1 4)
3
2019/7/14
2EI
EI 课件
§6-7 支座移动和温度改变时的内力计算
16
一、支座移动时的计算
(a 11
1 2
船舶结构力学:第三章力法

qi-1
qi
1 I1 2
i-1
Ii-1 i
Ii i+1
l1
li-1
li
图3-1(a)
M1
M2 Mi-1
qi-1
Mi Mi
qi
I1
Ii-1
Ii
l1
li-1 图3-1(b)
li
n-1
In-1 n
ln-1
Mi+1 Mn-1
Mn
In-1
ln-1
§ 3-3 刚性支座上连续梁与不可动节点简单刚 架计算
图(3.1a)所示的为n-1跨的刚性支座上的连续梁, 其两端刚性固定。首先判断它是一个n次超静定梁 (无轴向载荷,故无轴向约束反力),将连续梁两 端的刚性固定端改为固定铰支座,并以相应的多余 约束力(端面弯距)代替,在每个中间支座处将梁 切断,并以相应的约束反力(梁截面上的弯距)代 替。得到如图(3.1b)所示的基本结构—单跨梁。 它会使得力法方程简化。
第三章 超静定结构的解法—力法
Methods of Analysis of Statically Indeterminate Structures- Mechanics
§ 3-1 超静定结构的组成与超静定次数的确定
概述
超静定结构是相对于静定结构而言的。静定结构 是几何不变而又没有多余约束的体系,其反力和内力 只需静力平衡方程即可求得。所谓几何不变体系是指 如果不考虑材料应变所产生的变形,体系在受到任何 载荷作用后能够保持其固有的几何形状和位置的体系。 超静定结构有以下几个特征:
支座1处的 转角
1 0
支座2处的 转角
21 23
§ 3-2 力法的基本原理及典型方程
上式即为变形协调条件。利用两端自由支持单跨 梁的弯曲要素表,可以得到转角与弯矩和外载荷之间 的关系式,并将他们代入到上式,得到:
集美大学船舶结构力学(48学时)第三章 力法(1)2014(2学时)

R
静定基
这时原来仅受均布荷重q作用的静 不定的双跨梁变为受均布荷重q与集中 力R共同作用的静定的单跨梁;
2)比较前后两种梁的变 形情况,根据变形一致 (协调、连续)条件建 立方程式;
原超静定结构
v1 0
静定基
变形一致条件:
v1 0
静定基
变形一致条件:
v1 0
vq1 vR1 0
4
3
Rl 5ql 0 5 6 EI 24 EI R ql 4
P
M图
中点挠度大小
3
端点转角大小
2
m
Pl Pl EI , l 48EI 16EI Pl / 4 2 m ml ml ml 左 右 查单跨梁的弯曲要素表(附录A表A-2),得到: 3EI 6EI 16EI
Q
EI , l
Ql / 8
(力法基本未知数数目与结构的 静不定次数相同。)
2、在去掉约束或截断处, 列出变形一致(连续) 方程式以保证基本结构 的变形与原结构的变形 相同。
(方程数目与基本未知数数目相同。)
3、从变形一致(或连续、 协调)方程式中求出未 知“力”,进一步可求 出结构的其他弯曲要素。
五、三弯矩方程法 1、三弯矩方程式:一般来 说,在用力法的第二种方法 (截面法)解静不定杆系问 题时,列出的变形连续方程 式(或称节点转角连续方程) 是以各断面弯矩为未知数的 方程组,
1 2 M 1 ql 14
3 2 M2 ql 28
7)画弯矩图
求出了 M 1 、M 2 后, 就可以分别对两个单跨 梁1-2、2-3画弯矩图。
其中每一个单跨梁 的弯矩图都可以用叠加 法来画。最后组合起来 得到双跨梁的弯矩图, 图3-7(a)。
静定基
这时原来仅受均布荷重q作用的静 不定的双跨梁变为受均布荷重q与集中 力R共同作用的静定的单跨梁;
2)比较前后两种梁的变 形情况,根据变形一致 (协调、连续)条件建 立方程式;
原超静定结构
v1 0
静定基
变形一致条件:
v1 0
静定基
变形一致条件:
v1 0
vq1 vR1 0
4
3
Rl 5ql 0 5 6 EI 24 EI R ql 4
P
M图
中点挠度大小
3
端点转角大小
2
m
Pl Pl EI , l 48EI 16EI Pl / 4 2 m ml ml ml 左 右 查单跨梁的弯曲要素表(附录A表A-2),得到: 3EI 6EI 16EI
Q
EI , l
Ql / 8
(力法基本未知数数目与结构的 静不定次数相同。)
2、在去掉约束或截断处, 列出变形一致(连续) 方程式以保证基本结构 的变形与原结构的变形 相同。
(方程数目与基本未知数数目相同。)
3、从变形一致(或连续、 协调)方程式中求出未 知“力”,进一步可求 出结构的其他弯曲要素。
五、三弯矩方程法 1、三弯矩方程式:一般来 说,在用力法的第二种方法 (截面法)解静不定杆系问 题时,列出的变形连续方程 式(或称节点转角连续方程) 是以各断面弯矩为未知数的 方程组,
1 2 M 1 ql 14
3 2 M2 ql 28
7)画弯矩图
求出了 M 1 、M 2 后, 就可以分别对两个单跨 梁1-2、2-3画弯矩图。
其中每一个单跨梁 的弯矩图都可以用叠加 法来画。最后组合起来 得到双跨梁的弯矩图, 图3-7(a)。
船舶结构力学课件

教学中具体方法包括: 力法(Force method) 位移法(Displacement) 能量法(Energy method) 矩阵法(Matrix method) 有限元法(Finite element)
一、结构的几何不变性 ① 几何不变的意义 ② 几何不变系统 ③ 瞬时几何可变系统
二、几何不变性的判断
目的:
使学习者具有对船体结构进行 强度及变形分析的能力.
§1-2 船舶结构力学的研究方法
一般船舶结构分析方法
将船体的总强度与横向强度或局部 强度问题分开考虑;
在横向强度或局部强度问题中, 将空间结构拆成平面结构;
计算中又将船体的骨架和板分开考 虑;
计算机出现后的新方法: ➢将总强度与横向强度及局部强度
问题一起考虑; ➢完全可计算空间结构; ➢可不将骨架和板分开,而共同考
虑;
§1-3 船舶结构的计算图形 及典型结构
一般分析的原则: 将板与骨架分开进行分析
又可根据骨架受力以及结构变形特点将骨架 简化为更为简单的平面结构形式
板பைடு நூலகம்构
纵骨
船体结构中三种典型杆系 连续梁、刚架、板架
横梁
肋骨
❖板 板弯曲问题
板平面问题
垂直荷重 开口应力集中问题
板面内受到载荷 作用
组合载荷问题 稳定性问题
刚架
连续梁
船底
甲板结构
板架
平板结构 连续梁 刚架结构
板架结构
结构特点 结构受力特点 结构变形特点
❖空间和复杂结构
悬臂梁 甲板纵绗
肋骨
大舱口悬臂梁计算图形
大型油轮肋骨刚架离 散化计算图形
教学中具体内容: 杆及杆系的强度 板的强度 杆系和板的稳定性问题
集美大学船舶结构力学(48学时)第三章 力法(3)2014(2学时)

由于: R2 v2 / A
216EI v 2 3 11l
M 2 M1 5 R2 ql l 2
因此,有方程:
216 EI M 2 M1 5 v ql 2 3 11l l 2
将此式与上面两方程联立 问题则解决。
题9 求下图 M , v , R 。 1 1 1
据3.6改 (教材52页)
梁的左半段断面惯性矩 为 I 1 ,右半段断面惯性矩 为 I 2 ,可以设想在断面变 化处加上一个柔性系数 A= ∞ 的弹性支座,如图4-27b)所示, 于是就可以按弹性支座上双跨 梁的方法来计算了。
静定基
v AR
EI1
R10
R R12
EI 2
v
静力平衡方程?
R0
A
转角连续方程式?
因此,可列出中间支座断面的 转角连续方程式:
R10
R12
3
l v1 AR1 ( R10 R12 ) 12EI 2 R ql 3
题8
(教材49页例2) 图3-26a所示的具有弹 性支座的多跨梁,试求其断 面弯矩、节点挠度和作用在 弹性支座上的力。
解:1、静定基:
M1
q 1
EI , l
M2
q
E,4I ,4l
M2
3
11l 3 A 216EI
即: 原模型:
A l3 6 EI
静定基:
EI , l EI , l
变协方: 4 4 5 q(2l ) 1 R(2l ) AR 384 EI 48 EI
由此直接解得:
R
v1 AR
可以去掉 中间的弹性支 座代以支反力 R,再利用变 形连续条件列 方程式求解。
R 5ql / 8
216EI v 2 3 11l
M 2 M1 5 R2 ql l 2
因此,有方程:
216 EI M 2 M1 5 v ql 2 3 11l l 2
将此式与上面两方程联立 问题则解决。
题9 求下图 M , v , R 。 1 1 1
据3.6改 (教材52页)
梁的左半段断面惯性矩 为 I 1 ,右半段断面惯性矩 为 I 2 ,可以设想在断面变 化处加上一个柔性系数 A= ∞ 的弹性支座,如图4-27b)所示, 于是就可以按弹性支座上双跨 梁的方法来计算了。
静定基
v AR
EI1
R10
R R12
EI 2
v
静力平衡方程?
R0
A
转角连续方程式?
因此,可列出中间支座断面的 转角连续方程式:
R10
R12
3
l v1 AR1 ( R10 R12 ) 12EI 2 R ql 3
题8
(教材49页例2) 图3-26a所示的具有弹 性支座的多跨梁,试求其断 面弯矩、节点挠度和作用在 弹性支座上的力。
解:1、静定基:
M1
q 1
EI , l
M2
q
E,4I ,4l
M2
3
11l 3 A 216EI
即: 原模型:
A l3 6 EI
静定基:
EI , l EI , l
变协方: 4 4 5 q(2l ) 1 R(2l ) AR 384 EI 48 EI
由此直接解得:
R
v1 AR
可以去掉 中间的弹性支 座代以支反力 R,再利用变 形连续条件列 方程式求解。
R 5ql / 8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-4 弹性支座与弹性固定端的概念
本节主要通过力法解杆系结构的例子引出弹性支座与弹性固定端的 实际概念。
1、弹性支座
q
I
l/2 R l/2
R
l1/2
l1/2
3-4 弹性支座与弹性固定端的概念
根据原结构节点处位移连续条件,列出力法方程为:
ql4 Rl3 Rl13 384EI 192EI 48EI1
X n
Δnp
3-3 刚性支座上连续梁与不可动节点简单刚架 计算
1、刚性支座上连续梁与三弯矩方程
1
2
i-1
M1
1
M2
2
i
i+1
n-1
n
Mn Mn-1
n-1
n
1、刚性支座上连续梁与三弯矩方程
根据原结构在固定端处转角为0和在每一个中间支座处转角连续的条件, 可列出力法方程:
l 3EI
i1
M i1
i
i
Mi
Mi
i1
M i1
li 1
i-1
i
li
i
i+1
根据中间支座i处转角连续的条件: i=(2M i1
li 3EI i
Mi
i (qi1) i
i 1
li1
li 3EI i
Mi
li1 6 EI i 1
(2)去掉多余约束后的体系,必须是几何不变的体系,因 此,某些约束是不能去掉的。
3-2 力法的基本原理及典型方程
M1
1
M2
M2
2
2
为使新静定结构与原结构等效, 必须满足以下变形协调条件:
(1)固定端处的转角为0;
12 0
(2)中间支座处的转角连续;
21 23
3
3-2 力法的基本原理及典型方程
A
一次超静定结构的力法方程
A
式中δ11 、Δ1P被称为系数
和自由项,可用求解静定结构位移的方法求出。
B
B
X1
B
1P
δ11X111 B
X1
1×X1
3-2 力法的基本原理及典型方程
② 求系数δ11 、自由项Δ1P
ql 2 2
δ11 Δ1P——均为静定结构在已 A 知力作用下的位移,故可由积分 法或图乘法求得。
第三章
力法
3-1 超静定结构的组成与超静定次数的确定
力法是计算超静定结构最基本的方法之一。 1、超静定结构的组成
静定结构:几何不变而又没有多余联系的体系,其反力和内力只需根据静 力平衡方程即可求得;
超静定结构:几何不变但有多余联系的体系。其反力和内力仅根据静力平 衡方程无法确定。
3-1 超静定结构的组成与超静定次数的确定
ln1 3EI n1
Mn
n
(qn1
)
n
n 1
ln1
AnM n
1、弹性支座上连续梁计算
上述n个方程无法解出n个未知弯矩;因为还有n个未知数 1 n
因此还需要补充n个方程进行求解。
A R 根据以下关系: i
i i 支座反力R根据剪力求取。
根据i跨梁的平衡方程有:
2、超静定次数 通常将多余联系或多余约束力的数目称为结构的超静定次数。 如果从结构中去除n个约束结构就变为静定的,则原结构为超静 定结构。
一次超静定
3-1 超静定结构的组成与超静定次数的确定
3、去掉超静定的方法
① 撤去一个活动铰支座; 在支座处切断一根梁(支座保留);
去掉一个 多余联系
3-1 超静定结构的组成与超静定次数的确定
可为正、负或零,且由位移互等定理: δij =δji
3-2 力法的基本原理及典型方程
自由项Δ i P ——荷载FP单独作用于基本体系时,所引
起Xi方向的位移,可正、可负或为零。
δ11
L δ1n
LL
X1 M
Δ1p M
0
δn1 L
δnn
(n1)(n2)
(n1)(n1) (nn1)
( n 1) n
nn
M
n1
M n
(n
1)
p
np
1、刚性支座上连续梁与三弯矩方程
11
l1 3EI1
ii 1
li1 6EIi1
N ii
M i1 M i li1
Ni (qi )
支座处剪力与支座反力的关系为:
Ri Ni(i1) Nii
i跨梁上所有外载荷引起的 梁左端截面上的剪力
N i(i1)
qi
Mi
R1 N11 Rn Nn(n1)
Nii
N i1 M i1
1、弹性支座上连续梁计算
则总共有2n个方程,2n个未知数,整理得:
此方程不依结构形式变化而产生变化,称为力法的典型 方程。
3-2 力法的基本原理及典型方程
主系数δii(i =1,2, …n)——单位多余未知力 Xi=1
单独作用于基本结构时,所引起的沿其本身方向上 的位移,恒为正;
副系数δij(i ≠j)——单位多余未知力 Xj=1
单独作用于基本结构时,所引起的沿Xi方向的位移,
4
2 1
3 5
2、弹性固定端
图为双甲板船舱口部位的上甲板横梁与甲板间肋 骨组成的刚架。
基本结构如下图所示:
根据连接处转角连续,列出的力法方程如下:
l1 M l M ql3 3EI1 3EI 24EI
此表达式与下述结构左端转角表达式相同。
A M
l 3EI
M
ql3 24 EI
梁0-1相当于杆1-2的弹性固定端。
, ii
li1 3EIi1
li 3EIi
nn1
ln1 6EI n1
, nn
ln1 3EI n1
2、不可动节点简单刚架计算
船体刚架: 横梁; 肋骨; 肋板;
概念: (1)简单刚架:每一个节点处只有两根杆件; (2)复杂刚架:节点处的杆件多于两根; (3)不可动节点刚架:节点处线位移可以忽略不计,可视为固定铰支座; (4)可动节点刚架:节点处线位移需要计入。
(4)在杆系分析中,如果要计算某一根杆件,只需考虑与它相邻的那一 根杆件的影响而无需考虑选离此杆件的其他杆件对它的作用。
2、弹性固定端的固定系数
如果杆系结构中的所有杆件上都有外载荷作用,那么其中任何一根杆件 都不能作为另一根杆件的弹性固定端,因此,柔性系数无法求出。
因此引入一个关于弹性固定端固定程度的新定义,叫做固定系数。
A
l
B
M图
3-2 力法的基本原理及典型方程
4)力法的典型方程
对于n次超静定结构,其力法方程组可写成:
11X1 12 X 2 ...1n X n 0 21X1 22 X 2 ... 2n X n 0
...
n1X1 n2 X 2 ... nn X n 0
M1
M2
M2
1
2
l 3EI
M1
l 6EI
M2
ql3 24 EI
0
M 1l 6EI
M 2l 3EI
ql3 24 EI
l 3EI
M2
ql3 24 EI
2
变形3协调方程
力法方程
l 3EI
M1
l 6EI
M2
ql3 24 EI
0
l 6EI
M
1
2l 3EI
M2
ql3 12 EI
(1
1)
上述关系式并不普遍成立,但是:
A 0 A
1 0
3-5 弹性支座上连续梁计算
船体结构中也存在弹性支座上的连续梁计算: 如搁置在墩木上的船体,墩木对船体的支持相当于弹性支座。
1
2
i-1
i
n-1 n
弹性支座上连续梁的解法与刚性支座上的解法类似,采用力法进行求解。
1、弹性支座上连续梁计算
=0,自由支持端 =1,刚性固定端
M弹
M刚
固定系数为弹性固定端弯矩与假想为刚性固定端时的弯矩之比。
2、弹性固定端的固定系数
定义固定系数并不要求弯矩与转角成正比,因此固定系数与柔性系数并无关联。 为了实际的需要,目前在船舶结构分析中存在一个关系式:
1
1 2 A EI l
A
l 2EI
基本体系
X1 — 称为力法的基本未知量。
3-2 力法的基本原理及典型方程
q
(3)求基本未知量X1 ① 建立变形协调方程
A
B
l
==
基本体系与原结构在去掉多
q
余约束处沿多余未知力方向上
的位移应一致,即:Δ1 =0
A
由迭加原理,上式写成:
q
B
X1
B
Δ1 =Δ11+Δ1P=0
A
11
+
——变形协调方程。
Δ11:由多余未知力X1单独作用 A 时,基本结构B点沿X1方向产生的位移
...
...
.
.
.
M
n1
(n
1)
p
I
等效
l/2 R l/2
