三重积分习题ppt
合集下载
高等数学《三重积分》课件

3
注: 1.可积性: f 连续 可积
2.物理意义
如果f(x,y,z)表示某物体在点(x,y,z)处的体密度,Ω 是该物体所占的空间闭区域,f(x,y,z)在Ω上连续, 则
物体的质量 M f ( x, y, z)dv 3.几何意义
的体积 V dxdydz
4.性质 同二重积分 4
8.3.2、直角坐标系下的三重积分的计算法
f (z, x,
y)]dV
若为球面x 2 y 2 z 2 R2所围,则
x 2dV
y 2dV
z2dV
1 3
[ x 2
y2
z 2 ]dV
13
例 3 利用对称性简化计算
z ln( x2 y2 z2 1)
x2 y2 z2 1 dxdydz 其中积分区域 {(x, y, z) | x2 y2 z2 1}.
其中A(z)是Dz的面积
习题8.3.1
20
o
y
或D(z),即
x
{( x, y, z)( x, y) Dz ,c1 z c2}
f ( x, y, z)dv c2 dz f ( x, y, z)dxdy (3)
c1 Dz
15
f (x, y, z)dv c2 dz
z
f ( x, y, z)dxdy
c1
Dz
上式的适用范围:
其中在每vi表个示v第i上i个任小取闭一区点域(,i ,也i表, 示i)它,的作体乘积积。f ( i ,
i,
i)
vi
(i=1,2,…
n
,n)
,
并作和 f (i ,i , i )vi。
如果当各i 1小闭区域直径的最大值 趋于零时
这个和的极限总存在, 则称此极限为函数
三重积分ppt

0 2
在球面坐标下 x2 y2 z2 2, 因此
1. 若被积函数形如 f (x2 y2 z2);
2. 积分区域是由球面、锥面或平面所围成. 常用球面坐标计算
球面坐标下的三坐标面分别为
z
动点M(ρ, ,)
ρ=常数: 球面S
=常数:
M
S
ρ
0
x y
动点M(ρ, ,)
ρ=常数: 球面S
f
( x,
y, z)dxdy.
例4 计算三重积分 zdxdydz, 其中为三个坐
标面及平面x y z 1所围成的闭区域.
解 截面法(先二后一法)
zdxdydz
1
0
zdz
dxdy
Dz
Dz {(x, y) | x y 1 z}
z
1 x yz1
1O
x
Dz
1y
1
dxdy 2(1 z)(1 z)
z
• M (x, y, z)
z
O
Ax x
y
•P
y
向xOy平面投影, 记投影向量与x轴正方向的
夹角为 , 称 ( , , ) 为点M 的球面坐标. 规定: 0 , 0 , 0 2 .
直角坐标与球面坐标的关系为
x sin cos
y
sin
sin
z cos
0 0
z
C
=常数: 锥面C
=常数: 半平面P
M
S
P
0
x
y
球面坐标下的体积元素
z
元素区域由六个坐标面围成:
圆锥面
球面ρ+dρ
半平面 及+d ; ρsind
半径为ρ及ρ+dρ的球
在球面坐标下 x2 y2 z2 2, 因此
1. 若被积函数形如 f (x2 y2 z2);
2. 积分区域是由球面、锥面或平面所围成. 常用球面坐标计算
球面坐标下的三坐标面分别为
z
动点M(ρ, ,)
ρ=常数: 球面S
=常数:
M
S
ρ
0
x y
动点M(ρ, ,)
ρ=常数: 球面S
f
( x,
y, z)dxdy.
例4 计算三重积分 zdxdydz, 其中为三个坐
标面及平面x y z 1所围成的闭区域.
解 截面法(先二后一法)
zdxdydz
1
0
zdz
dxdy
Dz
Dz {(x, y) | x y 1 z}
z
1 x yz1
1O
x
Dz
1y
1
dxdy 2(1 z)(1 z)
z
• M (x, y, z)
z
O
Ax x
y
•P
y
向xOy平面投影, 记投影向量与x轴正方向的
夹角为 , 称 ( , , ) 为点M 的球面坐标. 规定: 0 , 0 , 0 2 .
直角坐标与球面坐标的关系为
x sin cos
y
sin
sin
z cos
0 0
z
C
=常数: 锥面C
=常数: 半平面P
M
S
P
0
x
y
球面坐标下的体积元素
z
元素区域由六个坐标面围成:
圆锥面
球面ρ+dρ
半平面 及+d ; ρsind
半径为ρ及ρ+dρ的球
重积分三重积分的应用课件.ppt

解 立体的图形为 设1为 在第一卦限内
的部分, 利用对称性得
z 1
M 4M1 4 ( x, y, z)dv
1
o
y
4( x y )dv 柱坐标变换 x
1
1
1
4 2 d rdr r(cos sin )dz
0
0
r2
4
2 (cos sin )d
1
r
2
(1
r
2
)dr
0
0
16。 15
13
设有一平面薄片占有 y
平面闭区域D, 在点(x,y)
处具有连续面密度
=(x,y),下面利用元素
y
•d
D
法求该平面薄片对两坐
标轴的转动惯量。
O
x
x
先将物体分割为许多小部分,考虑其中的一
个部分d,它的质量元素为
dm ( x, y)d
这个部分d对于x轴以及对于y轴的转动惯
量元素为
dIx y2( x, y)d dI y x2( x, y)d
F
x, y, a 一致。
F0
x r
,
y,a rr
o x
x
y
• P(x,y,0) y
cos,cos ,cos , (r x2 y2 a2 )
dF {dFx , dFy , dFz }
{| d F | cos,| d F | cos ,| d F | cos },
( x, y)xd ( x, y) yd a( x, y)d
14
y
以这些元素为被积表达 式,在闭区域D上积分, 可得
y
•d
D
Ix y2( x, y)d ,OD源自I y x2( x, y)d
三重积分的先二后一积分法(课堂PPT)

椭圆
x2 a2
y2 b2
1
的面积:
A ab
b
a
四川大学数学学院 徐小湛
May 2012
10.3 三重积分 7
Dz
{(x,
y) |
x2 a2 (1
z2 c2
)
y2 b2 (1
z2 c2
)
1}
dxdy
Dz
a2
(1
z2 c2
)
b2
(1
z2 c2
)
ab(1
z2 c2
)
椭圆的面积
z
2
dxdydz
Dz
d
z
DzLeabharlann c截面的质量 “切片法”
四川大学数学学院 徐小湛
May 2012
10.3 三重积分 4
适合“先二后一”积分法的一种特殊情形
d
f (x, y, z)dV c dz f (x, y, z)dxdy
Dz
d
D(z)
如果被积函数仅为 z 的函数,则
z
d
c
f (z)dV c dz f (z)dxdy
Dz
{(x,
y) |
x2 a2
y2 b2
1
z2 c2 }
椭圆域
四川大学数学学院 徐小湛
May 2012
例2 计算三重积分
z 2 dxdydz
10.3 三重积分 6
z
Dz
解 用“先二后一”的方法
o
y
x
{(x,
y, z) | c
z
c,
x2 a2
y2 b2
1
z c
2 2
}
三重积分习题ppt课件
z
2
解法1:利用“先二后一”方法计算。
1
因 {(x, y, z) | (x, y) Dz, 0 z 2}
oD
y
由于当 0 z 1 时, Dz : x 2 y 2 z 2;
x
而当 1 z 2 时, Dz : x2 y2 2 z2 。
机动 目录 上页 下页 返回 结束
故需用平面 z 1 将积分区域 划分为两部分: 1 2
h
所以本题也可采用柱面坐标计算
解法1:利用“先二后一”方法计算。
由于 {( x, y, z) | ( x, y) Dz , 0 z ,h}
o R x
Dz
R
y
其中 Dz : x 2 y 2 Rh22z,2 故
zdxdydz
h
zdz
dxdy
h
R2z2
z
dz
0 Dz
0
h2
R 2
注意:从上面两种解法的过程来看, 虽然本题可用两种方法
来计算,但“先二后一”法相对简便。
26/37
9(2). 计算三重积分 zdxdydz , 其中 是由圆锥面 z x2 y2 与上半球面 z 2 x2 y2 所围成的闭区域。
分析:本题可考虑用直角坐标系中的“先二后一”法和柱面
坐标方法进行计算。
D
a
b ax
xy
Dxy
dx a
dy c f ( x, y, z)dz 0
a
20/37
y x
x
机动 目录 上页 下页 返回 结束
4. 计算三重积分 xy2z 3dxdydz。其中 是由曲面 z xy
与平面
y
x,x
1
及
三重积分 ppt课件

0
n k 1
f
(
k
,k
,
k
)vk
记作
f (x, y, z)dv
存在, 则称此极限为函数 f (x, y, z) 在 上的三重积分.
dv称为体积元素, 在直角坐标系下常写作 dxdydz.
性质: 三重积分的性质与二重积分相似.
ppt课件
3
目录 上页 下页 返回 结束
二、三重积分的计算
其中 由抛物面
x2 y2 4z 与平面 z h (h 0)所围成 .
z
h
解: 在柱面坐标系下
原式 =
2π 2
d
0
0
h
1
2
d
h
2 d z
xO y
4 dv d ddz
2
2π
0
h
1
2
(h
2
4
)
d
ppt课件
10
目录 上页 下页 返回 结束
围成 , f (x, y, z) C( ).
提示:
:
1
y
2
1 2
x
I
2
dx
2
1 2
x
d
y
2
f (x, y, z)dz
01
x
ppt课件
14
目录 上页 下页 返回 结束
2. 设
计算
提示: 利用对称性
原式 = d x d y x2 y2 1 0
奇函数
ppt课件
因此有
d d r
r d
f (x, y, z)dxdydz
n k 1
f
(
k
,k
,
k
)vk
记作
f (x, y, z)dv
存在, 则称此极限为函数 f (x, y, z) 在 上的三重积分.
dv称为体积元素, 在直角坐标系下常写作 dxdydz.
性质: 三重积分的性质与二重积分相似.
ppt课件
3
目录 上页 下页 返回 结束
二、三重积分的计算
其中 由抛物面
x2 y2 4z 与平面 z h (h 0)所围成 .
z
h
解: 在柱面坐标系下
原式 =
2π 2
d
0
0
h
1
2
d
h
2 d z
xO y
4 dv d ddz
2
2π
0
h
1
2
(h
2
4
)
d
ppt课件
10
目录 上页 下页 返回 结束
围成 , f (x, y, z) C( ).
提示:
:
1
y
2
1 2
x
I
2
dx
2
1 2
x
d
y
2
f (x, y, z)dz
01
x
ppt课件
14
目录 上页 下页 返回 结束
2. 设
计算
提示: 利用对称性
原式 = d x d y x2 y2 1 0
奇函数
ppt课件
因此有
d d r
r d
f (x, y, z)dxdydz
同济大学 高数 三重积分ppt课件

对应雅可比行列式为 J (x, y, z) (u, v, w)
直角坐标与柱面坐标的关系:
x cos y sin zz
J (x, y, z)
(,, z)
x y
x y
xz cos sin 0
yz sin cos 0
z z zz
0
01
dv J dddz dddz
x2 y2 2
z
h
解: 在柱面坐标系下
原式 =
2π 2
d
0
0
h
1
2
d
h
2 d z
xO y
4 dv d ddz
2
2π
0
h
1
2
(h
2
4
)
d
22
目录 上页 下页 返回 结束
3. 利用球坐标计算三重积分
设 M (x, y, z) R3, 其柱坐标为(, , z), 令 OM r,
zOM ,则(r,, ) 就称为点M 的球坐标.
16
目录 上页 下页 返回 结束
f (x, y, z)dxdydz
d d dz
d
d 2 ( )
z2 (, ) F(, , z)dz
1 ( )
z1 ( , )
其中 F(, , z) f ( cos , sin , z )
(,, z) , 1( ) 2( ), z1(, ) z z2(, )
就称为点M 的柱坐标. 直角坐标与柱面坐标的关系:
x cos y sin
zz
坐标面分别为
00z2π
z z
M (x, y, z)
常数 常数
z 常数
圆柱面 半平面 平面
三重积分习题课优质课件
r=2a cos
M
r
例8
1
Dxy
1
0
x
z
y
【例9】
【解Ⅰ】
1
Dxy
1
0
x
z
y
【解Ⅱ】
1
Dxy
1
0
x
z
y
【解Ⅲ】
1
Dxy
1
0
x
z
y
【解Ⅳ】
【补充:利用对称性化简三重积分计算】
使用对称性时应注意:
1、积分区域关于坐标面的对称性;
2、被积函数在积分区域上的关于三个坐标轴 的
奇偶性.
一般,若在的表达式中,以y代x,以z代y,以x代z
(1) 交换积分顺序的方法
(2) 利用对称性简化计算
(3) 消去被积函数绝对值符号
(4)被积函数为1时巧用其几何意义
【例1 】计算
【解】
由对称性知
(球面坐标)
作业题
一、关于三重积分性质和应用的题类
【例2】
设
比较M,N,P的大小.
【分析】通过计算比较大小很烦琐,注意到积分区域为一以原点为球心的球体,具有对称性,于是想到是否可利用对称性直接作出比较呢?
问高度为130 cm 的雪堆全部融化需要
多少小时? (2001考研)
【例17】——机动备用
[提示]
记雪堆体积为 V, 侧面积为 S ,则
(用极坐标)
由题意知
令
得
(小时)
因此高度为130cm的雪堆全部融化所需的时间为100
小时.
【例5】
1
x+ y=1
y
o
z
x
1
M
r
例8
1
Dxy
1
0
x
z
y
【例9】
【解Ⅰ】
1
Dxy
1
0
x
z
y
【解Ⅱ】
1
Dxy
1
0
x
z
y
【解Ⅲ】
1
Dxy
1
0
x
z
y
【解Ⅳ】
【补充:利用对称性化简三重积分计算】
使用对称性时应注意:
1、积分区域关于坐标面的对称性;
2、被积函数在积分区域上的关于三个坐标轴 的
奇偶性.
一般,若在的表达式中,以y代x,以z代y,以x代z
(1) 交换积分顺序的方法
(2) 利用对称性简化计算
(3) 消去被积函数绝对值符号
(4)被积函数为1时巧用其几何意义
【例1 】计算
【解】
由对称性知
(球面坐标)
作业题
一、关于三重积分性质和应用的题类
【例2】
设
比较M,N,P的大小.
【分析】通过计算比较大小很烦琐,注意到积分区域为一以原点为球心的球体,具有对称性,于是想到是否可利用对称性直接作出比较呢?
问高度为130 cm 的雪堆全部融化需要
多少小时? (2001考研)
【例17】——机动备用
[提示]
记雪堆体积为 V, 侧面积为 S ,则
(用极坐标)
由题意知
令
得
(小时)
因此高度为130cm的雪堆全部融化所需的时间为100
小时.
【例5】
1
x+ y=1
y
o
z
x
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b
o
.
a
x
计I算 f(x,y,z)d xd yd z:czxy(c0),a x2 2b y2 21
及z0所围成的在区 第域 习一 题。 10卦 -3 限第的
z
x2 y2
a2
b2
1
1(4)题
y
cz=xy
b
o z=0
a
.
x
计I算 f(x,y,z)d xd yd z:czxy(c0),a x2 2b y2 21
ቤተ መጻሕፍቲ ባይዱ
a
20/37
y x
x
-
机动 目录 上页 下页 返回 结束
4. 计算三重积分 xy2z3dxdyd。z 其中 是由曲面 zxy 与平面 yx,x1及 z 0所围成的闭区域。
分析: 由于积分区域和被积函数不具有利用“先二后一”、 柱面 坐标和球面坐标计算的特点, 故本题考虑利用直角坐标来计算.
解: (1) 求 (如图)在平面 xo上y 的投影区域为 D xy
其中
1 { ( x , y , z ) |( x , y ) D z , 0 z 1 }
2 { ( x , y , z ) |( x , y ) D z , 1 z 2 }
于是,得
zdxdydz zdxdydzzdxdydz
1
2
1
2
0zdzdxdy1 zdzdxdy
Dz
Dz
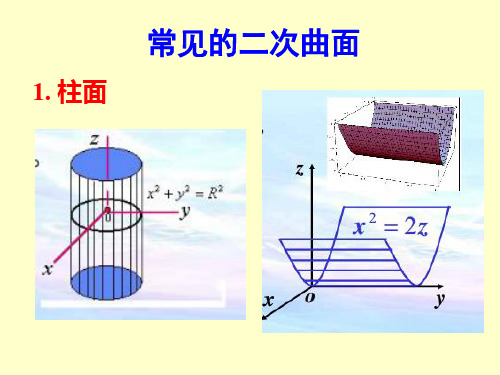
常见的二次曲面
1. 柱面
2. 锥面
3. 椭球面
4. 双曲面
5. 抛物面
习题10-3 第1(1)题
计I 算 f(x,y,z)d xd yd z
:zx与 y xy1,z0所围成的区域
x+ y=1
z
z=xy
y
1
o
1
.
x
习题10-3 第1(1)题
计I 算 f(x,y,z)d xd yd z
1zz2dz 2z(2z2)dz
0
1
1z41(z21z4) 2
40
41 2
解法2:利用柱面坐标计算。
在柱面坐标下 : z2 2 ,0 1 ,0 2
故有
zdxdydz 2d 1d 22 zdz
0
0
2 11(222)d 02
(2 1 4)1
20 2
注意:从上面两种解法的过程来看,虽然本题可用两种方法 来计算,但利用柱面坐标计算相对简便。
考虑到积分区域在xo坐y 标 面上的投影区域为圆域
z
Dxy: x2y2R2
h
所以本题也可采用柱面坐标计算
解法1:利用“先二后一”方法计算。
由于 { x ,( y ,z ) |( x ,y ) D z ,0 z ,h }
o R x
Dz
R
y
其中 Dz : x2y2 Rh22,z2 故
zdxdydz
1 x5 y6dxdy1
4 Dxy
4
1
d
x
x
x5
y6d
y
0
0
1 364
习题10-3
第7
题
8.
计算三重积分 zdxdydz. 其中 是由锥面
z h x2 y2 R
与平面z h(R0, h0)所围成的闭区域。
分析 由于被积函数 f(x, y,z)z只与变量 z有关, 且积分区域 被竖坐标为 z的平面所截的平面闭区域为圆域 Dz : x2y2 Rh22z2 故本题利用直角坐标系中“先二后一”的方法计算比较简便;
注意:从上面两种解法的过程来看, 虽然本题可用两种方法
来计算,但“先二后一”法相对简便。
26/37
9(2). 计算三重积分 zdxdydz, 其中 是由圆锥面 z x2 y2 与上半球面 z 2x2 y2所围成的闭区域。
分析:本题可考虑用直角坐标系中的“先二后一”法和柱面
坐标方法进行计算。
z
2
:zx与 y xy1,z0所围成的区域
x+ y=1
z
z=xy
y
1
o
z =0
1
.
x
习题10-3 第1(1)题
计I 算 f(x,y,z)d xd yd z
:zx与 y xy1,z0所围成的区域 。
。
x+ y=1
z
z=xy
y
1
o
z =0
1
.
x
xy
1 1x xy
Idxdy0
f(x,y,z)d z d x 00
解法1:利用“先二后一”方法计算。
1
因 { ( x ,y ,z )|( x ,y ) D z ,0 z 2 }
oD
y
由于当 0z1 时, Dz: x2y2z2;
x
而当 1 z 2 时, D z: x2y22z2。
-
机动 目录 上页 下页 返回 结束
故需用平面 z 1 将积分区域 划分为两部分:12
及z0所围成
的在区 第域 习一 题。 10卦 -3 限第的
1(4)题
z
cz=xy
.
b
o
a
y x
z
用哪种坐标? 直角坐标 cz=xy
是曲顶柱 由体,
xy
上顶 : z c
.
b
o
a
下底 : z = 0
Dxy:
x,
y,
x2 y
a
b
1
围成
y
xy
b
Idxdyc f(x,y,z)dz
D
a
bax
xy
Dxy
dxa dyc f(x,y,z)dz 0
D x: y 0yx ,0x1
(2)
确定上顶曲面
及下顶曲面
1
。2
因为当(x, y)Dx时y 满足 x ,0 y ,0
zxy0 。因此 1 :zxy 2 :z0
z zxy
o
(3) 转化为先对 z后对 x, y的三次积分计算:
y yx
x
xy2z3dxdydz
x
dxdy
yxy2z3dz
0
Dxy
d y f(x,y,z)d z 0
D
习题10-3
第
1(2)题
z
1
Dxy 0
y
1
x
习题10-3
第
1(3)题
计I算 f(x,y,z)d xd yd z:czxy(c0),a x2 2b y2 21
及z0所围成的在区 第域 习一 题。 10卦 -3 限第的
z
x2 y2
a2
b2
1
1(4)题
y
cz=xy
h
zdz
dxdy
h
R2z2
z dz
0 Dz
0
h2
R 2
h2
h z3dz 1 R 2 h2
0
4
解法2:利用柱面坐标计算。
在柱面坐标下 :hzh ,0R ,02
R
故有
zdxdydz
2
d
0
R
d
0
R hhzdz20R1 2(h2R h222)d
(1h22 2
4hR224)0R
1 4
R 2h2
