比例导引弹道仿真
过重力补偿比例导引弹道仿真研究

过重力补偿比例导引弹道仿真研究蒋 明, 宋卫东(军械工程学院兵器测试中心,河北 石家庄 050003)[摘 要] 激光半主动末制导炮弹能实现对目标的“攻顶”效应,分析了“攻顶”技术及其理论实质,即过重力补偿比例导引律的应用,以弹丸和目标的相对运动方程为基础,通过M atlab仿真计算的方法,分析了比例导引系数、弹丸与目标的速度比、过重力补偿值等主要参数的变化对弹道性能的影响,提出了导引律实现中注意的几个问题及改进制导系统的建议.[关键词] 导引规律; 比例导引法; 过重力补偿; 弹道; 仿真[中图分类号] TJ765.4 [文献标识码] AResearch on the Proporti ona l Nav i ga ti on w ith Co m pen s a ti on overGrav ity Tra jectory S im ul a ti onJ iang M ing, Song W eidong(W eapons Test Centre,O rdnance Engineering College,Shijiazhuang 050003,China)Abstract:Laser Se m i2active Ter m inal Hom ing Pr ojectile can actualize attack on the t op of the target.It is analyzed that the technique of t op2attack and its theoretical matter is the app licati on of the Pr oporti onal Navigati on with Compensati on over Gravity.Based on the relative move ment equati on gr oup of the p r ojec2 tile and the target,using Matlab t o make the si m ulati on and calculati on,it is analyzed that the affecti on of the maj or para meter’change t o the traject ory,such as p r oporti onal navigati on quotiety,the vel ocity ra2 ti o of p r ojectile and target,the compensati on over gravity,and s o on.Some p r oble m s in the actualizati on of guidance and s ome suggesti on on the i m p r ove ment of the guidance and contr ol syste m are offered in the paper.Keywords:guidance la w; p r oporti onal navigati on; compensati on over gravity; traject ory; si m ula2 ti on1 引 言比例导引(P N)是一种有效的寻的制导规律,广泛应用于自寻的战术导弹和制导炮弹的的末段制导[1].由于在实际应用中还要考虑到目标机动、许用过载、末段落角约束等条件的制约,因此须对比例导引加以改进以满足作战要求.以攻击工事和装甲目标的顶部(简称“攻顶”)为主要战术性能的激光半主动末制导炮弹在其弹道末制导段采用了一种论实质,以弹丸和目标的相对运动方程为基础,计算分析主要弹道参数对弹道性能的影响,提出制导系统设计和导引律实现中应注意的几个问题.2 末制导炮弹的“攻顶”技术激光半主动末制导炮弹的“攻顶”技术主要基于比例导引律的实现.2.1 比例导引在末制导中的实现制导炮弹的末制导段采用比例导引来提高命中精度,即弹丸速度矢量V 的转动角速度σ·正比于目标视线的转动角速度q ·,其数学表达式为:σ·=k ·q·(1) 弹丸头部的导引头是弹载核心部件,为一陀螺跟踪装置,它能测量出弹丸目标之间连线即目标视线的角速度,通过制导系统的运算和信号变换,形成与目标视线角速度成正比例的控制信号.在该控制信号的作用下导引头修正线圈产生修正力矩,使导引头陀螺向目标方向进动,驱使导引头光轴与目标视线间的误差角趋近于零.在制导过程中,该控制信号同时送入控制舵机,利用气动舵控制弹丸的飞行姿态从而实现弹丸的导引飞行,保证弹丸稳定跟踪目标.但是在比例导引的实现过程中还要考虑重力的影响,需要利用制导系统为弹丸提供重力补偿.2.2 “攻顶”技术的过程描述所谓的“攻顶”技术就是指在弹道的末制导段上给导引头引入重力补偿控制信号,使导引头产生附加进动,形成控制指令使弹丸以较大的落角攻击目标顶部的技术.该控制信号取自自动驾驶仪惯性陀螺产生的重力补偿信号,它给导引头施加一个附加力矩,驱使导引头的陀螺转子在铅垂平面内向下误进动,引起导引头产生反向调整的控制指令,与目标视线角速度形成的控制信号一起送入控制舵机完成比例导引.加入重力补偿信号之后其弹道特征为弹道在末制导段的前半段小幅上抬,后半段以较大的角度进行俯冲攻击,使弹丸的落角增大,实现“攻顶”[4].2.3 “攻顶”技术的理论实质由以上描述可知导引头测得的角速度信号包括两部分:一部分是目标视线角速度,一部分是重力补偿引起的附加进动角速度.测量值是这两个角速度的代数和.所以导引律(1)式应变为:σ·=k ·(q ·+w (t ))(2) 若令q ·g =q ·+w (t ),则式中q ·g 为导引头进动角速度,是测量值;q ·为目标视线角速度;w (t )为导引头附加进动角速度,本文仿真选取w (t )为一小值常量w g .考察弹丸的重力补偿情况可以发现,弹丸的惯导系统已经为弹丸提供了所需的重力补偿,而导引头附加进动角速度的产生相当于额外增加了一部分重力补偿值,故而重力补偿值比实际需要值大.而导引弹道的导引全过程又遵循比例导引,故可以称(2)式描述的导引律为过重力补偿比例导引律,w (t )视为过重力补偿信号.“攻顶”技术的理论实质即为过重力补偿比例导引的实践应用.3 弹道仿真的实现弹道仿真的实现分三个步骤[5]:建立弹道模型;建立仿真模型;改变参数,观察结果.(1)建立弹道模型d rd t=V T co sηT -V cos ηrd qd t=-V T sinηT +V sin ηq =ηT +σT q =η+σ(3) 由于假定弹丸处于理想控制状态,只研究其运动学特征,故选择弹丸和目标的相对运动方程(3)以及导引规律方程(2)为弹道模型.式(3)中各参数意义参见文献[3].(2)建立仿真模型根据方程(3),在Matlab 中建立仿真模型.(3)改变参数,观察结果改变各弹道参数,如初始弹道角、比例系数、弹丸目标速度比、过重力补偿值等,观察仿真结果,并进行相关分析.·27·战术导弹技术 TacticalM issile Technol ogy March,2008,(2)2012-05-18########################2012-05-18########################2012-05-18图2 c 变化时的弹道曲线图1 k 变化时的弹道曲线4 主要参数对弹道性能的影响本文主要分析了比例导引系数k 、弹丸与目标的速度比c 、过重力补偿值w g 等三个参数对弹道性能的影响.假定弹丸做等速飞行,目标做等速直线运动.4.1 比例导引系数k 对弹道性能的影响弹丸的末段速度相对较小,假定在200m /s 至400m /s 之间,而弹丸与目标的速度比c 较大,假定c =20.由图1可知:当k =1时末段弹道弯曲比较大,随着k 的增加,整个弹道的弯曲程度比较均匀,并且很明显制导初始段有一个小幅度上抬,后半段为俯冲弹道.通过分析可以得到以下结论:(1)弹道先上抬后俯冲的主要原因是由于引入了过重力补偿信号,导引头产生了附加进动角速度w g ,随着k 的增加,俯冲程度变大.(2)随着k 的增加,弹道初始段过载变大,弹末段过载趋近于某一常值.(3)弹道中间某点处将出现一个过载零点,这是因为视线角速度q ·是变化的,当q ·与w g 这两个角速度的代数和为零时,出现弹道过载零点,零点两侧过载方向相反.k 越大零点出现的时刻越早.4.2 弹丸与目标的速度比c 对弹道性能的影响由图2可以看出,弹丸与目标的速度比对弹道影响较大,c 越小弹道越弯曲;c 越大,弹道越光滑.c 对弹道的影响主要表现在:(1)c >15,弹道的弯曲程度变得均匀,表现为过载变化幅值不大;c <5,弹道初始段上抬程度变大,末段俯冲程度也变大,表现为弹道过载的急剧变化,例如图2中c =1.5时的情况.(2)c 越大,导引飞行的时间越短,如c =30时,t =10.5s ;c 越小,导引飞行的时间越长,如c=1.5时,t =31s .4.3 过重力补偿值w g 对弹道性能的影响过重力补偿值w g 为一小量,并且具有角速度的物理意义,所以在选取时取w g 为0(°)/s ~5(°)/s ,w g =0时即为重力补偿等于实际重力,其他即为过重力补偿的情况.由图3可以得出如下结论:(1)w g 越小,弹道越平直;w g 越大,弹道越弯曲,弹道的上抬和俯冲越明显,对目标的“攻顶”效果越好.(2)w g ≤2(°)/s ,弹道过载较小,当w g =0时,弹道末段过载趋于0;w g >2(°)/s ,弹道过载变大,弹道中间有过载零点.5 结 论通过以上分析和仿真计算可知,比例导引系数k,弹丸和目标的速度比c 以及过重力补偿值w g 是影响弹道性能的三个主要参数.因此在导引律的实·37·战术导弹技术 TacticalM issile Technol ogy March,2008,(2)2012-05-18########################2012-05-18########################2012-05-18图3 w g 变化时的弹道曲线现和设计弹丸的制导控制系统时,需要注意以下几个方面:(1)弹上的制导系统参数的选择要考虑其对弹道的综合影响,例如k 增大使得弹道中段和末段过载变化均匀,但加大了初始过载值;w g 的增大使得“攻顶”效果显著同时加大了全弹道上的过载.(2)由于弹丸末制导段速度变化不大,故c 对弹道性能的影响反应了弹丸对目标运动状态的选择和要求.因此在设计制导控制系统时要考虑其对目标的适用范围. (3)本文的计算主要基于k 和w g 在全弹道上为定量,但是制导控制系统的自适应和智能化的发展要求实现最优控制,故可以进一步改进导引律,使比例导引系数k 和过重力补偿值w g 随着弹道需求的变化而变化.(4)过重力补偿比例导引和传统比例导引一样过分依靠目标视线角速度q ·这一个观测量来控制,而在目标机动性加大或者出现测量误差时,难以实现精确控制而导致脱靶,因此可以发展新的比例导引律,使其能基于更多的观测量实现精确制导.[参 考 文 献][1] 雷虎民,刘兴堂,陈新海.比例导引的指令加速度[J ].电光与控制,1999(1):19~24.[2] 陈宏,雷鸣.激光寻的制导导引头技术[J ].光电子技术,2002,27(1):53~57.[3] 钱杏芳,张鸿端,林端雄.导弹飞行力学[M ].北京工业学院出版社.1987,12.[4] 翁彦,张天桥.激光半主动寻的制导在滚转导弹上的应用[J ].弹箭与制导学报,2002(1).[5] 张中南,童幼堂,张卫峰.比例导引法导引弹道仿真研究[J ].战术导弹技术,2005(2):56~59.(上接第48页)5.2 复合打击战法研究的内容对复合目标进行打击时,哪种型号的弹先打,哪种型号的弹后打,其总体毁伤效果是不一样的.复合式打法研究的内容还包括:导弹武器组合优化分析,即根据目标类型特性、战斗部毁伤效应和毁伤指标,科学组合各类型导弹对目标实施最有效的打击,以获取最大的军事效益;武器打击顺序研究,即根据目标价值、作战部队目前状态,结合作战任务,确定最佳的武器打击顺序;此外还包括多型号武器打击组合效应研究、耗弹量分析与优化及最佳复合打击方案的确定等.[参 考 文 献][1] 戴开政,王志平.伊拉克战争述评[M ].桂林:桂林陆军学院图书馆,2003.[2] 杨世荣.目标分析[M ].第二炮兵工程学院,2002,6:67.[3] 李新其等.美军在近期几场实战中目标选择的特点及对二炮的启示.二炮军事学术,2005(1):69~71.[4] 刘怡昕等.论对复合目标的复合式打法及其射击效率.射击学报,2004(2):4~6.[5] 章克凌,汪新红,张伟.精确制导武器对阵地工程损伤评估研究现状.科技研究,2002(5):4~6.·47·战术导弹技术 TacticalM issile Technol ogy March,2008,(2)2012-05-18########################2012-05-18########################2012-05-18file:///C|/Users/Administrator/Desktop/新建文本文档.txt通信/电子电脑、 杂志、 会议、 劳动合同、 生活休闲、 考试、 股票。
三维比例导引弹道的可视化仿真研究

第30卷 第4期2010年8月弹 箭 与 制 导 学 报Journal of Projectiles,Rockets,Missiles and GuidanceVol.30 No.4Aug 2010 三维比例导引弹道的可视化仿真研究*苏跃斌,辛长范,郭本亮,魏胜桃(中北大学机电工程学院,太原 030051)摘 要:为弥补二维平面内弹道仿真的缺陷,体现三维仿真多视角动态演示的优越性。
以比例导引法为例对弹道进行仿真,在MATLAB/Simulink环境下建立三维弹道的仿真模型,采用虚拟现实建模语言VRML(vir-tual-reality modeling language)建立三维虚拟场景,并通过Simulink接口将仿真模型导入,实现了对三维导引弹道的可视化仿真,形象地演示了导弹从发射到击中目标的整个过程,并且目标的运动轨迹可以实时控制,可以从不同角度观察导弹的飞行状态,更好的实现了对导引规律的仿真。
关键词:导引弹道;比例导引法;仿真模型;虚拟场景;可视化中图分类号:TJ765.3;V241.622 文献标志码:AResearch on Visualization Simulation of Three-dimensionalProportional Guidance TrajectorySU Yuebin,XIN Changfan,GUO Benliang,WEI Shengtao(School of Mechatronics Engineering,North University of China,Taiyuan 030051,China)Abstract:In order to counteract the defect of two-dimensional simulation and embody the advantage of three-dimensional simulation,taking the proportional guidance law as an example,the three-dimensional simulation model was established based on MATLAB/Simulink,the virtual-reality modeling language(VRML)was applied to establish the three-dimensional visual scene and with theSimulink to get the result of guidance equations.The whole flight process form different angles was demonstrated,and the guid-ance law can be completed much better.Keywords:guidance trajectory;proportional guidance law;simulation model;virtual scene;visualization0 引言比例导引法是自导引制导规律中最重要的一种制导规律,它是追踪法、前置点法、平行接近法制导规律的综合描述。
导弹最优导引律仿真分析(例子)
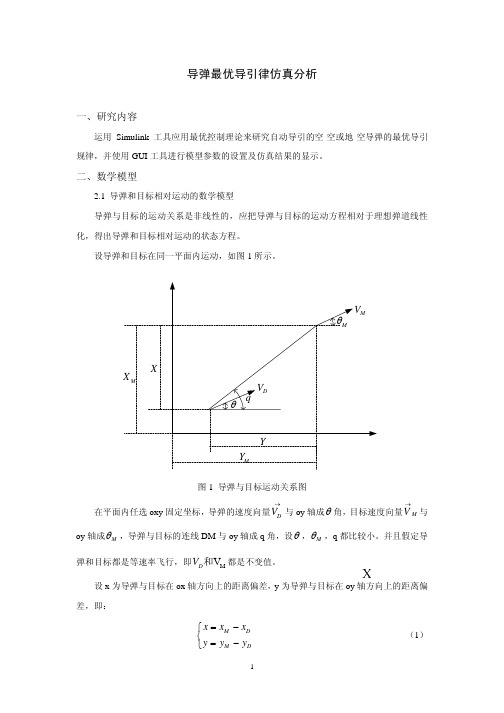
到限制,导弹结构能承受的最大过载也受到限制,所以控制信号 u 应该受到限制,因此,选
择下列形式的二次型指标函数
( ) ( ) ∫ ( ) J = 1 X T 2
tf
CX t f
+ 1 tf 2 t0
X T QX + U T RU dt
⎡c1 0 0 0 ⎤ ⎡0 0 0 0⎤
式中,
C
=
⎢ ⎢
0
c2
0
0
⎥ ⎥
,
Q
=
⎢⎢0
0
0
0⎥⎥
⎢0
⎢ ⎣
0
0 0
c3 0
0⎥
c4
⎥ ⎦
⎢0 0 0 0⎥ ⎢⎣0 0 0 0⎥⎦
2.2.2 最优导引律
(11)
完全考虑弹体二阶振荡环节时,假定目标不机动,导弹运动的状态方程见式(8),即
•
X = AX + Bu
(12)
⎡0 1 0 0 ⎤ ⎡ 0 ⎤
式中, A = ⎢⎢0 0 VD ⎢0 0 0
]
2(t f − t)2 + 6(t f − t)
ω
ω2
−
15 4ω
2
3
]
K3 (t) =
KDVD [(t f
− t)3
3 ω2 3 −
(t f
−t −
3 )2 ω
2(t f ω
− t)2
+
6(t f − t) ω2
−
15 4ω
2
3
]
最优导引方框图如图 3 所示。
6
u(σ )
KDω 2
+
1 s x4 1 s x3 VD +
“制导技术”课程教学模式改革的探索与体会

“制导技术”课程教学模式改革的探索与体会作者:朱建生王曙光陈栋来源:《教育界·下旬》2018年第10期【摘要】文章针对“制导技术”的课程特点,结合新形势对人才培养提出的新要求,对基于校园网微课资源的翻转课堂教学模式进行了积极探索和尝试,以比例导引法教学为例,分析了教学实践的实施过程及需要注意的几个问题,以期为其他课程教学模式改革提供借鉴和参考。
【关键词】“制导技术”;比例导引法;翻转课堂一、引言“制导技术”是弹药工程与爆炸技术专业本科生的一门限选课,通过课程学习,主要让学员理解和掌握制导装置及其原理在弹药工程领域的技术应用。
该课程涉及数学、力学和控制理论等相关知识,理论性较强,对于弹药工程相关专业本科学员来说,学习难度较大。
本文以“比例导引法”教学为例,探索翻转课堂教学模式在“制导技术”课程教学中的应用。
二、课前学习安排与传统课堂教学中的课前预习不同,翻转课堂教学模式中采用的是课前学习,包括线上自学与线下学习两部分内容。
(1)线上自学,根据教员提前下发的相应知识点,观看相关视频。
(2)线上学习,课前学员根据教员提前下发的课上讨论知识点进行视频学习、教材阅读、资料查阅、团队讨论,课后完成与知识点相对应的习题,进一步巩固学习知识点。
比例导引法教学内容包括比例导引法的弹目相对运动方程、弹道特性的讨论、比例系数K 的选择以及比例导引法弹道仿真,共计4学时。
课前给学员布置的预习任务包括两个方面。
(1)课前观看关于比例导引法的7个视频,并完成相应的讲间练习。
(2)尝试利用仿真软件,对比例导引法进行弹道仿真,并对结果进行分析。
三、课上讨论安排在课堂时间里,要组织学员对课前学习内容进行深入讨论,有针对性地解决每个学员在课下学习过程中遇到的问题,并根据学员情况对所学内容进行理论与应用两方面的拓展。
课堂讨论内容通常包括以下三个方面。
(1)课前所学内容的知识点讨论,并对各知识点之间的相互关系进行梳理,帮助学员认识其本质。
激光末制导炮弹比例导引律性能研究

2 激光末制导炮弹比例导引律回路模型
2.1 比例导引律的几何关系 由于激光末制导炮弹进行末制导时弹目距离较
近,比例导引律的弹道接近于直线,假设导引头噪声 干扰和初始指向误差等因素为使炮弹偏离理想弹道 的小扰动,可以将末制导炮弹比例导引律的几何关系 线 性 化 ,如 图 2 所 示[6]。
1 激光末制导炮弹比例导引律原理
252
红外与激光工程
第 38 卷
当激光光斑信号处于导引头探测器非线性区 (△q>1°)时 ,导 引 头 以 固 定 的 角 速 度 快 速 进 动 , 此 时 导
引头的进动角速度与探测器误差角并不成比例,而是
为一常值:
q觶 s =10 (°)/s
(1)
探 测 器 误 差 角 △q 迅 速 减 小 , 当 △q<3.5° 时 , 光 斑
图 2 末制导炮弹与目标相对几何关系 Fig.2 Relative geometrical relationship between TLGP and target
图中,t1 是末制导时间,t 是制导开始后的飞行时 间 ,t1 -t 是 剩 余 飞 行 时 间 ,Y 为 与 初 始 弹 目 线 垂 直 的 方向,vr 是炮弹相对目标沿初始弹目线方向的相对速 度,vm 表示炮弹速度,R=(t1 -t)vr 是炮弹与目标的相对 距 离 ;q 为 弹 目 视 线 角 ,qs 为 导 引 头 光 轴 在 惯 性 空 间 与水平面的夹角,对于采用发射后锁定攻击方式的末 制 导 炮 弹 ,往 往 存 在 初 始 指 向 误 差 q0 =q-qs ;初 始 时 刻炮弹飞行速度方向与弹目视线存在一个偏差角 ε, 则在垂直于弹目视线方向上存在着初始侧向速度干 扰 vsinε≈vε。 导 引 头 光 轴 在 初 始 时 刻 与 弹 体 同 轴 ,在 小攻角范围内,弹体纵轴与速度纵轴近似相同,因此 可认为 q0 ≈ε。 2.2 激光半主动陀螺式导引头动力学模型
一种新的扩展比例制导律设计与仿真

( 7)
制导律的实现 q - θ M ≈q - 若攻角很小, 即 α≈0 , 则 θ M ≈ M ,
·
从式 ( 7 ) 可知,为保证视线角速度收敛,必须 满足 N > 2 。
M = φ,并且 V M ≈a x1 。其中, φ 为离轴角; a x1 为弹 体纵向加速度。因此,式( 13 ) 转化为 a C1 =
· 30·
航空兵器 2011 年第 5 期
同时,设补偿项为 y,则扩展比例制导律为 +y aC = K R q 若认为弹体为理想环节,则有 M = a C - gcosθ M VM θ
· · ·
( 3) ( 4)
机动裕度就越大,可以用于克服未考虑的各种扰 动,末制导精度也就越高。因此,要求遭遇点的加 速度指令为零,即 a Ctf = 0 由式( 10 ) ,( 11 ) 得 y=
· · · ·
aT
cos( q - θ T ) + gcosθ M ] cos( q - θ M )
( 12 )
因此,导弹加速度指令为 aC =
· · N + N[ R q V tan( q - θM ) - cos( q - θM ) 2 M ·
V T sin( q - θ T ) + a T cos( q - θ T ) + gcosθ M cos( q - θ M ) - ycos( q - θ M ) ( 5 ) ( 6) 2. 2
N = K cos( q - θ M )
从式( 5 ) 可知,当目标加速度、导弹速度变化 率为零,补偿项为零,且不考虑重力影响时满足 + Rq ¨ =0 ( N - 2) R q
·
VT
sin( q - θT ) cos( q - θT ) + aT + gcosθM ] ( 13) cos( q - θM ) cos( q - θM )
(518618873) 典型导引规律三维弹道仿真分析

总第164 期200 8年第2期舰船电子工程Vo l.28No. 211 0Sh i p E lec tron ic En gin ee ringt3典型导引规律三维弹道仿真分析周纪元 1 ) 童幼堂2) 张磊1) 王亚1)(海军大连舰艇学院研究生1队1 )大连11 601 8)( 海军大连舰艇学院舰载武器系2 )大连11 601 8)摘要介绍几种典型导弹导引规律及其约束方程,运用MA T L AB 语言对纯追踪法、平行接近法和比例导引法的理想弹道进行了三维仿真。
绘制导弹速度和目标速度变化时,其对应的三维理想弹道,并进行比较分析。
关键词导引规律;弹道;仿真; MA T LAB中图分类号TP391. 91 引言导弹在攻击目标时,为了使导弹稳定的跟踪并命中目标,导引系统必须及时准确地提供导引信号,而导引信号又必须严格遵循某种规律,这种规律就是导引规律。
导引规律一般分为两大类,即两点法和三点法。
两点法又包括纯追踪法、比例导引法和平行接近法及固定前置角法等[ 1 ] 。
目前,大多数文献给出的两点法的运动学弹道多为导弹和目标在同一平面内的二维弹道,本文使用 MA T LAB 语言,对两点法前三种导引规律的理想弹道进行了三维仿真。
绘制出了三维仿真弹道,分析比较了不同导引规律对应的导弹和目标运动参数变化时的弹道变化特性。
2 两点法导引规律式中: r = d r/ d t:距离变化率;θ: V 与目标视线的夹角, 即目标运动前置角;β: Vm与目标视线的夹角;即导弹运动前置角;φ: 目标视线与x 轴夹角, 即视线角; r:目标与导弹之间的距离。
如图1所示。
图1导弹与目标相对关系图由图1可得各夹角之间的相互关系为:φ= η+θ (3)φ= β+γ(4)将( 3) 、( 4 )式代入(1)、( 2 ) 式可得:r = V t co s(φ- η) - V m co s(φ- γ) (5)两点法是确定导弹与目标两点在空间相对位置的方法。
比例导引法Matlab仿真

%三维制导模型,比例导引法求解%源代码作者不详,注释人:lylogn%Modified by lylogn,2012年4月17日clear all;close all;clcdt=0.1;%仿真时间步长alpha=pi/6;v_t=0.42;s_t=v_t*dt;%目标以0.42的速度沿alpha的角方向匀速飞行,s_t为目标在单位仿真步长前进的距离v_m=0.60;s_m=v_m*dt;%s_m为导弹在单位仿真步长沿目前速度方向前进的距离x(1)=0;y(1)=1.0;z(1)=0;pmr(:,1)=[x(1);y(1);z(1)]; %导弹初始位置,在坐标原点ptr(:,1)=[25;5;7]; %目标初始位置K=3; %比例导引系数q(1)=0; %初始的视线角,设定参考线为t和m初始位置的连线o(1)=0; %初始导弹速度向量方向角a(1)=0; %初始导弹相对目标的运动速度向量的方向角for(k=2:600)ptr(:,k)=[ptr(1,1)-v_t*cos(alpha)*dt*k;ptr(2,1);ptr(3,1)+v_t*sin(alpha)*k*dt]; %目标运行轨迹方程,匀速直线运动r(k-1)=sqrt((ptr(1,k-1)-pmr(1,k-1))^2+(ptr(2,k-1)-pmr(2,k-1))^2+(ptr(3,k-1)-pmr(3,k-1))^2); %k-1时刻导弹与目标在三维空间中的欧氏距离c=sqrt((ptr(1,k)-pmr(1,k-1))^2+(ptr(2,k)-pmr(2,k-1))^2+(ptr(3,k)-pmr(3,k-1))^2); %目标k时刻位置与导弹k-1时刻位置间的距离b=acos((r(k-1)^2+s_t^2-c^2)/(2*r(k-1)*s_t));%%%此处参见公式一%%%dq=acos((r(k-1)^2-s_t^2+c^2)/(2*r(k-1)*c));%k-1时刻到k时刻的视线角变化量(假设导弹不动,目标移动)%%%此处参见图一%%%if abs(imag(b))>0 %如果acos的值出现虚数,则说明该角度一定很小,对其进行近似操作b=0.0000001;endif abs(imag(dq))>0 %同上dq=0.0000001;endq(k)=q(k-1)+dq; %更新视线角o(k)=o(k-1)+K*dq; %更新导弹速度向量方向角a(k)=o(k)-q(k); %更新导弹相对目标的运动速度向量的方向角c1=r(k-1)*sin(b)/sin(a(k)+b); %计算k-1时刻角b所对边的长度%%%此处参见公式二%%%c2=r(k-1)*sin(a(k))/sin(a(k)+b); %计算k-1时刻角a(k)所对边的长度c3=sqrt((c1-s_m)^2+(c2-s_t)^2+2*(c1-s_m)*(c2-s_t)*cos(a(k)+b)); %计算k时刻导弹m与目标t之间的距离(在导弹不动,目标移动的假设条件下),为假值dq=a(k)-acos(((c1-s_m)^2+c3^2-(c2-s_t)^2)/(2*(c1-s_m)*c3)); %k-1时刻到k时刻的视线角变化量(假设导弹移动,目标也移动),以下代码重复以上过程,为假值%%%此处参见图二%%%if abs(imag(dq))>0dq=0.0000001;endq(k)=q(k-1)+dq;o(k)=o(k-1)+K*dq;a(k)=o(k)-q(k);c1=r(k-1)*sin(b)/sin(a(k)+b);c2=r(k-1)*sin(a(k))/sin(a(k)+b);c3=sqrt((c1-s_m)^2+(c2-s_t)^2+2*(c1-s_m)*(c2-s_t)*cos(a(k)+b)); %计算k时刻导弹m与目标t之间的距离(在导弹移动,目标也移动的假设条件下),逼近真值,以下计算使之更加精确dq=a(k)-acos(((c1-s_m)^2+c3^2-(c2-s_t)^2)/(2*(c1-s_m)*c3)); %k-1时刻到k时刻的视线角变化量(假设导弹移动,目标也移动),以下代码重复以上过程,为真值if abs(imag(dq))>0dq=0.0000001;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%�ded by lylogn 2012.04.17,To make 'dq' get closer to its true valueq(k)=q(k-1)+dq;o(k)=o(k-1)+K*dq;a(k)=o(k)-q(k);c1=r(k-1)*sin(b)/sin(a(k)+b);c2=r(k-1)*sin(a(k))/sin(a(k)+b);c3=sqrt((c1-s_m)^2+(c2-s_t)^2+2*(c1-s_m)*(c2-s_t)*cos(a(k)+b)); %计算k时刻导弹m与目标t之间的距离(在导弹移动,目标也移动的假设条件下),逼近真值,以下计算使之更加精确dq=a(k)-acos(((c1-s_m)^2+c3^2-(c2-s_t)^2)/(2*(c1-s_m)*c3)); %k-1时刻到k时刻的视线角变化量(假设导弹移动,目标也移动),以下代码重复以上过程,为真值if abs(imag(dq))>0dq=0.0000001;endq(k)=q(k-1)+dq;o(k)=o(k-1)+K*dq;a(k)=o(k)-q(k);c1=r(k-1)*sin(b)/sin(a(k)+b);c2=r(k-1)*sin(a(k))/sin(a(k)+b);c3=sqrt((c1-s_m)^2+(c2-s_t)^2+2*(c1-s_m)*(c2-s_t)*cos(a(k)+b)); %计算k时刻导弹m与目标t之间的距离(在导弹移动,目标也移动的假设条件下),逼近真值,以下计算使之更加精确dq=a(k)-acos(((c1-s_m)^2+c3^2-(c2-s_t)^2)/(2*(c1-s_m)*c3)); %k-1时刻到k时刻的视线角变化量(假设导弹移动,目标也移动),以下代码重复以上过程,为真值if abs(imag(dq))>0dq=0.0000001;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%q(k)=q(k-1)+dq;o(k)=o(k-1)+K*dq;a(k)=o(k)-q(k);c1=r(k-1)*sin(b)/sin(a(k)+b);c2=r(k-1)*sin(a(k))/sin(a(k)+b);c3=sqrt((c1-s_m)^2+(c2-s_t)^2+2*(c1-s_m)*(c2-s_t)*cos(a(k)+b)); %计算k时刻导弹m与目标t之间的距离,终于近似为真值了x1(k)=ptr(1,k-1)+c2/s_t*(ptr(1,k)-ptr(1,k-1));y1(k)=ptr(2,k-1)+c2/s_t*(ptr(2,k)-ptr(2,k-1));z1(k)=ptr(3,k-1)+c2/s_t*(ptr(3,k)-ptr(3,k-1)); %计算出角b所对边与目标运动轨迹的交点:(x1,y1,z1)%%%参见公式三%%%x(k)=pmr(1,k-1)+s_m/c1*(x1(k)-pmr(1,k-1));y(k)=pmr(2,k-1)+s_m/c1*(y1(k)-pmr(2,k-1));z(k)=pmr(3,k-1)+s_m/c1*(z1(k)-pmr(3,k-1)); %计算出导弹k时刻所运动到的位置:(x,y,z)%%%参见公式三%%%pmr(:,k)=[x(k);y(k);z(k)];r(k)=sqrt((ptr(1,k)-pmr(1,k))^2+(ptr(2,k)-pmr(2,k))^2+(ptr(3,k)-pmr(3,k))^2);if r(k)<0.06;break;end;endsprintf('遭遇时间:%3.1f',0.1*k);figure(1);plot3(pmr(1,1:k),pmr(2,1:k),pmr(3,1:k),'k',ptr(1,:),ptr(2,:),ptr(3,:));axis([0 25 0 5 0 25]);text(x(180),y(180),z(180),'\rightarrow 比例导引律制导下的导弹运动轨迹');text(ptr(1,280),ptr(2,280),ptr(3,280),'\rightarrow 目标运动轨迹');grid on之后,鉴于程序中很多地方不结合模型图也很难理解,将其中关键的图例与公式提取如下:最后,程序的运行过程分析完成,具体的细节详见注释,运行结果如下图所示:综上所述,本工作对比例导引法求解三维制导问题的仿真程序进行了详细的分析与注释,程序运行正常,希望对大家理解比例导引法有所帮助。
