简单的轴对称图形
简单的轴对称图形 教案
O E
B
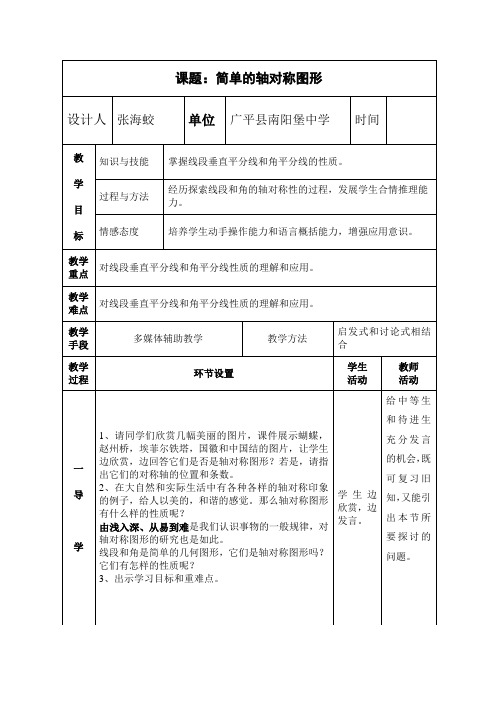
OC平分∠AOB, PD=PE PE⊥OB,
角平分线上的点到这个 角两边的距离相等。
轴对 称图 形
线段和角都是简单的轴对称图形。
课
A E
堂 学生独立完 成 (A) 检
C D
B
D
C
测
(BC)
B A E
小结
名称 图例 M P O N D 条件 结论 语言叙述 线段垂直平分线上的点 到这条线段两个端点的 距离相等。
六、 板 书 设 计
线段 垂直 平分 线 角平 分线
MN⊥AB, PA=PB AO=BO
B A C PD⊥OA, P
A
一 导
学
教学 过程
环节设置
学生活动
教师活动
二 自 学 与 交 流
自学指导 1: (1)按 51 页“做一做”画图; (2)说一说什么叫线段的垂直平分线? (3)完成 51 页“观察与思考”的第 1 题, 你认为线段是轴对称图形吗?若是, 它的对 学 生 先 自 学把自己 称轴是什么? (4)通过观察与思考第 2 题的折纸操作, 能 解 决 的 问题或者 你有何发现? (5) 小组讨论概括线段垂直平分线的性质。 是 折 纸 操 作独立完 成,然后 自学指导 2: (1)在一张半透明的纸上画一个∠AOB 再 组 内 交 (组长分工,每组要画出锐角,直角和钝 流 讨 论 , 概括得出 角) ; (2)不借助测量工具,画出∠AOB 的平分 线 段 垂 直 平分线和 线 OC; (3) ∠AOB 是轴对称图形吗?如果是, 角 平 分 线 的性质。 请说出它的对称轴; (4) 在∠AOB 的平分线 OC 上任取一点 P, 则该点到∠AOB 两边 OA、OB 的距离相等 吗?如何验证你的猜想?与同学交流。 (5)讨论概括角平分线的性质。
简单的轴对称图形
小结:
1、________是等腰三角形,要熟悉它的各部分名称。 2、等腰三角形具有哪些性质: 具有一般三角形的性质外,还有它的特殊性质:
1)等腰三角形的两底角相等(简写“等边对等角”)要利用此性 质,结合三角形内角和熟练求解等腰三角形的各角的度数。 2)等腰三角形的顶角平分线、底边上的高和底边上的中线互相 重合(简称“三线合一”)此三线是今后解决有关等腰三角形 问题常用的辅助线。
等腰三角形的性质
1、等腰三角形的两个底角相等(简称“等边对等角”) 2、等腰三角形的顶角平分线、底边上的高和底边上 的中线互相重合(简称“三线合一”)
一般的三角 形有这种性 质吗?
要注意是指顶角 的平分线、底边 上的高、底边上 的中线这三线重 合。
欢迎光临三角形之家 flash
如果一个三角形中有两个角相等, 那么这两个角所对的边也相等吗?
看看你本组其 他同学的情况, 共同交流, 能 得出什么结论?
B
D
C
现象
(1)等腰三角形是轴对称图形。
(2)∠B =∠C
(3 )∠BAD=∠CAD, AD为顶角的平分线
(4)∠ADB=∠ADC=90° AD为底边上的高
(5 )BD=CD,AD为底边上的中线。 现象(2)能用一句话归纳出来吗? 等腰三角形的两个底角相等 现象(3)、(4)、(5)能用一句话归纳出来吗? 等腰三角形的顶角平分线、底边上的高和底边 上的中线互相重合(简称“三线合一”) flash
C
A
达标练习二(A 水平)
一、填空题:
17 1、等腰三角形若两边长为3和7,则其周长为________。 50° 2、如果等腰三角形的一个底角为50°,那么其余两个角为______和 80° ______。 50° 3、如果等腰三角形的顶角为80°,那么它的一个底角为________。
七年级数学简单的对称图形1

发现:
(1)角是轴对称图形, 角平分线所在直线是它 的对称轴.
(2)角平分线上的点 到这个角的两边的距离 相等.
1.如图,在Rt△ABC中,BD 是∠ABC的平分线,DE⊥AB , 垂足为E .DE与DC 相等吗 ? 为什么?
E
B
A D C
2.如图用直尺和量角 器在直线MN上找一点P. 使点P到射线OA和OB的距 离相等. B N P M
A O 解:作∠AOB的角平 分线,交MN与一点,则 交点P即为所求.
﹙ ﹙
∵MN是线段AB的垂直平分线, 交AB于点O, 想一想:线段是轴对称图形吗 ? ∴AO = OB,∠AOC = ∠BOC; 如果是,你能找出他的一条对称轴吗? 在△AOC与△BOC中 试一试按下列步骤做一做 : M C CO = CO; (1)画一条线段AB,对折 ∠AOC = ∠BOC; AB使点A,B重合,折痕AB的 AO O =; BO 交点为 O A(B) N ∴ △AOC≌△BOC(SAS) (2)在折痕上任取一 ∴ CA=CB( 全等三角形,对应 点 C, 沿 CA 将纸折叠; 边相等)
§7.2 简单的轴对称图形 (一)
∵OC平分∠AOB A ∴ ∠DOC= ∠EOC D ( 1 )在一张纸上任意画 又∵CD⊥OA,CE C 一个角∠ AOB,沿角的两 ⊥OB ,垂足分别为点 D, 点E 边将其剪下。并将这个角对 折,使两边重合; O ) ∴∠ ODC= ∠OEC B E (CDO 2)在折痕(即角平分线) 在△ 与△CEO中 你在图中发 上任选一点 C ; ∠ODC= ∠OEC; ( 3)过点 C 折OA 边的垂 现了哪些相等的 ∠ DOC= ∠ EOC ; 线,得到新的折痕 CD,其中, 线段?换一点,再 OC=OC 点D是折痕与OA边的交点, ∴ △CDO≌△CEO 试一试? 即垂足; (AAS) (4)将纸打开,新的折痕与 OB边的交点为E. ∴CD=CE (全等三角形 对应边相等 )
简单的轴对称图形(等腰、等边)

AB CD 简单的轴对称图形---(等腰三角形,等边三角形)一、选择题 济宁附中李涛1、 等腰三角形的一个角为40°,则它的底角为( )A. 100°B. 40°C. 70°D. 70°或40°2、 等腰三角形的一个角为100°,则它的底角为( )A. 100°B. 40°C. 70°D. 100°或40°3、如图,在等腰三角形ABC 中,顶角∠A=36°.若BD 平分∠ABC ,则图中等腰三角形有( ) A . 1个 B . 2个 C . 3个 D . 4个4、已知,如图,在△ABC 中,OB 和OC 分别平分∠ABC 和∠ACB ,过O 作DE ∥BC ,分别交AB 、AC 于点D 、E ,若BD+CE=5,则线段DE 的长为( )A . 5 B . 6 C . 7 D . 85、如图所示.△ABC 中,∠B=∠C ,D 在BC 上,∠BAD=50°,AE=AD ,则∠EDC 的度数为( )A . 15°B . 25°C . 30°D . 50°6、如图,△ABC 的面积为1cm2,AP 垂直∠B 的平分线BP 于P ,则△PBC 的面积为( )A . 0.4 cm2B . 0.5 cm2C . 0.6 cm2D . 0.7 cm2二、选择题: 1、(1)已知等腰三角形的一边长等于5,一边长等于11,则它的周长为__________。
(2)已知等腰三角形一边长等于5,一边长等于7,则它的周长为__________。
2、如右图,∠A=200,∠C=400,∠ADB=800,则∠DBC=_ _,图中等腰三角形有_ 个。
3、如下图△ABC 中 AB=AC ,D 是BC 的中点,则AD BC,若∠B=35°,则∠CAD= ,∠BAC= 。
5.3 简单的轴对称图形(1)

20°
.
数学
返回目录
名师点拨:
(1)若题目中没有明确顶角或底角的度数,做题时要注意分情况
进行讨论计算;
(2)等腰三角形的顶角可以是直角、钝角或锐角,而底角只能是
锐角.
数学
返回目录
知识点三 等边三角形的定义和性质
1.定义:三边都相等的三角形是 等边三角形 ,也叫正三角形.
2.性质:等边三角形是特殊的等腰三角形,它除了具有等腰三角
等腰三角形的 顶角 ,腰与底边的夹角叫做等腰三角形的
底角
.
2.性质:①等腰三角形是轴对称图形,对称轴是它的顶角平分
线所在的直线;②等腰三角形顶角的平分线、底边上的高、
底边上的中线重合(简称“ 三线合一 ”).
数学
返回目录
▶▶ 典型例题
【例1】如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点
腰三角形的个数是
3
.
数学
返回目录
三、解答题
1.如图,在△ABC中,已知AB=AC,AD为∠BAC的平分线,且
∠2=36°,BD=2,求∠BAC,∠B的度数及BC的长.
解:因为AD为∠BAC的平分线,∠2=36°,
所以∠1=∠2=36°,∠BAC=2∠2=72°.
又因为AB=AC,所以AD⊥BC,BD=CD,
解:因为AB=AC,AD是∠BAC的平分线,
所以BD=CD.
因为△ABC的周长为16,
1
所以AB+BD= ×16=8.
2
因为△ABD的周长为12,所以AD=12-8=4.
数学
返回目录
6.如图,A,B是直线l同侧的两点.请在直线l上找一点C,使得
AC+CB最小,并说明理由.
简单的轴对称图形(二)等腰三角形

简单的轴对称图形(二)(一)教学设计●教学目标【知识与技能目标】1.进一步理解轴对称、轴对称图形的概念。
2.探索等腰三角形的性质,掌握等腰三角形的轴对称性及其相关性质。
3.会利用轴对称的有关性质解决实际问题。
【过程与方法目标】1.学生通过实验探索发现等腰三角形的性质,并能利用等腰三角形的性质解决实际问题。
2.学生亲自经历“问题情境——建立模型——求解——解释应用”的基本过程,体验数学知识在实际生活中的广泛应用。
3.通过轴对称图形的探究,培养形式分析、概括的能力【情感与态度目标】1.通过优美的等腰三角形“三线合一”的性质,体会几何图形的和谐美。
2.在学习活动中,学会与同伴交流,体会获得成功的喜悦。
3.通过对实际问题的解决,使学生感受数学与我们的生活息息相关。
●教学重点:探索等腰三角形的轴对称性●教学难点:掌握等腰三角形有关概念及特性;加深等腰三角形“三线合一”的理解和应用●教具准备:等腰三角形纸片、三角板、量角器、多媒体(若没有可直接用图片代替)多媒体动画展示折叠过程. (三)例题精选 例1 已知,如图,BC >AB ,BD 平分∠ABC ,且AD=DC ,求证:∠A+∠C=180°.例2 已知,如图(1),等边△ABC 和点P ,设点P 到△ABC 三边AB 、AC 、BC 的距离分别为h 1,h 2,h 3,△ABC 的高为h ,“若点P 在一边BC 上,此时h 3=0,可得结论:h 1+h 2+h 3=h ”请直接应用上述信息解决下列问题:当点P 在△ABC 内(如图2)、点P 在△ABC 外(如图3)这两种情况时,上述结论是否成立?若成立,请说明理由;若不成立,h 1,h 2,h 3与h 之间又有怎样的关系?请写出你的猜想,不需证明 .NKM M PP FE E DDCCB B AAM (2)F Q P(3)(1)EDCBA例3 如图,是某城市部分街道示意图,△ABC 、CDC BA A△CDE都为正三角形,A、B、C、D、E、F、G、H为公共汽车停靠站,公车甲从A站出发,按照A、H、G、D、E、C、F的顺序到达F站,公车乙从B站出发,沿F、H、E、D、C、G的顺序到达G站,如果甲、乙分别从A、B站出发,在各站耽误的时间相同,两车速度也一样,试问哪已辆公车先到达指定车站?为什么?.(四)练习精选1.等腰三角形的一腰为6,底边长为4,则这个等腰三角形的周长为()A.13;B.14;C.15;D.16.2.已知,等腰三角形的一边长为3,一边长等于6,则它的周长等于()A.12 B.15 C.12或15 D.15或18 3.在△ABC中,AB=AC,AB的中垂线与AC所在直线相交所得的锐角为50°,则底角B的大小为4.等腰三角形的一个角是110°,它的另外两个角是;等腰三角形的一个角是80°,它的另外两个角为5.如图,△ABC中,AB=AC,BD⊥AC于D,求证:∠DBC=21∠A6.如图,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=BE,求∠A的度数.(五)知识拓展与提高练习7.如图所示,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,则PM=PN,你认为这个结论对吗?请阐述你的理由。
北师大版初中数学一年级下册5.3简单的轴对称图形(共19张PPT)

如图:已知AO平分∠ BAC,OE⊥Fra bibliotekB,OD⊥AC。
求证:OE=OD
在AO上另取一点P, 作PH ⊥AB于H, PQ⊥AC于Q; 还会有PH=PQ吗?
结论:
角是轴对称图形.
角平分线所在的 直线是它的 对称轴。
角的平分线上的点 到
这个角的两边的距离
相等
∵AP是∠BAC的平分线, B
PD⊥AB,PE⊥AC D
17、儿童是中心,教育的措施便围绕他们而组织起来。上午12时53分31秒上午12时53分00:53:3121.9.5
You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
问题:
在上述的操作过程中, 你发现了哪些相等的线 段?说说你的理由。在 角平分线上另取一点, 再试一试。
B
C 距离分别是线段DE,
DC,所以DE=DC
∴PD=PE
P
(角平分线上的点到
这个角两边的距离相A 等) E C
做一做
1.线段是轴对称图 形吗?如果是,你能 找出它的一条对称轴 吗?
A(B)
O
B
2.画一条线段AB,对 折AB使A,B重合,折 痕与AB的交点为O;
C
A(B)
O
在折痕上任取一点C, 沿CA将纸折叠;
C
(1)CO与AB
有怎样的位置关系?
(4)将纸打开, 新的折痕与OB边的交 点为E。
9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。21.9.521.9.5Sunday, September 05, 2021
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下面这些图形是不是轴对称图形?为什么?
是
是
否
想一想下列图形有几条对称轴?动手画一画。
返回
返回
返回
返回
返回
返回
小结: 正方形有( 4 )条对称轴 长方形有(2)条对称轴 等腰三角形有( 1)条对称轴 等边三角形有( )条对称轴 3 1)条对称轴 等腰梯形有( 无数条 圆有( )条对称轴。
达
标
题
判断题: 1、如果一个图形沿着一条直线对折,两侧的图形能够 完全重合,这个图形就是轴对称图形。 ( √ ) 2、正方形只有两条对称轴。 选择题: (× )
1、长方形有( B )条对称轴。 A. 1
B. 2
C. 3 B. 9
2、下面的数字( A )是轴对称图形。A. 3 C. 7 操作题:(画出下面图形的对称轴)
总结:
·
·· · · · · ·· · ·
·
·
两个对称点到对称轴的距离相等
在轴对称图形中,对称轴 两侧相对着的对称点到对称轴 的距离相等,这就是轴对称图 形的性质。 我们可以用这个性质来判断 一个图形是否是一个轴对称图 形,或者作轴对称图形。
例2
画出下面图形的轴对称图形。
怎样画得又 好又快?
判断题: 1、飞机图不一定是轴对称图形。
2、半圆有无数条对称轴。 选择题: 1、 有( A )条对称轴。 A. 5 B. 10 B.小 2、下面汉字( C )是轴对称图形。 A.字 操作题:(画出下面图形的对称轴)
( √ )
×) (
C. 1 C.日
新的学期,新的开始,一起努力!
观察下列图形,说一说他们有什么样的特点?
• 简单的轴对称图形1
轴对称图形
如果一个图形沿着一条直 线பைடு நூலகம்折,两侧的图形能够 完全重合,这个图形就是 轴对称图形。
折痕所在的这条直线叫 做对称轴。
注意:
1、对称轴是一条虚线,画的时候 两端都要出头。 2、有些轴对称图形有一条对称 轴,有些轴对称图形可能有几条或无 数条对称轴,因此对称轴是不唯一的。
